Cellular Blebs and Membrane Invaginations Are Coupled through Membrane Tension Buffering

Abstract

Bleb-type cellular protrusions play key roles in a range of biological processes. It was recently found that bleb growth is facilitated by a local supply of membrane from tubular invaginations, but the interplay between the expanding bleb and the membrane tubes remains poorly understood. On the one hand, the membrane area stored in tubes may serve as a reservoir for bleb expansion. On the other hand, the sequestering of excess membrane in stabilized invaginations may effectively increase the cell membrane tension, which suppresses spontaneous protrusions. Here, we investigate this duality through physical modeling and in vivo experiments. In agreement with observations, our model describes the transition into a tube-flattening mode of bleb expansion while also predicting that the blebbing rate is impaired by elevating the concentration of the curved membrane proteins that form the tubes. We show both theoretically and experimentally that the stabilizing effect of tubes could be counterbalanced by the cortical myosin contractility. Our results largely suggest that proteins able to induce membrane tubulation, such as those containing N-BAR domains, can buffer the effective membrane tension—a master regulator of all cell deformations.

Significance

Many essential cell processes are characterized by the apparent expansion of the plasma membrane. Because the membrane is practically inextensible, cells accommodate shape changes by storing the membrane area in fluctuations, ruffles, microvilli, and various invaginations. In this work, we investigate how bleb-type protrusions expand by drawing area from either fluctuations or tubular invaginations. A quantitative framework is derived to understand how the formation of protrusions can be regulated through the structuring of the excess membrane area. We highlight the important role played by the curved membrane proteins that form the invaginations.

Introduction

Cellular blebs are protruding hemispherical bulges that form rapidly after local uncoupling of the plasma membrane from the cortical cytoskeleton (1, 2, 3). Protrusions of this type are instrumental in cellular processes, such as apoptosis, mitosis, and motility. The formation of blebs is driven by the intracellular hydrostatic pressure generated by actomyosin contractility (4, 5, 6, 7). Theoretical models of bleb initiation have thus far considered the membrane-cortex adhesion and the membrane tension as the forces that act against the detachment and deformation of the bulging membrane (8, 9, 10, 11, 12, 13). Although these parameters are indeed important, the common description of the membrane as a flat interface fails to represent the seemingly more complex expansion mechanism. Given that stretching a flat plasma membrane is limited to just 2–3% before rupture (14, 15) and that this extension requires a force that cells cannot generate (16), bleb expansion was suggested to depend on a local supply of membrane (16, 17, 18, 19). Such area exchange affects the stress-strain relationship of the plasma membrane in a manner that remains poorly understood. This stress-strain (or tension-expansion) relationship is an important aspect of bleb formation (20) and of all other cellular processes in which plasma membrane mechanics play a crucial role.

In a recent study (21), some of us investigated the in vivo motility of primordial germ cells (PGCs) in the zebrafish embryo. These cells migrate toward their target, the developing gonad, employing blebs as forward protrusions (22, 23, 24, 25). We found that the rapid membrane expansion associated with blebs relies on the local flattening of inwards-pointing tubular invaginations (or tubes) of the plasma membrane. Previous works suggest that cell membrane tubes may be formed and stabilized via a scaffolding mechanism involving crescent-shaped BAR domain proteins (26, 27, 28, 29) (for reviews see (30, 31, 32, 33)). Depending on their concentration, N-BAR proteins were shown to act both as membrane curvature sensors as well as curvature inducers (28, 34). Accordingly, in our experiments (21), we were able to track the membrane tubes by expressing the YFP-labeled Amph-N-BAR. At a low concentration, N-BAR served purely as a tubes sensor and had no effect on the blebbing capacity nor the motility of PGCs. At high concentrations of N-BAR, an increase in tubular membrane invaginations and thus an increase in membrane area sequestered within them was observed. Strikingly, this manipulation also resulted in impaired blebbing and defective migration. Whereas the apparent membrane reservoir for bleb expansion increased, the blebbing activity markedly decreased.

Motivated by this puzzle, we propose in this article a simplified physical description of membrane tubulation by curved proteins, coupled to the thermodynamics of bleb formation. In our model, we formulate the free energy of the membrane and the bound proteins that form scaffolds for membrane tubes. Discarding dynamics, we minimize this energy sequentially on a timescale hierarchy. Through this minimization, we calculate analytically both the folded membrane area and the effective membrane tension. We then show quantitatively how these properties control the expansion mechanism and the probability of bleb initiation. Our model yields a parametric regime under which cells could, in principle, regulate their blebbing activity through the expression of tube-forming proteins (such as N-BAR). A qualitative comparison with previous observations suggests that this regime is likely relevant to wild-type (WT) PGCs in the embryo. The model further provides another experimentally accessible prediction, namely that blebbing could be rescued post-N-BAR overexpression by elevating the myosin contractility. We were able to verify this prediction qualitatively in new in vivo experiments.

Model

Membrane tubes and expanding bleb are coupled by membrane tension

We begin by introducing our central hypothesis, which couples the tubular invaginations with the protruding bleb. This coupling is based on the area dependence of the membrane tension σ. In simple membrane systems such as giant vesicles, the membrane tension is primarily of entropic origin and is nonlinearly (exponentially) related to the “excess area,” broadly defined as the relative difference between the true membrane area (related to the number of lipid molecules) and the “apparent area”: the surface area of the average vesicle’s shape, which excludes thermal fluctuations (35). Conditions that increase the apparent area under constant true area, such as an hypo-osmotic shock, increase the membrane tension by flattening out thermal fluctuations. Such a simple relationship does not exist for cells, in which the membrane interact with the cytoskeleton and experiences active fluctuations in addition to the thermal ones (36). One may nevertheless expect that processes that increase the apparent cell membrane area, such as membrane tubulation and bleb formation, should also lead to an increase of membrane tension. To capture this at the phenomenological level, we postulate the following relationship between the cell membrane tension σ, the area held in tubes S_t, and the increase of (apparent) cell membrane area associated to bleb formation ΔS_b:

$$\sigma ={\sigma }_0+k_{\sigma }\frac{S_{\text{t}}+\mathit{\Delta }{S}_{\text{b}}}{A},$$ (1)

where σ₀ is the tension in a reference state with neither tubes nor a bleb, k_σ is an effective stretching modulus, and A is the area over which tension may be considered uniform. If tension equilibrates fast, A is the entire cell area. However, it has recently been shown that the cell membrane resists flow, possibly because of its tight interaction with the cytoskeleton (37), so that A could be restricted to the cortex-detached region underneath an expanding bleb. The phenomenological relationship is chosen to be linear for simplicity. Taking into account possible nonlinearities associated to large variations of the apparent cell membrane area (e.g., during the expansion of large blebs) would require introducing additional phenomenological parameters. We stress that many factors could plausibly affect σ₀ and k_σ, including the linkage of the membrane to the cytoskeleton (38). In our model, we treat both as constant parameters.

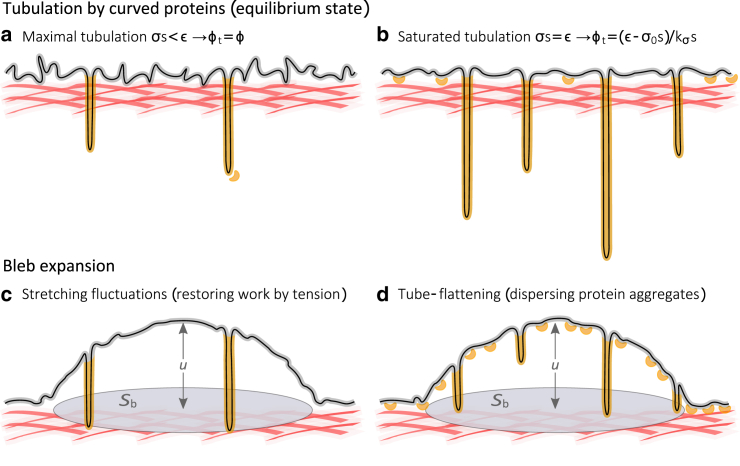
At equilibrium, meaning the stabilized folded state with no bleb, the membrane tension is an increasing function of the folded area, S_t, which is induced by the curved proteins (see Fig. 1 a). When the bleb does form, after the local membrane-cortex detachment, this heightened tension is the restoring force that acts against the deformation of the membrane (see Fig. 1 c). Thus, the bleb’s energy should be expected to grow as a function of the concentration of the curved protein. Notwithstanding, membrane area can be merely converted from the inward pointing tubules to the expanding bleb, such that no restoring work would be done by the membrane tension (see Fig. 1, b and d). Nevertheless, this expansion by means of unfolding (or tube flattening) presents its own free energy cost associated with dispersing the curved protein scaffolds that form the tubules. To accommodate the initial expansion of the bleb, the system minimizes its total free energy by paying with one energetic currency or another or possibly an optimized fraction of both stretching the membrane (that is, seizing area from fluctuations) and unfolding the membrane (releasing the area held in stabilized invaginations). Our model incorporates both of these processes, which are physically coupled through the area dependence of the membrane tension (Eq. 1).

Figure 1.

System illustration. The equilibrium state of the membrane under the regimes of low and high protein surface fraction is illustrated in figures (a) and (b), respectively. Figures (c) and (d) illustrate the initial expansion of the bleb, which bulges out of the equilibrium states (a) and (b), respectively. The gray-highlighted curve represents the “true” membrane area, including the thermal and active membrane fluctuations. The orange-highlighted curve represents S_t, the membrane area held in tubes. The small banana-shaped components (orange) depict N-BAR proteins. The red mesh represents the underlying actin cortex. The increase of apparent area due to bleb formation is ΔS_b = πu². To see this figure in color, go online.

Tubulation by curved membrane proteins

Although the cell membrane is clearly an out-of-equilibrium system, models based on equilibrium thermodynamics have proven valuable to understand aspects of membrane proteins self-aggregation of high physiological relevance (39). In this section, we propose such a model to determine the configuration of the membrane-bound curved proteins and the area stored in tubes at equilibrium and throughout the expansion of the bleb. We stress that our minimal aggregation model does not deal with the specifics of the N-BAR interaction with the membrane. We thus refer the reader to previous theoretical models (e.g., (40, 41, 42)) and molecular dynamics simulations (43, 44, 45, 46, 47, 48, 49) that describe this process at the molecular level. Here, our aim is to provide a simplified coarse-grained description of the equilibrated state of the membrane and to highlight the effect of tension buffering by tubulating proteins. Thus, our approach also differs from previous continuum models that have either focused solely on the onset of spontaneous tubulation (50) or described the enrichment of curved proteins on pre-existent (mechanically pulled) membrane tubes (51).

There exists direct experimental evidence that, at a high concentration, N-BAR proteins such as amphiphysin (51) and endophilin (52) can form protruding tubes on reconstituted membranes (giant vesicles). These tubes are enriched in N-BAR proteins and coexist with (almost) flat membrane regions. Similarly, in PGCs, we have observed membrane tubes pointing inwards from relatively flat regions (see Fig. 3 A and Video S3 in (21)). Thus, in our model, we consider membrane-bound proteins that can be either isolated on a flat membrane or aggregated on dense scaffolds that form stable membrane tubes. Note that this assumption naturally breaks down in several cases, e.g., in the limit of high temperature (as explained in Supporting Materials and Methods) or high tension and small system sizes that would not permit co-existence of tubes and flat membrane (53). The number of isolated proteins is given by n₁ = ρ₁A and the number of p-sized aggregates (tubes) is given by n_p = ρ_pA (where ρ₁ and ρ_p are uniform coarse-grained densities). We assume that the folded area held in each p-sized tube is ps, where s is the folded membrane area per protein. We also fix the protein surface fraction on tubes to unity to reduce the number of parameters. Accordingly, the tubes hold a total area of $S_{\text{t}}=A\sum _{p\ge p_{\text{c}}}{\rho }_{p}ps$ (where $p_{\text{c}}$ is a critical protein number for forming a tube cap), and the number of translational sites is A/s. In Eq. 2, we present the free energy associated with the curved proteins and the membrane tubes, including the work done by the membrane tension against the formation of the tubes and the expansion of the bleb. Note that the energy associated with membrane-cortex binding and the work done by the hydrostatic pressure will be considered later on in the analysis of the complete bleb energy.

$$F_{\text{t}}=A\left({\rho }_1\text{log}\frac{{\rho }_{1}s}{e}+\sum _{p\ge p_{\text{c}}}{\rho }_p\text{log}\frac{{\rho }_{p}s}{e}\right)+A\sum _{p\ge p_{\text{c}}}{\rho }_p\left(E_{\text{cap}}-\mathrm{\epsilon }p\right)+{\int }_{\text{0}}^{S_{\text{t}}+\text{Δ}{S}_{\text{b}}}\left({\sigma }_0+\frac{k_{\sigma }S}{A}\right)dS+\mu A\left({\rho }_1+\sum _{p\ge p_{\text{c}}}{\rho }_{p}p\right)$$ (2)

This formulation of F_t contains four essential contributions, given in units of k_BT. The first term comes from the translational entropy of all surface species (i.e., isolated proteins and tubes) (to lowest order in ρ₁s and ρ_ps). The second term accounts for the energy cost of forming the tube caps (E_cap per tube of any size) as well as the energy gain of aggregating proteins onto the tubular scaffolds (ε per recruited protein, accounting for any per-protein difference in the protein binding/membrane bending energy). The third term accounts for the restoring work done by varying the membrane tension against the extension of the tubes and the bleb (see Eq. 1). In effect, because of total membrane conservation (which is represented phenomenologically by Eq. 1), the area S_t + ΔS_b is drawn from thermal and active membrane fluctuations. Last, in the fourth term, μ denotes a Lagrange multiplier that fixes the total number of membrane-bound proteins. The parameters of this model (s, σ₀, k_σ, ε, and E_cap) are estimated in Table 1.

Table 1.

Quantitative Estimates of Our Tubulation Model Parameters

Description	Symbol	Estimate	Units	References/Comments
N-BAR surface area on membrane	s	30–50	nm2	(28, 59)
Membrane tension (without tubes)	σ0	10−4–1	pN/nm	(35, 36, 60)
Effective membrane stretching modulus	kσ	0.1–10	pN/nm	This phenomenological parameter is expected to be much smaller than the stretching modulus of pure lipid bilayer in the elastic regime ($\simeq 100$ pN/nm) because of thermal and active fluctuations (35, 61).
N-BAR affinity to tubes	ε	10–100	kBT	As a rough estimate, we consider the gain in the elastic energy of the membrane associated with clustering isolated N-BAR scaffolds (42, 62).
Energy of tube cap	Ecap	100–600	kBT	As a rough estimate, we consider the bending energy of a hemisphere, 4πKc, where Kc ∼ 10–50 kBT is the bending stiffness (63, 64).

With ${\text{k}}_{\text{B}}\text{T}\simeq 4$ pN/nm, we obtain ${\sigma }_{0}s\approx {10}^{-3}-10{\text{k}}_{\text{B}}\text{T}$, and $k_{\sigma }s\approx 1-100{\text{k}}_{\text{B}}\text{T}$.

We first minimize F_t with respect to the densities of isolated proteins and tubes (assuming ρ₁ and ρ_p are fast variables compared to the bleb expansion ΔS_b):

$$0=\frac{\partial F_{\text{t}}}{\partial {\rho }_1}\to {\rho }_1=\frac{1}{s}{e}^{-\mu },0=\frac{\partial F_{\text{t}}}{\partial {\rho }_p}\to {\rho }_p=\frac{1}{s}{e}^{-E_{\text{cap}}-\left(-\mathrm{\epsilon }+\sigma s+\mu \right)p},$$ (3)

where σ = σ₀ + k_σ (ϕ_t + ΔS_b/A), and ϕ_t = S_t/A is the surface fraction of proteins belonging to tubes (see Supporting Materials and Methods for detailed derivation).

The conservation of the total protein number is given by the following:

$$\varphi ={\varphi }_1+{\varphi }_{\text{t}}=s{\rho }_1+s\sum _{p\ge p_{\text{c}}}{\rho }_{p}p=e^{-\mu }+e^{-E_{\text{cap}}}\frac{e^{\left(1-p_{\text{c}}\right)\left(-\mathrm{\epsilon }+\sigma s+\mu \right)}\left(1+\left(e^{-\mathrm{\epsilon }+\sigma s+\mu }-1\right)p_{\text{c}}\right)}{{\left(e^{-\mathrm{\epsilon }+\sigma s+\mu }-1\right)}^2},$$ (4)

where ϕ is the total protein surface fraction, and ϕ₁ denotes the surface fraction of isolated proteins.

The conservation condition (Eq. 4) defines the Lagrange multiplier μ as a function of ϕ, with the closed nonlinear relationship obtained by substituting ϕ_t = ϕ − e^−μ back in σ. Unfortunately, we cannot extract μ explicitly from this implicit equation. Yet, in the limit $E_{\text{cap}}\gg 1$—which is in agreement with our estimation in Table 1—we find numerically that μ(ϕ) exhibits a sharp transition between two solvable asymptotic cases, namely: 1) at low ϕ, the surface fraction of isolated proteins ϕ₁ dominates over the surface fraction of proteins belonging to tubes ϕ_t, and 2) at higher ϕ, the fraction ϕ_t (last term on the right hand side) will start to dominate. The mathematical treatment, detailed in Supporting Materials and Methods, further reveals that when E_cap is the largest energy scale (as we indeed estimate), μ practically loses a quantitative dependency on both E_cap and p_c. Ultimately, we obtain an explicit piecewise approximation of ϕ_t:

$${\varphi }_{\text{t}}=\varphi -e^{-\mu \left(\varphi \right)}\simeq \{\begin{array}{cc}0& \varphi <{\varphi }^{\text{∗}}\\ \varphi -\frac{1}{k_{\sigma }s}W\left(k_{\sigma }s{e}^{-k_{\sigma }s\left(\frac{\mathrm{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}-\frac{\mathit{\Delta }{S}_{\text{b}}}{A}-\varphi \right)}\right)& \varphi >{\varphi }^{\text{∗}}\end{array},$$ (5)

where W(x) denotes the product log (Lambert function) and the crossover point of the two asymptotic limits (i.e., the point at which ${\mu }_{\varphi \simeq {\varphi }_1}={\mu }_{\varphi \simeq {\varphi }_{\text{t}}}$) is, in this $E_{\text{cap}}\gg 1$ approximation,

$${\varphi }^{\text{∗}}=e^{-\left(\mathrm{\epsilon }-{\sigma }_{0}s-k_{\sigma }s\mathit{\Delta }{S}_{\text{b}}/A\right)}$$ (6)

It is clear from Eq. 5 that ϕ^∗ represents a critical protein surface fraction for the onset of tubulation (corresponding to a critical density of proteins ϕ^∗/s). Note that this result is reminiscent of the “critical budding concentration” of the membrane proteins that induce caveolae, which are a spherical type of membrane invaginations (54). Also note that Eqs. 5 and 6 in essence depend only on three contracted parameters: (ε − σ₀s), k_σs, and ϕ as well as one additional variable: ΔS_b/A.

Results

Tubulation

Using Eqs. 5 and 6, we can compute the total folded area, S_t = Aϕ_t, as well as the membrane tension, σ = σ₀ + k_σ (ϕ_t + ΔS_b/A), for any set of parameters and any given bleb expansion. We first interpret the equilibrium result and then analyze how it is altered by the expanding bleb.

The equilibrium (prebleb) state

We focus on ${\varphi }_{\text{t}}^{\text{eq}}$, the surface fraction of proteins belonging to tubes at equilibrium (i.e., with ΔS_b = 0). To gain insight into Eq. 5, we briefly examine the limits $\left(\mathrm{\epsilon }-{\sigma }_{0}s\right)\gg 1$ and $k_{\sigma }s\gg 1$ (completely negligible entropy). First, we find that ϕ^∗ → 0 and thus,

$${\varphi }_{\text{t}}^{\text{eq}}\approx \varphi -\underset{k_{\sigma }s\to \infty }{\text{lim}}\frac{1}{k_{\sigma }s}W\left(k_{\sigma }s{e}^{-k_{\sigma }s\left(\frac{\mathrm{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}-\varphi \right)}\right)=\{\begin{array}{cc}\varphi & \varphi <\frac{\mathrm{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}\\ \frac{\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}& \varphi >\frac{\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}\end{array}$$ (7)

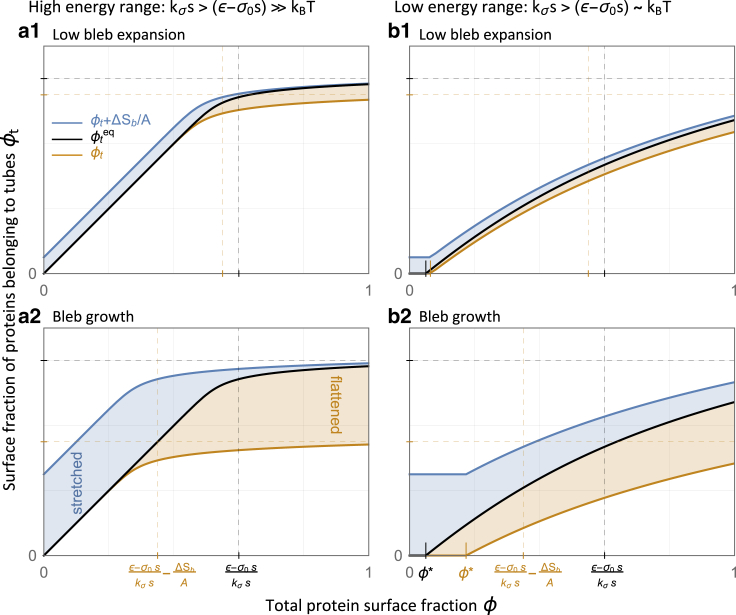
This result is expected and could be understood as follows. At low protein surface fraction (ϕ < (ε − σ₀s)/k_σs), the energetic gain of protein aggregation onto a few established tubes (of size p > E_cap/(ε − σ₀s)) dominates over the work that is done by the membrane tension against the per-protein extension of tubes (ε > σs). Because all added proteins are recruited to the tubes, we find that ${\varphi }_{\text{t}}\simeq \varphi$ in this limit (see Eq. 7; Fig. 1 a). However, as the amount of tube-forming proteins is increased, so does the folded area (S_t = Aϕ_t), which increases the membrane tension in accordance with our underlying assumption (Eq. 1). When this tension balances out the protein aggregation energy (i.e., when $\sigma s\simeq \mathrm{\epsilon }$, corresponding to${\varphi }_{\text{t}}\simeq \left(\mathrm{\epsilon }-{\sigma }_{0}s\right)/k_{\sigma }s$), any additional protein aggregation will not be energetically preferable (see Eq. 7; Fig. 1 b). Thus, the equilibrated ϕ_t and the membrane tension σ tend to saturate as a function of ϕ. The transition between the regimes of maximal tubulation (ϕ_t = ϕ) and saturated tubulation (ϕ_t = (ε − σ₀s)/k_σs) is smoothed out when increasing the relative weight of entropy (decreasing (ε − σ₀s) and k_σs proportionally) because that enhances the tendency to mix the distinguishable densities (isolated proteins and tubes of all sizes) at a high protein concentration. At a low protein concentration, the translational entropy favors isolated proteins over those clustered into large tubules. Thus, a decrease in (ε − σ₀s) increases the critical density ϕ^∗ for the onset of tubulation. All of these effects can be inferred from Fig. 2, where the black curves represent ${\varphi }_{\text{t}}^{\text{eq}}={\varphi }_{\text{t}}\left(\mathit{\Delta }{S}_{\text{b}}=0\right)$ using Eq. 5.

Figure 2.

Tubulation by curved proteins and the bleb tubes fluctuations area exchange. All plots are for $E_{\text{cap}}\gg 1$, as in Eqs. 5 and 6. In each plot, we present ${\varphi }_{\text{t}}^{\text{eq}}$ (black line), ϕ_t in the bleb state (orange line), and ϕ_t + ΔS_b/A (blue line, also proportional to the tension, σ = σ₀ + k_σ(ϕ_t + ΔS_b/A)) as functions of ϕ (see Eq. 5). The vertical gap between the black and orange curves (light orange region) is proportional to the tube-flattened area, and the vertical gap between the blue and black curves (light blue region) is proportional to the stretched area (seized from membrane fluctuations). The dependence on (ε − σ₀s) and on k_σs is indicated by the dashed grid lines (saturation limits) and the ticks that mark the critical density for tubulation, ϕ^∗ (Eq. 6), at equilibrium (black), and in the bleb state (orange). The entropic effects that arise from increasing the temperature (or decreasing all energy parameters proportionally) can be inferred from the different plots. In plots (a1) and (a2), the entropic effects are negligible because $\left(\mathit{\epsilon }-{\sigma }_{0}s\right)\gg 1$ (specifically, (ε − σ₀s) = 30 and k_σs = 50, well within our estimations in Table 1). In plots (b1) and (b2), where (ε − σ₀s) ∼ 1 (specifically, (ε − σ₀s) = 3 and k_σs = 5), one may notice a finite critical density for tubulation, ϕ^∗ > 0, as well as a smoother transition into saturation. The dependence on bleb growth can be inferred from plots (a2) and (b2), where ΔS_b/A is increased to 25% from 5% in plots (a1) and (b1). To see this figure in color, go online.

Using the numerical estimates of the parameters given in Table 1, we find that the aggregation of proteins into membrane tubes can increase the cell membrane tension up to a maximal value $\mathit{\epsilon }/s\simeq 1-10\text{p}\text{N}/\text{nm}$, corresponding to the saturation regime. This is a high value, which can exceed the membrane rupture tension. The saturation regime can be reached if the surface fraction of protein exceeds a value of order ε/(k_σs), which can be as low as $10\text{\%}$. For a lower composition, the system is in the regime of maximal tubulation; increasing the protein density by an amount Δϕ leads to an increase of the membrane tension by k_σΔϕ, which reach 1 pN/nm for Δϕ = 10%. We reiterate that these values should be considered as crude estimates because of the large uncertainty regarding the value of the effective stretching modulus k_σ. Nevertheless, they show that the effect of tube-forming proteins on the cell membrane tension can be highly physiologically significant.

The bleb state

The bleb expansion effectively increases the tension (Eq. 1), making the extension of tubes more costly. Therefore, we find that ϕ_t decreases as a function of ΔS_b (see orange curves in Fig. 2). Specifically, the limit at which the tension balances out the aggregation energy $\left(\sigma s\simeq \mathit{\epsilon }\right)$ corresponds to a lower saturation threshold for ϕ_t (see Fig. 2, a1 and a2). The change in the total folded area, $\mathit{\Delta }{S}_{\text{t}}=A\left({\varphi }_{\text{t}}^{\text{eq}}-{\varphi }_{\text{t}}\right)$, is the tube-flattened area that accounts for a fraction of ΔS_b (proportional to the orange vertical gaps in Fig. 2). The remaining expansion area, $\mathit{\Delta }{S}_{\text{b}}-\mathit{\Delta }{S}_{\text{t}}=A\left(\left(\mathit{\Delta }{S}_{\text{b}}/A\right)+{\varphi }_{\text{t}}-{\varphi }_{\text{t}}^{\text{eq}}\right)$, is drawn from fluctuations (membrane stretching, proportional to the blue vertical gaps in Fig. 2). Given ϕ > ϕ^∗, we may approximate, to first order in ΔS_b, the tube-flattened area and the stretched area:

$$\mathit{\Delta }{S}_{\text{t}}\approx -{A\frac{d{\varphi }_{\text{t}}}{d\text{Δ}{S}_{\text{b}}}|}_{\mathit{\Delta }{S}_{\text{b}}=0}\mathit{\Delta }{S}_{\text{b}}=\frac{k_{\sigma }s{\varphi }_1^{\text{eq}}}{k_{\sigma }s{\varphi }_1^{\text{eq}}+1}\mathit{\Delta }{S}_{\text{b}},\mathit{\Delta }{S}_{\text{b}}-\mathit{\Delta }{S}_{\text{t}}\approx \frac{1}{k_{\sigma }s{\varphi }_1^{\text{eq}}+1}\mathit{\Delta }{S}_{\text{b}},$$ (8)

where ${\varphi }_1^{\text{eq}}=\varphi -{\varphi }_{\text{t}}^{\text{eq}}\approx \left(1/k_{\sigma }s\right)W\left(k_{\sigma }s{e}^{-k_{\sigma }s\left(\left(\mathit{\epsilon }-{\sigma }_{0}s/k_{\sigma }s\right)-\varphi \right)}\right)$ is the surface fraction of isolated proteins at equilibrium. We find that there is a sharp transition in the mechanism of the initial bleb expansion, from stretching out fluctuations to flattening the tubes (illustrated in Fig. 1, c and d). This transition occurs at $\varphi \simeq \left(\mathit{\epsilon }-{\sigma }_{0}s/k_{\sigma }s\right)$, the limit at which the protein surface fraction belonging to tubes (${\varphi }_{\text{t}}^{\text{eq}}$) and the membrane tension $\left({\sigma }^{\text{eq}}={\sigma }_0+k_{\sigma }{\varphi }_{\text{t}}^{\text{eq}}\right)$ saturate (see Eq. 7; Fig. 2 a). As expected, an increase in the stiffness modulus k_σ, which increases the energetic cost of stretching out fluctuations, results in favoring the expansion via tube flattening. The effect of increasing (ε − σ₀s) is precisely the opposite because a higher energetic gain for protein aggregation stabilizes the membrane tubules.

The bleb nucleation energy

In this section, we first present the complete energy of a bleb that bulges out from the equilibrium state (folded membrane adhered to the cortex, see Fig. 1, a and b). We then use this expression to derive the energy barrier that limits the nucleation of blebs.

A compelling depiction of bleb formation as a nucleation process was first suggested in (8). In their treatment, Charras et al. began by minimizing the bleb energy with respect to curvature—ensuring normal force balance on the detached membrane (the Young-Laplace condition). They then found that the minimized bleb energy exhibits a nonmonotonic dependency on the cortex-detached area; the energy first increases with the membrane detachment and beyond some critical size it decreases, making it energetically preferable to form the macroscopic bleb. The maximal energy that corresponds to the critical detachment is thus interpreted as the energetic barrier for bleb nucleation. Here, we extend this fundamental description by coupling it directly to the total free energy associated with the membrane tubes and the curving proteins (Eq. 2).

The total energy difference between the bleb state and the equilibrium (prebleb) state is given by the following:

$$E_{\text{b}}=-P{V}_{\text{b}}+J{S}_{\text{b}}+\mathit{\Delta }{F}_{\text{t}}$$ (9)

where P is the hydrostatic pressure driven by actomyosin contractility, V_b is the inflated bleb volume, J is the membrane-cortex adhesion strength, S_b is the cortex-detached area (the base of the bleb, see Fig. 1), and ΔF_t is the difference in the free energy of the membrane and the curved proteins that results from the bleb expansion. It is calculated from the variation of the free energy F_t in Eq. 2. upon variation of the bleb expansion area from zero to ΔS_b. We assume that the tubular proteins equilibrate fast compared to the dynamics of bleb expansion so that the densities ρ₁ and ρ_p are given by Eq. 3. As we are interested in bleb nucleation, we consider the shallow bleb limit ($u^2/S_{\text{b}}\ll 1$, where u is the maximal height of the bleb, see Fig. 1), for which $\mathit{\Delta }{S}_{\text{b}}\simeq \pi u^2$ and $V_{\text{b}}\simeq S_{\text{b}}u/2$. Assuming S_b > K_c/σ (where K_c is the bending rigidity), we neglected in Eq. 9 the bending energy induced by the bleb deformation. Last, assuming that the change in tension is negligible during the nucleation stage of the bleb, we will also neglect contributions to ΔF_t that are quadratic in ΔS_b (quartic in u).

For a given ΔS_b, the minimized F_t can be expressed in terms of ϕ₁, ϕ_t (see Eq. S16). As shown in Supporting Materials and Methods, we use this expression to derive the following:

$${\frac{d{F}_{\text{t}}}{d\mathit{\Delta }{S}_{\text{b}}}|}_{\mathit{\Delta }{S}_{\text{b}}=0}\approx \{\begin{array}{cc}{\sigma }_0& \varphi <{\varphi }^{\text{∗}}\\ {\sigma }_0+k_{\sigma }{\varphi }_{\text{t}}^{\text{eq}}& \varphi >{\varphi }^{\text{∗}}\end{array}={\sigma }^{\text{eq}}$$ (10)

This result entails important physical meaning regarding the stress-strain relationship of the cell membrane. In the regime of low protein surface fraction (meaning ϕ < (ε − σ₀s)/k_σs), the free energy cost of bleb expansion increases with ϕ $\left(\mathit{\Delta }{F}_{\text{t}}\simeq {\sigma }^{\text{eq}}\mathit{\Delta }{S}_{\text{b}}=\left({\sigma }_0+k_{\sigma }\varphi \right)\mathit{\Delta }{S}_{\text{b}}\right)$. This is because the tubulating proteins effectively stiffen the membrane tension, which then works against the initial bleb expansion. In the regime of high protein surface fraction (ϕ > (ε − σ₀s)/k_σs), the cost of bleb expansion is given by $\mathit{\Delta }{F}_{\text{t}}\simeq \left(\mathit{\epsilon }/s\right)\mathit{\Delta }{S}_{\text{b}}$. In essence, this cost is attributed to unfolding the tubes (dispersing ΔS_b/s proteins from tubular aggregates at the cost of ε per protein). In other words, Eq. 10 concisely accounts for the transition between the two possible expansion mechanisms.

Substituting ΔF_t = σ^eqΔS_b back in Eq. 9,

$$E_{\text{b}}=-P{S}_{\text{b}}u/2+J{S}_{\text{b}}+{\sigma }^{\text{eq}}\pi u^2$$ (11)

Following (8), we proceed by minimizing E_b with respect to the bleb height u (assuming that the detached area S_b is the slowest variable). It follows that $u=\left(P{S}_{\text{b}}/4\pi {\sigma }^{\text{eq}}\right)$ and $E_{\text{b}}=-\left(P^2{S}_{\text{b}}^2/16\pi {\sigma }^{\text{eq}}\right)+J{S}_{\text{b}}$. The u-minimized bleb energy has a maximum at $S_{\text{b}}^{\text{nuc}}=8\pi {\sigma }^{\text{eq}}J/P^2$. This maximum corresponds to an energy barrier, which we call the bleb nucleation energy:

$$E_{\text{b}}^{\text{nuc}}=4\pi {\sigma }^{\text{eq}}{J}^2/P^2$$ (12)

Note that u^nuc = 2J/P and $\mathit{\Delta }{S}_{\text{b}}^{\text{nuc}}=4\pi J^2/P^2$ are the bleb height and the bleb expansion area at the nucleation point. The result given in Eq. 12 is valid so long as our simplifying assumptions (shallow deformation, negligible bending energy of the bleb, and negligible change in tension) are met throughout the nucleation stage (see range of validity in Supporting Materials and Methods).

Large bleb expansion might eventually lead to the complete flattening of all tubes, if ΔS_b is so large that ϕ < ϕ^∗(ΔS_b) (see Eq. 6)). We assume that this limit is not reached during the nucleation stage, which is valid provided that

$$\mathit{\Delta }{S}_{\text{b}}^{\text{nuc}}<\mathit{\Delta }{S}_{\text{b}}^{\text{∗}}\equiv A\frac{\text{log}\varphi +\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}\to J<P{R}_{\text{cell}}\sqrt{\frac{\text{log}\varphi +\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}},$$ (13)

where here we considered that the area A is roughly $4\pi R_{\text{cell}}^2$.

Model versus experiments

In this section, we discuss the relevance of our theory to the experiments. First, we infer which is the theoretical regime that bares the most qualitative resemblance to our previous observations. Second, we use the model to predict the consequences of performing two competing manipulations sequentially. We then verify this prediction in new in vivo experiments.

Comparison with previous observations

Let us first recall two major findings from our previous experimental study (21), namely that the folded area held in tubes increases with N-BAR expression and that the blebbing frequency decreases with N-BAR expression. These observed responses are supported theoretically by the model if both $S_{\text{t}}^{\text{eq}}$ (the equilibrium folded area) and $E_{\text{b}}^{\text{nuc}}$ (the bleb nucleation energy) are increasing functions of the total protein density. Because $S_{\text{t}}^{\text{eq}}=A{\varphi }_{\text{t}}^{\text{eq}}$ and $E_{\text{b}}^{\text{nuc}}=\left(4\pi J^2/P^2\right)\left({\sigma }_0+k_{\sigma }{\varphi }_{\text{t}}^{\text{eq}}\right)$, these two requirements are met so long as ${\varphi }_{\text{t}}^{\text{eq}}$ is not saturated as a function of ϕ (see black curves in Fig. 2). Assuming that entropic effects are negligible (that is, $\left(\mathit{\epsilon }-{\sigma }_{0}s\right)\gg 1$ and $k_{\sigma }s\gg 1$), this condition corresponds to ϕ < (ε − σ₀s)/k_σs. We thus infer that PGCs naturally express relatively low levels of tube-forming proteins. This regime seems favorable from an evolutionary standpoint as it allows for PGCs to regulate their blebbing activity (and consequent motility) by modulating their N-BAR expression.

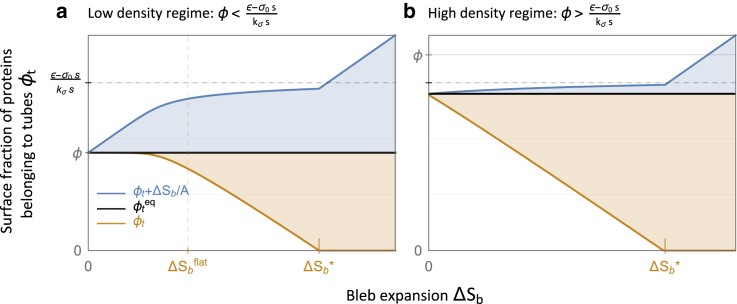
In the low ϕ regime, our model attributes at least a part of the initial bleb expansion to membrane stretching (seizing area from membrane fluctuations rather than from stabilized tubes, see Figs. 1 c and 2, a1 and a2). That being said, our experiments have suggested that bleb growth is concomitant with the local flattening of the membrane tubes (21). Yet, because the blebs form very rapidly and the spatiotemporal resolution of our imaging is limited, one cannot conclude from these observations that the mere onset of the bleb must rely strictly on tube flattening. Our model suggests that even if the bleb expands purely via stretching throughout the initial nucleation stage, it should enter a tube-flattening mode very quickly after nucleation. This is because the tension increases with bleb expansion (see Eq. 1), and when $\sigma s\simeq \mathrm{\epsilon }$, it becomes energetically preferable to draw area from the tubular reservoir. Tube flattening is triggered by bleb expansion when the expansion area reaches the following:

$$\mathit{\Delta }{S}_{\text{b}}\approx \mathit{\Delta }{S}_{\text{b}}^{\text{flat}}\equiv A\left(\frac{\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}-\varphi \right)\simeq 4\pi R_{\text{cell}}^2\left(\frac{\mathit{\epsilon }-{\sigma }_{0}s}{k_{\sigma }s}-\varphi \right)$$ (14)

Note that our assumption is $\mathit{\Delta }{S}_{\text{b}}^{\text{nuc}}<\mathit{\Delta }{S}_{\text{b}}^{\text{flat}}$, which translates into $J<P{R}_{\text{cell}}\sqrt{\left(\mathit{\epsilon }-{\sigma }_{0}s/k_{\sigma }s\right)-\varphi }$.

For high protein surface fraction, ϕ > (ε − σ₀s)/k_σs, our model predicts that the expansion via tube flattening (rather than stretching fluctuations) will ensue immediately after membrane-cortex detachment (see Figs. 1 d and 3 b). Thus, the very inception of the bleb would necessarily correlate with the flattening of membrane tubes. As discussed above, this regime cannot correspond to the WT experimental case because it is inconsistent with the fact that N-BAR overexpression increases the number of tubes and the membrane tension. Nonetheless, cells with overexpressed N-BAR may be in this regime.

Figure 3.

Area exchange during bleb expansion. In each plot, we present ${\varphi }_{\text{t}}^{\text{eq}}$ (black line), ϕ_t in the bleb state (orange line), and ϕ_t + ΔS_b/A (blue line, also proportional to the tension, σ = σ₀ + k_σ(ϕ_t + ΔS_b/A)) as functions of ΔS_b (see Eq. 5). The vertical gap between the black and orange curves (light orange region) is proportional to the tube-flattened area, and the vertical gap between the blue and black curves (light blue region) is proportional to the stretched area (seized from membrane fluctuations). The dependence on parameters is indicated by the black dashed grid line (saturation limit of tubulation), the orange dashed grid line ($\mathit{\Delta }{S}_{\text{b}}^{\text{flat}}$, given in Eq. 14, beyond which the bleb expansion induces tube flattening), the horizontal gray line (marking the total protein surface fraction ϕ), and the orange tick, which marks the critical bleb expansion, $\mathit{\Delta }{S}_{\text{b}}^{\text{∗}}$ (Eq. 13), beyond which ${\varphi }_{\text{t}}\simeq 0$. We vary the protein surface fraction ϕ, such that the equilibrium tubulation is maximal in plot (a) (${\varphi }_{\text{t}}^{\text{eq}}\simeq \varphi$), and saturated in plot (b) $\left({\varphi }_{\text{t}}^{\text{eq}}\simeq \left(\mathit{\epsilon }-{\sigma }_{0}s\right)/k_{\sigma }s\right)$. We set (ε − σ₀s) = 30 and k_σs = 50 as in Fig. 2, a1 and a2. To see this figure in color, go online.

Prediction and new supporting experiments

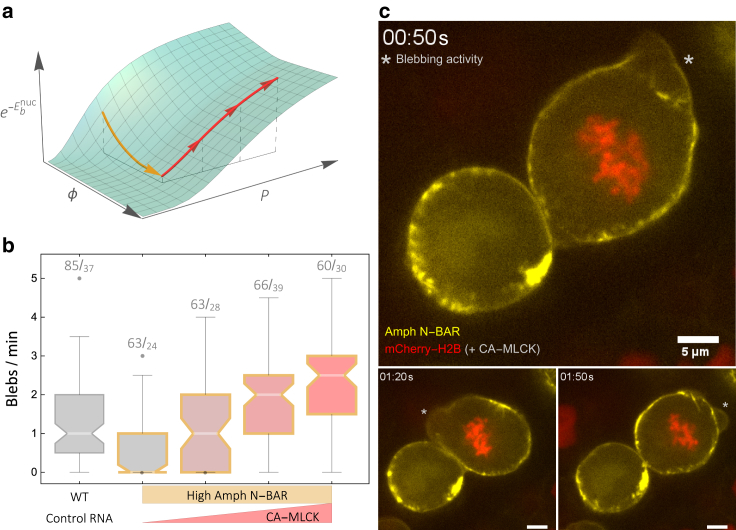
For all parameter regimes, the minimized bleb energy has a maximum as a function of S_b. This maximum corresponds to a finite bleb nucleation energy, $E_{\text{b}}^{\text{nuc}}$ (given in Eq. 12), which tends to saturate as a function of ϕ but is always proportional to 1/P². In other words, the stabilizing effect of the tubulating proteins is limited, whereas the destabilizing effect of the hydrostatic pressure is not. We may conclude then that regardless of ϕ, one can continuously increase the probability of bleb formation (proportional to $e^{-E_{\text{b}}^{\text{nuc}}}$) by gradually increasing P (see Fig. 4 a).

Figure 4.

Blebbing recovery in Amph N-BAR PGCs through CA-MLCK expression. (a) Shown is a plot of the theoretical probability of bleb formation, proportional to $e^{-E_{\text{b}}^{\text{nuc}}}$, as a function of the protein surface fraction ϕ and the hydrostatic pressure P (see Eq. 12). The arrows indicate the qualitative direction of the theoretically motivated manipulations. (b) Box whisker plot (with outliers) summarizes the in vivo blebbing frequency of WT and manipulated PGCs. White lines denote medians (with notched confidence interval), and each box extends from the 25% to the 75% quantile. Boxes with orange edges indicate datasets of cells expressing 250 pg of N-BAR domain of amphiphysin (Amph-N-BAR), and the red level fillings indicates the increasing levels of CA-MLCK (from 0 to 40 pg). Numbers indicate the number of cells quantified over the number of manipulated embryos. (c) Snapshots from Video S1 show a mosaic of cells that are overexpressing N-BAR (yellow). In contrast to the stable cell on the left, the blebbing cell on the right also expresses CA-MLCK. Blebbing activity is marked with asterisks, and the nuclear marker (mCherry-H2B) was used to tag cells that co-express both N-BAR and CA-MLCK. To see this figure in color, go online.

To test this prediction, we conducted a complementary study using zebrafish PGCs as an in vivo model. The experimental methods are similar to those reported in (21) (see Supporting Materials and Methods for details). In these new experiments, we first inhibited the blebbing activity by overexpressing the N-BAR domain of amphiphysin (Amph-N-BAR) specifically in the PGCs. We then expressed in these embryos varying concentrations of constitutively active MLCK (CA-MLCK), the enzyme which enhances myosin II contraction. Because the myosin contraction is known to increase the hydrostatic pressure, we expected to first rescue blebbing and then to increase the blebbing frequency as a function of the CA-MLCK concentration. Indeed, although we were not able to measure the pressure directly, our results show the expected trend (see Fig. 4 b). After this manipulation, the blebbing frequency of cells overexpressing Amph-N-BAR recovered to WT levels. Furthermore, by overexpressing the CA-MLCK protein, we were able to increase the blebbing activity beyond that observed in WT cells, which is also qualitatively consistent with the model. The recovery of blebbing in Amph-N-BAR PGCs by CA-MLCK overexpression is demonstrated in Fig. 4 c and Video S1. Here, two PGCs expressing elevated levels of Amph-N-BAR are presented (yellow label). One of the PGCs was engineered to express CA-MLCK (cell expressing mCherry in its nucleus), and this cell produces blebs (marked by asterisks).

Discussion

Our derivation of $E_{\text{b}}^{\text{nuc}}$ (see Eq. 12) shows how the bleb initiation probability scales with physical parameters, including the intracellular hydrostatic pressure (driven by actomyosin contractility), the membrane-cortex adhesion strength, and the fluctuations-driven membrane tension (8). We claim that bleb nucleation is controlled by the curved membrane proteins (N-BAR domains) through their capacity to control membrane tension by sequestering membrane area into tubular invaginations. Although a quantitative comparison with experiments remains limited, mostly due to the lack of precise independent measurements of our model parameters for this cell type, our theoretical results do provide a qualitative explanation of the observed responses of PGCs to manipulations in the level of the Amph-N-BAR and in the activity of the myosin light-chain kinase (MLCK) enzyme that induces actomyosin contraction. Indeed, increasing MLCK activity in WT somatic cells that do not normally bleb led to bleb formation in these cells (25). It would thus be interesting to examine this option in different cell types and at different steps, such as at the initiation of migration, during migration, and at the stage when the cells stop migration.

For simplicity, we have discarded possible couplings between the membrane-cortex adhesion strength, J; the density of the curved proteins, ϕ/s; and their aggregation energy, ε. However, a complex co-dependence between these factors is likely to arise because the tubes were observed to penetrate the cortex. Moreover, we found experimentally that tube flattening was mostly confined to the cortex-detached region of the expanding bleb (that is, tubes in distant parts of the membrane remained intact). This phenomenon could result from a possible stabilization of membrane tubes over the cortex-bound membrane through their interaction with cytoskeleton components. This could be taken into account in the model by assigning a larger value of the energy ε for tubes embedded in the cortex. Another possibility is that the increase of membrane tension after bleb expansion fails to propagate over the entire cell membrane because of friction with the cytoskeleton as was recently observed in HeLa cells (37). Such dynamical effects may be crudely accounted for in our equilibrium theory through the area A over which the tension is assumed to be uniform. If tension equilibrates fast compared to bleb expansion, A is the total cell area as was assumed in Eqs. 13 and 14. If friction over the cytoskeleton effectively prevents tension equilibration away from the growing bleb, A is equivalent to the cortex-detached area S_b. The only relevant parameters that depend on this area are the tension increase during bleb expansion $\mathit{\Delta }{\sigma }_{\text{bleb}}=k_{\sigma }\left(\mathit{\Delta }{S}_{\text{b}}/A\right)$ (see Eq. 1) and the total area stored in tubes S_t = Aϕ. Restricting tension propagation to the cortex-detached bleb membrane thus has two consequences: the bleb membrane tension increases much faster during bleb expansion and is more likely to reach the threshold tension at which tubes flatten, and tube flattening is restricted to the bleb membrane. Both consequences are in agreement with our observations.

Because of the fairly high uncertainty of the parameter values, precise quantitative predictions are beyond the scope of our model. We may nevertheless propose a realistic scenario based on our experimental evidence. In the context of our model, the inhibitory effect of N-BAR overexpression on bleb formation is evidence that WT PGCs are in the maximal tubulation regime (Fig. 1 a). Membrane tension is thus below a threshold set by the affinity of N-BAR proteins to tubular structures and the protein size: ${\sigma }_{\text{WT}}<\left(\mathrm{\epsilon }/s\right)\sim 1\text{p}\text{N}/\text{nm}$ (with ε = 10 k_BT and s = 50 nm², see Table 1). In this regime, increasing the protein density by an amount Δϕ leads to a relative increase of tension $\left(\mathit{\Delta }\sigma /\sigma \right)=\left(k_{\sigma }/\sigma \right)\mathit{\Delta }\varphi$. Because N-BAR overexpression strongly decreases the blebbing rate, we may expect that it leads to a large variation of the bleb nucleation energy (Eq. 12) $\left(\mathit{\Delta }{E}_{\text{b}}^{\text{nuc}}/E_{\text{b}}^{\text{nuc}}\right)=\left(\mathit{\Delta }\sigma /\sigma \right)\sim 1$. As we do not expect the protein surface fraction to be much larger than Δϕ = 0.1, this requires that k_σ is one order of magnitude larger than σ, which is consistent with our estimates (Table 1). We have shown that increasing actomyosin contractility can compensate for the effect of N-BAR overexpression on blebbing. According to Eq. 12, this requires that $\left(\mathit{\Delta }P/P\right)\sim \left(\mathit{\Delta }\sigma /2\sigma \right)\sim \left(1/2\right)$. An increase of contractility by $50\text{\%}$ is indeed a reasonable outcome of CA-MLCK overexpression.

Conclusions

Together, we have presented a comprehensive coarse-grained theory of bleb initiation and membrane tubulation by curved proteins, such as N-BAR domains. In this theory, the tubes control the rate of bleb formation by increasing the cell membrane tension. When the blebbing rate is sensitive to N-BAR expression, as in the case of WT PGCs, we infer from our model that the membrane reservoir contained in the tubes remains mostly folded during the nucleation stage of the bleb. We propose that the flattening of tubes is prompted when the energetic cost of stretching out fluctuations exceeds the free energy cost of dispersing the dense protein scaffolds that form the tubes. This unfolding mode is likely triggered at a later stage of bleb growth because the bleb expansion itself also increases the membrane tension. The results obtained in our description of the tubes at rest (that is, without a bleb) shed light on a more generic regulatory role for the curved membrane proteins. We suggest that these proteins significantly impact the tension by folding the cell membrane and could thus influence any cellular process in which membrane mechanics play an important role. The relevance of our findings is thus particularly broad as membrane tension is increasingly being regarded as a master regulator of important cellular process, such as cell motility (36, 55, 56) and cell spreading (57, 58).

Author Contributions

I.L. wrote the article and analyzed the model with N.S.G., R.V., and P.S. M.G. and E.R. designed and performed the experiments. P.S. supervised the theoretical work and edited the manuscript. All authors reviewed the manuscript.

Editor: Markus Deserno.