Mechanical Point Loading Induces Cortex Stiffening and Actin Reorganization

Abstract

Global cytoskeleton reorganization is well-recognized when cells are exposed to distinct mechanical stimuli, but the localized responses at a specified region of a cell are still unclear. In this work, we mapped the cell-surface mechanical property of single cells in situ before and after static point loading these cells using atomic force microscopy in PeakForce-Quantitative Nano Mechanics mode. Cell-surface stiffness was elevated at a maximum of 1.35-fold at the vicinity of loading site, indicating an enhanced structural protection of the cortex to the cell. Mechanical modeling also elucidated the structural protection from the stiffened cell cortex, in which 9–15% and 10–19% decrease of maximum stress and strain of the nucleus were obtained. Furthermore, the flat-ended atomic force microscopy probes were used to capture cytoskeleton reorganization after point loading quantitatively, revealing that the larger the applied force and the longer the loading time are, the more pronounced cytoskeleton reorganization is. Also, point loading using a microneedle combined with real-time confocal microscopy uncovered the fast dynamics of actin cytoskeleton reorganization for actin-stained live cells after point loading (<10 s). These results furthered the understandings in the transmission of localized mechanical forces into an adherent cell.

Significance

Mechanical reorganization of cellular components is crucial in biological homeostasis when a cell is exposed to the complicated mechanical environment in vivo. In contrast to global loading on an entire cell or cellular monolayer, point loadings usually induce confined cellular responses around the loading site. In a combination of experimental measurements and mechanical modeling, this study indicated that cell-surface stiffness was elevated around the loading site upon point loading with fast dynamics of cytoskeletal reorganization in <10 s, and this mechanical enhancement acted as structural protection of the cell cortex to intracellular components with reduced nucleus stress and strain. This work anticipated physical protection of single cells under point loading and furthered the understanding of localized force transmission inside a cell.

Introduction

Cells always situate in different mechanical milieus (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13) and have different responses to distinct physical or mechanical microenvironments. As the main structural elements for cells to resist physical perturbations (14, 15, 16, 17), the cytoskeleton is crucial for sensing and responding to different mechanical microenvironments. How the cytoskeleton responds to diverse mechanical stimuli has attracted much attention (7, 16, 18, 19). For instance, strong and polarized actin stress fibers are formed in osteoblastic cells even at a very short duration of shear flow (20), and similar shear-enhanced stress fiber structure and actin reorganization can also be observed in endothelial cells (21). Other mechanical stimuli show different impacts on cytoskeleton dynamics, as exemplified by the fact that cyclic stretching osteoblasts and fibroblasts can induce actin stress fibers reorienting to the direction perpendicular to the stretch to favor the stress release along the stretch direction (9).

Cytoskeleton responses under different mechanical loading are coupled with mechanical property changes of the cells. Under shear stress of 1–8 Pa for several hours, actin filaments are reorganized and aligned along the flow direction in osteoblastic and endothelial cells, followed by cell-stiffness enhancement (20, 22). Cell stiffness also increases or decreases when cells are placed in hypertonic or hypotonic solution and present varied surface tension (23, 24). Cell-stiffness enhancement is also detected for cells in dynamic stretch using magnetic tweezers (25, 26), and these mechanical changes vary with different loading modes (loading rate, duration, and amplitude) of substrate strain in distinct cell types (27, 28, 29). Interestingly, cyclic stretch helps the formation and strengthening of actin cap in mouse embryonic fibroblasts, which binds to nuclear lamina to maintain normal nuclear morphology and to reduce the stress applied on the nucleus (16). Evidently, cytoskeleton stiffening induced by mechanical loading also plays consequential roles in protecting cell components.

Although existing works mainly focus on cellular responses and mechanical changes upon specific loadings, most of them are bulk studies, and average effects from the cell population are analyzed. Thus, in situ change of mechanical properties upon cytoskeleton reorganization in a single cell remains unclear under mechanical loading. Although cell stiffness was compared before and after loading a cell using a force of 5–20 nN for 10 min (30), the related results only focused on a single point measurement without characterizing the whole cell. Meanwhile, cytoskeleton responses to mechanical loadings of varied extent (e.g., loading force magnitude and duration) have not been anatomized quantitatively, and the real-time dynamics of cytoskeleton reorganization to distinct mechanical loadings still remains to be unveiled. In this work, we aim to take in situ mechanical properties mappings of single cells before and after mechanical point loading and further explore the contribution of cytoskeleton structure to cell mechanical properties and the cytoskeletal reorganization dynamics upon mechanical point loading.

Materials and Methods

Multiple methods of mechanical loading were applied together with varied cell imaging protocols and then summarized for clarity. In brief, two kinds of mechanical point loading on the surfaces of single cells were performed by atomic force microscopy (AFM) tip and glass microneedle, respectively. The former was used for quantitative point loading with preset force and duration, together with offline confocal laser scanning microscopy of cellular actin and nucleus. The latter was used along with in situ confocal microscopy to record the real-time dynamics of actin cytoskeleton reorganization under controllable mechanical loading. The changes of cell-surface mechanical property of single cells were evaluated before and after the point loading of AFM measurements. In addition, mechanical modeling and numerical simulations were also performed for unveiling the roles of cytoskeletons in cell responses.

Cell culture

Three types of cells were used in this study. Human cervical carcinoma cell line HeLa cells were obtained from Dr. Feng Shao, and human foreskin fibroblast line HF and human umbilical vascular endothelial cell line HUVEC were both purchased from ATCC (American Type Culture Collection, Manassas, VA). HeLa cells and HFs were cultured in RPMI and DMEM(L) Medium (HyClone, Logan, UT) supplemented with 10% fetal bovine serum (Gibco, Thermo Fisher Scientific, Shanghai, China) and 100 U/mL penicillin-streptomycin (HyClone, Chicago, IL), respectively. Both kinds of cells were plated on poly-L-lysine-coated glass bottom dishes (Cellvis, Mountain View, CA) overnight for use. HeLa cells were used when they reached >80% confluence except for low-density experiments. In that case, cells were seeded in 1/8 density of normal seeding to isolate each cell. HFs were used when reaching around 50% confluence (mostly isolated cells). HUVECs were cultured in Medium 199 supplemented with 20% fetal bovine serum, 100 U/mL penicillin, 20 mM HEPES (HyClone, Logan, UT), 3 g/mL thymidine (Sigma-Aldrich, Shanghai, China), 1 mM L-glutamine (Sigma-Aldrich), 14 U/mL heparin sodium (Sigma-Aldrich), 25 g/mL amphotericin B (Amresco, Solon, OH), and 5 ng/mL bFGF (R&D Systems, Minneapolis, MN). They were plated on collagen I (Sigma-Aldrich)-coated glass-bottomed dishes to form a monolayer before using.

AFM experiments

AFM tests were performed on Bioscope Catalyst (Bruker, Billerica, MA) with an inverted fluorescence microscope IX71 (Olympus, Shinjuku, Tokyo, Japan) for point loading the top of the cell and mapping the cell-surface mechanical property. For point loading experiments, in-house-customized flat-ended CSG-10 probes, a general gift from Dr. Bin Tang (Fig. S1 A; nominal spring constant 0.07 N/m, tip diameter 1.5–2 μm), were used for applying a constant force of 2.5, 5, or 10 nN with different duration of 1 or 3 min upon the settings of ramp displacement 6 μm and ramp velocity 1 μm/s (ramp rate ≪ 1). Deflection sensitivity and spring constant of each AFM probe were calibrated through sapphire indentation and thermal tune method before loading, respectively. Cells were treated with 1:500 diluted Hoechst 33342 in culture medium (Thermo Fisher Scientific) for labeling nucleus for 10 min and followed by three times washing using prewarmed DPBS (HyClone, Logan, UT) before mechanical loading. In some cases, cells were first treated with 15 μM blebbistatin (Bleb) (Sigma-Aldrich) or 15 μM cytochalasin D (Cyto D) (TOCRIS, Bristol, UK or Cayman, Ann Arbor, MI) for 20 min, respectively, or with 100 nM trichostatin A (TSA) (Sigma-Aldrich) for 24 h, and then the nucleus was stained (all the drugs were diluted using culture medium). After point loading, the cells were fixed using 4% paraformaldehyde at room temperature for 15 min and then stained with respective fluorescent probes before the offline confocal microscopy observations.

For mechanical property mapping experiments, Bruker patent PeakForce-Quantitative Nano Mechanics (PF-QNM) mode was performed using precalibrated (spring constant around 0.07 N/m) PF-QNM-LC probes with 17-μm tip height and 65-nm tip radius. Parameter settings included peak force frequency 0.5 kHz, setpoint 1 nN (with deformation around 400 nm), and amplitude 300 nm. The resolution of imaging was 256 × 128 with a scanning size of 15 × 15 μm, which took ∼5 min to finish one round of scanning. To detect cell-surface mechanical property changes induced by point loading, the tip was ramped onto the cell surface for 3-min delay and 5-nN loading after the first 5-min scanning, and the same region was then scanned again. Finally, Sneddon model was used for extracting Young’s modulus E in the PF-QNM measurements.

Microneedle experiments

Microneedle manipulation combined with in situ confocal fluorescence microscopy was used to monitor point-loading-induced actin reorganization dynamics. Closed-end microneedles with radii around 1.5 μm were made from thin-wall glass capillaries (WPI, Sarasota, FL) using a Narishige PN-31 Micropipette-Puller (Narishige, Tokyo, Japan). A micropipette manipulation unit (Narishige) was used to manipulate loading on cells (Fig. S1 B). Microneedle loading was depicted using dashed downward arrow (Fig. S1 C), and the real-time actin reorganization was observed under point loading. Here, the microneedle approach serves as the qualitative supplement for AFM point loading. No quantitative indentation force values were obtained, mainly because of the difficulty of in situ spring constant calibration.

Immunofluorescence staining and imaging

For those fixed cells after AFM point loading, 1:40 rhodamine phalloidin (Thermo Fisher Scientific) diluted by 1% bovine serum albumin (BSA) (Sigma-Aldrich) was used to stain F-actin for 30 min at 37°C. In some cases, after treating with 5% BSA at 37°C for 1 h to block nonspecific epitopes, 1:200 γH2AX antibody (Abcam, Shanghai, China) diluted by 1% BSA was used to label DNA damage for 1 h at 37°C. Then the cells were rinsed three times using phosphate-buffered saline, and actin was stained as described above with another three times phosphate-buffered saline rinsing. Confocal laser scanning microscopy (Zeiss LSM 710; Zeiss, Oberkochen, Germany) with a 63×/1.35 NA oil-immersed objective was used for the imaging of stained cells in three modes as follows: three-dimensional (3D) reconstruction only (“3DR”) was performed with stack interval of 0.3 μm and pinhole in 1 AU; time series only (“TS”) was carried on with an interval of 2 s, maximum pinhole, and 30 frames in total; combination of 3D reconstruction with time series (“3DR” + “TS”) was taken with a stack interval of 1.5–1.6 μm, pinhole in 2–3 AU, 7–13 slices per cell, ∼0.77 s per slice, 10 s per Z-stack, and six frames in total.

Live-cell staining and transfection

SiR-Actin Spirochrome Kit (Cytoskeleton, Denver, CO) was used in 0.5 μM and 6-h incubation to stain F-actin for both HeLa cells and HUVECs, and the stained cells were rinsed three times using DPBS and replenished in culture medium before using. Verapamil was used in 10 μM and incubated for 6 h to favor actin staining as manufacturer’s instructions. Transfection on HeLa cells with Lifeact-RFP plasmid (a gift from Dr. Zhu Zeng) was performed using Lipofectamine 3000 Transfection Kit (Invitrogen, Shanghai, China). Cells were used after incubating 24–36 h.

FRAP

Fluorescence recovery after photobleaching (FRAP) was performed to confirm the fast actin recovery dynamics in a cell upon microneedle point loading. Imaging was performed with pinhole as 3 μm, bleaching iteration as 20, and pixel dwell time as 50.42 μs. Photobleaching started right after microneedle loading on the focal plane. First, a 2.5-μm-diameter circle centered on the loading site was set as the region to be bleached. Meanwhile, a ∼3-μm-diameter circle in the absence of cells was set as background (BG) and a ∼5-μm-diameter circle that located on another cell far from the bleached one as reference (REF) for fluorescence intensity normalization. The fluorescence normalization was done by $I_{norm}=\left[\left(I_{REF}^0-I_{BG}^0\right)\left(I_{Bleached}-I_{BG}\right)\right]/\left[\left(I_{Bleached}^0-I_{BG}^0\right)\left(I_{REF}-I_{BG}\right)\right]$, in which the superscript “0” denoted the initial fluorescence intensity right before bleaching. Then the data were fitted using $I_{norm}=\left(1-a\right)\left(1-b{e}^{-k_{off}\times t}\right)$, in which a and b denoted the fractions of immobile and bound actin, respectively, and k_off the unbinding rate constant of actin (31). Half-time, as the index defining actin recovery dynamics, was calculated as τ_1/2 = ln2/k_off.

Mechanical simulation

To unveil the roles of actin cytoskeleton (mainly cell cortex in this work) in cell responses, mechanical simulations were performed using Abaqus 6.14-2 (Dassault, France). The simulations were set as axisymmetric, and CAX3H/CAX4H elements were adopted. The geometry of the model was described in Fig. S1 D as “Cytoplasm” representing cell cortex with thickness δ_c = 1 μm and the nucleus δ_n = 8 μm (15). No slip was allowed on the interface between cell cortex and the nucleus. The indenter was set as analytical rigid (infinite stiffness), and the cell was set as neo-Hookean hyperelastic material and deformable. The stiffness of cytoplasm was set as E_c = 1, 3, or 5 kPa, and the nucleus was 1.5-fold stiffer than cytoplasm with E_n = 1.5, 4.5, or 7.5 kPa (32, 33) for parametric analysis, respectively. The Poisson’s ratio of cytoplasm (cell cortex) and the nucleus were both set as 0.36 (34).

Simulations were performed with even surface stiffness distribution. We first used a sharp-ended probe with tip radius of 100 nm to test the feasibility of the simulations and found that the finite element method was unable to rule out mesh-size dependence or high-strain-induced divergence when the indentation depth was beyond 300 nm (Fig. S2, A and B), as reported in (35, 36). Reduction of indentation depth or increase of tip radius is the common strategy to avoid mesh-size dependence and high-strain-induced divergence (35, 36). In our model, the tip radius was enlarged to 500 nm, and much denser mesh sizes up to 50 nm were applied near the loading site upon exerting the constant force (but not the constant indentation depth) of 5 nN (for all the cases except the one mentioned below) as in PF-QNM experiments (Fig. S2, C and D), even though the tip radius of the PF-QNM-LC probe was around 65 nm. It should be noted that the loading force was set around 2 nN in the condition of E_c = 1 kPa, with E_n = 1.5 kPa to ensure convergence. The simulations on the flat-ended probe were performed as the same as those of the above sharp-ended tips but with a different probe geometry.

Abaqus/Standard was used to run the general static simulations. The bottom of the cell was set as fixed to avoid rigid body motion. Displacement control was used to load the indenter and typical results from specified loading force (e.g., 5 nN) were extracted for analyses. Mesh sensitivity was tested before running the simulations.

Data analysis

Fluorescence images were analyzed using Imaris 7.4.2 (Bitplane, Belfast, UK) and ImageJ (National Institutes of Health, Bethesda, MD). Data fitting was done by MATLAB (The MathWorks, Natick, MA), and AFM QNM data were analyzed using NanoScope Analysis 1.4 and 1.8.

To quantify the extent of actin fluorescence reorganization after point loading upon microneedle or AFM probe, the cell was segregated into upper and lower regions using the red line (Fig. S1 C), and only those fluorescent intensities above the red line were collected to exclude the potential interference from the basal stress fibers in the lower region. The extent of the local actin intensity enhancement was assessed by the ratio of mean actin fluorescence intensity around the loading site I_ROI/mean actin fluorescence above the whole nucleus I_N (to exclude the interference from peripheral strong stress fibers) as I_Relative = I_ROI/I_N (details in Fig. S1, E–G). Note that all fluorescence data were shown in Z-projections except of those from “TS” mode only or for FRAP test.

To quantify cell-surface stiffness, 10 circular rings surrounding the center of loading point were segregated (R₁–R₁₀, R₁ was a circle) with ΔR = 0.75 μm for calculating the distributions of Young’s modulus E from PF-QNM mapping. The center of loading point was chosen based on contrasting topography and 3D height images before and after loading (the loading sites were always near the center of those images because the probe approximately shifts near the center of imaging regions when ramping). The E-value of each point was extracted (n = 260–4600 for each ring), and mean E for each ring was calculated. Self-written customized MATLAB codes were used for ring partition, raw data extraction, and modulus calculation.

All the statistics were run using GraphPad Prism 6 (San Diego, CA). One/two-way ANOVA analysis was performed with Dunnett’s or Tukey’s test (≥3 groups) or two-tailed t-test (two groups) to reveal difference between the different groups.

Results

Cell-surface stiffness increases after point loading

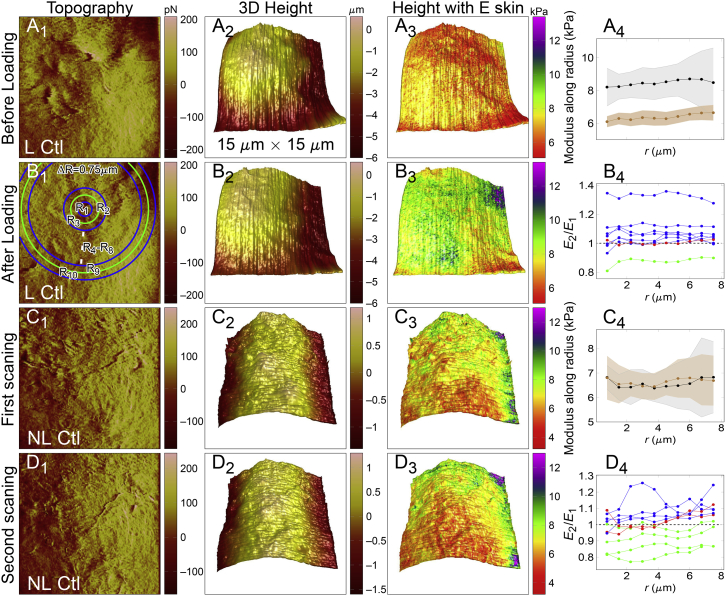
Because the cytoskeleton is one of the most important structural elements for cells to resist physical cues (14, 16, 17), it is reasonably anticipated that mechanical alteration of the cytoskeleton at the loaded region is required to reinforce cellular resistance to applied forces. To investigate the cell-surface mechanical alterations upon local point loading, a PF-QNM mode with PF-QNM-LC probes (37, 38, 39) was used to map surface topography, geometry, and Young’s modulus in a 15 × 15 μm region around the loading site, and all the loading sites were above the nucleus to rule out the potential interference from the substrate (Fig. 1). Here, tens of thousands of force curves were obtained from one scanning and one curve for each pixel. The region was selected and scanned first (Fig. 1 A; L Ctl, loading control), and then point loading was applied near the region center in 5 nN/3 min (loaded for 3 min with force 5 nN). The same region was scanned again just after loading without pause (Fig. 1 B). Negative control without point loading was performed with two successive scannings in the same region (Fig. 1, C and D; NL Ctl, nonloading control). Typical surface topography, 3D height, and Young’s modulus E in scanned cells were presented in the first, second, and third columns of Fig. 1, respectively. The Young’s modulus E at the same scanning region was determined twice and thus denoted as E₁ and E₂ for the first and second scannings. The center of point loading was determined by checking the changes in topography and 3D height images before and after loading, as indicated by the center of rings in Fig. 1 B₁. The ring center was set as the center of image in the cases of NL Ctl group. Representative mean E ± SD of scanned cells for each ring were plotted in Fig. 1, A₄ and C₄, and the ratios of E (= E₂/E₁) of all the cells for each ring were presented in Fig. 1, B₄ and D₄ for respective loading and nonloading cases. The results exhibited that cell-surface stiffness increases after point loading with E₂/E₁ > 1 (blue) for seven of nine cells, E₂/E₁ ≈ 1 (red) or <1 (green) for only one cell (Fig. 1 B₄). In nonloading group, both E₂/E₁ > 1 and <1 for 4 of 10 cells and E₂/E₁ ≈ 1 for two cells (Fig. 1 D₄). Quantitative statistics also revealed a significant cortex stiffening after point loading (Fig. S3).

Figure 1.

Comparisons of topography, 3D structure, and elasticity of HeLa cells before and after point loading. (A and B) AFM scanning within a 15 × 15 μm region was first performed on the top of the nucleus, and AFM tip was then point loaded near the center of the region at 5 nN for 3 min (shortly, 5 nN/3 min) (A). After loading, the scanning at the same region was performed again (B). (C and D) The first AFM scanning was performed from the top of the nucleus, and then the second scan followed at the same region with no pause. The first three columns showed typical topography of the scanned region, 3D height mapping, and Young’s modulus E mapped to 3D height images, respectively. (A₄) and (C₄) in the fourth column show representative E distributions before (brown) and after (black) the 3-min point loading (A₄) or two sequential scannings (C₄). The rule of extracting and computing E was interpreted in (B₁), and more details can be seen in Data Analysis, in which E ± SD for each ring (n = 260–4600 from R₁ to R₁₀) was plotted. (B₄) and (D₄) in the fourth column depict the ratio of E before (named E₁)/after (named E₂) point loading (B₄) or two sequential scannings (D₄). Here, each line represented the data of one cell with E₂/E₁ > 1 in blue, ∼1 in red, and <1 in green. E₂/E₁ = 1 in horizontal dashed lines was used for reference. All data were from two to three repeats. L Ctl, loading control; NL Ctl, nonloading control. To see this figure in color, go online.

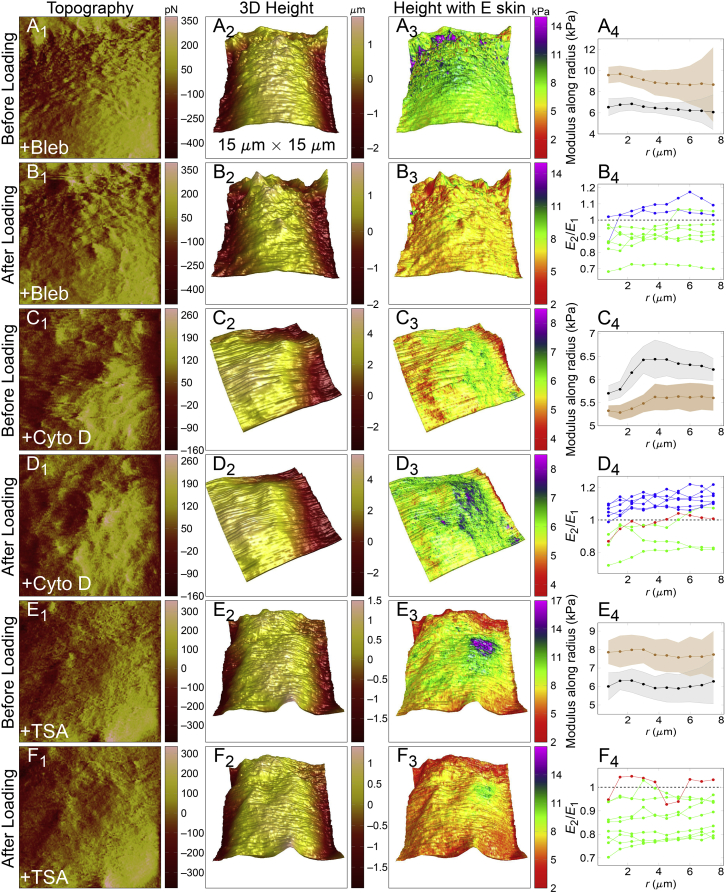
It has been known that cell-surface stiffness is dominated by cortex stiffness (40, 41), and no apical stress fiber is seen in some cancer cells (37). Because actomyosin contractility has been proved to help maintain cortex mechanical strength (15) and actin network integrity plays an important role in cellular responses to different mechanical loadings (42, 43, 44), it is interesting to test whether cortex is able to protect the cell when actomyosin contractility is inhibited or actin network integrity is disrupted. To inhibit actomyosin contractility, HeLa cells were treated with 15 μM Bleb for 20 min, and AFM scanning was then conducted before and after point loading as in Fig. 1, A and B. Results revealed a decrease of surface stiffness after point loading (six of eight cells in E₂/E₁ < 1, and 2 cells in E₂/E₁ > 1, Fig. 2, A and B; Fig. S3), indicating that actomyosin contractility is key to guarantee mechanical protection of the cortex. Next, 15 μM Cyto D was used to treat HeLa cells for 20 min to disrupt actin network integrity. Interestingly, a trend of increased cell-surface stiffness after point loading was recorded with E₂/E₁ > 1 for 6 of 10 cells, E₂/E₁ ≈ 1 for one, and <1 for three cells (Fig. 2, C and D; Fig. S3). Such an enhancement was presumably caused by actin abnormal clustering because Cyto D treatment could induce disruption of the actin network and the formation of actin foci or clumps (45, 46, 47, 48, 49). Also, cells treated with Cyto D lost the ability to recover their mechanical homeostasis after point loading, as can be seen in Fig. S4 D. Thus, mechanical compression to those foci and clumps induced the increase of cell-surface stiffness after Cyto D treatment.

Figure 2.

Comparisons of topography, 3D structure, and elasticity before and after point loading of HeLa cells upon various inhibitors. (A and B) For cells treated with 15 μM Bleb for 20 min, AFM scanning in a 15 × 15 μm region was first performed on the top of the nucleus and AFM tip, then point-loaded near the center of the region in 5 nN/3 min. After loading, scanning at the same region was performed again. Related results of cells treated with 15 μM Cyto D for 20 min or with 100 nM TSA for 24 h were shown in (C)–(F), respectively. The first column shows the topography of the scanned region, the second the 3D height mapping, and the third the Young’s modulus E mapped to 3D height images. (A₄), (C₄), and (E₄) from the fourth column showed the representative E distributions before (brown) and after (black) the 3-min point loading for Bleb, Cyto D, and TSA treatment, respectively. The principle of extracting and computing E was the same as in Fig. 1. (B₄), (D₄), and (F₄) from the fourth column depicted the ratio of E before (named E₁)/after (named E₂) point loading for Bleb, Cyto D, and TSA treatment, respectively, with E₂/E₁ > 1 in blue, ∼1 in red, and <1 in green. Here, E₂/E₁ = 1 as horizontal dashed lines was used for reference. Each line denoted one sample, and all samples were from two to three repeats. To see this figure in color, go online.

To eliminate the potential interference from the substrate, point loading was always performed above the nucleus in this work. This protocol also enabled us to investigate the contribution of physical condensation state of the nucleus in loading-induced surface stiffening because the condensation state and nuclear structure are also relevant to cell responses (50). The effect of chromatin condensation was then tested using TSA treatment in 100 nM for 24 h for HeLa cells, which inhibits histone deacetylase 1 and 2 and induces chromatin decondensation (51). Results also revealed a decrease of cell-surface stiffness after point loading with E₂/E₁ < 1 for eight of nine cells and E₂/E₁ ≈ 1 for another one (Fig. 2, E and F; Fig. S3), implying chromatin decondensation would largely weaken cortex’s protection to the cell. Collectively, mapping in situ cell-surface mechanical property before and after point loading exhibited that the cell cortex is stiffened with higher mechanical strength after point loading, and actomyosin contractility, actin network integrity, and nuclear condensation state were critical to maintain the stiffening response. Thus, the stiffening of the cell cortex after point loading hinted its protection role for the cell from external disruption.

Stiffened cell cortex is modeled as structural protection to mechanical loading

To further explore the protective role of cell cortex stiffening after point loading, the changes in stress, strain, and displacement fields in a model cell were investigated through mechanical modeling using the finite element method. The geometry of model cell was depicted in Fig. S1 D. Cytoplasm (cell cortex) and the nucleus were included in the simplified model, and neo-Hookean hyperelastic material was adopted in the modeling. A pyramid AFM indenter, representing a PF-QNM-LC probe used in AFM experiments with assumptive infinite stiffness, was set on the top of the cell.

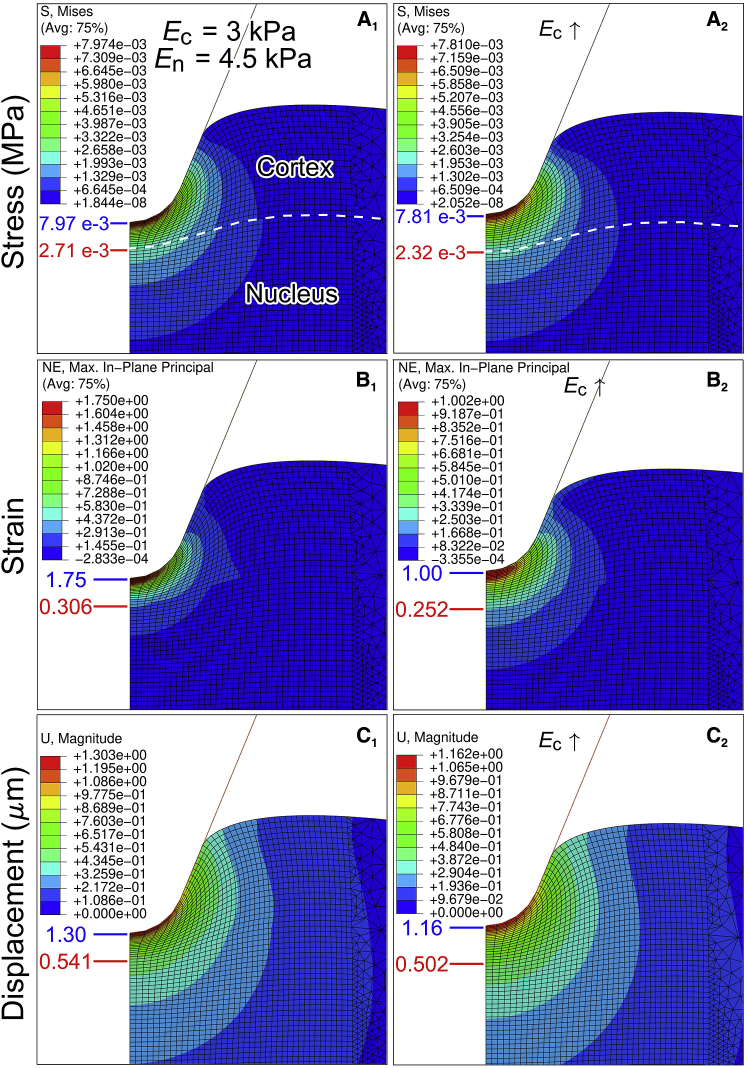
The simulations were performed with tip radius of 500 nm to reproduce comparable loading force (a constant force of 5 nN) and indentation depth of AFM experiments (Fig. S1 D) upon ruling out the mesh-size dependence and high-strain-induced divergence (see details in Materials and Methods). The stiffness of cytoplasm or the nucleus was set as E_c = 1, 3, or 5 kPa or E_n = 1.5, 4.5, or 7.5 kPa (32, 33), respectively, with 1.5-fold greater stiffness for the latter (Fig. 3; Fig. S5). The Poisson’s ratio was set as 0.36 (34). The effect of cortex stiffening was evaluated by increasing the cortex stiffness to 1.35-fold based on the upper limit value of E₂/E₁ in Fig. 1 B₄ when the corresponding nucleus stiffness kept unchanged. Fig. 3 exhibited the von Mises stress σ_von, maximum strain E, and magnitude of deformation U of the deformed cell when loading in 5 nN with the mediate stiffness settings of E_c = 3 kPa and E_n = 4.5 kPa. Compared with the values in the absence of cortex stiffening (Fig. 3, A₁–C₁), those with cortex stiffening resulted in 1.4, 42.9, and 10.8% decrease in maximal σ_von, E, and U for the cortex, respectively, and yielded 14.4, 17.6, and 7.2% decrease for the nucleus (Table 1). The higher reduction of maximum σ_von and E for the nucleus indicated that cortex stiffening strengthened structural protection to the nucleus. Further parametric analyses upon E_c = 1 and 5 kPa, E_n = 1.5 and 7.5 kPa showed similar tendency of structural protection of the stiffened cortex to the nucleus, in which the extent of protection in the case of E_c = 1 kPa and E_n = 1.5 kPa (Fig. S5, A–C) was similar to that of E_c = 3 kPa and E_n = 4.5 kPa (Fig. 3, A–C; Table 1). The reduction extent of maximum σ_von and E was slightly lower in the case of E_c = 5 kPa and E_n = 7.5 kPa (Fig. S5, D–F; Table 1). The impact of different Poisson’s ratios (0.36 and 0.49 (34, 52)) was also evaluated, and the results exhibited a similar trend (data not shown). Interestingly, the results with varied cortex stiffness revealed similar outcomes that the stiffened cortex could largely reduce maximum strain in cell cortex (∼40%) but slightly decreased the stress (<3%, Table 1), implying that the mechanical protection of cell cortex is likely stress-resistant.

Figure 3.

Mechanical modeling of the effect of cortex stiffening on nucleus mechanics. (A–C) Distributions of von Mises stress σ_von, maximum strain E, and magnitude of deformation U. The results of control settings with E_c = 3 kPa and E_n = 4.5 kPa (subscript “c” denotes the cytoplasm and “n” the nucleus) were shown in (A₁), (B₁), and (C₁) and those of cortex-stiffening settings with E_c′ = 1.35 E_c (E_c ↑) and E_n = 4.5 kPa are shown in (A₂), (B₂), and (C₂), respectively. Blue lines and values denote maximum σ_von, E, and U of cortex, and red lines and values were for the nucleus. Loading force was 5 nN. To see this figure in color, go online.

Table 1.

Maximum von Mises Stress σ_von, Maximum Strain E, and Magnitude of Deformation U of the Cytoplasm, Cell Cortex, and the Nucleus in Simulations Using Different Stiffness Settings

Stiffness (kPa)	Symbolsa	S (σvon, MPa)	Max. NEb (E)	U (μm)	Δ (S, NE, U)c
Ec = 1, En = 1.5	C	2.66e−3	1.75	1.30	−2.6%, −43.3%, −10.8%
	C (Ec↑)	2.59e−3	0.992	1.16
	N	9.02e−4	0.306	0.541	−14.7%, −18.6%, −7.8%
	N (Ec↑)	7.69e−4	0.249	0.499
Ec = 3, En = 4.5	C	7.92e−3	1.75	1.30	−1.4%, −42.9, −10.8%
	C (Ec↑)	7.81e−3	1.00	1.16
	N	2.71e−3	0.306	0.541	−14.4%, 17.6%, −7.2%
	N (Ec↑)	2.32e−3	0.252	0.502
Ec = 5, En = 7.5	C	8.44e−3	0.746	0.919	−0.7%, −39%, −12.9%
	C (Ec↑)	8.38e−3	0.455	0.800
	N	2.46e−3	0.143	0.320	−9.3%, −10.5%, −5.6%
	N (Ec↑)	2.23e−3	0.128	0.302

^aC, cytoplasm (cell cortex); N, nucleus; E_c, cortex stiffness; E_n, nucleus stiffness; E_c↑, 1.35-fold increased cortex stiffness.

^bNominal strain.

^cReduced percentage of σ_von, maximum strain E, and magnitude of deformation U after increasing cortex stiffness. Italic values are for the nucleus.

Actin reorganization is induced by point loading

The actin network is responsive to diverse mechanical stimuli, and mechanical protection of the cell cortex after point loading might be a hint of actin reorganization. To investigate actin reorganization more profoundly, an in-house-customized, flat-ended AFM probe (Fig. S1, with tip diameter 1.5–2 μm) was used to load the cells, attempting to cause the stress and strain redistribution more widely than pyramid probes (Fig. S6). Here, the geometrical jump at the periphery of the tip (a ring when considering the model as axisymmetric) could incur a large increase of stress (Fig. S6 A) and strain (Fig. S6 B), even though the change in displacement showed a different pattern.

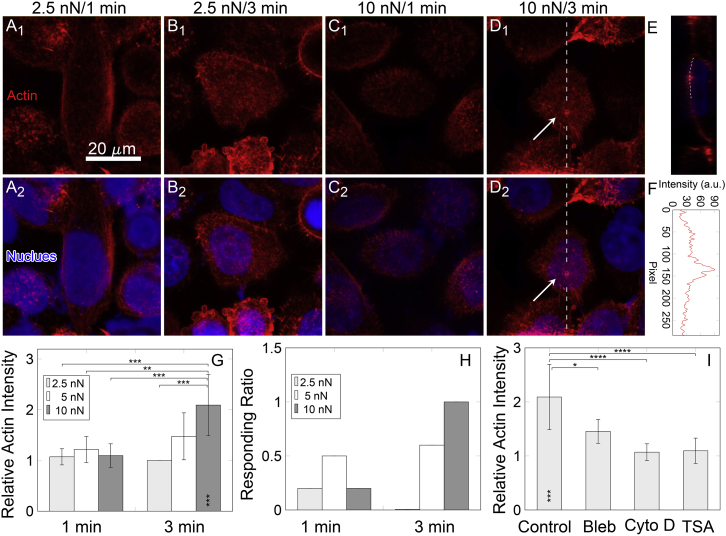
Varied loading forces of 2.5, 5, and 10 nN and durations of 1 and 3 min were applied, and the loading site was also set near the center of cells to exclude the potential interference from basal stress fibers. Typical actin distribution of HeLa cells showed that the actin reorganization was dependent on both loading force and duration (Fig. 4, A–D). Local actin intensity enhancement in the loading site of 10 nN/3 min (Fig. 4 D, as indicated using white arrows) was readily captured than in other loading groups (Fig. 4, A–C). A corresponding cross section along the white dashed line of the loading site (Fig. 4 D) showed obvious fluorescence enhancement (Fig. 4 E) with quantified actin fluorescence intensity peak (Fig. 4 F). Quantitative analyses and comparisons of relative fluorescence intensity (RFI) of actin among all the cases indicated that the longer the loading duration is, the higher local actin RFIs are, even though only the case of 10 nN/3 min group presented a significant difference to other cases. In addition, the RFI increased with loading force at the long duration of 3 min but not at the short duration of 1 min (Fig. 4 G). Consistent results were obtained for the corresponding ratio of the cells with distinguishable enhancement of local actin intensity (Fig. 4 H). Moreover, force dependence of local actin intensity enhancement after point loading using AFM probes was also tested in HF cells with the same loading duration of 3 min. Similar results were found, with the higher loading forces of 5 and 10 nN resulting in a more significant increase of RFI than that of 2.5 nN with full responses for all the tested cells (Fig. S7).

Figure 4.

Loading force and duration dependences of local actin fluorescence intensity of HeLa cell upon AFM assay. Here, force values of 2.5, 5, and 10 nN and loading durations of 1 and 3 min were applied. (A₁)–(D₁) depict the cell responses (actin in red) after loading for 1 min with force of 2.5 nN (2.5 nN/1 min), 3 min with force of 2.5 nN (2.5 nN/3 min), 1 min with force of 10 nN (10 nN/1 min), and 3 min with force of 10 nN (10 nN/3 min). Images for 1 and 3 min with force of 5 nN are not shown for clarity. Stained nuclei (blue) were merged in (A₂)–(D₂). (E) A typical cross section as indicated using white dashed line and white arrow in (D) shows the distribution of local actin intensity. (F) Fluorescence intensity (in a.u.) of actins along the white dotted line in (E) (along the membrane) was extracted and replotted. (G–I) Quantitative statistics of relative fluorescence intensity (RFI) are shown in (G). Percentage of cells with increased local actin intensity is shown in (H). Changes of mean RFI for the cells treated with Bleb, Cyto D, and TSA in 10 nN/3 min are shown in (I). Asterisks inside the bars of (G) and (I) showed significant difference of this bar to the baseline “1.” ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. n = 5–8 for each condition. To see this figure in color, go online.

Similar to those drug treatments in Fig. 1, HeLa cells treated with Bleb, Cyto D, and TSA were point-loaded to test how those drugs affect actin reorganization under a typical loading of 10 nN/3 min. The results exhibited significant decrease of actin reorganization for all three drug treatments, even though the extent of the decrease for Bleb treatment was slight lower than the two others (Fig. 4 I; the related fluorescence intensity images (SiR-actin or Lifeact-RFP-stained) were not shown). Taken together, these data indicated that the protective roles of the cell cortex are positively correlated with actin reorganization underneath the cortex.

Point loading induces rapid enhancement of local actin intensity

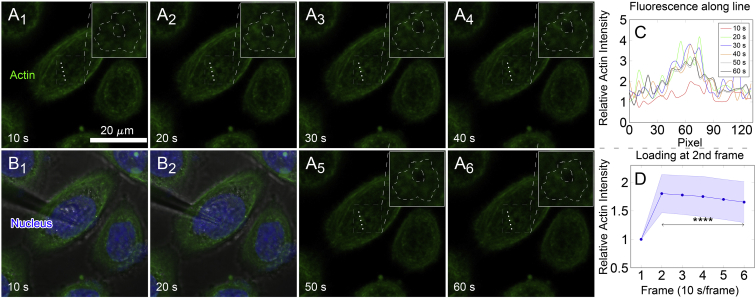
The aforementioned actin reorganization is a time-dependent, dynamic process. Here, actin reorganization dynamics under point loading were further investigated using microneedle with tip radius of around 1.5 μm (Fig. S1 B). After staining nuclei (Hoechst 33342) and F-actin (SiR-Actin) in live HeLa cells, the microneedle was then used to point load the cell from above the nucleus. The feasibility of microneedle loading was first confirmed with the similar observations that the local actin intensity was enhanced upon loading and the drug treatment resulted in decreased RFI (Fig. S8). Thus, time series along with 3D reconstruction protocol (“3DR” + “TS”) was adopted to monitor actin dynamics upon confocal microscopy. Before loading the cell, the focal plane was set at around the middle height of the cell as in Fig. S1 C. The needle was in hover at the first frame (first 10 s, Fig. 5, A₁ and B₁) on the top of the cell and then approached to the focal plane (indentation depth 3–5 μm) at the second frame (10–20 s, Fig. 5, A₂ and B₂). During the course of imaging, local actin intensity was detected as shown in the zoomed region in dash-boxed regions with irregularly dashed curves (Fig. 5, A_1–6). Quantitative RFI along the white dotted line was shown in Fig. 5 C, and a sharp enhancement of actin fluorescence after point loading was detected by comparing the lines of 20–60 s to that of original 10 s. Also, mean RFI of actin inside the irregularly dashed regions in the inserts of Fig. 5 A revealed the sharp enhancement in the second frame and the sequentially slow decay in the followed flames (Fig. 5 D). In fact, the actin reorganization might appear in even faster dynamics as shown in only “TS” mode for both HeLa cells (Fig. S9, A–F) and HUVECs (data not shown). To confirm the fast actin dynamics upon point loading, we further applied “3DR” + “TS” mode with only the upper half of the cell being reconstructed and five to six slices were captured in total with faster scanning velocity of 5 s/frame (Fig. S9, G–J). The results showed a similar trend with those of “TS” only mode (Fig. S9, A–F) or whole-cell “3DR” + “TS” mode (Fig. 5). Additionally, FRAP experiments were also performed to visualize actin dynamics induced by point loading. The results showed that the half-time τ_1/2 of actin recovery upon point loading was significantly faster (45.6 ± 25.7 s) than that in the absence of loading (130.1 ± 53.6 s) (Fig. S9, K–M). This significant speed-up at tens of seconds also gave a hint on the quick actin reorganization dynamics upon point loading.

Figure 5.

Loading dynamics of local actin fluorescence intensity enhancement at the point loading site of HeLa cells upon microneedle indentation assay. (A₁)−(A₆) denote the serial images of actin (green) fluorescent intensity in 1 min with 3D reconstruction every 10 s (thus, six frames in total). The needle was in hover at the first frame (first 10 s) as in (A₁) and (B₁) and then loaded on the top of the nucleus (blue) at the second frame (10–20 s) as in (A₂) and (B₂). Dashed square boxes in (A₁)−(A₆) depicted the region of local actin intensity enhancement as magnified in inserts (the region with local actin intensity enhancement was embraced by an irregular dashed contour, the central hole of which indicated the site occupied by the needle). (C) Spatiotemporal distribution of RFI along the white dotted line in dashed boxes in (A₁₋₆) is shown. (D) Evolution of mean RFI ± SD in the entire dashed regions in inserts is shown. Asterisks showed significant difference among two to six frames to the first one. ^∗∗∗∗p < 0.0001. n = 19 from two repeats. To see this figure in color, go online.

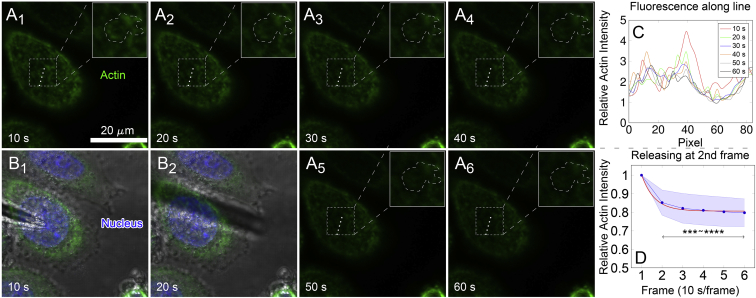
To further elucidate the reversibility of actin reorganization, the recovery dynamics of corresponding actin fluorescence after point unloading was also monitored using the imaging mode of “3DR” + “TS.” After point loading the cell for 50 s, imaging capture was started, and the needle was withdrawn after the first frame (Fig. 6, A_1–2 and B_1–2). RFI of actin along the dotted lines at the loading region presented an abrupt decrease right after needle withdrawal (Fig. 6 C, lines of 20–60 s to original 10 s in red line), followed by the evolution of gradual decay relative to that of original decrease (Fig. 6 D). The recovery curve was fitted using an exponential expression I(t) = I_base + exp(−t/τ₀) (red line), and the resulting half-life time was τ_1/2 = 14.3 s. Longer loading of 2 min 50 s before unloading did not affect the recovery dynamics with similar recovery phases and a comparable half-life time of 14.8 s (Fig. S10). Collective results of local actin organization upon force loading (Fig. 5; Fig. S9) and actin recovery after unloading (Fig. 6; Fig. S10) revealed that the former had faster dynamics than the latter, and the recovery dynamics was less sensitive to loading duration.

Figure 6.

Recovery dynamics of local actin fluorescence intensity of HeLa cells after removing the microneedle from the loading site. (A₁)–(A₆) denoted the serial images of actin (green) fluorescent intensity in 1 min with 3D reconstruction every 10 s (thus six frames in total). The needle had been loaded on the top of nucleus for 50 s before collecting fluorescence. After finishing first frame, the needle was lifted apart and kept in hover as in (B₁) and (B₂). Dashed square boxes in (A₁)−(A₆) depicted the region of local actin intensity enhancement as magnified in inserts (the region of local actin intensity enhancement was embraced by irregular dashed contour). (C) Spatiotemporal distribution of RFI along the white dotted line in dashed boxes in (A₁)−(A₆). (D) Evolution of mean RFI ± SD (blue) in the entire dashed regions in inserts. The mean RFI data was then fitted using an empirical equation, I(t) = I_base + exp(−t/τ₀) (red line), in which I_base denotes the baseline fluorescence and τ₀ the characteristic time. Half-life time of RFI decay was obtained from curve fitting as τ_1/2 = t₁ + τ₀ln2 = 14.3 s when t₁ = 10 s. Asterisks showed significant difference among two to six frames to the first one. ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. n = 9. To see this figure in color, go online.

Discussion

How the cellular cytoskeleton responds to different mechanical loadings has been widely investigated because the cytoskeleton empowers cellular structural integrity and mechanical stability to resist physical disturbances. It also plays crucial roles in various functions of cell migration, division, polarization, communication, endocytosis, vesicle transmission, autophagy, receptor recycling, invasion, etc. (53, 54). There are many mechanical manipulations to investigate the cytoskeletal responses for the cells exposed to different mechanical stimuli such as acoustic, magnetic, or optical tweezers; AFM; microneedle indentation; and micropipette aspiration (55). However, the majority of those mechanical property measurements are based on bulk responses of mechanical features to uncover the statistically averaged properties after a series of measurements, but in situ mechanical property measurements before and after mechanical loading of single cells are still not fully understood. In this study, an AFM assay was conducted to map the cell-surface mechanical property of single cells in situ before and after mechanical point loading. A mechanical model was also proposed to comprehend mechanical property variations upon AFM mapping, and then flat-ended AFM probes and microneedles were used to explore dynamical responses of cytoskeleton after point loading the cell. The results indicated that actin reorganization induced by point loading could act as protection shell with increased mechanical properties, resulting in corresponding decrease of maximum stress (−9 to −15%) and maximum strain (−10 to −19%) to the nucleus. This protective effect (i.e., decrease in stress and strain) was significant, though less enriched to the extent that actin cap favors decreasing maximum stress of the nucleus by 35% when cells undergoes dynamic stretch (16). In our microneedle experiments, actin reorganization upon point loading took place quickly within 10 s. Actually, similar rapid actin reorganization within 10 s had been recorded when loading the cell periphery using a sphere probe (56). Also, the cytoskeleton recovery dynamics after unloading, which has not been well investigated in the existing works, was elaborated in this work (with a half-life time of ∼14 s).

Impacts of dynamic and cyclic loading on actin reorganization are extensively investigated in cell biophysics. It is well known that an in vitro actin network test presents frequency-dependent stress stiffening under dynamic loading (14). Integrin-mediated actin recruitment is also found inside a cell upon dynamic loading using receptor-coated magnetic beads (57). Such actin recruitment results in the enhancement of cell mechanics (58). In similar tests of actin dynamics and cellular mechanics upon static AFM loading (30, 59), the studies exhibit that stress fibers are rearranged in the whole cell, and localized mechanical perturbation can induce responses of the whole cell (59). Specifically, no change of cellular stiffening is found before and after 5–20 nN point loading for 10 min (30). However, the obvious stiffness enhancement is observed after point loading in this work, almost over the entire mapping region of 15 μm in length, even though the actual length of the point loading indentation was around 4 μm (Fig. S4 D). This difference is presumably attributed to the following aspects: 1) mechanical measurement method. We performed in situ mechanical mapping that continuously spans over an entire region of interest centered on the loading site upon PF-QNM mode. In comparison to the Ramp mode with limited and discrete data points, applying the PF-QNM mode offers the larger data sets (two to three orders of magnitude higher) and the more detailed profile of mechanical features with higher spatial resolution. This enables us to define the mechanical alteration around the loaded point; 2) data analysis method. We quantified the in situ mechanical change upon the same region before and after point loading and compared the mechanical difference for each cell alone, but not the averaged changes of all the tested cells in a bulk way. This elaborative data analysis avoids the covering up of detailed features of an individual cell. Moreover, static point-loading-induced actin reorganization was rapid as <10 s. Those additional tests, by reconstructing only half of the cell after point loading, confirmed the above results and indicated that actin dynamics after point loading may even be faster, up to <5 s (Fig. S9, G–M). It is noticed that the fast actin dynamics presented here is different from the slower dynamics under dynamic loading reported in the literature, in which it takes 630 s for actin stiffening and obvious actin recruitment after 1440-s loading with the smaller loading magnitude (58). Collectively, we proposed a novel, to our knowledge, way to in situ probe mechanical changes of cell-surface stiffness before and after point loading with high spatial resolution to uncover cell cortex stiffening around the loading site. We also integrated the live-cell imaging with microneedle point loading to quantify the fast dynamics of actin reorganization (<10 s) upon 3D-reconstructed, time-lapsed images of actin remodeling. In addition, the tests using flat-ended AFM probes reveal that the larger the applied force and the longer the loading time are, the more pronounced actin reorganization is. Meanwhile, computational modeling helps to propose the structural protection from the stiffened cell cortex. Thus, the in situ, high-spatial-resolution mechanical mapping and the combination of experimental measurements and mechanical modeling further our understanding of the transmission of localized mechanical forces into an adherent cell.

Cell density or confluence is known to intervene in many processes such as cell-cell communication, cell survival, and cell responses to external signals (60, 61, 62, 63). Testing the relevance between cell density and cell responses to point loading indicated that local actin reorganization was still captured stably in low seeding density of 1/8 high density (Fig. S11, A₁–F₁), similar to those in high density (Fig. S11, A₂–F₂). Quantitative statistics exhibited similar tendencies in that the higher the loading force and duration, the higher the RFI (Fig. S11 G) and responding ratio (Fig. S11 H) are, regardless of cellular seeding density. These results indicated that a cell locating within monolayer or individually presents similar mechanical responses to point loading, at least qualitatively.

To rule out the potential interference from basal stress fibers and strong actin signal along cell periphery, point loading was always performed above the nucleus (mostly geometrical center of the cell). Thus, it is required to confirm if the nucleus is damaged mechanically. In fact, no matter what the state of actin network integrity is, DNA damage around the point loading site was not evident (data not shown), indicating the self-resistance capacity of the nucleus to external mechanical loadings. Also, the differences of actin reorganization after point loading on cell periphery was tested using the well-spread HUVECs with fully extended periphery. The disruption of stress fibers and retraction of actin network was readily captured around the point loading site using a microneedle (Fig. S12, A–D). Meanwhile, when AFM point loading was right above a stress fiber, the disruption of that stress fiber was able to be captured (Fig. S12, E–G). From this perspective, the responses of the cell cortex and stress fiber were different upon point loading.

The potential impacts of cell viscoelasticity were also evaluated for both AFM and microneedle loading assays. First, we double-checked the cell deformation recovery after AFM point loading. The results showed that the cells had almost recovered to their unloaded states except those of the Cyto D-treated group (Fig. S4), indicating that the role of cell creeping could be neglected for cell elasticity mapping, at least, within this experimental setting. Second, we attempted to outline the cellular viscous features in the microneedle loading tests. For example, the data collected from “3DR” + “TS” mode exhibited that the cellular deformation occurs at the second frame and recovers partially during the followed four frames (Fig. S13 A), indicating the existence of stress relaxation. This relaxing may be the reason for the slow decrease of actin intensity during point loading (Fig. 5 D; Fig. S9, E and F). Meanwhile, mechanical unloading resulted in quick recovery of cellular deformation after 1- or 3-min loading (Fig. S13, B and C), implying the reasonability of neglecting the viscous effect as in AFM point loading tests. It is also noticed that these features are consistent with the results of fluorescence recovery (Fig. 6 D; Fig. S10 D). Collectively, cellular viscous effect is represented by relaxation/creeping during microneedle loading/unloading and also quick cellular deformation recovery when the loading is abrogated by AFM.

For the underlying mechanisms of mechanically induced actin reorganization, it is still an open question as to what the mechanotransductive pathways for cell responses to the local point loading are. For example, a perinuclear actin rim could be formed along with actin filaments around nuclear periphery soaring in <10 s when loading cell periphery using sphere probes in National Institutes of Health 3T3 cells, in which the process is possibly mediated by formin protein (56). Fast scratch upon cell surface induces fast F-actin to G-actin homeostasis, and the force-induced actin nucleation is also mediated by formin protein mDia1 (64). Also, actin nucleation protein, Arp2/3, may be another candidate for the underlying process (65). Mechanical point loading may induce rapid lipid raft disruption and cause the altered actin dynamics (66) because actin tethers raft clusters directly (67). Mechanical loading on the cell surface may also prompt actin recruitment by activating membrane-resided integrin and downstream talin (68). Although this study focused on the features of actin reorganization dynamics and the corresponding cell mechanical property induced by point loading, it is worthwhile to investigate intrinsic signaling in the future. Other technical issues should also be fixed in the future works. One is that the sharp tip geometry caused a divergence problem in our simulations, as reported in the literature (35, 36). To load the cell effectively, a blunted tip with radius of 500 nm was adopted to run the simulations (Fig. 3; Fig. S5) because only in that way could we apply a large indentation force of 5 nN to the cell. In addition, the idealized modeling is to simulate the cortex-stiffening dynamics after constant force loading upon those complicated signal pathways of actin reorganization, which should be a future focus. The motivation for choosing this simplified model is just to elucidate the effect of cortex stiffening on mechanical protection but not the underlying mechanisms of occurrence of cortex stiffening. Another issue is that it is difficult to obtain cell-surface mechanics mapping along with real-time actin reorganization because the PF-QNM-LC probe used for mechanics mapping is not able to load the cell in large force amplitude, and thus the flat-ended probe is chosen to detect local actin reorganization after point loading.

Conclusions

In this work, cortex stiffening of single cells was specialized after point loading the cell in situ, playing a role of structural protection to the cell/the nucleus. Such stiffening was attributed to the localized actin reorganization. This actin reorganization presented a fast dynamics (<10 s) at the vicinity of the loading site. These localized responses of a cell are different from those bulk responses to applied mechanical stimulus in a force- and duration-dependent manner.

Author Contributions

J.H., S.L., and M.L. designed the research and wrote the article. J.H. and W.H. carried out all experiments. J.H. and S.C. performed the simulations and analyzed the data.

Editor: Philip LeDuc.