On the Interpretation of Force-Induced Unfolding Studies of Membrane Proteins Using Fast Simulations

Abstract

Single-molecule force spectroscopy has proven extremely beneficial in elucidating folding pathways for membrane proteins. Here, we simulate these measurements, conducting hundreds of unfolding trajectories using our fast Upside algorithm for slow enough speeds to reproduce key experimental features that may be missed using all-atom methods. The speed also enables us to determine the logarithmic dependence of pulling velocities on the rupture levels to better compare to experimental values. For simulations of atomic force microscope measurements in which force is applied vertically to the C-terminus of bacteriorhodopsin, we reproduce the major experimental features including even the back-and-forth unfolding of single helical turns. When pulling laterally on GlpG to mimic the experiment, we observe quite different behavior depending on the stiffness of the spring. With a soft spring, as used in the experimental studies with magnetic tweezers, the force remains nearly constant after the initial unfolding event, and a few pathways and a high degree of cooperativity are observed in both the experiment and simulation. With a stiff spring, however, the force drops to near zero after each major unfolding event, and numerous intermediates are observed along a wide variety of pathways. Hence, the mode of force application significantly alters the perception of the folding landscape, including the number of intermediates and the degree of folding cooperativity, important issues that should be considered when designing experiments and interpreting unfolding data.

Significance

Single-molecule force spectroscopy, such as atomic force spectroscopy and magnetic tweezers, has proven extremely beneficial in elucidating folding pathways for membrane and other proteins, especially in detecting sparsely populated intermediates. These measurements are challenging from both experimental and computational standpoints, partly because of the demanding computation resources required. Here, we introduce a fast computational tool that can accurately replicate forced unfolding measurements of membrane proteins in a variety of different experimental modes, with a resolution comparable to the highest resolution measurements. We find that the mode of applying force can greatly alter the perception of the folding landscape, an important issue that should be considered when designing experiments and interpreting unfolding data.

Introduction

Single-molecule force spectroscopy (SMFS) is a powerful tool to investigate the dynamics of biomolecules. The ever-expanding repertoire of single-molecule manipulation techniques includes atomic force microscope (AFM), optical tweezers, and magnetic tweezers (MT) (1). These methods have been proven beneficial in detecting sparsely populated intermediates and elucidating unfolding pathways of soluble (2, 3, 4, 5) and membrane proteins (6, 7, 8, 9, 10, 11, 12, 13, 14). Simulations and theory have aided the experimental SMFS studies by revealing the complexity of the folding process (15, 16, 17, 18, 19, 20, 21). These measurements are challenging from the computational standpoint, in part because of the demanding computation resources required to simulate the experimental timescales (17). Coarse-grained models enable more extensive sampling and allow for slower, more realistic pulling velocities and lower forces (20) that better match the experimental studies in providing increased likelihood of observing transient intermediates.

A major challenge in coarse graining is to establish the right balance between accelerating the simulations and retaining the critical features of the system. We have addressed this challenge with our new Upside model, which can fold de novo proteins shorter than 100 residues in cpu-hours (22, 23). To this physics-based model, which uses six atoms per residue and realistic Ramachandran maps, we have incorporated a new knowledge-based membrane burial potential that accounts for the changing level of side-chain exposure to lipids (thereby correcting for the replacement of lipid-protein interactions by protein-protein interactions as helices approach) (24). The membrane burial potential also includes unfavorable energies for unsatisfied H-bond donors and acceptors in the membrane, which allows helices to fold and unfold within the bilayer during the simulations.

Here, we conduct numerous simulations mimicking two high-resolution SMFS unfolding experimental studies. The first is an AFM study of bacteriorhodopsin (bR) (11), a light-driven proton pump with seven transmembrane (TM) helices (25). The second is an MT study of GlpG, a rhomboid intramembrane protease from Escherichia coli with six TM helices (9). We perform hundreds of trajectories to test our ability to reproduce the experimental data and then investigate the effects of pulling under various protocols, including different spring stiffness and operating in constant velocity or constant force mode (Fig. 1). The logarithmic dependence of pulling velocities on the observed rupture forces is also examined to compare our values to those obtained in experiment, which are conducted at lower pulling velocities, as well as to obtain the distance to the transition state (6, 26, 27).

Figure 1.

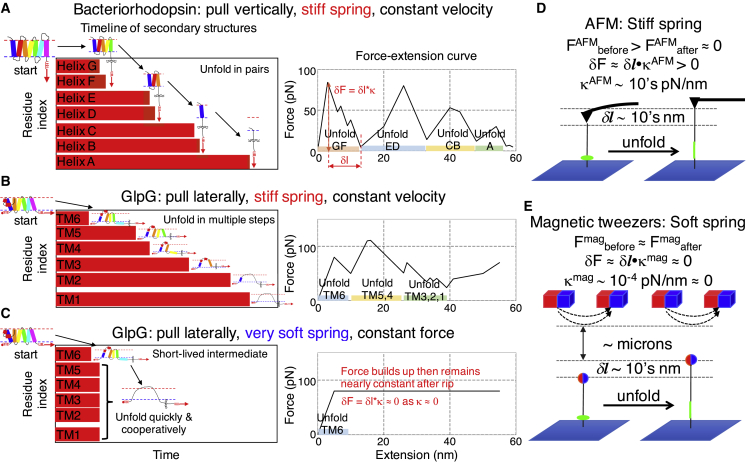
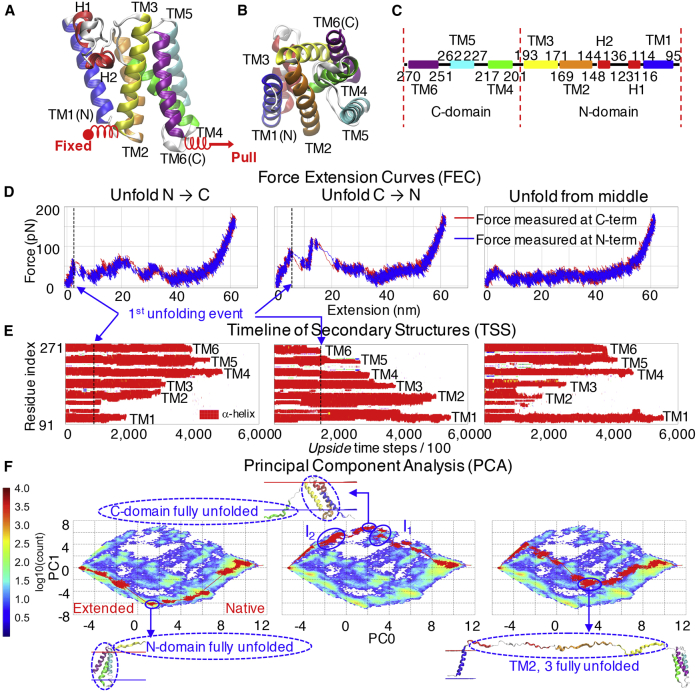
Idealized forced unfolding trajectories for bR and GlpG highlighting how different pulling protocols influence the observation of intermediates. The virtual springs (in red) exert force by moving perpendicular (bR) or parallel (GlpG) to the bilayer surface at a constant velocity. (A and B) After a region unfolds in either pulling geometry, a significant drop in force, δF, occurs with a stiff spring as the unfolded chain length increases by an amount δl. This rapid drop increases the probability that another intermediate will be observed. (C) However, with a very soft spring, force is maintained as δForce = –δl × κ^mag ≈ 0, and the probability of observing another intermediate is lowered. The horizontal red bars represent the unfolding of helical structures versus time and illustrate the timeline for the secondary structures (TSS). For simplicity, GlpG’s two small interfacial helices are not shown. (D and E) The experimental setup with the AFM and MT is shown. Whereas AFM studies often use a stiff spring (10 ∼10⁵ pN/nm), MT studies intrinsically employ a soft spring (∼10⁻⁴ pN/nm) because of the weak spatial dependence of the magnetic field, which varies on the scale of microns (1). Because the force is nearly unchanged after the unfolding event, MT effectively operate in a constant force mode. To see this figure in color, go online.

Simulations of bR unfolding provide an example where force is applied normal to the bilayer on the C-terminus. The simulations largely match the experimental AFM data; for example, many of the same unfolding intermediates are observed (11). The trajectories for the unfolding of the monomeric bR are similar, but not identical to those for the unfolding of the trimeric form. In the MT study of GlpG, in which force is applied parallel to the bilayer to match the experimental geometry, a principal component analysis (PCA) (28) identifies that unfolding occurs stepwise from either end or the middle of the protein when the same spring stiffness is used as in the AFM simulations of bR. This behavior is in apparent disagreement with the experimental study in which few intermediates were found and only the C- to N-terminal unfolding route was observed (9). However, when we better mimic the MT experiment by using a softer spring, the experimental findings are reproduced. This strong dependence on the spring constant highlights that the details of force application can significantly alter the perception of the folding landscape.

Methods

Structure and sequence of bR and GlpG

The bR structure (Protein Data bank [PDB]: 1qhj) and orientation within the lipid bilayer was obtained from the Orientations of Proteins in Membranes (OPM) database (29). The membrane thickness were set to 30.0 nm as identified by OPM. Truncated versions of bR (used in the calibration of the contour length per amino acid) were made from the native structure of bR, and are in the same orientations as in the native bR.

The native structure and orientation within the lipid bilayer of GlpG (PDB: 2xov) were taken from the OPM database (29). The membrane thickness was set to 28.8 nm as predicted by OPM. Two GlpG mutants were made from the native structure using Swiss-Pdbviewer (30): E166A and G261V.

Upside algorithm modified for application of force

Upside is a non-Gō, physics-based model where each residue is represented with five atoms (N, Cα, C, H, O) and a side-chain bead, and with the polypeptide backbone having a geometry given by residue- and neighbor-dependent Ramachandran maps (31). The energy function includes H-bonds, side chain/side chain and side chain/backbone interactions (including helix capping), and a solvation term. The energy function is trained using contrastive divergence. The side chains are represented by multiposition, amino acid-, and directional-dependent beads. Their positional probabilities are given by the probability distribution having the lowest global free energy for all side chains (minimize G = E – TS). The use of an instantly equilibrated side-chain probability distribution (i.e., repacking) calculated at every molecular dynamics (MD) step is, to our knowledge, novel and greatly smooths the energy surface and enables Upside simulations to be extremely fast. Force is applied to the chosen Cα based on the virtual cantilever’s spring constant (κ) and position, which moves at a velocity v. The applied force is computed as –κ × (tip position – Cα position).

In terms of the Upside program, the force function is implemented in the AFMPotential class in Upside (in bond.cpp). The tension function used in the force clamp simulation is implemented in the TensionPotential class in bond.cpp. Its implementation is simpler because there is no need to estimate the time and store the tip position and residue position.

PCA of unfolding trajectories of GlpG

The programs MDTraj (32) and scikit-learn (33) were used to perform the PCA using the Cα-Cα distances below 8 Å in the native state to define contacts. Structures from all trajectories under the same set of simulation conditions were included in the PCA. To derive the principal components (PCs), we used the Cα-Cα distances obtained at T = 1.0 (∼300 K), spring constant κ = 0.05 k_BT/Ų (∼21 pN/nm at 300 K), and a pulling velocity v = 0.001 Å/Upside time step (∼10⁶ nm/s). These PCs are used for the projection at the other conditions for comparison purposes.

Results

Testing of our implementation of force in MD simulations

We first conducted a variety of tests of the new capability of our Upside algorithm (22, 23, 24) (Supporting Materials and Methods) to describe force unfolding. The calibration of the force levels is verified by evaluating the thermal fluctuations (in the z direction) of the tip of the virtual cantilever when attached to different masses. These fluctuations are found to be proportional to the spring constant κ as required by the equipartition theorem: k_BT = κ<z²> (Fig. S1; (34)). In addition, the unfolded segments are well described by a worm-like chain (WLC) model (Figs. S2 and S3 E; (35)). This behavior provides evidence that our pulling rate of 0.001 Å/Upside time step is slow enough that the unfolded polypeptide has enough time to sample conformational space and behave as an entropic spring.

To further examine our force calibration and Upside’s ability to replicate all-atom simulations, we also compared our simulations to those observed in all-atom, explicit solvent studies of already unfolded ubiquitin molecules (Fig. S3; (18)). Upside closely matches the force-extension curve (FEC) and contour length Lc of the all-atom simulations. However, the Ramachandran maps of the (ϕ, ψ) backbone dihedral angles are moderately different over the force range 30–100 pN. Our maps have more β-angles and less polyproline 2 and helical-like angles. Our dihedral potentials are obtained from a coil library (31), which can be used to predict local chain behavior (e.g., NMR residual dipolar couplings (36)), whereas the maps seen in all-atom simulations are known to depend strongly on the particular force field (37). Overall, these tests provide confidence for us to proceed with the study of forced-induced unfolding of membrane proteins.

AFM simulations of bR unfolding

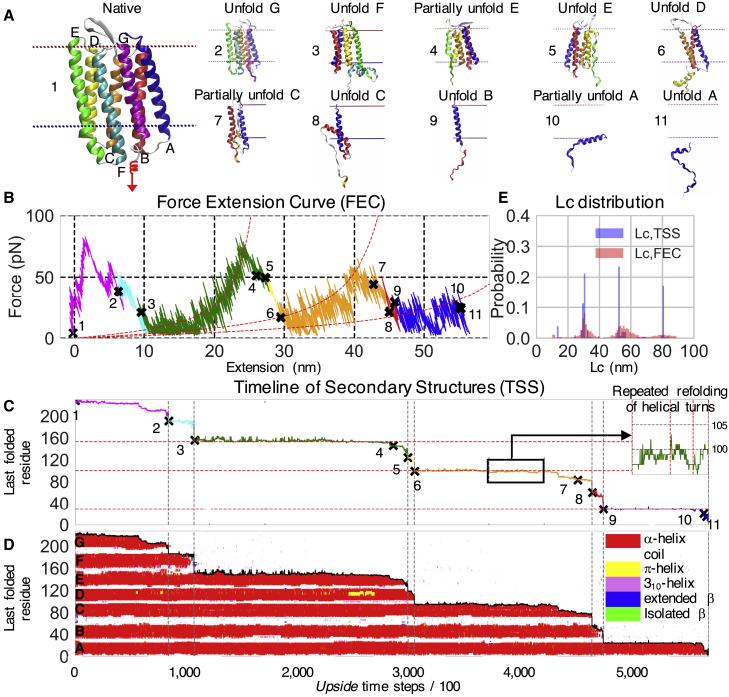
In the experimental AFM study, bR molecules are arranged in a lattice of closely packed trimers embedded in purple membranes, and monomers are removed one by one (11). In our simulations, we also pull on single bR molecules, both as monomers and as trimers in a bilayer. Compared to the experiment, our simulations of trimers lack the protein-protein interactions between adjacent trimers found in the purple membranes; these interactions are replaced with protein-lipid interactions in the simulations. The molecules are located within an implicit membrane bilayer modeled using our new membrane burial potential (24) with force being applied with a virtual spring attached at bR’s C-terminus. Fig. 1 A depicts the experimental setup and introduces the plot of the timeline of secondary structure (TSS), a convenient pictorial representation of the folding simulations that highlights the time evolution of helix unfolding (22). Here, each solid horizontal red bar denotes the presence of a folded helix, with the height reflecting the extent of the folded portion in the helix. Fig. 2 A presents an actual trajectory produced by our simulations.

Figure 2.

A representative unfolding trajectory of bR. (A) Typical unfolding intermediates (Video S1A) are shown. (B) The force-extension curve (FEC) is shown. The red dashed curves are fit to the WLC model, using the contour lengths (Lc) of the most populous states (as seen in C). (C) Shown is the demarcation of index of the most C-terminal residue that remains folded as determined from the TSS plot (D, where each red strip represents a helix and hence identifies the folded regions in the protein). The “X” marks and the associated numbers in (B) and (C) denote reference points of the trajectory in (A) and serve to map the FEC to the TSS. The red horizontal dashed lines in (C) identify the most populous intermediates during the unfolding of the ED and CB helix pairs and of helix A. The green line in the inset in (C) is an example of repeated fraying/refolding of helical ends in the C helix; other examples of back-and-forth folding transitions are presented in Fig. S4. Secondary structure designations follow conventions in the Dictionary of Secondary Structure of Protein (48) in which coil refers to either H-bonded turn, bend and loop, and irregular elements. Gray vertical dashed lines in (C) and (D) define the time points at which a given TM helix has completely unfolded. (E) Probability distributions of the Lc values obtained from the FEC (as in B) fit with the WLC model and directly from the TSS (as in C). To see this figure in color, go online.

The force is increased by moving the spring vertically at a constant velocity normal to the bilayer (z direction) (Figs. 1 A and 2 A; Video S1 A). Force typically accumulates to ∼100 pN before becoming an unfolding event occurs, whereupon a newly unfolded portion of the protein extends in the z direction. As a result, the spring returns toward its equilibrium position and the force drops. The magnitude of the drop, δF, is proportional both to δl, the length of the newly unfolded segment, and κ, the stiffness of the cantilever: δForce = –δl × κ. Each unfolding event signals the presence of an intermediate or the final release of the entire protein from the bilayer. Sequential unfolding events produces a sawtooth FEC curve with the depth of the valleys reflecting how close the cantilever returns to its neutral position. Our simulated FECs recapitulate key features of the experiments, including the extension of the unfolded segments being well described by the WLC model (6, 7, 8, 11) (Eq. S1).

Video S1

Unfolding Trajectories of bR and GlpG Simulations are run with a spring constant κ = 0.05 k_BT/Ų and pulling velocity = 0.001 Å/Upside time step at T ≈ 300 K. A. Force-induced unfolding of bR in the AFM (stiff spring) mode. Force is applied vertically to the membrane surface. B. Force-induced unfolding of GlpG in the AFM (stiff spring) mode, unfolding from N→C, from C→N, and from the middle, respectively. Force is applied laterally to the membrane surface.

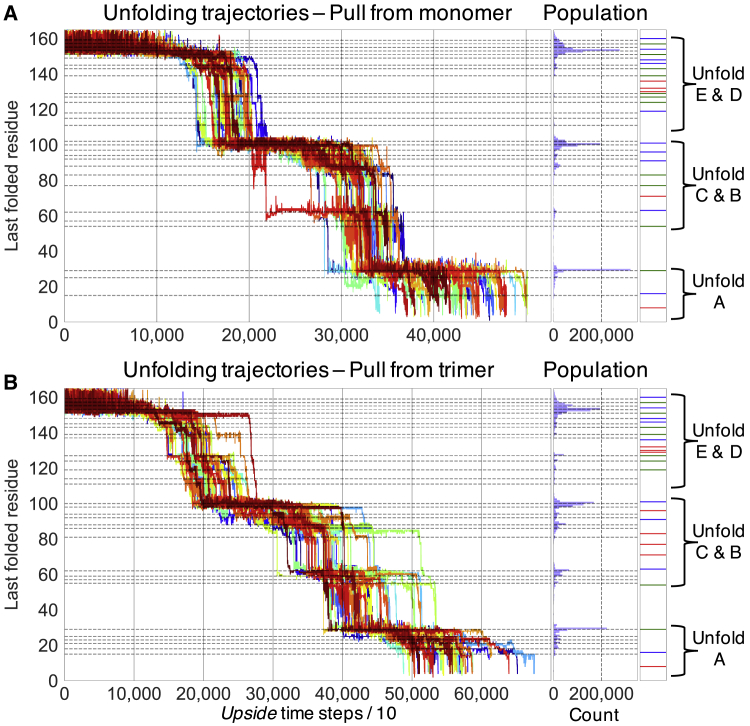
Because the conformation of the protein is known at every time point in the simulations, we may identify the sawtooth pattern as reflecting the sequential unfolding of pairs of TM helices, starting sequentially from the C-terminal helices in the order of GF, ED, and then CB. The pairwise unfolding is a known consequence of the up-down topology of the protein (pulling out a single helix would yield an energetically unfavorable conformation with a single unfolded segment traversing the bilayer) (11). The pairwise unfolding of TM helices is readily observed in the TSS plot.

The first GF helix pair unfolds relatively quickly because the pair is connected directly to the cantilever and the force rapidly accumulates upon movement of the spring. Our simulations lack the capability of including the retinal, which is attached to helix G (38). As the retinal stabilizes the protein (39), our simulations probably underestimate the force that is required to remove helix G. Fortunately, helix G is removed first as the spring is attached to the C-terminus so that the rest of the trajectory should be unaffected and can be reasonably compared to experiments. The FEC for the remainder of the trajectory is dominated by the buildup of force as the unfolded segments are stretched (entropic tension), punctuated with drops in force reflecting the unfolding of the pairs of helices. The final step involves the release of helix A from the bilayer.

The position of the last residue remaining folded at a given time point is readily identified from the simulations. This position is used to construct a plot highlighting the structure of the intermediates, their boundaries, and the lengths of the unfolded segments (Fig. 2 C). The helical regions are plotted as a function of time in the TSS plot (Fig. 2 D). The contour length (Lc) and folded regions also can be inferred from the FEC, as done experimentally. We find that they generally agree with their true values obtained directly from the simulated conformations (as shown in the TSS; Fig. 2 E). This agreement supports the standard experimental assumption that the unfolded region is located only at the C-terminus, whereas the remaining TM helices remain stationary within the bilayer (11). However, the agreement is not absolute because our simulations find that partially folded helices can translate vertically in the bilayer (Fig. 2 A10) or change from α-helix to 3₁₀ helix or π-helix conformations (Fig. S5 A) and even unfold at the amino terminus (Fig. S5 B). These events, although infrequent, are likely to be missed in experiments.

An impressive feature of the experimental AFM study (11) is the ability to observe back-and-forth unfolding and refolding events at the ends of the helices for two to four residues, representing a half to a full helical turn. We likewise observe these back-and-forth transitions between microstates in all three major regions (ED, CB, and A helices) (Figs. 2 C and 3; Fig. S4).

Figure 3.

Unfolding trajectories and intermediates of bR. Unfolding behavior of (A) monomeric and (B) trimeric bR is shown. Unfolding trajectories plotted according to the index of the last folded residue (left), the corresponding population distribution (middle), and the intermediates found in the experiment (11) (right) are shown. The time spent at each position is histogrammed (blue bars) and fit using multiple Gaussians to identify the population and position of the simulated intermediates (designated with the black dashed lines in the left and middle regions). The blue, green, or red solid lines (right) denote intermediates exactly matching the experiment, matching within one residue, or not observed in our simulations, respectively. Of the 45 trajectories conducted on trimeric bR, helix A unfolds by itself in 43 trajectories. Of the 90 trajectories of monomeric bR, helix A unfolds by itself in 48 trajectories. In the rest of the trajectories, more than 2 TM helices are pulled out of the membrane in the last observed unfolding event (these abbreviated trajectories are not shown for simplicity). Helix A is more stable in the trimers because it can interact with the other two bR molecules. Therefore, more helix A intermediates are observed (Table S2), and the mean unfolding force for the major intermediate in helix A is higher (Table S1). Note, the last four residues (I4, Q3, A2, E1) are not in the PDB: 1qhj file and therefore are not included in the simulations and the comparison. To see this figure in color, go online.

Unfolding intermediates of monomeric and trimeric bR

To further test the agreement between our simulations and the AFM measurements (11), we compare the populations and structures of the intermediates. Following the procedure employed for soluble proteins (3), the population distribution of intermediates obtained from the TSS plot are fit with multiple Gaussian functions, assuming a width of one amino acid (Fig. S6). More and longer-lived intermediates are observed in simulations of trimeric versus monomeric bR (Fig. S8 G; Tables S1 and S2). Presumably, this difference is due to the additional protein-protein contacts in the trimer. In the simulations of monomeric (trimeric) bR, we identify 29 (32) intermediates with 15 (15), 11 (11), and 3 (6) having folded-unfolded boundaries in the ED, CB, and A helices, respectively (Fig. 3; Table S2). Among this group of 29 (32) intermediates, 11 (9) exactly correspond to 1 of the 26 experimental intermediates and another 10 (10) are within 1 residue of an experimental intermediate. For both the monomer and trimer, we fail to identify 5 intermediates (3 near the bottom of the E helix, 1 in the middle of the loop connecting the CB helices, and 1 at the bottom of the A helix) while identifying 8 (13) that are not observed experimentally (Table S2).

The disparity in identifying intermediates may reflect real differences, such as errors in our energy function, pulling speed, effective temperature, or the study of isolated trimers rather than the full lattice of trimers. However, the different protocols for identifying intermediates, either the use of the experimental FEC or the simulated TSS, can also affect the determination of the intermediates. For example, we observe that the protein can have unfolded regions between folded regions (Fig. S5 B), a possibility that is not considered in the experimental analysis.

Force levels and pulling velocities in bR simulations

Generally, the use of a fast pulling speed or a soft spring constant can produce an FEC where the applied force has insufficient time to relax back to zero after an unfolding event and the trough-to-peak depth in the sawtooth pattern is reduced. Our study sets the velocities of the cantilever and spring constant to 0.001 Å/Upside time step (∼10⁶ nm/s; see Estimating Upside Temperature and Time Scale in Supporting Materials and Methods) and 21 pN/nm, respectively, chosen partly so that the simulations match the experimental sawtooth pattern (11) and to be computationally feasible. The experimental and simulated FEC traces are similar over the range of experimental velocities and spring constants of 30–3000 nm/s and 13–58 pN/nm, respectively. To further test whether our pulling velocities are appropriate for making comparisons to the experimental data, we decreased our speed by a factor of 10. This change has minimal effect on the depth of our sawtooth pattern except at the fastest pulling speeds (Fig. S8; Table S1), supporting the view that we employ sufficiently slow pulling speeds to enable the unfolded regions to equilibrate.

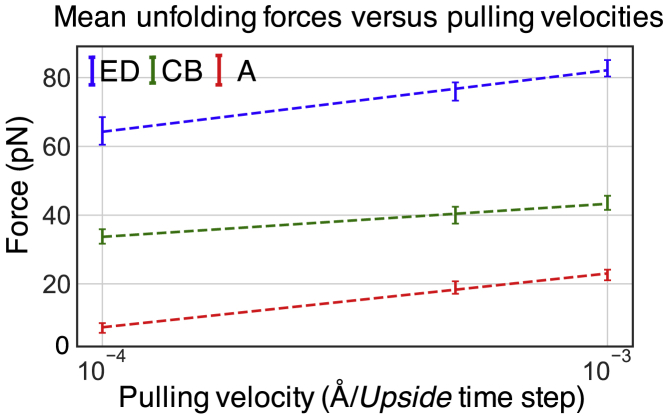
In the simulations, the major intermediate of the helix pair ED exhibits an average simulated unfolding force of 88.7 ± 3.0 and 83.4 ± 2.4 pN for bR in trimeric and monomeric forms, respectively (Table S1). These values are close to the experimental value of 94 ± 1 pN (11). However, our pulling velocities are three to four orders of magnitude faster, which should result in higher rupture forces. According to the Bell-Evans model (26), the most probable rupture force, F_mp, is partly determined by the pulling velocity v and the width of the potential barrier $\mathit{\Delta }{x}^{\ne }$ (the distance from initial state to transition state where the separation distance is the reaction coordinate), as well as the natural transition rate k₀ according to $F_{mp}={\left(\beta \times \mathit{\Delta }{x}^{\ne }\right)}^{-1}ln(\beta \times \mathit{\Delta }{x}^{\ne }\times \kappa \times v/k_0)$ where β = (k_BT)⁻¹, assuming the potential barrier does not move under force (6, 27). By fitting the mean unfolding forces with log(pulling velocities), the barrier distances for helix pairs ED, CB, and helix A (Fig. 4; Table S7) are obtained. We observe the logarithmic relationship for the three unfolding events involving helix pairs ED, CB, and helix A (Fig. 4). This finding indicates that our pulling velocity is slow enough that force is still linear with log(velocity). At the experimental pulling speed, the extrapolated values of the rupture force are 19.1, 9.4, and −32 pN for the ruptures of the ED, CB, and A helices, respectively, whereas the experimental values are 94, 49, and 62 pN. This discrepancy could be due to an error in our conversion of the Upside time step to real time (see Supporting Materials and Methods), our membrane potential being too weak, or other inaccuracies in the Upside energy function. For example, doubling of the membrane potential significantly stabilizes the last helix, helix A, in the membrane bilayer and increases the rupture force of helix A from 22.6 to 38.9 pN (Table S1).

Figure 4.

Mean unfolding force and pulling velocity. The mean unfolding forces of the major helix pairs ED, CB, and helix A (Table S1) are computed from the trajectories at each pulling velocity. A logarithmic dependence of the unfolding force on the pulling velocity is observed in the range 0.0001–0.001 Å/Upside time step (∼10⁵–10⁶ nm/s). The distributions of the mean unfolding forces are shown in Fig. S7, and the transition distances are provided in Table S7. The error bars indicate the standard deviation of the rupture forces at each velocity. To see this figure in color, go online.

GlpG can unfold along multiple routes with well-populated intermediates

Pulling simulations on GlpG were performed using the same pulling velocity and spring stiffness as used in the bR simulations. But, to match the experimental pulling geometry used in the MT apparatus, the force was applied horizontally, pulling on both GlpG’s N- and C-termini that are located on the same side of the bilayer (Figs. 1 B and 5 A; Video S1 B). Specifically, the C-terminal spring is translated horizontally to the membrane surface to generate force parallel to the surface, whereas the N-terminal spring is held fixed (similar outcomes are produced when the N-terminal spring moves at the same velocity and the C-terminal spring is fixed; Fig. S12 A; Table S3).

Figure 5.

Unfolding pathway diversity for GlpG. (A and B) Side and bottom views of GlpG (PDB: 2xov) and (C) secondary structure and definition of N- and C-domains are shown. (D–F) FEC, TSS, and PCA plots illustrate unfolding beginning from the N-terminus (left; 14th trajectory from Fig. S9A), the C-terminus (middle, first trajectory in Fig. S9D), and the middle (right, 41st trajectory in Fig. S9C). Videos of the three unfolding trajectories can be found in Video S1B. In the FEC plots (D), the forces generated by the two springs (blue and red lines) are very similar, indicating that the force has sufficient time to equilibrate across the protein, a necessary condition for meaningful comparisons to experiment, except for an occasional small time lag at one end of the protein just when an unfolding event occurs at the other end of the protein. For instance, when the TM1 helix unfolds first, the force measured at the N-terminus drops faster than that at the C-terminus ((D) left, at extension ∼5 nm), whereas the force at the C-terminus drops faster when TM helices close to that end unfold first ((D) middle, at extension ∼10 and 20 nm). Unfolding pathways are defined by the sequence order of the unfolding of TM helices. In (F), the PCA heat map is evaluated from 50 trajectories. Red curves depict an unfolding pathway from the native to the fully extended state. PC0 relates to the end-to-end distance, whereas PC1 relates to whether unfolding begins from one end of GlpG or the other. The N→C and C→N pathways diverge first (proceeding along the lower and upper edge of the heat map, respectively) as the protein expands under force. The structures along the two pathways become the most distinct at the bottom and top of the heat map, where either the N- and C-domain are unfolded along the N→C and C→N pathways, respectively. Then, the two pathways converge as more TM helices unfold. The two blue circles in the middle subplot of (F) replicate the two experimentally observed unfolding intermediates I₁ and I₂, formed by the unfolding of TM6 and TM5, followed by TM4 and TM3, respectively, with the final step being the unfolding of TM2 and TM1 (9). To see this figure in color, go online.

Figs. 5 E and S9 illustrate the diversity of unfolding pathways, including examples of unfolding starting at either terminus or, more rarely, starting with the central helices. Unfolding from the N-terminus (“N→C pathway”) typically proceeds sequentially for three helices: TM1→TM2→TM3 followed by the unfolding of TM4, TM5, and TM6 in any order (Figs. 4 C and 5 E, left; 29 of 50 trajectories in Figs. S9 A and S10). Unfolding from the C-terminus (“C→N pathway”) typically proceeds sequentially: TM6→TM5→TM4→TM3→TM2→TM1 (Fig. 5 E, middle; 3 of 50 trajectories in Figs. S9 D and S11). Other pathways are shown in Fig. S9.

A PCA often is employed to interpret high-variance collective protein motions in simulations such as those observed along folding pathways (28). Internal coordinates, such as interresidue separations, are a poor separation, (e.g., two very different structures can have the same N-to-C separation depending on whether the unfolding initiates at the N- or C-terminus). Hence, we used the native Cα-Cα contacts to derive our PCs (Fig. 5 F).

The results of the PCA are plotted as a population heat map for the first two PCs, PC0 and PC1. The interpretation of PCs can be challenging because these mathematical constructs typically do not refer to any specific real-space conformation or motion. For the unfolding of GlpG, however, we empirically find PC0 is related to the lateral expansion of the protein, whereas PC1 is related to whether unfolding occurs from the N-terminus, the center, or the C-terminus. Each of these three scenarios is illustrated with a single unfolding trajectory (Fig. 5 F, thin red line in the three maps). The unfolding pathway begins from the right, fully folded side and proceeds to the left, fully extended side. For unfolding from the N- or C-terminus, respectively, the path goes along the lower edge (Fig. 5 F, left; Fig. S9 A) or the upper edge (Fig. 5 F, middle; Fig. S9 D). For unfolding beginning in the middle of the protein, the pathway traverses the center of the map (Fig. 5 F, right; Fig. S9 C). Beyond highlighting the pathway heterogeneity, the PCA heat maps also emphasize that unfolding may occur through ∼10 intermediates (Figs. S10 and S11), including both the intermediates observed in the MT experiment (I₁ and I₂ in Fig. 5 F, middle) (9).

The dependence on spring velocity and constant were also examined, as done with bR. The reduction of the velocity by 10-fold or the spring constant by 5-fold had minimal effect on the PCA plots (Fig. S12 A). These results support the robustness of our method. We are unable to readily apply Bell-Evans-style correction to determine the disruption forces extrapolated to the experimental pulling velocity because of the diversity of unfolding barriers in the GlpG landscape. Nevertheless, the correction should be similar to that for bR.

More stable N-domain of GlpG is more likely to unfold

Unexpectedly, we find that the more stable N-terminal domain (40) has higher tendency to unfold before the C-terminal domain (Fig. S9; Table S3). This counterintuitive observation arises from the differential hydrophobicity of the TM helices (41). TM2, TM5, and TM1 are the most hydrophobic, whereas TM6 is the least. Although hydrophobicity promotes helix insertion into the bilayer (stage I folding (42)), it has the complementary effect of promoting dissociation of helices from the other hydrophobic helices in the bilayer because these helices are “well solvated” by the lipids in the bilayer. In fact, TM5 is completely dissociated from the other TM helices in the crystal structure of GlpG (43). The dissociation of TM1 and TM2 is energetically less costly than the dissociation of TM6 and TM4 because the latter process exposes polar and charged groups (Fig. 6 A; and the near-native and N1 intermediates in Fig. S10 C).

Figure 6.

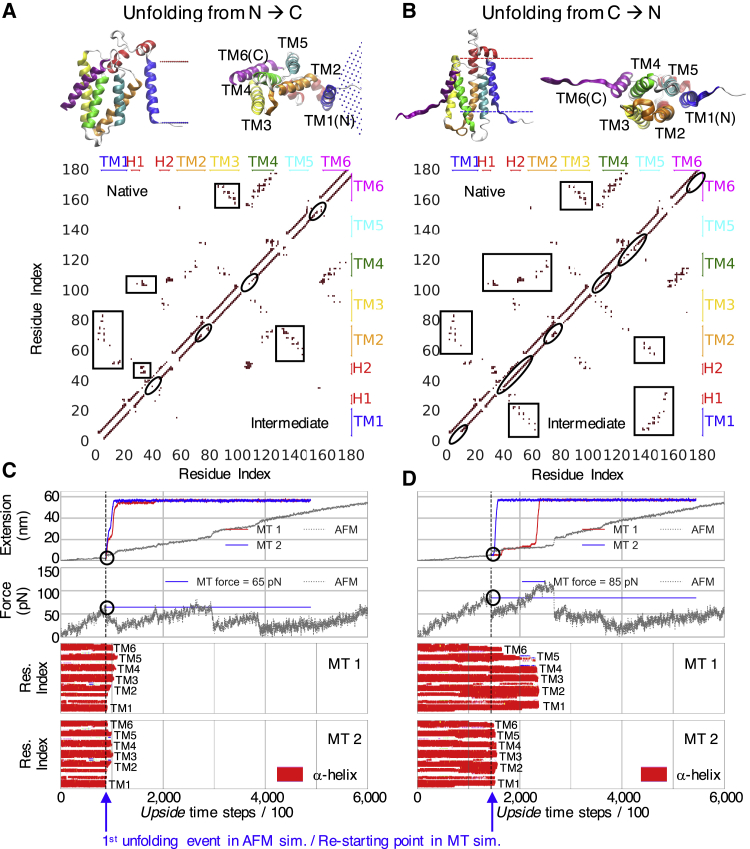
GlpG simulations using a soft spring, as in a MT measurement. (A and B) Structures and contact maps of the major unfolding intermediate on the N→C and the C→N pathways are shown. The intermediates selected for restarting simulations from the N→C and the C→N pathways correspond to the near-native intermediate in Fig. S10C and the C2 intermediate in Fig. S11C, respectively. Differences in contacts between the native state and the intermediates are marked by black rectangles and ellipses (along the main diagonal). The length of the maroon lines near the main diagonal identifies the length of the folded portion of the helices (e.g., TM6 in the N→C pathway is present in the first intermediate but is partially unfolded in its counterpart along the C→N pathway). (C and D) Shown are extension and force profiles over time, along with TSS plots for two examples of unfolding trajectories (denoted MT1 and MT2). After an initial force loading period, the protein begins to unfold (blue arrows), and the force is held constant for the rest of the trajectory reflecting the use of a soft spring. For comparison, the extension and force profiles (gray) for the N→C and C→N trajectories are shown for a simulation conducted using a stiff spring (denoted AFM) where the force builds up and relaxes after unfolding events (Fig. 5). To see this figure in color, go online.

In addition, the 34-residue segment between TM1 and TM2 is of sufficient length to allow TM1 to dissociate from the other TM helices and remain upright in the bilayer. However, the linker between TM5 and TM6 has only 10 residues, so TM6 must tilt in the bilayer or the GlpG structure must distort for TM6 to dissociate. As a result, the TM6 helix does not readily dissociate on the C→N pathway; rather, the ends of the TM1 and TM6 helices unfold first (Fig. 6 B; C2 intermediate in Fig. S11 C). These multiple factors explain the preference for unfolding to occur along the N→C pathway.

Cooperative unfolding of GlpG occurs with a force clamp and a soft spring

The extensive pathway diversity and large number of intermediates found in the simulations discussed in the previous section were not observed in the experimental MT study. That study also concluded that unfolding initiates only from the C-terminus and goes through two intermediates (9). We propose that the differences between experiment and the simulations shown in the prior sections are primarily a result of a difference in the mode of force application, possibly compounded by limited experimental time resolution.

The GlpG unfolding simulations presented above mimic a typical AFM measurement in that force builds up as the cantilever is translated, followed by a rapid drop in the force after each unfolding event as the newly unfolded region provides sufficient slack to allow the cantilever to relax back toward its equilibrium position: Force_after = Force_before – δl × κ ≈ 0 (Fig. 1, B and D). The rapid relaxation of force reduces the probability that any other part of the protein unfolds in the same kinetic event. Consequently, unfolding occurs with multiple distinguishable intermediates, and the FEC has multiple peaks and the distinctive sawtooth pattern.

In a typical MT experiment, the pulling force increases as magnets move toward the bead, which is attached to the protein. However, once a portion of the protein unfolds, the force on the bead is largely unchanged because the magnetic field varies on a scale of microns, whereas the bead moves only tens of nanometers as a protein segment unfolds (Fig. 1 E). Hence, the bead still resides in nearly the same magnetic field as it did before the unfolding event and it therefore experiences the same force. As Force_after = Force_before – δl × κ ≈ Force_before, or δl × κ ≈ 0, the MT intrinsically function as a very soft spring (Fig. 1, C and E). Consequently, the force level present at the beginning of the first unfolding event is retained for the remainder of the measurement (as found in Fig. 3 a in (9)).

At this elevated force given by the level at the first rupture event, the protein often is pulled apart in a few or even a single all-or-none process. Hence, few intermediates are observed. Generally, folding appears more cooperative with softer springs. This effect is most pronounced for “brittle” proteins where the first unfolding event requires a higher force than the subsequent unfolding events so that only the first event is kinetically distinguishable from the unfolding of the rest of the protein.

Appreciating this effect of having a soft spring, we mimic the MT experiment by employing a modified force clamp protocol (Fig. 1 C). Force is gradually increased until the first unfolding event, whereupon the force is held constant for the remainder of the trajectory (Fig. 6, C and D). Using this protocol, the N→C and C→N pathways are investigated in detail by restarting 40 total simulations from the structure present right at the point of first rupture on each route (1 structure for 20 N→C trajectories (Fig. 6 A) and another structure for 20 C→N trajectories (Fig. 6 B). The ruptures occur at a force of 65 and 85 pN, respectively, for the N→C and C→N pathways.

As anticipated, the unfolding of GlpG under this modified protocol of force clamp is more cooperative along both unfolding pathways as compared to those pathways when a stiff spring is used. After the first unfolding event with the softer spring, all the remaining helices are seen to unfold almost immediately and nearly in unison (Fig. 6, C and D, all red bars disappear at the same time in the TSS, unlike the behavior in Fig. 5 E). Additionally, fewer intermediates are seen, and they are more transient especially along the N→C unfolding pathway.

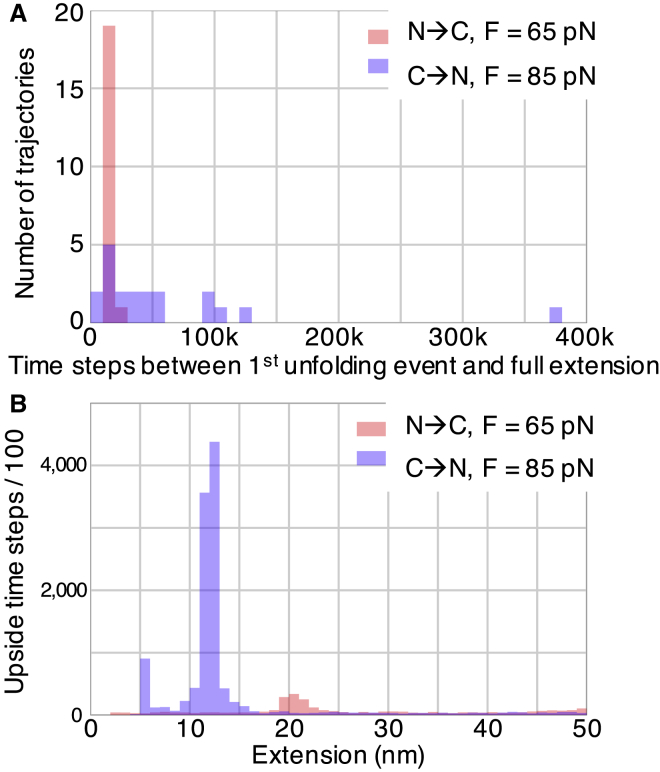
For the 20 trajectories conducted on each of the N→C and C→N pathways, we observe 1 major intermediate (at extension of ∼20.5 nm) and 2 major intermediates (at extensions of ∼5.5 and ∼12.5 nm), respectively (Figs. 6, C and D and 7 B). The difference between the use of a stiff and soft spring is readily apparent in the PCA heat maps in which the soft spring measurement yields only one well-populated intermediate on either the N→C or C→N pathway, and little population appears elsewhere on the PCA heat map (Fig. S12 C). In contrast, the measurement using a stiff spring populates dozens of intermediates across the entire map (Figs. 5 F, S10 A, S11 A, and S12 A).

Figure 7.

Lifetime and position of GlpG intermediates observed when using a soft spring for 40 simulations. (A) The number of trajectories as a function of lifetime between the first unfolding event and the fully extended state for the 20 unfolding trajectories originating from either end of GlpG are shown. (B) The corresponding aggregate time spent at each extension in an intermediate is shown. Each peak represents an intermediate (one is observed for the N→C pathway and two for the C→N pathway). The fully unfolded state has an extension above 50 nm, which defines the upper limit of the x axis. To see this figure in color, go online.

Furthermore, the behaviors of the simulations along the two pathways differ in a manner consistent with experiments. Simulated intermediates formed on the C→N pathway live longer than those on the N→C route (Fig. 7). After the first rupture and formation of an intermediate on the N→C unfolding pathway, the intermediate unfolds in less than 20,000 time steps for 19 of 20 simulations, whereas on the C→N unfolding pathway, the intermediate does not unfold even within 50,000 steps for 7 of 20 simulations despite the elevated level of force (65 vs. 85 pN, respectively; Fig. 7 A). Consequently, more intermediates are observed on the C→N pathway despite the fact that more molecules unfold though the N→C route (Fig. S9; Table S3).

The use of a 60 Hz CCD camera in the experiment (9) also could result in the unfolding of GlpG appearing more cooperative with a preference for unfolding beginning from the C-terminus. At this relatively slow frame rate, intermediates populated for less than ∼16 ms could elude detection. Because the intermediates are longer lived on the C→N pathway, they are more likely to be detected than those on the N→C pathway. Thus, the use of a slow camera could increase the apparent degree of folding cooperativity and introduce a bias for observing intermediates on the C→N route.

Other SMFS modes applied to GlpG

To explore other SMFS modes of unfolding, we pulled on GlpG in the same manner as in the AFM simulations of bR with force being applied vertically with a stiff spring attached to either the N- or the C-terminus. As with bR, we observe the characteristic sawtooth pattern (Fig. S14). However, the TM helices of GlpG are not as hydrophobic as bR’s (41), so GlpG’s TM helices are pulled out at lower force (∼60 pN for the first pair of helices versus ∼80 pN for bR). TM1 is pulled out in a distinct event in 4 of 20 simulations when the force is applied to the C-terminus, whereas TM6 is pulled out in 3 of 20 trajectories when the force is applied to the N-terminus. In the rest of the trajectories, more than one TM helix is pulled out in the same final unfolding event. Moreover, TM6 sometimes unfolds before TM5 when the N-terminus is pulled (Fig. S14 B), a behavior consistent with TM6 being intrinsically unstable within the bilayer (41). This inversion in the order of unfolding would be hard to infer from the FEC because it violates the assumption that the helices unfold according to their sequence order. The difference between this AFM mode and other modes well illustrated in the PCA plots, which display a series of intermediates going along the edges of the heat map (Fig. S12 B). Because no corresponding AFM experiment has yet been conducted with GlpG, these simulations provide testable predictions. Studies of other SMFS modes and the effects of mutations and temperature can be found in the Supporting Materials and Methods.

Discussion

We have modified our fast Upside MD algorithm (22, 23) to include our new membrane burial potential (24) to study the forced unfolding of bR and GlpG in a variety of different modes of force application. Upside models the polypeptide backbone with five atoms and residue-dependent Ramachandran maps. Each type of side chain is represented with a multiposition, orientation-dependent bead. The side chains are repacked with a probability distribution that minimizes their free energy using belief propagation at every MD step. The great acceleration in speed afforded by this method allows us to run hundreds of simulations and conduct PCA to map out the energy surface. Unfolding trajectories of membrane proteins as large as trimeric bR are generated in less than 10 cpu-days with results that agree well with experimental studies (Figs. 2 and 3; (11)). That Upside captures many of the experimental features and identifies most intermediates is a positive indication that a reasonably accurate representation of the system has been achieved, including having a membrane burial potential with an appropriate energetic penalty for unfolding helices within the bilayer.

A major finding of our study is that the mode of force application and the strength of the spring strongly affect the observed details and apparent unfolding cooperativity. The use of a stiff spring constant κ (and one with a very fast response time) enables the system to rapidly lower the force right after an unfolding event having extension δl, as Force_after = Force_before – δl × κ < Force_before. Because the force on the rest of the protein has rapidly dropped, little additional unfolding occurs until the force is increased again. Hence, many intermediates are likely to be observed, and the FEC will have a distinct sawtooth pattern. With a soft spring, however, the force after an unfolding event remains at the same elevated level even after the extension of the chain because of unfolding, as Force_after = Force_before – δl × κ ≈ Force_before. Because subsequent species often are less likely to withstand the same high level of force as more folded species can (such as the native protein), unfolding will occur with few distinct steps and high apparent cooperativity (Fig. S12, C and D).

Conceptually, the applied force also can remain high after a rupture if the length of the already unfolded segments is sufficiently long that the chain (and whatever handles are used to connect the protein to the instrument) can act as weak entropic springs. This possibility will reduce the effective spring constant of the entire system. This effect becomes more pronounced in the later stages of unfolding because the length of the unfolded regions becomes increasingly longer with each unfolding event. This bias may reduce the probability of observing late intermediates.

Membrane proteins can be unfolded by either pulling vertically at one terminus or laterally at both ends. Each mode explores different regions of the energy surface (Fig. S12). Pulling vertically produces a more deterministic unfolding route because TM helices often unfold sequentially and in pairs, whereas the remaining portion of the protein largely remains intact. Pulling laterally tends to break interhelical contacts at a variety of locations, which leads to gross structural rearrangements even before any TM helix unfolds.

Few SMFS simulations have been conducted for membrane proteins, partly because of the computation resources required. One all-atom MD study (17) identified a number of key residues that resist mechanical unfolding in the intermediate states probed by the experiment (11), although its pulling speed (1–50 m/s) was too fast to observe WLC behavior for the unfolded segments. A 2016 CG study used the same pulling rate as ours (∼10⁶ nm/s) and found WLC behavior (20). Although many features are similar between this and our studies, we observed more intermediates (Table S2).

A recent GlpG force-induced unfolding study concluded that the two-stage membrane folding model (44) is overly simplistic because isolated helices can coexist with a folded domain, and all the helices do not have to be in the bilayer before the initiation of folding (45). Although our study reproduces these two items, some technical differences between the two studies are worth noting. We explore different parts of the landscape as we explicitly simulate the experimental pulling process by directly applying force with springs, whereas the other study performs umbrella sampling with an energetic bias determined by the N-to-C separation. Also, we allow helices to unfold and do not employ a Gō model nor stabilize the N-terminus to promote the C→N pathway. The group’s earlier study found that folding could occur along either the N→C or C→N pathways (46) as we observe, although we also observe unfolding from the center of the protein.

Although our method has widespread applications, several issues exist. First, we cannot refold the membrane proteins by relaxing the force, whereas refolding to the native is observed in the experimental studies (9, 10, 13). Second, we assume an infinite flat membrane bilayer, which is valid for bR, but experimentally, GlpG (9) is embedded in bicelles, which may not be large enough to accommodate all the states we generate in our simulations. Third, our estimated force rupture values have some uncertainty. We largely match the values for bR at our typical pulling speed. However, the extrapolation is low for the values appropriate for the experimental pulling speeds using the Bell-Evans relationship between log(pulling velocity) and rupture force. Improvements in our energy function are in progress that may address these issues.

Conclusions

We have developed an accurate and fast atomic-level method to conduct hundreds of realistic unfolding simulations to characterize the energy surface for force-induced unfolding. The method reproduces many of the experimental features of SMFS studies for the unfolding of bR (11) and GlpG (9). Our simulations can assist experimental studies by helping convert FECs to structures, pathways, and energies. For example, we identified the more stable amino-terminal domain of GlpG as the more likely terminus to unfold, but it escaped detection in experiment because of the cooperative unfolding behavior along this route. The counterintuitive unfolding of this more stable end (40) arises in part from higher hydrophobicity of the amino-terminal TM helices, a finding that highlights a general folding property for membrane helices: although increased hydrophobicity promotes insertion into the bilayer, it also enhances dissociation because the lipid bilayer effectively behaves as a good solvent for isolated hydrophobic helices. In contrast, TM helices that bury polar or charged groups upon association tend to remain associated because the cost of exposing their nonhydrophobic moieties to the bilayer is high.

Our major finding is that the mode of force application significantly alters the properties of the energy surface. The use of a constant force, either explicitly or by employing a soft spring, reduces the probability of observing intermediates while increasing the apparent unfolding cooperativity as compared to the use of stiff springs that can rapidly relax after an unfolding event. Finally, our simulation tools can be employed to investigate SMFS transition paths (47) as well as conduct complicated “gedanken” pulling experiments beyond current experimental capabilities, such as pulling on multiple sites in multiple directions with different strengths of the springs, and with either membrane or soluble proteins.

All data and analysis codes supporting the findings of this study are available from the corresponding authors upon reasonable request. The full simulation package of Upside as well as the necessary parameter files are available to public access on GitHub: https://github.com/sosnicklab/upside-md.

Author Contributions

Z.W. conceived the study, designed the research, implemented the AFM function into Upside, performed the simulations, analyzed the results, and wrote the manuscript. J.M.J. developed Upside and reviewed the codes of AFM function. K.F.F. provided theoretical guidance and wrote the manuscript. T.R.S. designed the research, analyzed the results, and wrote the manuscript.

Editor: Thomas Perkins.