Abstract
Extraction from simulations of the area compressibility moduli of the monolayers in a bilayer is considered theoretically. A statistical mechanical derivation shows that the bilayer modulus is the sum of the two monolayer moduli, as is often supposed but contrary to a recent study. Seemingly plausible assumptions regarding fluctuations are tested rigorously. Prospects for future research are discussed.
Significance
It is important to describe the properties of both leaflets of generally asymmetric biomembranes. One such property is the area compressibility modulus. This manuscript rigorously establishes the fundamental theory that corrects a recent Biophysical Journal article. The theory is straightforward but substantial enough that it was not readily apparent why the previous theory was incorrect. This is why this paper should be considered a new article and not just a comment. Another reason is that this paper points to an alternative method, used only once previously, for extracting the leaflet area compressibility modulus from simulations.
Introduction
Biomembranes are generally asymmetric, so increasing attention has been paid to creating asymmetric model systems, both in vitro and in silico. Then, it is appropriate to consider separately the physical properties of each of the two monolayers in asymmetric lipid bilayers. Separating some of those properties experimentally is difficult, so it is appropriate to turn to simulations. Those simulations that agree with the experiment for all the properties that experiment can measure can then be considered for extracting properties that experiments do not measure (1, 2). The property of interest in this article is the area compressibility modulus. There are two well-known methods of extracting the bilayer modulus from simulations. This article focuses on the extraction of the individual monolayer moduli.
An area compressibility modulus k is generally defined as follows:
| (1) |
where A is the area, and γ is the surface tension. This modulus is essentially a spring constant. Assuming that there is negligible coupling between the two monolayers, j = 1 and 2, each monolayer can be thought of as analogous to a spring with modulus kj, and the bilayer would then be two springs of equal length in parallel. The forces on the springs would be Fj = kj x, and the force on the two springs would be F12 = F1 + F2 = (k1 + k2) x, which is then identified as k12 x. It would then follow by analogy from elementary mechanics of springs that the modulus k12 for a bilayer is the sum of the monolayer moduli, which would be as follows:
| (2) |
Eq. 2 for symmetric bilayers is the conventional wisdom in the lipid bilayer field that has often been used for symmetric bilayers, usually in passing without even being remarked upon (3, 4, 5, 6).
In contrast to Eq. 2, a recent article (7) derived a rather different equation as follows:
| (3) |
This equation has two highly unusual features. The first comes from applying it to a symmetrical bilayer. Then, the two monolayer moduli must be equal, k1 = k2, so Eq. 3 requires that each monolayer modulus must equal the bilayer modulus k12. This unusual feature was specifically noted, and a rationalization was provided (7). The second unusual feature comes from considering a bilayer that is highly asymmetric; for example, monolayer one might consist of gel phase 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine at room temperature, and monolayer two might consist of highly fluid 1,2-dioleoyl-sn-glycero-3-phosphocholine. In the limit when k1 is very much larger than k2, Eq. 3 predicts that the bilayer modulus k12 is only twice the smaller monolayer modulus k2. This violates the definition in Eq. 1 because the tension γ1 to change the area of monolayer 1 should be enormous compared to the tension γ2 to effect the same change to the area of monolayer 2. A macroscopic analogy would be to construct a bilayer consisting of a sheet of rubber on a sheet of steel and claim that the area compressibility is unrelated to that of the steel. As the derivation provided for Eq. 3 has gaps and makes unproven assumptions (7), it is appropriate to return to basics.
After laying the statistical mechanical foundation in Methods, the current article provides a rigorous derivation of Eq. 2 in the Thermodynamic relations subsection. The Correlations subsection reveals exactly which assumptions employed in (7) are incorrect for the case of uncoupled monolayers considered there. It also allows for the consideration of features not considered theoretically (7) that would nevertheless affect that method of analyzing simulations. The Discussion assesses the prospects for applying the small patch method of (7), and attention is called to a different simulation method that would not be subject to the same artifacts.
Methods
The theoretical system
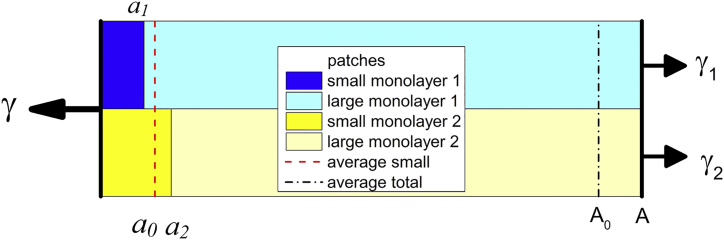
Consider a bilayer with fluctuating area A and average area <A> = A0. The monolayer fluctuating areas A1 and A2 are necessarily constrained to be equal to the bilayer fluctuating area, A1 = A2 = A. The simulation method proposed in (7) analyzes the fluctuating areas of small portions of each monolayer j with fluctuating areas . For convenience, we will set the average small areas <> on both monolayers to be the same value . Of course, the fluctuating areas a1 and a2 are not generally equal unless there is very strong coupling between the two monolayers. A schematic of this setup is shown in Fig. 1.
Figure 1.
A schematic of fluctuations of the patches in two monolayers in a bilayer. To see this figure in color, go online.
Assuming that there is also no coupling between these small fluctuating areas and between the remaining Bj = Aj − areas in each monolayer leads, via the equipartition theorem, to the monolayer moduli:
| (4) |
where kB is Boltzmann’s constant, and kBT is thermal energy. This equation is well established as one of the two main ways to obtain k12 when bilayer areas A and A0 replace and (8, 9). The interesting issue is how k12 is related to the k1 and k2 that are obtained from Eq. 4. For this, we return to the same statistical mechanics used to derive the equipartition theorem, but we now have to realize that even if the two monolayers are uncoupled locally, there is the global constraint A1 = A2 = A.
The formal description of the system begins by writing the basic fluctuation energy for the small patches and also for the remaining large areas Bj − B0:
| (5) |
Of course, analysis of simulations would analyze many small patches to obtain better statistics, but there is no loss of generality in a derivation that considers small patches one at a time, each embedded in a reservoir that consists of the remaining small patches considered as a group. Also, the average area per molecule, suitably defined, is generally different in the two monolayers, and those areas may not coincide with the areas of the free-standing monolayers. Again, with no loss of generality, the areas of the small patches are not those of lipid molecules but have been chosen for notational convenience to contain an appropriate amount of material in each monolayer such that the average small patch area is the same in both monolayers.
Each of the four terms in Eq. 5 has the conventional harmonic form for the fluctuation energy with monolayer moduli kj. This equation looks like it has four independent fluctuating variables, but there are only three because + Bj = Aj = A. Although this complicates the ensuing derivation, it is crucial for explaining the difference between Eqs. 2 and 3. We therefore replace (Bj − B0) by (A − A0) − ( − ) in Eq. 5. It will be convenient to condense the notation in subsequent equations by writing the three independent fluctuating variables as x = A − A0 and yj = − . Then, Eq. 5 becomes the following:
| (6) |
As is often the case in statistical mechanics, it is advantageous to formally distinguish nominally identical terms such as has been done for the kj′ in the first term in Eq. 6 and to add terms to the basic energy as follows:
| (7) |
The first term in Eq. 7 is crucial because it will enable finding the relation between the bilayer k12 and the monolayer moduli kj by taking the derivative of the partition function with respect to w and then setting w = 0. The h12 term provides for the coupling between the two monolayers. For h12 > 0, the coupling energy increases when the areas of the small patches are correlated. With the usual volume conservation assumption, such correlated fluctuations correspond to total bilayer thickness fluctuations (sometimes called peristaltic modes); h12 > 0 therefore suppresses thickness fluctuations, whereas h12 < 0 enhances them. The hj terms provide a kind of coupling between the small patches and the large patches in the monolayers; even more importantly, that term will enable finding the correlation functions that were previously presumed to be zero (7).
Statistical mechanical derivation
The partition function for this system is defined as follows:
| (8) |
where β = 1/kBT. The result of the integrations is as follows:
| (9) |
Defining R = (B0/) and r=(B0/A0), the fs are as follows:
| (10) |
and for j = 1 and 2 as follows:
| (11) |
and
| (12) |
The evaluation of the partition function in Eq. 8 was performed by first grouping all the exponential factors involving x2 and x. Completion of the square in the form (ax − c)2 − c2 provides a Gaussian x integral, which gives the factor 2πkT/B0f0 in Eq. 9. The factors involving y12 and y1, including those in the c2 factor left over from the x integration, were then similarly treated, finally ending with a Gaussian integral over y2. The results of the y1 and y2 integrations together give the remaining factor in Eq. 9.
Results
Thermodynamic relations
Derivatives of the partition function in Eq. 9 give thermodynamic quantities of interest. First, consider the average energy as follows:
| (13) |
defined by the first equality in Eq. 13. The calculation using Eq. 9 gives the second equality. This recovers the usual equipartition result for three classical harmonic degrees of freedom.
The most interesting derivative is of ln Z with respect to the parameter w. By definition of the partition function in Eq. 8 and the definition of Eadd in Eq. 7, this derivative gives the first identity in the following equation:
| (14) |
The second equality is just the identity for the bilayer modulus k12 as in Eq. 4. The last equality is the result of taking the derivative in Eq. 9 and then setting w = 0 as well as hj = h12 = 0; this returns the energy to the basic terms in Eq. 6. Eq. 14 is a primary result that confirms Eq. 2 which was suggested in the Introduction by analogy to springs. This fully rigorous result proves that Eq. 3 is incorrect.
When h12 is nonzero, there are corrections to Eq. 14, which, however, are of order r and therefore vanish in the small subsystem limit ≪A0. This is consistent with the infinitely strong h12 limit, which is independently calculable because then y1 = y2 is constrained and the tightly coupled monolayers reduce to a single layer with modulus k1 + k2. However, the h12 coupling between the monolayers is far from innocuous for the interpretation of small patch fluctuations. These fluctuations are obtained by taking a derivative with respect to kj′ and setting hj = 0 = w, designated by 0′ in the first term in the following equation:
| (15) |
The first equality in Eq. 15 follows simply from Eqs. 7 and 8. The second equality in Eq. 15 defines the apparent monolayer modulus k1app that the small patch simulation method would report. The last equality in Eq. 15 shows the result of the calculation using Eq. 9. Importantly, k1app is not the true monolayer modulus k1 but becomes k1+ h12. Encouragingly, one could determine h12 = 1/2 (k1app + k2app − k12) and thence obtain k1 and k2 using the final equality in Eq. 15. However, this assumes that the only coupling is between patches on opposite monolayers.
Although the hj terms might appear to provide the in-plane coupling equivalent to the h12 out of plane term, there is a difference that makes the hj terms unsatisfactory for determining k1 and k2. For either sign of hj, some fluctuations decrease the hj energy term, which even leads to instability of the system for modest values of hj. However, it may be noted that these terms decrease k1app and k12 but only proportional to hj2 and to r = /A0. A better model for in-plane coupling might involve adding terms like (a−)2(B−B0)2 to the energy, but this would introduce quartic terms, which, even if calculable, would complicate an already complicated derivation of the partition function.
Correlations
It is interesting to see exactly how plausible assumptions for correlations between the patches fail because of the A1 = A2 = A constraint. Let us begin with the following identity, alluded to in (7), that follows from A = 1/2 (A1 + A2):
| (16) |
The left-hand side is just A0kBT/k12. Expanding the right-hand side gives the following:
| (17) |
where
| (18) |
and
| (19) |
W was previously assumed to be zero (7), but it is trivially equal to 1/2 <(A − A0)2> by inspection. The authors of Doktorova et al. (7) have acknowledged this correction to W in a recent erratum (15) although not to the subsequent corrections in the next paragraph.
Eq. 17 can now be rewritten as follows:
| (20) |
If there is no specific coupling between patches, application of Eq. 4 shows that <( – )2> + <(Bj – B0)2> = A0kBT/kj, so Eq. 20 can be further rewritten as follows:
| (21) |
If Q1 + Q2 were zero, then this would be a derivation of Eq. 3. However, the Qj are straightforwardly determined to be nonzero by taking derivatives of the partition function with respect to hj. The result for Q1 is as follows:
| (22) |
and the result for Q2 simply exchanges the indices 1 and 2, so Q1 + Q2 is not zero. The product Q1Q2 depends only upon the sum k1 + k2, but the ratio Q1/Q2=(k2/k1)2 shows that the Qj have quite different values for asymmetric bilayers with larger values of Qj for the softer monolayer than for the stiffer one. Finally, combining 2Qj in Eq. 22 with the kj terms in Eq. 21 gives, for both j = 1 and 2, the result 1/2A0kBT/(k1 + k2), thereby giving the following:
| (23) |
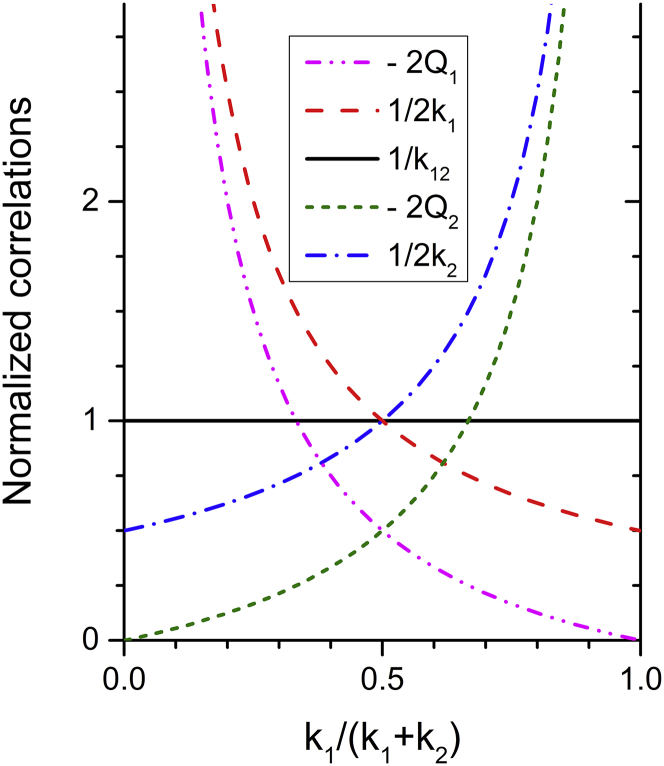
which again confirms that the bilayer modulus k12 is the sum of the monolayer moduli as in Eq. 2. Fig. 2 plots the terms in Eq. 21 as the relative stiffness of the two monolayers varies.
Figure 2.
The terms in Eq. 21 are normalized to A0kBT/(k1+ k2). The algebraic sum of the four terms on the right-hand side of Eq. 21 equals 1/k12= 1 because k1+ k2 is normalized to 1. To see this figure in color, go online.
It is interesting that the simple constraint that both monolayers have the same area has such a large effect on the Qj and W correlations. Compared with a system consisting of a single monolayer, W is not defined, and the only defined Q1 is zero as one would expect from the assumption that the small patch is uncoupled from the large patch reservoir. It is also interesting to note that W + Q1+Q2 = 0 for symmetric bilayers but only for symmetric bilayers.
Discussion
The difference between the derivations of Eqs. 2 and 3 is the treatment of the crucial constraint that the monolayers in a bilayer must have the same total area. Although the derivation of Eq. 3 in the previous subsection recognizes this constraint, it then had to make assumptions about various correlations. The derivation of Eq. 2 makes no such assumptions and actually calculates the correlation functions and shows that they do not agree with the assumptions in the derivation of Eq. 3. The derivation of Eq. 2 confirms what has been assumed for a long time, at least for symmetric bilayers.
Although Eq. 3 is incorrect, it is a reasonable prospect that the fluctuations in small patches will reveal differences in the monolayer moduli in asymmetric bilayers. If there is no coupling of the patches with the remainder of the bilayer, then the rigorous theory in this article shows that this analysis will give the monolayer moduli quantitatively. However, if the sum of the apparent monolayer moduli obtained from small patches k1app + k2app does not equal the well-determined bilayer modulus k12, then there must be coupling. If the coupling is only between patches on opposite monolayers, then the analysis using h12 allows the extraction both of the coupling and the individual kj. One could also have equality with coupling if the in-plane coupling competes with the h12 coupling, but we do not have a good theory for the effect of coupling within each monolayer.
The simulations previously reported (7) gave k1app + k2app = 2k12, indicating strong coupling. However, the method employed there to convert area fluctuations to thickness fluctuations may have been flawed by the assumption that the volume was constant in a region consisting of only about half the hydrocarbon region as it was determined by the location of specific methylenes. A similar assumption has been found to be false in a current analysis of the Poisson ratio (unpublished data).
Given these problems with the small patch analysis method, it is appropriate to consider a second method that stems from the second method that has routinely been employed to obtain the bilayer modulus k12. This second method simply plots the area A versus surface tension γ to obtain the area compressibility modulus directly from its definition in Eq. 1. This method was noted in (7), but it was apparently not realized that it could also be used to obtain the kj moduli separately. For each value of γ in the simulation, one would first calculate the average lateral pressure profile Π(z) = −γ(z) of the bilayer (9, 10, 11). The integral of γ(z) along z across the whole bilayer is the value of γ. The idea is that one may also choose to integrate only over each monolayer separately to obtain γ1 and γ2. Then, one would calculate the separate moduli as follows:
| (24) |
using the average <A> for each value of γj. The only assumption in this method, as in the proposed method (7), is that it makes sense to separate the bilayer into two monolayers. One might argue that it does not make sense to apply it to bilayers with fully interdigitated hydrocarbon chains, but it does appear to be a reasonable conceptual division for most bilayers that have only mini-interdigitation (12) of the monolayers near the center of the bilayer. Furthermore, one does not have to just separate k12 into two monolayer values. Indeed, k12 has already been further refined into a modulus k12(z) that varies with depth z for a coarse-grained simulation of a symmetric bilayer (13). When applied to an asymmetric bilayer, that method would provide an even more detailed view than just obtaining k1 and k2. As noted (7), this second method requires more simulations at different surface tensions, and the lateral pressure profiles would probably be subject to more noise. However, this method would not be subject to the difficulties involved in the small patch method.
Finally, it may also be noted that (7) tackled the thorny issue of the relation between the area compressibility modulus KA (=k12) and the bending modulus KC. It focused on the appropriate thickness t to use in the following:
| (25) |
rather than on the factor of 24 that comes from the polymer brush formulation that assumes independent monolayers (6). The choice of the total hydrocarbon thickness for t has worked rather well (2, 6). However, the most significant exception was found when cholesterol was added to lipid bilayers, and a large change in the definition of t was proposed (14). In agreement with (7), further analysis using reliable determinations of both KA and KC, both from experiment and from simulations, are indeed needed to refine what effectiveness thickness t is appropriate to relate the mechanical properties of specific lipid bilayers.
Conclusions
The statistical mechanical relation of the leaflet area compressibility moduli to that of the bilayer has been rigorously derived. Coupling between the two leaflets has been incorporated theoretically and that can be addressed using the small patch simulation method. However, an alternative method is likely to be superior for obtaining more, and more reliable, information about the area compressibility of asymmetric membranes.
Editor: D. Peter Tieleman.
References
- 1.Klauda J.B., Kucerka N., Nagle J.F. Simulation-based methods for interpreting x-ray data from lipid bilayers. Biophys. J. 2006;90:2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nagle J.F. Introductory lecture: basic quantities in model biomembranes. Faraday Discuss. 2013;161:11–29. doi: 10.1039/c2fd20121f. discussion 113–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brannigan G., Brown F.L.H. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophys. J. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Helfrich W. Bending elasticity of fluid membranes. In: Luisa P.L., Walde P., editors. Giant Vesicles. John Wiley & Sons Ltd.; 2000. pp. 51–70. [Google Scholar]
- 5.Seifert U., Lipowsky R. Morphology of vesicles. In: Lipowsky R., Sackmann E., editors. Elsevier; 1995. pp. 403–463. Structure and Dynamics of Membranes. [Google Scholar]
- 6.Rawicz W., Olbrich K.C., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Doktorova M., LeVine M.V., Weinstein H. A new computational method for membrane compressibility: bilayer mechanical thickness revisited. Biophys. J. 2019;116:487–502. doi: 10.1016/j.bpj.2018.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Waheed Q., Tjörnhammar R., Edholm O. Phase transitions in coarse-grained lipid bilayers containing cholesterol by molecular dynamics simulations. Biophys. J. 2012;103:2125–2133. doi: 10.1016/j.bpj.2012.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Venable R.M., Brown F.L.H., Pastor R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ollila O.H.S., Vattulainen I. Lateral pressure profiles in lipid membranes: dependence on molecular composition. In: Sansom M.S.P., Biggin P.C., editors. Volume 20. Royal Society of Chemistry; 2010. Molecular Simulations and Biomembranes: From Biophysics to Function. [Google Scholar]
- 11.Hu M., de Jong D.H., Deserno M. Gaussian curvature elasticity determined from global shape transformations and local stress distributions: a comparative study using the MARTINI model. Faraday Discuss. 2013;161:365–382. doi: 10.1039/c2fd20087b. discussion 419–459. [DOI] [PubMed] [Google Scholar]
- 12.Nagle J.F. Theoretical modeling of experimentally determined tilt modulus of lipid bilayers. Biophys. J. 2018;114:94a. [Google Scholar]
- 13.Campelo F., Arnarez C., Kozlov M.M. Helfrich model of membrane bending: from Gibbs theory of liquid interfaces to membranes as thick anisotropic elastic layers. Adv. Colloid Interface Sci. 2014;208:25–33. doi: 10.1016/j.cis.2014.01.018. [DOI] [PubMed] [Google Scholar]
- 14.Pan J., Tristram-Nagle S., Nagle J.F. Effect of cholesterol on structural and mechanical properties of membranes depends on lipid chain saturation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:021931. doi: 10.1103/PhysRevE.80.021931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Doktorova M., LeVine M.V., Weinstein H. A new computational method for membrane compressibility: bilayer mechanical thickness revisited. Biophys. J. 2019;117:790. doi: 10.1016/j.bpj.2019.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]