Abstract
Invasion of erythrocytes by merozoites is an essential step for the survival and progression of malaria parasites. To invade red blood cells (RBCs), apicomplexan parasites have to adhere with their apex to the RBC membrane. This necessary apex-membrane contact (or alignment) is not immediately established because the orientation of a free merozoite with respect to the RBC membrane is random when an adhesion contact first occurs. Therefore, it has been suggested that after the initial adhesion, merozoites facilitate their proper alignment by inducing considerable membrane deformations, frequently observed before the invasion process. This proposition is based on a positive correlation between RBC membrane deformation and successful invasion; however, the role of RBC mechanics and its deformation in the alignment process remains elusive. Using a mechanically realistic model of a deformable RBC, we investigate numerically the importance of RBC deformability for merozoite alignment. Adhesion between the parasite and RBC membrane is modeled by an attractive potential that might be inhomogeneous, mimicking possible adhesion gradients at the surface of a parasite. Our results show that RBC membrane deformations are crucial for successful merozoite alignment and require interaction strengths comparable to adhesion forces measured experimentally. Adhesion gradients along the parasite body further improve its alignment. Finally, an increased membrane rigidity is found to result in poor merozoite alignment, which can be a possible reason for a reduction in the invasion susceptibility of RBCs in several blood diseases associated with membrane stiffening.
Significance
Plasmodium parasites invade erythrocytes during the progression of malaria. To start invasion, parasites adhered to erythrocytes have to reorient themselves such that their apex establishes a direct contact with erythrocyte membrane. The reorientation (or alignment) process is often associated with strong membrane deformations, which are believed to be induced by the adhered parasite and are positively correlated with its alignment. We employ a mechanically realistic erythrocyte model to investigate the interplay of membrane deformations and merozoite alignment. Our model demonstrates that erythrocyte deformations are essential for successful parasite alignment because parasite reorientation at rigidified membranes is generally poor. Therefore, our results suggest a possible mechanism for the reduction in erythrocyte invasion susceptibility in several blood diseases associated with membrane stiffening.
Introduction
Malaria remains one of the most devastating diseases in the world, especially in African and South Asian regions, claiming over 400,000 lives per year (1). This motivates significant research efforts directed toward understanding various aspects and stages of malaria infection (2, 3, 4). Malaria is caused by a unicellular parasite from the genus Plasmodium that is transmitted to humans through a mosquito bite. Five different types of malaria parasites are known to infect humans. Among them, Plasmodium falciparum causes most severe cases of the infection. During the blood stage of malaria, merozoites invade red blood cells (RBCs) and asexually reproduce inside them. The invasion of RBCs by merozoites is a critical step in their survival (3, 4, 5) because inside RBCs, the parasites remain invisible to the host’s immune system. As a result, this step in malaria has attracted considerable scientific interest because it can reveal potential targets for antimalarial drugs (3).
Merozoites belong to the phylum Apicomplexa, which is characterized by the existence of an apical complex consisting of structural components and secretary organelles required for successful invasion of RBCs (6). Therefore, to start the invasion process, parasites have to establish first a direct contact between their apex and the RBC membrane (5, 6). For adhesion, merozoites have a surface coat with a number of embedded proteins that can bind to RBC membrane (6, 7, 8). The first contact between the merozoite and RBC can be considered to occur with a random orientation. However, such random parasite adhesion is unreliable for the establishment of the direct apex-RBC contact because after about 3 min, parasites become nonviable and are not able to invade RBCs anymore (9). Therefore, it is hypothesized that merozoites are able to facilitate the alignment of their apex toward the RBC membrane after their initial adhesion with a random orientation (10). This alignment or preinvasion stage occurs within the range of 2–50 s (10, 11, 12), which is fast enough to proceed to RBC invasion afterwards.
Even though the alignment process has been observed in a number of experiments (11, 12, 13, 14), the mechanisms that lead to a successful parasite alignment are still under discussion. One proposition is that the reorientation of an adhered parasite at RBC membrane is guided by a gradient of adhesive agonists along the parasite’s body such that their density increases toward the apex (15). This proposition is based on some evidence for the release of adhesive agonists from the parasite’s apex during invasion (3, 16, 17). An interesting feature that is frequently observed in the preinvasion stage is RBC membrane deformations of various intensity (11, 12, 13, 14). In fact, a recent experimental study (18) has suggested that a positive correlation between the magnitude of membrane deformations and the efficiency of RBC invasion exists. Interestingly, such membrane deformations subside right after the alignment is achieved and the merozoite starts initiating cell invasion. This suggests that the parasite may use membrane deformations to facilitate its apex-membrane alignment.
At present, several questions regarding possible mechanisms for the parasite alignment remain unanswered. Can a purely mechanistic model of passive parasite adhesion to a RBC reproduce successfully merozoite alignment? Is an adhesion gradient along the parasite’s body required for successful alignment? How do membrane deformations aid parasite alignment? Are they necessary for a proper alignment? To address these questions, we perform simulations of parasite adhesion to an RBC membrane (19). In particular, we focus on the so-called passive compliance hypothesis (20), which assumes that observed membrane deformations simply result from the parasite adhesion to the RBC. Parasite-membrane adhesion is modeled by an attractive potential, whose local strengths are adapted to represent different adhesion intensities and gradients. Our results show that the parasite-RBC adhesion interactions, whose strength is comparable with experimentally measured adhesion forces (9), produce membrane deformations of various intensity, qualitatively matching experimental observations (11, 12, 13, 14, 18). More importantly, we find that membrane deformations significantly aid parasite alignment because the parasite becomes partially wrapped by the RBC membrane, making contact between the apex and RBC much more likely. Furthermore, simulations of parasite adhesion to a rigidified RBC show poor parasite alignment, indicating that RBC deformation is a key aspect for the successful alignment of a merozoite. Simulations with an adhesion gradient along the parasite’s body confirm that such gradients facilitate better alignment; however, their presence seems not to be necessary for a successful apex-membrane alignment. In conclusion, our results obtained from a purely mechanistic model for parasite-membrane adhesion suggest that the passive compliance hypothesis is sufficient to reproduce merozoite alignment.
The study is structured as follows. In the next section, the models for a deformable RBC and rigid parasite and adhesive interactions between them are discussed in detail. Then, the Results section starts with a calibration of the parasite-membrane adhesion model, which is required to establish a relation between the adhesive strength and the degree of membrane deformation. The second part of the Results section presents the quality of parasite alignment with respect to the adhesion strength and membrane deformation and compares parasite alignment for deformable and rigid RBCs. Finally, the importance of RBC membrane deformation for parasite alignment is discussed.
Methods and Models
To investigate adhesion interactions between an RBC and a parasite, we employ models of cells with membranes having bending and stretching elasticity (19, 21, 22), which are embedded into a fluid represented by the dissipative particle dynamics (DPD) method (23, 24). All models are implemented within the LAMMPS package (25), and specific setups are available upon request.
RBC membrane model
The RBC membrane is described by a triangulated network model (19, 21, 22, 26) with Nrbc = 3000 vertices that are distributed at the membrane surface of the cell. These vertices are connected by NS = 8994 springs that form NT = 5996 triangles. Mechanical properties of the RBC are described by the potential energy (21, 22)
| (1) |
where Esp models the elasticity of the spectrin network that is attached to the cytoplasmic side of the lipid bilayer and Ebend represents the bending resistance of the bilayer. Earea and Evol constrain the area and volume of the RBC membrane, mimicking incompressibility of the lipid bilayer and cell’s cytosol, respectively.
The spring energy Esp is expressed as (21, 22)
| (2) |
where kBT is the unit of energy, li is the length of the i-th spring, is the maximal spring extension, and . The other parameters are the persistence length pi and the spring constant λi. To set a stress-free state for the elastic network, a nonzero equilibrium length is assigned to each spring individually, according to the initial triangulation of the RBC biconcave shape (22). This implies a force balance represented by for each spring within the network. The membrane shear modulus μ is approximated as (21, 22)
| (3) |
where is constant for all springs. Then, from known lengths and selected values of μ and x0, individual spring parameters pi and λi can be calculated using the force balance and Eq. 3 for each spring.
The bending energy Ebend is given by (26, 27)
| (4) |
where κ is the bending modulus and is a unit normal to the membrane surface at the vertex i (the average normal of the faces surrounding vertex i). The second sum in Eq. 4 runs over all bonded neighbors j(i) of vertex i, and the vector rij = ri − rj is the bond vector between vertices i and j and rij = |rij|. Moreover, is the area of the dual cell of vertex i, where σij = rij[cotθ1 + cotθ2]/2 is the length of a bond in the dual lattice and the angles θ1 and θ2 represent the two angles opposite to the shared bond vector rij.
The area Earea and volume Evol constraints are given by (21, 22)
| (5) |
| (6) |
where A and V are the instantaneous total surface area and volume of the membrane. The corresponding values A0 and V0 are targeted values of these quantities. Ai represents the area of triangle i, and is the corresponding rest area set according to the initial RBC triangulation. The coefficients ka, kl, and kv define strengths of the global and local area constraints as well as the volume constraint, respectively.
The elasticity of an RBC is characterized by the shear modulus μ and a Young’s modulus Y = 4μK/(μ + K), where K = 2μ + ka + kl is the area-compression modulus. This model has been verified to properly reproduce RBC mechanics (19, 21, 22) and membrane fluctuations (28).
Parasite model
The parasite is much less deformable than the RBC because no deformations of parasite body are visible from different experimental observations (9, 18). Therefore, it is modeled as a rigid body, which is represented by Npara vertices distributed on its surface (see Fig. 1 A). All vertices of the parasite are moving as a rigid cluster, similar to the raspberry model for colloidal particles (29). In this model, the total force and torque on the parasite is computed each time step as the sum of forces and torques (from interactions with fluid and RBC particles) on Npara particles. Then, the positions and velocities of parasite particles are updated such that it moves and rotates as a rigid body (30).
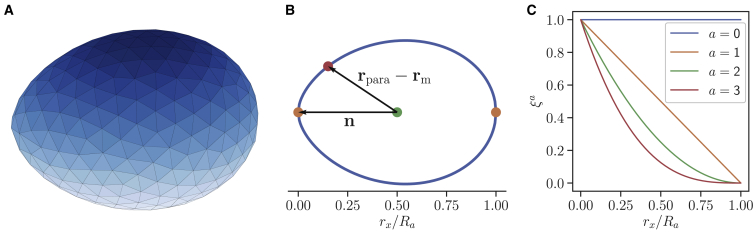
Figure 1.
Parasite model and its adhesion interaction with RBC membrane. (A) The parasite is modeled by Npara vertices that form an egg-like shape given by Eq. 7 and move as a rigid cluster. (B) The interaction for each parasite vertex with RBC membrane depends on its relative position with respect to the parasite head (or apex), described by the dot product n ⋅ (rpara − rm) in Eq. 10. Here, n is a directional vector from the parasite midpoint (rx/Ra = 0.5) to the head (rx/Ra = 0). (C) Function ξa, describing a position-dependent density of adhesive agonists for various exponents a, is shown. ξ(rpara) in Eq. 10 is chosen in such way that the interaction for a = 1 increases linearly along the parasite’s directional vector. Higher powers of a lead to interactions that are strongly localized around the parasite head. To see this figure in color, go online.
Merozoites possess an egg-like shape with a size within the range of 1–2 μm (7, 15, 31). The egg-like shape of a merozoite is approximated by (15)
| (7) |
where Ra is the parasite’s length and Rb is the diameter. Discretization of the parasite surface is performed using DistMesh (32) in MATLAB (The MathWorks, Natick, MA).
RBC-parasite adhesion interaction
The parasite and the RBC membrane interact through a Lennard-Jones (LJ) potential, which includes both repulsive and attractive parts. The pairwise interaction energy between one membrane vertex at rrbc and one parasite vertex at rpara separated by the distance r = |rpara − rrbc| is given by
| (8) |
where σ is the characteristic length of repulsive interaction and rcut is the cutoff radius for the adhesion potential. The potential is repulsive below and attractive above. The position-dependent interaction strength ϵ(rpara) is defined as
| (9) |
Here, we assume that the area of each vertex Ac = Apara/Npara in the discretization of a parasite with the total area Apara contains Acρ(rpara) adhesive agonists, where ρ(rpara) = ρa[ξ(rpara)]a is a position-dependent surface density. ρa is the density coefficient, a is the gradient exponent, and the function ξ(rpara) defines the distribution of agonists with respect to the position rpara at the parasite surface
| (10) |
where rm marks the midpoint of the cylindrical symmetric axis of the parasite (see Fig. 1 B). The vector n is the directional vector of the parasite, pointing from rm toward its apex. As shown in Fig. 1 C, different exponents a introduce various gradients of adhesive agonists at the parasite surface. Note that for a > 0, the adhesion interaction is highly localized at the apex. Other parameters in Eq. 9 are the interaction strength of each agonist ϵ1, ϵa = Acρaϵ1, and an additional position-independent interaction ϵ0 between the RBC membrane and the parasite. In all simulations, ϵ0 is set to zero. The total interaction energy is obtained by summing over all RBC-parasite vertex pairs.
Hydrodynamic interactions
The RBC and parasite are embedded in a Newtonian fluid, which is modeled by a particle-based hydrodynamics method, DPD (23, 24). In short, the fluid environment is represented by a collection of fluid particles, which interact through three pairwise forces. Thus, the total force between particles i and j is given by
| (11) |
where , , and are conservative, dissipative, and random forces, respectively. The conservative force determines static pressure in the fluid and controls its compressibility. FD governs fluid viscosity η, which depends on several simulation parameters and is evaluated using a reverse-Poiseuille flow setup (33, 34). Finally, FR describes thermal fluctuations such that the pair of dissipative and random forces serves as a thermostat, maintaining a desired equilibrium temperature.
Note that the DPD forces act only between the particle pairs fluid-fluid, fluid-membrane, and fluid-parasite, whereas the pairs of membrane-membrane and parasite-parasite particles are not subject to any DPD forces. Furthermore, conservative interactions are omitted for fluid-membrane and fluid-parasite pairs of particles. No-slip boundary conditions at the surface of the parasite and RBC membrane are enforced by an appropriate choice of the dissipative interaction between fluid particles and suspended cells (22).
Simulation setup
The simulation setup consists of one RBC and a parasite suspended in a fluid. The simulated domain assumes periodic boundary conditions in all directions. The parasite is initially placed within the interaction range of the RBC so that it can immediately adhere to the membrane. The initial orientation of the parasite is chosen such that the apex of the parasite is pointing away from the membrane, i.e., with its back to the RBC, the most unfavorable orientation for binding. We mainly focus on parasite adhesion at the rim (or side) of RBC, and several simulations are performed for merozoite adhesion at the highest point (top) of the membrane (see Fig. S1). For convenience, RBC center of mass is fixed by a harmonic spring so that the cell does not diffuse away.
Table 1 summarizes the main simulation parameters. To relate parameters in simulation and physical units, we define basic length, energy, and timescales. The length scale is defined by an effective RBC diameter , where A0 is the RBC membrane area. The basic energy scale is kBT, where kB is the Boltzmann constant and T is temperature. Finally, the timescale τ corresponds to an RBC relaxation time defined as . For average properties of a healthy RBC with D0 = 6.5 μm and κ = 3 × 10−19 J and for the fluid viscosity η = 1 mPa s, we obtain τ ≈ 0.92 s.
Table 1.
Overview of Main Parameters in Simulation and Physical Units
| Parameter | Simulation Value | Physical Value |
|---|---|---|
| A0 | 133.5 | 133.5 × 10−12 m2 |
| V0 | 93.8 | 93.8 × 10−18 m3 |
| D0 | 6.5 | 6.5 × 10−6 m |
| kBT | 0.01 | 4.282 × 10−21 J |
| τ | 725.8 | 0.92 s |
| η | 70 kBTτ/ | 1 × 10−3 Pa s |
| κ | 70 kBT | 3.0 × 10−19 J |
| μ | 4.6 × 104kBT/ | 4.8 × 10−6 Nm−1 |
| Y | 1.82 × 105kBT/ | 1.89 × 10−5 Nm−1 |
| σ | 0.15 | 0.15 μm |
| rcut | 0.4 | 0.4 μm |
The effective RBC diameter with A0 being the membrane area, the thermal energy kBT, and the characteristic RBC relaxation time are selected as length, energy, and timescales. κ is the membrane bending rigidity, μ is the shear modulus, Y is the Young’s modulus, and η is the fluid’s dynamic viscosity. σ and rcut are parameters of the LJ potential. The RBC properties correspond to average characteristics of a healthy RBC.
To assess the importance of parasite size for the adhesion to and alignment toward RBC membrane, two different merozoite sizes are considered:
-
1)
small size: Ra = 1.0 μm and Rb = 0.70 μm,
-
2)
large size: Ra = 1.5 μm and Rb = 1.05 μm,
which will often be referred to as small and large parasites, respectively. The small parasite is discretized with Npara = 310 vertices, whereas the large parasite contains Npara = 664 vertices, so they have the same particle density at their surface. Because of the hard-core LJ interaction between the merozoite and the RBC with σ = 0.15 μm, parasite particles cannot approach RBC membrane closer than the distance σ. Therefore, simulated parasites are effectively larger than the values of Ra and Rb defined above, corresponding to a length of 1.15 μm and a diameter of 0.85 μm for the small parasite and to a length of 1.65 μm and a diameter of 1.2 μm for the large parasite. All simulations were performed on the supercomputer JURECA (35) at Forschungszentrum Jülich. To obtain reliable averages of quantities of interest, all presented data points are averaged over ∼10 statistically independent simulations. Shaded lanes around simulated data curves represent SDs.
Results
To allow quantitative predictions of RBC-merozoite interaction, our model first requires a detailed calibration for various adhesion strengths and interaction gradients. Subsequently, the quality of parasite alignment is connected to the adhesion strength and corresponding membrane deformation. In addition, we compare parasite alignment at the surface of deformable and rigid RBCs.
Adhesion-induced membrane deformations
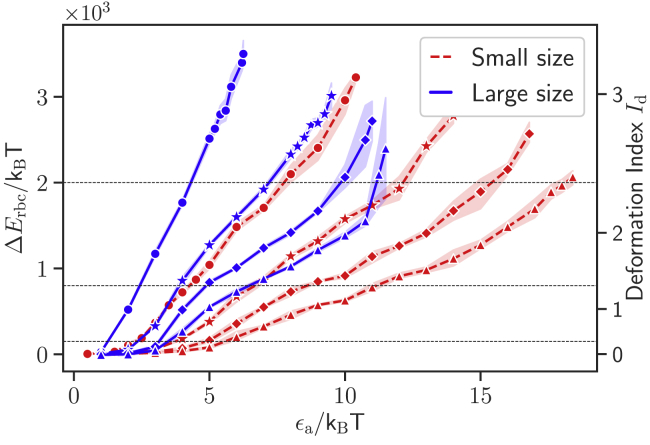
To establish a connection between the interaction strength ϵa and visual RBC deformation, a number of simulations are performed for various ϵa values for the two parasite sizes (see Fig. 2; Videos S1 and S2). RBC deformation is quantified by the deformation energy ΔErbc, defined as
| (12) |
where is the total membrane energy from Eq. 1 for a biconcave RBC shape in its relaxed state at equilibrium and is the total energy of an RBC deformed because of parasite adhesion. Fig. 3 presents membrane deformation energy as a function of the interaction strength ϵa for different exponents a and the two parasite sizes. The deformation energy increases with increasing ϵa, and strong deformations are induced by a partial wrapping of the parasite by the membrane to maximize the area of contact. Note that the adhesion between the parasite and RBC membrane reaches a stable configuration, which does not change over time anymore, after a very fast reorientation (see Videos S1 and S2). The deformation energies are computed after this stationary configuration is achieved. The large parasite leads to stronger membrane deformations than the small merozoite for the same interaction strengths because it forms a larger area of adhesion. The data in Fig. 3 are for side contact. The deformation energy for top contact has a similar dependence on ϵa; see the comparison in Fig. S2 for the small parasite with a = 0.
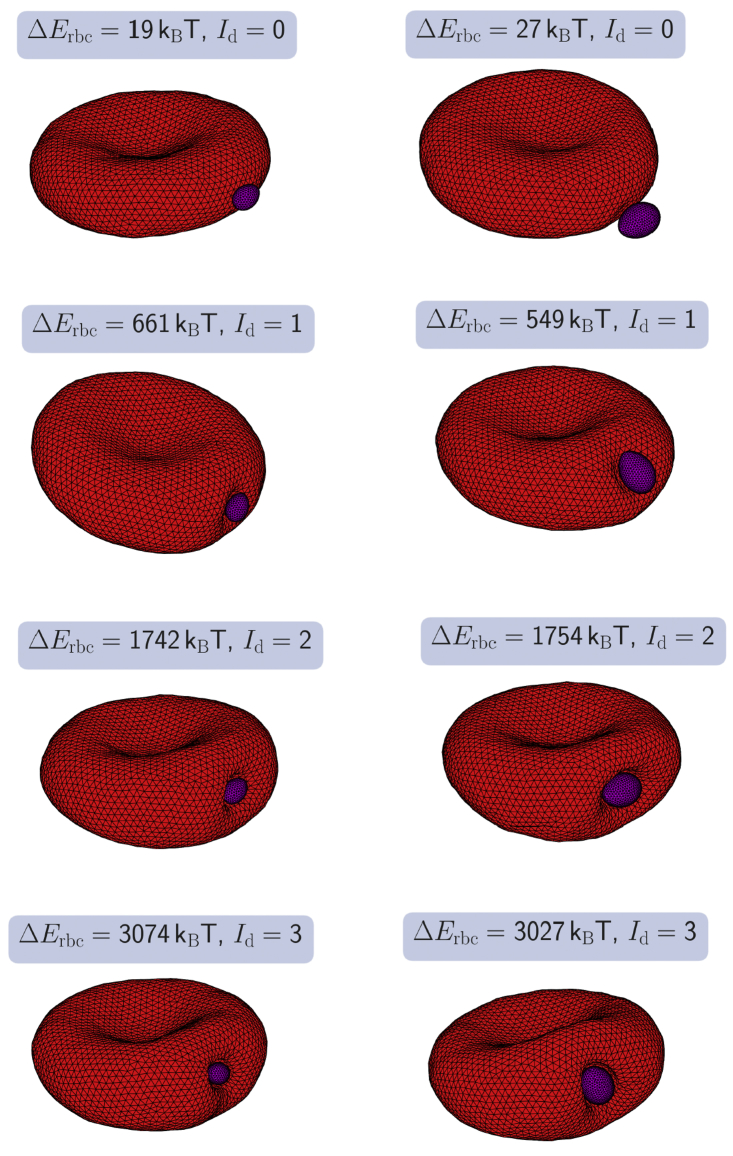
Figure 2.
Snapshots of RBCs deformed because of parasite adhesion with a side contact, including small (left column) and large (right column) merozoites. Interaction strengths from top to bottom are ϵa/kBT = 1, 4, 7, 10 for the small merozoite and ϵa/kBT = 1, 2, 4, 5.4 for the large parasite. Depending on the interaction strength, the parasite induces membrane deformations of various intensity. These deformations are classified visually by a deformation index Id (see Table 2) and quantified by the deformation energy ΔErbc shown in Fig. 3. Because of the interaction strength and partial wrapping of the parasite by the membrane, the parasite reorients itself toward a configuration with a minimal total energy and shows no significant motion afterwards; see Videos S1 and S2. Here, a = 0 (homogeneous adhesion). To see this figure in color, go online.
Figure 3.
Deformation energy ΔErbc and deformation index Id as a function of the interaction strength ϵa for small (red dashed lines) and large (blue solid lines) parasites and different exponents (from left to right): a = 0 (circles), a = 1 (stars), a = 2 (diamonds), and a = 3 (triangles). The shown values are for side contact between the parasite and RBC membrane. The horizontal black dashed lines indicate ranges of assigned deformation indices; see Table 2. To see this figure in color, go online.
Small, ϵa/kBT = 4; large, ϵa/kBT = 2. For Id, see snapshots in Fig. 2. Here, a = 0 (homogenous adhesion).
Small, ϵa/kBT = 10; large, ϵa/kBT = 5.4. For Id, see snapshots in Fig. 2. Here, a = 0 (homogenous adhesion).
To characterize RBC deformations, a discrete deformation index Id was introduced in experiments (18). This index divides membrane deformations into four categories and is assigned based on the visual inspection of RBC deformations. These categories are summarized in Table 2. In addition, we also associate the deformation indices with different ranges of deformation energy (see Table 2) using our simulation results. The RBC-parasite configurations in Fig. 2 are representative examples of different index categories.
Table 2.
Definition of the Deformation Index Id, which Is Determined by a Visual Inspection of RBC Membrane Deformations
| Id | Visible deformations | ΔErbc/kBT |
|---|---|---|
| 0 | No visible deformations | [0, 150) |
| 1 | Small and local deformations | [150, 800) |
| 2 | Partial wrapping of the parasite, local deformations | [800, 2000) |
| 3 | Wrapping of the parasite, RBC shape is globally deformed | ≥2000 |
See (18). Connecting visual membrane deformations to the computed deformation energy ΔErbc allows us to define deformation energy ranges, which describe well different deformation indices.
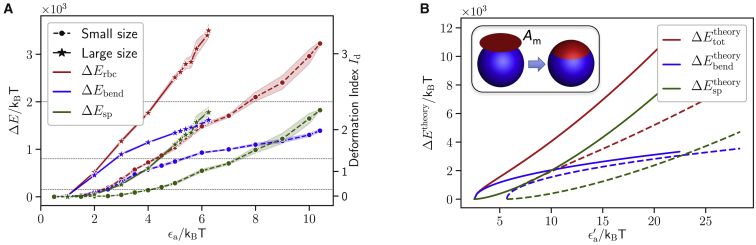
ΔErbc represents deformation energy in which all contributions are lumped together. Fig. 4 A shows different contributions to ΔErbc as a function of the interaction strength ϵa for the case of a = 0 and the two parasite sizes. The main contributions to the deformation energy correspond to bending elasticity (i.e., Ebend in Eq. 1) of the lipid bilayer and shear elasticity (i.e., Esp in Eq. 1) of the spectrin network. Contributions from the area- and volume-conservation constraints are very small and can be neglected. For small membrane deformations (i.e., for Id = 1), the bending energy contribution ΔEbend dominates over ΔEsp. For large RBC deformations with Id = 2 or 3, the stretching-energy contribution ΔEsp becomes dominant, pointing to significant stretching of the spectrin network. Note that for a > 0, the results for different contributions to ΔErbc are similar to the case a = 0.
Figure 4.
(A) Different contributions to the deformation energy, including bending elasticity (blue) of the lipid bilayer and shear elasticity (green) of the spectrin network, as a function of the interaction strength ϵa for small (dashed lines with circles) and large (solid lines with stars) parasite sizes. Small membrane deformations primarily correspond to membrane bending characterized by ΔEbend, whereas at large deformations, the contribution of stretching energy ΔEsp dominates. Here, a = 0 (homogeneous adhesion). (B) Bending and stretching energy contributions are shown, computed from the theoretical model in Eqs. 13 and 14 for the RBC parameters from Table 1 and the two sphere radii Rs = 0.5 μm (dashed lines) and Rs = 0.75 μm (solid lines), mimicking small and large parasite sizes, respectively. Here, . The inset illustrates wrapping of the sphere mimicking merozoite by a membrane patch with area Am. To see this figure in color, go online.
The dependence of different membrane deformation energies on ϵa in Fig. 4 A can be understood qualitatively from a theoretical model for wrapping of a sphere (mimicking the parasite) by a membrane patch with area Am, as illustrated schematically in the inset of Fig. 4 B. The total energy of the wrapped state can be approximated as (36, 37)
| (13) |
where Rs is the sphere radius and the sphere area. The first term in Eq. 13 represents stretching energy of the wrapped patch, the second corresponds to bending energy , and the third is the energy gained through adhesion. Therefore, the coefficient represents a gain in the adhesion energy per area Ac or the corresponding interaction energy between a single parasite particle and all membrane vertices within the cutoff radius rcut (i.e., is a function of ϵa). Minimization of Etheory with respect to Am yields
| (14) |
Therefore, the area of the adhered membrane is proportional to the square root of the interaction strength for other parameters fixed. Using this expression for Am, different energy contributions as a function of can be estimated from Eq. 13 and are shown in Fig. 4 B for the RBC parameters from Table 1 and the two sphere radii Rs = 0.5 μm and Rs = 0.75 μm, mimicking small and large parasite sizes, respectively. The dependence of different energies from the theoretical model is qualitatively consistent with the RBC energies in Fig. 4 A measured from simulations. Note that the stretching-energy contribution becomes larger than that from the bending energy for large enough or ϵa values because , whereas . Finally, this theory confirms qualitatively that the large parasite should induce stronger membrane deformations than the small parasite for the same interaction strengths because it has a larger adhesion area.
Parasite adhesion force
As shown above, strong enough adhesion interactions between parasite and RBC lead to strong membrane deformations, which are visually similar to experimentally observed cell deformations (18). However, it is not clear whether the employed values of ϵa quantitatively correspond to realistic adhesion forces. Interaction strength of spent merozoites has been measured in experiments by attaching a merozoite to two RBCs with the parasite in the middle (9). This is possible because spent parasites have lost their ability to invade RBCs but still adhere to them. The elongation of one RBC pulled away by optical tweezers is used to quantify the force required for rupturing RBC-parasite adhesion contact. Experimental detachment forces are in the range of 10–40 pN (9).
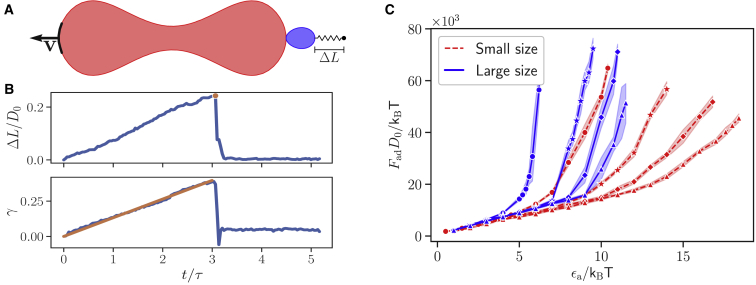
We perform simulations mimicking these experiments to quantify adhesion forces for different interaction models and strengths. The corresponding simulation setup is shown schematically in Fig. 5 A. A parasite is adhered with its head (or apex) to an RBC that is pulled away with a constant velocity v (see Video S3). Note that this apex-membrane orientation in simulations yields detachment measurements, which represent maximal adhesion forces, whereas in experiments (9), parasite adhesion orientation is neither controlled nor tracked, so it is likely random. The second RBC in the experimental setup is replaced by a harmonic spring with a spring constant /kBT = 211,250 ( 20 pN μm−1), which tethers the parasite’s center of mass to its initial position. The pulling velocity is applied to a cluster of 0.025Nrbc membrane particles at the rim position opposite to the parasite and is chosen such that the strain rate for RBC deformation remains close to an experimentally used strain rate of ( 0.1 s−1) (9), where Dr is the diameter of an RBC at rest and ΔD is the elongation of this diameter as a result of the applied strain γ (see Fig. 5 B). Detachment force is then measured as a maximal force Fad = kΔLmax on the harmonic spring tethering the parasite, as shown in Fig. 5 B. Here, ΔLmax is the spring elongation at the time when the connection between the parasite and RBC ruptures.
Figure 5.
(A) Schematic illustration of a simulation to determine the detachment force Fad. A parasite, whose center of mass is tethered by a harmonic spring, is adhered to an RBC. The rim of the RBC (a cluster of 0.025Nrbc membrane particles) opposite to the parasite is pulled away with a constant velocity v (see Video S3). (B) Fad is measured through the elongation ΔL of the harmonic spring tethering the parasite when it detaches from the RBC, i.e., the maximal measured force. Applied strain γ for RBC deformation corresponds to a nearly constant strain rate of 0.1 s−1 employed in experiments (9). Here, ΔL/D0 and γ are plotted for the small parasite with a = 0 and ϵa/kBT = 10. (C) Fad as a function of the interaction strength ϵa is shown for small (red dashed lines) and large (blue solid lines) parasites and different exponents (from left to right): a = 0 (circles), a = 1 (stars), a = 2 (diamonds), and a = 3 (triangles). The adhesion force increases for all values of a with increasing the interaction strength. To see this figure in color, go online.
See Fig. 5 A. Here, the small parasite with a = 0 and ϵa/kBT = 10 is employed.
Fig. 5 C presents detachment forces as a function of the interaction strength ϵa for different values of the exponent a and the two parasite sizes. Fad increases nonlinearly with increasing ϵa because larger interaction strengths lead to a stronger wrapping (i.e., a larger interaction area) of the parasite by RBC membrane. The curve for a = 0 represents the steepest increase in Fad because it corresponds to the strongest interaction between the parasite and RBC (see Fig. 1 C). The large parasite exhibits larger detachment forces than the small parasite for same interaction models and strengths. The detachment forces from simulations in Fig. 5 C can be compared to experimentally measured forces (9), e.g., FadD0/kBT = 60 × 103 corresponds to Fad 40 pN. Therefore, Fad in Fig. 5 C is smaller than 50 pN for all shown cases so that the range of employed adhesion strengths realistically represents interactions between the parasite and the RBC membrane.
Parasite alignment
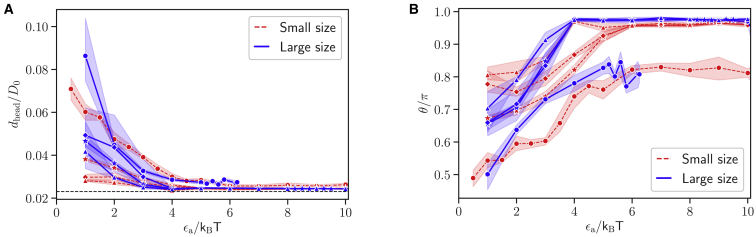
For a successful RBC invasion, the parasite needs to align its apex (or head) toward cell membrane. Experiments indicate that the parasite head has to be in close proximity to the membrane surface, and a successful invasion strongly correlates with a perpendicular alignment of the parasite toward RBC membrane (5, 7). Therefore, we introduce the head distance dhead and alignment angle θ, illustrated in Fig. 6, which allow the quantification of parasite alignment required for RBC invasion. dhead is defined as the distance between the parasite head rhead and a membrane vertex ri that minimizes the distance dhead = mini|rhead − ri|. θ is measured between the directional vector n of the parasite and the normal vector ni of a triangular face whose center is closest to the parasite head, as sketched in Fig. 6. With these definitions, an optimal alignment is achieved for small values of dhead and an alignment angle θ ∼ π. Note that this optimal value of θ may not be reached even for a perfect perpendicular alignment because only the closest triangle is used to calculate θ, and this triangle may not lie directly in front of the apex. Therefore, every angle θ ≥ 0.8π is considered to correspond to good alignment.
Figure 6.
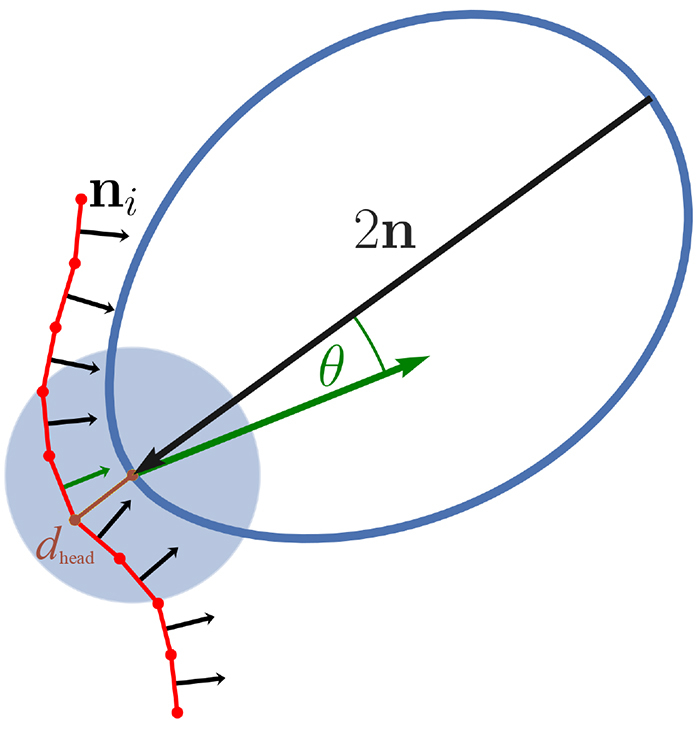
A sketch illustrating the measurement of a head distance dhead and alignment angle θ. dhead is calculated as the distance between the parasite head and the closest membrane vertex (brown color). θ is determined as the angle between the directional vector n of the parasite and the normal of a triangular face (green arrow) whose center is closest to the parasite head. The alignment angle is calculated only if the head of the parasite is within a certain interaction range with the membrane, as indicated by the blue circle. To see this figure in color, go online.
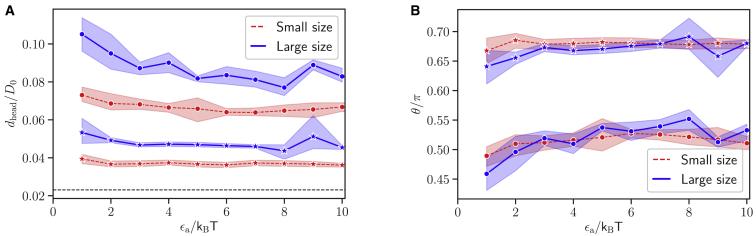
Fig. 7 shows the two alignment characteristics as a function of the interaction strength ϵa for different exponents a and the two parasite sizes. For all adhesion models, the values of dhead in Fig. 7 A decrease with increasing ϵa and closely approach the minimal possible distance represented by the repulsive range σ of the LJ interaction. The alignment angle θ in Fig. 7 B increases with increasing interaction strength. Thus, both characteristics show a positive correlation of parasite alignment with interaction strength ϵa or equivalently with RBC deformation. This is mainly due to the fact that a larger ϵa value leads to a stronger wrapping of the parasite by the RBC membrane, bringing the parasite head closer to the membrane surface. For weak interaction strengths ϵa/kBT 4, both alignment characteristics show some quantitative differences for the two parasite sizes; however, qualitative behavior of these characteristics is similar for both merozoite sizes. For strong parasite-membrane interactions, the alignment properties become nearly independent of the parasite size. Furthermore, an interaction gradient along the parasite’s body for a > 0 aids the alignment because such gradients favor parasite adhesion with an orientation of its head toward RBC membrane. The effect of interaction gradient on the parasite alignment can be clearly seen in Fig. 7, in which both alignment properties are better for a > 0 in comparison to the case of a = 0. For instance, values of θ for a = 0 in Fig. 7 B do not closely approach π even for large ϵa values. Nevertheless, all models show good parasite alignment properties for interaction strengths ϵa/kBT 4, which correspond to small levels of membrane deformations (Id ≥ 1), as shown in Fig. 3.
Figure 7.
(A) Average head distance dhead and (B) average alignment angle θ for different interaction strengths ϵa, small (red dashed lines) and large (blue solid lines) parasites, and different exponents: a = 0 (circles), a = 1 (stars), a = 2 (diamonds), and a = 3 (triangles). The black dashed line in plot (A) represents the minimal possible distance σ of the repulsive LJ interaction. An optimal parasite alignment corresponds to small values of dhead and an alignment angle close to π. Both characteristics show a positive correlation between the parasite alignment and the interaction strength (or equivalently the level of RBC deformation) for both parasite sizes. To see this figure in color, go online.
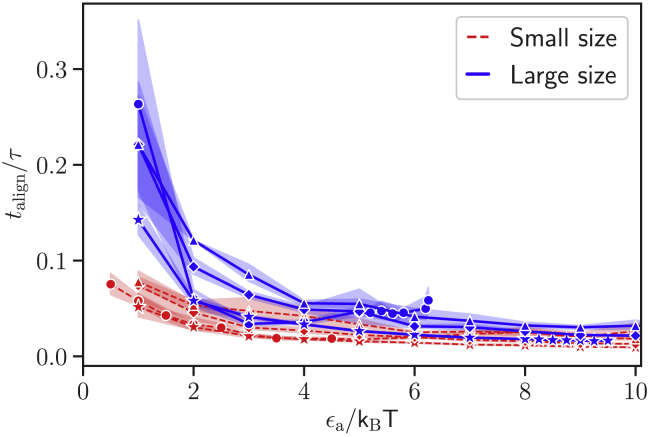
Another important aspect of the parasite alignment is the average time required for this process. Experimental observations indicate that parasite alignment generally occurs within a time range between a few seconds and 1 min (18). Fig. 8 shows average alignment times from simulations for different interaction strengths ϵa, values of a, and the two parasite sizes. The alignment time corresponds to a time difference between the moments the parasite starts to interact with the membrane and when it reaches its stationary adhesion configuration. The simulated alignment times in Fig. 8 are similar for various models with different interaction gradients. The large parasite is subject to a slower reorientation in comparison to the small merozoite, which is likely due to differences in rotational friction that scale as size cubed. Nevertheless, all simulated alignment times are significantly smaller than 1.1τ ( 1 s). This means that the alignment times in simulations are about two orders of magnitude smaller than those found experimentally (18).
Figure 8.
Average alignment time as a function of the interaction strength ϵa for small (red dashed lines) and large (blue solid lines) parasites, and different exponents: a = 0 (circles), a = 1 (stars), a = 2 (diamonds), and a = 3 (triangles). All models result in alignment times talign that are significantly smaller than 1.1τ ( 1 s). To see this figure in color, go online.
Rigid RBC membrane
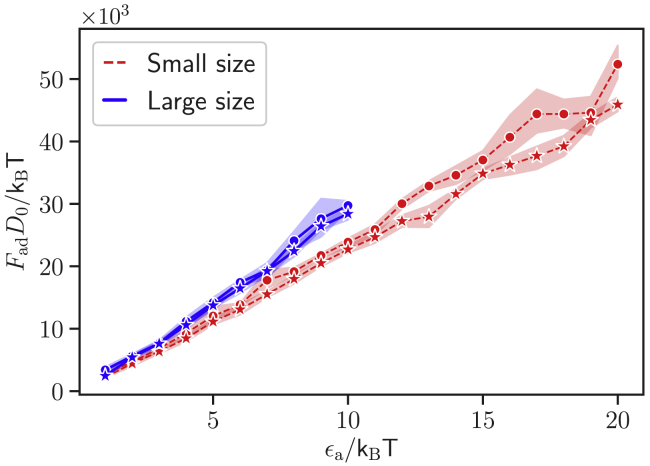
To investigate the effect of membrane deformations on the parasite alignment, simulations are performed with stiffened RBCs. Here, the bending rigidity and the Young’s modulus of RBC membrane are increased by two orders of magnitude in comparison to a healthy cell so that the membrane can be considered rigid. As a result, the parasite does not induce deformations for all studied interaction strengths. Fig. 9 shows the adhesion force Fad as a function of ϵa for a = 0 and a = 1 and the two parasite sizes. Fad has a linear dependence on the interaction strength for both parasite sizes and values of a. This is due to the fact that interaction area between the parasite and RBC is independent of ϵa and remains constant because the parasite cannot deform the RBC membrane. The detachment force can still reach magnitudes of up to 40 pN for large enough ϵa values. Fad in Fig. 9 is similar for both a = 0 and a = 1 models; however, the detachment force is slightly larger for the large parasite in comparison to the small merozoite because the large parasite has a smaller local curvature, allowing the formation of a slightly larger interaction area than that for the small parasite.
Figure 9.
Adhesive force Fad of the parasite to a rigid RBC for different interaction strengths ϵa, small (red dashed lines) and large (blue solid lines) parasites, and two exponents: a = 0 (circles) and a = 1 (stars). Fad for a rigid RBC grows more slowly with increasing ϵa than that for a deformable RBC in Fig. 5C and has a nearly linear dependence on the interaction strength; as for the rigid cell, the adhesion area is independent of ϵa. To see this figure in color, go online.
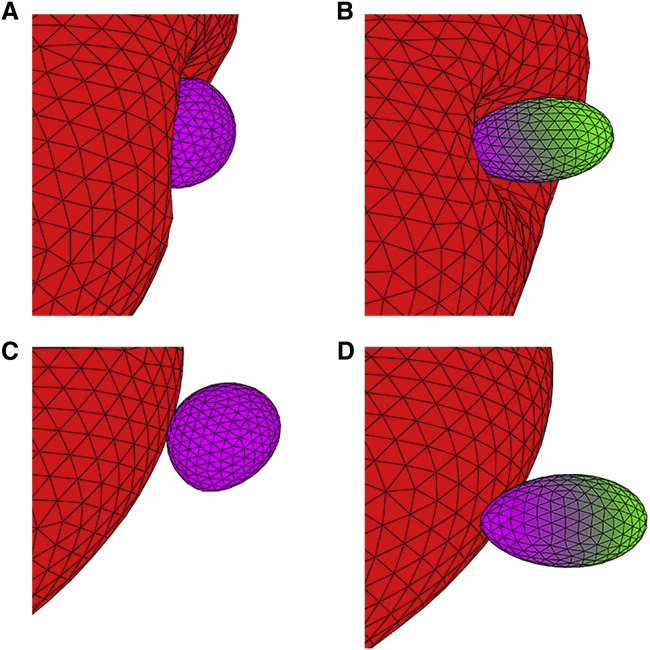
Fig. 10 presents the head distance dhead and the alignment angle θ for a parasite adhering to a rigid RBC. Both dhead and θ remain nearly constant independently of ϵa. This means that the quality of parasite alignment is not influenced by the interaction strength and remains rather poor. This is due to the inability of the parasite to deform the RBC membrane so that it positions itself sideways on the membrane (i.e., its directional vector is nearly perpendicular to membrane normal for a = 0; see Fig. 11 C) because this configuration represents a maximal adhesion energy. The large parasite has slightly larger dhead than the small parasite (see Fig. 10 A); however, for both sizes, the alignment is poor. The case of a = 1 shows a better alignment in comparison to a = 0 because the interaction gradient facilitates the reorientation of parasite head toward the RBC membrane. However, both interaction models for parasite adhesion to a rigid RBC yield worse alignment results than those for deformable RBCs. This can be seen in Fig. 11, which shows conformations of the parasite adhered to rigid and flexible membranes. For a = 1, the parasite has a good alignment for both membrane rigidities because the interaction gradient (marked by color at the parasite surface) brings the parasite’s head close to the membrane (see Fig. 11, B and D). For a = 0, the energetically favorable adhesion configuration is a sideways positioning of the parasite with θ ≈ 0.5π (see Fig. 11, A and C; Videos S4 and S5), which represents poor alignment. However, in the case of a deformable RBC, the parasite can become partially wrapped by the RBC membrane, making the membrane-apex contact probable.
Figure 10.
Alignment characteristics given by (A) head distance dhead and (B) alignment angle θ for the parasite interacting with a rigid RBC. Both characteristics are nearly independent of the interaction strength ϵa and generally show a poor parasite alignment. Data for both small (red dashed lines) and large (blue solid lines) parasites and the two exponents a = 0 (circles) and a = 1 (stars) are shown. The black dashed line in plot (A) represents the minimal possible distance σ of the repulsive LJ interaction. To see this figure in color, go online.
Figure 11.
Comparison of parasite alignment at flexible RBCs (A and B) and rigid RBCs (C and D) for a = 0 with ϵa/kBT = 5 (A and C) and a = 1 with ϵa/kBT = 8 (B and D), where the interaction gradient is marked by a color code on the parasite surface (purple: maximal interaction strength, green: minimal interaction strength). For flexible RBCs, the observed alignment is better than for the rigid membrane because the parasite can become partially wrapped by the flexible cell membrane (see Videos S4 and S5). For a = 1, the alignment is good in both cases because a configuration with the parasite’s head toward the membrane minimizes the total energy. Here, the illustrations are for the small parasite size. To see this figure in color, go online.
See Fig. 11 A.
See Fig. 11 C.
Discussion
Our simulation results support the passive compliance hypothesis (20), which states that the alignment of merozoites arises from mechanical adhesion interactions between the parasite and RBC and induced membrane deformations. Here, both bending and stretching properties of the RBC membrane contribute to the resistance against parasite-induced deformations. For small local deformations, bending energy dominates, whereas strong membrane deformations lead to significant stretching of the RBC spectrin network. More importantly, the adhesion forces required for such deformations are within the range of experimentally measured forces 10–40 pN (9). The detachment force increases superlinearly with elevated interaction strength because the parasite becomes strongly wrapped by the RBC membrane, resulting in a significant increase of the interaction area. Thus, an increase in the interaction strength quickly leads to a very stable parasite-membrane adhesion. Larger parasites induce stronger membrane deformations and lead to larger adhesion forces in comparison to smaller parasites for the same strength of surface interactions. Nevertheless, the adhesion characteristics are qualitatively similar for the considered parasite sizes. More importantly, both the level of deformations and the adhesion forces reproduce well experimentally observed behavior (9, 18).
Analysis of parasite alignment characteristics such as the head distance dhead and the alignment angle θ shows that stronger membrane deformations lead to a better parasite alignment for all considered interaction models and parasite sizes. The primary reason for the good alignment due to strong parasite-RBC interactions is that the parasite gets partially wrapped by RBC membrane, facilitating a contact between the membrane and the parasite head. For instance, in the case of weak adhesion interactions, which do not induce significant membrane deformations, an equilibrium adhesion configuration corresponds to the parasite lying on its side because of the parasite’s egg-like geometry. This configuration makes a contact between the parasite head and the membrane unlikely. Therefore, strong membrane deformations serve as a hallmark of efficient parasite alignment followed by RBC invasion. This result compares favorably with recent experiments (18), in which RBC deformations characterized by a deformation index were found to correlate positively with the parasite invasion frequency.
Furthermore, parasite models with an adhesion gradient along the parasite body show that such gradients facilitate a better alignment because they introduce stronger adhesion interactions toward the parasite’s head. Strong enough adhesion gradients result in a perfect parasite alignment, which is generally not observed in experiments. In addition, the existence of adhesive gradients leads to very fast parasite alignment in a subsecond regime. The main reason for this quick reorientation due to adhesion gradients is that they lead to a well-controlled, directed, and fast motion of the parasite toward perfect alignment by maximizing the interaction energy. A comparison with experimental observations in (18) shows that the alignment in our simulations is about two orders of magnitude faster and that the real motion of the parasite at RBC membrane is often much more erratic than the parasite motion modeled with an interaction gradient. These results suggest that there should not be strong permanent adhesion gradients along the parasite body because they lead to very fast reorientation times and suppress diffusive parasite behavior.
The importance of RBC membrane deformations for the parasite alignment is further emphasized by the simulations of parasite adhesion to rigid RBCs. These simulations show that there is no correlation between the adhesion strength and the quality of parasite alignment. Furthermore, the alignment quality for the parasite interaction with a rigid RBC is quite poor in comparison to a deformable membrane. This is due to the fact that the minimal energy for parasite adhesion to a rigid surface corresponds to a configuration in which the parasite lies on its side because of its egg-like shape. This adhesion configuration is independent of the interaction strength and represents a poor alignment. Addition of the interaction gradient along the parasite’s body improves the parasite alignment on a rigid RBC but does not make it perfect, as in the case of a deformable membrane. An increased rigidity of the RBC membrane is relevant for several blood diseases and disorders such as sickle-cell anemia (38), thalassemia (39), and stomatocytosis (40). For example, the invasion efficiency of merozoites is reduced for sickle-cell and thalassemic RBCs (41). Our simulation study suggests that a poor parasite alignment due to RBC membrane stiffening can contribute to the reduction in the invasion of RBCs by merozoites.
Even though the parasite adhesion model with a fixed interaction potential reproduces important aspects of the parasite alignment, it does not capture the frequently observed erratic dynamics of a merozoite at an RBC membrane. The fixed interaction potential leads to a stationary adhesion configuration in which the parasite does not exhibit significant motion. This model captures the behavior of spent or inactive parasites, but it fails to describe parasite dynamics, which is generally much more vivid. One possible reason for this model behavior can be the activity of parasite agonists. The fixed interaction potential mimics a situation in which the density of adhesive agonists at the parasite surface is large enough to allow an averaged description. A more realistic approach for the parasite adhesion would be an explicit representation of the discrete nature of binding agonists, which can be modeled by the formation and dissociation of discrete bonds between the parasite and the RBC membrane. Such a model is likely to lead to a more dynamic parasite adhesion to RBC membrane due to the stochasticity and dynamics of the discrete bonds. Clearly, further investigation is needed to clarify the discrepancies in the adhesion dynamics between model predictions and experimental observations and to establish a reliable mechanism for the parasite alignment process.
Finally, it is worth mentioning that the invasion of RBCs by merozoites is certainly a combination of mechanical and biochemical processes. The purely mechanistic model presented here realistically captures important features of parasite-RBC interactions and demonstrates that the passive compliance hypothesis is sufficient for parasite alignment. Of course, it does not exclude the possibility of active contributions to RBC deformation by the parasite at later stages. As an example, it has been suggested in several studies (10, 42) that the parasite may mediate RBC membrane properties by changing local concentration of calcium (Ca2+) ions. This suggestion has been eliminated as a potential cause for parasite alignment in recent experiments (20), which showed that RBC deformations are also observed in the absence of Ca2+, and calcium release by the parasite starts only at the invasion stage. However, to a large extent, the question about the importance of biochemical activity of a merozoite during the alignment process remains unanswered. Such biochemical processes, if known, can be incorporated into mechanical models of parasite-RBC adhesion in the future.
Author Contributions
S.H. and A.K.D. performed simulations and analyzed the computational results. G.G. and D.A.F. designed the research project. All authors interpreted the results and wrote the manuscript.
Acknowledgments
The authors thank Virgilio L. Lew and Pietro Cicuta from the University of Cambridge for insightful and fruitful discussions.
S.H. acknowledges support by the International Helmholtz Research School of Biophysics and Soft Matter (IHRS BioSoft). D.A.F. acknowledges funding by the Alexander von Humboldt Foundation. The authors also gratefully acknowledge the computing time granted through JARA-HPC on the supercomputer JURECA (35) at Forschungszentrum Jülich.
Editor: Mark Alber.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.08.027.
Supporting Material
References
- 1.World Health Organization World malaria report 2018. 2018. https://www.who.int/malaria/publications/world-malaria-report-2018/en/
- 2.Miller L.H., Baruch D.I., Doumbo O.K. The pathogenic basis of malaria. Nature. 2002;415:673–679. doi: 10.1038/415673a. [DOI] [PubMed] [Google Scholar]
- 3.Cowman A.F., Berry D., Baum J. The cellular and molecular basis for malaria parasite invasion of the human red blood cell. J. Cell Biol. 2012;198:961–971. doi: 10.1083/jcb.201206112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.White N.J., Pukrittayakamee S., Dondorp A.M. Malaria. Lancet. 2014;383:723–735. doi: 10.1016/S0140-6736(13)60024-0. [DOI] [PubMed] [Google Scholar]
- 5.Koch M., Baum J. The mechanics of malaria parasite invasion of the human erythrocyte - towards a reassessment of the host cell contribution. Cell. Microbiol. 2016;18:319–329. doi: 10.1111/cmi.12557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cowman A.F., Crabb B.S. Invasion of red blood cells by malaria parasites. Cell. 2006;124:755–766. doi: 10.1016/j.cell.2006.02.006. [DOI] [PubMed] [Google Scholar]
- 7.Bannister L.H., Mitchell G.H., Cohen S. Structure and development of the surface coat of erythrocytic merozoites of Plasmodium knowlesi. Cell Tissue Res. 1986;245:281–290. doi: 10.1007/BF00213933. [DOI] [PubMed] [Google Scholar]
- 8.Gilson P.R., Nebl T., Crabb B.S. Identification and stoichiometry of glycosylphosphatidylinositol-anchored membrane proteins of the human malaria parasite Plasmodium falciparum. Mol. Cell. Proteomics. 2006;5:1286–1299. doi: 10.1074/mcp.M600035-MCP200. [DOI] [PubMed] [Google Scholar]
- 9.Crick A.J., Theron M., Rayner J.C. Quantitation of malaria parasite-erythrocyte cell-cell interactions using optical tweezers. Biophys. J. 2014;107:846–853. doi: 10.1016/j.bpj.2014.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lew V.L., Tiffert T. Is invasion efficiency in malaria controlled by pre-invasion events? Trends Parasitol. 2007;23:481–484. doi: 10.1016/j.pt.2007.08.001. [DOI] [PubMed] [Google Scholar]
- 11.Dvorak J.A., Miller L.H., Shiroishi T. Invasion of erythrocytes by malaria merozoites. Science. 1975;187:748–750. doi: 10.1126/science.803712. [DOI] [PubMed] [Google Scholar]
- 12.Gilson P.R., Crabb B.S. Morphology and kinetics of the three distinct phases of red blood cell invasion by Plasmodium falciparum merozoites. Int. J. Parasitol. 2009;39:91–96. doi: 10.1016/j.ijpara.2008.09.007. [DOI] [PubMed] [Google Scholar]
- 13.Glushakova S., Yin D., Zimmerberg J. Membrane transformation during malaria parasite release from human red blood cells. Curr. Biol. 2005;15:1645–1650. doi: 10.1016/j.cub.2005.07.067. [DOI] [PubMed] [Google Scholar]
- 14.Crick A.J., Tiffert T., Cicuta P. An automated live imaging platform for studying merozoite egress-invasion in malaria cultures. Biophys. J. 2013;104:997–1005. doi: 10.1016/j.bpj.2013.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dasgupta S., Auth T., Gompper G. Membrane-wrapping contributions to malaria parasite invasion of the human erythrocyte. Biophys. J. 2014;107:43–54. doi: 10.1016/j.bpj.2014.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mitchell G.H., Thomas A.W., Bannister L.H. Apical membrane antigen 1, a major malaria vaccine candidate, mediates the close attachment of invasive merozoites to host red blood cells. Infect. Immun. 2004;72:154–158. doi: 10.1128/IAI.72.1.154-158.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Singh S., Alam M.M., Chitnis C.E. Distinct external signals trigger sequential release of apical organelles during erythrocyte invasion by malaria parasites. PLoS Pathog. 2010;6:e1000746. doi: 10.1371/journal.ppat.1000746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weiss G.E., Gilson P.R., Crabb B.S. Revealing the sequence and resulting cellular morphology of receptor-ligand interactions during Plasmodium falciparum invasion of erythrocytes. PLoS Pathog. 2015;11:e1004670. doi: 10.1371/journal.ppat.1004670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fedosov D.A., Noguchi H., Gompper G. Multiscale modeling of blood flow: from single cells to blood rheology. Biomech. Model. Mechanobiol. 2014;13:239–258. doi: 10.1007/s10237-013-0497-9. [DOI] [PubMed] [Google Scholar]
- 20.Introini V., Crick A., Lew V.L. Evidence against a role of elevated intracellular Ca2+ during Plasmodium falciparum preinvasion. Biophys. J. 2018;114:1695–1706. doi: 10.1016/j.bpj.2018.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fedosov D.A., Caswell B., Karniadakis G.E. Systematic coarse-graining of spectrin-level red blood cell models. Comput. Methods Appl. Mech. Eng. 2010;199:1937–1948. doi: 10.1016/j.cma.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fedosov D.A., Caswell B., Karniadakis G.E. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 2010;98:2215–2225. doi: 10.1016/j.bpj.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hoogerbrugge P.J., Koelman J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992;19:155–160. [Google Scholar]
- 24.Español P., Warren P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995;30:191–196. [Google Scholar]
- 25.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Chem. Phys. 1995;117:1–19. [Google Scholar]
- 26.Gompper G., Kroll D.M. Triangulated-surface models of fluctuating membranes. In: Nelson D.R., Piran T., Weinberg S., editors. Statistical Mechanics of Membranes and Surfaces. World Scientific; 2004. pp. 359–426. [Google Scholar]
- 27.Gompper G., Kroll D.M. Random surface discretizations and the renormalization of the bending rigidity. J. Phys. I (France) 1996;6:1305–1320. [Google Scholar]
- 28.Turlier H., Fedosov D.A., Betz T. Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat. Phys. 2016;12:513–519. [Google Scholar]
- 29.Lobaskin V., Dünweg B. A new model for simulating colloidal dynamics. New J. Phys. 2004;6:54. [Google Scholar]
- 30.Heard W.B. Wiley-VCH; Weinheim: 2006. Rigid Body Mechanics: Mathematics, Physics and Applications. [Google Scholar]
- 31.Hanssen E., Dekiwadia C., Ralph S.A. Electron tomography of Plasmodium falciparum merozoites reveals core cellular events that underpin erythrocyte invasion. Cell. Microbiol. 2013;15:1457–1472. doi: 10.1111/cmi.12132. [DOI] [PubMed] [Google Scholar]
- 32.Persson P.-O., Strang G. A simple mesh generator in MATLAB. SIAM Rev. 2004;46:329–345. [Google Scholar]
- 33.Backer J.A., Lowe C.P., Iedema P.D. Poiseuille flow to measure the viscosity of particle model fluids. J. Chem. Phys. 2005;122:154503. doi: 10.1063/1.1883163. [DOI] [PubMed] [Google Scholar]
- 34.Fedosov D.A., Karniadakis G.E., Caswell B. Steady shear rheometry of dissipative particle dynamics models of polymer fluids in reverse Poiseuille flow. J. Chem. Phys. 2010;132:144103. doi: 10.1063/1.3366658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Krause D., Thörnig P., Jülich Supercomputing Centre JURECA: modular supercomputer at Jülich supercomputing centre. J. Large-scale Res. 2018;4:A132. [Google Scholar]
- 36.Bowick M.J., Nelson D.R., Travesset A. Interacting topological defects on frozen topographies. Phys. Rev. B Condens. Matter Mater. Phys. 2000;62:8738–8751. [Google Scholar]
- 37.Schneider S., Gompper G. Shapes of crystalline domains on spherical fluid vesicles. Europhys. Lett. 2005;70:136–142. [Google Scholar]
- 38.Barabino G.A., Platt M.O., Kaul D.K. Sickle cell biomechanics. Annu. Rev. Biomed. Eng. 2010;12:345–367. doi: 10.1146/annurev-bioeng-070909-105339. [DOI] [PubMed] [Google Scholar]
- 39.Peters M., Heijboer H., Giordano P.C. Diagnosis and management of thalassaemia. BMJ. 2012;344:e228. doi: 10.1136/bmj.e228. [DOI] [PubMed] [Google Scholar]
- 40.Caulier A., Rapetti-Mauss R., Badens C. Primary red cell hydration disorders: pathogenesis and diagnosis. Int. J. Lab. Hematol. 2018;40(Suppl 1):68–73. doi: 10.1111/ijlh.12820. [DOI] [PubMed] [Google Scholar]
- 41.Tiffert T., Lew V.L., Mohandas N. The hydration state of human red blood cells and their susceptibility to invasion by Plasmodium falciparum. Blood. 2005;105:4853–4860. doi: 10.1182/blood-2004-12-4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McCallum-Deighton N., Holder A.A. The role of calcium in the invasion of human erythrocytes by Plasmodium falciparum. Mol. Biochem. Parasitol. 1992;50:317–323. doi: 10.1016/0166-6851(92)90229-d. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Small, ϵa/kBT = 4; large, ϵa/kBT = 2. For Id, see snapshots in Fig. 2. Here, a = 0 (homogenous adhesion).
Small, ϵa/kBT = 10; large, ϵa/kBT = 5.4. For Id, see snapshots in Fig. 2. Here, a = 0 (homogenous adhesion).
See Fig. 5 A. Here, the small parasite with a = 0 and ϵa/kBT = 10 is employed.
See Fig. 11 A.
See Fig. 11 C.