Mouth Function Determines the Shape Oscillation Pattern in Regenerating Hydra Tissue Spheres

Abstract

Hydra is a small freshwater polyp capable of regeneration from small tissue pieces and from aggregates of cells. During regeneration, a hollow bilayered sphere is formed that undergoes osmotically driven shape oscillations of inflation and rupture. These oscillations are necessary for successful regeneration. Eventually, the oscillating sphere breaks rotational symmetry along the future head-foot axis of the animal. Notably, the shape oscillations show an abrupt shift from large-amplitude, long-period oscillations to small-amplitude, short-period oscillations. It has been widely accepted that this shift in oscillation pattern is linked to symmetry breaking and axis formation, and current theoretical models of Hydra symmetry breaking use this assumption as a model constraint. However, a mechanistic explanation for the shift in oscillation pattern is lacking. Using in vivo manipulation and imaging, we quantified the shape oscillation dynamics and dissected the timing and triggers of the pattern shift. Our experiments demonstrate that the shift in the shape oscillation pattern in regenerating Hydra tissue pieces is caused by the formation of a functional mouth and not by shape symmetry breaking as previously assumed. Thus, model assumptions must be revised in light of these new experimental data, which can be used to constrain and validate improved theoretical models of pattern formation in Hydra.

Significance

Hydra spheres originating from tissue pieces or aggregates of body column cells undergo dramatic osmotically driven shape oscillations during regeneration. Previous works proposed a causal link between a characteristic abrupt shift in the frequency of shape oscillations of regenerating spheres and de novo axis specification via the establishment of morphogen gradients. Here, we break this link by demonstrating that regeneration without an oscillation pattern shift is possible and that the shift is a direct consequence of mouth function and its use in osmoregulation. Because the link between oscillation dynamics and axis specification was a key assumption in current models of Hydra regeneration, our results indicate that we must reexamine the mechanisms driving pattern formation in Hydra.

Introduction

Hydra is a small (∼1 cm long), transparent, radially symmetric freshwater cnidarian polyp (Fig. 1 A). It consists of a cylindrical body column with a tentacle ring and a dome-shaped hypostome containing the mouth on one end and a foot that anchors the animal to the substrate on the other. Hydra is composed of only two tissue layers: an outer ectodermal epithelium and an inner endodermal epithelium, separated by a basal lamina called the mesoglea. Body shape is regulated by contractile processes on the epithelial cells called myonemes, which are oriented longitudinally along the head-foot axis in the ectoderm and circumferentially in the endoderm (1). This simple anatomy, combined with the ability to regenerate a complete polyp from tissue pieces and from aggregates of body column cells, made Hydra an important model system for biologists and physicists alike to study regeneration, axis formation, and patterning (2).

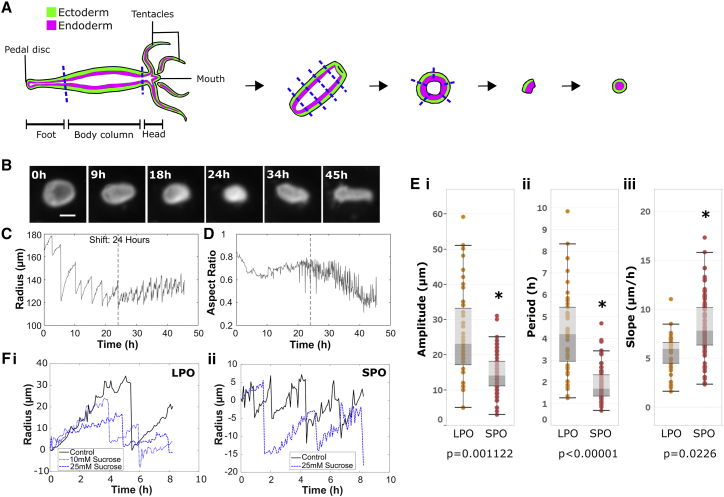
Figure 1.

Generation of tissue spheres and quantification of oscillation dynamics. (A) Preparation of tissue pieces from a Hydra polyp (see Materials and Methods) is shown. (B) Representative images of regenerating tissue spheres at various time points during regeneration are shown. In the 45 h image, the regenerated head with tentacles is to the left. Scale bars, 150 μm. (C) Shown is a plot of effective radius, calculated as the radius of a circle with an area equal to that of the tissue piece, as a function of time for the sphere shown in (B). (D) Shown is a plot of aspect ratio as a function of time for the same tissue sphere. The dashed line indicates the time of shift from LPO to SPO. (E) Box-whisker plots of (i) amplitudes, (ii) time periods, and (iii) slopes for LPOs and SPOs for body column tissue pieces regenerating in HM are shown. The asterisk indicates a statistically significant difference from LPO (p < 0.05): amplitude p = 0.0011; period p < 1e−5; slope p = 0.0226. (F) A plot of effective radius (adjusted to set initial radius to zero) as a function of time at different sucrose concentrations in the external medium during (i) LPOs and (ii) SPOs is shown. To see this figure in color, go online.

One of the earliest attempts at modeling axial patterning in Hydra was made by Alfred Gierer and Hans Meinhardt (3), who proposed a reaction-diffusion model consisting of a short-range head activator, a long-range head inhibitor, and a gradient for the activator source. The model qualitatively explains pattern formation from a homogeneous starting state. However, a lack of quantitative experimental data has limited progress on validation and refinement of this and subsequent models (4). Recently, the availability of a fully sequenced genome (5), various transgenic reporter lines (6, 7) and CRISPR genome editing tools (8) has allowed researchers to reexamine earlier models and studies of Hydra regeneration and gain new insights.

Here, we revisit a striking phenomenon that occurs during Hydra regeneration from tissue pieces (9) and aggregates of cells (3). As they regenerate, both tissue pieces and aggregates form a hollow bilayered sphere with ectodermal cells on the outside and endodermal cells on the inside. These Hydra spheres undergo osmotically driven cycles of swelling and subsequent rupture, referred to as shape oscillations (10, 11). The shape oscillations are sawtooth shaped, consisting of cycles of a long inflation phase followed by an abrupt deflation of the sphere due to local tissue rupture (12). The inflation phase is caused by the uptake of water and the active pumping of sodium ions into the lumen of the sphere (13). Initially, inflation is isotropic. The Hydra sphere’s aspect ratio, defined as the ratio of the minor axis to the major axis of an ellipse fit to the sphere, is close to unity. As time progresses, the swelling becomes increasingly anisotropic: the aspect ratio decreases with sharp dips during deflation of the hollow sphere. The regenerating animal breaks spherical symmetry to establish a body axis and develops a mouth and tentacles by ∼48 h (11).

Previous studies have utilized different definitions and criteria for symmetry breaking. First, morphological, or shape symmetry breaking, refers to the tissue sphere becoming ellipsoidal, which has been quantified by shape analysis either through a decrease in the aspect ratio of an ellipsoid fit to the tissue sphere (14) or as changes in the Fourier modes of the two-dimensional contour of the tissue over time (11). Second, biochemical symmetry breaking involves spatial patterning of morphogens such as Wnt3 (15) to specify a body axis and the position of the head, foot, and tentacles. Finally, structural symmetry breaking involves the reorganization of supracellular structures such as myonemes (16). Although these aspects have been studied individually and feedback between morphological and biochemical symmetry breaking has been proposed by some studies (4, 14, 17), the lack of tools to visualize morphogen gradients in vivo has prevented researchers from demonstrating a causal connection.

It has long been hypothesized that shape symmetry breaking coincides with or occurs shortly after the morphogen patterning proposed by Gierer and Meinhardt (3), leading models to use the time of oscillation pattern shift as the time of biochemical symmetry breaking. To the best of our knowledge, the mechanism underlying the oscillation pattern shift has not been determined. Sato-Maeda and Tashiro (12) were the first to probe the connection between shape oscillations and axis formation two decades ago. They reported the sawtooth shape of the oscillations and described a method of detecting shape symmetry breaking in cell aggregates by quantifying the divergence of orthogonal radii as the regenerating animal elongated along one axis. This approach represented a measure of body axis formation that could be quantitatively linked to other morphological fluctuations. Fütterer et al. (11) subsequently analyzed the shape of regenerating Hydra spheres originating from tissue pieces in greater detail, using Fourier decomposition to reveal three distinct temporal stages: 1) large-amplitude, long-period oscillations (LPOs) of the zeroth mode (size of the tissue piece); 2) small-amplitude, short-period oscillations (SPOs) of the zeroth mode associated with fluctuations of the second mode (elongation); and 3) strong increase in the second mode during contractions. They reported that shape anisotropy always occurred after the completion of LPOs, suggesting a correlation between oscillation dynamics and formation of the body axis as implied by shape symmetry breaking (11).

Hydra spheres derived from cell aggregates and from small tissue pieces exhibit similar oscillation dynamics. It was also reported that regenerating spheres reoriented their body axes in alignment with an applied temperature gradient regardless of their origin, so long as the gradient was applied before the onset of SPOs (18). Consequently, it was conjectured that both tissue pieces and cell aggregates begin from a homogenous state and must break symmetry de novo. The idea that the pattern shift occurs at the same time as biochemical symmetry breaking was supported by the finding that the time of pattern shift from LPO to SPO coincides with the emergence of critical scaling in the patch size distribution of the Hydra head-specific gene ks1 (18). Secondly, β-catenin, which acts as a mechanotransducer in other model organisms (19), is involved in Hydra head specification via the canonical Wnt pathway (20, 21). Because the timing of oscillation pattern shift at ∼24 h (15) was comparable to the timing of the emergence of expression patches of Wnt3, the earliest known marker expressed during Hydra head regeneration (22, 23), in larger cell aggregates, Soriano et al. (14) concluded that the oscillation pattern shift must also coincide with the establishment of biochemical asymmetry. Consequently, it has been proposed that β-catenin may link the mechanical forces caused by tissue stretch or rupture with biochemical patterning in Hydra (14). This remains to be experimentally verified, but the theory is attractive because of the known role of mechanotransduction pathways in a wide range of morphogenetic and developmental processes (24).

Thus, the pattern shift was regarded as a reliable and easily detectable marker of the morphological and biochemical symmetry breaking event in both aggregates and small tissue pieces (18). Because of this apparent link, subsequent theoretical models by Soriano et al. (14) and Mercker et al. (4) coupled tissue mechanics with reaction-diffusion of morphogens to explain axis formation in Hydra. Both authors acknowledge that equating the time of oscillation pattern shift to that of biochemical symmetry breaking is a possible overestimation but use this assumption to constrain their models for lack of viable alternatives.

Recently, the assumption that both small tissue pieces and aggregates break symmetry de novo has been challenged. It was shown that spheres derived from small tissue pieces inherit the parent animal’s myoneme organization and, as such, have structural asymmetry from the beginning (16). How this structural asymmetry relates to morphological or biochemical symmetry breaking remains elusive. However, it suggests that regenerating tissue spheres possess a predetermined body axis, which is incompatible with existing models of Hydra regeneration, assuming that small regenerating tissue fragments and regenerating aggregates both begin from an isotropic state and exhibit a true symmetry breaking event. In light of this apparent paradox in the existing literature, there is a need to determine the cause of the LPO-SPO shift and understand its relevance.

Here, we use in vivo manipulation and imaging to quantify shape oscillation dynamics and experimentally dissect the timing and triggers of the pattern shift. First, we demonstrate that both LPOs and SPOs are driven by osmotic pressure, suggesting that the observed differences do not arise from different swelling mechanisms but from changes in the local yield strength of the tissue spheres. Consistent with this idea, we find that the site of tissue rupture is random during LPOs but conserved during SPOs, suggesting the existence of a fixed mechanical weak point during SPOs. We demonstrate that this weak spot is the mouth. Furthermore, we show that mouth structure alone is insufficient to cause an oscillation pattern shift because tissue pieces derived from nerve-free animals, which are unable to open their mouths, regenerate fully but exhibit only LPOs. Additionally, tissue pieces derived from the heads of normal animals containing a functional mouth were found to exhibit only SPOs, whereas tissue pieces from the heads of nerve-free animals with a structurally normal but nonfunctional mouth only exhibit LPOs. Together, these experiments demonstrate that the shift in oscillation pattern observed in regenerating Hydra tissue pieces is caused by the onset of mouth function. Therefore, the pattern shift is an indicator of active control of mouth opening, providing an easily observable readout for an important regeneration milestone. In addition to providing a mechanistic explanation for shape oscillation dynamics, this study also allowed us to estimate a lower bound for the tissue yield strength, a parameter which may prove useful for future models of Hydra regeneration.

Materials and Methods

Hydra strains and culture

Hydra vulgaris strain AEP, Hydra vulgaris (formerly Hydra magnipapillata strain 105) strain sf-1 (temperature-sensitive interstitial stem cells), Hydra vulgaris strain A10 (chimera consisting of Hydra vulgaris epithelial cells and sf-1 interstitial cells) (25), and Hydra vulgaris “watermelon” (AEP expressing GFP in the ectoderm and DsRed2 in the endoderm) (7) were used for experiments. Polyps were kept in Hydra medium (HM) composed of 1 mM CaCl₂ (Spectrum Chemical, New Brunswick, NJ), 0.1 mM MgCl₂ (Sigma-Aldrich, St. Louis, MO), 0.03 mM KNO₃ (Fisher Scientific, Waltham, MA), 0.5 mM NaHCO₃ (Fisher Scientific, Hampton, NH), and 0.08 mM MgSO₄ (Fisher Scientific) prepared with MilliQ water, with pH between 7 and 7.3, at 18°C in a Panasonic incubator (Panasonic MIR-554, Kadoma, Japan) in the dark. The Hydra were fed three times per week with Artemia nauplii (Brine Shrimp Direct, Ogden, UT). Animals were cleaned daily using published procedures (26).

Generation of nerve-free Hydra

Nerve-free Hydra were generated using either of two methods. Watermelon animals were made nerve free as described by Tran et al. (27). Briefly, the animals were incubated in 0.4% colchicine (Acros Organics, Thermo Fisher Scientific, Waltham, MA) in HM for 8 h in the dark. This 8 h incubation was then repeated 3 weeks after the first treatment. Colchicine-treated Hydra are susceptible to bacterial infection, so the animals were kept in HM supplemented with 50 μg/mL rifampicin (EMD Millipore, Burlington, MA) at 18°C in the dark in the incubator. Nontransgenic nerve-free animals were generated by heat shock treatment of the sf-1 and A10 strains (25, 28, 29). Sf-1 and A10 animals were heat shocked in an incubator at 29°C in the dark for 48 h and then moved back into the 18°C incubator. All nerve-free animals were force fed and “burped” as per the protocol described in Tran et al. (27).

Preparation of tissue pieces

Tissue pieces were cut with a scalpel (Sklar Instruments, West Chester, PA) from the body columns of adult nonbudding Hydra starved for 24 h, as shown in Fig. 1 A. The head was amputated immediately below the tentacles. A second cut was made above the foot to isolate the body column. Depending on the size of the resulting body column piece, one to three cross-sectional cuts were made to extract rings. The rings were cut into four or more pieces and allowed to round up in HM for ∼2 h (measured from the time of initial excision of the body column piece). Once rounded up, tissue pieces were selected by size (<200 μm radius) by visual examination under a stereo microscope for use in experiments (Fig. 1 A).

Preparation of head and foot tissue pieces

Head tissue pieces were prepared under a stereo microscope. The animals’ heads were removed immediately below the tentacle ring, and then the tentacle bases were excised. The remaining head tissue pieces were given ∼1 h to round up and placed individually into custom-made agarose wells for time-lapse imaging. Foot tissue pieces were prepared by cutting the animals immediately above the basal disk and allowing the resulting tissue pieces to round up for 2 h. In both cases, rounded tissue pieces of the same approximate size as body column tissue pieces were selected for imaging.

Imaging of shape oscillations

Regenerating tissue pieces were placed in agarose wells made using a 1% solution of agarose or low melting point agarose (Invitrogen, Carlsbad, CA) in HM. The two types of agarose were used interchangeably. To make the wells, molten agarose solution was poured into 30 mm Falcon petri dishes (Thermo Fisher Scientific), and a comb with 1-mm-wide teeth was placed vertically into the dishes to create wells. Once the agarose had solidified, the comb was removed, the wells were filled with HM, and the tissue pieces were moved into the wells using a pipette. Imaging was accomplished using an Invitrogen EVOS FL Auto 2 microscope (Thermo Fisher Scientific) and the Invitrogen EVOS FL Auto 2.0 Imaging System software. Images were acquired every 5 min and stored as Tagged Image File Format files. Viability of the tissue pieces was assayed by observing the presence of a body axis at 48 h and the formation of tentacles and mouth opening upon presentation of Artemia at 96 h.

Altering osmolarity of HM

To test the effect of changes in osmotic pressure on regenerating tissue pieces, tissue pieces were prepared and imaged as described above. However, the tissue pieces were kept in sucrose-supplemented HM for imaging instead of HM. Sucrose (Sigma-Aldrich) was added to HM to final concentrations of 10 or 25 mM. Rifampicin (EMD Millipore) was added to a final concentration of 50 μg/mL to prevent bacterial growth in the presence of sucrose.

Injections of microbeads and rupture site tracking

Tissue pieces were incubated at room temperature until at least 5 h after cutting to allow them to round up and form an internal cavity. An agarose trough for microinjection was cast as previously described (30). Hollow tissue spheres were placed in the trough in HM and injected with 1 μm green fluorescent (excitation/emission: 468/508 nm) microbeads (Thermo Fisher Scientific G0100) using a WPI Pneumatic PicoPump (PV 820) (Sarasota, FL) and needles pulled using a Sutter Instrument P-1000 (Novato, CA). Successfully injected spheres were placed in agarose wells and imaged for 24 h as described above. The resulting videos were used to determine the location of rupture events by tracking the locations of ejection of fluorescent beads relative to a fixed feature on the sphere. The smaller of the two angles between the fixed feature and the rupture location was recorded.

Visualization of myoneme arrangement in the head

Nerve-free Hydra prepared by heat shock treatment of strain A10 and untreated controls were fixed and stained with rhodamine-phalloidin (Biotium, Fremont, CA). The polyps were relaxed in 1 mL of 1 mM linalool (Sigma-Aldrich) in HM for 10 min (https://www.biorxiv.org/content/10.1101/584946v1) and then fixed in 4% paraformaldehyde (Thermo Fisher Scientific) in HM for 20 min at room temperature. They were washed with HM thrice for 10 min each before being incubated overnight at 4°C in rhodamine-phalloidin diluted 1:100 in HM. The fixed stained samples were washed 5 times for 10 min each with HM. They were then placed on 22 × 40 mm glass coverslips (Corning, Corning, NY), which had a piece of double-sided tape (3M, Maplewood, MN) running along the short edges of the coverslips. These coverslips were then sealed by placing 22 × 22 mm glass coverslips (Fisher Scientific) on top, and the samples were imaged using an Olympus IX81 inverted microscope (Olympus Corporation, Tokyo, Japan) with an ORCA-ER camera (Hamamatsu Photonics, Hamamatsu, Japan). Slidebook version 5 (Intelligent Imaging Innovations, Denver, CO) was used to interface with the microscope and acquire z-stacks. Maximum intensity projections of the z-stacks were used to determine the orientation of the myonemes.

Oscillation analysis

Images collected using the EVOS microscopes were opened in ImageJ (http://imagej.nih.gov/ij/; National Institutes of Health, Bethesda, MD), and full regeneration was verified. Full regeneration was defined as the regenerated tissue piece exhibiting a well-defined body axis, head formation, and tentacle growth. Only tissue pieces that showed full regeneration were included in further analysis. The obtained images were processed to extract the radius of the tissue piece as a function of time as described in the next paragraph. Only those tissue spheres whose minimum radius was ≤150 μm were included in further analysis. This cutoff was chosen based on the literature, in which it has been suggested that spheres with <200 μm average minimum radius, defined as the average of the minimum radi across oscillation cycles for a single tissue sphere, exhibited a pattern shift (14).

Each image set was analyzed using built-in functions in a custom Python script (Python 3.7.0; Python Software Foundation). The script first applies morphological image opening and closing to distinguish the sphere from the background, followed by watershed segmentation to detect and eliminate ejected cell debris (Fig. S1). If the script failed to segment the raw image set, debris was removed from the images by manually tracing over the debris in ImageJ before analysis. For each image in a set, the script traces the boundary of the regenerating tissue to determine its area. Effective radius is calculated as the radius of the circle having the same area as the tissue piece. Shape is approximated by fitting an ellipse to the two-dimensional contour of the tissue piece and recording major and minor axes to determine the aspect ratio. Effective volume of the tissue piece was determined as the volume of an ellipsoid obtained by revolution of the fit ellipse about its major axis as described in Soriano et al. (18). We found that the effective radius and the effective volume, normalized so that the minimum radius and volume are unity, qualitatively show the same temporal dynamics (Fig. S2). Subsequent processing and analysis of the data were carried out in MATLAB 2017b (The MathWorks, Natick, MA). The code is available online at https://github.com/Collinslab-swat/Oscillation-Analysis.git. The existence and timing of oscillation pattern shift in a data set was determined by having five researchers independently examine the radius-time plots for the data set and provide an estimate of the presence and timing of the shift. The data set was accepted as having a shift at a particular time if there was consensus of at least four of the researchers, defined as all scores being within a 4 h interval.

After shift presence and timing were determined, the amplitude, time period, and slope of each oscillation were extracted. The amplitude was defined as the difference between maximum and minimum radius during the inflation phase. The time period was defined as the time difference between the beginning of the inflation phase and end of the deflation phase. The swelling rate (slope) was obtained from a linear fit to the inflation phase of the oscillation.

As individual oscillations within a single biological replicate cannot be considered independent and their parameters are not normally distributed, we calculated the median values for each biological replicate and used these as inputs in our statistical analysis.

A two-sided Mann-Whitney U test was used to determine whether two sets of oscillation parameters originated from the same distribution. A p-value of 0.05 or lower rejects the null hypothesis that the two samples were drawn from the same distribution. For all conditions other than body column tissue pieces taken from wild-type animals regenerating in HM, the oscillations were classified as LPO or SPO based on comparison to wild-type LPO and SPO time periods. We used time periods for classifying an oscillation as LPO or SPO because the time periods are fairly consistent across biological replicates and the LPO time period distribution has very little overlap with the SPO time period distribution.

Calculation of the yield strength of the tissue

The Hydra tissue sphere was treated as a linear elastic hollow spherical shell. Then, the elastic pressure experienced by the sphere is given by the following:

$$P=2Eh\frac{A}{R_0^2\left(1-\mathit{\nu }\right)}.$$

Here, E is the Young’s modulus of the tissue, ν is the Poisson’s ratio, h is the thickness of the shell, A is the amplitude of the sphere at the time of rupture, and R₀ is the minimum radius of the sphere. The tissue was assumed to be incompressible, so ν = 0.5. However, the results are not strongly dependent on the choice of ν. For example, if ν = 0.25 is used, as in Kücken et al. (10), the pressure is only reduced by a factor of 1.5. For the Young’s modulus, a value of 185 N/m² was used based on experiments by Veschgini et al. (31), who measured the response of tissue spheres to uniaxial compression. The median values of minimum radius and amplitude were used, with R₀ = 119 μm and A = 28 μm for LPOs and A = 15.5 μm for SPOs, respectively. The shell thickness, h, was obtained from images presented in Buzgariu et al. (32) and was found to be ∼25 μm. The size of the hole caused by rupture was estimated from images that captured debris leaving the tissue sphere during a rupture event. The narrowest portion of the debris immediately adjacent to the sphere was averaged over three events and treated as an upper limit approximation of the size of the exit point, yielding a mean diameter of 26 μm, corresponding to one to two cell diameters.

Comparison of the oscillation parameters to previously published values

Published histograms of the slopes during LPOs and SPOs were taken from Soriano et al. (14). Using the freely available WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/), we converted the histograms into frequency distribution tables, calculated medians for the slopes for LPO and SPO, and compared those to the medians we calculated for our data. Because histograms were not available for time periods and amplitudes, we used other published plots of radius and volume over time to obtain time periods and amplitudes. The median time periods were obtained after digitizing the volume over time plot in Soriano et al. (18). Median amplitudes were also obtained in the same manner from the radius over time plot in Kücken et al. (10). We used medians as the summary statistic for the data because the data distributions were nonnormal.

Results and Discussion

As a freshwater animal, Hydra experiences a continuous inflow of water from the medium, through the tissues and into the gastric cavity (33, 34). The resulting internal pressure is periodically relieved by opening of the mouth (35). Regenerating Hydra spheres initially lack a mouth and therefore must relieve pressure from water accumulation by passive tissue rupture. This creates an oscillatory pattern of gradual osmotically driven swelling and rapid deflation due to tissue rupture, followed by healing of the rupture site. These cycles of swelling and rupture show an abrupt shift in oscillation pattern from LPOs to SPOs, coincident with a change in the aspect ratio of the regenerating Hydra sphere.

LPOs and SPOs have distinct oscillation parameters but a common driving mechanism

To examine the cause of the observed shift in oscillation pattern, we prepared tissue spheres (Fig. 1 A) and imaged them over the course of regeneration (Video S1). We only analyzed data from tissue spheres that regenerated fully, showing a defined body axis with head and tentacles (Fig. 1 B). A shift in oscillation pattern was observed to coincide with a gradual decline in aspect ratio (Fig. 1, C and D), as previously reported (10, 11, 14). From these radius-versus-time plots (Fig. 1 C), we extracted amplitude, period, and swelling rate (slope) for LPOs and SPOs (see Materials and Methods) and found all parameters to differ significantly between the two oscillation types (Fig. 1 E). A comparison of our data to the literature (10, 14) using the medians of the oscillation parameters (see Materials and Methods) shows similar differences in these three parameters between LPO and SPO.

Video S1. Regeneration of Wild-Type Tissue Piece

Raw video of the tissue piece represented in Figure S4 A. Scale bar 200 μm, total time 48 h. Recorded at 1 frame every 5 minutes (0.003 fps), playback at 10 fps.

The median amplitudes observed for LPOs and SPOs (Table 1) correspond to changes of ∼25% and 15%, respectively, in the radius of the tissue spheres. Because a sphere’s radius scales linearly with the linear size of the epithelial cells, we infer that the cells undergo linear deformations of 25% during LPOs and ∼15% during SPOs. Although these are significant cell deformations, similar and more extreme deformations are observed during mouth opening in intact polyps over the course of tens of seconds (35). These numbers illustrate the remarkable deformability of Hydra tissue.

Table 1.

Summary of Oscillation Parameters

	Period Length (h)	Amplitude (μm)	Slope (μm/h)	Number of Biological Replicates
Wild-type (HM) LPO	4.2 (3.7, 5.8)a	28.0 (21.0,36.6)a	6.3 (5.6, 7.1)b	15
Wild-type (HM) SPO	1.8 (1.5, 1.9)c	15.5 (13.0, 19.7)c	7.5 (6.7, 9.8)d	15
Sucrose 10 mM 2 h	2.3 (1.9,3.0)a,c	13.5 (10.9,19.1)c	4.9 (4.4,6.3)a	14
Sucrose 25 mM 2 h	3.0 (2.8, 4.3)a	14.3 (11.7, 19.8)c	3.5 (3.1, 4.1)a,c	17
Sucrose 25 mM 24 h	4.1 (2.7, 4.5)a	21.2 (13.5, 29.2)	4.0 (3.6, 5.0)a,c	15
Wild-type head tissue piece	1.1 (0.9, 1.4)a,c	8.7 (6.3, 12.1)b,c	9.7 (7.4, 10.9)d	4
Foot tissue piece	2.8 (2.3, 4.0)a	21.0 (14.2, 30.3)	7.6 (5.5, 7.9)	5

Parameters are reported as the median of biological replicates with the first and third quartiles.

^aIndicates significant difference from wild-type SPOs at p < 0.01.

^bIndicates significant difference from wild-type SPOs at p < 0.05.

^cIndicates significant difference from wild-type LPOs at p < 0.01.

^dIndicates significant difference from wild-type LPOs at p < 0.05.

Previous studies and models assumed that both LPOs and SPOs are driven solely by osmotic pressure (4, 10). However, this was only experimentally tested for LPOs (10). To verify that SPOs are also osmotically driven, we incubated tissue pieces in hypertonic medium made by adding 10 or 25 mM sucrose to HM. Because the osmolarity between the inside and the outside of a tissue sphere equilibrates after several rupture events, we began incubation either 2 h postamputation to probe the effect of altered osmotic pressure on LPOs or 24 h postamputation to probe its effect on SPOs. Consistent with previous work (10), we observed a concentration-dependent decrease in swelling rates during the LPO cycle in the 2-h postamputation treatments (Table 1). Similarly, we obtained a decrease in slope in the 24-h postamputation treatment with 25 mM sucrose. Moreover, the increase in slope from LPOs to SPOs was not affected by sucrose concentrations (Table 1).

This suggests that SPOs are also primarily osmotically driven and that the increased rate of inflation is due to a secondary mechanism, such as a change in tissue properties associated with regeneration (e.g., an increase in tissue permeability to water or an increase in the number or activity of ion pumps), as previously suggested (11). As slopes are even further increased in head tissue piece oscillations, the change may be linked to the development of a head, which has been reported to differ in terms of cell composition and matrix thickness (36).

The decrease in maximum amplitude of SPOs compared to LPOs indicates that the pressure required to trigger a rupture event has decreased. This can be explained either by the weakening of the tissue’s tearing strength (globally or locally) or the rupture becoming an actively controlled process. Both of these are attributes of the Hydra mouth. The mouth is a structural weak spot because it has a thinner mesoglea and an absence of myonemes running across it (36). The mouth also allows for active pressure release in the intact polyp through the control of the nervous system (35). Soriano et al. (18) proposed the first possibility, suggesting that the formation of a protomouth created a weak spot, but this idea was not tested experimentally.

Rupture site becomes constant as regeneration progresses

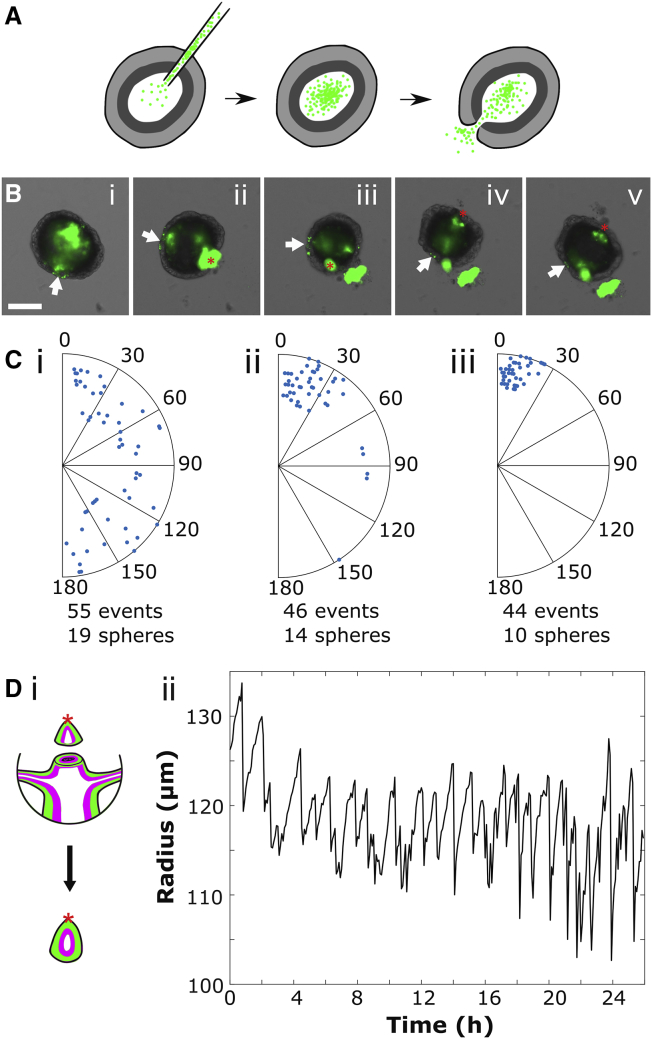
To determine whether a fixed rupture site consistent with a permanent mechanical defect appears during regeneration, we used fluorescent microbead injections to visualize the rupture site in oscillating tissue spheres (Fig. 2, A and B). We observed that cell debris was frequently ejected from spheres throughout the regeneration process and thus conclude that the introduction of microbeads does not represent a significant alteration to natural behavior (Fig. S4). Because rupture events can no longer be visualized after all beads are ejected from a sphere, we injected 5 h postamputation to track rupture events during LPOs or 24 h postamputation to track ruptures during SPOs. We observed that rupture sites are randomly distributed in spheres injected at 5 h (Fig. 2 Ci) but are significantly more localized in spheres injected at 24 h (Fig. 2 Cii). We compared rupture site locations for both LPOs and SPOs to data drawn from a uniform distribution using a two-sample Kolmogorov-Smirnov test and found that the 5 h data are not significantly different from a uniform distribution (p = 0.9702), whereas the 24 h data are (p = 1.0047e−07.) This suggests that a mechanical weak spot in the tissue sphere forms as regeneration proceeds.

Figure 2.

The rupture site becomes constant with head development. (A) An experiment schematic shows injection of fluorescent microbeads into a hollow sphere. Beads are ejected from the sphere during rupture events. (B) A representative image series of sphere ejecting beads during successive ruptures is shown. The white arrow indicates the feature used to track rotation, and the red asterisk represents the observed rupture site (see Materials and Methods). Scale bars, 100 μm. (C) Shown is the location of the rupture site relative to the first rupture, with each radius representing a single sphere. (i) Beginning 5 h after cutting is shown. (ii) Beginning 24 h after cutting is shown. (iii) Head tissue pieces containing the mouth of the parent animal are shown. (D) (i) A schematic illustrating the creation of a head tissue piece is shown. The red asterisk indicates the location of the mouth. (ii) Representative oscillation plot of a head tissue piece is shown. To see this figure in color, go online.

To confirm that this structural weak point corresponded to the Hydra mouth, we tracked ruptures in excised head tissue pieces. These were created by excising the intact mouth of the parent animal and a small amount of surrounding tissue, then allowing the piece to round in the same way as a body column tissue piece (Fig. 2 Di). Head tissue pieces are not viable long term because of being composed mainly of terminally differentiated cells, but they remain healthy for at least 24 h and exhibit trackable oscillations during that time (Fig. 2 Dii). They also retain the parental mouth structure, which can be visualized via phalloidin staining (Fig. S5). We found that these head piece spheres had an invariant rupture site (Fig. 2 Ciii), supporting the idea that the emergence of a fixed rupture site is coincident with mouth development during regeneration. Finally, to confirm a link between the mouth and oscillation dynamics, we analyzed the oscillations of head pieces and found that they only exhibit SPOs as seen from the distribution of time periods (Fig. 2 Dii; Table 1). These data demonstrate that the presence of a mouth in a tissue piece is sufficient for SPOs.

Because it had been proposed that the aboral pore acts as a second weak point in the intact animal that may be used for pressure regulation (37), we also imaged foot tissue pieces containing the entire basal disk (Fig. 1 A). Foot tissue pieces showed oscillation parameters with a greater similarity to LPOs than to SPOs (Table 1). The statistically significant difference in period between foot tissue pieces and SPOs indicates that the presence of an aboral pore does not increase rupture frequency in the same way the presence of a mouth does. Thus, the aboral pore does not play a role in regulating osmotic pressure during regeneration. We suspect that the similarity in the swelling rate between the foot piece and body tissue piece SPOs results from a difference in tissue composition in the foot. Both the hypostomal region and the basal disk have significantly higher proportions of epitheliomuscular and nerve cells than the body column (38), which may cause differences in mechanical properties or permeability.

In summary, these results support the hypothesis that ruptures during LPOs are caused by osmotically driven inflation until the yield strength of the tissue is reached, resulting in random rupture locations. In contrast, SPOs are caused by the development of a mouth structure, creating a permanent, localized weak point on the sphere. This is consistent with previous observations that insertion of head tissue into cell aggregates decreases the time required for a shift to SPOs to occur (14). The presence of a head organizer would allow the aggregate to more rapidly define a head and develop a mouth, resulting in a faster oscillation pattern shift. Whether the forming mouth acts solely as a mechanical defect, as previously suggested (18), or actively regulates osmotic pressure cannot be distinguished based on these data.

Mouth function is required for a shift to SPO

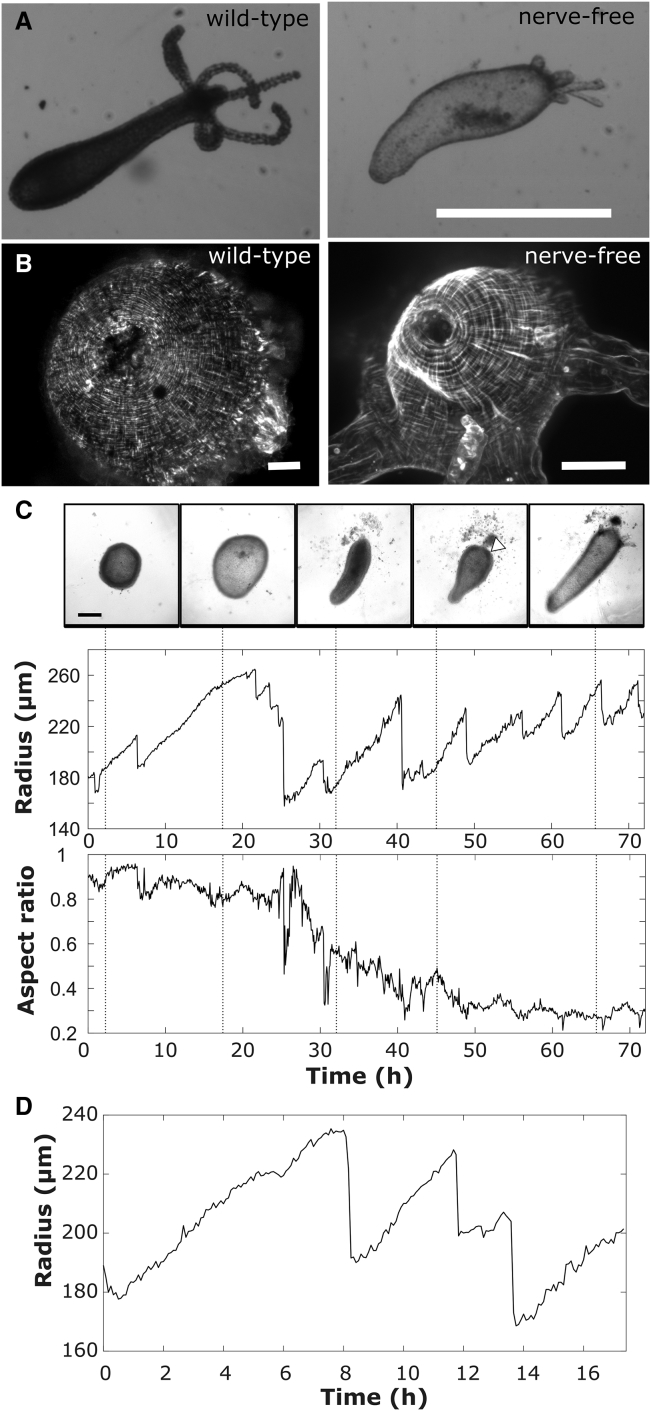
To determine whether the mouth plays an active osmoregulatory role in regenerating tissue spheres, we decouple mouth function from mouth structure by examining nerve-free Hydra, which are capable of complete regeneration but are unable to open their mouths to relieve pressure or respond to chemical stimuli (33, 39, 40). In contrast to normal animals, nerve-free Hydra take on a characteristic bloated appearance (27) (Fig. 3 A) because of their inability to relieve internal pressure by mouth opening. The mouth appears morphologically normal in nerve-free animals (Fig. 3 B), suggesting that lack of function is caused by the absence of neurons and thus an inability to sense pressure (41). Body column tissue spheres derived from nerve-free animals showed only LPOs, with a period slightly longer than LPOs in wild-type spheres (Fig. 3 C; Table 2). The small difference in parameters may be due to differences in tissue strength given that nerve-free animals lack all cell types derived from the interstitial cell lineage: neurons, gland cells, and nematocytes (42). Although it has been suggested that nerve-free animals may use an alternate, slower regeneration pathway for regeneration than enervated animals (43), we observe that nerve-free animals are able to form a head and tentacles within 72 h without ever exhibiting SPO behavior (Figs. 3 C and S3; Video S2). Thus, nerve-free animals break shape symmetry and have a clearly specified axis without ever experiencing SPOs.

Figure 3.

Mouth opening impacts oscillation dynamics. (A) Shown is a comparison between wild-type and nerve-free polyps, showing characteristic bloated phenotype of nerve-free Hydra (scale bars, 1 mm). (B) A comparison of myoneme organization in the hypostome of wild-type and nerve-free animals (scale bars, 50 μm) is shown. (C) Full regeneration of a nerve-free tissue sphere showing only LPOs (the time periods of all the oscillations are much greater than that of SPOs) is shown. Representative images are taken at times indicated on radius and aspect ratio plots. Scale bars, 200 μm. (D) A representative oscillation plot of nerve-free head tissue sphere showing only LPOs is shown.

Table 2.

Oscillation Parameters for Various Experimental Conditions

	Period length (h)	Amplitude (μm)	Slope (μm/h)	Number of Biological Replicates
Wild-type body column tissue pieces LPO	4.2 (3.7, 5.8)a	28.0 (21.0,36.6)a	6.3 (5.6, 7.1)b	15
Wild-type body column tissue pieces SPO	1.8 (1.5, 1.9)c	15.5 (13.0, 19.7)c	7.5 (6.7, 9.8)d	15
Wild-type head tissue pieces	1.1 (0.9, 1.4)a,c	8.7 (6.3, 12.1)b,c	9.7 (7.4, 10.9)d	4
Nerve-free body column pieces	6.6 (5.6, 9.3)a,c	28.5 (25.8, 37.7)a	4.1 (3.3, 4.5)a	11
Nerve-free head tissue pieces	3.2 (2.8,4.0)a	20.8 (16.0, 29.9)	6.5 (5.5, 7.8)	4

Parameters are reported as median of biological replicates with the first and third quartiles.

^aIndicates significant difference from wild-type SPOs at p < 0.01.

^bIndicates significant difference from wild-type SPOs at p < 0.05.

^cIndicates significant difference from wild-type LPOs at p < 0.01.

^dIndicates significant difference from wild-type LPOs at p < 0.05.

Video S2. Regeneration of Nerve-Free Tissue Piece

Raw video of the tissue piece represented in Figure 3, showing formation of body axis and head structures. Scale bar 200 μm, total time 72h. Recorded at 1 frame every 5 minutes (0.003 fps), playback at 10 fps.

Because it is still possible that the development of mouth structures is delayed in nerve-free Hydra, we use excised head pieces from nerve-free Hydra containing the mouth to fully decouple mouth structure from mouth function. If the presence of a mouth structure was sufficient to increase rupture frequency, we would expect to observe SPOs in spheres derived from nerve-free head pieces as we do in untreated wild-type head pieces (Fig. 2 D). Alternatively, if active control of the mouth structure is necessary for SPOs to occur, nerve-free head pieces should not show SPOs. We observe that spheres from nerve-free head pieces show only LPOs (Fig. 3 D; Table 2) and therefore conclude that mouth function is a requirement for the occurrence of SPOs.

Taken together, these data demonstrate that the shift in oscillation pattern observed in regenerating Hydra tissue spheres is caused by the formation of a functional mouth and its use in osmoregulation. A tissue sphere derived from a wild-type polyp initially exhibits LPOs in which rupture is dictated by the yield strength of the tissue. Rupture events in this regime are randomly located because mechanical failure is equally likely to occur at any point on the sphere. Approximately 24 h into the regeneration process, we observed the development of a functional mouth, which allows for active osmoregulation, causing the shift to SPOs.

Implications for theoretical models of Hydra regeneration

Various attempts have been made to model axis determination from a homogenous initial state in Hydra spheres. The core of these models lies in some form of feedback between morphogen concentrations and mechanical properties of the tissue such as elasticity. The dynamics of the morphogen concentrations are modeled using the Gierer-Meinhardt model (3), whereas feedback between mechanics and the morphogens is modeled using a relation between tissue stretch and morphogen diffusion. In the model proposed by Soriano et al. (14), this takes the form of a linear relationship between tissue strain and the diffusion coefficient of one of the morphogens. Axis formation is posited to occur when a stable morphogen gradient is established (a consequence of the diffusion coefficient exceeding a certain threshold (14)), which makes the timescale for gradient formation much shorter than the timescale for shape oscillations. In a more recent model by Mercker et al. (4), the local diffusion coefficient is a function of the local area strain of the tissue, and the elastic modulus is a function of morphogen concentration. This allows for a growth instability: high local strain causes accumulation of the morphogen and morphogen accumulation allows for higher local strains in response to the same stress (4).

To date, there are no quantitative experimental data on concentration patterns of morphogens, their diffusion constants, or the feedback between morphogen concentration and mechanical properties in Hydra. Therefore, models rely entirely on relations between morphological parameters, such as swelling rate, initial tissue size, and the time of shape symmetry breaking, to constrain model parameters and validate predictions. The results presented here force us to reconsider the assumption that the time of shape and biochemical symmetry breaking always coincide with the time of the oscillation pattern shift from LPO to SPO. Nerve-free tissue pieces only exhibit LPOs but nevertheless break shape symmetry and specify a body axis (Fig. 3 C; Fig. S3). This demonstrates that one of the key observables used to constrain the existing models is not universally applicable. Instead, we show that the shift in the oscillation pattern is caused by a change in local yield strength of the tissue because of mouth formation, a property whose variation is not considered by existing models.

We estimate the local yield strength of the tissue by treating it as an elastic shell (see Materials and Methods). The order of magnitude estimate is made using only quantities that can be measured or calculated from experimental data presented here or elsewhere in the literature, except for Poisson’s ratio, which does not affect the order of magnitude (see Materials and Methods). The estimated elastic pressure inside the sphere at the time of rupture is on the order of 20 Pa during LPOs. Because the pressure scales linearly with oscillation amplitude (see Materials and Methods) and the SPO amplitude is approximately half the LPO amplitude, the pressure at the time of rupture during SPOs is ∼10 Pa acting on an area of the order of two to three cell diameters across. Therefore, the elastic force must be on the order of a few nano-Newtons at the time of rupture during SPOs.

The magnitude of this force is comparable to that exerted by myonemes to create a mouth opening (35) and to the separation force associated with tight junctions involved in cell-cell adhesion (44). Although the sources of the elastic forces estimated here for SPOs are different from those involved in mouth opening, they act on the same tissue producing the same effect (breaking cell-cell contacts to create an opening), suggesting that the estimates are reasonable. We thus provide an experimentally determined value that can be used to constrain the maximum stress associated with tissue rupture in models.

We can infer that axis specification must precede mouth function. Previous work shows that Wnt3 expression occurs by 24 h in large aggregates that give rise to multiple body axes (15) or by 1.5 h after amputation in a decapitated animal (22). Because a tissue piece retains more structure than an aggregate but less than a decapitated animal, we expect Wnt3 signaling to be established between these times. By combining these constraints with the time of the oscillation pattern shift as an upper bound, we can improve our estimate of the time of axis specification over that used in previous models.

Finally, although this and other recent works (10, 11, 16) have focused on regenerating spheres originating from tissue pieces, the oscillation behavior of spheres originating from cell aggregates should be revisited. A direct comparison of the results from these two starting scenarios is likely to provide further insights into the mechanisms that drive regeneration and patterning. Exploring these possibilities and leveraging them to improve existing models should be the next step in our attempt to understand axis specification in Hydra.

Conclusions

During Hydra regeneration from small tissue pieces or aggregated cells, a hollow bilayered sphere forms that undergoes dramatic shape oscillations. A switch in oscillation pattern, from long-period, large-amplitude to short-period, small-amplitude oscillations, occurs approximately 1 day into regeneration. Because previous explanations for the shift in oscillation pattern have recently been invalidated, we reexamined this fundamental process during Hydra regeneration from tissue spheres and demonstrate that the oscillation pattern shift is a direct consequence of the onset of mouth function and its use in osmoregulation. This allows us to infer the development of an important physiological function through a morphological readout. The results from this work also enable the field to reexamine and improve existing models of Hydra regeneration that rely on the concurrence of the shift in oscillation pattern and decrease in aspect ratio to constrain model parameters.

Author Contributions

E.-M.S.C. designed research. R.W. and T.G. performed experiments. R.W., T.G., K.K., H.J.Q., and Z.S. analyzed data. K.K. contributed analytical tools. P.H.D. consulted on data analysis and interpretation. R.W., T.G., P.H.D., and E.-M.S.C. wrote the manuscript.

Editor: Lisa Manning.