Automated Model-Based Segmentation of the Left and Right Ventricles in Tagged Cardiac MRI

Abstract

We describe an automated, model-based method to segment the left and right ventricles in 4D tagged MR. We fit 3D epicardial and endocardial surface models to ventricle features we extract from the image data. Excellent segmentation is achieved using novel methods that (1) initialize the models and (2) that compute 3D model forces from 2D tagged MR images. The 3D forces guide the models to patient-specific anatomy while the fit is regularized via internal deformation strain energy of a thin plate. Deformation continues until the forces equilibrate or vanish. Validation of the segmentations is performed quantitatively and qualitatively on normal and diseased subjects.

1. Introduction

Cardiovascular disease is the leading cause of death for both men and women in most developed countries. However, improved understanding of the regional heterogeneity of myocardial contractility can lead to more accurate patient diagnosis and potentially reduce its morbidity. SPAMM-MRI [1],[2] is a non-invasive technique for measuring the motion of the heart by magnetically tagging parallel sheets of tissue at end-diastole. The sheets appear as dark lines that deform during systole. Quantification of the deformation requires accurate segmentation of the epicardial and endocardial surfaces and tag sheets.

A highly automated method is needed to make the technique clinically viable. Previously, an expert anatomist required 5+ hours per subject to interactively segment these structures. Segmenting the epicardial and endocardial surfaces typically takes up 80% of the total extraction time. This paper presents an automated method for extracting these surfaces. Prior to this paper, there have not been fully automated methods to extract these surfaces from tagged cardiac MR for the following reasons:

• Image artifacts & noise must be suppressed and the tag lines must be removed.

• Features outlining the boundaries must be identified.

• The image data samples the heart coarsely and irregularly over space (Fig 1a).

• The geometry of the heart is complex making surfaces difficult to initialize.

Due to the challenges, people have resorted to semi-automated methods that rely on extensive human operator interaction. This paper presents the first fully-automated model-based segmentation and it is composed of a sequence of steps:

1. Image processing methods are applied to prepare images for use by the models.

2. Image features are automatically extracted for model initialization.

3. Internal forces are defined to regularize the fit of the models.

4. A deformable model-fitting approach is employed, which balances the forces.

Fig. 1.

The full data set (a) is composed of two SA sets (b) and (c) and a LA set (d)

We employ an automated model-based segmentation that segments 3D surfaces rather than a set of 2D contours as in [5] because the 3D models enable integration of constraints from all images. In this paper we propose novel methods for initializing the models and for extracting 3D forces from the 2D images. Other researchers [7] have fit surface models to cardiac data. However their methods were not directly applicable to our objectives since our data is tagged and we have sparse, non-uniformly arranged images. Other researchers [9], have extracted 3D myocardial motion from tagged MR; however, their methods assume the segmentation is provided. This paper fills the void left by such researchers by providing an automated method to obtain the required segmentation. The segmented surfaces will likely be beneficial for (1) inter-subject alignment and (2) classical descriptors of cardiac function.

2. Methodology

2.1. Image Processing Methods to Prepare Images for Model Fitting

We used a 1.5T GE MR imaging system to acquire the images, and an ECG-gated tagged gradient echo pulse sequence. Every 30ms during systole, 2 sets of parallel short axis (SA) images are acquired; one with horizontal tags and one with vertical tags. These images are perpendicular to an axis through the center of the left ventricle (LV). One set of long axis (LA) images are acquired along planes having an angular separation of 20 degrees and whose intersection approximates the long axis of the LV.

To prepare the images for segmentation, we use low level image processing methods, detailed in [6], that (1) suppress intensity inhomogeneity induced by surface coils and (2) suppress differences in MR intensities between subjects.

2.2. Apply Deformable Surface Models to Segment the Myocardium

2.2.1. Description of the Deformable Models that We Use

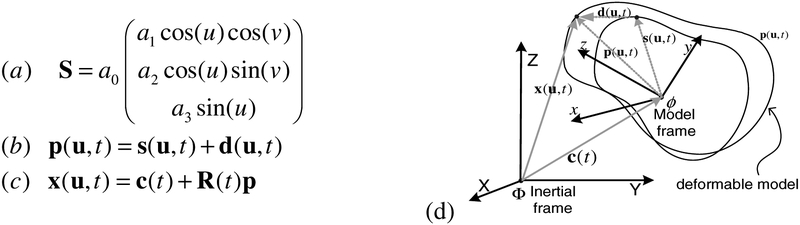
The myocardium can be delineated by 3 surfaces the endocardial surface of the right ventricle (RV), the endocardial surface of the left ventricle (LV), and a combined LV and RV epicardial surface surrounding both ventricles [9]. Consequently, we fit 3 surface models to the image data to segment the myocardium. We denote these models: RVEndo, LVEndo, EPI, respectively. Each model is initialized to a very rough approximation of the desired surface. For example, the LVEndo model is initialized to a ellipsoid shape ( S in Fig 2a). The model is parametric in material coordinates u = (u, v) , where u and v are latitudinal and longitudinal coordinates respectively. Each point on the surface model, (x, y, z) is governed by a function of{u, v,a_i} : a₀ controls the overall size of the shape, while a₁, a₂, and a₃ control the aspect ratio parameters in the x, y and z directions respectively. The shape is defined in a model frame, ϕ. The surface model is roughly aligned to the image data by applying a translation, c(t), and a rigid body rotation, R(t), to the model frame. Once the model has been initialized, it deforms under image forces to fit to the MR data. A free form deformation is represented by the displacement field d. The initial surface plus the current deformation at time, t , is the surface model, denoted p(u,t) . The relationship between the deformable model p and the surface model points, x(u,t) in an inertial reference frame, Φ , is given in Fig 2c. The combined epicardial surface model (EPI) can also be roughly described by an ellipsoid, while we model the RVEndo model using a blending of two ellipsoids as in [9].

Fig. 2.

(a) Reference shape, S . (b) Deformable model, p . (c) Model points, x , in inertial reference frame. (d) Relationship between model frame, ϕ, and inertial frame, Φ.

2.2.2. Extract Image Features for Each Model

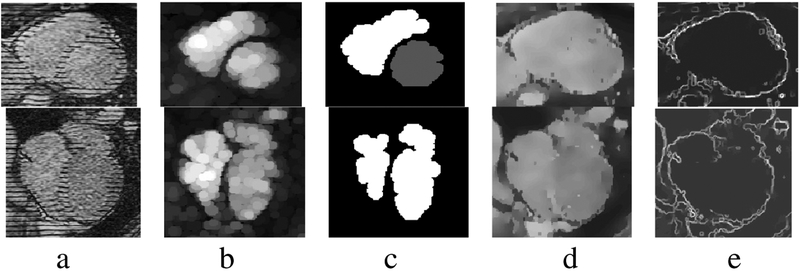
We extract image features for each model so that we can (1) initialize the pose, c(t) and R(t), and aspect parameters {a₀,a₁,a_2,a_3,} and (2) generate forces for the displacement, d , of the deformable models. Fig 3b shows the result after applying a grayscale opening with a disk-shaped structuring element to the input in Fig 3a. Fig 3c depicts the result after thresholding and pruning non-heart related regions from (b). Fig 3d shows the result after applying a grayscale closing operation to the images in (a) with a linear structuring element to fill in the tags. In [5] we detailed the process for extracting features from SA images. In this paper we (1) extend the process to LA images and (2) implement a new thermal noise suppression filter which combines scale based diffusion [8] with median filtering to a) suppress thermal noise b) preserve salient edges and c) suppress impulse noise. Fig 3e shows the magnitude of the intensity gradient of (d). We use the regions (Fig 3c) as the features that attract the RVEndo and LVEndo models, and edge features (Fig 3e) to attract the EPI model.

Fig. 3.

Features derived from SA images (first row) and LA images (second row).

2.2.3. Automatically Initialize the Pose and Aspect Parameters of Each Model

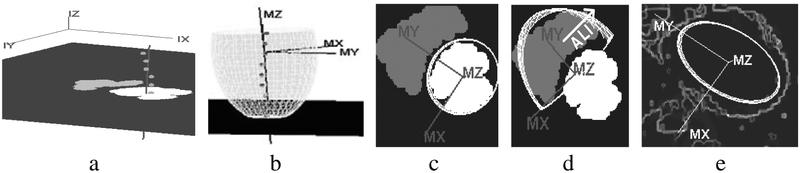
Region features, (Fig 3c), are used to estimate the initial pose and aspect parameters of the surface models. For example, to initialize the pose of the principal axis of the LVEndo, we robustly fit a line (Fig 4a) through the centroids of each LV endo region in each SA image. The center of the ellipsoid is defined to be on this line and roughly near the center of mass of the LV endo features. We align the y axis of the model reference frame along the line from the ellipsoid center to the center of mass of the RV endo features as shown in Fig 4c. The pose also defines the LVEndo model frame. In this frame we scan the LV endo features in the SA images (Fig 3c, top) for the extremal pixels to determine aspect parameters, {a₁,a₂,a_3,}. Fig 4b depicts how we stretch the ellipsoid by adjusting a₃ until the apex fits the LV endo feature in the most inferior SA slice. In Fig 4c, we have scaled the ellipsoid along MX and MY using parameters a₁,a₂ . We set the overall scale, a₀, to unity. A similar approach is used for the RVEndo model and EPI model.

Fig. 4.

(a) Robust line fit through centroids of LVEndo blood regions (b) The initial LVEndo model (c) LVEndo model frame and initial shape: top down view with a SA slice (d) RVEndo model frame and initial shape (e) EPI model frame and initial shape.

2.2.4. Compute 2D Image Forces to Attract Each Model to the Appropriate Features

The 2D images are radially-arranged and parallel-arranged and sparse (Fig 1a). To fit our 3D models to patient-specific anatomy, we derive 3D image forces through these steps:

1. compute a 2D image force field (vector field) on each feature image

2. compute the intersection points, u_i , of each image plane with model edges

3. Extrapolate image forces exerted on u_i to nodes bounding the intersected edges.

4. Combine the multiple 2D forces felt by each node into 3D forces that move it

Compute a 2D Vector Field of Image Forces from Each Feature Image:

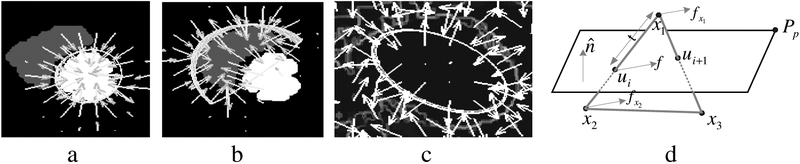
We generate a vector field of image forces by computing the gradient of each feature image and interpolate it via the gradient vector flow (GVF) computation [3]. Fig 5a shows the force field (subsampled for readability) for the LVEndo model for one SA image; the gray RV region is suppressed (set to zero) during GVF computation for the LVEndo model. A similar process is used for the RVEndo model (Fig 5b) while the force field (Fig 5c) for the EPI model comes from an edge image.

Fig. 5.

(a) GVF forces that attract the LVEndo model (b) Forces that attract the RVEndo model (c) Forces that attract the EPI model (d) a model element intersected by an image plane

Compute the Image Plane/Model Edge Intersection Points, u_i:

We compute the intersection points of model edges and image planes by searching edges to find those which straddle an image plane (Fig 5d). Which-side-of-plane tests are preformed for each edge endpoint. We represent the image plane with the implicit equation, n ∙(x – P_p) , where $\widehat{n}$ is the unit normal to the image plane, P_p is a point in the plane, and m is the distance of the test point X from the image plane. Edge $\overline{x_1{x}_2}$ is intersected by the plane, if this equation yields opposite signs for x₁ and x₂. We substitute the line equation l(t) , l(t) = x₁ + t(x₂ – x₁) for X to compute the point of intersection, u_i.

Extrapolate the Forces Exerted by the Vector Fields to the Nodes:

We compute the image force acting on each intersection point, u_i, by bilinearly interpolating the GVF field. The shape of each surface model is defined by the position of the model nodes comprising the triangular tessellation (e.g. Fig 7b). The nodes are the intersection of 2 or more edges. To deform the model with the image forces, we linearly interpolate the force felt by each intersection point, u_i, to the endpoints of the edge on which u_i lies. If the force felt by u_i is f , the endpoint forces are $f_{x_1}=(1-t)f$ and $f_{x_2}=tf$.

Fig. 7.

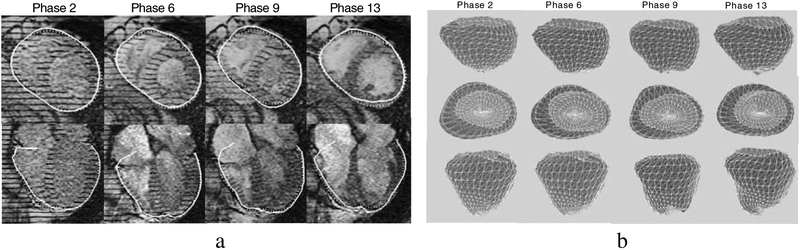
(a) Segmented EPI surface intersection line (solid line), 2D contour drawn by the expert (dashed line). (b) The surface contracts throughout systole (phases 2–9) and expands during diastole (phase 9–13).

2.2.5. Compute 3D Image Forces by Combining 2D Image Forces

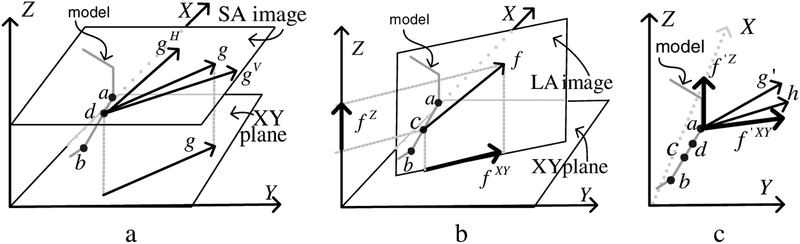
Multiple image forces are typically extrapolated to each node. For example, in Fig 6a, a short sequence of edges from a surface model is shown. The SA image plane intersects the model edge $\overline{ab}$ at the point d. There are two image forces that influence d: the force from the horizontally tagged image, g^H and the force g^V from the vertically tagged image. We denote as g the weighted sum of g^H and g^V . Depending on the orientation in space of the surface we desire to segment the images yield different degrees of information about the location and orientation of the surface: as the angle between a model surface and the initial horizontal tag direction (the direction laid down in the pulse sequence) approaches 90 degrees, we increase the weight of g^H relative to g^V and vice-versa as the angle approaches zero. The force, g , is parallel to the XY plane. Often $\overline{ab}$ will also be intersected by a LA image. For example, Fig 6b shows an image that intersects $\overline{ab}$ at the point c. The force from this image, f has one component, f ^XY , parallel to the XY plane and another, f ^Z , parallel to the Z axis. If these are the only images intersecting the edge connected to the node a, then we have the situation shown in Fig 6c in which three forces “pull” node a: two forces from c: f ^‘Z and f ^‘XY and one from d: g ‘. Both f ^‘XY and g ‘ are parallel to the XY plane, hence we compute a weighted average of them, denoted h . The 3D image force felt by a is then f_a = (h_x,h_y,f ‘^Z)^T. A similar process is applied for all nodes.

Fig. 6.

(a) Image forces from a SA image plane (b) Image forces from a LA image plane (c) The forces are extrapolated to the edge endpoints.

2.2.6. Compute 3D Internal Forces Which Make Each Fitted Surface Model Smooth

Using image forces alone, yields an unsatisfactory fit for the 3 surfaces, due to the presence of residual MR artifacts. We improve the results dramatically by adding internal model regularization forces. Using the regularization framework of a thin plate under tension and the finite element method, we embed smoothing “material” properties into each model. We model the deformation strain energy, ε(d) , using eqn (1). The deformation strain energy comes from the partial derivatives of the displacement, d , of material points (u,v) on the model’s surface in the model frame, ϕ :

$$\epsilon (d)=\int w_{20}{\left(\frac{{\partial }^{2}d}{\partial u^2}\right)}^2+w_{11}{\left(\frac{{\partial }^{2}d}{\partial u\partial v}\right)}^2+w_{02}{\left(\frac{{\partial }^{2}d}{\partial v^2}\right)}^2+w_{10}{\left(\frac{\partial d}{\partial u}\right)}^2+w_{01}{\left(\frac{\partial d}{\partial v}\right)}^2+w_{00}{(d)}^{2}du$$ (1)

Increasing coefficients, {w₂₀,w₁₁,w₀₂}, makes the model behave more like a thin plate; increasing {w₁₀,w₀₁} increases model elasticity; increasing {w₀₀} increases the tension. The coefficients which work best on experimentation with 5 subjects have been adopted for model fitting. To compute the displacement, d(u, v) , which is everywhere C¹, we let the nodal variable be q_d as in (eqn 2a). The nodal shape functions are{N₁,…, N₁₈} as in [6]. Using the theory of elasticity, the deformation strain energy at a node of the j^th element, E_j, can be expressed in terms of the strain matrix, Γ ^j , (eqn (2b,c)), and a diagonal matrix of material properties, D ^j (eqn (2d)). Using this formulation, the elemental stiffness matrix, $K_{d{d}_k}^j$, (eqn (2e)), is derived from the deformation strain energy. We expand the $K_{d{d}_k}^j$ matrices to form the global stiffness matrix K.

$$\begin{array}{ll}\text{(a) }{q}_d={\left(d,\frac{\partial d}{\partial u},\frac{\partial d}{\partial v},\frac{{\partial }^{2}d}{\partial u^2}\frac{{\partial }^{2}d}{\partial u\partial v},\frac{{\partial }^{2}d}{\partial v^2}\right)}^T\hfill & (\text{d})\hfill \\ \text{(b) }{\mathrm{\Gamma }}_k^j=\left({\gamma }_1^j{\gamma }_2^j\dots {\gamma }_{18}^j\right)\hfill & D_k^j=\mathit{\text{diag}}\left(\left[w_{00},w_{10},w_{01},w_{20},w_{11},w_{02}\right]\right)\hfill \\ \text{(c) }{\gamma }_i^j={\left[N_i^j,\frac{\partial N_i^j}{\partial u},\frac{\partial N_i^j}{\partial v},\frac{{\partial }^2{N}_i^j}{\partial u^2},\frac{{\partial }^2{N}_i^j}{\partial u\partial v},\frac{{\partial }^2{N}_i^j}{\partial v}\right]}^T\hfill & \text{(e) }{K}_{d{d}_k}^j=\underset{E_j}{\int }{\left({\mathrm{\Gamma }}_k^j\right)}^T{D}_k^j{\mathrm{\Gamma }}_k^j\mathit{\text{dudv}}\hfill \end{array}$$ (2)

2.2.7. Deform the Models with All 3D Forces Until the Forces Equilibrate or Vanish

The motion of our model nodes are governed by the Lagrangian equations of motion. We set the mass matrix to zero and the dampening matrix to the identity which yields the first order equation: $\stackrel{.}{q}+Kq=f$ where K is the stiffness matrix derived earlier, and f and Kq are the image and internal forces, respectively. We solve this equation with the explicit Euler difference scheme: q(t + Δt) = q(t) + Δt (f – Kq(t)) and evolve our model until the external and internal forces equilibrate or vanish.

3. Results

3.1. Qualitative Results

We compare the intersecting contour of our surface model with the LA and SA images to the contours drawn by experts. In Fig 7a contours are shown for four phases throughout the cardiac cycle. Displaying both types of contours in the images provides convincing evidence of our algorithm’s accuracy. At the base of the RV we can see a “flap” which curls over the right atrium. To accurately segment the atria, we would (1) model the atria and (2) acquire SA images intersecting the atria. We see additional evidence for the correctness of our algorithm by examining the fit of our 3D model throughout the cardiac cycle (Fig 7b).

In addition, we have preliminary results for the endocardial surfaces. Fig 8 shows the fitted RVEndo and LVEndo models. They have fit the endocardial surfaces quite well. The fit of the apex of the LV particularly benefits from the LA images.

Fig. 8.

Endocardial surfaces:(a)axial (b)coronal views; with EPI superimposed:(c) and (d).

3.2. Quantitative Results

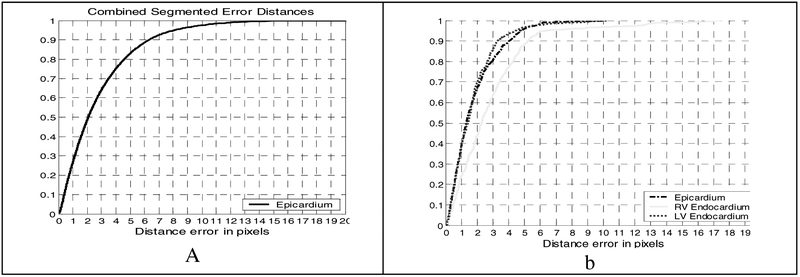
We compute the distance between each segmented contour, A (the intersection between our 3D models and the image plane) and the corresponding 2D contour, B, drawn by the expert, by computing the distance $d(a,B)=\underset{b\in B}{\text{min}}\Vert a-b\Vert$ for all points a on the segmented contour and d (b, A) for points, b on the expert contours. Fig 9a shows the cumulative distribution of these error distances for the contour points over all slices in all volumes from end diastole to end systole and into the next diastole for 5 normal and diseased subjects comprising over 1500 images. The plot shows that 50% of the segmented epicardium contour points are within 2.1mm (a pixel is 1mm × 1mm) and that 90% of the points are within 6.3 pixels. Fig 9b shows the quantitative results for the endocardium models for one subject. For the LVEndo, 50% of the points are within 1.5mm, 90% are within 3.3mm. The RV endocardial surface: 50% of its points are within 2.3mm, 90% are within 5.3mm. The RV errors that occur are concentrated near (1) the narrow apex which is often not visible in both the LA and the SA images and (2) at the bifurcation of the RV into inflow and outflow tracts, which we are not currently modeling.

Fig. 9.

A. EPI distance errors for 5 subjects b. distance errors for all surfaces for one subject.

4. Conclusions

We have presented an automated model-based segmentation method for extracting surfaces delineating the myocardium in tagged MRI. To achieve excellent segmentation we have developed novel methods to (1) initialize the models and (2) to compute 3D model forces from 2D images. Our method is fully automated and its running time is less than 15% of the time required for manual expert segmentation.