Mutation rate variability as a driving force in adaptive evolution

Abstract

Mutation rate is a key determinant of the pace as well as outcome of evolution, and variability in this rate has been shown in different scenarios to play a key role in evolutionary adaptation and resistance evolution under stress caused by selective pressure. Here we investigate the dynamics of resistance fixation in a bacterial population with variable mutation rates, and we show that evolutionary outcomes are most sensitive to mutation rate variations when the population is subject to environmental and demographic conditions that suppress the evolutionary advantage of high-fitness subpopulations. By directly mapping a biophysical fitness function to the system-level dynamics of the population, we show that both low and very high, but not intermediate, levels of stress in the form of an antibiotic result in a disproportionate effect of hypermutation on resistance fixation. We demonstrate how this behavior is directly tied to the extent of genetic hitchhiking in the system, the propagation of high-mutation rate cells through association with high-fitness mutations. Our results indicate a substantial role for mutation rate flexibility in the evolution of antibiotic resistance under conditions that present a weak advantage over wildtype to resistant cells.

I. INTRODUCTION

The ability to predict the possible trajectories of a naturally evolving complex living system is key to describing and anticipating varied ecological and biomedical phenomena. Such predictability rests on an understanding of the potential for evolutionary adaptability of a given system. In asexual populations, a major mechanism responsible for evolutionary adaptation under environmental stress is the generation via genetic mutations of phenotypes able to better withstand and thrive under the stressor: resistant populations arising from within a wildtype population that may “rescue” the population from the source of stress by eventually coming to dominate the population. The rate at which such resistant mutations occur and the balance between these and more deleterious mutations are major determinants of whether the population may survive and adapt to selective evolutionary pressure [1–5], an environmental stressor that targets strain variants, or phenotypes, nonuniformly. Although the baseline mutation rate in bacteria is quite low, at about ∼10^–3 per genome per generation [6,7], high prevalences of mutator strains in natural bacterial populations and clinical isolates have been observed in various studies (see [8–11] for early work and [12] for a survey), and in certain cases “hypermutability,” an increase in the mutation rate over the baseline rate, was shown to result in fitness increases and faster adaptation [5,13–18] and even be essential for survival under stress [19] by enabling genetic hitchhiking on beneficial mutations [5,20–22]. Mutation rates can increase under environmental stress [23–26], and, in particular, hypermutability may play a significant role in the rise of antibiotic resistance [27–32].

The potential for adaptability via genetic mutations is dependent on the interplay between the ensemble of phenotypes that the system can access via mutations and the rate at which such transitions may occur within this ensemble. Phenotypes are typically characterized by some intrinsic measure of evolutionary fitness, such as their growth rate or lag phase, that contributes to evolutionary success, with extrinsic conditions, such as the probability of acquisition of this trait, initial population distribution, or resource availability, held fixed. Yet evolutionary advantage is determined by an interplay of these intrinsic and extrinsic factors, and separating these dependences while considering only a subset of them is of limited utility in establishing a global picture of a system’s evolvability potential as well as specific response to selective pressure. Here, we address both with a view to investigating the extent to which mutation rate variability drives adaptation under selective pressure.

The main purpose of this paper is to demonstrate that evolution under selective pressure—an external stressor that induces a fitness gradient in a given population—may not be uniformly sensitive to mutation rate as a function of the selective pressure as well as additional fitness-determining conditions, and that this nonuniform behavior should be taken into account when deciding on an appropriate antibiotic dosing protocol. In such a situation, there is generally no information available on the mutation rate in the pathogenic bacterial population, and this rate may also change in the course of therapy, as noted above. If dosing can be restricted to ranges for which the expected evolutionary outcome is less sensitive to the mutation rate, there will be higher predictive certainty about the treatment outcome, and more reliable strategies can be developed for avoiding antibiotic resistance arising in the course of treatment.

By considering a simple deterministic model of bacterial evolution under limited resources, we show that evolutionary outcome is most sensitive to the mutation rate when there exist phenotypes in the population that have a weak advantage—expressed through either intrinsic traits or extrinsic conditions—over the phenotype that is initially dominant in the population. In Sec. II we introduce and describe our evolutionary dynamics model; in Sec. III we define and motivate our measure of mutation rate sensitivity and quantify how sensitive the evolutionary success of a population is to increases in the mutation rate. We show that the fitness advantage of the resistant mutant—as given by both intrinsic fitness and extrinsic advantage-conferring conditions—is a determining factor in the extent of this sensitivity. In Sec. IV, we focus our analysis on selective evolutionary pressure in the form of a bacterial growth inhibitor (antibiotic), and we quantify (i) the dependence of mutation rate sensitivity to this source of pressure, and (ii) the extent to which the antibiotic drives the fixation of hypermutation in the population. We conclude with a brief discussion of the ramifications of our findings in Sec. V.

II. THE MODEL

We consider a system under non-neutral selection in which up to two distinct phenotypes—defined by their growth rates g_i—may coexist under limited resources. We denote them by “wt” for wildtype and r for resistant—designations that are intended to indicate that the r phenotype is more resistant to the evolutionary pressure considered (e.g., antibiotic, as in Sec. IV) under the non-neutral selection experienced by the population. Each of these phenotypes may be found with some baseline mutation rate μ_bl or with an elevated mutation rate of f × μ_bl, f > 1. Both forward and backward mutations are permitted with equal probability¹ p_wt,r; transitions between baseline-mutation phenotype and its elevated-mutation counterpart (of identical growth rate) occur with rate r_μ. In addition, to account for the fitness penalty incurred due to an increased rate of deleterious mutations at higher values of f, we assume that either phenotype may experience deleterious mutations with probability P_del. Since at non-negligible levels of selective pressure phenotypes whose resistance to the pressure is weaker than wildtype will have very low growth, we do not keep track of such low-growth populations explicitly, but they are implicitly accounted for in our model as the loss of cells from higher-growth populations via deleterious mutations. Since we assume that such loss occurs with uniform probability P_del, when the overall genetic mutation rate of a cell is μ, the rate of deleterious mutations is given by μP_del. Note that when P_del is high, increases in μ carry a higher penalty, implying that for hypermutation to be beneficial and counteract this penalty, resistant phenotypes would have to be significantly advantageous either by having a much higher growth rate (intrinsic advantage) or, e.g., by occurring with a high probability or being initially present in relatively high proportions (extrinsic advantage). Figure 1 shows a schematic of this model. We assume deterministic evolution under limited resources, as resources needed for growth are nearly always constrained in real biological systems, driving competition between organisms consuming the same resources. The equations governing the time evolution of this system are given by

$${\dot{x}}_{k,\alpha }(t)=\left(1-\frac{x_{\text{tot}}(t)}{K}\right)[g_k{x}_{k,\alpha }(t)+{\mu }_{\text{bl}}{f}_{\alpha }{p}_{j,k}{g}_j{x}_{j,\alpha }(t)+r_{\mu }{g}_k{x}_{k,\beta }(t)-f_{\alpha }{\mu }_{\text{bl}}{g}_k\left(p_{k,j}+P_{\text{del}}\right)-r_{\mu }{g}_k{x}_{k,\alpha }(t)],$$ 2.1

FIG. 1.

Schematic indicating the allowed single-step transitions and their rates between phenotypes.

where $j\ne k,j,k\in \left\{\text{wt,}r\right\},\alpha \ne \beta ,$ and a stationary population distribution is established when the total population size $x_{\text{tot}}={\sum }_{m,\gamma }{x}_{m,\gamma }$ reaches the resource capacity K. Note that faster-growing phenotypes will also produce exponentially more deleterious mutants as a result of their more frequent divisions, resulting in the previously noted fitness tradeoff. The four-dimensional system (Fig. 1) of Eq. (2.1) is given explicitly in Appendix A. We consider here the case in which the effect of selective pressure is limited to selecting for hypermutant variants if they are advantageous but not directly inducing hypermutability (for work on the latter, see, e.g., [35–39]). Under this assumption, hypermutation occurs independently of selective pressure, and therefore some proportion of the initial-state population would be expected to already exhibit elevated mutation rates. We assume in all that follows that cells with elevated mutation rates constitute 1% of the total initial population (distributed in proportion to the phenotype distribution) and a corresponding rate at which hypermutation-conferring mutations occur of 0.25% of cells per generation (see Appendix B for an extended discussion of these parameter choices).

III. SENSITIVITY OF EVOLUTIONARY SUCCESS TO THE MUTATION RATE

The ability of a population to survive evolutionary pressure depends on the extent to which resistant phenotypes come to dominate it and withstand potential subsequent applications of the stressor (e.g., in a serial dilutions experiment). To understand how mutation rate affects this, we consider how the stationary-state ratio of resistant cells in the population, x_r/x_tot, at elevated mutation rates compares with this ratio if all mutations in the system were restricted to occur at the baseline rate μ_bl,

$$\frac{R_r\left(\mu >{\mu }_{\text{bl}},\overrightarrow{\rho }\right)}{R_r\left({\mu }_{\text{bl}},\overrightarrow{\rho }\right)}\equiv \frac{{\left[x_r(\overrightarrow{\rho })/x_{\text{tot}}(\overrightarrow{\rho })\right]}_{\mu >{\mu }_{\text{bl}}}}{{\left[x_r(\overrightarrow{\rho })/x_{\text{tot}}(\overrightarrow{\rho })\right]}_{\mu ={\mu }_{\text{bl}}}}$$ 3.1

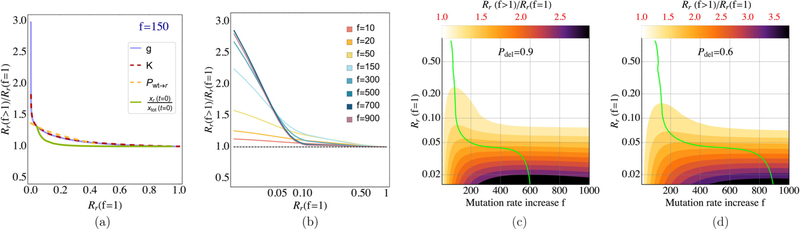
as a function of the main parameters that arise in our model, $\overrightarrow{\rho }=\left(g_r,K,p_{\text{wt},r},x_r(t=0)/x_{\text{wt}}(t=0)\right).$ The ratio (3.1) represents the extent to which a particular (elevated) mutation rate is able to drive a successful evolutionary outcome: a larger proportion of resistant cells in the stationary-state distribution. We refer to this as the sensitivity of evolutionary success to the mutation rate. In Fig. 2(a), we show how this sensitivity correlates with our measure of baseline “evolutionary advantage” of the resistant mutant, $R_r\left({\mu }_{\text{bl}},\overrightarrow{\rho }\right),$ as different components of $\overrightarrow{\rho }$ are varied.² For each of these model parameters, we see that at some fixed mutation rate (shown in the plot is a 150-fold increase over the baseline), sensitivity to the elevation in mutation rate is highest at low (but positive) levels of the resistant mutant’s evolutionary advantage; it decreases and eventually becomes negligible (≈1) as its evolutionary advantage increases.

FIG. 2.

The sensitivity of evolution success to hypermutation [R_r(f > 1)/R_r(f = 1)] is negatively correlated with the baseline-mutation rate evolutionary advantage R_r(f = 1) of the resistant mutant and is optimized at a mutation rate increase (f ) that depends on the extent of advantage, diminishing upon further increases in this rate. (a) R_r(f > 1)/R_r(f = 1) vs R_r(f = 1) curves for individual parameters $\overrightarrow{\rho }$ affecting the resistant mutant’s evolutionary advantage at f = 150. (b) Averages of the single-ρ_i curves in the appropriate ranges put through a low-pass filter for smoothness shown at multiple values of f (on a log-linear scale, for clarity of resolution between different mutation rates). The dashed black line (parity in R_r at baseline and elevated f ) indicates the point of no benefit from hypermutation; initial increases in f yield significant benefit at low-advantage conditions, which decreases and eventually becomes negligible at high-advantage conditions [R_r(f = 1) → 1]. At very high f (here $f\underset{\sim }{>}700$ ) even low-advantage mutants experience diminishing benefit from hypermutation. (c) and (d) R_r(f > 1)/R_r(f = 1) contours corresponding to plot (b) in f – R_r(f = 1) space. The green curve shows the optimal [i.e., yielding highest R_r(f > 1)/R_r(f = 1)] mutation rate increase factor f as a function of R_r(f = 1). The probability of deleterious mutations was set at P_del = 0.9 for plots (a)–(c) and at P_del = 0.6 in plot (d). When held constant, $\overrightarrow{\rho }$ parameters were set at g_r/g_wt = 3, K/x_tot(t = 0) = 10², p_wt,r = 0.01, and x_r(t = 0) = 0. Wildtype E. coli growth was set at g_wt = 0.34 h⁻¹ and μ_bl = 2 × 10⁻¹⁰ × N_g, with N_g the size of the E. coli genome.

Before proceeding in our analysis, we consider how the different parameters in $\overrightarrow{\rho }$ are in fact indicative of evolutionary advantage: while it is clear how a higher growth rate g_r, a larger initial proportion x_r(t = 0)/x_wt(t = 0), and a higher nondeleterious mutation rate lead to advantageous conditions for the resistant mutant to increase its proportions in the population, it is perhaps less obvious why a higher resource capacity produces an advantage specifically for the resistant mutant given that resource utilization is uniform in our model among the two phenotypes. The reason for this is that while the resource capacity appears a priori to be a nonselective environmental stressor, due to the exponential growth phase involved in the evolution of the system (2.1), higher resource capacity puts off the time of resource saturation, thus compounding the advantage enjoyed by phenotypes with higher growth rate g_k.

By averaging over individual-ρ_i interpolations [Fig. 2(b)] and varying f [Figs. 2(c) and 2(d)], we observe that the largest impact of the presence of elevated mutation rates in the population is under parameter combinations that, due to any one or multiple advantage-determining parameters, result in the resistant phenotype having a weak advantage. In these circumstances, the evolutionary advantage of the resistant cells may be insufficient to establish these populations in high proportions due to competition for limited resources, and certain increases in the mutation rate may thus be critical for adaptation, even at the cost of increased deleterious mutations. When initial conditions confer a high advantage on the resistant phenotype, mutation rate increases offer negligible to negative benefit. The high growth rate of these populations and hence frequent cell divisions imply that increases in their mutation rate also drive approximately exponentially increases in deleterious mutations, and that when a strong advantage exists, the baseline-mutation phenotype will thus rise to fixation faster than its hypermutant counterpart.

As shown in the contour plots of Figs. 2(c) (P_del = 0.9) and 2(d) (P_del = 0.6), for any level of resistant mutant evolutionary advantage, there exists an optimal mutation rate (green curves) yielding the highest proportion of resistant cells. Increasing the mutation rate up to this rate provides substantial benefit for lower-advantage mutants, and further increases lead to diminishing (albeit more gradually) returns due to the tradeoff with an increased loss caused by deleterious mutations. We see [Fig. 2(c) compared with 2(d)] that the level of evolutionary advantage past which there is no gain from hypermutation is fairly robust to variations in the rate of deleterious mutations (f μ_blP_del), but a lower P_del extends the range of mutation rates conferring benefit, as in that case there is little loss to deleterious mutations even at high f (see the supplemental material [40] for additional plots corresponding to different choices of P_del and r_μ).

IV. EFFECT OF SELECTIVE PRESSURE ON MUTATION RATE SENSITIVITY AND ON GENETIC HITCHHIKING

In this section, we focus on the effect of selective pressure in the form of an antibiotic that inhibits bacterial growth, and we quantify how the extent of selective pressure—different antibiotic concentrations—affects the sensitivity of evolutionary outcome to the mutation rate. The effect of antibiotic concentration on this quantity arises from the respective dependences of the phenotypes’ growth rates on this concentration. Motivated by work [34] on the response of E. coli to variations in the dosage of trimethoprim, a competitive inhibitor of dihydrofolate reductase, we assume a hyperbolic decay functional dependence for the growth rate g on the inhibitor concentration [I],

$$g([I])=\frac{g_0}{1+[I]/g_I},$$ (4.1)

where g₀ is the growth rate in the absence of an inhibitor and g_I controls the extent to which the population may grow in the presence of the inhibitor. In [34] this functional dependence, with g₀ and g_I given explicitly as functions of various protein biophysical and cellular properties, was shown to agree with experimental measurements for several mutant phenotypes over a range of [I], and similar methods can in principle be used to derive g₀ and g_I from biophysical principles for a wider range of biologically relevant scenarios.

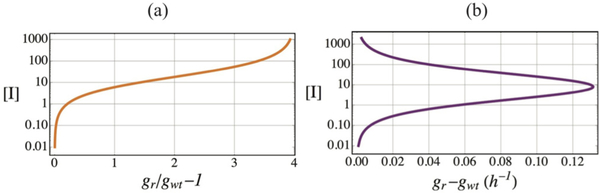
By computing the sensitivity to mutation rate, (Eq. 3.1), as a function of only the inhibitor with other parameters held fixed, we show [Fig. 3(a)] that at low levels of inhibition, where g_I carries only a small fitness advantage and mutant and wildtype growth rates g([I]) are similar, there is substantial benefit to be gained from hypermutation. As inhibition is increased, the difference between mutant and wildtype growth increases, resulting in the resistant mutant easily increasing in proportions without much benefit from hypermutation; but at yet higher levels of inhibition, the role of elevated mutation rates in determining adaptation once again becomes significant. The behavior of the (intrinsic) selection coefficient g_r/g_wt – 1 is not revealing in this respect: it monotonically approaches a constant value at high [I]. However, the difference between g_r and g_wt peaks at an intermediate value of [I] and decreases at lower and higher values of [I] (Fig. 4). While the peak does not numerically coincide with the [I] concentrations yielding the lowest R_r(f > 1)/R_r(f = 1), we note that additional parameters in $\overrightarrow{\rho }$ also affect this ratio.

FIG. 3.

(a) Hypermutation has a strong impact on resistance fixation at low and at very high levels of inhibition that is optimized at a mutation rate that depends on the inhibition level. (b) Genetic hitchhiking on resistant mutations is most pronounced in intermediate levels of inhibition. The black contour (=1) indicates no hitchhiking on resistant mutations. Parameters were set at g_0,r = g_0,wt = 0.34 h⁻¹, g_r,I = 5g_wt,I, where gwt,I = 3.6 μg/mL, P_del = 0.9; and K, p_wt,r, and x_r(t = 0) as in Fig. 2.

FIG. 4.

While the intrinsic selection coefficient g_r/g_wt – 1 increases monotonically as a function of inhibition (a), the difference in growth rates g_r – g_wt is maximized at intermediate levels of inhibition (b).

We next consider the extent to which selective pressure, the antibiotic, affects the extent of hypermutation in the population by computing the stationary-state proportion of hyper mutants in the population $x_h(\overrightarrow{\rho })/x_{\text{tot}}(\overrightarrow{\rho })$ when an inhibitor is applied (resistant cells have a positive evolutionary advantage) relative to when no inhibition is present (neutral selection),

$$\frac{R_h([I]>0,\overrightarrow{\rho })}{R_h([I]=0,\overrightarrow{\rho })}\equiv \frac{{\left[x_h(\overrightarrow{\rho })/x_{\text{tot}}(\overrightarrow{\rho })\right]}_{[I]>0}}{{\left[x_h(\overrightarrow{\rho })/x_{\text{tot}}(\overrightarrow{\rho })\right]}_{[I]=0}}$$ 4.2

as a function of the inhibition [Fig. 3(a)]. Figure 3(b) shows contours of R_h([I] > 0)/R_h([I] = 0) in a two-dimensional space of f and [I]. We find [Fig. 3(b)] that genetic hitchhiking on resistant mutations as measured by R_h is most pronounced in an f – [I] phase space that up to intermediate mutation rate increases is approximately complementary to that in which hypermutation has the most pronounced beneficial effects. This effect can be explained by noting that at low inhibition, where the resistant mutant does not have significant advantage over wildtype, the acquisition of such mutations does not drastically increase the growth rate of hypermutant cells; on the other hand, when resistant mutations are highly advantageous (high inhibition), the baseline-mutation resistant mutant rises to fixation largely unaided by hypermutation, which under finite resources limits the growth potential of other subpopulations (resistant hypermutants). We note that the range of mutation rates at which we observe hitchhiking to be strongest is in keeping with experimental observations (see [12] for a review and [41] for additional recent data) of an O(10¹−10²) increase over baseline in E. coli clinical isolates [with some data pointing to a nearly O(10³) in certain cases [42]].

V. DISCUSSION

In obtaining the results presented here, we assumed deterministic dynamics. While mutations typically arise randomly and can introduce a large degree of stochasticity into the dynamics, deterministic evolution can provide important insights into processes with varying degrees of stochasticity: large populations are expected to sample a large extent of the available mutational phase space (with infinite populations sampling every possible configuration, or genotype), and experimental work [43] on evolutionary pathways in E. coli to drug resistance found that similar mutational trajectories across populations evolved in parallel. Our deterministic results, moreover, suggest that stochastic fluctuations in the mutation rate can have an outsized effect on the stationary state of the system under a broad range of conditions that suppress the evolutionary advantage of emergent resistant populations. Knowledge of the effects of these conditions in conjunction with a quantitative understanding of changes in a controllable selective pressure, such as the one we modeled here in the case of a growth inhibitor, are crucial for forming informed predictions on how variations in this main driving force of adaptation affect the dynamics of complex, high-dimensional systems and on how to best minimize the effects of stochastic fluctuations to establish a desired evolutionary outcome, such as a clinical antibiotic protocol minimizing the risk of resistance evolution.

APPENDIX A: EVOLUTION EQUATIONS

We consider a population subdivided into wildtype with growth rate g_wt and baseline mutation rate μ_bl, a resistant phenotype with this baseline mutation rate and growth rate g_r, and corresponding phenotypes of equal growth rate but increased mutation rate f μ_bl, f > 1. Population levels at time t are given by x_wt,1(t), x_r,1(t), x_wt,f (t), and x_r,f (t), respectively. Transitions (mutations) between the subpopulations are permitted in accordance with the schematic Fig. 1. We assume limited resources set by an environmental carrying capacity K, so that the subpopulation levels thus evolve in time according to the equations

$$\begin{array}{l}{\dot{x}}_{\text{wt},1}(t)=\left(1-\frac{x_{\text{tot}}(t)}{K}\right)\left\{\left[1-{\mu }_{\text{bl}}\left(p_{r,\text{wt}}+P_{\text{del}}\right)-r_{\mu }\right]g_{\text{wt}}{x}_{\text{wt,1}}(t)+{\mu }_{\text{bl}}{p}_{r,\text{wt}}{g}_r{x}_{r,1}(t)+r_{\mu }{g}_{\text{wt}}{x}_{\text{wt,}f}(t)\right\},\\ {\dot{x}}_{\text{wt},f}(t)=\left(1-\frac{x_{\text{tot}}(t)}{K}\right)\left\{\left[1-f\times {\mu }_{\text{bl}}\left(p_{r,\text{wt}}+P_{\text{del}}\right)-r_{\mu }\right]g_{\text{wt}}{x}_{\text{wt},f}(t)+f\times {\mu }_{\text{bl}}{p}_{r,\text{wt}}{g}_r{x}_{r,f}(t)+r_{\mu }{g}_{\text{wt}}{x}_{\text{wt},1}(t)\right\},\\ {\dot{x}}_{r,1}(t)=\left(1-\frac{x_{\text{tot}}(t)}{K}\right)\left\{[1-{\mu }_{\text{bl}}\left(p_{r,\text{wt}}+P_{\text{del}}\right)-r_{\mu }]g_r{x}_{r,1}(t)+{\mu }_{\text{bl}}{p}_{r,\text{wt}}{g}_{\text{wt}}{x}_{\text{wt},1}(t)+r_{\mu }{g}_r{x}_{r,f}(t)\right\},\\ {\dot{x}}_{r,f}(t)=\left(1-\frac{x_{\text{tot}}(t)}{K}\right)\left\{\left[1-f\times {\mu }_{\text{bl}}\left(p_{r,\text{wt}}+P_{\text{del}}\right)-r_{\mu }\right]g_r{x}_{r,f}(t)+f\times {\mu }_{\text{bl}}{p}_{r,\text{wt}}{g}_{\text{wt}}{x}_{\text{wt},f}(t)+r_{\mu }{g}_r{x}_{r,1}(t)\right\},\end{array}$$ A1

where r_μ is the rate of mutation from a baseline-mutation rate (f = 1) phenotype to an f > 1 phenotype (the rate at which mutations leading to elevated mutation rates f μ_bl occur) and its reverse (assumed to be equal), p_r,wt ≡ p_wt→r = p_r→wt is the probability of mutation from wildtype to the resistant phenotype and backward, and P_del is the probability of mutation to deleterious phenotypes, x_tot = x_wt,1 + x_wt,1f + x_r,1 + x_{r, f}.

To compute the relative advantage or disadvantage conferred by hypermutation on the fixation of drug-resistant subpopulations [Eq. (3.1)], we numerically compute the ratio of resistant mutants (combined nonhypermutant and hypermutant types) in the total population at $2⩽f⩽1000$ to the ratio that would result if no hypermutations were allowed in the system, i.e., if we set r_μ = 0 and consider only phenotypes x_wt,1 and x_r,1. When computing these quantities for a system with an initial distribution of hypermutants of either phenotype, we assume that the r_μ = 0 system has a corresponding distribution in which

$x_{i,r_{\mu }=0}(t=0)=x_{i,1,r_{\mu }\ne 0}(t=0)+x_{i,f,r_{\mu }\ne 0}(t=0),$ with i representing either wildtype or the resistant phenotype.

In the figures shown in the main text and in the supplemental material, μ_bl was set at 2 × 10⁻¹⁰ × N_genome per generation per cell [6], where N_genome = 4.64 × 10⁶ is the number of base pairs in the E. coli genome. In the results shown in the main text, when the population is not purely wildtype at t = 0, the proportion of hypermutants chosen is assumed to be distributed proportionally among the wildtype and resistant populations.

APPENDIX B: RATE OF ACQUISITION r_μ OF INCREASED MUTATION RATE AND INITIAL PROPORTION OF HYPERMUTANTS

To estimate a biologically reasonable r_μ, we consider a simple system consisting of a wildtype f = 1 phenotype and a wildtype f > 1, both with fitness g_wt, which can mutate into

each other with rate r_μ:

$$\begin{array}{l}{\dot{x}}_{\text{wt},1}(t)=\left(1-\frac{x_{\text{wt},1}(t)+x_{\text{wt},f}(t)}{K}\right)\\ \times \left[\left(1-r_{\mu }\right)g_{\text{wt}}{x}_{\text{wt},1}(t)+r_{\mu }{g}_{\text{wt}}{x}_{\text{wt},f}(t)\right],\\ {\dot{x}}_{\text{wt},f}(t)=\left(1-\frac{x_{\text{wt},1}(t)+x_{\text{wt},f}(t)}{K}\right)\\ \times \left[\left(1-r_{\mu }\right)g_{\text{wt}}{x}_{\text{wt},f}(t)+r_{\mu }{g}_{\text{wt}}{x}_{\text{wt},1}(t)\right].\end{array}$$ (A2)

The steady-state (stationary distribution) proportion of hypermutants in the total population will be given by

$$R=\frac{x_{\text{wt},f}(\tau )}{x_{\text{wt},1}(\tau )+x_{\text{wt},f}(\tau )}$$ 3

at time τ after resources have been saturated.³ Hypermutation can be caused by various mechanisms; studies that focused on pathogenic E. coli have found comparatively high (>1%) proportions of mutators in bacterial isolates (3.6% in [44] and 1.9% in [9]); a separate study that looked specifically for MMR deactivation in E. coli found a much lower proportion (0.24%) when both commensal and pathogenic E. coli were included [8]. A later study [10] found, however, that when other sources of hypermutation were included besides MMR, E. coli cells exhibiting increased mutation rates—of up to two orders of magnitude from the baseline mutation rate—constituted as much as 14% of the total population, most being mild mutators, with both commensal and pathogenic strains included in the study. The highest mutation rates were found to correspond to MMR deficiencies, with lower increases due to other mechanisms. Note that since r_μ is a neutral-selection rate, studies of mutator proportions that were conducted under conditions of adaptive evolution will likely overestimate this parameter, and we therefore restrict our data to studies of natural isolates, noting that even in those cases adaptive evolution in the recent past may have taken place.

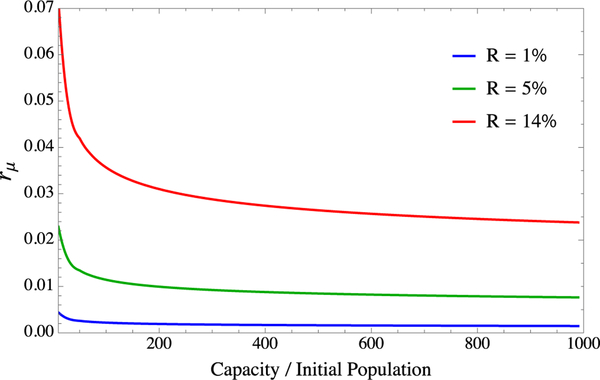
We compute which r_μ values yield the stationary distribution ratio (3) for different carrying capacities by taking g_wt as in the main text to be 0.34 h⁻¹ under no inhibition. The results for different values of R are shown in Fig. 5. Since we consider a uniform distribution⁴ of mutation rate increase factors f and the 14% figure is heavily tipped toward mild mutators, using this figure will likely overestimate the mutation rate r_μ in our model for higher values of f. For the purpose of the plots in the main text, we set on the lower end at r_μ = 0.25% and an initial proportion of 1% hypermutating cells in the population.

FIG. 5.

Computed values of r_μ from the system (2) for different expected steady-state proportions of resistant cells as the availability of resources is varied. Across a wide range of carrying capacities, r_μ only varies from ∼0.5% to ∼1.5%. Plots in the main text employ r_μ = 0.25%, corresponding to an initial hypermutant population of 1% of the total population.