Exchange Saturation Transfer and Associated NMR Techniques for Studies of Protein Interactions Involving High-Molecular-Weight Systems

Abstract

A brief overview of theoretical and experimental aspects of the Dark state Exchange Saturation Transfer (DEST) and lifetime line broadening (ΔR₂) NMR methodologies is presented from a physico-chemical perspective. We describe how the field-dependence of ΔR₂ can be used for determining the exchange regime on the transverse spin relaxation time-scale. Some limitations of DEST/ΔR₂ methodology in applications to molecular systems with intermediate molecular weights are discussed, and the means of overcoming these limitations via the use of closely related exchange NMR techniques is presented. Finally, several applications of DEST/ΔR₂ methodology are described from a methodological viewpoint, with an emphasis on providing examples of how kinetic and relaxation parameters of exchange can be reliably extracted from the experimental data in each particular case.

Dark state Exchange Saturation Transfer (DEST) and lifetime line broadening (ΔR₂) methodologies, introduced about 8 years ago, have provided a powerful means of investigating exchange processes involving very high-molecular weight species by NMR (Fawzi et al., 2010; Fawzi et al., 2011; Fawzi et al., 2012; Anthis and Clore, 2015). Examples include early stages of peptide/protein aggregation processes (Fawzi et al., 2010; Fawzi et al., 2011; Conicella and Fawzi, 2014; Fawzi et al., 2014), binding of peptides to and protein folding on large supra-molecular machines such as the chaperonin GroEL (Libich et al., 2013; Libich et al., 2015; Libich et al., 2017; Wälti et al., 2018), and interactions of proteins and peptides with nanoparticles (Ceccon et al., 2014; Ceccon et al., 2016a; Ceccon et al., 2016b; Ceccon et al., 2017; Egner et al., 2017; Ceccon et al., 2018a; Ceccon et al., 2018b; Ceccon et al., 2019). Dennis Torchia, to whom this brief review is dedicated on the occasion of his 80^th birthday, played an important role in the initial stages of development of these NMR techniques (Fawzi et al., 2010; Fawzi et al., 2011; Fawzi et al., 2012). Dennis’s profound knowledge of NMR theory in general and of NMR applications for the studies of chemical exchange processes in particular, proved invaluable for laying the groundwork for the development of these NMR methods, as well as a theoretically sound interpretation of early-stage experimental results.

In recognition of Dennis’s extensive contributions to the field of exchange NMR, as well as his role in the development of DEST/ΔR₂ methodology, here we provide a brief overview of NMR developments in studies of exchange processes involving high-molecular-weight systems with a special emphasis on the physico-chemical aspects of the methodology. This account is therefore not intended to survey in detail all the applications of the DEST/ΔR₂ methodology that have appeared in the scientific literature in recent years, but rather focuses on certain quantitative aspects of DEST/ΔR₂ and associated NMR techniques. We anticipate that our treatment of some of the NMR nuances of this methodology will be useful for those NMR researchers actively engaged in studying chemical exchange processes involving high-molecular-weight systems.

We start with a description of the theoretical underpinnings of exchange-induced lifetime line broadening (ΔR₂) and describe how the field-dependence of ΔR₂ can be used to determine the exchange regime on the transverse spin relaxation time-scale. In what follows, we describe some limitations of DEST/ΔR₂ methodology in applications to molecular systems with intermediate molecular weights (and hence transverse spin relaxation rates), and delineate the means of overcoming these limitations by supplementing DEST and ΔR₂ data with data obtained from closely related NMR techniques. Finally, several applications of DEST/ΔR₂ methodology are described from a methodological perspective with an emphasis on providing examples of how the kinetic and relaxation parameters of exchange can be reliably and unambiguously extracted from the NMR data in each particular case.

Lifetime line broadening, chemical exchange-induced line broadening and chemical shifts.

The magnetization of a molecular system exchanging between two states A and B with first-order rate constants k_a and k_b, $\text{A}\underset{\underset{k_{\text{b}}}{\leftarrow }}{\overset{k_{\text{a}}}{\to }}\text{B}$ evolves according to,

$$\frac{d}{dt}\left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]=-\left[\begin{array}{cc}{R}_2^{\text{A}}+k_{\text{a}}& -k_{\text{b}}\\ -k_{\text{a}}& R_2^{\text{B}}+k_{\text{b}}+i\Delta \omega \end{array}\right]\left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]$$ (1)

where M^A and M^B are the transverse magnetization operators of states A and B, respectively; $R_2^{\text{A}}$ and $R_2^{\text{B}}$ are the respective intrinsic transverse relaxation rates of the two states in the absence of exchange; and Δω is the difference in chemical shifts (ω_B – ω_A) between states A and B (in rad/s), where the on-resonance condition with respect to state A is assumed (ω_A = 0 ). In the context of molecular association, k_a is a pseudo-first order (‘apparent’) association rate constant, $k_{\text{on}}^{\text{app}}$, and k_b is the first-order dissociation rate constant, k_off. Exact analytical solutions of the differential equations given by Eq. 1 are straightforward to obtain. However, simple approximations for chemical exchange line broadening, R_ex, and the exchange-induced chemical shift, δ_ex, can be derived under conditions where the populations of states A and B are highly skewed $\left(k_{\text{b}}\gg k_{\text{a}}\right)$. Retaining only the leading term in the characteristic polynomial, and taking the real, $R_{ex}=-Re\left(E_1\right)-R_2^{\text{A}}$, and imaginary, ${\delta }_{ex}=Im\left(E_1\right)$, components of the smaller eigenvalue E₁ of the 2×2 matrix in the right-hand side of Eq. 1, leads to

$$R_{\text{ex}}=k_{\text{a}}\frac{k_{\text{b}}\Delta R+\Delta R^2+\Delta {\omega }^2}{{\left(k_{\text{b}}+\Delta R\right)}^2+\Delta {\omega }^2}$$ (2)

$${\delta }_{\text{ex}}=k_{\text{a}}\frac{k_{\text{b}}\Delta \omega }{{\left(k_{\text{b}}+\Delta R\right)}^2+\Delta {\omega }^2}$$ (3)

where $\Delta R=R_2^{\text{B}}-R_2^{\text{A}}$. These expressions were initially derived by Anet and Basus (1969) in the limit where ΔR = 0, and later in a more general form by Skrynnikov et al. (2002). We denote the component of R_ex that ‘survives’ in the absence of chemical shift differences between states A and B (Δω = 0) and arises from large differences between the transverse spin relaxation rates $R_2^{\text{A}}$ and $R_2^{\text{B}}$ (large ΔR ) as ‘lifetime line broadening’ or ΔR₂ given by,

$$\Delta R_2=\frac{k_{\text{a}}\Delta R}{k_{\text{b}}+\Delta R}$$ (4)

As we focus here on exchanging systems where $R_2^{\text{B}}\gg R_2^{\text{A}}$ and $k_{\text{b}}\gg k_{\text{a}}$, we can write that

$$\Delta R_2\approx \frac{k_{\text{a}}}{1+\left(k_{\text{ex}}/R_2^{\text{B}}\right)}$$ (5)

where the exchange rate $k_{\text{ex}}=k_{\text{b}}+k_{\text{a}}\approx k_{\text{b}}$. A plot of ΔR₂ in units of k_a versus the ratio $\left(k_{\text{ex}}/R_2^{\text{B}}\right)$ is shown in Figure 1.

Figure 1.

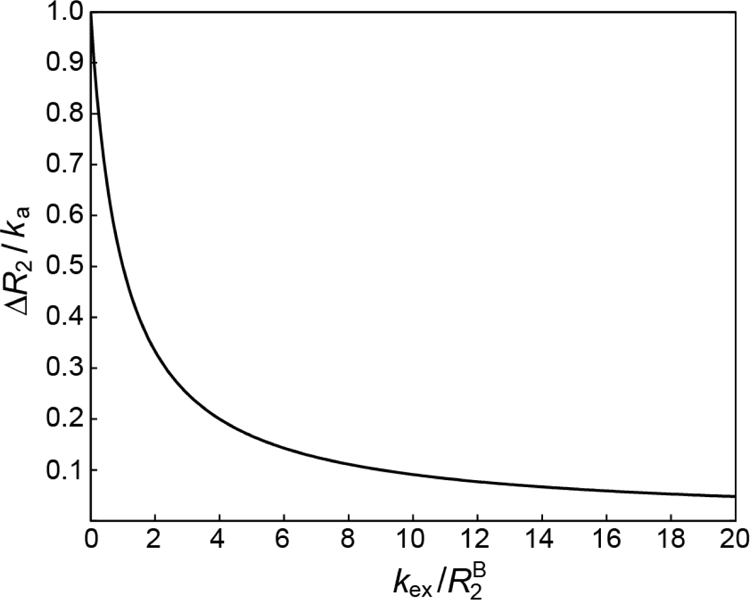
Plot of ΔR₂/k_a (y-axis) versus $k_{\text{ex}}/R_2^{\text{B}}$ (x-axis). The value of ΔR₂/k_a, spanning a range from 0 to 1, is a measure of the exchange regime in relation to the time-scale of transverse relaxation.

It is immediately evident from Eq. 5 and the plot in Figure 1 that when exchange is fast on the transverse relaxation time scale $(k_{\text{ex}}/R_2^{\text{B}}\gg 1)$, $\Delta R_2\approx p_{\text{B}}{R}_2^{\text{B}}$; and when exchange is slow relative to the transverse relaxation rate $(k_{\text{ex}}/R_2^{\text{B}}\ll 1)$, $\Delta R_2\approx k_{\text{a}}$. Experimentally, lifetime line-broadening (ΔR₂ ) is easily measured as the difference between transverse spin relaxation rates in the presence and absence of exchange under conditions where the contributions to R_ex arising from a finite (non-zero) value of Δω are minimized (e.g. by using R_1ρ measurements with strong on-resonance spin-lock fields). Therefore, any detailed investigation of exchange, in a biological system involving a large molecular weight component, usually starts with the measurement of ΔR₂ as a function of controllable experimental parameters such as concentration, temperature and the strength of the static magnetic field.

The exchange regime on the relaxation time-scale (generally, not known a-priori for a given system in the absence of prior information on the rate constants) can be established from the dependence of ΔR₂ on the strength of the static magnetic (spectrometer) field B₀. The effect of B₀ on $R_2^{\text{B}}$ is easily predictable from nuclear spin relaxation theory (Abragam, 1961). The analysis below pertains almost exclusively to backbone ¹⁵N nuclei in proteins as their sizable chemical shift anisotropy (CSA; ~ −160–170 ppm) ensures that substantial (and predictable) changes in ${}^{15}\text{N-}{R}_2^{\text{B}}$ accompany changes in B₀. Following the analysis of Millet et al. (2000) and Vallurupalli et al. (2011) of the dependence of R_ex and δ_ex on B₀, it is straightforward to show that,

$$\frac{d\ln \Delta R_2}{d\ln R_2^{\text{B}}}=\alpha \approx \frac{1}{1+(R_2^{\text{B}}/k_{\text{ex}})}$$ (6)

where 0 ≤ α ≤ 1. From Eq. 6, it follows that for small changes in $R_2^{\text{B}}$ and the static field, ΔB, ΔR₂ measured at a higher magnetic field $(\Delta R_2^{B_0+\Delta B})$ is related to that measured at the lower field $(\Delta R_2^{B_0})$ via the relationship,

$$\frac{\Delta R_2^{B_0+\Delta B}}{\Delta R_2^{B_0}}\approx n^{\alpha }$$ (7)

where n is a factor by which $R_2^{\text{B}}$ is predicted to increase theoretically (e.g. ~1.3 between 900 and 600 MHz, and ~1.2 between 800 and 600 MHz for ¹⁵N nuclei of the protein backbone), and the exchange regime is determined by the value of the exponent $\alpha =\ln (\Delta R_2^{B_0+\Delta B}/\Delta R_2^{B_0})/\ln n$. Thus, the ratio of experimental ΔR₂ values (or their averages for different residues in a protein) measured at two spectrometer fields allows one to establish the exchange regime via the relationship in Eq. 7. Three regimes can be distinguished in this regard: (1) if the ratio, n^α, is equal or close to 1, $\Delta R_2\approx k_{\text{a}}$ (slow exchange on the transverse relaxation time-scale, $k_{\text{ex}}/R_2^{\text{B}}\ll 1$); (2) if the ratio is close to the factor n, exchange is fast relative to transverse relaxation rates, $k_{\text{ex}}/R_2^{\text{B}}\gg 1$; and (3) if the ratio adopts an intermediate value (<n and >1), the exchange rate k_ex is comparable to $R_2^{\text{B}}$ (intermediate exchange regime on the transverse relaxation time scale with $R_2^{\text{B}}/k_{\text{ex}}={\alpha }^{-1}-1$). Further, although all the parameters of exchange cannot be determined unambiguously from the field-dependence of ΔR₂, even if the measurements are performed at more than two spectrometer fields, the forward rate constant k_a in the intermediate exchange regime (case 3 above) can be estimated from ΔR₂ recorded at two fields using the following relationship,

$$k_{\text{a}}=\frac{(n-1)\Delta R_2^{B_0}\Delta R_2^{B_0+\Delta B}}{n\Delta R_2^{B_0}-\Delta R_2^{B_0+\Delta B}}$$ (8)

where average values of ΔR₂ over all residues of a protein can be used. Eq. 8 provides a means of estimating the value of k_a in the intermediate exchange regime from ΔR₂ data acquired at two spectrometer fields even in the absence of other experimental information.

Dark state Exchange Saturation Transfer (DEST) spectroscopy and associated NMR techniques.

To characterize the kinetics of an exchanging system in detail, ΔR₂ measurements are usually combined with analysis of Dark state Exchange Saturation Transfer (DEST) profiles (Fawzi et al., 2010; Fawzi et al., 2011). DEST experiments involve the application of off-resonance radiofrequency (RF) radiation at a series of offsets from the resonance positions of the directly observable state A in order to saturate the nuclei of the large, spectroscopically invisible (‘dark’) state B. The magnetization is then transferred from the (partially) excited ‘dark’ state to the major, observable state A via exchange. Intensities of the NMR cross-peaks of the major visible species obtained at each offset frequency are subsequently normalized to those obtained without saturation or very far off-resonance where even the ‘dark’ state is not excited. The acquisition of such intensity profiles as a function of offset frequencies both up-field and down-field of the frequency range of the observable spectrum, is usually carried out at two or more RF saturation field strengths, which are chosen to maximize the broadening of the profiles in the presence of exchange while ensuring minimal saturation of cross-peaks in the absence of exchange. DEST profiles are commonly analysed via numerical integration of a set of homogeneous Bloch-McConnell differential equations (McConnell, 1958; Helgstrand et al., 2000) (represented by a 7×7 matrix for a 2-state system), as no analytical expressions exist for the general case of exchange saturation transfer. Simultaneous analysis of DEST/ΔR₂ data allows the kinetic parameters of exchange, as well as the values of $R_2^{\text{B}}$, to be determined unambiguously under conditions where $R_2^{\text{B}}>{\omega }_1$ (the strength of the RF saturation field applied to the resonances of the ‘dark’ state). This was the case in the initial applications of the DEST/ΔR₂ methodology to studies of early stages of amyloid aggregation (Fawzi et al., 2010; Fawzi et al., 2011). Below, we provide a brief description of the limitations of the DEST/ΔR₂ approach in cases when the above condition is not fulfilled, namely for intermediate values of $R_2^{\text{B}}$ lying the range between ~500 s⁻¹ and 5000 s⁻¹ and therefore either smaller than or comparable to the strength of the saturation fields employed in the DEST experiments.

Although the equations derived by Baldwin and Kay (2013) for R_1ρ, in the case where $R_2^{\text{B}}>R_2^{\text{A}}$, can be used to reproduce DEST profiles, the expressions are bulky and give little insight into how the parameters of exchange and relaxation relate to one another. That is why we choose to draw an analogy with the recent work of Kay and co-workers (Yuwen et al., 2018), where the authors probed a slowly exchanging protein system via off-resonance R_1ρ experiments. For a two-state exchanging system in the limit where the strength of the radio-frequency (RF) field ${\omega }_1\gg R_2^{\text{B}}$; k_ex, the evolution of magnetization, in the absence of chemical shift differences between the inter-converting species (Δω = 0), can be approximated by,

$$\frac{d}{dt}\left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]=-\left[\begin{array}{cc}{k}_{\text{a}}& -k_{\text{b}}\\ -k_{\text{a}}& k_{\text{b}}+R_2^{\text{B}}{\sin }^2\theta \end{array}\right]\left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]$$ (9)

where the notation of Eq. 1 is preserved, and θ is the angle between the spin-locked magnetization and the z-axis of the laboratory frame (Yuwen et al., 2018). The longitudinal relaxation rates of states A and B ($R_1^{\text{A}}$ and $R_1^{\text{B}}$), as well as the transverse relaxation rate of state A, $R_2^{\text{A}}$, are assumed to be zero in this approximation. The solution of Eq. 9 is given by,

$$\begin{gathered} M^{\text{A}}(t)=A{e}^{{\lambda }_{s}t}+B{e}^{{\lambda }_{f}t} \\ {M}^{\text{B}}(t)=C{e}^{{\lambda }_{s}t}+D{e}^{{\lambda }_{f}t} \end{gathered}$$ (10)

where the small (‘slow’) and large (‘fast’) eigenvalues, λ_s, and λ_f, are

$${\lambda }_{f,s}=-\frac{1}{2}\left(k_{\text{ex}}+R_2^{\text{B}}{\sin }^2\theta \pm \sqrt{{\left(k_{\text{ex}}+R_2^{\text{B}}{\sin }^2\theta \right)}^2-4p_{\text{B}}{k}_{\text{ex}}{R}_2^{\text{B}}{\sin }^2\theta }\right)$$ (11)

Expressions for the terms A-D in Eq. 10 when Δω = 0, are given by,

$$\begin{gathered} A={\lambda }_f\left(1-p_{\text{B}}\right)/\left({\lambda }_f-{\lambda }_s\right) \\ B=-{\lambda }_s\left(1-p_{\text{B}}\right)/\left({\lambda }_f-{\lambda }_s\right) \\ C=p_{\text{B}}\left({\lambda }_f+R_2^{\text{B}}{\sin }^2\theta \right)/\left({\lambda }_f-{\lambda }_s\right) \\ D=-p_{\text{B}}\left({\lambda }_s+R_2^{\text{B}}{\sin }^2\theta \right)/\left({\lambda }_f-{\lambda }_s\right) \end{gathered}$$ (12)

−λ_s represents the effective relaxation rate measured as a function of offset. From Eqs. 9–11, it therefore follows that the contribution to the transverse relaxation rate arising from exchange, R_ex, in the limit of skewed populations (p_B << p_A) is given by,

$$R_{\text{ex}}=-{\lambda }_s/{\sin }^2\theta \approx {\left[\frac{1}{p_{\text{B}}{R}_2^{\text{B}}}+\frac{{\sin }^2\theta }{p_{\text{B}}{k}_{\text{ex}}}\right]}^{-1}$$ (13)

Eq. 9 and its solutions in Eqs. 10–12 are a good approximation to the full Bloch-McConnell equations in the limit ${\omega }_1\gg R_2^{\text{B}}$; k_ex for the analysis of off-resonance R_1ρ experiments where the magnetization is aligned (‘locked’) along the effective RF field for each value of the offset (angle θ).

In exchange saturation transfer experiments such as DEST, however, the magnetization is saturated during the relaxation period by application of a continuous RF field so that the angle between the magnetization and the z-axis of the laboratory frame becomes time-dependent. Nevertheless, the DEST profiles generated via the full set of Bloch-McConnell equations can be reproduced reasonably well using the expression for R_1ρ relaxation rate, $R_{1\text{ρ}}=R_1{\cos }^2\theta +R_{2,\text{eff}}{\sin }^2\theta$, where $R_{2,\text{eff}}=R_2^{\text{A}}+R_{\text{ex}}$ and $R_{\text{ex}}$ is calculated using Eq. 13, provided that the transverse relaxation rates $R_2^{\text{B}}$ are sufficiently large. To further illustrate this point, the differences in normalized intensities Δ between DEST profiles generated using the full set of Bloch-McConnell equations and those calculated from R_1ρ rates using Eq. 13 for R_ex are shown in Figure 2A. As might be expected, the largest differences Δ are localized at intermediate offset values, but even the latter become very small by absolute magnitude as the transverse relaxation rates of state B increase (Figure 1A). Interestingly, the agreement between the DEST profiles does not deteriorate for faster rates of exchange as shown in Figure 2B, where the maximal deviations (by absolute magnitude) between the two profiles are plotted as a function of ${\log }_{10}(R_2^{\text{B}})$ for exchange rates ranging from 100 to 10,000 s⁻¹. Since, for the purposes of this discussion, we are mostly interested in ‘intermediate’ relaxation rates, that is ${\log }_{10}(R_2^{\text{B}})$ values spanning a range between ~2.8 and ~3.8 where a shallow minimum of |Δ|_max is observed in Figure 2B in the case of faster exchange, we can conclude that the simplified treatment represented by Eqs. 9 and 13 above serves our illustrative purposes.

Figure 2.

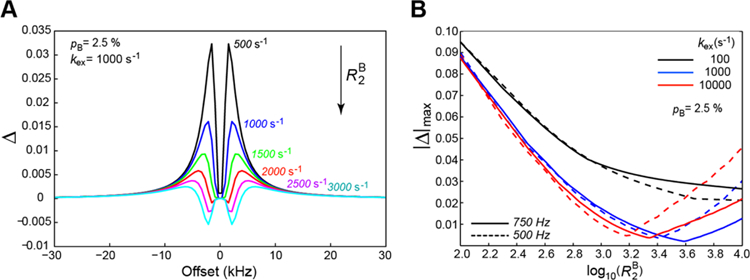
(A) Difference (Δ) between normalized intensities of DEST profiles (scaled between 0 and 1) calculated using the full Bloch-McConnell equations and those calculated using Eq. 13 for a set of $R_2^{\text{B}}$ values ranging from 500 to 3,000 s⁻¹. The exchange parameters used are: p_B = 2.5% and k_ex = 1000 s⁻¹. The plots are color-coded according to $R_2^{\text{B}}$ values as indicated on the plot. (B) Maximal (by absolute magnitude) deviations |Δ|_max (y-axis) between the differences of the DEST profile calculated as in (A) plotted versus ${\log }_{10}(R_2^{\text{B}})$ (x-axis) for three regimes of exchange, color-coded as indicated on the plot. Dashed and solid lines in all exchange regimes correspond to DEST RF saturation field of 500 and 750 Hz, respectively. p_B is fixed at 2.5 % in all calculations.

Eq.13 is particularly useful in illustrating the limitations of DEST/ΔR₂ analysis for intermediate $R_2^{\text{B}}$ rates because it shows that whereas the value of $k_{\text{a}}=p_{\text{B}}{k}_{\text{ex}}$ in the denominator of the right term can be determined from ΔR₂ data acquired at two spectrometer fields and/or the combination of ΔR₂ and DEST profiles, the product $p_{\text{B}}{R}_2^{\text{B}}$ in the denominator of the first term is the only quantity that can be determined with certainty from DEST/ΔR₂ analysis under condition where $R_2^{\text{B}}$ is not much larger than the strength of the applied saturation field ω₁ (in rad/sec).

Numerical simulations using synthetic DEST data at three RF saturation fields in combination with ΔR₂ data at two spectrometer fields, confirm that as the value of $R_2^{\text{B}}$ increases beyond the highest of the ω₁ fields employed in DEST measurements, the limitation of the DEST/ΔR₂ approach described above slowly disappears, i.e. accurate values of p_B and $R_2^{\text{B}}$ can be extracted at the same time from the data to within the uncertainties in the fitted parameters without resort to other/additional NMR experimental observables.

The approach used to de-correlate p_B and $R_2^{\text{B}}$ for intermediate $R_2^{\text{B}}$ values will depend upon the exchange regime on the transverse relaxation time-scale. For slow exchange $(k_{\text{ex}}/R_2^{\text{B}}<1)$, another observable quantity introduced by Kay and co-workers (Yuwen et al., 2018) can be used. This experimental observable, denoted as C_fast, relates to the fractional contribution of the fast decaying component of R_1ρ relaxation to the total signal intensity: namely, (B+D) in Eq. 10, with the sum of all eigenvectors (A+B+C+D) normalized to unity. From Eq. 10, the decay of ‘spin-locked’ magnetization for each state in R_1ρ experiments is inherently biphasic. When care is taken in R_1ρ measurements to carefully equilibrate magnetization before and after each relaxation period (‘spin-lock’ element), the magnetizations of the A and B states after each relaxation period are given by, $M_{\text{eq}}^{\text{A}}(T)=(1-p_{\text{B}})\left[M^{\text{A}}(T)+M^{\text{B}}(T)\right]$ and $M_{\text{eq}}^{\text{B}}(T)=p_{\text{B}}\left[M^{\text{A}}(T)+M^{\text{B}}(T)\right]$, where T is the duration of relaxation delay. The C_fast component can then be reliably estimated from extrapolation of the R_1ρ decay to zero time provided that normalization of signal intensities is performed relative to those measured in the absence of a relaxation period (i.e. at T = 0). The latter correspond to (A+B+C+D) in Eq. 10. The measurement of a single C_fast value per residue at or close to on-resonance frequency is sufficient to de-correlate p_B and $R_2^{\text{B}}$ (Ceccon et al., 2018a). On resonance (sinθ = 1 in Eqs. 9–12), C_fast reaches its maximal value, denoted as $C_{\text{fast}}^{\max }$ in the following. For skewed populations $\left(p_{\text{B}}\ll p_{\text{A}}\right)$, $C_{\text{fast}}^{\max }$ can be simplified to,

$$C_{\text{fast}}^{\max }=\frac{p_{\text{B}}}{1+{\left(k_{\text{ex}}/R_2^{\text{B}}\right)}^2+\left(2k_{\text{ex}}/R_2^{\text{B}}\right)\left(1-p_{\text{B}}\right)}\approx \frac{p_{\text{B}}}{{\left(1+\frac{k_{\text{ex}}}{R_2^{\text{B}}}\right)}^2}$$ (14)

Eq. 14 shows that $C_{\text{fast}}^{\max }$ is directly proportional to p_B. Thus, provided that $k_{\text{ex}}/R_2^{\text{B}}<1$, $C_{\text{fast}}^{\max }$ serves as a good measure of the population of the bound state p_B, even if only a single (on-resonance) measure of C_fast is available. Inclusion of an additional term that accounts for $C_{\text{fast}}^{\max }$ data into the DEST/ΔR₂ target function, then enables unambiguous determination of p_B (and therefore k_off), as well as the set of residue-specific $R_2^{\text{B}}$ values (Ceccon et al., 2018a).

If, however, the ratio $k_{\text{ex}}/R_2^{\text{B}}$ is significantly larger than unity (fast exchange on the transverse relaxation time-scale) or p_B is small (< ~1%), $C_{\text{fast}}^{\max }$ will decrease to unmeasurably low values (Eq. 14), and the application of other NMR techniques, such as the measurement of chemical exchange line-broadening R_ex (Eq. 2) and exchange-induced chemical shifts δ_ex (Eq. 3), is required to characterize the parameters of exchange unambiguously. The latter can be measured directly if the state of the system without exchange (state A only) is experimentally accessible or assessed indirectly from the dependence of the chemical shifts of state A on the spectrometer field (Skrynnikov et al. 2002), while the former is usually quantified via Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion (Meiboom and Gill, 1958; Palmer, 2014) measured in a constant time manner (Mulder et al., 2000).

For two-site exchange the evolution of the magnetization vector $M={\left[M^{\text{A}};M^{\text{B}}\right]}^T$ in Eq. 1 (where T denotes transposition) during the CPMG constant time period is represented by,

$$M\left(t\right)={\left(AA*A*A\right)}^{ncyc}M\left(0\right)$$ (15)

where $A=\exp \left(-\tilde{R}{\tau }_{CP}/2\right)$; A* is the complex conjugate of A, ncyc is the number of CPMG cycles employed, τ_CP is the time-period between two consecutive 180° pulses in the CPMG pulse train, and $\tilde{R}$ is the 2×2 matrix on the right-hand side of Eq. 1. Although this approach adds additional parameters to the analysis in the form of chemical shift differences Δω note that neither DEST nor lifetime line-broadening ΔR₂ data are sensitive to differences in chemical shifts between the states), the significantly different dependence of R_ex and δ_ex on the parameters of exchange (cf. Eqs. 2 and 3; see also (Vallurupalli et al., 2011)), and the use of R_ex and δ_ex in combination with DEST and ΔR₂ data, solves the problem of correlated parameters in DEST/ΔR₂ analysis and provides Δω values (Libich et al., 2013). Of note, CPMG relaxation dispersions are used in this type of analysis in a somewhat unconventional way by allowing the values of $R_2^{\text{B}}$ to be variable parameters in the fit. Numerical simulations of fits to synthetic DEST data at three RF fields, ΔR₂ data and CPMG profiles at two spectrometer fields, and δ_ex at the highest spectrometer field, show that the minimal |Δω| value required for reliable extraction of exchange parameters is quite small, on the order of 0.8–1.0 ppm for ¹⁵N nuclei. The larger are the values of ¹⁵N-|Δω|, the greater is the accuracy of the fitted exchange parameters.

In this context, we note that it may be tempting to forgo the measurement of ΔR₂ altogether as CPMG relaxation dispersion profiles contain the same information in the limit of fast pulsing (at high CPMG frequencies). We therefore investigated this issue in more detail. The general analytical solution for the measured effective relaxation rate ΔR_2,eff in a two-site exchanging system is given by the Carver-Richards equation (Carver and Richards, 1972; Davis et al., 1994). It is straightforward to show that in the limit where Δω = 0 (no chemical shift differences between states A and B), the Carver-Richards equation reduces to the expression for the effective relaxation rate equal to $R_2^{\text{A}}+\Delta R_2^{CR}$, where the superscript ‘CR’ denotes ‘Carver-Richards’, and $\Delta R_2^{CR}$ is given by,

$$\Delta R_2^{CR}=\frac{1}{2}\left[\Delta R+k_{\text{ex}}-{\left\{\Delta R^2+k_{\text{ex}}^2+2\Delta R\left(k_b-k_a\right)\right\}}^{1/2}\right]$$ (16)

The expression in Eq. 16 is equivalent to ΔR₂ calculated from the exact solution of Eq. 1 in the Δω = 0 limit, i.e. equal to $-Re\left(E_1\right)-R_2^{\text{A}}$ where E₁ is the smaller eigenvalue of the matrix in Eq. 1. It is important, however, to realise that since CPMG relaxation dispersions are recorded in a constant-time manner, the resulting ΔR_2,eff values will involve a (small) correction. The analytical form of this correction in the general case was derived earlier by Baldwin (2014). Here, we are concerned with the fact that this small correction adopts a finite (non-zero) value even in the limit where 0. In this limit, using the expressions of Baldwin (2014), this correction, which we denote in the following by $\delta \Delta R_2^{\text{CPMG}}$, is given by,

$$\delta \Delta R_2^{\text{CPMG}}=-\frac{\ln Q}{T_{\text{relax}}}$$ (17)

where $Q=\frac{1}{2}\left(1+e^{-T_{\text{relax}}\sqrt{\epsilon }}+\left(\Delta R+k_{\text{ex}}\right)\left(1-e^{-T_{\text{relax}}\sqrt{\epsilon }}\right)/\sqrt{\epsilon }\right)$; T_relax is the duration of the constant time period used in the CPMG experiment; and $\epsilon ={\left(\Delta R+k_{\text{b}}-k_{\text{a}}\right)}^2+4k_{\text{a}}{k}_{\text{b}}={\left(\Delta R+k_{\text{ex}}\right)}^2-4\Delta R{p}_{\text{B}}{k}_{\text{ex}}$. The correction $\delta \Delta R_2^{\text{CPMG}}$ is very small under most circumstances, almost inversely proportional to the duration of the CPMG constant-time period, and dependent mostly on the fractional population of the minor state (p_B). $\delta \Delta R_2^{\text{CPMG}}$ is plotted as a function of p_B for exchange rates ranging from 200 s⁻¹ to 3500 s⁻¹ with $R_2^{\text{B}}=900{\text{ s}}^{-1}$ in Figure 3. The function in Eq. 17 can be shown to have a minimum (the largest value of the correction achieved by absolute magnitude) when $k_{\text{ex}}/R_2^{\text{B}}\approx 1$. That is why the lowest curve (shown in magenta in Figure 3) corresponds to $k_{\text{ex}}\approx R_2^{\text{B}}$ (see also the inset in Figure 3 where $\delta \Delta R_2^{\text{CPMG}}$ is plotted as a function of k_ex for p_B = 10 %). Numerical simulations of R_2,eff rates, obtained from constant-time CPMG relaxation dispersion measurements for two-site exchange in the 0 limit using the evolution law in Eq. 15, are fully consistent with those obtained from the relationship, $R_{2,\text{eff}}=R_2^{\text{A}}+\Delta R_2+\delta \Delta R_2^{\text{CPMG}}$, where $\delta \Delta R_2^{\text{CPMG}}$ is calculated using Eq. 17. Overall, the values of $\delta \Delta R_2^{\text{CPMG}}$ are likely to be well below the experimental uncertainties in CPMG relaxation dispersion measurements unless the ‘dark’ state B is highly populated (≥ ~10–15 %). We note, however, that much higher accuracy for ΔR₂ values can be achieved if the latter are measured separately via dedicated R_1ρ experiments. It is therefore generally not advisable to rely on CPMG relaxation dispersion data for the measurement of ΔR₂.

Figure 3.

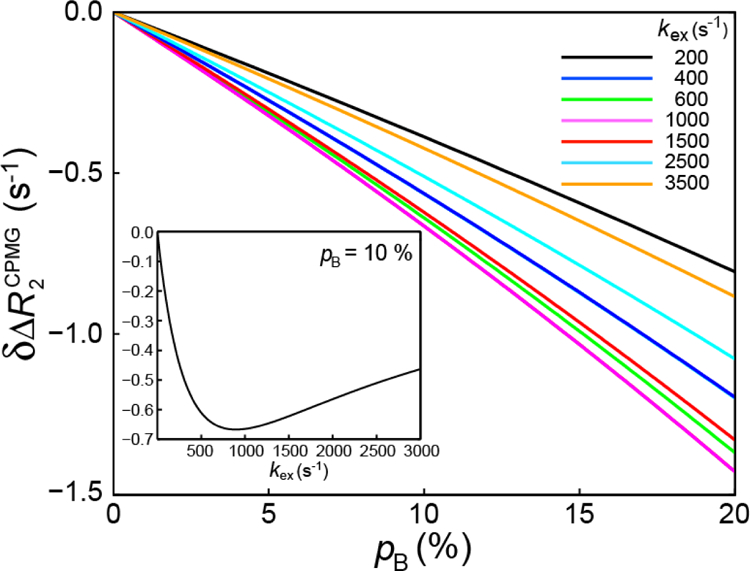
Plot of $\delta \Delta R_2^{\text{CPMG}}({\text{s}}^{-1})$ as a function of the population of the minor state, p_B, for exchange rates (k_ex) ranging from 200 to 3,500 s⁻¹, $R_2^{\text{B}}=900{\text{ s}}^{-1}$, and T_relax = 40 ms. Eq. 17 was used for all calculations of $\delta \Delta R_2^{\text{CPMG}}$. The curves are color-coded according to the value of k_ex as indicated in the plot. The inset shows a plot of $\delta \Delta R_2^{\text{CPMG}}$ as a function of k_ex for p_B = 10 % and $R_2^{\text{B}}=900{\text{ s}}^{-1}$.

Applications to exchanging systems involving high-molecular-weight species.

In this section we present a concise survey of the applications of DEST/ΔR₂ methodology for a number of interesting biological systems with special emphasis on the quantitative aspects of extraction of kinetic and spin relaxation parameters in different regimes of chemical exchange.

The first applications of DEST/ΔR₂ methodology focussed on the early stages of self-aggregation of amyloid β(Aβ) peptides, where the transverse relaxation rate $R_2^{\text{B}}$ of the dark state, corresponding to Aβ proto-fibrillar assemblies, was very large, typically reaching tens of thousands per second. Hence, $R_2^{\text{B}}\gg {\omega }_1$, where ω₁ is the strength of the applied RF field in DEST experiments, typically not exceeding ~4700 rad/sec (Fawzi et al., 2010; Fawzi et al., 2011). Exchange between Aβ free in solution and on the surface of Aβ proto-fibrils is slow on the transverse relaxation time scale $\left(k_{\text{ex}}/R_2^{\text{B}}\ll 1\right)$ and, hence, $\Delta R_2$ is independent of either spectrometer field or type of nucleus: $\Delta R_2\approx k_{\text{on}}^{\text{app}}$, where $k_{\text{on}}^{\text{app}}$ is the ‘apparent’ pseudo-first-order association rate constant. In terms of our analysis above, this corresponds to a value of α in Eq. 7 close to 0. In this exchange regime, the very high transverse relaxation rate of the dark state ensured that accurate values of the kinetic parameters of exchange and $R_2^{\text{B}}$ could be obtained reliably from the combined analysis of DEST profiles acquired at two RF field strengths and ΔR₂ profiles acquired at two spectrometer fields.

Subsequently, the DEST/ΔR₂ methodology was applied to exchanging systems with ${}^{15}\text{N-}{R}_2^{\text{B}}$ rates smaller than ω₁. Examples include binding of Aβ40 (Libich et al., 2013) and Aβ42 (Wälti et al., 2018) to the 800-kDa chaperonin GroEL. In these two cases, exchange (binding) occurs on a much faster time-scale ($k_{\text{ex}}/{}^{15}\text{N-}{R}_2^{\text{B},600}$ ranges from ~3 to ~16 depending on the residue) leading to a steep dependence of ΔR₂ on the type of nucleus probed (backbone amide ¹H relaxation rates compared to those of backbone ¹⁵N nuclei) as well as spectrometer field. The value of α calculated from Eq. 6 ranges from 0.75 to 0.94, which compares well with the corresponding values of 0.65 and 1.0 calculated using Eq. 7 from the smallest and largest ΔR₂ ratios respectively, at 900 and 600 MHz spectrometer fields). In these systems, simultaneous extraction of the kinetic parameters of exchange (namely, the dissociation rate constants of the complexes, k_off, and consequently the population of the dark/bound state, p_B) together with the rates $R_2^{\text{B}}$, is no longer possible without additional information obtained from CPMG relaxation dispersion experiments and/or exchange-induced chemical shift measurements. Without these additional experiments, the DEST/ΔR₂ data only, acquired on an exchanging system with $R_2^{\text{B}}<{\omega }_1$, are not sufficient for determination of p_B (and hence k_off ) and $R_2^{\text{B}}$ rates independently, even if high-quality DEST profiles at several RF field strengths are available. Although chemical shift differences between free and GroEL-bound forms of Aβ40 and Aβ42 are quite small (not exceeding ~1 and ~0.1 ppm for ¹⁵N/¹³Cα and ¹H_N nuclei, respectively), the shifts induced by these differences together with CPMG relaxation dispersion and DEST/ΔR₂ data proved sufficient for unambiguous determination of all parameters of exchange.

The same correlation between kinetic (p_B and k_off) and relaxation $\left(R_2^{\text{B}}\right)$ parameters of exchange was described in our studies of the truncated VPL-mutant of the Fyn-SH3 domain (FynSH3^Mut 56) bound to GroEL (Libich et al., 2017), where the field-dependence of ¹⁵N-ΔR₂ yields a value of α in Eq. 7 of ~0.27, indicating that binding to GroEL proceeds in the slow-to-intermediate regime on the transverse relaxation time-scale $\left({}^{15}\text{N-}{R}_2^{\text{B},600}/k_{\text{ex}}={\alpha }^{-1}-1\approx 2.7\right)$. The ¹⁵N-DEST/ΔR₂ data of FynSH3^MutΔ56 in the presence of GroEL could be fit equally well for a continuum of $\left\{p_{\text{B}};R_2^{\text{B}}\right\}$ combinations (Libich et al., 2017), indicating that a strong correlation exists between these two parameters. De-correlation of p_B from $R_2^{\text{B}}$ was achieved in this case by assuming a certain average transverse ¹⁵N spin relaxation rate in the bound state, ${<}^{15}\text{N-}{R}_2^{\text{B}}>$, based on the molecular weight of the FynSH3^MutΔ56-GroEL complex (~950 s⁻¹ at 900 MHz and 10 °C for a well-ordered N-H bond vector). We note that the earlier study of the folding-unfolding equilibrium of the full-length Fyn-SH3 VPL-mutant, FynSH3^VPL in the free and GroEL-bound states (Libich et al., 2015) (characterized by intermediate-to-fast binding, with the field-dependence of ¹⁵N-ΔR₂ corresponding to in the range ~0.6–0.8), was largely driven by quantitative analysis of (and the observed differences in) CPMG relaxation dispersion profiles in the presence (4-state model) and absence (2-state model) of GroEL. Therefore, no correlations between ${}^{15}\text{N-}{R}_2^{\text{B}}$ rates and the population(s) of the GroEL-bound state(s) were observed in this work.

In another recent study, the binding of two huntingtin exon-1 peptides, htt^NT and htt^NTQ₇, to ~30 nm-diameter small unilamellar lipid vesicles (SUVs; ${}^{15}\text{N-}{R}_2^{\text{B}}~2,000{\text{ s}}^{-1}$ at 600 MHz) occurs in a very slow exchange regime $\left(k_{\text{ex}}/{}^{15}\text{N-}{R}_2^{\text{B}}~0.1\right)$ (Ceccon et al., 2018a). Not surprisingly, ¹⁵N-ΔR₂ profiles in this case do not show any traces of field-dependence (α ~ 0). The low value of the $\left(k_{\text{ex}}/{}^{15}\text{N-}{R}_2^{\text{B}}\right)$ ratio ensures that reliable estimates of p_B can be obtained from the measurement of $C_{\text{fast}}^{\max }$ (see Eq. 14). To amplify the value of $C_{\text{fast}}^{\max }~2\text{-fold}$, two spin-lock periods were used in the total relaxation delay, each preceded and followed by a magnetization equilibration delay ${\tau }_{\text{eq}}\ge 2/k_{\text{ex}}$ (Yuwen et al., 2018). In this instance, exchange is very slow on the transverse relaxation time-scale, and the measurements of $C_{\text{fast}}^{\max }$ for htt^NT and htt^NTQ₇ peptides in the presence of SUVs proved indispensable for de-correlating the kinetic (p_B and k_off) and relaxation ${(}^{15}\text{N-}{R}_2^{\text{B}})$ parameters of exchange. The inclusion of an additional term that accounts for $C_{\text{fast}}^{\max }$ data into the DEST/ΔR₂ target function, enabled unambiguous determination of p_B and k_off for htt^NT and htt^NTQ₇ binding to SUVs, as well as the set of residue-specific ${}^{15}\text{N-}{R}_2^{\text{B}}$ values, without compromising the quality of the fit to the DEST or ΔR₂ profiles (Ceccon et al., 2018a).