Imaging the spontaneous flow of thought: Distinct periods of cognition contribute to dynamic functional connectivity during rest

Abstract

Brain functional connectivity (FC) changes have been measured across seconds using fMRI. This is true for both rest and task scenarios. Moreover, it is well accepted that task engagement alters FC, and that dynamic estimates of FC during and before task events can help predict their nature and performance. Yet, when it comes to dynamic FC (dFC) during rest, there is no consensus about its origin or significance. Some argue that rest dFC reflects fluctuations in on-going cognition, or is a manifestation of intrinsic brain maintenance mechanisms, which could have predictive clinical value. Conversely, others have concluded that rest dFC is mostly the result of sampling variability, head motion or fluctuating sleep states. Here, we present novel analyses suggesting that rest dFC is influenced by short periods of spontaneous cognitive-task-like processes, and that the cognitive nature of such mental processes can be inferred blindly from the data. As such, several different behaviorally relevant whole-brain FC configurations may occur during a single rest scan even when subjects were continuously awake and displayed minimal motion. In addition, using low dimensional embeddings as visualization aids, we show how FC states—commonly used to summarize and interpret resting dFC—can accurately and robustly reveal periods of externally imposed tasks; however, they may be less effective in capturing periods of distinct cognition during rest.

INTRODUCTION

As the field of functional Magnetic Resonance Imaging (fMRI) moves away from group-level reports and becomes increasingly interested in the types of single-subject evaluations that are necessary for clinical diagnosis and prognosis; there is an increasing focus on examining how brain states change over time rather than treating each scan as a static snapshot of a person’s brain function (Hutchison et al., 2013a; Preti et al., 2017; Saggar et al., 2018). For example, individual scans today are often described in terms of a limited set of recurring, short-duration (tens of seconds), whole-brain FC configurations named FC states (Allen et al., 2014; Damaraju et al., 2014; Gonzalez-Castillo et al., 2015). Metrics describing their dwell times, ordering and frequency of transitions can then be used to quantify different aspects of empirically observed dFC (Calhoun et al., 2014). Many questions remain both about the etiology of empirically observed systems-level FC dynamics; as well as regarding the ability of current models to accurately capture behavioral, cognitive and clinically relevant dynamic phenomena.

One well accepted principle is that task performance can modulate dFC across the brain (Gonzalez-Castillo and Bandettini, 2018), even if the brain never abandons an overall small-world configuration (Di et al., 2013). As humans perceive external stimuli and engage with cognitive tasks, patterns of communication across brain networks reshape (Cole et al., 2014), modularity decreases (Kitzbichler et al., 2011), communication hubs relocate (Leske et al., 2015), and overall variability of FC estimates drops (Elton and Gao, 2015). FC modulations induced by tasks are sufficiently profound as to allow prediction of subsequent perceptual outcomes such as response time (Thompson et al., 2013) and pain levels (Ploner et al., 2010). Furthermore, FC estimates computed from only seconds long portions of data can be used to classify scans according to tasks (Shirer et al., 2012) and to segment multi-task scans into task-homogenous periods (Gonzalez-Castillo et al., 2015).

Nonetheless, despite empirical reports of dFC in resting humans (Allen et al., 2014), macaques (Hutchison et al., 2013b) and rodents (Keilholz et al., 2013), a similar level of consensus does not exist regarding the significance of dFC phenomena while at rest—with rest referring to a subject’s state when instructed to stay awake and not required to perform any given task or pay attention to any specific external stimuli. Those who hypothesize rest dFC to be neuronally relevant have explored the phenomenon in the context of consciousness (Barttfeld et al., 2015), development (Qin et al., 2015) and clinical disorders (Damaraju et al., 2014; Falahpour et al., 2016; Wee et al., 2016). These studies have shown how the complexity of dFC decreases as consciousness levels decline (Barttfeld et al., 2015), how dynamic inter-regional interactions can be used to predict brain maturity (Qin et al., 2015), and how dFC derivatives (e.g., dwell times) can be diagnostically informative for conditions such as schizophrenia (Damaraju et al., 2014), mild cognitive impairment (Wee et al., 2016), and autism (Falahpour et al., 2016). Yet, many others have raised valid concerns regarding the ability of current dFC estimation methods to capture neuronally relevant dFC at rest (Handwerker et al., 2012; Hindriks et al., 2016; Leonardi and Van De Ville, 2015; Shakil et al., 2016). These concerns include a lack of appropriate null models to discern real dynamics from sampling variability (Hindriks et al., 2016), improper pre-processing leading to spurious dynamics (Leonardi and Van De Ville, 2015), and excessive temporal smoothing that hinder our ability to capture sharp and rapid transitions of interest (a real concern for sliding window techniques used to estimate FC states; (Keilholz et al., 2017; Shakil et al., 2016)). Finally, some have stated that resting dFC is primarily a manifestation of sampling variability, residual head motion artifacts, and fluctuations in sleep state; and that as such, it lacks clear cognitive or psychological significance (Laumann et al., 2017).

One cause of such discrepant views is that it is challenging to demonstrate the potential cognitive correlates of resting dFC; especially given the unconstrained cognitive nature of rest and scarcity of methods to reliably infer the cognitive correlates of whole-brain FC patterns. When subjects are instructed to quietly rest, retrospective reports demonstrate that subjects often engage in a succession of self-paced cognitive processes including inner speech, musical experience, visual imagery, episodic memory recall, future planning, mental manipulation of numbers, and periods of heightened somatosensory sensations (Delamillieure et al., 2010). Reconfigurations of FC patterns during rest could, to some extent, be a manifestation of this flow of covert self-paced conscious cognition (Barttfeld et al., 2015); even if other factors such as random exploration of cognitive architectures (Deco et al., 2013), fluctuations in autonomic system activity (Chang et al., 2013), intrinsic unconscious processes (Kucyi, 2018), self-initiated body motion (Tan et al., 2017) and arousal levels (Laumann et al., 2017), also contribute. Here we present a series of experiments aimed at exploring this hypothesis, namely that distinct periods of covert cognition are significant contributors to observable resting dFC. We use the term “covert cognition” in the previous sentence as an umbrella term to refer to all different mental states a subject undertakes while lying still inside the MRI scanner. These will differ in nature, order, timing and length across subjects; and may include both ongoing subjective experiences as well as spontaneous memory replays or fluctuations in attention, among many others. In other words, we use the term “cognition during rest” as an equivalent concept to William James “flights” and “perchings” of the mind; and as such, it encompasses the different types of spontaneous thoughts—namely daydreaming, mind-wandering, and creative thinking—described by Christoff et al. (2016) when describing a neuroscientific framework for the study of mind-wandering. In parallel, we also evaluate the ability of FC states—one of the most prominent approaches to summarize rest dFC—to capture those hypothesized periods of distinct cognition during rest.

To explain these diverse and sometimes contradictory observations regarding dFC, we extend current FC state methodology in two ways. First, we combine hemodynamic deconvolution (Caballero Gaudes et al., 2013) and activity-based reverse-inference (Yarkoni et al., 2011) to map FC states onto cognitive states. An FC state is commonly defined in terms of a representative FC matrix and a timeline (when it occurs). The deconvolution step allows us to also generate a representative “activity” map per FC state. Those FC state “activity” maps are subsequently input to a pre-existing decoding framework (Neurosynth; (Yarkoni et al., 2011)) able to map whole-brain activity patterns into ranked lists of cognitive processes likely associated with the input map. A direct mapping from representative FC matrices to cognitive processes might be preferable but, unfortunately as of today, such systems do not exist. In the past, hemodynamic deconvolution and reverse-inference have proven successful at decoding the nature of self-driven body motion during rest scans (Tan et al., 2017). Here, we extend that approach for the purpose of attaining open-ended cognitive decoding of FC states. The second way in which we extend current FC state methodology is the use of manifold learning techniques to generate low dimensional representations of time-varying FC that help visualize how connectivity evolves and identify periods of distinct cognition during rest. Projection of dynamic FC patterns into low dimensional spaces to ease interpretation has also been proposed by Dodero et al. (2016), as well as by Shine et al. (2019) to explore system-wide brain dynamics as a function of cognition.

The proposed methods are first evaluated on a multi-task¹ fMRI dataset (Gonzalez-Castillo et al., 2015) for which precise information about the timing and nature of cognitive states (as dictated by task demands) is available. Next, we apply the same methods to 15 mins long resting state scans with low head motion and infrequent eye closures from the human connectome project (HCP, (Van Essen et al., 2013)). This way, we examine the possible presence of periods of distinct cognition during rest, and the ability of FC states to uncover such periods. Comparative analyses across both scenarios (multi-task and rest) are important as substantial differences in the timing and nature of externally driven versus self-paced cognitive processes, and their manifestations in terms of dFC phenomena, may modulate the ability of models to capture cognitively relevant information across both scenarios.

Our results confirm both that FC states can accurately capture periods of distinct cognition driven by external task demands, as previously shown (Gonzalez-Castillo et al., 2015), and also that the proposed extension for the FC state framework permits accurate inference of the cognitive processes underlying each task FC state. Next, we show that although periods of distinct task-like cognition are present during pure rest, and their cognitive correlates can be inferred in a similar manner, FC state modeling—at least in the specific form examined here—does not identify discrete cognitive states as consistently as with the task data. Overall, our work suggests that resting dFC is influenced by periods of task-like cognition, and therefore more than a single correlation structure may be necessary to entirely describe rest scans. At the same time, our results suggest that FC states do not consistently capture periods of distinct cognition during rest, and that their estimation and interpretation as a model for rest dFC should be updated accordingly.

METHODS

Multi-Task Dataset

The multi-task dataset used here has been previously described in detail in (Gonzalez-Castillo et al., 2015). In summary, it contains data from 22 subjects (13 females; age 27 +/− 5 y.o.) who gave informed consent in compliance with a protocol approved by the Institutional Review Board of the National Institute of Mental Health in Bethesda, MD. The data from two subjects were discarded from the analysis due to excessive spatial distortions in the functional time series.

The MRI data have been deposited in Xnat Central, https://central.xnat.org (project ID: FCStateClassif).

Multi-Task Experimental Paradigm

Subjects were scanned continuously for 25 min and 24 s while performing four different tasks: rest with eyes open (REST), simple mathematical computations (MATH), 2-back working memory (MEMO), and visual attention/recognition (VIDEO). Each task occupied two separate 180-s blocks, preceded by a 12-s instruction period. Task blocks were arranged so that each task was always preceded and followed by a different task. Additional details can be found on the supplementary materials accompanying Gonzalez-Castillo et al. (2015).

Multi-Task Data Acquisition

Imaging was performed on a Siemens 7 Tesla MRI scanner equipped with a 32-element receive coil (Nova Medical). Functional runs were obtained using a gradient recalled, single shot, echo planar imaging (gre-EPI) sequence: (TR=1.5 s; TE=25 ms; FA=50°; 36 interleaved slices; slice thickness = 2 mm; in-plane resolution = 2×2 mm; GRAPPA=2). Each multi-task scan consists of 1,017 volumes acquired continuously as subjects engage and transition between the different tasks. In addition, high resolution (1mm³) T1-weighted magnetization-prepared rapid gradientecho and proton density (PD) sequences were acquired for presentation and alignment purposes.

Multi-Task Data Preprocessing

Data preprocessing was conducted with AFNI (Cox, 1996). Preprocessing steps match those described in Gonzalez-Castillo et al. (2015), and include: (i) despiking; (ii) physiological noise correction (in all but four subjects, due to the insufficient quality of physiological recordings for these subjects); (iii) slice time correction; and (iv) head motion correction. In addition, mean, slow signal trends modeled with Legendre polynomials up to seventh order, signal from eroded local white matter, signal from the lateral ventricles (cerebrospinal fluid), motion estimates, and the first derivatives of motion were regressed out in a single regression step to account for potential hardware instabilities and remaining physiological noise [ANATICOR model] (Jo et al., 2010). Finally, time series were converted to signal percent change, bandpass filtered [0.03 – 0.18Hz], and spatially smoothed (FWHM = 4mm). The cutoff frequency of the high pass filter was chosen to match the inverse of window length (WL = 30s); following recommendations from Leonardi and Van De Ville (2015).

In addition, spatial transformation matrices to go from EPI native space to Montreal Neurological Institute (MNI) space were computed for all subjects following procedures previously described in (Gonzalez-Castillo et al., 2013). These matrices were then used to bring publicly available regions of interest (ROI) definitions from MNI space into each subject’s EPI native space.

Resting-State Dataset

In addition to the previously described multi-task scan dataset, we also conducted analyses on a set of 20 resting-state scans part of Human Connectome Project (Van Essen et al., 2013). In particular, we used the first resting-state scan [TR=1s; TE=22.2ms; FA=45°; Voxel Resolution = 1.6×1.6×1.6mm³; Multiband Factor = 5; GRAPPA = 2] from 20 subjects part of the 1200 Release (March 2018) for which FIX (Salimi-Khorshidi et al., 2014) pre-processed resting-state scans acquired on a 7T MR system were available. Subject selection proceeded as follows. First, out of the 175 subjects available, we selected the 144 subjects that completed both the NIH and non-NIH toolbox behavioral batteries, as well as alcohol and smoking questionnaire, and the family history of psychiatric and neurological disorders. Of these remaining 144 subjects, we further restricted our sample to the subset of 106 subjects for which eye tracking data was available for the first resting scan. Next, based on windowed estimates of percent time of eye closure per window, we selected the 37 subject subjects that never had their eyes closed for more than 40% of the duration of any sliding window utilized in our analyses (Suppl. Fig. 6). Finally, we restricted our study to the 20 subjects with the least amount of maximum absolute motion among those 37 subjects (Suppl. Fig. 7).

In addition to the pre-processing performed via the HCP FIX-ICA denoising pipeline, we also applied band-pass filtering (0.03 – 0.18Hz]), and spatial smoothing (FWHM = 4mm) to match equivalent filtering and spatial smoothing steps performed on the multi-task dataset. Following these steps, scan segmentation analyses proceeded as described below for both datasets (e.g., multi-task and rest).

Scan Segmentation into Cognitively Homogenous Segments

Segmentation of multi-task scans into cognitively homogenous segments was performed on the basis of short-term 30 s long functional connectivity patterns (snapshots) following procedures previously described in Gonzalez-Castillo et al. ((2015); Supp. Fig. 1.B). First, representative time-series ROIs from the Craddock (2012) 200-ROI atlas were obtained and input to a PCA (keep 97.5% of the variance) to reduce the dimensionality of the data. This resulted, on average, in connectivity matrices of size 72 × 72 instead of the original 200 × 200. Remaining PCA time series were subsequently segmented in time using overlapping windows of duration 30s. Sliding step was set to 1.5 s (one TR). For each window, we computed all pairwise correlations between PCA time series, transform them into Z-scores using the Fisher transform, and put them in vector form. For each multi-task scan this procedure resulted in 988 vectors (one per-window). We often refer to these vectors of windowed connectivity as connectivity snapshots or simply snapshots throughout the manuscript.

Lastly, these connectivity vectors were inputted into the k-means (k=4 given the number of tasks; distance metric=correlation) clustering algorithm in MATLAB 2017b, which groups connectivity vectors into four groups by maximizing within-group similarity and between-group dissimilarity, using correlation as a distance metric between snapshots. The algorithm ran 10,000 times with different random initializations so that the clustering results do not depend on the initialization of the algorithm. Then, the algorithm selects as optimal partition the one with the lowest within-cluster sums of point-to-centroid distances.

We hypothesize that each group will contain primarily vectors from the same task based on the original results from Gonzalez-Castillo et al. (2015). If so, the time spanned by all windows in a given group define a segment from the original scan during which the subject was engaged with primarily one type of cognitive activity (e.g., one task). As an unsupervised clustering algorithm, k-means only informs us about groupings in the data, not about the meaning (e.g., the task or main cognitive process) associated with each group.

Computation of Activity Map per Segment

For the computation of representative “activity” maps we relied on hemodynamic deconvolution because it does not require any information about the timing or nature of what subjects are doing in order to estimate activity. This is key to ensure the applicability of the procedure to rest data.

Pre-processed voxel-wise time series—excluding the low pass filtering step—were input to AFNI program 3dPFM, which implements the fMRI deconvolution algorithm named Sparse Free Paradigm Mapping (SPFM; (Caballero Gaudes et al., 2013)). This program takes as input voxel-wise fMRI time series and a canonical hemodynamic response model—here we used the SPFM canonical response (SPGM1 function on AFNI program 3dDeconvolve). The output consists on voxel-wise time series of sparse activity-inducing events (Suppl. Fig. 1.C) that best explain the input fMRI time series. The deconvolution algorithm enforces sparsity in time via an L₁ norm regularized estimator using the LASSO. Here, the Akaike’s Information Criterion (AIC) was used to select the regularization parameters per voxel.

First, voxel-wise time-series of activity inducing events were computed with AFNI program 3dPFM using entire scan time series. Subsequently, activity-like maps were computed for each cognitively homogenous scan segment as dictated by the k-means analysis described above. In these maps, the intensity of a given voxel corresponds to the average intensity of all activity-inducing events detected by SPFM that fall within the temporal constrains of the given segment (see Suppl. Fig. 1.D). A such, this procedure resulted on one “activity” map per cognitively homogenous segment. These maps constitute the input to the decoding step described next.

It is worth noting that activity and connectivity views associated with a given scan segment (e.g., an FC-state), although complementary in nature, should not be expected to be fully independent. They both constitute summary views of the same data. In addition, connectivity estimates based on Pearson’s correlation can be expected to be dominated by large synchronized hemodynamic signal fluctuations, which are the target of the deconvolution technique used in the generation of the activity summary views(Petridou et al., 2013).”

Cognitive Decoding

To minimize limitations in terms of the number of cognitive processes that could be decoded, we decided to rely on existing meta-analytical databases of brain activity for this last step of the analysis. More particularly, we decided to use the reverse inference capabilities of the Neurosynth system; which permits decoding at two different levels: that of individual terms (Yarkoni et al., 2011) or that of topics (Poldrack et al., 2012). Because topics are collections of terms that frequently co-occur in the neuroscientific literature, they provide a more meaningful level of decoding; and were chosen as the decoding target here. Two different topic sets were used: the 50- and 400-cognitive state topic sets described in (Poldrack et al., 2012). In this manner, we were able to evaluate the efficiency of the method under two different difficulty levels.

Topic-level decoding with Neurosynth proceeds as follows. First, for each topic set, Neurosynth computes a reverse inference map (see Suppl. Figs. 3 & 4 for some examples) based on activity foci reported in large corpus of neuroscientific literature as described in (Poldrack, 2011; Poldrack et al., 2012). Next, when an instance for decoding (e.g., the maps generated in “Computation of Activity Map per Segment”) is available, Neurosynth computes the spatial correlation between this input and all available topic maps. This correlation informs about the likelihood of a given topic being associated with the input map. The output of Neurosynth usually consists on a sorted list of topics and their associated correlations with the input. The higher the “correct” topic for a given input appears in this rank, the more accurate the decoding was. Below we describe how we evaluated the quality of the decoding.

Evaluation of Scan Segmentation and Decoding

Scan Segmentation Evaluation

To quantitatively evaluate success at recovering the periods during which subjects were performing the same mental task, we used the adjusted rand index (ARI) (Hubert and Arabie, 1985). The ARI measures the quality of data-driven clustering (k-means) against an existing gold-standard (experimental tasks). It ranges from 1 to below 0, with 1 indicating perfect recovery of clusters. Ranges established in the literature describe an ARI > 0.9 as excellent, 0.9 > ARI > 0.8 as good, 0.8 > ARI > 0.65 as moderate, and ARI < 0.65 as poor recovery, respectively (Steinley, 2004).

Clustering was attempted under two scenarios: (a) considering all available windows; and (b) after removal of all non-task homogenous windows (e.g., those spanning one or two tasks plus instruction periods). Independently of the scenario, the ARI was computed only considering task-homogenous windows. In other words, no matter which windows entered the k-means analysis, the ARI was computed only based on the grouping of task-homogenous windows as those are the only ones for which an unambiguous correct answer clearly exists.

Decoding Evaluation

Decoding was performed using two different topic sets: 50 and 400 cognitive topic sets. These two sets contain one or more topics that strongly relate to the four tasks under scrutiny. For example, within the 50 topic-set, only one topic (TOPIC 022) contains the terms “memory”, “working memory”, “wm”. Accordingly, decoding success for the MEMO segments is quantified in terms of the decoding ranking for TOPIC 022. Similarly, within the 400 topic-set, two topics (TOPIC14 and TOPIC376) contains those terms. In this case, decoding success for MEMO segments will be quantified considering the average decoding ranking for these two terms. Suppl. Tables 1 and 2 list the “correct” topics for our four tasks in the 50 and 400 topic-set, respectively. Neurosynth reverse inference maps for all “correct” topics are displayed on Supplementary Figures 3 (50-topic set) and 4 (400-topic set).

Decoding accuracy was evaluated quantitatively using the ranking accuracy (RA) metric (Pereira et al., 2018), which has the desirable property of attributing partial credit proportional to how close the correct answer is to the top of the ranking; therefore providing a more nuanced picture than accuracy. Rank accuracy is defined as follows for a given subject (s) and task (t):

$$R{A}_{s,t}=1-\frac{{\mathit{RankCorrect}}_t-1}{\mathit{Ntopics}-1}$$

where Ntopics is the number of topics in the set (e.g., 50 or 400), and RankCorrect_t is the decoding rank for the correct topic. One limitation of the rank accuracy metric, derived from its reliance on rankings, is its inability to provide information regarding actual decoding strength values (i.e., is the correct topic ranked high even though the decoding strength is low). Therefore, we also report the mean and standard deviation of decoding strengths for correct topics across the multi-task population.

The p-value for each mean rank accuracy score across subjects was obtained using draws from the distribution under the null hypothesis of chance performance (uniform rank position). Given a sample of null results for each subject, we computed the mean across subjects, to yield a null distribution for the mean score. The p-value for the actual rank accuracy score was the probability mass in the tail for values greater than or equal to that score. When there is more than one correct topic, RankCorrect_t refers to the average decoding rank across all those correct topics.

Visualization of Windowed Connectivity

Windowed connectivity matrices, following vectorization contain thousands of elements, and consequently are hard to visualize; even with high-dimensional visualization tools such as parallel coordinate plots (Inselberg and Dimsdale, 1990) or star glyphs (Chambers, 1983). In such high dimensional scenarios, an alternative for aiding with visualization is to use manifold learning to bring the data into a 2 or 3-dimensional spaces while preserving, as much as possible, the structure of the data in its native high-dimensional space. Here, we use one particular manifold learning technique, Laplacian Eigenmaps (LE; (Belkin and Niyogi, 2003)), to help interpret results and compare between rest and task conditions. Laplacian embeddings were chosen because of their computational tractability, their interpretational value from a clustering perspective, and because they place emphasis on the preservation of local geometry in the higher dimensional originating space.

Laplacian eigenmaps were computed with the scikit-learn Python library (Abraham et al., 2014). The algorithm for the computation of the embeddings proceeds as follows. First, an affinity matrix for the data in the original high dimensional space was computed using the k-nearest neighbor algorithm (NN = 100) and correlation distance as the dissimilarity metric (to be consistent with the k-means portion of the study). This provides the algorithm with a network-like representation of the data. Next, the algorithm computes the Graph Laplacian Matrix of the affinity matrix. Finally, an eigenvalue decomposition of the Graph Laplacian is done to estimate the embedding dimensions.

It is important to notice that the NN parameter can affect the resulting embeddings. Several NN values, ranging from NN=25 to NN=250, were evaluated in the multi-task dataset. For all NN values equal or greater than 75, the embeddings contained the structures discussed throughout the manuscript (i.e., clusters of task-homogenous windows at distal spokes, task inhomogeneous windows forming trajectories between sub-spaces occupied by the initial and ending task). All embeddings reproduced here are for NN=100. For NN below 75, the embeddings were able to solely capture temporal autocorrelation, resulting in “spaghetti-like” structures with windows ordered simply according to time; but not otherwise meaningful configurations.

Operations on Low Dimensional Embeddings

Community Detection

To help evaluate the structure of the data in the low 3D space, we decided to estimate affinity matrices separately for each subject, once transformed to this low dimensional space. Each cell on those embedding affinity matrices represents the Euclidean similarity (1 / [1 + Euclidean distance]) between the location for two snapshots in 3D space.

In addition, these affinity matrices were used as input to a community detection algorithm to estimate the number of communities—namely groups of tightly grouped snapshots, separated for the rest of the set—present in the data. For the community detection step, we relied on the “community detection for NetworkX” python library (https://github.com/taynaud/python-louvain), which implements the Louvain method described in Blondel et al. (2008). Analyses were conducted using default parameters (resolution=1) for the best_partition function.

Corner Detection

Groups of elements at distal corners of Laplacian embeddings are known to signal the presence of meaningful clusters in the data (Belkin and Niyogi, 2003). Automatic detection of corners for the embeddings of the rest-only dataset proceeded as follows. For each subject, we found the x most distal windows in the embedding (in terms of Euclidean distance), with x being equal to the number of FC-states. Next, for each distal end, we selected all windows sitting within a given distance d from it (d = average inter-snapshot distance for all task-homogenous windows in the multi-task dataset). This procedure allowed us to automatically identify sets of spatially contiguous snapshots sitting near the distal ends of the embeddings.

Data and Code Availability Statement

The multi-task dataset is publicly available in the XNAT Central repository (Project ID: FCStateClasif). The rest data used in this work is part of the Human Connectome Project. Analyses were conducted with publicly available packages, including: AFNI, MATLAB, Python, scikit-learn and the NeuroSynth Python API.

RESULTS

FC States and Cognition in Multi-task Scenario

After pre-processing, FC states were estimated for the multi-task dataset. We performed these analyses under two different scenarios: (a) using only task homogenous windows—namely those that fall completely within the temporal span of individual task blocks (as was previously published (Gonzalez-Castillo et al., 2015)); and (b) using all available windows, which also include windows spanning more than one task block. The goal of comparing these two scenarios is to evaluate to what extent having cognitively inhomogeneous windows may affect our ability to correctly segment the multi-task scans. On average (see Suppl. Fig. 2), FC states faithfully recovered task timing in both scenarios: ARI = 0.89 ± 0.18 for the case when all windows entered the analyses; and ARI = 0.97 ± 0.10 when only task homogenous windows are considered. Yet, there was a significant difference in ARI across scenarios (T=2.25; p=0.02). For the “all windows” scenario, which is the primary focus here, 5 subjects out of 20 had an ARI < 0.8 (moderate or poor).

Figure 1.A & D show FC timelines, in the “all windows” scenario, for two representative subjects with different levels of success at reproducing task timing structure. In these timelines, windows are represented as dots, with their X-axis position indicating time, and their Y-axis position indicating FC state assignments. Underlay colors provide a visual reference for the task that subjects were performing during each window (grey = rest, blue = memo, yellow = video, green = math, white = more than one task). Fig. 1.A shows a case with perfect agreement (ARI=1) between FC states and mental states dictated by tasks. Fig 1.D shows a case where recovery was poor (ARI=0.46) and FC states extended across contiguous tasks independently of their distinct cognitive demands.

Figure 1.

(A) FC state timeline, (B) 3D embedding, and (C) associated affinity matrix for one multi-task subject that showed good agreement (ARI = 1.0) between FC-states and mental states dictated by task. In (A), the X-axis signals time in terms of window units, and the Y-axis indicates FC-sate membership. Snapshots of windowed connectivity are represented as black dots. Underlay colors provide a visual reference for the task that subjects were performing during each window (grey = rest, blue = memo, yellow = video, green = math, white = more than one task). (D-F) show equivalent information for a second subject with poor agreement (ARI = 0.46) between FC-states and mental states. (G) Group-level average affinity matrix for all subjects with ARI > 0.8 (15 subjects out of 20).

Next, 3D visualizations of windowed connectivity for each subject (Fig. 1.B & E) were generated via Laplacian Embeddings (Belkin and Niyogi, 2003; Thirion and Faugeras, 2004). In these visualizations, each snapshot of windowed connectivity is represented as a color-coded point in 3D space. The color of a snapshot informs us about the task, or tasks, occurring during its temporal span (grey = rest; green = math; blue = memo; yellow = visual attention; white = more than one task). The location of snapshots in these embeddings is solely a consequence of their pair-wise similarity. Task information is only used for coloring purposes, to aid with visualization, but does not contribute to the computation of the embeddings. For subjects whose FC states faithfully reproduced task states (ARI > 0.8), we observe that task homogeneous snapshots cluster together into “spoke” formations (red arrows)—one “spoke” per task—that extent away from the center of the embedding; while transition-snapshots (white dots; those spanning across tasks) form links between those spokes that go through the center of the embedding. This type of structure is less well-defined in instances of poor agreement between FC states and tasks (Fig. 1.E). Fig. 1.C & F show affinity matrices for the embeddings depicted in Fig. 1.B & E. In these matrices, a given cell represents the Euclidean similarity (1 / [1 + Euclidean distance]) between the location for two snapshots in 3D space. Fig 1.C shows a matrix with clear blocks of high affinity for task homogenous snapshots, in agreement with its originating embedding (Fig 1.B). This pattern becomes even more apparent when we average affinity matrices for all 15 subjects with ARI > 0.8 (Fig. 1.G).

Data-driven estimation of number of FC States

One limitation of FC states as a model for dFC stems from the use of unsupervised clustering (most commonly k-means (Lloyd, 1982)) for their estimation, which often requires the experimenter to provide an a-priori estimation for the number of FC states (e.g., how many clusters should k-means generate). Although data-driven techniques, such as the elbow criterion, can be used to estimate this hyper-parameter; their effectiveness is limited when applied to fMRI data (Shakil et al., 2016). Given how well the affinity matrices for the 3D embeddings presented in Fig. 1 represent the task structure of the multi-task scans, we decided to apply a Louvain community detection algorithm (Blondel et al., 2008) to each subject matrix to estimate the number of separate communities (e.g., tasks or FC states) present in the data. For 17 out of 20 subjects, the algorithm predicted 4 communities (in agreement with the number of distinct tasks). For the remaining 3 subjects (one of them being the one depicted in Fig 1.D-F) the algorithm estimated the presence of 3 communities.

Cognitive Correlates of FC States in the Multi-task Scenario

Cognitive decoding of FC states proceeded in two steps: 1) computation of a representative “activity” map for each FC state and 2) mapping from “activity” map into ranked lists of cognitive processes. This two-steps process was necessary for circumventing the lack of systems able to directly map FC matrices into cognitive processes.

Fig. 2 and Suppl. Fig. 5 show decoding results for two representative subjects using the 400-topics set (Fig. 2) and the 50-topics set (Supp. Figure 5). Both figures have the same structure. Panel A shows FC state timelines. Panels B-E shows “activity” maps for each FC state. Panels F-I show decoding results per FC state both as a table listing the top-five topics with the highest decoding strength and as cloud plots with the distribution of decoding strength across all available topics. For qualitative evaluation purposes, the location of correct topics (i.e., those with the most direct relationship to the task; see Suppl. Tables 1 & 2) are clearly marked for all FC states in panels F-I. In particular, for Sbj17 (Fig. 2), we can observe how the FC state timeline faithfully follows the experimental task timing (ARI=1.0). For this subject, FC state 1 spanned periods of MATH and FC state 2 periods of the MEMO task. Activity maps for these two states contain prominent clusters of activity in dorsolateral pre-frontal cortex and parietal regions (Fig. 2.B & C); consistent with tasks with a heavy working memory component. Similarly, FC state 3, which overlaps in time with the visual attention task (VIDEO), has prominent areas of activity around the MT/V5 region and other visual regions in ventral temporo-occipital cortex (Fig. 2.D). Finally, for FC state 4—which spans rest periods—we observe activity in regions of the default mode network (Fig. 2.E). As for the actual decoding, for FC states 1 and 2, we observe topics with terms such as “memory”, “working”, “arithmetic”, “calculation” and “numbers” among the top decoding topics (Fig 2.F & G). For FC state 3 (VIDEO), top topics include the terms “visual”, “motion”, “biological”, “moving” and “scenes” (Fig. 2.H). Finally, for FC state 4 (REST), the three topics that best describe rest (see Suppl. Table 2) appear as the top three decoding terms for this FC state (Fig 2.I). Similar results can be seen in Suppl. Fig. 5 when decoding was done using the 50-topics set on a different representative subject.

Figure 2.

Individual subject task decoding results for the 400-topics set. (A) Scan segmentation results. Each dot represents a snapshot of windowed connectivity. The position of the dot in the y-axis indicates to which FC-state the snapshot of windowed connectivity was assigned. Tasks periods are depicted as colored bands for reference (REST: gray; MEMO: blue; MATH: green; VIDEO: yellow). (B-E) Activity maps for each FC-state obtained with SPFM. (F-I) Decoding results in the form of cloud plots and top-five lists. Cloud plots depict the probability distribution of decoding strength values across all 400 topics for each FC state in the form of kernel density estimates (colored curves), swarm plots (colored dots; one per topic) and boxplots (black). In these plots the location of “correct” topics per task are clearly marked by boxed text with arrows. Finally, the tables on the right of the figure lists the top 5 topics with the highest decoding strength for each FC state. Topic names are constructed using the top three terms associated with the topic.

Mean and standard deviation decoding strength values for correct topics across the multi-task population were 0.18 ± 0.08 (400-topics set) and 0.19 ± 0.10 (50-topics set). Fig. 3 shows group-level task decoding results. Fig. 3.A-B show rank accuracy (Pereira et al., 2018)—a measure of how often the correct topics appeared at the top of the decoding rank—for all task segments and subjects as colored dots, and across-subject mean rank accuracy per task as grey bars for the 50-topics set (Fig. 3.A) and the 400-topics set (Fig. 3.B). Mean rank accuracy was above 0.8 for all tasks for most subjects. Worse decoding results were obtained for the visual attention (VIDEO) task when using 50-topics. Overall, decoding was more successful when using the 400-topics set relative to the 50-topics set; this despite a large increase in the ratio of wrong-to-correct choices. In all instances, mean rank accuracy was significantly higher than chance (p<0.05; see SI for details). Figure 3.C-J show average cumulative distributions of decoding strength for the different tasks (black curves). In addition, individual decoding strength for correct topics are depicted as dashed colored lines. A colored continuous bold line marks the mean correct decoding strength across all subjects. In all instances, except for VIDEO using the 50-topics set (panel 3.E), the mean decoding strength for correct topics fell to the right of 95% of the cumulative distribution of decoding strengths (shaded region).

Figure 3.

Group Evaluation of Task Decoding. (A) Rank accuracy for all subjects and tasks when using the 50-topics set. (B) Same as (A) but when using the 400-topics set. (C-F) Cumulative distribution of decoding strength values for the 50-topics set. Each panel shows results for a different task. The mean cumulative distribution across all subjects is depicted in black. Individual decoding strengths for the correct term are shown as dashed lines and the mean decoding strength across all subjects as a continuous line. In all panels, we mark the region that corresponds to 95% of the cumulative distribution with grey. (G-J) Same as (C-F) but for the 400-topics set.

Periods of Distinct Cognition during Rest

Next, we applied the same methods to a subset of twenty 15 mins-long eyes-open resting scans acquired on a different 7T system part of the HCP (Van Essen et al., 2013). Subjects were selected to minimize motion and sleepiness confounds (detailed selection criteria in SI materials). Suppl. Fig. 6 show traces of windowed eye closure times per subject. It can be observed that all subjects remained awake for the whole scan duration. Supp. Fig 7 shows traces of absolute and relative motion for all 20 subjects. Average absolute motion was 0.27 ± 0.18 mm, and average relative volume-to-volume motion was 0.10 ± 0.07 mm.

Figure 4 summarizes results of these analyses for one representative resting subject (sbj05). Panel A shows the 3D embedding for this subject, with connectivity snapshots colored by FC state (3D embeddings for all rest subjects in Suppl. Figure 8.A). Number of FC-states for the rest datasets varied between three and four. Large inter-subject variability in 3D embedding patterns can be observed in Suppl. Fig. 8.A for this second dataset. Although “spoke-like” structures are present for some subjects (e.g., the one in Fig. 4), this motif is not as prominent as in the multi-task dataset (Supp. Fig. 8.B). Moreover, FC-states in rest scans do not necessarily align with distinct spokes in the same manner they did in the multi-task scans (e.g., in Fig. 4.A, FC1 extends into a second spoke that is shared between FC1 and FC4). Panel 4.B shows the affinity matrix for the 3D embedding shown in 4.A. Dashed lines identify the confines of estimated FC-states, which were very similar in size and contain only temporally contiguous windows. This behavior was common across the majority of rest scans, suggesting that FC-states did not fully capture the structure depicted by the corresponding 3D embeddings.

Figure 4.

Cognitive decoding for one representative subject from the rest only dataset. (A) 3D embedding with connectivity snapshots colored according to automatically extracted FC states. (B) Affinity matrix for the embeddings in panel A. (C-F) Activity maps computed via SPFM for each of the FC states. (G-J) Distributions of decoding strengths for the 400-topics set and lists with the top-5 topics for each FC-state. (K) Same embedding as in (A), but this time colors signal the windows assigned to spoke-like structures following the procedures described in the SI materials. Two different views (different rotation angles) are presented to help better appreciate the structure of the embedding. (L-O) Activity maps computed using only the windows identified as members of spoke-like structures (e.g., non-white windows). (P-S) Distribution of decoding strengths for the maps shown in L-O.

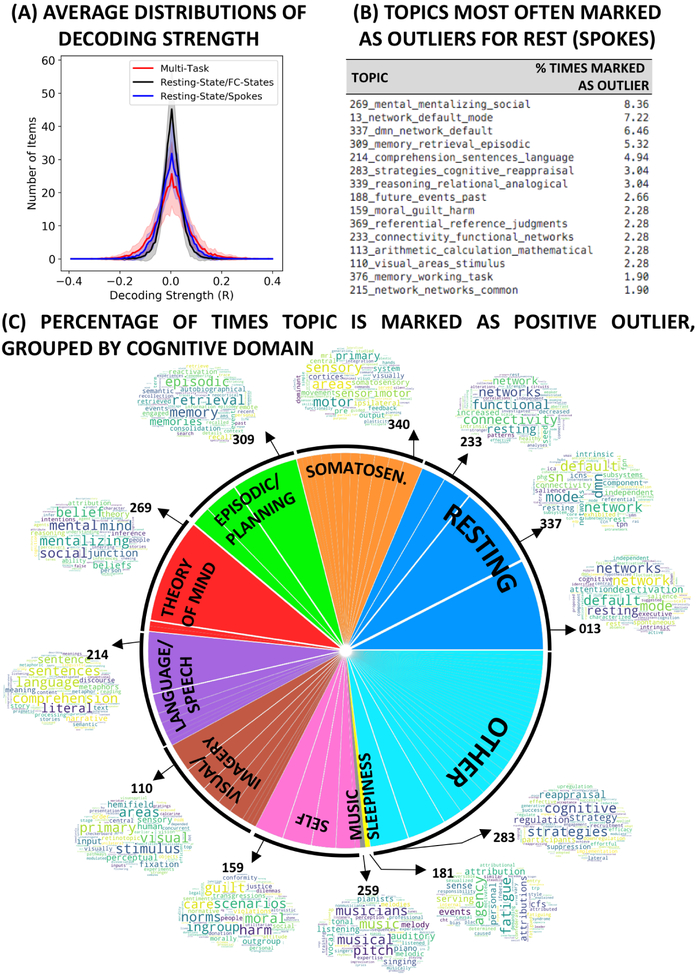
Panels 4.C-F show “activity” maps for all four FC-states detected in sbj05. Activity maps are very similar across states, particularly for FC-states one, two and three. Panels 4.G-J show corresponding distributions of decoding strength per FC-state for the 400-topics set. Distributions are often narrower than in the multi-task scenario, suggesting fewer topics show strong positive associations with activity maps. This is particularly clear for FC states one and two, whose top-ranking terms have decoding strengths below 0.1. This same narrowing effect can be observed at the group level by looking at group-averaged distributions of decoding strength (Fig. 5.A). Average distributions are wider and have longer tails for the multi-task dataset (red) than for the rest dataset (black). We quantified this effect by looking at the number of topics that constitute positive outliers for each FC-state (i.e., those above the third quantile plus 1.5 times the interquartile range) in both scenarios. We found that there are significantly more outlier topics for the multi-task dataset than the rest dataset (T=2.74; p=0.007).

Figure 5.

(A) Average decoding strength distributions for the 400 topic-set under three different scenarios: (red) FC-states detected in the multi-task dataset; (black) FC-states detected in the pure rest scenario; (blue) windows in the vicinity of spoke-like structures in the pure rest scenario. (B) List of the top 15 topics marked as positive outliers (e.g., signaled to have a strong relationship with provided activity maps) during the decoding of spoke-like structures in pure rest 3D embeddings. Topic names were constructed concatenating the topic ID in NeuroSynth with the three top terms part of the topic. The percentage on the right indicate the number of times the topic became an outlier relative to the total number of outlier detection in the whole sample. (C) Depiction of the distribution of outlier topics for spoke-like structures in the pure rest scenario grouped by cognitive domains previously reported to describe most common cognitive processes subjects engage with during rest.

Lastly, to explore if observable spoke-like structures in pure rest embeddings correspond to periods of distinct cognition—even if automatically estimated FC states were not able to effectively capture them—we decided to apply our cognitive state decoding method focusing only on windows sitting at the distal ends of rest 3D embeddings. For each subject, we found the x most distal windows in the embedding (in terms of Euclidean distance), with x being equal to the number of FC-states. Next, for each distal end, we selected all windows sitting within a given distance d from it (d = average inter-snapshot distance for all task-homogenous windows in the multi-task dataset). This procedure allowed us to automatically identify sets of spatially contiguous snapshots sitting near the distal ends of the embeddings. Fig 4.K shows the output of this procedure for sbj05. Both 3D plots in the panel show the same data viewed from different angles. Suppl. Fig. 9 shows the same information for all rest subjects. Next, we took these newly defined groups of windows and proceeded with the cognitive decoding step. Fig. 4.L-O show activity maps for the four groups of windows sitting at distal ends of the embedding for sbj05. Activity maps are now more clearly differentiable across clusters. The map for Spoke01 shows activity in lateral parietal and frontal regions. The map for Spoke02 has activity mostly focused on sensory motor regions. The map for Spoke03 presents strong activity in occipital, limbic and insular regions. And, finally, the map for Spoke04 shows activity primarily concentrated in the calcarine region. Fig 4.P-S shows corresponding decoding results. Distributions now have widened and have longer tails, suggesting activity maps are now more strongly associated with distinct topics. This effect is also appreciable at the group level (Fig 5.A – blue trace). Consequently, decoding strengths for top topics are larger; with all top 5-topics having R > 0.1. Moreover, top topics are now associated with distinct cognitive domains. For example. Spoke01 contains topic associated with numeric mental activity (e.g., “arithmetic_calculation_mathematical” and “number_numerical_numbers”). Spoke02 seems to encompass periods of strong somatosensory activity, as indicated by the terms “motor_sensory_areas”, “motor_finger_movements”, “movement_movements_motor”, etc. Finally, Spoke03 and Spoke04 point to scan segments dominated by strong visual activation perhaps associated with visual imagery.

Across all subjects, out of the 400 available topics, only 78 topics became positive outliers for one or more spokes. Fig 5.B lists the top 15 topics most commonly marked as outliers. This includes topics clearly associated with pure rest (topics 13, 337, 233, 215), thinking about the past or future (topics 309 and 188), theory of mind (topic 269), language/inner speech (topic 214), self-evaluation (topics 159 and 369), mental computations (topics 113 and 376), and visual activity (topic 110). Those all correspond to cognitive domains previously reported as describing the types of mental processes subjects commonly engage with during rest (Delamillieure et al., 2010; Diaz et al., 2013; Hurlburt et al., 2015). Finally, Fig 5.C provides a summary view of all topics marked as positive outliers for spoke-like structures in pure rest scans. Topics are grouped into the above-mentioned cognitive domains describing resting mental activities. Approximately 75% of topics fall within one of these categories: resting (17.87%), somatosensory (9.89%), episodic/planning (9.51%), theory of mind (9.13%), language/speech (9.13%), visual/imagery (9.13%), self (8.37%), music (0.4%) and sleepiness (0.4%).

DISCUSSION

Resting dFC is an empirically observed phenomenon with promising translational value (Calhoun et al., 2014; Gonzalez-Castillo and Bandettini, 2018) for which several methodological and mechanistic questions remain unresolved (Keilholz et al., 2017). We address some of them here. First, we show evidence in support of the hypothesis that on-going self-paced cognition is a contributor to dFC phenomena during rest, although the degree of contribution may vary across subjects, as well as across cognitive domains. Second, we demonstrate that data-driven estimates of FC states based on fixed-sized sliding window approaches—one of the most prominent modeling approaches for dFC—do not always capture periods of distinct cognitive processing during rest, even though FC states robustly align with cognitive processes imposed by external task demands (i.e., multi-task scenario). Overall, our results highlight the cognitive relevance of resting dFC, how a single FC static structure may not be sufficient to capture the diversity of cognitive processes occurring during rest, and the need to update the definition, computation and thus interpretation of FC states, especially when it comes to how they may relate to cognitive processing during rest.

Cognition contributes to observable dFC during Rest

Snapshots of time-varying FC spanning task-homogenous periods in the multi-task scenario clustered together at the distal ends of spoke-like structures in the 3D embeddings (Fig. 1; Suppl. Fig. 8.B). This motif of similar elements sitting together at corners of Laplacian embeddings has been previously reported for different domains, including speech (Belkin and Niyogi, 2003) and neuronal spike sorting (Chah et al., 2011). For the HCP rest scans, similar structures could be observed in a subset of subjects, suggesting the presence of isolated periods of homogenous FC distinct from other portions of the scan. Moreover, reverse-inference results suggest that such periods are associated with different types of task-like cognition (Figs. 4 & 5), although definitive validation would require behaviorally annotated (e.g., via experience sampling (Kahneman et al., 2004)) resting datasets (please see next paragraph and the limitations section below). Overall, these results support our working hypothesis that covert on-going cognition affects short term estimates of FC in a similar manner to how overt externally imposed cognition does (Gonzalez-Castillo et al., 2015); and, subsequently, that cognitively meaningful dynamics can be a contributing factor to resting dFC.

In the multi-task scenario, we were able to objectively validate cognitive inferences. Unfortunately, our ability to do so for rest scans is severely limited. Nonetheless, the cognitive processes inferred for spoke-like structures in rest embeddings agree with previous reports of the most common mental operations subjects undertake during rest (Delamillieure et al., 2010; Diaz et al., 2013; Hurlburt et al., 2015), and different spokes tend to be associated with a different set of mental processes (Fig. 4). Future work should better validate the neural accuracy of the cognitive mappings. For example, concurrent skin conductance, electromyography and video recordings of subjects in the scanner bore may help validate inferences regarding periods of somatosensory activity, self-generated body movements (Tan et al., 2017) or strong emotional content. Additional validation may be possible using rest scans accompanied by retrospective descriptions of subject’s mental processes during the scan. Delamillieure et al. (2010) suggested that subjects can be grouped according to the most prominent type of mental activity they conduct while resting. Future work should evaluate if similar groupings can be obtained on the basis of retrospective reports and data-driven decoding. Finally, dFC phenomena of limited complexity have been reported in the absence of consciousness (Amico et al., 2017; Barttfeld et al., 2015). Should spoke-like structures in dFC embeddings be the manifestation of covert cognitive processes, those structures should dissolve for rest scans conducted under deep anesthesia.

The timing and nature of cognition occurring during rest is heterogenous across subjects (Delamillieure et al., 2010; Hurlburt et al., 2015). The same is true for other postulated contributing factors such as arousal, motion or sleep. The embeddings presented here demonstrate that resting dFC is quite heterogenous across subjects even when both motion and sleep contributions were minimized via sample selection. Future work should help isolate all these factors and quantify their relative contributions at the individual subject level. For example, templates of regional activity correlated with pupil dilation may help isolate the contributions of arousal (Chang et al., 2016). Such quantification efforts are key for merging current discrepant views on the origin of rest dFC. As previously mentioned, Laumann et al. (2017) recently stated that rest dFC is primarily the result of sampling variability, arousal fluctuations, sleep and motion. One supporting argument made by the authors was the observation of limited changes in multi-variate kurtosis for pure rest scans as compared to task/rest alternating scans (Fig. 6 in (Laumann et al., 2017)). Yet, reported histograms of multi-variate kurtosis for pure rest scans (blue) have a long right tail and bump that overlaps with the kurtosis distribution for alternating task/rest scans (green and red traces). Our results suggest that cognition may contribute to resting dFC differently across subjects, with potentially negligible contribution in some subjects (those with very diffuse spokes). It could be argued that the right tail of the distribution of multi-variate kurtosis values reported in (Laumann et al., 2017) for pure rest (Fig 6, blue trace) represents the presence of a limited group of subjects with strong contributing on-going cognition. Moreover, assessing the contribution of different factors will not only help settle this argument, but also understand the origin of previously reported systematic differences in dFC across normal and patient populations (Damaraju et al., 2014; Falahpour et al., 2016; Wee et al., 2016). For example, it may be the case that differences in both static or dynamic estimates of FC across populations are not solely indicative of differences in intrinsic patterns of connectivity but may be also contributed by subjects from different populations engaging systematically into different forms of cognitive processing as they lay inside the scanner. For example, depressed patients may engage more often in regurgitative thinking; while a different population may be more prone to perform mathematical computations as a form of distraction while being scanned.

Open-ended Cognitive Inference for fMRI Scans

Here we describe and test a pipeline for blindly inferring periods of distinct cognition occurring during fMRI scans. The primary components of the pipeline are: 1) dFC estimates are used to temporally segment scans into FC homogenous periods; 2) hemodynamic deconvolution is used to generate activity-like maps for each period; and 3) activity-based reverse inference is used to deduce the cognitive processes occurring during those periods. All these steps can be performed on individual scans and require no training dataset. As such, decoding is not limited to group-level inferences and the breadth of cognitive states to be inferred is ultimately set by the breadth of the neuroimaging literature mined by the NeuroSynth platform.

Nonetheless, each of these steps set limitations regarding the specificity and sensitivity of resulting inferences. For example, the temporal segmentation step is designed to accommodate more than one cognitive state per scan. Unfortunately, the present results suggest its ability to effectively do so in a meaningful manner is limited to externally imposed cognition. Similarly, the correctness of the hemodynamic deconvolution step will depend on the degree of correspondence between canonical and actual hemodynamic response shapes (which will vary per location and subject). Errors in the estimation of activity levels may occur for regions where actual hemodynamic responses differ the most from the model provided to the SPFM algorithm—even though the SPFM algorithm shows certain robustness against mismatches in the shape of the HRF (Caballero Gaudes et al., 2013); which in turn will affect the efficacy of the decoding. Finally, limitations inherent to the NeuroSynth platform—such as limited specificity of topics, vocabulary biases and inability to incorporate priors that may help contextualize predictions (e.g., this scan corresponds to a subject under sedation) also apply here (Rubin et al., 2017; Yarkoni et al., 2011) also apply. Moreover, the Neurosynth platform was chosen here because it provides an open-ended decoding engine; yet it must be kept in mind that its breadth is limited to the set of mental processes sampled by the literature in its database; which, to a large extent, is driven by task studies. One key assumption in our work is that manifestations of a given mental state (e.g., mental arithmetic) share the same neuronal code—as captured by fMRI—in both task-cued and task-free (rest) scenarios. Although, previous work on affective content suggests this is a valid first approximation (Tusche et al., 2014), one can expect subjects to engage on certain cognitive processes unique to rest (e.g., spontaneous initiation of thought), which Neurosynth may decode incorrectly. Similarly, perceptual decoupling (a signature of some mind-wandering processes (Smallwood and Schooler, 2015) and overlapping unconscious intrinsic brain activity (Kucyi, 2018) may also constitute significant confounds affecting the correctness of the decoding in some instances. In a recent review on the relationship between dFC and mind-wandering, Kucyi (2018) poses the following question: “to what degree do spontaneous changes in network states reflect intrinsic activity, and to what degree do such changes reflect an individual’s current behavioral state?”. The contributing ratio of these two components to dFC and how they fuse in fMRI recordings (e.g., linear vs. non-linear, mostly parallel vs. mostly sequential) will affect the quality of our inferences. Nonetheless, we expect that by focusing only on strongly distinct and homogenous periods of connectivity signaled by the spoke structures present on the low dimensional embeddings, we are capturing fluctuations in dFC mostly driven by the second component—namely individual current behavioral states—and therefore Neurosynth inferences to be appropriate.

Future developments should help address many of these limitations. For example, multi-echo fMRI can improve the accuracy of the deconvolution (Caballero-Gaudes et al., 2019); and improved probabilistic decoding frameworks may increase the specificity of the inferences (Rubin et al., 2017) by providing researchers with the ability to generate context-sensitive interpretations of whole-brain activity maps. In addition, it will be valuable to develop systems able to directly map FC matrices into cognitive states in an open-ended fashion, erasing the need to generate representative “activity” maps for each FC state as an intermediate step. The development of such systems is intricate given the diversity of brain parcellations used to compute functional connectivity matrices and the fact that matrices tend to be reported only in graphic form—i.e., images—and not as numerical arrays. Developments in image recognition that could automatically mine and transform images of FC matrices into numerical arrays, and novel meta-analytic tools able to merge connectivity information from diverse parcellations may make those systems readily available in the near future.

FC states as a Model for Resting dFC

FC states currently constitute a mainstream approach to model, summarize, and report within-scan dFC. Repeatedly, researchers have reported on the behavioral (Gonzalez-Castillo et al., 2015; Sadaghiani et al., 2015) and clinical relevance (Damaraju et al., 2014; Li et al., 2014) of this model. Yet, FC states present important limitations resulting from the use of fixed-size sliding windows and k-means as key steps in their estimation. First, the FC-states framework commonly assumes that dFC is effectively characterized in terms of a limited set of distinct FC configurations (those detected by k-means). As the multi-task embeddings demonstrate (Fig 1), even if that were true, the limited temporal resolution of sliding windows will often result in adulterated FC estimates—spanning several unique cognitive configurations—that sit at interspaces between clusters (white dots) and diffuse true clustering structure in the data (task-colored dots). Because k-means enforces membership (all inputs must be assigned to a cluster) and tends to generate clusters of equal size when true cluster structure is diffused or missing, k-means is not effective at capturing periods of distinct FC in the rest scenario (Fig. 4.A). This is clearly exemplified by the fact that, for the multi-task scenario, the ARI significantly decreased when all overlapping windows enter the analysis relative to when only task-homogenous windows do (Suppl. Fig. 2). To avoid such issues, future FC state modeling should rely on variable size windows that align with FC transitions (Jia et al., 2014) or rely on non-windowed estimates of time-varying connectivity such as dynamic conditional correlation (Lindquist et al., 2014). In addition, modeling approaches than can accommodate for both multiple membership (e.g., one element can be part of two or more different clusters) and null membership (inputs may be assigned to no cluster at all) should also be adopted. Examples of such models include the use of principal component analysis (Leonardi et al., 2013; Leonardi et al., 2014), dictionary learning (Li et al., 2014), and temporal independent component analysis (Miller et al., 2016). More importantly, future research should elucidate whether dFC should be conceptualized as a continuous or discrete phenomenon (Hansen et al., 2015). Ultimately, it may be that a hybrid framework able to accommodate both the presence of discrete, transient meaningful configurations (signaling distinct periods of cognition or sensory activity whenever present) and underlying meta-states (potentially capturing intrinsic maintenance and exploratory processes) may be the most appropriate conceptualization (Karahanoglu and Van De Ville, 2015; Petridou et al., 2013). In fact, Roberts et al. (2019) have demonstrated that metastable states and waves are compatible dynamical regimes for the human connectome and can be explained with a unified mechanism.

Finally, it is worth mentioning that ours is not the only approach one can use to generate meaningful “activity-like” summary views for portions of an fMRI scan when timing information about cognitive processes is missing. For example, Karahanoglu et al. (2015) proposed the use of innovation co-activation patterns (iCAPs) to describe transient activity patterns in resting state scans. Moreover, groups of iCAPs—as generated by hierarchical clustering based on temporal overlap—showed a relationship with broad behavioral profiles (i.e., action, cognition, perception, interoception and emotion) obtained using the BrainMap database (Fox and Lancaster, 2002). Despite differences in the deconvolution operation (SPFM assumes isolated events, while Total Activation (Karahanoglu et al., 2013) looks for temporally contiguous blocks of activity), and in the decoding engine (NeuroSynth vs. BrainMap); our results, and those of Karahanoglu and colleagues (2015), suggest that multiple functional connectivity and activity maps are needed to describe the richness of resting state data, especially if one seeks to capture the multiple mental states subjects navigate through while they “rest” in the scanner.

Extensions to Prior Work, Limitations, Future Directions

Our original study conducted on this multi-task dataset demonstrated that FC states derived from non-overlapping task-homogenous windows robustly recovered temporally disjoint periods of homogenous cognition (Gonzalez-Castillo et al., 2015). Here we extend those results in several ways. First, we demonstrate a robust data-driven way to infer the number of states (i.e., tasks) using affinity matrices in the embedded 3D space. In our original work, the number of states was provided by the experimenters. Second, we not only describe a way to temporally segment multi-task scans into task homogenous periods, but also how to deduce the cognitive processes underlying those periods in an open-ended fashion that requires zero timing information or training data. Third, we demonstrate that those results can be accomplished even if overlapping task-inhomogeneous windows enter the analyses. In the original study, the onset/offset times of task blocks were used to restrict analyses to only task-homogenous non-overlapping windows.

Several limitations, in addition to those regarding imperfect ability for validation in the resting scenario, apply here. First, dFC phenomena most likely resides on a higher dimensional space beyond three dimensions. Three dimensions were selected for the current analyses because of their representational ease and because they were able to capture task structure much better than their 2D counterparts (Supp. Fig. 10). Yet, 3D embeddings were not able to explain all clustering errors. For example, Fig. 1.D&E shows an example of how 3D embeddings were able to capture the proximity of snapshots from the first MEMO, VIDEO and MATH blocks in the original higher dimensional space leading to their mistakenly joint membership to FC-State 1; but failed at capturing the same information regarding the mistaken joint assignment of windows from the second MATH and VIDEO blocks to FC-state 3. Higher dimensional spaces may better capture all relationships of interest as they will not distort original pair-wise relationships so abruptly. Yet, tools for visualizing such spaces are limited and may be difficult to interpret. Future work should evaluate the effectiveness of working with higher dimensional spaces, and the ability of visualization tools such as parallel coordinates (Inselberg and Dimsdale, 1990) and glyphs (Chernoff, 1973) to render meaningful representations of dFC in such higher dimensional spaces. In addition, future studies should evaluate the ability of other manifold learning methods, such as T-SNE (Van der Maaten and Hinton, 2008), to aid in the visualization and interpretation of dFC phenomena during task and rest. A second limitation of the current study is that we only worked with one implementation of FC-states. We previously demonstrated that methodological decisions can significantly alter the strength of the relationship between FC-states and cognitive states dictated by tasks (Gonzalez-Castillo et al., 2015). As alternative methods to estimate FC-states exist in the literature (Allen et al., 2014; Leonardi et al., 2014), future work should elucidate how well our conclusion of limited ability of FC-states to capture periods of distinct cognition during rest generalizes to these other variants of FC state modeling.

Regarding the proposed procedure for data-driven estimation of the number of states, we note that community detection on the embedding’s affinity matrix—a key step in this procedure—was conducted with default parameters. Such defaults may not be optimal. For example, a random graph model may not be appropriate for matrices whose edges denote statistical relationships such as correlations or Euclidean distance (the case here). In its current configuration, the algorithm resulted in a number of communities that agrees, in the majority of the subjects, with the number of tasks present in the multi-task dataset. The ability of the algorithm to detect the correct number of mental states or tasks under other circumstances must be evaluated and compared to other methods commonly used to estimate the number of clusters in datasets, such as the elbow criteria or the gap statistic (Tibshirani et al., 2001).

Despite the above-mentioned limitations, we believe that the current results advance our understating of dFC during both rest and task. They provide evidence in support of the hypothesis that resting dFC includes manifestations of covert cognition; suggesting that several different behaviorally relevant whole-brain FC configurations may occur during a single rest scan. In addition, we confirmed that data-driven estimates about the cognitive nature of most common mental processes occurring during rest agree with those inferred via retrospective questioning in other subject samples. Finally, our results also underscore how differences in effect size and temporal characteristics of externally-imposed and self-driven cognition may obstruct direct translation of methods and conclusions across both scenarios.