Abstract
Quantitative susceptibility mapping (QSM) estimates the underlying tissue magnetic susceptibility from MRI gradient-echo phase signal and typically requires several processing steps. These steps involve phase unwrapping, brain volume extraction, background phase removal and solving an ill-posed inverse problem relating the tissue phase to the underlying susceptibility distribution. The resulting susceptibility map is known to suffer from inaccuracy near the edges of the brain tissues, in part due to imperfect brain extraction, edge erosion of the brain tissue and the lack of phase measurement outside the brain. This inaccuracy has thus hindered the application of QSM for measuring susceptibility of tissues near the brain edges, e.g., quantifying cortical layers and generating superficial venography. To address these challenges, we propose a learning-based QSM reconstruction method that directly estimates the magnetic susceptibility from total phase images without the need for brain extraction and background phase removal, referred to as autoQSM. The neural network has a modified U-net structure and is trained using QSM maps computed by a two-step QSM method. 209 healthy subjects with ages ranging from 11 to 82 years were employed for patch-wise network training. The network was validated on data dissimilar to the training data, e.g., in vivo mouse brain data and brains with lesions, which suggests that the network generalized and learned the underlying mathematical relationship between magnetic field perturbation and magnetic susceptibility. Quantitative and qualitative comparisons were performed between autoQSM and other two-step QSM methods. AutoQSM was able to recover magnetic susceptibility of anatomical structures near the edges of the brain including the veins covering the cortical surface, spinal cord and nerve tracts near the mouse brain boundaries. The advantages of high-quality maps, no need for brain volume extraction, and high reconstruction speed demonstrate autoQSM’s potential for future applications.
Keywords: MRI – magnetic resonance imaging, QSM – quantitative susceptibility mapping, deep learning, neural network
Introduction
Quantitative susceptibility mapping (QSM) is a relatively new MRI technique that measures the spatial distribution of magnetic susceptibility within an object (Acosta-Cabronero et al., 2016; Bilgic et al., 2012; Haacke et al., 2015; Li et al., 2016; Liu et al., 2015a; Liu et al., 2015b; Schweser et al., 2013; Shmueli et al., 2009; Wang and Liu, 2015; Wharton and Bowtell, 2010). QSM computes the susceptibility from the phase signal of gradient-recalled echoes (GRE) and typically requires several processing steps. These steps involve phase unwrapping, tissue volume (e.g., brain) extraction, background phase removal and solving an inverse problem relating the tissue phase to the underlying susceptibility distribution. Phase unwrapping can easily be performed using path-based (Jenkinson, 2003) or Laplacian-based (Li et al., 2011; Schofield and Zhu, 2003; Sun and Wilman, 2013) algorithms. The widely-used automatic Brain Extraction Tools (BET) are typically model-based (Smith, 2002) or learning-based (Iglesias et al., 2011). Removal of background fields may be performed using a number of algorithms, including projection onto dipole fields (Liu et al., 2011a), SHARP processing and its variants (Schweser et al., 2011; Wu et al., 2012) and HARPERELLA (Li et al., 2013). However, estimating the susceptibility map from a local tissue field map is more complex. To account for regions where the amplitude of dipole kernel is small and its inverse is undefined, some algorithms use threshold-based masking or dipole kernel modification (Schweser et al., 2013; Wharton et al., 2010). These algorithms are efficient and easy to implement; however, they contain severe streaking artifacts and bias susceptibility values due to the information loss through the masking process, and a compromise must be made between noise amplification and the reduction of streaking artifacts. Streaking in the focal areas of objects with large susceptibility values, e.g., blood vessels, may be reduced by estimating the missing data using iterative (Sun et al., 2016; Tang et al., 2013; Wei et al., 2015) or compressed sensing (Wu et al., 2012) algorithms. However, these iterative methods are considerably slower than direct inverse via thresholding, and care must be taken on the assumptions made when selecting spatial priors to avoid over-regularization and the reduction of image contrast (Liu et al., 2012b; Liu et al., 2011b; Wharton and Bowtell, 2010).
A new class of QSM algorithms that directly relate the GRE phase signal to the unknown susceptibility distribution has been proposed recently (Chatnuntawech et al., 2017; Liu et al., 2017; Sun et al., 2018). By performing background phase removal and dipole inversion in a single step, these algorithms prevent potential error propagation across successive operations. For example, to eliminate the background phase removal step, one study proposed a single-step QSM reconstruction technique which combined single-kernel spherical mean value (SMV) filtering with dipole inversion using the Laplacian operator (Chatnuntawech et al., 2017). Others used total generalized variation (TGV) regularization to develop a single-step QSM model (SS-TGV-QSM) that mitigated the artifacts observed in total variation (TV)-based reconstructions (Chatnuntawech et al., 2017; Langkammer et al., 2015). These Laplacian-based QSM methods implicitly eliminate the background field. However, the practical implementation of the Laplacian requires a tradeoff between robustness to error amplification and the integrity of the cortical brain tissue (Chatnuntawech et al., 2017; Langkammer et al., 2015). Recently, total field inversion (TFI) and least square norm (LN-QSM) methods were proposed to directly perform dipole inversion on the total field (Liu et al., 2017; Sun et al., 2018). However, these methods still need a mask to aid QSM reconstruction. Moreover, automatically generating an optimal mask is challenging, especially near the brain boundary, where large air-tissue or tissue-bone susceptibility differences can cause substantial signal loss on the magnitude images used to define the mask. Using a mask that is too big can include noisy phase information and lead to streaking artifacts, while a mask that is too small results in loss of brain tissue in the final image. In particular, erosion of the brain mask can prevent visualization of important structures at the brain boundaries, e.g., human brain cortical vessels, the spinal cord and nerve tracts of mouse brain.
Deep neural networks have been applied to iterative methods for solving variety of inverse problems (Oktem, 2017; Qin et al., 2018). Over the last few years, deep learning methods have been shown to outperform previous state-of-the-art machine learning techniques in several fields, computer vision being one of the most prominent cases. Deep networks have been also applied to medical image reconstruction, e.g., PET, CT and MRI (Han et al., 2018; Leynes et al., 2018; Zhu et al., 2018). Recently, Yoon et al. trained a neural network to predict high-quality COSMOS (Calculation of Susceptibility through Multiple Orientation Sampling) (Liu et al., 2009) QSM from single-head-orientation data (Yoon et al., 2018). However, this trained model for COSMOS QSM does not describe magnetic susceptibility anisotropy. Another study proposed a deep convolutional network that utilizes real-world single-orientation phase to solve the inverse problem from simulated phase to magnetic susceptibility (Rasmussen et al., 2018).
In this study, we propose to train a deep neural network that reconstructs QSM directly from the field map while maintaining the contrast resulting from brain tissue’s magnetic susceptibility anisotropy. The proposed method, referred to as autoQSM, is iteration-free, skipping skull stripping and thus enabling efficient reconstruction. The model is trained on subjects with ages ranging from 11 to 82 years old, and the ground truth is the reconstruction by the established two-step STAR-QSM method (Wei et al., 2015). We investigate the capability of the trained neural network to directly reconstruct QSM from the measured magnetic field shift. We demonstrate the feasibility of autoQSM for fast and high-quality QSM reconstruction without skull stripping and show that it preserves more tissues at the brain boundaries, e.g., blood vessels and the spinal cord. Moreover, we validate the network by generating QSM maps of the in vivo mouse brain which has dissimilar tissue contrast to the human brain training data, suggesting that the network generalized and was able to learn the underlying mathematical relationship between magnetic field shift and magnetic susceptibility. The advantages of high-quality maps, no need for brain volume extraction, high reconstruction speed and recovering more cortical blood vessels demonstrate autoQSM’s potential for future applications.
Methods
MRI data acquisition and processing
A total of 209 healthy subjects with ages ranging from 11 to 82 years old were included for training. The subjects were scanned at the Brain Imaging and Analysis Center (BIAC) at Duke University using a 3T scanner (MR 750, GE Healthcare, Milwaukee, WI) equipped with an 8-channel head coil. Imaging was carried out with the approval of the institutional review board (IRB) and informed consent from the adult subjects or from the legal guardians of the teenage subjects. The 21 teenage (ages 11–20, 10M/11F) subjects were scanned using a 3D GRE sequence with field of view (FOV) = 22×22 cm2, matrix size = 256×256, flip angle (FA) = 20°, TR = 41 ms, TE1/spacing/TE8 = 4/2.82/29.4 ms, spatial resolution = 0.86×0.86×2 mm3, number of slice = 64, and reconstruction spatial resolution = 0.86×0.86×1 mm3, SENSE factor = 2, total imaging acquisition time = 5.7 min. The 188 adult (ages 21–82) subjects were scanned with the following parameters: FOV = 22×22 cm2, matrix size = 256×256, FA = 20°, TR = 34.6 ms, TE1/spacing/TE8 = 5.468/3/26.5 ms, spatial resolution = 0.86×0.86×1 mm3. SENSE factor = 2, number of slice = 136, total imaging acquisition time = 9.7 min. Detailed information about the subjects at each age interval is shown in Fig. S1 in the supplemental material.
QSM reconstruction of the training dataset for the neural network was performed in STI Suite (https://people.eecs.berkeley.edu/~chunlei.liu/software.html). The sum of squares of GRE magnitude images across echo times , where n is the number of echoes, was used to mask and extract the brain tissue using the brain extraction tool (BET) in FSL (Smith et al., 2004). The raw phase was unwrapped using Laplacian-based phase unwrapping (Schofield and Zhu, 2003). The normalized total phase ψ was calculated as: where ω is the unwrapped phase. The normalized background phase was removed with the SMV method (Wu et al., 2012). The variable radius of the SMV filter increased from 1 pixel at the brain boundary to 25 towards the center of the brain with singular value decomposition truncated at 0.05 for the SMV filter during the deconvolution process (Wu, Li et al. 2012). Lastly, susceptibility maps were computed by inverting the filtered phase using the STAR-QSM algorithm (Wei et al., 2015; Wei et al., 2016).
Deep network architecture
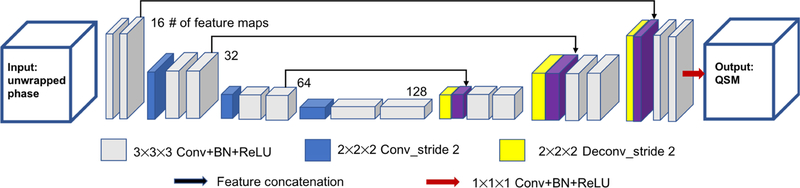
Our network architecture is modified from an established architecture (U-net) (Ronneberger et al., 2015). The overall network architecture used in this study is summarized in Fig. 1. It consists of repetitive applications of 1) 3×3×3 convolutional layer, 2) batch normalization layer, 3) rectified linear unit (ReLU), 4) 2×2×2 convolution with stride 2, 5) 2×2×2 deconvolution with stride 2, 6) identity mapping layer that adds the left-side feature layer to the right side, and 7) a 1×1×1 convolution kernel as the last layer. The architecture can be divided into a contracting section and an expanding section. The left half of the architecture aims to compress the input path layer by layer, acting as an encoder, while the right half expands the path, acting as a decoder. The network has 15 convolutional layers in total and the largest feature size is 128. The network parameters including the depth of the layers were empirically optimized.
Figure 1.
The schematic diagram of the neural network structure of autoQSM. A 3D U-net was implemented with 14 convolutional layers with kernel size of 3×3×3, 1 convolutional layer with kernel size of 1×1×1, 3 convolutional layers with kernel size of 2×2×2 applied with stride 2, 3 deconvolutional layers with kernel size of 2×2×2 applied with stride 2, and 3 feature concatenations.
The normalized 3D total phase images, ψ, were used as the input of the neural network and STAR-QSM images were used as the label. Out of the 209 healthy datasets, 42 subjects (6 subjects with 3F/3M from each age interval of 10 years) were used as a validation set. The size of 3D patch for training and testing is 64×64×64. The patch was generated with an overlapping scheme of 2/3 overlap between adjacent patches. 100 patches were randomly extracted from each dataset for training. Mean squared error (MSE) within the brain tissue between the reconstruction from the autoQSM and the label data served as the cost function for the optimizer, and it was minimized using the alternating direction method of multipliers (ADAM) optimizer (Kingma and Ba, 2015). The learning rate decay was exponential with a factor of 10−4 every 600 steps until it reached 10−7. The batch size was set to 8 and the network converged after 100 epochs. To avoid overfitting, dropout was used to randomly turn off neurons with a rate of 10% (Srivastava et al., 2014). The proposed network structure was implemented using Python 3.6.2 and Tensorflow v1.4.1 using NVIDIA 1080TI GPU. The total training time was approximately 24 hours.
Evaluation of autoQSM
To test the network’s ability to reconstruct QSM directly from total phase images, different datasets acquired at different sites were used as test datasets. These datasets had different acquisition parameters from the training data, so the following experiments would test autoQSM’s ability to learn the underlying physical principle of the QSM reconstruction rather than simply the anatomy.
Experiment 1:
A numerical brain phantom was built according to a previous QSM study with a matrix size of 192×256×150 and a spatial resolution of 1mm3 isotropic (Chatnuntawech et al., 2017). The phantom was generated with the following susceptibility values (SI units): hippocampus, 0.05ppm; hypothalamus, 0.05 ppm; medulla oblongata, 0.05 ppm; white matter, – 0.03 ppm; cerebellum, –0.0065 ppm; pons, –0.0065 ppm; thalamus, –0.0065 ppm; midbrain, – 0.0065 ppm; cerebrospinal fluid (CSF), 0 ppm; skull, –2.1 ppm. The magnetic susceptibility sources at 0.6 ppm were included to resemble subcutaneous fat without the chemical shift effect. The magnetic susceptibility sources at 9.2 ppm were included within the head to mimic internal air in the nasal cavity. The skull, fat and air act as the background susceptibility sources compared to brain tissues. The resulting phantom was convolved with the dipole kernel to generate the total phase. The total phase defined within the brain mask was used as the input of the trained neural network and the result was compared to those computed by the truncated k-space division (TKD) (Wharton and Bowtell, 2010) and the improved sparse linear equation and least-squares (iLSQR)-algorithm (Li et al., 2015).
Experiment 2:
Six subjects were scanned using a 3D GRE sequence on a GE 3T Hdxt scanner equipped with an 8-channel head coil with the following parameters: FOV = 25.6×25.6 cm2, matrix size = 256×256, FA = 20°, TR = 41 ms, TE1/spacing/TE16 = 3.2/2.2/36.2 ms, spatial resolution = 1×1×1 mm3, number of slice = 144. The same scans were repeated at three additional head orientations with respect to the B0 field, SENSE factor = 2, total imaging acquisition time = 13 min per orientation. The four orientations were used to perform COSMOS QSM reconstruction. In addition, TKD and iLSQR QSM images were generated from the filtered phase for comparison. For the TKD method, the threshold was 0.2 as suggested in the literature (Shmueli et al., 2009). For the iLSQR method, the parameters were set as suggested in the original paper (Li et al., 2015). To assess its performance, the results of autoQSM were compared with STAR-QSM, TKD, iLSQR and the gold-standard COSMOS QSM. We used several quantitative metrics assessed by the 2016 QSM Reconstruction Challenge to evaluate the reconstruction quality of these QSM algorithms. The metrics were normalized root-mean-squared error (RMSE), high-frequency error norm (HFEN), and structure similarity index (SSIM) (Langkammer et al., 2018). For example, RMSE (%) was calculated as norm(χ(:) - χ_true(:))/norm(χ_true(:)). χ denotes the calculated susceptibility map while χ_true is the COSMOS QSM. Norm denotes the normalization, defined as in matlab, where ai is the ith element of the vector χ. Note that all the metrics were assessed within the brain tissue mask. To further quantify the accuracy and consistency of the QSM maps, region-of-interest (ROI) analysis was performed. ROIs were extracted by registering a QSM atlas (Zhang et al., 2018) to the reconstructed QSM images. The QSM dataset was treated as the target brain and the QSM atlas was registered using large deformation diffeomorphic mapping (LDDMM) (Beg et al., 2005). Deep gray matter (DGM) ROIs, including caudate nucleus (CN), putamen (PUT), globus pallidus (GP), red nucleus (RN), substantia nigra (SN), and representative white matter (WM) ROIs, including internal capsule (IC), corpus callosum (CC), optic radiation (OR), were defined using the QSM atlas. The mean and standard deviation for each ROI was calculated for the QSM maps reconstructed by different methods. One-way analysis of variance with repeated measurement was performed for each ROI and corrected for multiple comparisons using SPSS (SPSS Inc., Chicago, IL). Differences were considered statistically significant when P<0.05. To demonstrate the preserved susceptibility anisotropy of autoQSM, the autoQSM’s results were compared against those of QSMnet (Yoon et al., 2018).
Experiment 3:
AutoQSM was also tested using the data provided by the 2016 QSM Reconstruction Challenge (Langkammer et al., 2018). RMSE, HFSN, SSIM, and ROI error were calculated with respect to the susceptibility tensor component χ33.
Experiment 4:
This experiment aimed to test autoQSM’s performance on infant and child brain datasets, which exhibit lower iron deposition and less myelination compared to the adult brain thus significantly different contrast. Imaging was carried out with approval of IRB and parental consent for babies and children. Ten 2-years-old infant subjects were scanned with the following parameters: FOV = 220×220 mm2, matrix size = 220×220, TR = 40 ms, TE1/spacing/TE16 = 2.9/2.9/46.4 ms, and spatial resolution = 1×1×1 mm3, number of slices = 128, SENSE factor = 2, total imaging acquisition time = 11 min. Infant earmuffs were used for hearing protection, and possible motion artifacts were mitigated by immobilization with a cotton pillow. An experienced neonatologist and a neuroradiologist were in attendance throughout the imaging process. Fifteen children (ages 5–7) were scanned with the following parameters: FOV = 220×220 mm2, matrix size = 384×384, TR = 42 ms, TE1/spacing/TE7 = 4.35/4.76/32.91 ms, and spatial resolution = 0.58×0.58×1 mm3, number of slices = 128, SENSE factor = 2, total imaging acquisition time = 12 min.
Experiment 5:
The fifth experiment attempted to explore the clinical applicability of autoQSM to data from patients with brain lesions, which were not present in the subjects seen by the network during training. Fifteen multiple sclerosis (MS) patients were scanned with the following parameters: FOV = 220×220 mm2, matrix size = 256×256, TR = 44 ms, TE1/spacing/TE8 = 3/4.18/32.3 ms, and spatial resolution = 0.86×0.86×1 mm3, number of slices = 136, SENSE factor = 2, total imaging acquisition time = 13.5 min. Fifteen patients with brain hemorrhage was scanned with the following parameters: FOV = 220×220 mm2, matrix size = 256×256, TR = 41 ms, TE1/spacing/TE8 = 3.16/4.85/37.1 ms, and spatial resolution = 0.86×0.86×1 mm3, number of slices = 136, SENSE factor = 2, total imaging acquisition time = 12 min.
Experiment 6:
We also applied the trained network to total phase maps of fifteen in vivo mouse brains that were scanned using a 7T 20-cm-bore magnet (Bruker BioSpec 70/20 USR, (Dibb et al., 2015; Dibb et al., 2017; Liu, 2010a; Xie et al., 2015), Billerica, MA, USA) interfaced to an Avance III system. A high-sensitivity cryogenic radiofrequency coil was used for transmission and reception (Bruker CryoProbe). The mice were scanned using a 3D spoiled-gradient-recalled (SPGR) sequence with the following scan parameters: TR = 250 ms, TE1/∆TE/TE10 = 3.72/5.52/53.4 ms, FA = 35°, FOV = 19.2×14.4×9.6 mm3 with 87 µm isotropic resolution, number of slices = 110, total imaging acquisition time = 90 min. Data acquisition was respiratory gated with two pulse sequence repetitions per respiratory cycle.
Experiment 7:
Three subjects were scanned using a 3D fast low angle shot (FLASH) sequence on a whole body 7T scanner (Magnetom; Siemens Healthcare, Erlangen, Germany) equipped with an 32-channel head coil with the following parameters: sagittal view, FOV = 19.2×19.2 cm2, matrix size = 320×320, FA = 10°, TR = 30 ms, TE1/spacing/TE4 = 2.3/6.9/23 ms, spatial resolution = 0.6×0.6×0.6 mm3, number of slices = 320, GRAPPA factor = 2, total scan time = 25.6 min. To assess autoQSM’s performance on image the magnetic susceptibility of spinal cord, the results of autoQSM were compared with STAR-QSM’s results.
Results
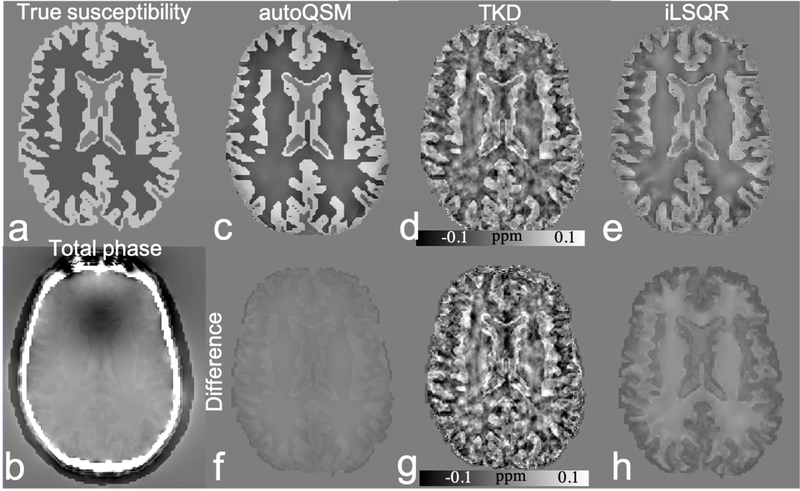
Fig. 2 shows the testing results on numerical phantom susceptibility model using different methods. The difference map between the results of autoQSM and true susceptibility shows substantially smaller differences related to brain tissues. Compared to TKD and iLSQR, autoQSM delivers substantially lower error level with RMSE of 83%, 76% and 58% respectively.
Figure 2.
Results of autoQSM, TKD and iLSQR for QSM reconstruction on the brain numerical phantom susceptibility model as well as the difference with respect to the ground truth. The input is the masked total phase map from a simulated background field superimposed onto the simulated brain phantom. Compared to TKD and iLSQR, autoQSM delivers substantially lower error level. (a) true tissue magnetic susceptibility; (b) simulated total phase image; (c-e) reconstructed QSM images using autoQSM, TKD and iLSQR, respectively; (f-h) the difference maps of autoQSM, TKD and iLSQR with respect to the true magnetic susceptibility map.
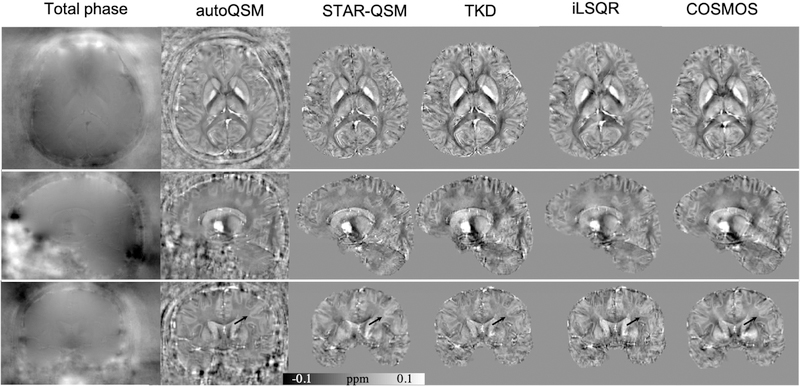
Fig. 3 shows the three orthogonal views of total phase and QSM images on one representative healthy subject using the five methods. It is clear from Fig. 3 that autoQSM can effectively recover the cortical tissues, such as vessels. In contrast, TKD-QSM and iLSQR showed a substantially noisy susceptibility contrast between the cortical gray and white matter. The predicted QSM is similar to that of STAR-QSM, with slightly lower susceptibility contrast compared to COSMOS visually. The quantitative metrics, e.g., RMSE, HFEN, and SSIM of the five reconstruction methods are summarized in Table 1. AutoQSM results achieved the lowest RMSE, lowest HFEN and highest SSIM, suggesting better performances based on these criteria than the TKD-QSM and iLSQR methods.
Figure 3.
Comparison of different QSM reconstruction methods on a healthy subject referenced to COSMOS QSM. Arrows pointed to the cortical gray and white matter delineation can be visible on autoQSM’s results which hardly seen on TKD and iLSQR QSM images.
Table 1.
Quantitative performance metric, RMSE, HFEN, and SSIM from the four different QSM reconstruction methods referenced to COSMOS QSM. AutoQSM shows better performances in all criteria than other QSM methods.
| RMSE (%) | HFEN(%) | SSIM | |
|---|---|---|---|
| TKD | 75.6 | 75.1 | 0.88 |
| iLSQR | 74.5 | 73.3 | 0.86 |
| STAR-QSM | 72.6 | 68.8 | 0.91 |
| autoQSM | 72.2 | 68.8 | 0.91 |
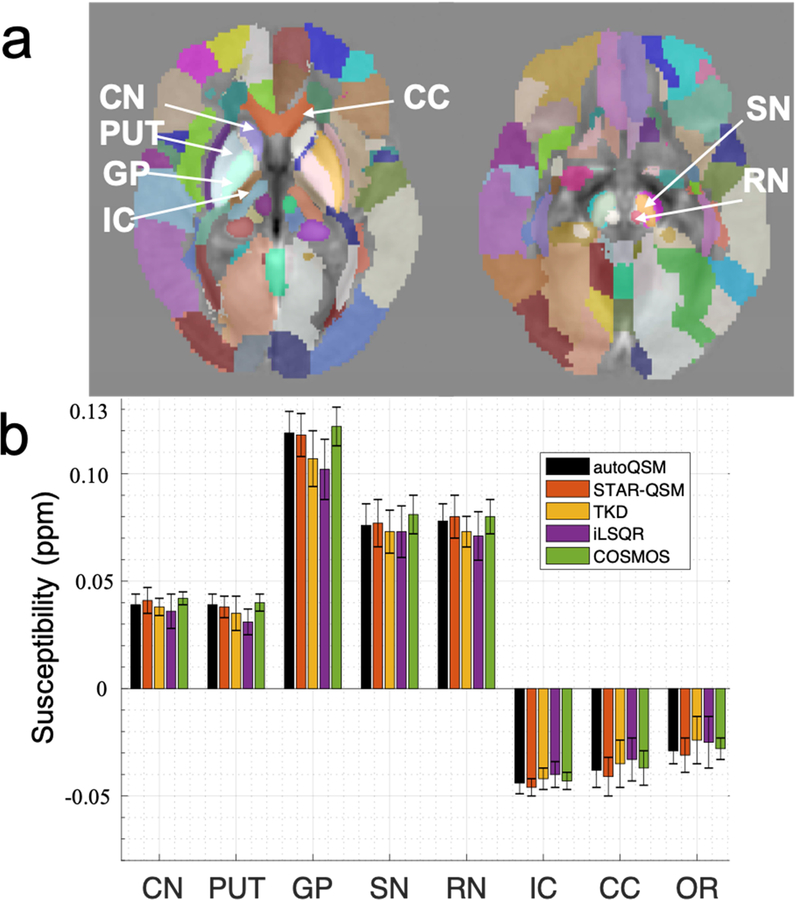
With respect to the mean susceptibility and standard deviation of the representative ROIs as shown in Fig. 4a, the autoQSM results show comparable values when compared to STAR-QSM and slightly lower susceptibility contrast than those on the COSMOS QSM. However, no significant difference was found for any deep gray matter region between autoQSM and COSMOS, P>0.05.
Figure 4.
ROI analysis of the five different methods. The susceptibility values of the ROIs (CN, PUT, GP, SN, RN, IC, CC, OR) are plotted, the autoQSM’s results match well with the gold-standard COSMOS QSM results. Data are presented as mean ± standard deviation. No statistically significantly difference was found in the eight ROIs within the group of subjects.
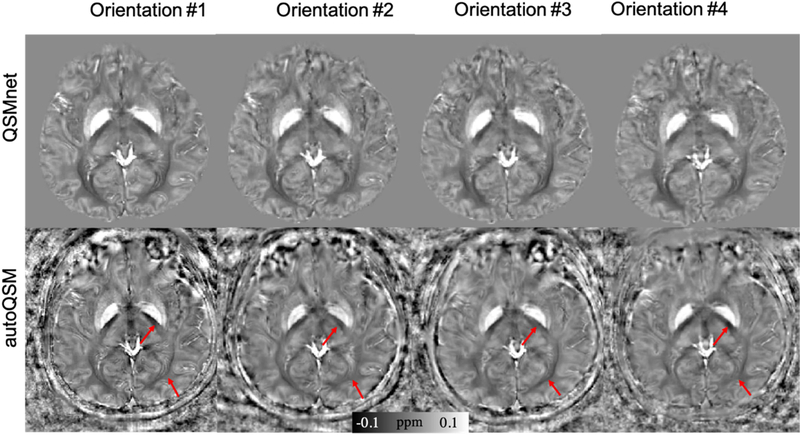
Fig.5 shows a representative healthy volunteer acquired at four different orientations relative to the B0 field to demonstrate the preserved susceptibility anisotropy. The QSM maps predicted by autoQSM exhibit strong susceptibility anisotropy of white matters as pointed by arrows, is consistent with the orientation-dependent susceptibility measured by STAR-QSM (Fig. S2 in the supplemental material). However, these regions show more consistent contrast on QSMnet’s results across different head orientations (Yoon et al., 2018). The comparison of the magnetic susceptibility in internal capsule and optic radiation are presented in Table 2. This difference is expected as QSMnet is trained using multi-orientation COSMOS while autoQSM is trained using single-orientation QSM.
Figure 5.
Axial views of the QSM images from four head orientations. Compared to QSMnet’s results, the images predicted using autoQSM show strong orientation-dependent magnetic susceptibility within the white matter. The red arrows point to regions where autoQSM predicts susceptibility differences across different head orientations, while QSMnet predicts the same susceptibilities.
Table 2.
Quantitative comparison of magnetic susceptibility in internal capsule and optic radiation calculated from STAR-QSM, autoQSM and QSMnet at four different head orientations. The values are presented as mean± standard deviation (ppm).
| Internal Capsule | ||||
|---|---|---|---|---|
| Orientation 1 | Orientation 2 | Orientation 3 | Orientation 4 | |
| autoQSM | −0.044±0.006 | −0.031±0.004 | −0.056±0.002 | −0.043±0.005 |
| STAR-QSM | −0.046±0.004 | −0.029±0.006 | −0.052±0.003 | −0.040±0.004 |
| QSMnet | −0.042±0.003 | −0.044±0.005 | −0.046±0.004 | −0.045±0.005 |
| Optic Radiation | ||||
| Orientation 1 | Orientation 2 | Orientation 3 | Orientation 4 | |
| autoQSM | −0.029±0.006 | −0.024±0.008 | −0.045±0.005 | −0.034±0.008 |
| STAR-QSM | −0.028±0.008 | −0.024±0.006 | −0.043±0.004 | −0.036±0.004 |
| QSMnet | −0.043±0.005 | −0.044±0.005 | −0.045±0.003 | −0.042±0.004 |
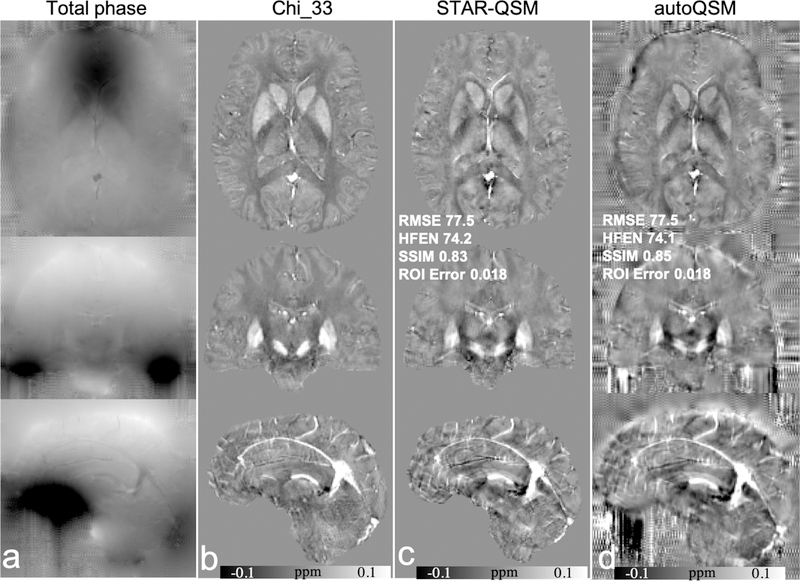
Using data provided from the 2016 Challenge and χ33 as the ground truth, we compared the performance metrics between STAR-QSM and autoQSM. AutoQSM returned comparable scores to STAR-QSM for RMSE and HFEN metrics, and ROI-level errors equivalent to those observed for STAR-QSM and χ33. Qualitatively, we note that autoQSM yielded susceptibility values and contrast at brain edges that are lost in STAR-QSM and χ33, as shown in Fig. 6d. We also observe checkerboard and ringing artifacts near the cortical surface were observed on the autoQSM’s results. These artifacts are due to noisy unwrapped phase values with a checkerboard pattern outside of the brain that acquired using a simultaneous multiple slice (SMS) sequence. However, these artifacts are not present in the data acquired using conventional GRE sequences. The comparison of unwrapped phase images acquired using SMS and GRE sequences are shown in Fig. S3 in the supplemental material.
Figure 6.
Comparison of Chi_33, STAR-QSM and autoQSM using the 2016 QSM Challenge data. (a) total phase, (b) Chi_33, (c) STAR-QSM, (d) autoQSM. Note that the noisy phase values with checkerboard pattern outside of the brain in d are due to artifacts on the unwrapped phase images, rather than autoQSM reconstruction. The RMSE, HFEN, SSIM are calculated within the mask defined based on Chi_33.
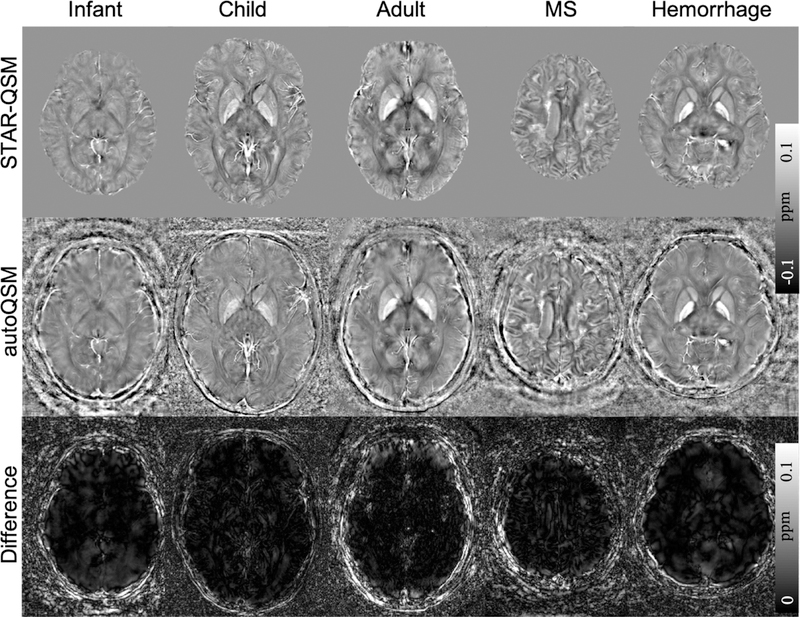
The autoQSM method was applied to the infant, child and adult subjects which were not included in the training dataset. The predicted results by autoQSM revealed comparable contrasts to those of STAR-QSM. As shown in the difference maps (Fig. 7c), there are negligible susceptibility differences related to gray and white matter. The clear differences at the edge of the brain were caused by blood vessels that were predicted by the trained neural network but lost in STAR-QSM. The observed high signal intensities at the edge of the brain on the autoQSM’s results were confirmed as the cortical veins by R2* and unwrapped phase maps as pointed by red arrows in Fig. S4 in the supplemental material. Nevertheless, further validation by angiography is needed. Similar results were observed when autoQSM was applied to the patients with MS lesions and hemorrhage.
Figure 7.
Comparison of QSM images computed using STAR-QSM and autoQSM methods. The last row shows the clear differences at the edge of the brain were caused by blood vessels that were predicted by the trained neural network but lost in STAR-QSM.
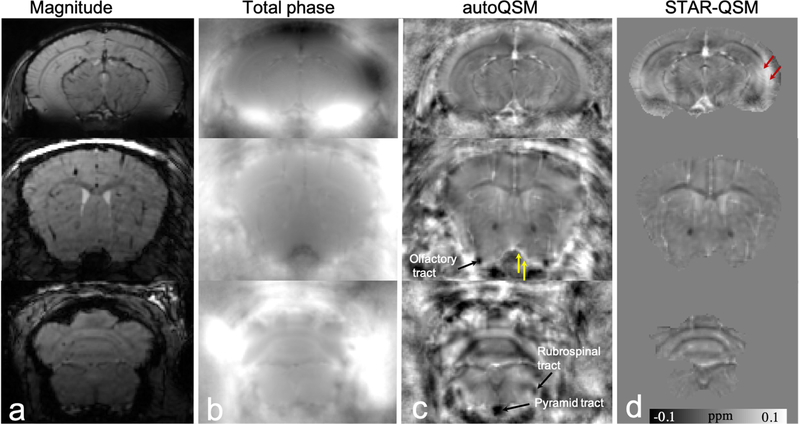
It is well known that brain volume extraction from in vivo mouse brain MRI images is more complex because the brain is surrounded by tissues that have similar image intensity. In addition, the gap between the brain and non-brain tissue is very narrow. At some locations, the edges of the brain cannot even be identified at an isotropic spatial resolution of 86 µm, as shown in Fig. 8a. Consequently, human brain extraction techniques are error prone when applied to mouse brain MRI. For example, the medulla region including nerve tracts as shown in Fig. 8d is significantly eroded. Fig. 8c illustrates autoQSM’s remarkable capability of preserving the cortical regions of the in vivo mouse brain without skull striping during reconstruction. Red arrows pointed to cortical regions with shadowing artifacts that are significantly reduced using the trained network. Yellow arrows point to brain erosion that can be recovered using autoQSM. For example, we can observe the white matter tracts as pointed by black arrows in Fig. 8c, which is completely inaccessible on the STAR-QSM images.
Figure 8.
Representative axial slices of QSM images computed using STAR-QSM and autoQSM methods in an in vivo mouse brain. (a) Magnitude images, (b) total phase maps, (c) QSM images predicted using trained neural network, (d) QSM image reconstructed using STAR-QSM. Red arrows point to reduced artifacts by the trained neural network. Yellow arrows point to paramagnetic susceptibility of blood vessel preserved near the cortex. Black arrows point to the recovered nerve tracts near the edges of the brain revealed by autoQSM while eroded by skull stripping.
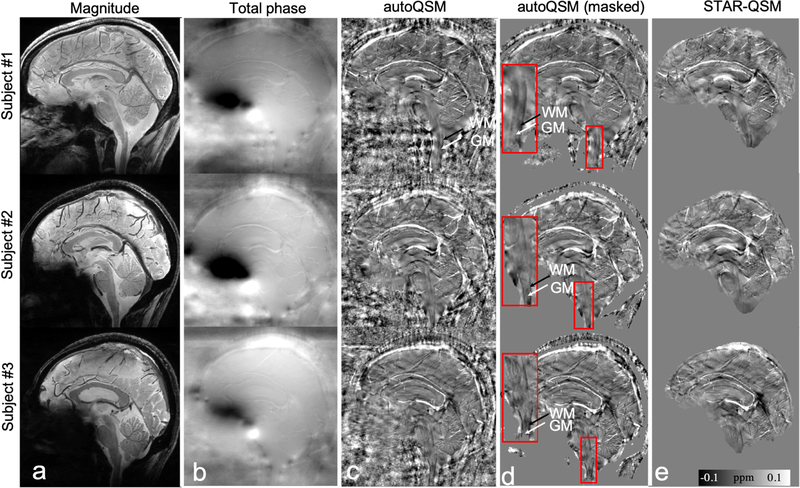
Additionally, the trained neural network may have the potential to image the magnetic susceptibility of tissues near the neck, e.g., spinal cord. AutoQSM’s images show clear susceptibility contrast between gray and white matter. Black arrows pointed to the diamagnetic lateral white matter tracts while white arrows pointed to the gray matter regions which have relatively paramagnetic susceptibility values. All three healthy subjects show the consistent contrast between white matter and gray matters in the zoomed-in regions as shown in Fig. 9d. However, these spinal cord regions are significantly eroded during the skull stripping procedure as shown by STAR-QSM images. The comparison of magnetic susceptibility of spinal cord using autoQSM and STAR-QSM processing is shown in Fig. 9. Similar susceptibility contrast was observed in the spinal gray and white matters between Fig. 9d and Fig. 9e except that the erosion exists in STAR-QSM due to background phase removal procedure.
Figure 9.
Comparison of QSM reconstructed by STAR-QSM and autoQSM on three healthy volunteers scanned at sagittal view with spinal cord included at 7 T. Black and white arrows point to white matter and gray matter in zoomed-in spinal cord respectively. Note that the paramagnetic susceptibility of gray matters is surrounded by diamagnetic white matters in the spinal cord. (a) magnitude images, (b) total phase images, (c) autoQSM’s results, (d) masked autoQSM’s results by applying a masked derived from magnitude images, a zoomed-in region of spinal cord is shown for each subject as outlined by the red box, (e) STAR-QSM results.
One main advantage of the autoQSM is the fast reconstruction speed. The average reconstruction time was only 5 ± 0.8 s measured in a GPU, which was much fast than STAR-QSM (146 ± 16.2 s; with background removal measured in a CPU) and iLSQR (360 ± 32.5 s; with background removal measured in a CPU).
Discussion
In this study, we constructed a deep neural network that performs QSM reconstruction from total phase images without brain volume extraction. One significant advantage is the high computational efficiency of the trained neural network achieved by combining two techniques: (i) eliminating the need of brain skull stripping during QSM reconstruction, and (ii) end-to-end QSM processing computed by GPU. Compared to conventional QSM reconstruction methods involving background phase removal followed by dipole field inversion, our results show better quality of reconstructed susceptibility maps. In particular, skipping the skull stripping for QSM reconstruction significantly improves the robustness of QSM reconstruction to brain volume extraction bias. Additionally, the training data used in this study covers a wide age range (11 to 82 years old), which is important for high reproducibility in longitudinal studies. The preliminary results tested on infant brain data, in vivo mouse brain data, and patients with brain lesions suggest that autoQSM can be applied to brain data dissimilar to the training data, which suggests that the network has generalized the underlying principles of QSM inversion. Finally, the high computational efficiency allows for clinical routine QSM reconstruction within a few seconds.
Previously, deep neural networks have shown the ability to reconstruct QSM from simulated phase, similarly to any other dipole deconvolution methods (Rasmussen et al., 2018). In this study, we reconstructed a neural network to incorporate background phase removal and compared the susceptibility reconstructions from autoQSM to the state-of-the-art QSM algorithms. Other single-step QSM reconstruction method, e.g., the SS-TGV-QSM method combined Laplacian-based background phase removal and local field inversion into a single step. However, Laplacian-based methods suffer from brain erosion since it is implemented using the finite difference operator or the spherical kernel operator, both require the ROI mask to be eroded. The LN-QSM and TFI methods perform dipole inversion directly on the total field instead of on the filtered phase and thus avoid the Laplacian operator, but still require brain masks to aid QSM reconstruction. Additionally, it was shown that the reconstruction speed and the quantification accuracy are both influenced by the choice of the preconditioner in TFI and regularization parameters in LN-QSM (Liu et al., 2017; Sun et al., 2018). In this study, the trained neural network enables end-to-end single-step QSM processing and it does not require explicit regularization parameters.
The neural network was trained using the total phase as the input and STAR-QSM as the label. Thus, autoQSM’s results is expected to be similar to STAR-QSM. Fig.3 shows that autoQSM has lower susceptibility contrast than COSMOS visually, potentially from underestimation of high susceptibility values in some brain nuclei or may be caused by the limited range of susceptibility values used in training. The latter can be potentially corrected with data augmentation that enlarges the dynamic range of the training data.
Brain extraction is required for all the existing QSM reconstruction methods. A number of automated brain extraction algorithms have been developed using morphology, morphology combined with edge detection (Shattuck and Leahy, 2001), deformable models (Smith, 2002), graph cuts, watershed and others. Each algorithm has its merits and pitfalls. More generally, the accuracy of brain extraction depends on the segmentation algorithms and parameters (Iglesias et al., 2011; Smith, 2002). Each method either keeps some non-brain tissue or removes extra brain tissue. Thus, using brain extraction is problematic when applying QSM to a large cohort with varying scanning parameters and manual adjustment of program parameters and manual editing of extraction results are inevitable. Brain extraction is especially problematic for baby brain MRI images because they lack edge information and contain ambiguous tissue information. Similarly, the in vivo mouse brain has a narrow gap between skull and brain tissue, which hampers the ability of QSM to evaluate the magnetic susceptibility of brain tissue. With autoQSM, brain QSM maps without brain extraction is possible by direct prediction on the total phase within the whole FOV. Furthermore, superficial veins can be recovered by the trained neural network. The recovered magnetic susceptibility at the cortical surface may extend potential QSM applications to functional QSM imaging (Sun et al., 2017) and quantitative full brain susceptibility venography (Buch et al., 2019). In addition, the recovered magnetic susceptibility of spinal cord may extend potential QSM applications to investigate the magnetic susceptibility between spinal cord lesions and brain lesions for Multiple Sclerosis (MS) patients.
Recently, there was a proposal of using deep neural network (QSMnet) to predict high quality COSMOS QSM maps from filtered phase acquired from a single orientation (Yoon et al., 2018). This result overcomes the drawback of long scanning time for the multiple head orientation acquisitions. Although the QSM maps produced by COSMOS have high quality with higher SNR, the disadvantage of the COSMOS model is that it does not account for anisotropy of magnetic susceptibility and structural tissue anisotropy. The comparison of QSM images reconstructed using QSMnet and autoQSM is shown in Fig. 5. Quantification of susceptibility anisotropy in white matter is crucial for investigation of myelin membrane lipids (Li et al., 2017; Li and van Zijl, 2014; Li et al., 2012; Liu, 2010b; Liu et al., 2012a). It is has been reported that prenatal alcohol exposure significantly reduces susceptibility anisotropy of the white matter (Cao et al., 2014). Another study proposed using deep neural networks trained to solve the inverse problem from simulated phase to magnetic susceptibility (Rasmussen et al., 2018). The input data for training was created by convoluting the labeled synthetic real-world data with the dipole kernel following well-posed forward solutions. The trained network was then used to solve an ill-posed field-to-susceptibility inversion. However, the quantification accuracy of the trained model using simulated data needs further investigation.
The measured magnetic susceptibility of cortical surface blood depends on flow velocity, oxygenation level of hemoglobin, and the angle between the vessel and B0 field. As shown in the current study, the magnetic susceptibility of blood vessels near the edges of the brain were recovered by autoQSM. From the difference map (Fig. S5), there were negligible susceptibility differences related to brain tissues between autoQSM and STAR-QSM. In contrast, clear differences near the brain boundary by the blood vessels do appear in the difference maps. These images show that autoQSM produces similar susceptibility values of the brain tissue to STAR-QSM while preserving the cortical vessels, suggesting autoQSM’s potential to recover the cortical vessels. In the future, quantitative full brain susceptibility venography needs to be investigated.
The test datasets currently used in this study have different spatial resolutions, e.g., 1 mm isotropic spatial resolution in Experiment 1; 0.86×0.86×1 mm3 used in Experiment 4, 87 µm isotropic resolution used in experiment 5, 0.6 mm isotropic resolution in Experiment 7 and 0.86×0.86×2 mm3 in Experiment 8 and with different matrix sizes. Different spatial resolutions will alter the SNR level of phase images which may bring some error in the background. A previous study has reported that the calculated susceptibility values were erroneous at low resolution (Karsa et al., 2019). The robustness of the neural network to the test datasets with large slice thickness (>3mm) is needed to test in the future. The matrix size does not have any effects on the predicted images since the neural network was trained patch by patch. We may note to users that the test dataset should not have a large slice thickness size (e.g., larger than 3 mm) since the training and prediction patch is 64×64×64. Any matrix dimension smaller than 64 will corrupt the currently trained model. Also, the image orientation should be consistent between training and test data. In addition, the input unwrapped phase images should be normalized both for training and testing. In this study, the training datasets have axial orientation as input. Thus, sagittal and coronal input datasets should be resliced to the axial orientation in order to align with the B0 field.
We observe the residual susceptibility contrast left outside of the brain. The autoQSM maps are not intended to estimated susceptibility of the air outside the head or regions without data support, except for special cases such as small air pockets surrounded by tissues. While phase unwrapping methods extrapolated phase values outside of the brain tissue resulting in the observed susceptibility contrast outside of the brain predicted by the neural network. The phase pattern and signal-to-noise ratio (SNR) of the unwrapped phase images also vary at different acquisition sites, depending on the phase reconstruction methods (e.g., coil combination method), severity of motion artifacts and phase unwrapping algorithms. As shown in Fig. S6, the phase pattern has huge difference between different MR sites. The neural network cannot distinguish the brain and non-brain regions from the unwrapped phase image. Thus, the predicted QSM image keep background contrasts when the background has non-zero unwrapped phase values. The mask can be applied afterwards to mask out the non-brain tissues only for visualization purpose, as shown in Fig.9 and Fig.S7–S9 in the supplemental material.
The data of the 2016 QSM reconstruction challenge was acquired using a simultaneous multiple slice (SMS) sequence, which has much lower signal-to-noise ratio and some residual reconstruction artifacts compared to 3D gradient echo sequences. The blooming artifacts near the cortical surface of autoQSM’s results are also present in the total phase, as pointed by the red arrow in Fig. S7. These artifacts are due to acceleration in SMS sequence and phase unwrapping. Note that the cortical structures on STAR-QSM’s result are eroded compared to autoQSM. In this study, the training datasets were acquired using 3D GRE sequences, so this noisy phase image acquired using SMS sequence and phase unwrapping artifacts may degrade the trained network’s performance. However, these artifacts are not present in the QSM images acquired using conventional 3D GRE sequences. In the future, more efforts are needed to quantitatively evaluate the effects of noise and reconstruction artifacts on the performance of deep neural networks.
The trained deep neural network performs QSM reconstruction from total phase images which functions as the background phase removal method. The autoQSM’s performance for background phase removal on the numerical brain phantom experiment was shown in Fig.S10 in the supplemental material.
Limitations
The trained neural network has some limitations. One of the biggest challenges of deep networks is that they are difficult to characterize conceptually. The design of the autoQSM architecture and the training parameters require empirical tuning of the network structure.
The trained neural network was applied to the unwrapped phase image, assuming the phase wraps were accurately removed. Further research is necessary to fully explore the capability of deep neural network to reconstruct QSM from raw phase with phase wraps. However, the location and number of phase wraps are highly dependent on the scan parameters. The phase wrap pattern varies significantly if the brain tilts at different angles with respect to the B0 field. All these factors challenge the performance of deep neural network to reconstruct QSM from raw phase images. Alternatively, we can extend the training dataset to a much larger scale including datasets acquired at different echo times, different head rotations, and at different field strengths. We expect that more research will explore this possibility for QSM reconstruction in the future.
It is known that the skull has very short T2* relaxation time and there is no MR signal in air. Measuring the magnetic susceptibility values of skull is still challenging based on 3D GRE data with echo times of a few milliseconds. The autoQSM maps are not intended to accurately estimated susceptibility of the skull in regions without data support. Ultra-short echo time (UTE) and zero echo time (ZTE) sequences (Larson et al., 2016; Wei et al., 2018) bring higher MR signals from tissues with short T2 decay times, which may be suitable for studying the magnetic susceptibility of the skull. Thus, magnetic susceptibility of air and skull outside of the brain may not be correctly estimated by autoQSM.
Conclusion
Our results demonstrate a powerful new paradigm for QSM reconstruction without the need for brain volume extraction, which is implemented with a deep neural network that learns the underlying mathematical relationship between total field and the magnetic susceptibility. Quantitative and qualitative comparisons demonstrate that autoQSM has superior image quality compared to other QSM methods. Additionally, the autoQSM maps show its potential to explore the magnetic susceptibility of whole brain vasculature, spinal cord and cortical nerve tracts of mouse brain. The advantages of high-quality maps, no need for brain volume extraction, and high reconstruction speed demonstrate autoQSM’s potential for future applications.
Supplementary Material
Acknowledgements
This study is supported in part by the National Institutes of Health through grants NIMH R01MH096979 and U01EB025162. We thank Woojin Jung and Prof. Jongho Lee for QSMnet reconstruction used in the Figure 5.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Acosta-Cabronero J, Betts MJ, Cardenas-Blanco A, Yang S, Nestor PJ, 2016. In Vivo MRI Mapping of Brain Iron Deposition across the Adult Lifespan. J Neurosci 36, 364–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beg MF, Miller MI, Trouvé A, Younes L.J.I.j.o.c.v., 2005. Computing large deformation metric mappings via geodesic flows of diffeomorphisms 61, 139–157. [Google Scholar]
- Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E, 2012. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. NeuroImage 59, 2625–2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buch S, Chen Y, Mark Haacke E, 2019. Susceptibility mapping of the dural sinuses and other superficial veins in the brain. Magn Reson Imaging 57, 19–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao W, Li W, Han H, O’Leary-Moore SK, Sulik KK, Allan Johnson G, Liu C, 2014. Prenatal alcohol exposure reduces magnetic susceptibility contrast and anisotropy in the white matter of mouse brains. NeuroImage 102 Pt 2, 748–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatnuntawech I, McDaniel P, Cauley SF, Gagoski BA, Langkammer C, Martin A, Grant PE, Wald LL, Setsompop K, Adalsteinsson E, Bilgic B, 2017. Single-Step Quantitative Susceptibility Mapping with Variational Penalties. NMR Biomed 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dibb R, Qi Y, Liu C, 2015. Magnetic susceptibility anisotropy of myocardium imaged by cardiovascular magnetic resonance reflects the anisotropy of myocardial filament alpha-helix polypeptide bonds. J Cardiovasc Magn Reson 17, 60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dibb R, Xie L, Wei H, Liu C, 2017. Magnetic susceptibility anisotropy outside the central nervous system. NMR Biomed 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Liu S, Buch S, Zheng W, Wu D, Ye Y, 2015. Quantitative susceptibility mapping: current status and future directions. Magn Reson Imaging 33, 1–25. [DOI] [PubMed] [Google Scholar]
- Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC, 2018. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magn Reson Med 80, 1189–1205. [DOI] [PubMed] [Google Scholar]
- Iglesias JE, Liu CY, Thompson PM, Tu Z, 2011. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Trans Med Imaging 30, 1617–1634. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, 2003. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med 49, 193–197. [DOI] [PubMed] [Google Scholar]
- Karsa A, Punwani S, Shmueli K, 2019. The effect of low resolution and coverage on the accuracy of susceptibility mapping. Magn Reson Med 81, 1833–1848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma D, Ba J, 2015. Adam: A Method for Stochastic Optimization. The International Conference on Learning Representations (ICLR) San Diego. [Google Scholar]
- Langkammer C, Bredies K, Poser BA, Barth M, Reishofer G, Fan AP, Bilgic B, Fazekas F, Mainero C, Ropele S, 2015. Fast quantitative susceptibility mapping using 3D EPI and total generalized variation. NeuroImage 111, 622–630. [DOI] [PubMed] [Google Scholar]
- Langkammer C, Schweser F, Shmueli K, Kames C, Li X, Guo L, Milovic C, Kim J, Wei H, Bredies K, Buch S, Guo Y, Liu Z, Meineke J, Rauscher A, Marques JP, Bilgic B, 2018. Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn Reson Med 79, 1661–1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson PE, Han M, Krug R, Jakary A, Nelson SJ, Vigneron DB, Henry RG, McKinnon G, Kelley DA, 2016. Ultrashort echo time and zero echo time MRI at 7T. Magma 29, 359–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leynes AP, Yang J, Wiesinger F, Kaushik SS, Shanbhag DD, Seo Y, Hope TA, Larson PEZ, 2018. Zero-Echo-Time and Dixon Deep Pseudo-CT (ZeDD CT): Direct Generation of Pseudo-CT Images for Pelvic PET/MRI Attenuation Correction Using Deep Convolutional Neural Networks with Multiparametric MRI. J Nucl Med 59, 852–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Avram AV, Wu B, Xiao X, Liu C, 2013. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR Biomed 27, 219–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Liu C, Duong TQ, van Zijl PC, Li X, 2017. Susceptibility tensor imaging (STI) of the brain. NMR Biomed 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Wang N, Yu F, Han H, Cao W, Romero R, Tantiwongkosi B, Duong TQ, Liu C, 2015. A method for estimating and removing streaking artifacts in quantitative susceptibility mapping. NeuroImage 108, 111–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Wu B, Liu C, 2011. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. NeuroImage 55, 1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Harrison DM, Liu H, Jones CK, Oh J, Calabresi PA, van Zijl PC, 2016. Magnetic susceptibility contrast variations in multiple sclerosis lesions. J Magn Reson Imaging 43, 463–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, van Zijl PC, 2014. Mean magnetic susceptibility regularized susceptibility tensor imaging (MMSR-STI) for estimating orientations of white matter fibers in human brain. Magn Reson Med 72, 610–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Vikram D, Lim I, CK J, Farrell J, Zijl P.v., 2012. Mapping magnetic susceptibility anisotropies of white matter in vivo in the human brain at 7T. NeuroImage 62, 314–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, 2010a. Susceptibility tensor imaging. Magn Reson Med 63, 1471–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, 2010b. Susceptibility tensor imaging. Magn Reson Med 63, 1471–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W, Tong KA, Yeom KW, Kuzminski S, 2015a. Susceptibility-weighted imaging and quantitative susceptibility mapping in the brain. J Magn Reson Imaging 42, 23–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W, Wu B, Jiang Y, Johnson GA, 2012a. 3D fiber tractography with susceptibility tensor imaging. NeuroImage 59, 1290–1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Wei H, Gong NJ, Cronin M, Dibb R, Decker K, 2015b. Quantitative Susceptibility Mapping: Contrast Mechanisms and Clinical Applications. Tomography 1, 3–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Liu T, de Rochefort L, Ledoux J, Khalidov I, Chen W, Tsiouris AJ, Wisnieff C, Spincemaille P, Prince MR, 2012b. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. NeuroImage 59, 2560–2568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris a.J., Wang Y, 2011a. A novel background field removal method for MRI using projection onto dipole fields (PDF). NMR Biomed, 1129–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y, 2011b. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging. Magnetic Resonance in Medicine 66, 777–783. [DOI] [PubMed] [Google Scholar]
- Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y, 2009. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med 61, 196–204. [DOI] [PubMed] [Google Scholar]
- Liu Z, Kee Y, Zhou D, Wang Y, Spincemaille P, 2017. Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping. Magn Reson Med 78, 303–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oktem JAO, 2017. Solving ill-posed inverse problems using iterative deep neural networks. Inverse Problems arXiv:1704.04058 [Google Scholar]
- Qin C, Hajnal JV, Rueckert D, Schlemper J, Caballero J, Price AN, 2018. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging [DOI] [PubMed] [Google Scholar]
- Rasmussen KGB, Kristensen MJ, Blendal RG, Ostergaard LR, Plocharski M, O’Brien K, Langkammer C, Janke A, Barth M, Bollmann S, 2018. DeepQSM - Using Deep Learning to Solve the Dipole Inversion for MRI Susceptibility Mapping. BioRxiv [DOI] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T, 2015. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, pp. 234–241. [Google Scholar]
- Schofield MA, Zhu Y, 2003. Fast phase unwrapping algorithm for interferometric applications. Optics letters 28, 1194–1196. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Lehr BW, Reichenbach JR, 2011. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? NeuroImage 54, 2789–2807. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Sommer K, Reichenbach JR, 2013. Toward online reconstruction of quantitative susceptibility maps: Superfast dipole inversion. Magn Reson Med 69, 1581–1593. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Leahy RM, 2001. Automated graph-based analysis and correction of cortical volume topology. IEEE Trans Med Imaging 20, 1167–1177. [DOI] [PubMed] [Google Scholar]
- Shmueli K, de Zwart JA, van Gelderen P, Li TQ, Dodd SJ, Duyn JH, 2009. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med 62, 1510–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, 2002. Fast robust automated brain extraction. Hum Brain Mapp 17, 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, 2004. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage 23, S208–S219. [DOI] [PubMed] [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R, 2014. Dropout: a simple way to prevent neural networks from overfitting J. Mach. Learn. Res 15, 1929–1958. [Google Scholar]
- Sun H, Kate M, Gioia LC, Emery DJ, Butcher K, Wilman AH, 2016. Quantitative susceptibility mapping using a superposed dipole inversion method: Application to intracranial hemorrhage. Magn Reson Med 76, 781–791. [DOI] [PubMed] [Google Scholar]
- Sun H, Ma Y, MacDonald ME, Pike GB, 2018. Whole head quantitative susceptibility mapping using a least-norm direct dipole inversion method. NeuroImage 179, 166–175. [DOI] [PubMed] [Google Scholar]
- Sun H, Seres P, Wilman AH, 2017. Structural and functional quantitative susceptibility mapping from standard fMRI studies. NMR Biomed 30. [DOI] [PubMed] [Google Scholar]
- Sun H, Wilman AH, 2013. Background field removal using spherical mean value filtering and Tikhonov regularization. Magn Reson Med [DOI] [PubMed] [Google Scholar]
- Tang J, Liu S, Neelavalli J, Cheng Y, Buch S, Haacke E, 2013. Improving susceptibility mapping using a threshold-based K-space/image domain iterative reconstruction approach. Magn Reson Med 69, 1396–1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Liu T, 2015. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn Reson Med 73, 82–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei H, Cao P, Bischof A, Henry RG, Larson PEZ, Liu C, 2018. MRI gradient-echo phase contrast of the brain at ultra-short TE with off-resonance saturation. NeuroImage 175, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei H, Dibb R, Zhou Y, Sun Y, Xu J, Wang N, Liu C, 2015. Streaking artifact reduction for quantitative susceptibility mapping of sources with large dynamic range. NMR Biomed 28, 1294–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei H, Zhang Y, Gibbs E, Chen NK, Wang N, Liu C, 2016. Joint 2D and 3D phase processing for quantitative susceptibility mapping: application to 2D echo planar imaging. NMR Biomed 30. [DOI] [PubMed] [Google Scholar]
- Wharton S, Bowtell R, 2010. Whole-brain susceptibility mapping at high field: a comparison of multiple-and single-orientation methods. NeuroImage 53, 515–525. [DOI] [PubMed] [Google Scholar]
- Wharton S, Schäfer A, Bowtell R, 2010. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med 63, 1292–1304. [DOI] [PubMed] [Google Scholar]
- Wu B, Li W, Guidon A, Liu C, 2012. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med 67, 137–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L, Dibb R, Cofer GP, Li W, Nicholls PJ, Johnson GA, Liu C, 2015. Susceptibility tensor imaging of the kidney and its microstructural underpinnings. Magn Reson Med 73, 1270–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon J, Gong E, Chatnuntawech I, Bilgic B, Lee J, Jung W, Ko J, Jung H, Setsompop K, Zaharchuk G, Kim EY, Pauly J, Lee J, 2018. Quantitative susceptibility mapping using deep neural network: QSMnet. NeuroImage 179, 199–206. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Wei H, Cronin MJ, He N, Yan F, Liu C, 2018. Longitudinal atlas for normative human brain development and aging over the lifespan using quantitative susceptibility mapping. NeuroImage 171, 176–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS, 2018. Image reconstruction by domain-transform manifold learning. Nature 555, 487–492. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.