Abstract
This work introduces a novel algorithm for deconvolution of the BOLD signal in multi-echo fMRI data: Multi-echo Sparse Paradigm Free Mapping (ME-SPFM). Assuming a linear dependence of the BOLD percent signal change on the echo time (TE) and using sparsity-promoting regularized least squares estimation, ME-SPFM yields voxelwise time-varying estimates of the changes in the apparent transverse relaxation without prior knowledge of the timings of individual BOLD events. Our results in multi-echo fMRI data collected during a multi-task event-related paradigm at 3 Tesla demonstrate that the maps of changes obtained with ME-SPFM at the times of the stimulus trials show high spatial and temporal concordance with the activation maps and BOLD signals obtained with standard model-based analysis. This method yields estimates of having physiologically plausible values. Owing to its ability to blindly detect events, ME-SPFM also enables us to map associated with spontaneous, transient BOLD responses occurring between trials. This framework is a step towards deciphering the dynamic nature of brain activity in naturalistic paradigms, resting-state or experimental paradigms with unknown timing of the BOLD events.
Keywords: BOLD FMRI, MULTI-ECHO, DECONVOLUTION, SINGLE-TRIAL
INTRODUCTION
Task-based functional magnetic resonance imaging (fMRI) data is typically analyzed through the use of linear regression of BOLD signal change models on voxel time series. These regressors are defined assuming a linear model of the BOLD response as the convolution of a known activity with the hemodynamic response function (HRF). Recently, there has been an increasing interest in methods that enable to extract activation information without prior information of the timing of the BOLD events. Such methods can provide useful information about brain function in cases when insufficient knowledge about the neuronal activity driving the BOLD events is available, including naturalistic paradigms, resting state, and clinical conditions. In the absence of timing information, a potential approach is to estimate the activity-inducing signal underlying the BOLD responses; a process also known as deconvolution. Deconvolution allows detecting individual BOLD events (i.e. single trials) (Gaudes et al., 2011; Caballero-Gaudes et al., 2013), minimizing hemodynamic confounds in measures of functional connectivity (Gitelman et al., 2003; McLaren et al., 2012; Rangaprakash et al., 2018) and exploring time-varying activity of resting state fluctuations (Keilholz et al. 2017; Petridou et al., 2013; Karahanoğlu and Van de Ville, 2015, 2017). Note that in this work deconvolution refers to estimate the processes underlying the BOLD responses, rather than to extract the pattern of even-related hemodynamic responses when using a known timing (for example see Buckner et al., 1996; Goutte et al., 2000; Ciuciu et al., 2003; Chaari et al., 2013).
Deconvolution can also be understood as solving an inverse problem where the forward model is defined from the assumed hemodynamic model. If the deconvolution is performed with least squares estimation, estimates will exhibit large variability due to the high collinearity of the model. To overcome this, some type of regularization or prior information must be applied to the estimates of the activity-inducing signal. Initially, the deconvolution was done via empirical Bayesian estimators with Gaussian priors (Gitelman et al., 2003) or regularized least-squares estimators where the regularization term penalized the Euclidean norm (i.e. L2-norm) of the estimates (i.e. ridge regression) (Gaudes et al., 2011). Other approaches have employed sparsity-promoting regularized estimators based on the L1-norm or L2,1-norm of the estimates to improve the interpretability of the estimates, such as the Dantzig Selector, the Least Absolute Selection and Shrinkage Operator (LASSO) (Caballero-Gaudes et al., 2013, Khalidov et al., 2011) and a non-negative version of the fused LASSO (Hernandez-Garcia and Ulfarsson, 2011). The method of Total Activation incorporated spatio-temporal regularization terms based on generalized total variation and structured mixed L2,1-norms to improve the robustness of the deconvolution across neighboring voxels (Farouj et al., 2017; Karaganoglu et al., 2015). Structured mixed-norm regularization terms can also be used to account for variability in the shape of the assumed hemodynamic model (Gaudes et al., 2012). A nonparametric deconvolution method based on homomorphic filtering was proposed in Sreenivasan et al. (2015). Nonlinear regression methods using logistic functions have also been proposed to avoid assuming a linear model for the BOLD response (Bush and Cisler, 2013; Bush et al., 2015). Approaches using nonlinear state-space models (Riera et al., 2004), dynamic expectation maximization (Friston et al., 2018), generalized filtering (Friston et al., 2010) and its adaptation to a cubature Kalman filtering (Havlicek et al., 2011) have also been implemented to estimate the hidden activity-inducing signal and physiological parameters of the Balloon model of the BOLD response, which operate at a regional level to gain signal-to-noise ratio due to their higher complexity.
Relevant for the current work, all the aforementioned methods perform the deconvolution of fMRI data with one time series per voxel acquired at an echo time (TE). Acquisition at a single echo (1E) is commonly used for BOLD fMRI data, where the TE is usually chosen close to the average apparent transverse relaxation parameter of the grey matter region of interest (Bandettini et al., 1994; Menon et al., 1993) to maximize the contrast-to-noise ratio of the signal. However, fMRI data can be alternatively acquired at multiple echo times so that a weighted combination of the multiple echo signals can result in an enhancement in BOLD sensitivity, mainly in regions close to air-tissue boundaries that are prone to large signal dropouts and susceptibility distortions (Gowland and Bowtell, 2007; Poser et al., 2006; Posse et al., 1999; Posse, 2012). With multi-echo fMRI (ME-fMRI) estimation of on a per-TR basis and voxel (i.e. a -time series) is feasible, which can be used for subsequent analysis of task-related activity (Peltier and Noll, 2002) and functional connectivity (Wu et al., 2012, Power et al., 2018). Furthermore, ME-fMRI enables improved denoising of artefactual and confounding physiological signal fluctuations with dual-echo approaches (Bright and Murphy, 2013; Buur et al., 2009; Ing and Schwarzbauer, 2012) or multi-echo independent component analysis (MEICA) (Kundu et al., 2012; 2013; 2017; Evans et al., 2015; Gonzalez-Castillo et al., 2016). Other denoising methods based on ME-fMRI acquisitions are discussed in Caballero-Gaudes and Reynolds (2017).
In this work, we propose a novel method for the temporal deconvolution of ME-fMRI data, named multi-echo sparse paradigm free mapping (ME-SPFM). To our knowledge, no algorithm has been previously proposed for deconvolution of ME-fMRI data. Although previous approaches can be applied on ME-fMRI data after weighted combination of the multiple echo signals in a single dataset, the proposed approach directly operates with the multiple echo signals without combining them. Assuming a mono-exponential decay model of the gradient-echo signal, this method is able to estimate the activity-inducing signal associated with single BOLD events without prior information of their timing, which can be also related to quantifiable changes in the apparent transverse relaxation rate , i.e. . Using multi-echo fMRI data acquired on 10 subjects (16 datasets) during an event-related paradigm including five distinct tasks (Gonzalez-Castillo et al., 2016), we demonstrate that the ME-SPFM algorithm considerably improves the accuracy of the deconvolution of individual BOLD events compared with its counterpart that operates in a single dataset or echo, namely sparse paradigm free mapping (hereafter denoted as 1E-SPFM) (Caballero-Gaudes et al., 2013). Furthermore, ME-SPFM yields voxel-wise quantitative estimates of in interpretable units (s−1), which is relevant for functional analysis across different acquisition protocols and field strengths.
METHODS
Multi-echo signal model
Assuming a mono-exponential decay model, the MR signal of a gradient echo acquisition in a voxel x at time t for an echo time TEk can be approximated as
| (1) |
where and are the signal changes in the net magnetization S0 and the apparent transverse relaxation rate of the voxel x at time t, and n(x, t) is a noise term. Hereinafter, the noise term and the voxel index x are omitted for simplicity in the notation. Describing and in terms of relative changes with respect to the average values in the voxel (Kundu et al., 2017), i.e. and , the MR signal can be written as
| (2) |
where the mean of the signal is . Typically, ∆S0(t) and are considerably smaller than and , respectively. Hence, the last term in Eq. (2) can be approximated using a first-order Taylor approximation as . Substituting this term into Eq. (2) and defining , the MR signal can be approximated as
| (3) |
where the term resulting from the multiplication of small values of ∆S0(t) and is neglected. Finally, signal percentage changes with respect to the mean of the signal, i.e. , can be described as
| (4) |
This signal model can be understood as a linear regression model in which the slope (i.e. dependent on the echo time TEk) captures the fluctuations related to , whereas the intercept captures the fluctuations related to ∆S0(t). In BOLD fMRI, signal changes related to are more likely linked to neuronal processes than changes due to ∆S0(t), which are normally related to confounding effects such as motion or blood inflow.
Following the linear convolution model usually adopted in fMRI data analysis, let us also assume that changes in generating the BOLD response in the signal can be described as , where ∆a(t) denotes an activity-inducing signal that is related to changes in neuronal activity, and ℎ(t) is the hemodynamic response function (HRF). Without lack of generality, we will assume that the shape of ℎ(t) is independent of TE and also normalized to a peak amplitude equal to 1 so that estimates of ∆a(t) can be expressed in units of the hemodynamic signal changes . Substituting in Eq. (4), signal percentage changes can then be approximated as
| (5) |
If signal changes related to variations in the net magnetization ∆ρ(t) are reduced during data preprocessing, the BOLD component of the signal can then be approximated as
| (6) |
The continuous time MR signal is sampled every repetition time (TR), i.e. t = nTR, where n = 1, …, N, and N is the number of volumes acquired during the acquisition. In discrete time, the previous equations can be reformulated in matrix notation. We can define , where , , and . Gathering all time points as a vector, , we can write , where is a column vector of length N that represents an activity-inducing signal that is related to , and is a Toeplitz convolution matrix whose columns are shifted versions of the hemodynamic response function (HRF) of duration L time points at TR temporal resolution, i.e. . If K echoes are acquired at echo times TEk, k = 1, …, K, the signal percentage changes of each echo signal can be vectorized in a column vector of length NK. Since the activity-inducing signal can be considered identical for all echoes, the ME signal model can be written as
| (7) |
or simply .
Multi-echo Sparse Paradigm Free Mapping
The deconvolution algorithm of multi-echo sparse paradigm free mapping (ME-SPFM) aims to deconvolve the changes in the BOLD ME-fMRI signal related to neuronal activity without knowledge of their timings. This involves the estimation of ∆a according to the model in Eq. (7). Figure 1 illustrates a schematic of the assumed ME-fMRI signal model and the ME-SPFM algorithm. Assuming that after preprocessing, the noise follows an uncorrelated Normal distribution, an unbiased estimate of the activity-inducing signal ∆a can be obtained by means of an ordinary least-squares estimator. Nevertheless, in practice, the least-squares solution would produce estimates with large variability due to the large collinearity between the columns of . Therefore, it is advisable to incorporate some type of regularization term to the least-squares minimization. Following previous algorithms for the temporal deconvolution of the BOLD fMRI signal, we propose to estimate ∆a with the following L1-norm regularized least-squares estimator
| (8) |
This mathematical optimization problem is known as Basis pursuit denoising (Chen et al., 1998), which is equivalent to the well-known LASSO (Tibshirani, 1996). The L1-norm regularization term encourages sparse estimates with few non-zero coefficients in , performing both variable selection and regularization in order to enhance the prediction accuracy and the interpretability of the estimates. This implies that will tend to be non-zero in only the coefficients that explain a large variability of the ME-fMRI signals according to the TE-dependent hemodynamic model described previously.
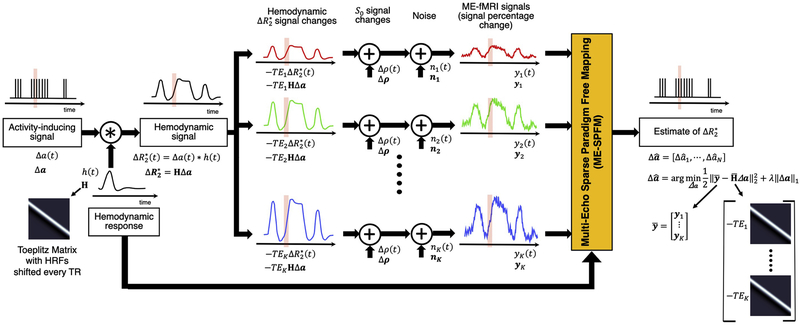
Figure 1.
Schematic of the ME-fMRI signal model and the ME-SPFM algorithm. From left to right: An activity-inducing signal (∆a(t)) is convolution with the hemodynamic response (ℎ(t)) resulting in the activity-induced hemodynamic signal or BOLD responses (i.e. ). The convolution step can be modelled as multiplying the activity inducing signal with a Toeplitz matrix whose columns are shifted HRFs every TR. Percentage signal changes of the fMRI signal acquired at TEk can be modelled as the sum of the hemodynamic signal scaled by TEk (i.e. ), fluctuations of the net magnetization (∆ρ(t)), and other noisy sources (e.g. thermal noise) (∆n(t)). The percentage signal changes of all echoes (or their MEICA denoised versions) are concatenated and input to ME-SPFM algorithm, which solves a regularized least squares problem, to obtain estimates of the activity inducing signal.
The choice of the regularization parameter λ is critical to obtain an accurate estimate of . In this work, instead of selecting a fixed value of λ, we compute the entire regularization path by means of the least angle regression (LARS) procedure (Efron et al., 2004). This homotopy procedure initializes with zero coefficients and then efficiently estimates the entire regularization path for decreasing values of λ where a coefficient of becomes non-zero or shrinks to zero again. After computing the regularization path, we propose to select the estimate of based on the Bayesian Information Criterion (BIC) as follows
| (9) |
where and df(λ) are the residual sum of squares and effective degrees of freedom for each estimate as a function of λ, respectively. Note that the BIC scales with NK, i.e. the number of time points by the number of echoes. Here, the effective degrees of freedom is approximately equal to the number of non-zero coefficients of the activity-inducing estimate. Besides, the BIC has shown appropriate selection of the regularization parameter in LASSO-like problems for variable selection (Tibshirani and Taylor, 2011; Zou et al., 2007).
Finally, to compensate for the shrinkage towards zero of the coefficients owing to the L1-norm regularization term, we propose to perform debiasing of the BIC estimate, known as the relaxed LASSO (Meinshausen, 2007). Debiasing is performed as the ordinary least-squares estimate on the reduced model corresponding to the subset of non-zero coefficients of the estimate. More specifically, let denote the support of , i.e. , the coefficients of the debiased estimate in the support are re-computed as
| (10) |
where is the reduced matrix with the subset of columns of corresponding to the support , whereas the coefficients not included in remain as zero.
MRI data acquisition
The evaluation of ME-SPFM was performed on ME-fMRI data acquired in 10 subjects (5 males, 5 females, mean ± SD age = 25 ± 3 y.o.) using a multi-task rapid event-related paradigm. Six subjects performed two functional runs, and 4 subjects only performed 1 run due to scanning time constraints (i.e. a total of 16 datasets). All participants gave informed consent in compliance with the NIH Combined Neuroscience International Review Board-approved protocol 93-M-1070 in Bethesda, MD. A complete description of the MRI acquisition protocols and experimental tasks in the experimental design can be found in Gonzalez-Castillo et al. (2016), and relevant details are given here for completeness.
MRI data was acquired on a General Electric 3 Tesla 750 MRI scanner with a 32-channel receive-only head coil (General Electric, Waukesha, WI). Functional scans were acquired with a ME gradient-recalled echo-planar imaging (GRE-EPI) sequence (flip angle=70° for 9 subjects, flip angle=60° for 1 subject, TEs=16.3/32.2/48.1 ms, TR=2 s, 30 axial slices, slice thickness=4 mm, in-plane resolution=3×3 mm2, FOV 192 mm, acceleration factor 2, number of acquisitions=220). Functional data was acquired with ascending sequential slice acquisitions, except in one subject where the acquisitions were interleaved. In addition, high resolution T1-weighted MPRAGE and proton density images were acquired per subject for anatomical alignment and visualization purposes (176 axial slices, voxel size=1×1×1 mm3, image matrix=256×256).
Experimental paradigm
The PsychoPy software (Peirce, 2009) was used for stimulus delivery. Eye tracking data were collected to check subject’s performance. Each run included 6 trials of each of the 5 different tasks (i.e. a total of 30 trials per run). Subjects were instructed on the task types prior to the scanning session. The 5 tasks were:
Finger tapping (FTAP). Subjects were instructed to press one button of a response box with a single finger at a fixed rate of approximately 0.5 Hz for a duration of 4 s. Visual cues were shown to help subjects press the button at a constant rate. All subjects performed this task with the left hand except two, who were inadvertently provided with the response box on their right hand.
Biological motion observation (BMOT). Subjects were instructed to observe 4-second videos of dot patterns resembling biological motion such as walking, jumping, dancing, drinking and climbing steps. The videos were shown on only one of the two visual hemi-fields (right or left) and their position was randomized across trials.
Passive viewing of houses (HOUS). Subjects were instructed to watch a succession of pictures of houses shown in the center of the screen. Each trial lasted 4 s and contained pictures of 6 different houses. Each house appeared for approximately 170 ms with a gap of 500 ms between pictures.
Listening to music (MUSI). Subjects were instructed to attentively listen to 4-seconds recordings of music clips played by a single instrument (violin, piano, or drums) and to direct their gaze to one of the three pictures on the screen (one per instrument) that represented the instrument being played as soon as they had identified it.
Sentence reading (READ). Subjects were instructed to covertly read sentences presented on the screen one word at a time. For each trial, words were presented in one of the two hemifields (right or left) to aid with analysis of eye tracking data. All words of a trial appeared on the same hemifield. Each word was presented for 250 ms with gaps of 100 ms in between. Sentence length was between 10 and 11 words, so each trial lasted either 3400 or 3750 ms.
Onset times for trials were generated with optseq2 in Freesurfer (https://surfer.nmr.mgh.harvard.edu/optseq). Three different schedules (onset times) were randomly used in these experiments. For all three schedules the minimum inter-stimulus interval (ISI) was 10 s. Mean and standard deviation ISIs for the three different schedules were: 13 ± 24, 13 ± 18 and 13 ± 15 s.
FMRI data preprocessing
Each ME-fMRI dataset was preprocessed through four different pipelines implemented in AFNI (Cox et al., 1996) resulting in the following datasets:
Individually preprocessed echoes (E01, E02 and E03): (1) removal of the initial 10 s to achieve steady-state magnetization, (2) slice timing correction, (3) volume realignment, registration to anatomical image, and warping to MNI template, and computation of the combined spatial transformation, (4) spatial normalization of each echo dataset to the MNI template at 2 mm isotropic voxel size with a single spatial transformation, (5) nuisance regression (Legendre polynomials up to 5th order, realignment parameters and their 1st temporal derivatives, and 5 largest principal components of voxels within the lateral ventricles), (6) spatial smoothing with a 3D Gaussian kernel with Full Width Half Maximum of 6 mm, and (7) calculation of signal percentage change as described in Eq. (4). The preprocessed E02 acquired at TE=32.2 ms will be used as the representative dataset for a conventional single echo fMRI acquisition at 3T.
Optimally combined dataset (OC): same preprocessing as A) but with optimal weighted combination of the three echoes based on non-linear voxelwise estimation of (Posse et al., 1999) between steps (4) and (5).
Multi-echo Independent Component Analysis plus Optimally Combined dataset (DN): same preprocessing as A) but with multi-echo independent component analysis (MEICA) denoising (Kundu et al., 2012) and optimal combination between steps (4) and (5). MEICA was applied using the code available in https://github.com/ME-ICA/me-ica (version 3.2).
Multi-echo Independent Component Analysis denoised echoes (MEICA-E01, MEICA-E02, MEICA-E03): same preprocessing as A) but including MEICA between steps (4) and (5). The purpose of this pipeline was to evaluate the influence of denoising the echoes with a ME-based denoising approach in order to remove fluctuations related to changes in the net magnetization (∆S0) prior to ME-SPFM, as assumed in the proposed model.
The mask of the lateral ventricles was computed in the original functional space of each dataset as those voxels showing a value of . The maps were obtained based on a nonlinear fit of the mono-exponential decay model of the gradient-echo signal using the average signal intensity of each echo, and were eroded to reduce partial volume effects and remove CSF voxels in the edges of the brain.
FMRI data analysis
The three preprocessed echo datasets (E01, E02 and E03) and the three MEICA denoised echo datasets (MEICA-E01, MEICA-E02 and MEICA-E03) were analyzed with the multi-echo sparse paradigm free mapping algorithm described above. The ME-SPFM algorithm was implemented for AFNI using functions for compatibility with R and used the LARS package (version 1.2) for the computation of the regularization path of the LASSO. The canonical HRF (SPMG1 option of 3dDeconvolve in AFNI) was used as the hemodynamic response function (HRF) to define the convolution matrices in . Since the ME-SPFM algorithm outputs a 4D-dataset with voxelwise time-varying estimates of the activity-inducing signal ∆a, for validation purposes we defined ME-SPFM activation maps for each trial by computing the maximum of the ∆a volumes when each trial occurred (i.e. 3 TRs for a duration of 4 s per trial).
The performance of ME-SPFM was compared with the results of the deconvolution with the Sparse Paradigm Free Mapping for a single (or echo) dataset (1E-SPFM, Caballero-Gaudes et al., 2013) and traditional GLM analyses implemented with 3dREMLfit in AFNI. These analyses were performed in the E02, OC and DN datasets. As for 1E-SPFM, datasets were analyzed with the implementation of SPFM available in AFNI (3dPFM program) using the LASSO algorithm, the Bayesian Information Criterion (BIC) for selection of the regularization parameter and the canonical HRF to define the corresponding convolution matrix. Similar to ME-SPFM, 1E-SPFM activation maps were created from the deconvolved coefficients (beta output dataset in 3dPFM) as the maximum of the volumes when each trial occurred. No additional processing steps were applied to the ME-SPFM and 1E-SPFM activation maps.
In addition, we performed two different GLM analyses in the E02, OC and DN datasets, where the design matrix was either defined considering all trials of a task in one regressor (TASK-LEVEL) or each trial individually modulated, i.e. each trial has its own regressor (‘IM’ or TRIAL-LEVEL). The SPM canonical HRF was used in both analyses, assuming a trial duration of 4 s. The task-based activation maps were thresholded at FDR-corrected q ≤ 0.05 (TASK-q05). The trial-based activation maps were thresholded at FDR-corrected q ≤ 0.05 (IM-q05), as well as uncorrected p ≤ 0.05 (IM-p05) and p ≤ 0.001 (IM-p001). The number of components removed by MEICA was considered in the computation of the degrees of freedom of the GLM analyses when it was employed in preprocessing (i.e. the DN dataset).
Evaluation of spatial concordance with GLM analyses
We evaluated the ability of the 1E-SPFM and ME-SPFM to detect the activation revealed by the GLM analyses in terms of the spatial sensitivity, spatial specificity and spatial overlap using a dice coefficient metric. This evaluation only considered activations that produce a positive BOLD signal change (i.e. a positive effect size in GLM analyses), a positive coefficient in 1E-SPFM and a negative (i.e. ∆a < 0) coefficient in the analyses with ME-SPFM.
First, we performed the comparison at the task level by using the task-based activation maps obtained with the DN dataset (TASK-q05/DN) as the reference maps. These can be considered as the gold standard of activation maps per task in each dataset that can be obtained with an analysis that is aware of the trials’ onsets and durations using the same hemodynamic model (i.e. SPMG1). For this comparison, we also considered the following activation maps: IM-q05, IM-p001, IM-p05; 1E-SPFM with the E02, OC and DN as input datasets, as well as ME-SPFM using the triplets E01, E02 and E03 or MEICA-E01, MEICA-E02 and MEICA-E03 as input datasets.
Second, we performed the comparison at the trial-level by using the trial-based activation maps at p ≤ 0.05 obtained with the DN dataset (IM-p05/DN) as the reference maps, which considers a model of a single trial based on its onset and duration and, thus, is closer to the assumptions of the ME-SPFM activation maps. For this evaluation at the single trial level, we considered the following activation maps: 1E-SPFM with the E02, OC and DN datasets, as well as ME-SPFM using the triplets E01, E02 and E03 or MEICA-E01, MEICA-E02 and MEICA-E03 as input datasets.
Evaluation of temporal concordance with GLM-IM analysis
We also computed maps of the Pearson correlation between the fitted signal of the GLM-IM model with the fitted signal of 1E-SPFM and ME-SPFM (i.e. convolution of the detected events with the canonical HRF) in order to evaluate the temporal concordance of the detected events in comparison with a conventional model-based analysis using timing of the experimental trials. Moreover, we computed the correlation between these models with the preprocessed DN dataset (i.e. including MEICA and optimal combination) to examine whether the deconvolution approaches can explain additional variance of the preprocessed data, particularly in regions that might not be involved during the known tasks. These temporal correlation analyses can serve as an evaluation criterion that is not threshold-dependent and therefore complements the aforementioned spatial evaluation.
Quantitative Analysis of estimates
We evaluated the ability of ME-SPFM deconvolution to estimate events in the activity-inducing signals that correspond to changes within physiologically plausible limits, which was established as according to previous reports of neurobiologically-driven values at 3T (van der Zwaag et al., 2009). First, we computed histograms of the activity-inducing estimates for both ME-SPFM and MEICA-ME-SPFM activation maps in three conditions: a) during the entire dataset in all whole-brain voxels to assess the efficacy of the algorithms to yield physiologically-plausible estimates independently of the paradigm, b) during the timings of trials in the whole brain, and c) during the timings of trials in only those voxels showing positive activation in the TASK-q05 maps for the DN dataset, i.e. assumed to have a clear positive BOLD response to the task that is associated with . In addition, we computed the percentage of estimates exceeding per trial, per task, per dataset and per ME-SPFM analysis.
RESULTS
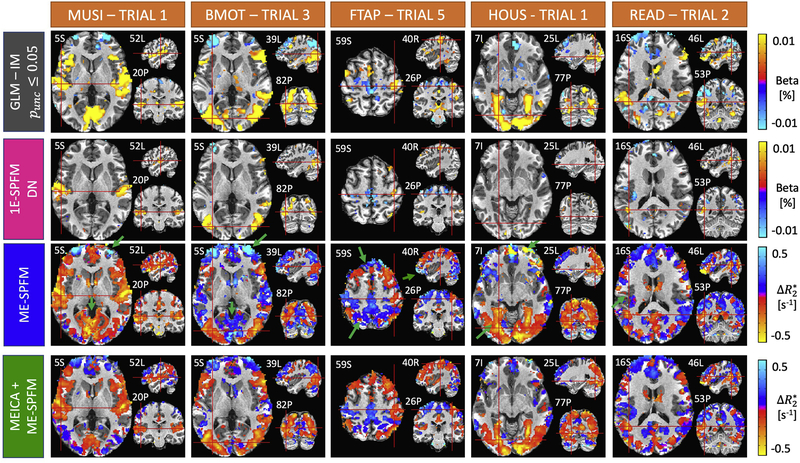
The output of ME-SPFM is a 4D dataset with an identical number of time points as the input dataset, which can be visualized as a sequence of deconvolved maps. A movie showing the activity-inducing signal (given in the same units as ) and the hemodynamic response signal (i.e. signal changes as the convolution of the activity-inducing signal with the HRF) of a run of a representative subject is available as supplementary material. The movies of the rest of the runs and subjects are available in https://ccaballero.pages.bcbl.eu/me-spfm-videos/. Figure 2 depicts the corresponding activation maps for representative single trial events of each task type for the same run for IM-p05, 1E-SPFM with the DN dataset, and ME-SPFM with the preprocessed echo datasets and after ME-ICA. The activation maps obtained with ME-SPFM have a larger resemblance with the maps obtained with the trial-based GLM analysis (IM-p05) than the activations maps obtained with 1E-SPFM. Even though the 1E-SPFM maps generally depict clusters of activation in the same locations as the GLM maps (i.e. high spatial specificity), they exhibit lower spatial sensitivity than the ME-SPFM activation maps, especially observed in FTAP-5, HOUS-1 and READ-2. In general, the ME-SPFM activation maps exhibit activity-inducing signals with negative in brain regions showing positive BOLD signal changes, and conversely activity-inducing signals with positive in brain regions showing negative BOLD signal changes, in the IMp05 and 1E-SPFM maps. The MEICA+ME-SPFM activation maps illustrate that applying MEICA prior to ME-SPFM reduces spurious activations in the borders of clusters and draining veins, probably related to inflow fluctuations, and in brain edge voxels related to effects of head motion. Some examples of these effects are marked with green arrows.
Figure 2.
Activation maps of an individual single-trial event for each experimental condition obtained with an individually-modulated (IM) GLM analysis (T-test, uncorrected p ≤ 0.05) (first row), 1E-SPFM (second row), ME-SPFM (third row) and MEICA+ME-SPFM (fourth row). The maps of IM-GLM and 1E-SPFM show estimated beta coefficients in signal percentage change (i.e. % amplitude), whereas ME-SPFM and MEICA-ME-SPFM show estimated values in units of s−1. Note the ME-SPFM and MEICA+ME-SPFM activations maps are shown with reverse colorbars so that negative (positive) values shown in red (blue) induce positive (negative) BOLD signal changes.
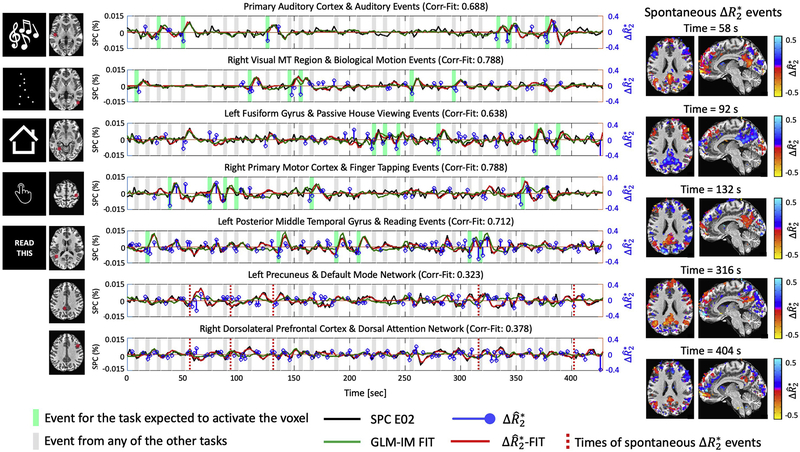
Figure 3 plots the preprocessed and estimated signals for the trial-based GLM and MEICA+ME-SPFM analyses for the same dataset in seven representative voxels, relevant to each task (shown in the left maps) and in left precuneus and right dorsolateral prefrontal cortex (DLPFC), which are regions typically associated with the default mode network and dorsal attention network, respectively. For the voxels related to the tasks, the activity-inducing time series obtained with ME-SPFM exhibit negative (deflection in blue traces) that are reliably detected at the time of all experimental events (light green bands). These negative result in positive BOLD signal changes (red traces) that agree with the signals estimated by the GLM-IM model in the DN dataset (green traces). The Pearson’s correlation between the BOLD signal estimated with ME-SPFM and with the GLM-IM model is shown on top of each time course (Corr-FIT values). Clearly the correlation values are larger in the task-activated voxels than in the left precuneus and right DLPFC. In addition to the task-related events, ME-SPFM is able to detect BOLD events that often occur during the timing of other tasks or in the absence of any task, i.e. during rest periods. The ME-SPFM activation maps shown on the right correspond to five representative task-unrelated spontaneous BOLD events marked with red dashed lines in the plots of the left precuneus and DLPFC. These maps depict spatial patterns with clusters of activation in regions of the default mode network (negative at 58, 132, 316 and 404 s and positive at 92 s) that act in synchrony with clusters of activation in areas of the dorsal attention network. Importantly, these transient events occurring at times without any task cannot be revealed by conventional GLM approaches, but are detected by ME-SPFM owing to its ability to operate without timing information.
Figure 3.
Time courses of signal percentage change in E02 dataset (SPC E02, black line), GLM-IM fitted signal (green), (blue) and BOLD estimates, i.e. convolved with canonical HRF (red) obtained with MEICA+ME-SPFM in seven representative voxels in task-related regions, and left precuneus and right dorsolateral prefrontal cortex (DLPFC) of the same dataset as Figure 1. The voxel’s location is shown in the left maps. Dark and light grey bands indicate the times of trials of the relevant task for each voxel and the rest of the tasks, respectively. The maps shown on the right display instances of spontaneous events occurring at rest, whose timing is marked with dashed lines in the time courses of the left precuneus and right DLPFC.
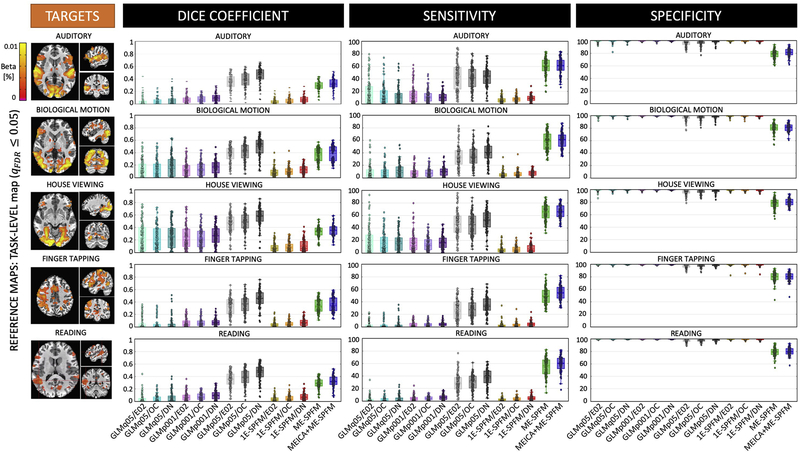
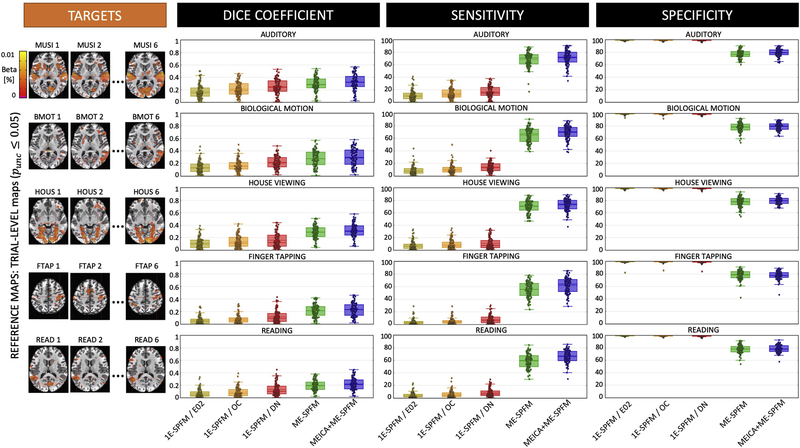
Considering all datasets, Figures 4 and 5 show the average spatial dice coefficient, sensitivity and specificity for the different methods using the task-based GLM (TASK-q05/DN) and trial-based GLM maps (IM-p05/DN) as reference maps, respectively. Both figures illustrate the ME-SPFM algorithm outperforms its 1E-SPFM counterpart regardless of the prior use of ME-ICA, achieving considerably larger spatial overlap and sensitivity with a reduction in specificity. As shown in Figure 4, ME-SPFM achieves similar spatial concordance with the TASK-q05 maps to the one obtained with trial-based GLM analyses using a statistical significance threshold between punc ≤ 0.05 (IM-p05) and punc ≤ 0.001 (IM-p001). In general, denoising the fMRI signal with MEICA (i.e. the DN dataset) is beneficial to increase the sensitivity and the spatial concordance of the TRIAL-LEVEL (i.e. IM) GLM maps with respect to the TASK-LEVEL maps. In all cases, the spatial concordance of the IM-p001 maps is similar to the TRIAL-q05 maps. MEICA-based denoising is more advantageous than preprocessing based on optimal combination of echoes (i.e. the OC dataset) or a standard single echo (E02) dataset for detecting single-trial BOLD events in both 1E-SPFM and ME-SPFM analyses. The advantage of MEICA is also seen in the IM-p05 maps. Similar conclusions can be drawn from the results in Figure 5 wherein the TRIAL-LEVEL IM-p05/DN activation maps become the reference maps. MEICA+ME-SPFM yields larger spatial concordance, sensitivity and specificity than ME-SPFM, and both of them outperform 1E-SPFM analyses in terms of spatial overlap for all the conditions.
Figure 4.
Dice coefficient (i.e. spatial overlap), sensitivity and specificity values of single-trial activation maps obtained with each of the analysis methods (GLM-IM, 1E-SPFM, ME-SPFM and MEICA+ME-SPFM) for each of the experimental conditions. Each box depicts the median and the mean (dashed line) across all trials. Its width is defined by the interquartile range (IQR) defined by the 1st quartile (Q1) and 3rd quartile (Q3) quartiles. The whiskers define the 1.5xIQR below Q1 and 1.5xIQR above Q3. TASK-LEVEL activation maps thresholded at FDR-corrected q ≤ 0.05 (TASKq05) and only including voxels with positive activation were used as reference maps, shown on the left for a representative dataset. The GLM-IM and 1E-SPFM activation maps were computed from the E02, OC and DN (i.e. MEICA and OC) preprocessed datasets, and GLM-IM maps were obtained at thresholds FDR-corrected q ≤ 0.05 (IMq05), as well as uncorrected p ≤ 0.05 (IMp05) and p ≤ 0.001 (IMp001).
Figure 5.
Dice coefficient (i.e. spatial overlap), sensitivity and specificity values of the single-trial activation maps obtained with 1E-SPFM, ME-SPFM and MEICA+ME-SPFM for each of the experimental conditions. Each box depicts the median and the mean (dashed line) across all trials. Its width is defined by the interquartile range (IQR) defined by the 1st quartile (Q1) and 3rd quartile (Q3) quartiles. The whiskers define the 1.5xIQR below Q1 and 1.5xIQR above Q3. TRIAL-LEVEL activation maps thresholded at uncorrected p ≤ 0.05 (IMp05) and only including voxels with positive activation were used as reference maps, shown on the left for a representative dataset. The 1E-SPFM activation maps were computed from the E02, OC and DN (i.e. MEICA and OC) preprocessed datasets.
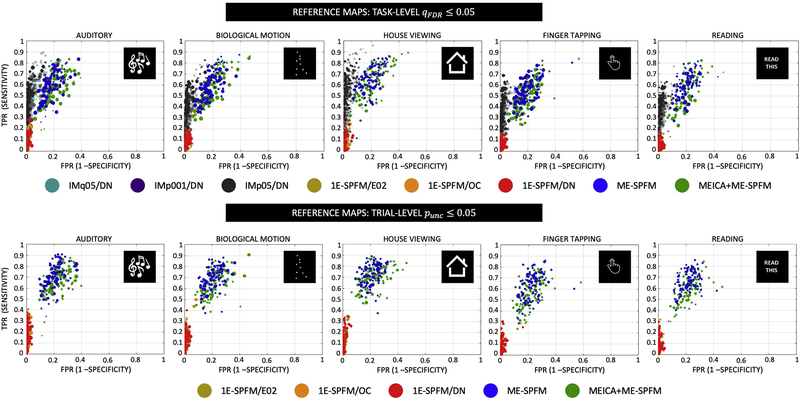
Figure 6 shows the corresponding receiver operating characteristic (ROC) curves with the sensitivity and specificity of each individual trial’s activation map for all conditions and the two types of reference maps: TASK-q05/DN are shown at the top and IM-p05/DN are shown at the bottom. For visualization purposes, only the IM-q05, IM-p001 and IM-p05 with the DN dataset are shown in the ROC plots at the TASK-LEVEL. The radius of each circle is relative to the number of voxels showing activations (i.e. total number of positives) in the reference maps. Similar to Figures 4 and 5, the ROC curves illustrate that ME-SPFM offers larger sensitivity in detecting single-trial events than 1E-SPFM, which instead achieves nearly perfect specificity values (i.e. above 95%) similar to GLM-IM activation maps. Interestingly, ME-SPFM achieves larger sensitivity values than GLM-IM for certain trials, particularly for the house viewing and reading conditions. The use of MEICA in preprocessing slightly improves the performance of ME-SPFM, particularly when compared with the IM-p05/DN activation maps.
Figure 6.
Receiver operating characteristic (ROC) curves with the sensitivity and specificity of each individual trial’s activation map for all conditions and the two types of reference maps: TASK-q05/DN (top) and IM-p05/DN (bottom). The number of dots per type of analysis is the total number of trials across all datasets (i.e. 16 datasets with 30 trials each equals 480 trials). For visualization purposes, only the IM-q05, IM-p001 and IM-p05 with the DN dataset are shown in the ROC plots at the TASK-LEVEL. The radius of each circle is relative to the number of positives in the reference map, i.e. trials with bigger circles activations had more activated voxels in the reference maps, wherein the largest radius is the maximum number of positives across all trials and conditions. For the TASK-q05/DN plots, the maximum/minimum number of positives for each task were: 57558/7278 for MUSI, 60915/8210 for BMOT, 37303/8089 for HOUS, 53249/10456 for FTAP, 46860/5542 for READ. For the IM-p05/DN plots, the maximum/minimum number of positives for each task were: 50825/1120 for MUSI, 59764/1892 for BMOT, 39137/2603 for HOUS, 33380/804 for FTAP, 29539/933 for READ.
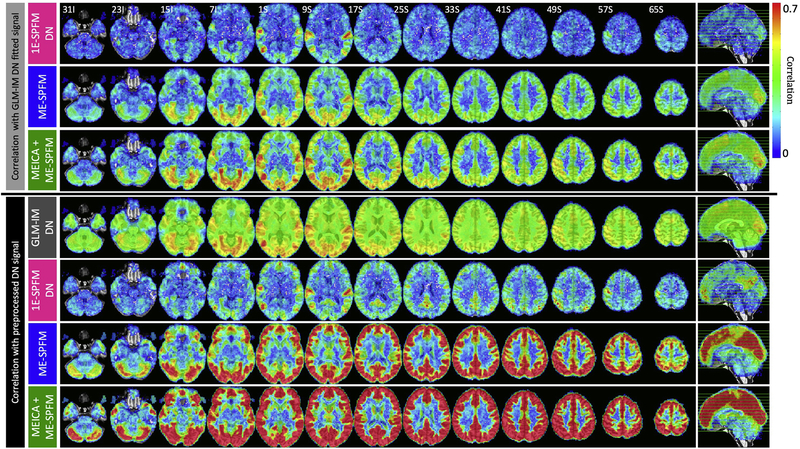
To demonstrate the temporal concordance of the detected activation, Figure 7 shows the average Pearson’s correlation coefficients of the hemodynamic signal estimated with the GLM-IM model (top three rows) and the preprocessed DN dataset (bottom four rows) with the hemodynamic signals estimated with 1E-SPFM/DN, ME-SPFM and MEICA+ME-SPFM. Fisher’s z-transformation was applied to the correlation coefficients prior to averaging across datasets and then inversely applied for visualization purposes. Also, notice that the range of the correlation maps only covers positive values because negative correlations were only identified in few disperse voxels in white matter. As for the correlation with the GLM-IM hemodynamic signal, both ME-SPFM analyses show higher temporal correlation values than those obtained with 1E-SPFM, particularly confined to gray matter voxels. The peaks of the correlation maps occur in brain regions involved in the processing of the multiple tasks, such as the primary auditory cortex for listening to music, the primary motor cortex for finger tapping, the ventral occipitotemporal cortex involved for viewing of houses and reading, the posterior temporal-occipital cortex for passive viewing of biological motion, and the primary occipital cortex for the multiple tasks with visual input. The 1E-SPFM maps only display large correlation values in these cortical regions.
Figure 7.
(Top three rows) Maps of Pearson’s correlation coefficients between the BOLD signals estimated with the GLM-IM analysis and the BOLD signals estimated with the 1E-SPFM, and ME-SPFM and MEICA+ME-SPFM deconvolution algorithms. (Bottom four rows) Maps of Pearson’s correlation coefficients between the preprocessed DN dataset and the fitted signals estimated with the GLM-IM analysis, and the 1E-SPFM, and ME-SPFM and MEICA+ME-SPFM deconvolution algorithms.
The bottom four rows of Figure 7 illustrate the average correlation maps of the corresponding hemodynamic signals with the preprocessed MEICA+OC denoised (DN) dataset. The correlation maps of the DN dataset with the GLM-IM fitted signal are spatially smooth with non-negligible correlation across all brain voxels and peaks in task-related areas. Similar to the correlation maps with the GLM-IM hemodynamic signals, the ME-SPFM correlation maps reveal a pattern of larger correlation values in voxels across the entire cortex and in some subcortical areas (e.g. putamen and caudate nucleus) and low correlation values in voxels in white matter and cerebrospinal fluid where the deconvolution normally produces null estimates. The correlation values of the MEICA+ME-SPFM hemodynamic signal with the DN dataset is larger than those obtained with the ME-SPFM maps. This can be expected since the reference signal has also been denoised with MEICA. Both ME-SPFM clearly exhibit larger correlations than the 1E-SPFM due to their higher temporal sensitivity. The widespread pattern of correlation in grey matter can also be observed, but less evidently so in the maps obtained with 1E-SPFM. The deconvolution approaches are able to explain variance of the preprocessed DN signal in regions such as the anterior and posterior cingulate cortices, precuneus and prefrontal regions, which cannot be described with the GLM-IM model.
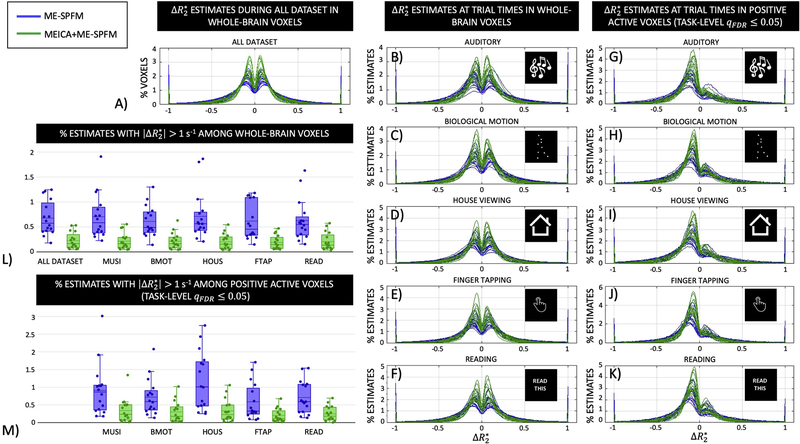
Figure 8 displays the histograms of the activity-inducing estimates in the same units as obtained with ME-SPFM and MEICA+ME-SPFM for all subjects: (A) during the entire run, (B-F) during the timings of each task in all intracranial voxels, and (G-K) only in the voxels with significant positive response in the corresponding TASK-q05/DN activation map. Voxels with zero are discarded in the histogram plots. In general, the activity-inducing estimates are within values of between [−1, 1] s−1, which is a physiologically-plausible range of in grey matter at 3T. In addition, the percentage of voxels showing activity-inducing estimates with was considerably reduced in the MEICA+ME-SPFM analyses (see plots L and M). A table with the percentage of voxels showing activity-inducing estimates with for ME-SPFM and MEICA+ME-SPFM for all datasets is available as supplementary material. The histograms illustrate that the activity-inducing estimates obtained with MEICA+ME-SPFM show smaller amplitudes than the those obtained with ME-SPFM. Furthermore, the histograms become skewed towards negative -estimates when the mask only includes voxels with significant positive task-related BOLD signal changes. Interestingly, the histograms exhibit a noticeable symmetry around 0 s−1 with all intracranial voxels, particularly when the entire duration of the run is considered.
Figure 8.
Histograms of values estimated with ME-SPFM (blue lines and boxes) and MEICA+ME-SPFM (green lines and boxes) in: A) whole-brain voxels during the entire dataset, (B-F) in whole-brain voxels during times of trials for each condition, and (G-K) in voxels with positive activation according to the TASK-LEVEL IMq05 activation map during the times of trials for each condition. (L-M) Box plots with the percentage of voxels with for the analysis, showing one circle per dataset.
DISCUSSION
The proposed deconvolution algorithm for ME-fMRI, named multi-echo sparse paradigm free mapping (ME-SPFM), achieved larger spatial overlap with maps obtained using conventional GLM analyses and greater sensitivity than single echo deconvolution but reduced specificity relative to its 1E-SPFM counterpart (Caballero-Gaudes et al., 2013). Even though the deconvolution with 1E-SPFM generated single-trial activation maps with very high specificity, it exhibited a significant reduction in sensitivity that caused the algorithm to fail in the detection of activations in brain regions related to the task for certain events (see 1E-SPFM activation map of HOUS Trail 1 in Figure 2) probably due to insufficient contrast-to-noise ratio in these trials. Here, the deconvolution with ME-SPFM was performed with the same combination of sparsity-promoting regularized estimator of LASSO and the Bayesian Information Criterion as for 1E-SPFM. From these results, it can be inferred that the superior performance of ME-SPFM is due to its ME-based formulation as this accounts for the linear dependence of the BOLD signal on TE according to a mono-exponential decay model. Importantly, the advantage of ME-SPFM over 1E-SPFM was observed for the three ways of preprocessing to generate a single dataset from the multiple echo datasets, even after MEICA denoising and optimal echo combination which can be considered one of the most advanced preprocessing approaches for ME-fMRI data (Gonzalez-Castillo et al., 2016). Based on these results, it can be concluded that, for the purpose of voxelwise deconvolution, leveraging the information available across the multiple echo datasets through a TE-dependent model is more advantageous than weighted combination of the multiple echoes in a single dataset (Posse et al., 1999; Gowland and Bowtell, 2007; Poser et al., 2006), even with MEICA denoising (Kundu et al., 2012). In addition, the advantage of ME-SPFM with respect to 1E-SPFM increased when the reference activation maps were defined based on a GLM analysis with task-level regressors, rather than with individually modulated regressors for each trial. This result may be associated to the higher level of uncertainty of the single-trial activation maps used as reference, which results in higher variability in the specificity, sensitivity and spatial overlap estimates.
We observed that applying MEICA prior to ME-SPFM in order to denoise the multiple echo datasets did improve, but not substantially, the sensitivity, specificity and spatial overlap with the TASK-LEVEL or TRIAL-LEVEL reference maps. Hence, we conclude that the improved ability to blindly detect individual BOLD events is more associated with the ME-SPFM algorithm rather than due to denoising with MEICA. To some degree, this result also demonstrates that the proposed ME-SPFM algorithm can cope with S0-related fluctuations of the signal despite these being neglected in the deconvolution. Moreover, the slight improvements in performance of the 1E-SPFM and ME-SPFM algorithms when the echo datasets are denoised with MEICA are similar to the ones observed when GLM analyses are performed, which is concordant with previous results (Gonzalez-Castillo et al., 2016).
Denoising the echo datasets with MEICA prior to the proposed ME-SPFM algorithm is still recommended (i.e. the MEICA+ME-SPFM analysis), since the corresponding activation maps become more focal, showing a reduced number of voxels with non-zero values that may originate from inflow effects, movement-related artefacts and physiological fluctuations (see green arrows in Figures 1). Moreover, the number of voxels showing activity-inducing signals with non-physiologically plausible values of is significantly reduced in MEICA+ME-SPFM (see Figure 8). The smaller amplitude of the MEICA+ME-SPFM estimates also agrees with previous observations of diminished effects sizes in task-related activations observed in Gonzalez-Castillo et al. (2016).
As shown in Figure 7, the ME-SPFM algorithm also exhibited higher temporal correlation with the hemodynamic signals estimated by GLM-IM than by the 1E-SPFM algorithm, suggesting a higher temporal sensitivity of the estimated signals. Even though the peaks of the temporal correlation maps were located in brain regions assumed to strongly engage in the experimental tasks, the correlation maps of ME-SPFM also exhibited non-negligible correlation values in grey matter voxels across the entire cortex, subcortical regions and cerebellum, whereas the correlation was clearly reduced in white matter voxels. This indicates that ME-SPFM offers not only higher temporal sensitivity, but also does not detect hemodynamic (i.e. ) signal changes at random, but they are specific to brain regions of potential functional relevance. These BOLD signal changes (i.e. -events) are missed by 1E-SPFM and cannot be explained from the experimental design with GLM analyses. There can be multiple causes for the origin of these activations. First, the higher contrast-to-noise ratio of the BOLD signal in grey matter voxels than in white matter (Krüger and Glover, 2001). Second, due to the sluggishness of the hemodynamic response, BOLD signal changes associated with occurring prior to the trials may also extend in time and overlap with the BOLD signal changes in response to the trials. Third, part of the activations observed in brain regions beyond those primarily involved in the performance of the tasks could also be explained in terms of behavioural differences across trials, for instance due to changes in attention, self-awareness or executive control mechanisms that engage other brain regions in a less prominent manner and thus are only detected with ME-SPFM due its enhanced sensitivity relative to 1E-SPFM. Here, we confirmed that subjects performed all task-related events based on eye-tracking measurements, thus ensuring that variability across trials is not associated to inappropriate performance of the tasks (Gonzalez-Castillo et al., 2016).
Importantly, ME-SPFM also enabled us to detect hemodynamic events with physiologically plausible values in periods between trials when the subjects are not assumed to engage in any evoked task. These spontaneous events detected during rest would be neglected by any analysis approach that only model events with timing known by the experimenter. Figure 3 shows several instances of these transient, spontaneous -events for a representative dataset (see also the movie available as supplementary material) in brain regions of the default mode network (Raichle, 2015) as well as the attention and frontoparietal executive control networks (Dixon et al., 2018; Fox et al., 2006). Similar patterns of spontaneous -events were observed across all datasets. The maps and amplitude of these spontaneous activations highly resemble the functional connectivity maps observed in resting state fMRI and also exhibit similar between-network relationships in the sign of the detected activations. For instance, the illustrative maps in Figure 3 show the well-known opposite polarity of BOLD signal changes, and thus also in , between regions of the default mode network (i.e. precuneus, posterior cingulate, inferior parietal lobule and medial prefrontal cortex) and the dorsal attention network (i.e. dorsolateral prefrontal cortex, frontal eye fields, intraparietal sulcus, superior parietal lobule) (Fox et al., 2005). Although the datasets were not acquired in resting state, these findings corroborate previous evidence of involvement of resting state functional networks during event-related paradigms obtained in single-echo datasets with SPFM (Caballero-Gaudes et al., 2013; Petridou et al., 2013) and Total Activation (Karahanoğlu et al., 2013). Point process analyses have also revealed the presence and relevance of these extreme events in resting-state analyses (Liu et al., 2018; Tagliazucchi et al., 2012; Tagliazucchi et al., 2016), and they can serve as a proxy of the onset of significant BOLD deflections to estimate the shape of a resting-state HRF (Wu et al., 2013).
The activity-inducing signals estimated with ME-SPFM have the same interpretable units as , i.e. s−1. As shown in Figure 8, most of the ME-SPFM estimates fell within limits of neuronally-driven at 3T. For positive BOLD signal changes, Donahue et al. (2011) and van der Zwaag et al. (2009) reported total values of −0.74 ± 0.05 s−1 and −0.98 ± 0.08 s−1 in the human visual and motor cortices at 3T for a block-design tasks with long stimuli. These values are higher than those obtained with our deconvolution in response to more complex tasks and with shorter trial duration. Should we have a prior hypothesis of the maximum induced by neuronally-driven events per brain region, this information can be exploited to characterize the nature of the detected events and identify those events with exceeding values that might be more related to artefactual changes in the BOLD signal (i.e. due to severe motion) than to neurobiological processes. For that, it is important to consider that values may vary due to differences in anatomy across brain regions (e.g. vascularization), imaging parameters (e.g. magnetic field strength, RF coil type, voxel size, flip angle) and experimental paradigm (e.g. block vs. fast event-related designs).
Furthermore, the histograms of were symmetrical at the whole-brain level, particularly when considering the entire run. Similar results were obtained for all analyses when a gamma function (GAM option in 3dDeconvolve) without post-stimulus undershoot was used for deconvolution (data not shown). This observation indicates that the observed symmetry in the histograms of the estimates cannot be completely explained due to spurious estimates that try to compensate mismatches between the assumed and real HRF shapes. The hemodynamic equilibrium in number and magnitude is intriguing, but agrees with our previous observations of whole-brain, widespread activations with equivalent number of positive and negative BOLD signal changes at 3T (Gonzalez-Castillo et al., 2012). Although this work does not aim to explore this issue, we conjecture that the observed hemodynamic equilibrium has a main neuronal contribution probably due to inhibition (Devor et al., 2007; Shmuel et al., 2006), rather than purely hemodynamic due to blood stealth of positively active regions from neighboring regions (Harel et al., 2002). Our support to this claim is that positive occurred in spatially distributed regions across distinct vascular territories, were observed across all tasks, and were also confined to regions of the same functional network (e.g. default mode, dorsal attention) in periods of rest.
Remarks, limitations and future directions
Estimates of the activity-inducing signal obtained by ME-SPFM are related to changes in the apparent relaxation rate , which is closely related to changes in the concentration of deoxygenated hemoglobin and blood oxygen saturation, which in turn are described by localized changes in blood flow, oxygen metabolism and blood volume in response to neuronal activity (Buxton et al., 2004). Hence, it is important to emphasize that the origin of the events detected by ME-SPFM is governed by a complex mixture of neurophysiological and metabolic processes that would need additional imaging data to describe their intrinsic dynamics and a more valid quantification, for example by means of combining multiecho BOLD with ASL acquisitions (Havlicek et al., 2017) or calibrated fMRI procedures (Blockley et al., 2013).
Furthermore, the ME-SPFM formulation proposed here, as well as the ME-ICA algorithm, builds upon the assumption of linear TE-dependence of fractional BOLD signal changes based on a mono-exponential decay model of the gradient-echo fMRI signal. This is valid for the extra-vascular contribution to the BOLD signal, which increases linearly with TE (Donahue et al., 2011). However, in the gradient echo signal at 3T and for a TE equal to the tissue T2, the relative intra-vascular contribution can represent approximately 36% and 11% of the signal variation for the micro- and macro-vasculature, respectively (Uludağ et al., 2009; Croal et al., 2017). The intra-vascular signal shows a nonlinear dependence on TE with a peak for TEs between 20–50 ms and decreasing values for longer TEs (Uludağ et al., 2009; Havlicek et al., 2017), probably due to changes in the average chemical exchange time during the stimulation (Kang et al., 2018). As a consequence, the model assumed might not be valid for the percentage of intra-vascular signal changes within the total signal changes; instead they could be more accurately characterized using the Luz-Meiboom exchange model (Uludağ et al., 2009; Duong et al., 2003). At field strengths larger than 4.7 T, the contribution of the intravascular signal to total gradient echo fMRI signal change would be nearly zero regardless of the TE (Uludağ et al., 2009). Moreover, recent experiments using a combination of multi-echo BOLD and cerebral blood flow measurements in the human visual cortex at 3T have shown that the amount of nonlinearity in the model with TE might also change during the time course of the BOLD response (Havlicek et al., 2017), suggesting different physiologically-driven dynamics for the intercept time-course and the BOLD component of the signal. Yet, these non-linear findings were obtained with long stimulus durations (e.g. visual stimuli of 55 s duration were used in Havlicek et al. (2017) and 16 s duration in Donahue et al. (2011) and Kang et al. (2018)), whereas our data comprised short stimuli of 4 s duration. Even if the assumption of linearity on TE failed, which would make the model assumed in ME-SPFM and other ME-based approaches such as MEICA slightly imperfect, our results showed large agreement with the results of GLM analyses, proving the viability of a ME-based deconvolution approach. Finally, fitting a multi-exponential model might also be more accurate in voxels with large partial volume effects, particularly for CSF with considerably longer than that of grey matter (Speck et al., 2001).
A potential limitation of our approach is the use of sparsity-promoting L1-norm regularized estimators such as LASSO for deconvolution. We used the Least Angle Regression (LARS) algorithm (Efron et al., 2004) to efficiently compute the entire regularization path in combination with the Bayesian Information Criterion (BIC) for selection of the regularization parameter (Zou et al., 2007). Although the BIC curve is voxel-dependent, we observed homogenous maps of the regularization parameter (both the BIC curves and the maps of the regularization parameter are also available in 3dMEPFM in AFNI). Other approaches based on Bayesian procedures, stability selection, or other less strict model selection criteria such as the Akaike Information Criterion (AIC), could also be investigated. In promoting a sparse solution the activity-inducing signal might show very few events in some gray matter voxels, with periods where no activity is found. We do not interpret this absence of activation as that the brain region does not have neuronal activity, but as that the voxel’s fMRI signal does not show sufficiently relevant hemodynamic response according to the assumed HRF model to be found by the algorithm using the BIC. Note that the BIC establishes an inherent trade-off between fitting perfectly the signal (i.e. sensitivity) and sparsity (i.e. specificity) in detecting events. Even though the rule of the BIC selects sparser estimates than for example the AIC, we observed that sparse hemodynamic events are sufficient to achieve a high correlation between the preprocessed denoised signals and the BOLD signals estimated with ME-SPFM, particularly in grey matter regions (see Figure 7). Even so, the sparsity assumption might not be appropriate for prolonged blocked stimuli or faster event-related paradigms. In such cases, the proposed ME-based deconvolution framework could be adapted to use other regularization terms, such as the L2-norm (i.e. ridge regression) to relax the sparsity assumption, or generalized total variation (Karahanoğlu et al., 2013) or synthesis-based regularization scheme including a first order difference / integrator operator in the model (Cherkaoui et al., 2019) to capture blockwise activity-inducing signals. Furthermore, the deconvolution algorithm could also incorporate spatial regularization terms (e.g. following Karahanoğlu et al., 2013) or formulate a multivariate version to account for the spatial correlation across voxels, and thus similarity of the estimates. We will investigate the implementation of these approaches in future studies. Importantly, the proposed ME-based deconvolution method can be modified straightforwardly to estimate both and ∆ρ(t) (i.e. also estimating time-varying changes in the net magnetization ∆S0(t)), even using different types of regularization for each component so as to adapt to the nature of their fluctuations (Caballero-Gaudes et al., 2018a; 2018b).
Another possible limitation of the PFM framework is that it uses a particular HRF shape as the model for deconvolution. To explore the robustness of our evaluations to a mismatch in the HRF shape, we also computed the spatial concordance with GLM analyses in a scenario where the ME-SPFM and 1E-SPFM algorithms used the canonical HRF (SPMG1) and the GLM analyses used the BLOCK model in AFNI. This evaluation did not change the patterns observed in Figures 4, 5 and 6 (data not shown), suggesting that ME-SPFM is robust to mismatches in the shape of the HRF similar to the observations obtained for 1E-SPFM (Caballero-Gaudes et al., 2013) and probably gained by the regularization terms of the deconvolution. Beyond that, since ME-SPFM is not locked to the timing of the trials, it can clearly account for variability in the onset of the response. It can also describe more complex patterns, such as the transient stimulus onset/offset responses reported in Gonzalez-Castillo et al. (2012) in terms of two hemodynamic events. Further flexibility in the HRF model can be incorporated by using multiple basis functions like the informed basis set with the canonical HRF and its temporal and dispersion derivatives, or the FLOBS approach in FSL and employing structured-sparse regularization terms for the deconvolution, such as the Group LASSO, to promote the fact that the activity-inducing signals of the different functions must exhibit activity simultaneously (see Gaudes et al., 2012 for a proof of concept with 1E-SPFM). Alternatively, a semi-blind deconvolution approach that alternates between the deconvolution of the activity-inducing signal and estimation of the HRF shape could also be explored (Cherkaoui et al., 2019).
In addition, the proposed discrete model operates at the sampling period of the fMRI acquisition (i.e. TR) and, as such, the deconvolution obtains as many estimates of the activity-inducing signal as number of scans (N). To allow the detection of events with greater temporal precision, the activity-inducing signal could also be estimated at a finer temporal resolution (i.e. where the number of estimates is n times larger than N) by modifying the convolution matrix H accordingly, which will not be Toeplitz, or performing the deconvolution in the Fourier domain. Relevantly, any mismatch between the assumed HRF shape and the HRF of the real BOLD fluctuations in the data will also interact with the temporal accuracy of the estimates. In that respect, considering more complex models that account for temporal shifts in the HRF model, such as the canonical HRF and the temporal and dispersion derivatives, could also help to increase the temporal precision of the deconvolution (Caballero-Gaudes et al., 2012).
The evaluations of spatial concordance in terms of dice coefficients, sensitivity and specificity were constrained to the activations resulting in positive BOLD signal changes. This decision was based on the fact that the HRF model is more firmly established for positive BOLD responses, rather than negative ones. In terms of mathematical modelling, it is important to highlight that coefficients in the activity-inducing signal with positive , i.e. generating negative BOLD response, can also be estimated to counteract mismatches in the HRF shape, for example to model a deeper post-stimulus undershoot than the one described by canonical HRF. As noted above, changing the HRF model did not alter the symmetry of the histograms of the activity-inducing signals across the entire brain depicted in Figure 8. If a different temporal HRF model was to be formulated for negative BOLD signal changes (see Goense et al. (2016), Sten et al. (2017) and references therein), the algorithm could be modified to use two different complementary HRF models for the positive and negative signal changes and establish non-positive (or non-negative) constraints in the estimates of the activity-inducing signals of each of the models, or even limiting the algorithm to capture the signal changes with a polarity of interest.
Apart from possible updates in the ME-SPFM algorithm, its performance will depend on the parameters and optimization of the multi-echo data acquisition. Similar to ME-ICA, the algorithm relies on a linear dependence of the BOLD signal with TE. Consequently, the quality of the deconvolution may improve if more echoes are acquired in the same range of TE by reducing the timing between echoes with more efficient k-space trajectories, e.g. with spirals. Additional echoes can also be acquired at longer TEs providing these echoes are not detrimental due to possible reduction in contrast-to-noise ratio (Gowland and Bowtell, 2007; Chiew and Graham, 2011), at the cost of reducing the temporal resolution. For these reasons, three or four equally spaced echoes have been typically acquired for standard multi-echo acquisitions (e.g., Kundu et al., 2012; Kundu et al., 2013; Kundu et al., 2017; Poser et al., 2006; Posse 2012; Power et al., 2018). The acquisition of two echoes have also shown good denoising performance, especially when the first echo signal is sampled as close to zero TE and, as such, it primarily captures fluctuations of the net magnetization with no BOLD weighting (Bright and Murphy, 2013; Buur et al., 2009). Nowadays, simultaneous multi-slice (a.k.a. multiband) multi-echo acquisitions can circumvent the trade-off between the number of echoes and the spatial/temporal resolution. The combination of multiecho with multiband acquisitions can be leveraged to improve the sensitivity and specificity relative to conventional multiecho approaches particularly at ultra-high 7T field strength (Boyacioğlu et al., 2015) and in subcortical nuclei of the basal ganglia (Puckett et al., 2018). It can also yield additional advantages such as removal of physiological noise, high frequency artefacts and slice-leakage components with MEICA (Olafsson et al., 2015). We hypothesize that ME-SPFM will also benefit from multiecho multiband acquisitions in a similar fashion, particularly if MEICA is part of the preprocessing. However, further systematic empirical evaluations are required. For example, further research should examine the inflow contribution to the hemodynamic events detected by ME-SPFM, and if its other formulations (Caballero-Gaudes et al., 2018a; 2018b), can disentangle these effects from the real BOLD contrast. In addition, the effect of other important acquisition parameters that change the signal- or contrast-to-noise ratio of the data and the performance of the algorithm, such as TR, the flip angle, in-plane acceleration, could also benefit from systematic evaluations.
Regardless of the HRF shape and the parameters of the acquisition, it is important to emphasize that, similar to other deconvolution algorithms assuming a linear convolution model to link the activity-inducing signal and hemodynamic signal changes (i.e. ), ME-SPFM cannot disentangle the mixture of active neuronal/metabolic processes and passive vascular processes that underlay the BOLD signal as long as they show the linear TE-dependence. Biophysical generative nonlinear models such as the Balloon model (Buxton et al., 1998; 2004; Friston et al., 2000) or the physiologically-informed dynamic causal model (P-DCM) (Havlicek et al., 2015) are required to distinguish them. Bayesian filtering algorithms have been proposed to invert the Balloon model and estimate the activity-inducing signal (Friston et al., 2008, 2010; Havlicek et al., 2011) (to our knowledge, no algorithm has been proposed for blind estimation of neuronal input and the model parameters for P-DCM). These approaches have been typically evaluated with regional time series due to the high number of model parameters to estimate. The inability of less parameterized deconvolution algorithms to disentangle the underlying neuronal and vascular processes might be a cost to pay in order to deconvolve the activity-inducing signal without prior knowledge of the timing of the BOLD responses at the voxelwise level, without the penalty of obtaining less accurate estimates at the regional level (Sreenivasan et al. 2015). More work is necessary to compare both types of algorithms with realistic simulations and a variety of experimental paradigms.
In this work, we used datasets with a known experimental paradigm for validation of ME-SPFM, confirming subject’s compliance with concurrent eye-tracking data. The usage of ME-SPFM in a completely blind scenario with no knowledge of the experimental conditions would be more challenging. This may require the combination of the deconvolution with reverse inference approaches that attempt to decode the subject’s engagement in a particular cognitive process from the activation maps (Poldrack, 2011; Poldrack and Yarkoni, 2016), for example by comparing the activation maps to a predefined set of meta-maps formed using the Activation Likelihood Estimation method of the BrainMap database (Tan et al., 2017). Decoding could be performed at the same rate as the TR of the acquisition, even though successive spatial maps can be averaged to reduce the level of noise in the activation maps and uncertainty in the decoding scores.
Finally, deconvolution algorithms can also be understood as a way of denoising the fMRI signal, like a filtering process matched to the shape of the HRF, wherein the denoised signal comprises the BOLD fluctuations triggered by the deconvolved activity-inducing signal. By some means, this interpretation is supported by the correlation maps of Figure 7 that illustrate a very high correlation between the ME-SPFM hemodynamic dataset without MEICA, and the preprocessed DN dataset (i.e. with MEICA denoising and optimal combination). A comprehensive comparison of ME-SPFM with other ME-based denoising approaches, such as dual-echo regression (Bright and Murphy, 2013) or MEICA-based approaches (Kundu et al., 2012; Power et al., 2018), for denoising the fMRI signal in resting-state and task-based paradigms is beyond the scope of this study. The application of ME-SPFM for denoising will likely involve refinement of the proposed methods (e.g. degree of sparsity, choice of regularization parameters) particularly for connectivity-based analyses.
In summary, in this paper we have introduced the algorithm of multi-echo sparse paradigm free mapping (ME-SPFM) for the deconvolution of BOLD fMRI data collected with ME acquisitions. The ME-SPFM method obtains estimates of the associated with single-trial BOLD events, outperforming our previous method for single-echo acquisitions (1E-SPFM), and exhibiting more concordance with the maps obtained with conventional GLM-based analyses despite being unaware of the timings of the events (i.e. blind detection). The new algorithm is available in AFNI as 3dMEPFM.
Supplementary Material
Supplementary material 1. Movie displaying (top left) a sequence with the icons for each experimental condition according the timing of the experimental paradigm, (top middle) the same sequence of icons but temporally blurred according to the HRF, and (top right) the histogram of -estimates for each time point. The middle maps display the maps of and the bottom maps display the maps of fitted signals, i.e. after convolution with the HRF, in synchrony with timings of the experimental paradigm.
Supplementary material 2. Table with the percentage of voxels with estimated with ME-SPFM and MEICA+ME-SPFM for all datasets, experimental conditions and corresponding trials.
ACKNOWLEDGEMENTS
We thank Prof. Penny A. Gowland for helpful discussion regarding the contents of this manuscript, as well as the anonymous reviewers for their valuable comments and feedback. This research was possible thanks to the support of the Spanish Ministry of Economy and Competitiveness through the Juan de la Cierva Fellowship (IJCI-2014-20821) and Ramon y Cajal Fellowship (RYC-2017-21845), the Spanish State Research Agency through the BCBL “Severo Ochoa” excellence accreditation (SEV-2015-490), the Basque Government through the BERC 2018–2021 program, the National Institute of Mental Health Intramural Research Program (NIH clinical protocol number , protocol ID 93-M-0170, Annual report ZIAMH002783-16), the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 713673, and a fellowship from La Caixa Foundation (ID 100010434) (fellowship code LCF/BQ/IN17/11620063). Portions of this study used the high-performance computational capabilities of the NIH High Performance Cluster (Biowulf) at the National Institutes Health, Bethesda, MD (http://hpc.nih.gov).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Bandettini PA, Wong EC, Jesmanowicz A, Hinks RS, Hyde JS, 1994. Spin-echo and gradient-echo epi of human brain activation using bold contrast: A comparative study at 1.5 T. NMR Biomed 7, 12–20. 10.1002/nbm.1940070104 [DOI] [PubMed] [Google Scholar]
- Blockley NP, Griffeth VEM, Simon AB, Buxton RB, 2013. A review of calibrated blood oxygenation level-dependent (BOLD) methods for the measurement of task-induced changes in brain oxygen metabolism. NMR Biomed 26, 987–1003. 10.1002/nbm.2847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyacioğlu R, Schulz J, Koopmans PJ, Barth M, Norris DG, 2015. Improved sensitivity and specificity for resting state and task fMRI with multiband multi-echo EPI compared to multi-echo EPI at 7 T. Neuroimage 119, 352–361. 10.1016/j.neuroimage.2015.06.089 [DOI] [PubMed] [Google Scholar]
- Bright MG, Murphy K, 2013. Removing motion and physiological artifacts from intrinsic BOLD fluctuations using short echo data. Neuroimage 64, 526–537. 10.1016/j.neuroimage.2012.09.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Bandettini PA, O’Craven KM, Savoy RL, Petersen SE, Raichle ME, Rosen BR, 1996. Detection of cortical activation during averaged single trials of a cognitive task using functional magnetic resonance imaging. Proc. Natl. Acad. Sci 93, 14878–14883. 10.1073/pnas.93.25.14878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush K, Cisler J, 2013. Decoding neural events from fMRI BOLD signal: A comparison of existing approaches and development of a new algorithm. Magn. Reson. Imaging 31, 976–989. 10.1016/j.mri.2013.03.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush K, Cisler J, Bian J, Hazaroglu G, Hazaroglu O, Kilts C, 2015. Improving the precision of fMRI BOLD signal deconvolution with implications for connectivity analysis. Magn. Reson. Imaging 33, 1314–1323. 10.1016/j.mri.2015.07.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buur PF, Poser BA, Norris DG, 2009. A dual echo approach to removing motion artefacts in fMRI time series. NMR Biomed 22, 551–560. 10.1002/nbm.1371 [DOI] [PubMed] [Google Scholar]
- Buxton RB, Uludağ K, Dubowitz DJ, Liu TT, 2004. Modeling the hemodynamic response to brain activation. Neuroimage 23, S220–S233. 10.1016/j.neuroimage.2004.07.013 [DOI] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR, 1998. Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magn. Reson. Med 39, 855–864. 10.1002/mrm.1910390602 [DOI] [PubMed] [Google Scholar]
- Caballero-Gaudes C, Moia S, Bandettini PA, Gonzalez-Castillo J, 2018a. Quantitative Deconvolution of fMRI Data with Multi-echo Sparse Paradigm Free Mapping, in: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) Springer, Cham, pp. 311–319. 10.1007/978-3-030-00931-1_36 [DOI] [Google Scholar]
- Caballero-Gaudes C, Reynolds RC, 2017. Methods for cleaning the BOLD fMRI signal. Neuroimage 154, 128–149. 10.1016/j.neuroimage.2016.12.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero Gaudes C, Bandettini PA, Gonzalez-Castillo J, 2018b. A temporal deconvolution algorithm for multiecho functional MRI, in: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). pp. 608–611. 10.1109/ISBI.2018.8363649 [DOI] [Google Scholar]
- Caballero Gaudes C, Petridou N, Francis ST, Dryden IL, Gowland PA, 2013. Paradigm free mapping with sparse regression automatically detects single-trial functional magnetic resonance imaging blood oxygenation level dependent responses. Hum. Brain Mapp 34, 501–518. 10.1002/hbm.21452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaari L, Vincent T, Forbes F, Dojat M, Ciuciu P, 2013. Fast joint detection-estimation of evoked brain activity in event-related fMRI using a variational approach. IEEE Trans. Med. Imaging 32, 821–837. 10.1109/TMI.2012.2225636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen SS, Donoho DL, Saunders MA, 2001. Atomic Decomposition by Basis Pursuit. SIAM Rev 43, 129–159. 10.1137/S003614450037906X [DOI] [Google Scholar]
- Cherkaoui H, Moreau T, Halimi A, Ciuciu P, 2019. Sparsity-based Blind Deconvolution of Neural Activation Signal in FMRI, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). pp. 1323–1327. 10.1109/ICASSP.2019.8683358 [DOI] [Google Scholar]
- Chiew M, Graham SJ, 2011. BOLD Contrast and Noise Characteristics of Densely Sampled Multi-Echo fMRI Data. IEEE Trans. Med. Imaging 30, 1691–1703. 10.1109/TMI.2011.2143424 [DOI] [PubMed] [Google Scholar]
- Ciuciu P, Poline JB, Marrelec G, Idier J, Pallier C, Benali H, 2003. Unsupervised robust nonparametric estimation of the hemodynamic response function for any fMRI experiment. IEEE Trans. Med. Imaging 22, 1235–1251. 10.1109/TMI.2003.817759 [DOI] [PubMed] [Google Scholar]
- Croal PL, Driver ID, Francis ST, Gowland PA, 2017. Field strength dependence of grey matter R2*on venous oxygenation. Neuroimage 146, 327–332. 10.1016/j.neuroimage.2016.10.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devor A, Tian P, Nishimura N, Teng IC, Hillman EMC, Narayanan SN, Ulbert I, Boas DA, Kleinfeld D, Dale AM, 2007. Suppressed Neuronal Activity and Concurrent Arteriolar Vasoconstriction May Explain Negative Blood Oxygenation Level-Dependent Signal. J. Neurosci 27, 4452–4459. 10.1523/JNEUROSCI.0134-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixon ML, De La Vega A, Mills C, Andrews-Hanna J, Spreng RN, Cole MW, Christoff K, 2018. Heterogeneity within the frontoparietal control network and its relationship to the default and dorsal attention networks. Proc. Natl. Acad. Sci 115, E1598–E1607. 10.1073/pnas.1715766115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donahue MJ, Hoogduin H, van Zijl PCM, Jezzard P, Luijten PR, Hendrikse J, 2011. Blood oxygenation level-dependent (BOLD) total and extravascular signal changes and ΔR2* in human visual cortex at 1.5, 3.0 and 7.0 T. NMR Biomed 24, 25–34. 10.1002/nbm.1552 [DOI] [PubMed] [Google Scholar]
- Duong TQ, Yacoub E, Adriany G, Hu X, Kim S, 2003. Microvascular BOLD Contribution at 4 and 7 T in the Human Brain : Gradient-Echo and Spin-Echo fMRI With Suppression of Blood Effects 1027, 1019–1027. 10.1002/mrm.10472 [DOI] [PubMed] [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R, 2004. Least angle regression. Ann. Stat 32, 407–499. 10.1214/009053604000000067 [DOI] [Google Scholar]
- Evans JW, Kundu P, Horovitz SG, Bandettini PA, 2015. Separating slow BOLD from non-BOLD baseline drifts using multi-echo fMRI. Neuroimage 105, 189–197. 10.1016/j.neuroimage.2014.10.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farouj Y, Karahanoglu FI, Van De Ville D, 2017. Regularized spatiotemporal deconvolution of fMRI data using gray-matter constrained total variation, in: 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017). IEEE, pp. 472–475. 10.1109/ISBI.2017.7950563 [DOI] [Google Scholar]
- Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME, 2006. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc. Natl. Acad. Sci 103, 10046–10051. 10.1073/pnas.0604187103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME, 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci 102, 9673–9678. 10.1073/pnas.0504136102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Stephan K, Li B, Daunizeau J, 2010. Generalised filtering. Math. Probl. Eng. 2010 10.1155/2010/621670 [DOI]
- Friston KJ, Mechelli A, Turner R, Price CJ, 2000. Nonlinear responses in fMRI: The balloon model, Volterra kernels, and other hemodynamics. Neuroimage 12, 466–477. 10.1006/nimg.2000.0630 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Trujillo-Barreto N, Daunizeau J, 2008. DEM: A variational treatment of dynamic systems. Neuroimage 41, 849–885. 10.1016/j.neuroimage.2008.02.054 [DOI] [PubMed] [Google Scholar]
- Gaudes CC, Karahanoǧlu FI, Lazeyras F, Van De Ville D, 2012. Structured sparse deconvolution for paradigm free mapping of functional MRI data, in: Proceedings - International Symposium on Biomedical Imaging. IEEE, pp. 322–325. 10.1109/ISBI.2012.6235549 [DOI] [Google Scholar]
- Gaudes CC, Petridou N, Dryden IL, Bai L, Francis ST, Gowland PA, 2011. Detection and characterization of single-trial fMRI bold responses: Paradigm free mapping. Hum. Brain Mapp 32 10.1002/hbm.21116 [DOI] [PMC free article] [PubMed]
- Gitelman DR, Penny WD, Ashburner J, Friston KJ, 2003. Modeling regional and psychophysiologic interactions in fMRI: The importance of hemodynamic deconvolution. Neuroimage 19, 200–207. 10.1016/S1053-8119(03)00058-2 [DOI] [PubMed] [Google Scholar]
- Goense J, Bohraus Y, Logothetis NK, 2016. fMRI at High Spatial Resolution: Implications for BOLD-Models. Front. Comput. Neurosci 10, 1–13. 10.3389/fncom.2016.00066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Castillo J, Panwar P, Buchanan LC, Caballero-Gaudes C, Handwerker DA, Jangraw DC, Zachariou V, Inati S, Roopchansingh V, Derbyshire JA, Bandettini PA, 2016. Evaluation of multi-echo ICA denoising for task based fMRI studies: Block designs, rapid event-related designs, and cardiac-gated fMRI. Neuroimage 141, 452–468. 10.1016/j.neuroimage.2016.07.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Castillo J, Saad ZS, Handwerker DA, Inati SJ, Brenowitz N, Bandettini PA, 2012. Whole-brain, time-locked activation with simple tasks revealed using massive averaging and model-free analysis. Proc. Natl. Acad. Sci. U. S. A 109, 5487–92. 10.1073/pnas.1121049109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte C, Nielsen F.Å. a, Hansen LK, 2000. Modeling the haemodynamic response in fMRI using smooth FIR filters. IEEE Trans. Med. Imaging 19, 1188–201. 10.1109/42.897811 [DOI] [PubMed] [Google Scholar]
- Gowland PA, Bowtell R, 2007. Theoretical optimization of multi-echo fMRI data acquisition. Phys. Med. Biol 52, 1801–1813. 10.1088/0031-9155/52/7/003 [DOI] [PubMed] [Google Scholar]
- Harel N, Lee SP, Nagaoka T, Kim DS, Kim SG, 2002. Origin of negative blood oxygenation level-dependent fMRI signals. J. Cereb. Blood Flow Metab 22, 908–917. 10.1097/00004647-200208000-00002 [DOI] [PubMed] [Google Scholar]
- Havlicek M, Friston KJ, Jan J, Brazdil M, Calhoun VD, 2011. Dynamic modeling of neuronal responses in fMRI using cubature Kalman filtering. Neuroimage 56, 2109–2128. 10.1016/j.neuroimage.2011.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havlicek M, Ivanov D, Poser BA, Uludag K, 2017. Echo-time dependence of the BOLD response transients – A window into brain functional physiology. Neuroimage 159, 355–370. 10.1016/j.neuroimage.2017.07.034 [DOI] [PubMed] [Google Scholar]
- Havlicek M, Roebroeck A, Friston K, Gardumi A, Ivanov D, Uludag K, 2015. Physiologically informed dynamic causal modeling of fMRI data. Neuroimage 122, 355–372. 10.1016/j.neuroimage.2015.07.078 [DOI] [PubMed] [Google Scholar]
- Hernandez-Garcia L, Ulfarsson MO, 2011. Neuronal event detection in fMRI time series using iterative deconvolution techniques. Magn. Reson. Imaging 29, 353–364. 10.1016/j.mri.2010.10.012 [DOI] [PubMed] [Google Scholar]
- Ing A, Schwarzbauer C, 2012. A dual echo approach to motion correction for functional connectivity studies. Neuroimage 63, 1487–1497. 10.1016/j.neuroimage.2012.07.042 [DOI] [PubMed] [Google Scholar]
- Kang D, Sung Y-W, Shioiri S, 2018. Estimation of physiological sources of nonlinearity in blood oxygenation level-dependent contrast signals. Magn. Reson. Imaging 46, 121–129. 10.1016/j.mri.2017.10.017 [DOI] [PubMed] [Google Scholar]
- Karahanoǧlu FI, Caballero-Gaudes C, Lazeyras F, Van De Ville D, 2013. Total activation: FMRI deconvolution through spatio-temporal regularization. Neuroimage 73, 121–134. 10.1016/j.neuroimage.2013.01.067 [DOI] [PubMed] [Google Scholar]
- Karahanoğlu FI, Van De Ville D, 2017. Dynamics of Large-Scale fMRI Networks: Deconstruct Brain Activity to Build Better Models of Brain Function. Curr. Opin. Biomed. Eng 28–36. 10.1016/j.cobme.2017.09.008 [DOI]
- Keilholz SD, Caballero-Gaudes C, Bandettini P, Deco G, Calhoun VD, 2017. Time-resolved resting state fMRI analysis: current status, challenges, and new directions. Brain Connect 7, brain.2017.0543 10.1089/brain.2017.0543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalidov I, Fadili J, Lazeyras F, Van De Ville D, Unser M, 2011. Activelets: Wavelets for sparse representation of hemodynamic responses. Signal Processing 91, 2810–2821. 10.1016/j.sigpro.2011.03.008 [DOI] [Google Scholar]
- Krüger G, Glover GH, 2001. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn. Reson. Med 46, 631–637. 10.1002/mrm.1240 [DOI] [PubMed] [Google Scholar]
- Kundu P, Brenowitz ND, Voon V, Worbe Y, Vértes PE, Inati SJ, Saad ZS, 2013. Integrated strategy for improving functional connectivity mapping using multiecho fMRI 110 10.1073/pnas.1301725110 [DOI] [PMC free article] [PubMed]
- Kundu P, Inati SJ, Evans JW, Luh WM, Bandettini PA, 2012. Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. Neuroimage 60, 1759–1770. 10.1016/j.neuroimage.2011.12.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Voon V, Balchandani P, Lombardo MV, Poser BA, Bandettini PA, 2017. Multi-echo fMRI: A review of applications in fMRI denoising and analysis of BOLD signals. Neuroimage 154, 59–80. 10.1016/j.neuroimage.2017.03.033 [DOI] [PubMed] [Google Scholar]
- LaConte SM, Peltier SJ, Hu XP, 2007. Real-time fMRI using brain-state classification. Hum. Brain Mapp 28, 1033–1044. 10.1002/hbm.20326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Zhang N, Chang C, Duyn JH, 2018. Co-activation patterns in resting-state fMRI signals. Neuroimage 180, 485–494. 10.1016/j.neuroimage.2018.01.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLaren DG, Ries ML, Xu G, Johnson SC, 2012. A generalized form of context-dependent psychophysiological interactions (gPPI): A comparison to standard approaches. Neuroimage 61, 1277–1286. 10.1016/j.neuroimage.2012.03.068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N, 2007. Relaxed Lasso. Comput. Stat. Data Anal 52, 374–393. 10.1016/j.csda.2006.12.019 [DOI] [Google Scholar]
- Menon RS, Ogawa S, Tank DW, U??urbil, K, 1993. 4 Tesla gradient recalled echo characteristics of photic stimulation-induced signal changes in the human primary visual cortex. Magn. Reson. Med 30, 380–386. 10.1002/mrm.1910300317 [DOI] [PubMed] [Google Scholar]
- Olafsson V, Kundu P, Wong EC, Bandettini PA, Liu TT, 2015. Enhanced identification of BOLD-like components with multi-echo simultaneous multi-slice (MESMS) fMRI and multi-echo ICA. Neuroimage 112, 43–51. 10.1016/j.neuroimage.2015.02.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JW, 2009. Generating stimuli for neuroscience using PsychoPy. Front. Neuroinform 2, 1–8. 10.3389/neuro.11.010.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peltier SJ, Noll DC, 2002. T2* Dependence of Low Frequency Functional Connectivity. Neuroimage 16, 985–992. 10.1006/nimg.2002.1141 [DOI] [PubMed] [Google Scholar]
- Petridou N, Gaudes CC, Dryden IL, Francis ST, Gowland PA, 2013. Periods of rest in fMRI contain individual spontaneous events which are related to slowly fluctuating spontaneous activity. Hum. Brain Mapp 34, 1319–1329. 10.1002/hbm.21513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, 2011. Inferring Mental States from Neuroimaging Data: From Reverse Inference to Large-Scale Decoding. Neuron 72, 692–697. 10.1016/j.neuron.2011.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Yarkoni T, 2016. From Brain Maps to Cognitive Ontologies: Informatics and the Search for Mental Structure. Annu. Rev. Psychol 67, 587–612. 10.1146/annurev-psych-122414-033729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poser BA, Norris DG, 2009. Investigating the benefits of multi-echo EPI for fMRI at 7 T. Neuroimage 45, 1162–1172. 10.1016/j.neuroimage.2009.01.007 [DOI] [PubMed] [Google Scholar]
- Poser BA, Versluis MJ, Hoogduin JM, Norris DG, 2006. BOLD contrast sensitivity enhancement and artifact reduction with multiecho EPI: Parallel-acquired inhomogeneity-desensitized fMRI. Magn. Reson. Med 55, 1227–1235. 10.1002/mrm.20900 [DOI] [PubMed] [Google Scholar]
- Posse S, 2012. Multi-echo acquisition. Neuroimage 10.1016/j.neuroimage.2011.10.057 [DOI] [PMC free article] [PubMed]
- Posse S, Wiese S, Gembris D, Mathiak K, Kessler C, Grosse-Ruyken M-L, Elghahwagi B, Richards T, Dager SR, Kiselev VG, 1999. Enhancement of BOLD-contrast sensitivity by single-shot multi-echo functional MR imaging. Magn. Reson. Med 42, 87–97. [DOI] [PubMed] [Google Scholar]
- Power JD, Plitt M, Gotts SJ, Kundu P, Voon V, Bandettini PA, Martin A, 2018. Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proc. Natl. Acad. Sci 201720985 10.1073/pnas.1720985115 [DOI] [PMC free article] [PubMed]
- Puckett AM, Bollmann S, Poser BA, Palmer J, Barth M, Cunnington R, 2018. Using multi-echo simultaneous multi-slice (SMS) EPI to improve functional MRI of the subcortical nuclei of the basal ganglia at ultra-high field (7T). Neuroimage 172, 886–895. 10.1016/j.neuroimage.2017.12.005 [DOI] [PubMed] [Google Scholar]
- Raichle ME, 2015. The Brain’s Default Mode Network. Annu. Rev. Neurosci 38, 433–447. 10.1146/annurev-neuro-071013-014030 [DOI] [PubMed] [Google Scholar]
- Rangaprakash D, Wu GR, Marinazzo D, Hu X, Deshpande G, 2018. Hemodynamic response function (HRF) variability confounds resting-state fMRI functional connectivity. Magn. Reson. Med 80, 1697–1713. 10.1002/mrm.27146 [DOI] [PubMed] [Google Scholar]
- Riera JJ, Watanabe J, Kazuki I, Naoki M, Aubert E, Ozaki T, Kawashima R, 2004. A state-space model of the hemodynamic approach: Nonlinear filtering of BOLD signals. Neuroimage 21, 547–567. 10.1016/j.neuroimage.2003.09.052 [DOI] [PubMed] [Google Scholar]
- Shmuel A, Augath M, Oeltermann A, Logothetis NK, 2006. Negative functional MRI response correlates with decreases in neuronal activity in monkey visual area V1. Nat. Neurosci 9, 569–577. 10.1038/nn1675 [DOI] [PubMed] [Google Scholar]
- Speck O, Ernst T, Chang L, 2001. Biexponential modeling of multigradient-echo MRI data of the brain. Magn. Reson. Med 45, 1116–1121. 10.1002/mrm.1147 [DOI] [PubMed] [Google Scholar]
- Sreenivasan KR, Havlicek M, Deshpande G, 2015. Nonparametric hemodynamic deconvolution of fMRI using homomorphic filtering. IEEE Trans. Med. Imaging 34, 1155–1163. 10.1109/TMI.2014.2379914 [DOI] [PubMed] [Google Scholar]
- Sten S, Lundengård K, Witt ST, Cedersund G, Elinder F, Engström M, 2017. Neural inhibition can explain negative BOLD responses: A mechanistic modelling and fMRI study. Neuroimage 158, 219–231. 10.1016/j.neuroimage.2017.07.002 [DOI] [PubMed] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR, 2012. Criticality in Large-Scale Brain fMRI Dynamics Unveiled by a Novel Point Process Analysis. Front. Physiol 3, 1–12. 10.3389/fphys.2012.00015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Siniatchkin M, Laufs H, Chialvo DR, 2016. The Voxel-Wise Functional Connectome Can Be Efficiently Derived from Co-activations in a Sparse Spatio-Temporal Point-Process. Front. Neurosci 10, 1–13. 10.3389/fnins.2016.00381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan FM, Caballero-Gaudes C, Mullinger KJ, Cho S-Y, Zhang Y, Dryden IL, Francis ST, Gowland PA, 2017. Decoding fMRI events in sensorimotor motor network using sparse paradigm free mapping and activation likelihood estimates. Hum. Brain Mapp 38, 5778–5794. 10.1002/hbm.23767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R, 1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Statistical Methodol 58, 267–288. [Google Scholar]
- Tibshirani RJ, Taylor J, 2012. Degrees of freedom in lasso problems. Ann. Stat 40, 1198–1232. 10.1214/12-AOS1003 [DOI] [Google Scholar]
- Uludağ K, Müller-Bierl B, Uğurbil K, 2009. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage 48, 150–165. 10.1016/j.neuroimage.2009.05.051 [DOI] [PubMed] [Google Scholar]
- van der Zwaag W, Francis S, Head K, Peters A, Gowland P, Morris P, Bowtell R, 2009. fMRI at 1.5, 3 and 7 T: Characterising BOLD signal changes. Neuroimage 47, 1425–1434. 10.1016/j.neuroimage.2009.05.015 [DOI] [PubMed] [Google Scholar]
- Wu CW, Gu H, Zou Q, Lu H, Stein EA, Yang Y, 2012. TE-dependent spatial and spectral specificity of functional connectivity. Neuroimage 59, 3075–3084. 10.1016/j.neuroimage.2011.11.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G-R, Liao W, Stramaglia S, Ding J-R, Chen H, Marinazzo D, 2013. A blind deconvolution approach to recover effective connectivity brain networks from resting state fMRI data. Med. Image Anal 17, 365–374. 10.1016/j.media.2013.01.003 [DOI] [PubMed] [Google Scholar]
- Zou H, Hastie T, Tibshirani R, 2007. On the “degrees of freedom” of the lasso. Ann. Stat 35, 2173–2192. 10.1214/009053607000000127 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material 1. Movie displaying (top left) a sequence with the icons for each experimental condition according the timing of the experimental paradigm, (top middle) the same sequence of icons but temporally blurred according to the HRF, and (top right) the histogram of -estimates for each time point. The middle maps display the maps of and the bottom maps display the maps of fitted signals, i.e. after convolution with the HRF, in synchrony with timings of the experimental paradigm.
Supplementary material 2. Table with the percentage of voxels with estimated with ME-SPFM and MEICA+ME-SPFM for all datasets, experimental conditions and corresponding trials.