Evaluation and Intercomparison of Five North American Dry Deposition Algorithms at a Mixed Forest Site

Abstract

To quantify differences between dry deposition algorithms commonly used in North America, five models were selected to calculate dry deposition velocity (V_d) for O₃ and SO₂ over a temperate mixed forest in southern Ontario, Canada, where a 5-year flux database had previously been developed. The models performed better in summer than in winter with correlation coefficients for hourly V_d between models and measurements being approximately 0.6 and 0.3, respectively. Differences in mean V_d values between models were on the order of a factor of 2 in both summer and winter. All models produced lower V_d values than the measurements of O₃ in summer and SO₂ in summer and winter, although the measured V_d may be biased. There was not a consistent tendency in the models to overpredict or underpredict for O₃ in winter. Several models produced magnitudes of the diel variation of V_d (O₃) comparable to the measurements, while all models produced slightly smaller diel variations than the measurements of V_d (SO₂) in summer. A few models produced larger diel variations than the measurements of V_d for O₃ and SO₂ in winter. Model differences were mainly due to different surface resistance parameterizations for stomatal and nonstomatal uptake pathways, while differences in aerodynamic and quasi-laminar resistances played only a minor role. It is recommended to use ensemble modeling results for ecosystem impact assessment studies, which provides mean values of all the used models and thus can avoid too much overestimations or underestimations.

1. Introduction

The lifetime of atmospheric pollutants is governed by several processes including emission, transport, transformation, and deposition (Seinfeld & Pandis, 2006). Deposition is the only process that ultimately removes pollutants from the atmosphere and controls pollutants input into ecosystems. Deposition can be wet or dry; the relative importance of each depends on the pollutant species, underlying surface, and precipitation amount. On a regional or global scale, the amounts of dry and wet deposition are roughly equally important but can vary considerably on a local scale (Lamarque et al., 2013; Liu et al., 2017; Vet et al., 2014).

At monitoring sites for atmospheric deposition studies, wet deposition is typically monitored through the collection of precipitation and subsequent laboratory analysis of precipitation composition (Amodio et al., 2014). Directly measuring dry deposition is expensive and technically challenging (Mohan, 2016; Wright et al., 2016); thus, ambient concentrations of pollutants of interest are measured for subsequent dry deposition estimation using the inferential method (e.g., Ban et al., 2016; Baumgardner et al., 2002; Flechard et al., 2011; Zhang et al., 2016). However, in chemical transport models (CTMs), both dry and wet deposition processes are parameterized and are mostly semiempirical or empirical algorithms (Gong et al., 2011; Pleim & Ran, 2011; Vivanco et al., 2017).

Uncertainties in wet deposition measurements are considered to be small, ranging from 10% to less than a factor of 2 depending on the precipitation concentration level (Otoshi et al., 2001; Sirois & Vet, 1999). However, uncertainties in dry deposition measurements as well as in the dry and wet deposition fluxes estimated using empirical algorithms are considerably higher, as seen from model intercomparison studies on deposition budgets (Hardacre et al., 2015; Vivanco et al., 2017). Dry deposition estimated using different dry deposition algorithms can differ by up to a factor of 2 for monthly to annual average values for ozone, sulfur, or nitrogen species (Flechard et al., 2011; Schwede et al., 2011; Wu et al., 2011, 2012). These chemical species are among the most frequently studied, supported by a relatively rich set of field flux measurements (Fowler et al., 2009). However, dry deposition estimates for these species still have large uncertainties due to the many chemical, biological, and meteorological factors affecting dry deposition processes. Uncertainties for other chemical species are even larger (Fowler et al., 2009; Hicks et al., 2016; Mohan, 2016; Wesely & Hicks, 2000; Wright et al., 2016).

To identify the causes of the large discrepancies in the calculated dry deposition fluxes between two monitoring networks (Canadian Air and Precipitation Monitoring Network [CAPMoN] in Canada and Clean Air Status and Trends Network [CASTNET] in the United States), an intercomparison project was initiated about a decade ago. In the first stage of the project, Schwede et al. (2011) compared the estimated deposition fluxes at a colocated site (Egbert, Ontario) and found that the observed concentrations were very similar between the two networks while large differences existed in the model-derived V_d. Considering that most dry deposition algorithms have been evaluated against measurements conducted over short time periods ranging from several days to weeks, a long-term monitoring of O₃ and SO₂ concentration gradient data at a temperate mixed forest (Borden, 15 km northwest of Egbert) was then initiated, aiming to provide long-term flux data for further model evaluation. The present study is a continuation of the above-mentioned intercomparison project to further evaluate the two dry deposition algorithms used in the two networks using the recently generated 5-year flux data of O₃ and SO₂ (Wu et al., 2016), but we chose to expand the evaluation to include three additional community dry deposition algorithms widely used in North America in order to assess the uncertainties in and discrepancies between these algorithms. The magnitudes of the uncertainties of the modeled dry deposition velocities (and fluxes) were quantified, the dominant factors causing the differences were identified, and the ensemble modeling results were examined. Knowledge gained from the study will help the scientific community improve the capability of these models for better application to monitoring networks and CTMs, the results of which are used for developing air quality management strategies and regulatory policies. The dry deposition algorithms are briefly described in section 2, the measurement data in section 3, model evaluation and intercomparison results in section 4, and major conclusions and recommendations in section 5.

2. Brief Description of the Five Dry Deposition Algorithms

Five dry deposition algorithms commonly used in air quality models and national monitoring networks in North America were selected for investigation. These include (1) the Zhang et al. (2003) scheme used in the CAPMoN and several Canadian and American air quality models (referred to as ZHANG below), (2) the Noah land surface model coupled with a photosynthesis-based Gas Exchange Model described in Niyogi et al. (2009) and Wu et al. (2012) (referred to as Noah-GEM below), (3) the dry deposition module of the Community Multiscale Air Quality (CMAQ) model version 5.0.2 described in Pleim and Ran (2011) (referred to as C5DRY below), (4) the dry deposition module of Weather Research and Forecasting model coupled with Chemistry (WRF-Chem) that employs the widely used Wesely (1989) scheme (referred to as WESELY below), and (5) the multilayer model used in the United States CASTNET based on Meyers et al. (1998; referred to as MLM below). These algorithms are briefly described here; detailed descriptions can be found in the references mentioned above.

All the five dry deposition algorithms are based on the resistance-analogy approach for calculating dry deposition velocity (V_d), although with substantial differences in their formulations (Table 1). MLM derives its aerodynamic (R_a) and quasi-laminar (R_b) resistance from routinely measured wind speed and direction, and the other four algorithms calculate R_a and R_b as a function of surface properties, such as surface roughness (z₀), friction velocity (u_*), and atmospheric stability (z/L) using Monin-Obukhov similarity theory (MOST). In MLM, the entire canopy is divided into multiple layers; resistance is first calculated for each layer before being integrated into canopy-scale resistance (R_c). In the other four algorithms, a single-canopy layer is used for calculating R_c. R_c is commonly split into two parallel paths, nonstomatal and stomatal resistance. For non-stomatal uptake, prescribed land use-dependent constants, adjusted by surface wetness, coldness, leaf area index (LAI), and humidity, are used in the models. ZHANG and Noah-GEM also includes the effect of u_* on nonstomatal resistance (see Table 1).

Table 1.

Formulation Comparisons Across the Five Dry Deposition Models

	ZHANG	Noah-GEM	C5DRY	WESELY	MLM
Modeling framework	Vd(z) = (Ra(z) + Rb + Rc)−1 and $\frac{1}{R_c}=\frac{1-W_{\mathrm{st}}}{R_s+R_m}+\frac{1}{R_{\mathrm{ns}}}$ $\frac{1}{R_{\mathrm{ns}}}=\frac{1}{R_{\mathrm{cut}}}+\frac{1}{R_{\mathrm{ac}}+R_g}$				$V_{\text{d}}={\left(R_a+\frac{1}{{\int }_0^{h_c}S(z)dz+\frac{1}{R_{\mathrm{ac}}+R_g}}\right)}^{-1}$ and $S\left(z\right)=\mathrm{LAI}\left(z\right)\left(\frac{\begin{array}{l}1\end{array}}{r_s\left(z\right)+r_b\left(z\right)+r_m}+\frac{2}{r_b\left(z\right)+r_{\mathrm{cut}}}\right)$
Aerodynamic resistance (Ra)	For stable conditions, $R_a=\frac{0.74\ln \left(\frac{z}{z_0}\right)+4.7\frac{z}{L}}{\kappa u_{*}}$ For unstable conditions, $R_a=\frac{0.74}{\kappa u_{*}}$ $\left[\ln \left(\frac{z}{z_0}\right)-2\ln \left(\frac{\sqrt{1-9\frac{z}{L}}+1}{2}\right)\right]$	$R_a=\frac{\ln \left(\frac{z}{z_0}\right)+{\psi }_h\left(\frac{z}{L}\right)-{\psi }_h\left(\frac{z_0}{L}\right)}{k{u}_{*}}$ For stable conditions, ${\psi }_h=5\frac{z}{L}$ For unstable conditions, ${\psi }_h=-2\ln \left(\frac{\sqrt{1-16\frac{z}{L}}+1}{2}\right)$	$R_a=\frac{0.95\left[\ln \left(\frac{z}{z_0}\right)+{\psi }_h\left(\frac{z}{L}\right)-{\psi }_h\left(\frac{z_0}{L}\right)\right]}{k{u}_{*}}$ For stable conditions, ${\psi }_h=5\frac{z}{L}$ For unstable conditions, ${\psi }_h=-2\ln \left(\frac{\sqrt{1-16\frac{z}{L}}+1}{2}\right)$	For stable conditions, $R_a=\frac{0.74\ln \left(\frac{z}{z_0}\right)+4.7\frac{z-z_0}{L}}{k{u}_{*}}$ For unstable conditions, $R_a=\frac{0.74}{\kappa u_{*}}$ $\left\{\ln \left[\frac{\sqrt{1-9\frac{z}{L}}-1}{\sqrt{1-9\frac{z}{L}}+1}\right]-\ln \left[\frac{\sqrt{1-9\frac{z_0}{L}}-1}{\sqrt{1-9\frac{z_0}{L}}+1}\right]\right\}$	For stable conditions, $R_a=\frac{4}{u{\sigma }_{\theta }^2}$ For unstable conditions, $R_a=\frac{9}{u{\sigma }_{\theta }^2}$
Quasi-laminar sublayer resistance (Rb)	Rb = 2(κu*)−1(Dθ/Dc)2/3		Rb = 2(κu*)−1(SC/Pr)2/3		$r_b(z)=\alpha {\left(\frac{\delta }{u}\right)}^{0.5}$
Stomatal resistance (Rs)a	$R_s=\frac{R_s(\mathrm{PAR})}{f_T{f}_{\mathrm{vpd}}{f}_w}$ $\frac{1}{R_s(\mathrm{PAR})}=\frac{{\mathrm{LAI}}_{\mathrm{sun}}}{r_s({\mathrm{PAR}}_{\mathrm{sun}})}+\frac{{\mathrm{LAI}}_{\mathrm{shade}}}{r_s({\mathrm{PAR}}_{\mathrm{shade}})}$ $r_s(\mathrm{PAR})=\frac{r_{s,\min }}{f_{\mathrm{PAR}}}$	$R_s={\left[\mathrm{LAI}(m\frac{A_n{h}_s}{C_s}P+b)\right]}^{-1}$	$R_s=\frac{r_{s,\min }}{{\mathrm{LAI}f}_{\mathrm{PAR}}{f}_T{f}_{\mathrm{vpd}}{f}_w}$	$R_s=R_{s,\min }\left\{1+\frac{1}{{[200(R_G+0.1)]}^2}\right\}\frac{400}{T_s(40-T_s)}$	$r_s(z)=\frac{r_{s,\min }}{f_{\mathrm{PAR}}{f}_T{f}_{\mathrm{vpd}}{f}_w}$
Cuticular resistance (Rcut)	For dry surface, $R_{\mathrm{cut}}=\frac{R_{\mathrm{cut}d0}}{e^{0.03RH}{\mathrm{LAI}}^{0.25}{u}_{*}}$ For wet surface, $R_{\mathrm{cut}}=\frac{R_{\mathrm{cut}w0}}{{\mathrm{LAI}}^{0.5}{u}_{*}}$		Prescribed values for dry and wet surfaces; Rcut,dry for O3 is adjusted if RH >70%: Rcut = Rcut, dry(1 − FRH) + Rcut, wet × FRH FRH = (RH − 70)/30	Prescribed values for dry and wet surfaces	Prescribed values for dry and wet surfaces
In-canopy aerodynamic resistance (Rac)	$R_{\mathrm{ac}}=\frac{R_{\mathrm{ac}0}{\mathrm{LAI}}^{0.25}}{{u_{*}}^2}$		$R_{\mathrm{ac}}=14\mathrm{LAI}\frac{h_c}{u_{*}}$	Prescribed values	$R_{\mathrm{ac}}={\left[h_{\mathrm{free}}+6.86\times {10}^{-6}\frac{1+2i_u}{L_c\ln (z/z_0)}{\mathrm{Re}}^{0.8}\right]}^{-1}$
Ground resistance (Rg)	Prescribed values for dry and wet surfaces; adjusted if frozen		Prescribed values for dry and wet surfaces; adjusted if frozen	Prescribed values for dry and wet surfaces; adjusted if frozen	Prescribed values for dry and wet surfaces; adjusted if frozen

Note. W_st = the fraction of stomatal blocking under wet conditions; R_m/r_m = the mesophyll resistance; z = reference height; z₀ = the roughness length for momentum; L = the Obukhov length; κ = the von Karman’s constant; u_* = the friction velocity; u = the mean wind speed; σ_θ = the standard deviation of the wind direction; D_θ = the thermal diffusivity; D_c = the molecular diffusivity of a specific gas; S_c = the Schmidt number; P_r = the Prandtl number for air; α = the constant depending on gas species; δ = the characteristic leaf dimension; f_PAR = the environmental stress function of radiation; f_T = the environmental stress function of temperature; f_vpd = the environmental stress function of humidity; f_w = the environmental stress function of leaf water potential; LAI_sun = the total sunlit leaf area indexes; LAI_shade = the total shaded leaf area indexes; PAR_sun = the photosynthetically active radiation (PAR) received by sunlit leaves; PAR_shade = PAR received by shaded leaves; r_s,min = the minimum leaf stomatal resistance for water vapor; R_s,min = the minimum canopy stomatal resistance for water vapor; A_n = net CO₂ assimilation/photosynthesis rate; h_s = the relative humidity (RH) fraction at the leaf surface, C_s = CO₂ partial pressure at the leaf surface; P = the atmospheric pressure; m = the slope obtained by linear regression analysis of data from gas exchange experiments; b = the intercept obtained by linear regression analysis of data from gas exchange experiments; R_G = the solar irradiation; T_s = surface air temperature; R_cutd0 = the reference value for dry cuticle resistance; R_cutw0 = the reference value for wet cuticle resistance; R_cut,dry = dry cuticle resistance; R_cut,wet = wet cuticle resistance; R_ac0 = the reference value for in-canopy aerodynamic resistance; h_free = the free convection offset; i_u = the turbulence intensity; L_c = a within canopy length scale; R_e = the local Reynolds number.

^aStomatal resistance for a specific gas x (R_s,x) is scaled by the ratio of molecular diffusivities (D) between the gas of interest and water vapor as follows: R_s,x = R_sD_H2O/D_x.

For stomatal uptake (R_s), WESELY, Noah-GEM, and C5DRY employ a one big-leaf approach, which treats the whole canopy as a single big leaf. ZHANG uses a two big-leaf approach that divides the whole canopy into sunlit and sunshade portions. MLM also uses sunlit and sunshade approach at each canopy layer. R_s is modeled following either the empirical Jarvis-type approach (Jarvis, 1976) or the semiempirical Ball-Berry approach (Ball et al., 1987). The Jarvis model predicts R_s based on a prescribed minimum stomatal resistance (R_s,min; resistance at maximum stomatal opening), which is regulated by a series of empirical environmental stress functions. ZHANG, C5DRY, and MLM apply the Jarvis-type approach and include the stress effects of solar radiation, temperature, humidity, and soil water availability. WESELY uses a simplified Jarvis-type approach and only considers the effects of solar radiation and temperature. Noah-GEM employs a photosynthesis-based Ball-Berry approach that estimates R_s by considering the physiological process of the leaf response to net CO₂ assimilation/photosynthesis rate (A_n), the relative humidity fraction at the leaf surface (h_s), and CO₂ partial pressure at the leaf surface (C_s).

3. Model Run Configuration and Field Data Description

3.1. Model Run Configuration

WESELY was extracted from the WRF-Chem model V3.1.1. C5DRY was extracted from the Pleim-Xu (PX) land surface model in WRF V3.4 and the CMAQ model V5.0.2, but the cuticular resistance for O₃ was updated to the parameterization introduced in CMAQ V5.1. All the dry deposition models were executed in a single-point mode, driven by consistent on-site meteorology, and with the same parameters for site characterization (e.g., LAI, roughness length, and canopy height). The land use type was set as mixed forest in Noah-GEM, WESELY, and C5DRY. Since ZHANG does not include a land use type as mixed forest, V_d was calculated for deciduous broadleaf forest and evergreen needleleaf forest and then averaged into a mixed forest with V_d being based on the area fractions of the two forest types listed in Table S1 in the supporting information. Similarly, V_d from MLM was calculated for each tree species and then also averaged into a mixed forest V_d using the weighting factors in Table S1. Hourly measurements of temperature (T), relative humidity (RH), wind speed (WS), wind direction (WD), friction velocity (u_*), Obukhov length (L = −ρC_pu_*³θ/kgH), atmospheric pressure (Pa), downward shortwave radiation (R_{g_in}), downward long-wave radiation (R_{long_in}), canopy wetness (C_wet), ground wetness (G_wet), precipitation rate (Precip), and snow depth (SD) were used as meteorological inputs to the models. The ZHANG model also required the input of cloud fraction, which was extracted from the archived data produced by the Canadian weather forecast model, Global Environmental Model (GEM). WESELY determines canopy wetness caused by dew or rain based on relative humidity and precipitation rate. In ZHANG, Noah-GEM, MLM, and C5DRY, the canopy wetness was determined from the leaf wetness sensor at 18 m (closest to the crown of the canopy) and the ground wetness was taken from the sensor at 1.3 m height. Note that in the operational version in CMAQ, C5DRY uses a canopy wetness fraction calculated in the PX land surface model. Since this information is not available at the study site, the canopy wetness in C5DRY was set to 0 (dry) or 1 (wet) based on the information obtained from the leaf wetness sensor at the canopy height. In operational mode, CMAQ uses the same wetness fraction for both the canopy wetness and the ground wetness. For this study, we took advantage of the additional information provided by the wetness sensor at 1.3-m height and used this to determine the surface wetness of the ground. A sensitivity test of C5DRY was conducted by setting the canopy and ground wetness to 0 (dry). The differences of the averaged V_d between the sensitivity test and the base run were < 1% for O₃ and about 6.6% for SO₂ during the study period, which should be the upper limits of the uncertainties caused by the choice of the canopy/ground wetness in C5DRY. In operational mode, the vegetation fraction is used in PX and CMAQ representing the fraction of the grid that is covered with vegetation that is varied seasonally and ranges from 0.60 to 0.95 for a mixed forest. This parameter could be set for individual sites based on the flux footprint of the tower. Here we use the seasonally varying value that would correspond to a grid cell that was 100% mixed forest. The operational version of MLM at CASTNET was used in this study, which turns off the snow effects as the snow measurements are not available at the CASTNET sites and do not include the revision recently proposed by Saylor et al. (2014). Saylor et al. (2014) revised the resistance framework for the leaf-level R_b, which does not significantly impact the calculated V_d for O₃ and SO₂ (<3%).

3.2. Field Data Description

The Borden Forest Research Station (hereafter referred to as Borden Forest) is located in a mixed deciduous and coniferous boreal-temperate transition forest in southern Ontario, Canada (44°19′N, 79°56′W). A permanent 42-m tower was used as the main structure supporting instruments that measured O₃ and SO₂ concentration profiles and related meteorological variables. Eddy covariance fluxes of sensible heat, water vapor, momentum, and CO₂ were measured above the canopy using a sonic anemometer coupled with a closed-path infrared gas analyzer. Details on the site and the instrumental methods can be found in Froelich et al. (2015) and Wu et al. (2016).

A database of hourly V_d values for O₃ and SO₂ covering 1 May 2008 to 30 April 2013 was previously developed at Borden Forest (Wu et al., 2016). In the process of developing this database, dry deposition fluxes (F) of O₃ and SO₂ were calculated using concentration gradients between a level above and a level below the canopy top based on a modified gradient method (MGM) described in Wu et al. (2015). Briefly, the MGM is similar to the classic aerodynamic gradient method (AGM) in that fluxes are calculated by combining measurements of concentration gradients and micrometeorology (e.g., u_*, L) with empirical models of wind and thermodynamic profiles. Like the AGM, the MGM applies empirical stability corrections for the calculation of R_a above the canopy. The AGM and MGM differ in that the latter incorporates measurements of concentration within the canopy crown to determine the gradient. This approach is advantageous from a measurement standpoint as gradients between the atmosphere and canopy crown are larger than gradients above the canopy (i.e., AGM), the magnitude of which is often less than the precision of the measurement itself. For the MGM, the eddy diffusivity for momentum within the crown space must therefore be specified, which in this case is estimated as a function of the empirically derived wind speed profile within the canopy. Additional detail on the MGM is provided by Wu et al. (2015).

The MGM-estimated V_d values agreed well with previous eddy covariance measurements at this and other locations reported in the literature in the context of the magnitude, diel and seasonal variations, and some contrasting features between O₃ and SO₂ (Wu et al., 2016). However, uncertainties of the order of approximately 20% in the estimated V_d values likely exist due to the assigned canopy characteristics, limitation of the algorithm, and measurement uncertainties in concentrations. Uncertainties are expected to be higher in stable conditions (e.g., nighttime and winter) when accuracy of the stability correction functions decreases (Wu et al., 2015) and are higher for SO₂ than O₃ as concentrations of SO₂ were relatively low through the measuring period (Wu et al., 2016). These uncertainties are considered when using the V_d database to evaluate the five dry deposition models below.

4. Results and Discussion

4.1. Comparison of Modeled Dry Deposition Velocities

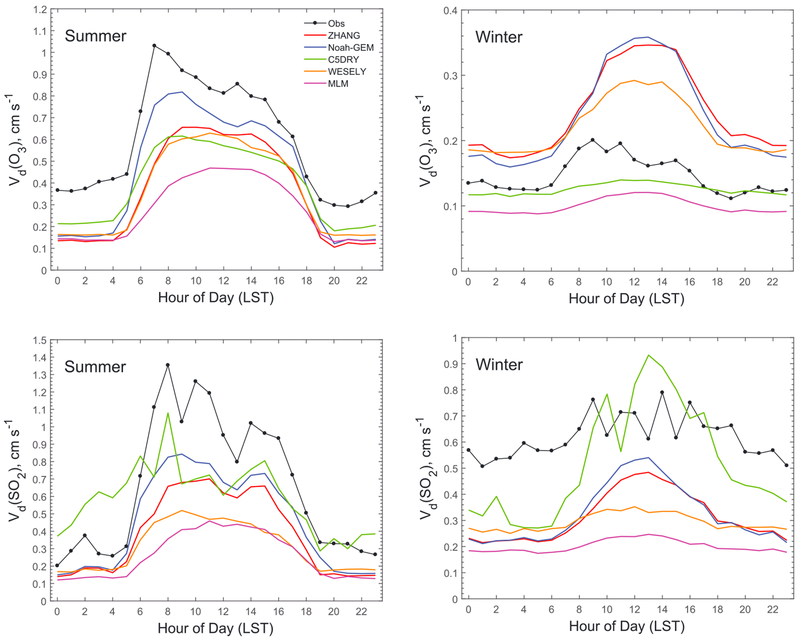
The dry deposition velocities of O₃ and SO₂ calculated by the five models were compared against each other and with those estimated from concentration-gradient measurements (see Figures 1 and S1–S5 and Table 2). For the summer seasons (June–September), all the models reproduced the diel pattern to some extent when compared to measurements. The summer-average diel variations of hourly V_d from the models were in the range of 0.1 up to 0.8 cm/s for both SO₂ and O₃ (Figure 1). In comparison, measurements showed a range of 0.3 to 1.0 cm/s for O₃ and 0.2 to 1.3 cm/s for SO₂. Thus, a few models produced the same magnitudes as measurements of diel variations of O₃ V_d, but all models produced smaller diel variations than measurements of SO₂ V_d. As shown in Table 2, models produced 20–60% lower V_d for both O₃ and SO₂ than the measurements, keeping in mind that measurement-based V_d values also had large uncertainties as mentioned in section 3. MLM estimated the lowest V_d while Noah-GEM/C5DRY the highest, with differences between the models up to a factor of 2.4 on the summer average. Correlations between model estimates and measurements were similar for all the models for O₃ with correlation coefficients between 0.55 and 0.64 (Table 2). Correlation for SO₂ in summer for most models ranged from 0.6 to 0.7. However, for C5DRY, the correlation was lower (0.19) due to a number of very high values (Figure S3). The deposition to wetted surfaces in C5DRY is a function of the Henry’s law constant. For cold, wet surfaces, the Henry’s law constant in C5DRY is quite high. Many of the other models employ a minimum resistance of 10 s/m; however, C5DRY does not set a minimum resistance.

Figure 1.

Comparison of averaged diel cycles of observed and modeled dry deposition velocities (V_d) of O₃ and SO₂ in summer (June–September) and winter (November–April). LST = local standard time.

Table 2.

Statistical Results of the Observed and Modeled Dry Deposition Velocities (V_d) of O₃ and SO₂ (cm/s)

	Vd (O3), all (N = 14385)			Vd (O3), summer (N = 5342)			Vd (O3), winter (N = 5630)			Vd (SO2), all (N = 6748)			Vd (SO2), summer (N = 1845)			Vd (SO2), winter (N = 3585)
	Mean	Median	R	Mean	Median	R	Mean	Median	R	Mean	Median	R	Mean	Median	R	Mean	Median	R
Observation	0.34	0.25	-	0.58	0.49	-	0.14	0.12	-	0.59	0.53	-	0.61	0.48	-	0.60	0.56	-
ZHANG	0.30	0.25	0.55	0.34	0.29	0.64	0.23	0.20	0.36	0.30	0.24	0.49	0.35	0.26	0.66	0.29	0.24	0.35
Noah-GEM	0.33	0.25	0.58	0.42	0.36	0.64	0.22	0.19	0.35	0.33	0.24	0.51	0.41	0.30	0.67	0.29	0.24	0.35
C5DRY	0.22	0.16	0.56	0.38	0.33	0.62	0.12	0.13	<0.1	0.47	0.18	0.16	0.56	0.39	0.19	0.46	0.17	0.13
WESELY	0.28	0.21	0.52	0.35	0.22	0.55	0.21	0.19	0.24	0.27	0.24	0.37	0.29	0.22	0.60	0.28	0.27	0.25
MLM	0.17	0.12	0.58	0.27	0.23	0.57	0.10	0.10	0.28	0.20	0.20	0.50	0.24	0.19	0.66	0.19	0.22	0.39
MLM-Ra	0.20	0.13	0.59	0.31	0.28	0.57	0.11	0.10	0.30	0.24	0.22	0.47	0.29	0.22	0.66	0.22	0.23	0.40
ZHANG-rs,min	0.32	0.26	0.57	0.39	0.31	0.65	0.24	0.20	0.36	0.31	0.24	0.51	0.38	0.28	0.69	0.29	0.24	0.35
ZHANG-SD	0.30	0.19	0.60	0.39	0.31	0.65	0.17	0.10	0.32	0.38	0.30	0.45	0.38	0.28	0.69	0.41	0.33	0.27
Noah-GEM-SD	0.30	0.20	0.61	0.42	0.36	0.64	0.17	0.11	0.32	0.37	0.29	0.48	0.41	0.30	0.67	0.38	0.31	0.30
C5DRY-fw	0.21	0.13	0.59	0.38	0.33	0.62	0.09	0.09	0.17	0.42	0.13	0.15	0.56	0.39	0.19	0.35	0.11	0.12
Ensemble	0.25	0.18	0.65	0.36	0.30	0.65	0.15	0.12	0.33	0.33	0.25	0.40	0.38	0.32	0.59	0.32	0.26	0.25
ZHANG-SD (forecast driven)	0.39	0.40	0.53	0.48	0.47	0.58	0.24	0.12	0.26	0.48	0.43	0.35	0.52	0.52	0.53	0.45	0.38	0.19
WESELY (forecast driven)	0.30	0.24	0.51	0.36	0.26	0.55	0.23	0.22	0.22	0.25	0.23	0.31	0.28	0.21	0.56	0.26	0.27	0.17

Note. Note that summer is June-September, winter is November–April, N is the number of samples, and R is the correlation coefficient between observation and model simulation. MLM-Ra is the same as MLM except the C5DRY-modeled R_a is used; ZHANG-r_s,min is the same as ZHANG except that r_s,min was reduced by 25%; ZHANG-SD is the same as ZHANG-r_s,min except that sd_max is reduced from 200 cm to 10 cm; forecast driven refers to drive the model by forecasted meteorology, instead of on-site observations; Noah-GEM-SD is the same as Noah-GEM except that sd_max is reduced from 200 cm to 10 cm. C5DRY-fw is the same as C5DRY except the resistance framework is revised to make the ground resistance to be parallel pathways of snow covered and bare ground. Ensemble is the mean of ZHANG-SD, Noah-GEM-SD, C5DRY-fw, WESELY, and MLM.

For the winter seasons (November–April), no consistent patterns were found between the models or between O₃ and SO₂. Measurements showed small diel variations of V_d (O₃) and V_d (SO₂), which were in the range of 0.1 to 0.2 cm/s and 0.5 to 0.8 cm/s, respectively. Two models (MLM and C5DRY) produced lower O₃ V_d than measurements with nearly no diel variation while the three other models produced higher V_d than measurements with considerable diel variations. All models produced lower SO₂ V_d than measurements (by 50–70% or larger than a factor of 2.0), but C5DRY produced closer magnitudes of diel variations to the measurements, for example, 0.3–0.9 cm/s versus 0.5–0.8 cm/s. Correlation between the C5DRY estimates and measurements was relatively low (0.13), which is also due to the extremely high values of V_d (SO₂) produced by C5DRY (Figure S3). V_d (SO₂) by MLM and WESELY was relatively low and showed very small diel variations (similar to V_d [O₃] by MLM and C5DRY), which is mainly caused by nonstomatal resistances (R_ns) having large values but small diel cycles (see Figure 5). The model-measurement correlations were similar between the other models with correlation coefficients in the range of 0.24 to 0.39, which were much lower than those in summer.

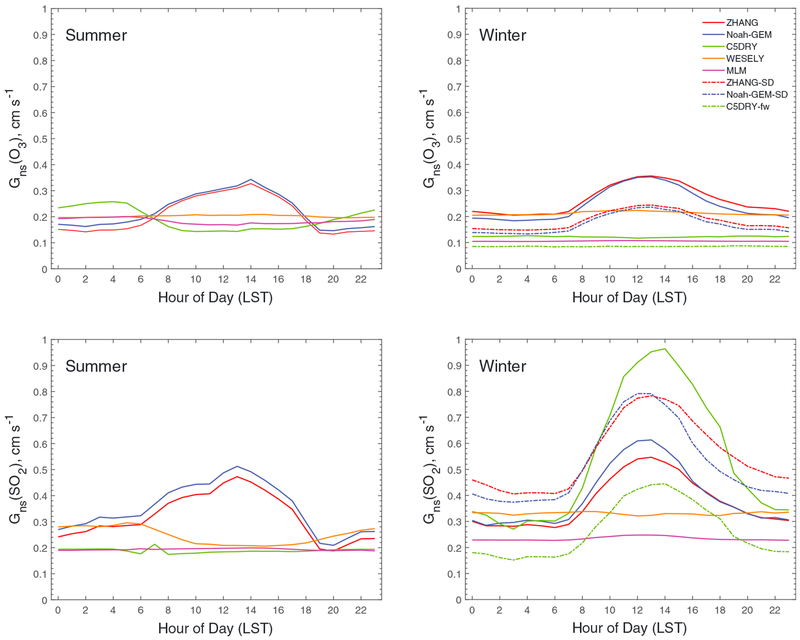
Figure 5.

Comparison of averaged diel cycles of modeled nonstomatal conductance (G_ns) in summer (June–September) and winter (November–April). LST = local standard time.

Large differences in modeled V_d have been reported in several previous studies. For example, Park et al. (2014) found differences in O₃ V_d between the WESELY and a CMAQ dry deposition version reached a factor of 2 when driven by identical meteorology. Flechard et al. (2011) estimated the reactive nitrogen fluxes across the NitroEurope network using three European and one Canadian (ZHANG) dry deposition models and found considerable differences (a factor of 2–3) in the estimated fluxes. Schwede et al. (2011) compared V_d between MLM and ZHANG at four CASTNET sites using consistent meteorological input and showed that ZHANG produced higher V_d for O₃ and SO₂ at the forest sites but lower V_d at the grassland site compared to MLM. Myles et al. (2012) reported a similar finding to that of Schwede et al. (2011) for SO₂ at a grassland site.

4.2. Comparison of Modeled Resistance Components and Sensitivity Tests

To investigate the causes of the differences in V_d across the models, the calculated resistance components were compared. For MLM, most resistances were calculated for 21 layers within canopy and the canopy-average resistance components were extracted by using a “zero-out” approach that sets all the other resistance/conductance components to zero except the one for output. Since the resistance can vary by 2–3 orders in magnitude (from 10 s/m to 10⁴/s m), the conductance, which is the inverse of resistance, is shown below.

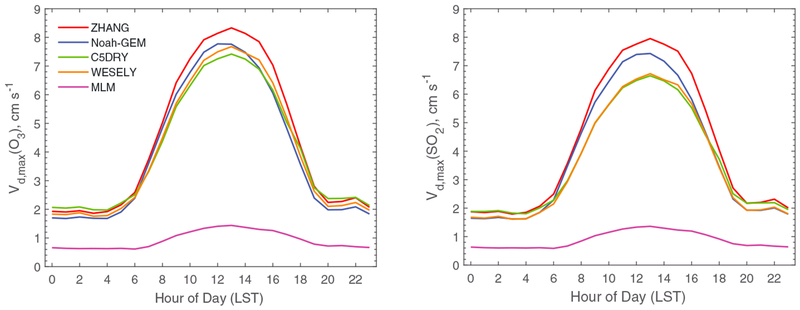
Figure 2 shows the comparison of the maximum possible dry deposition velocity (V_d,max) that is the inverse of the sum of atmospheric resistances (R_a and R_b). The models employing the MOST approach (i.e., ZHANG, Noah-GEM, WESELY, and C5DRY) produced very similar V_d,max values (varying within 20%). The contribution of atmospheric resistances to the total resistances of O₃ and SO₂ was generally small (5–15% in this study), and the differences in the calculated R_a and R_b among the four MOST-based models are thought to have no noticeable effect on the overall differences in modeled V_d of O₃ and SO₂. MLM uses a simplified approach to calculate R_a for a practical reason (Hicks et al., 1987), making use of on-site measurements of mean wind speed and standard deviation of wind direction. R_b is calculated at each level in the canopy and is treated as being in series with each of the deposition pathways to the leaf. This approach has been questioned by Saylor et al. (2014), and an alternative model was proposed. However, here we retain the original MLM parameterization as used in the operational runs at CASTNET. The peak V_d,max by MLM was 4–5 times lower than those of the MOST-based models (Figure 2). Results from Schwede et al. (2011) also showed MLM produced a lower V_d for HNO₃ than ZHANG by a factor of 2 on average over a maple forest site close to Borden Forest. V_d (HNO₃) should be close to V_d,max as R_c (HNO₃) is generally very small if not negligible (Meyers et al., 1989; Nguyen et al., 2015).

Figure 2.

Comparison of averaged diel cycles of modeled maximum possible dry deposition velocities (V_d,max) of O₃ and SO₂. Note that V_d,max = 1/(R_a + R_b). LST = local standard time.

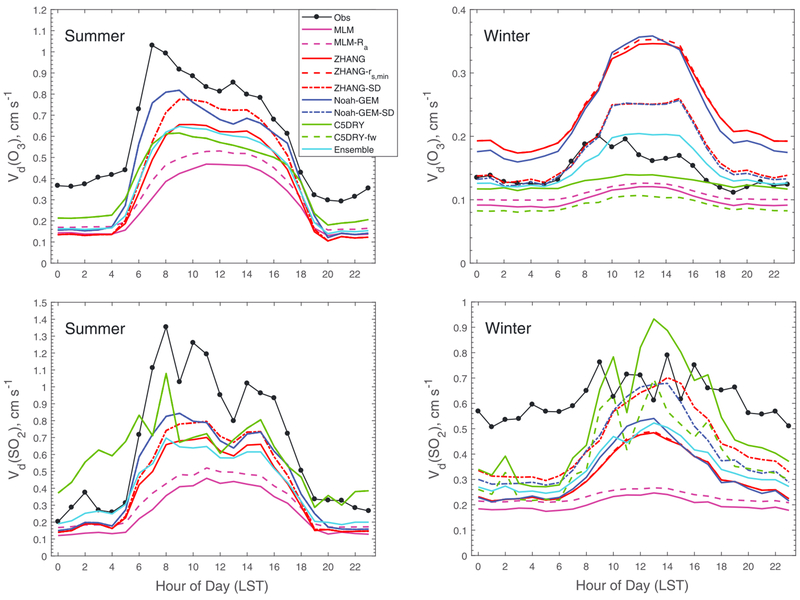
A sensitivity test was conducted by replacing R_a in MLM with the C5DRY-calculated R_a (hereafter as MLM-R_a; the MOST-based R_b formula is difficult to insert into the MLM modeling framework). As shown in Figures S12 and S13, R_a is similar with R_b in magnitude and there is a consistent pattern in the differences between the MOST-based models and MLM for R_a and R_b. Thus, it is expected that the effect of differences in R_b should be similar to that of R_a. With reduced R_a in MLM, mean V_d only increased by about 10% (Table 2 and Figure 3). As the mean modeled V_d by MLM was only about half of the highest model estimates (Table 2), the main causes of the differences in V_d across the models is mainly due to the differences in the calculated R_c, especially for MLM. It is worth noting that the differences of R_a and R_b between the models found in this study should be important for some fast-depositing chemical species such as HNO₃ that has near-zero R_c.

Figure 3.

Sensitivity tests of modeled dry deposition velocities (V_d) of O₃ and SO₂. LST = local standard time.

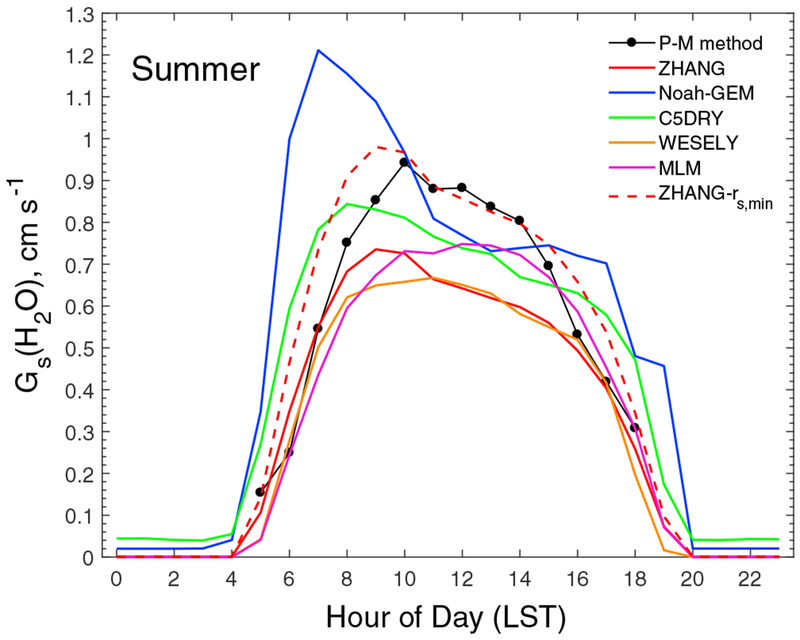
To identify which portion of R_c dominated the differences in modeled V_d of O₃ and SO₂, stomatal and non-stomatal uptake pathways were investigated separately. Figure 4 shows the comparison of the canopy stomatal conductance for water vapor (G_s = 1/R_s; conductance for gaseous pollutants are scaled to that of water vapor in the models). In addition to the modeled G_s, the observed G_s was also estimated for summer daytime by using the inversion of the Penman-Monteith (P-M) equation (Monteith & Unsworth, 1990), which establishes a relationship of G_s mainly with water vapor flux and vapor pressure deficit. The evaporation from soil water and liquid water on the vegetation surfaces is usually a minor contribution to the total water vapor flux observed above canopy during summer daytime, and it was assumed that 85% of the water vapor flux originates from transpiration (Turnipseed et al., 2006) in this study. The models captured well the diel variations in G_s. The Jarvis-type models (i.e., ZHANG, C5DRY, WESELY, and MLM) produced lower G_s than that estimated by the inverted P-M method. Noah-GEM (Ball-Berry type) produced G_s close to the inverted P-M method in the afternoon but overestimated it during the early morning.

Figure 4.

Comparison of modeled and observed averaged diel cycles of stomatal conductance (G_s) for water vapor in summer (June–September). G_s for water vapor is about 1.6 and 1.9 times of that for O₃ and SO₂, respectively. LST = local standard time.

WESELY uses a simplified Jarvis-type stomatal submodule for which the main limitations are a lack of consideration of key biological (e.g., LAI) and meteorological (e.g., humidity and soil moisture) variables. The standard Jarvis stomatal submodule is implemented in ZHANG, C5DRY, and MLM. The stress effects of temperature, solar radiation, humidity, and soil moisture are included in the models, although different stress functions or parameters are used (see Tables S1 and S2). The Jarvis-type stomatal model is known for its linear dependence on the prescribed minimum stomatal resistance (r_s,min; Kumar et al., 2011; Wu et al., 2011). However, this parameter is mainly derived from empirical fits to field measurements and suffers from large uncertainties. Additionally, the value is usually derived from leaf-scale measurements for specific plant species, so values for a land use/land cover classification will depend on the assumed mix of species. For the models in this study and the tree species present in the vicinity of the tower, the value of r_s,min ranges from 100 to 250 s/m.

In order to investigate the impact of uncertainties of r_s,min on modeled V_d, a series of sensitivity tests were conducted using the ZHANG model by adjusting the r_s,min values. It was found that R_s modeled by ZHANG would match that of the inverse P-M method if r_s,min was reduced by 25% (from 150–250 s/m to 113–188 s/m, hereafter referred to as ZHANG-r_s,min; Figure 4). The mean V_d for O₃ and SO₂ in ZHANG-r_s,min increased by 14% and 12%, respectively, in summer compared to the base case (i.e., ZHANG; see Table 2 and Figure 3). The reduced r_s,min value is still within the range of reported results by field measurements or the other models (see Table S1). The change of r_s,min had a minimal effect in winter for O₃ and SO₂ V_d since LAI was small and stomatal uptake was limited at Borden Forest (Wu et al., 2016). As shown in Figure 3, large discrepancies still exist in V_d between ZHANG-r_s,min and the observations, which can be further attributed to the nonstomatal parameterization of the model, as discussed below. The important role of r_s,min on modeled V_d was confirmed by conducting similar tests on the other Jarvis-type models. For example, the C5DRY V_d for O₃ and SO₂ in summer would increase by 16% and 14%, respectively, if r_s,min is reduced by 25%.

While stomatal conductance for water vapor can be inferred from field measurements and used for quantifying stomatal conductance of gaseous pollutants, the nonstomatal conductance (e.g., cuticular and ground) is difficult to measure or infer directly in field studies. Existing nonstomatal uptake parameterizations all use simple approaches without explicitly considering the complication of chemistry effects in the canopy air space. Figure 5 presents a comparison of nonstomatal conductance (G_ns) for O₃ and SO₂ in different seasons. There were substantial differences of the G_ns among the five models in both the magnitude and the diel variations. MLM produced small G_ns values compared to the other models that mainly contributed to the low MLM V_d values. ZHANG and Noah-GEM employ the nonstomatal scheme of Zhang et al. (2003), which was derived from an empirical regression analysis of the field measurements cited above and includes a dependence on u_*² in the calculation of the in-canopy aerodynamic resistance and parameterizes the cuticular uptake as a function of u_*. The calculated G_ns by ZHANG and Noah-GEM was relatively high and produced a distinct diel cycle showing maxima around noon as expected given the strong dependence of the parameterization on u_*. The G_ns calculations by the other models showed relatively small diel variations as the in-canopy resistance is a weaker function of u_* and they mostly relied on the prescribed constants for the cuticular resistance with minimal consideration of meteorological effects (e.g., u_* and RH) other than canopy wetness (see Table 1). Field study measurements (Lamaud et al., 2002, 2009; Zhang et al., 2003, 2002) show a correlation between total nonstomatal conductance and u_*; however, these studies did not contain measurements to identify the processes responsible for this relationship. In the absence of more detailed measurements to better understand the nonstomatal conductance and in-canopy resistance, it is not possible to determine which modeling approach is most realistic. The intermodel differences emphasize the need for additional experimental work to inform improvements to parameterizations of in-canopy processes.

The nonstomatal pathways dominated the total surface uptake in winter. The Borden Forest was frequently covered with snow in winter, and analysis of the observation data found that the snow surface became an effective sink for SO₂ but inhibited O₃ deposition (Wu et al., 2016). Measurements of deposition velocity over snow covered surfaces are challenging, and the observed values can have a high degree of uncertainty. Recent studies (e.g., Helmig et al., 2014; Zeller, 2000) indicate that O₃ fluxes over snow may be positive or negative and can be influenced by many factors including the temporal storage in the air space within snow and reactions with chemicals contained within the snowpack.

The snow effects are considered in the models in this study explicitly or implicitly, although in very simplified ways. ZHANG considers snow effects separately for different surface types and adjusts the ground resistance (R_g) and cuticle resistance (R_cut) by including a snow cover fraction (f_snow). f_snow is defined as the ratio of the snow depth (sd) to the maximum snow depth (sd_max), the latter is a prescribed land use-dependent constant representing the threshold value above which canopy leaf and ground surfaces are fully covered by snow. A value of 200 cm is assigned to the tall canopies such as deciduous broadleaf forest and evergreen leaf forest. A sensitivity test was conducted by reducing sd_max to a value of 10 cm, the same as the default value for the short canopies (e.g., grass and crops), in ZHANG-r_s,min (hereafter as ZHANG-SD). G_ns for O₃ in ZHANG-SD was decreased by as much as 40% in winter, and, on the other hand, G_ns for SO₂ increased by a similar percentage (Figure 5). The measured snow depth at Borden Forest did not exceed 80 cm during the study period (see Figure 6 in Wu et al., 2016). The value of 200 cm is likely too high to get any meaningful snow cover fraction (f_snow) for underlying surfaces inside forests. Note that snow cover enhances SO₂ uptake but inhibits O₃ deposition; improper definition on f_snow will thus affect the overall ground/cuticle uptake. After reducing sd_max, the winter G_ns (O₃) by ZHANG was within the range of results by the other models and the G_ns (SO₂) by ZHANG in winter was much larger than the results by the other models (Figure 5). Compared with ZHANG-r_s,min, V_d in ZHANG-SD decreased about 30% for O₃ and increased by about 40% for SO₂ in winter, both approaching the observations (Table 2).

As Noah-GEM employs the same nonstomatal parameterization as in ZHANG, the reduction of sd_max impacted the Noah-GEM V_d to a similar extent (see Noah-GEM-SD). C5DRY also considers the effects of snow cover but uses a different approach than ZHANG. In CMAQ V5.0.2, the model considers parallel pathways to the snow, vegetation, and bare ground. For snow covered ground, the snow resistance is additionally divided into ice and liquid fractions of snow. The model calculates the liquid water content of the snow using the approach of Bales et al. (1987) to distinguish between wet snow and dry snow on the ground. The resistance to wet snow is driven by Henry’s law constant, so soluble species such as SO₂ will readily deposit to the wet snow covered surfaces. For cold (< 0°C), wet conditions, the cuticular resistance is set to the resistance for dry snow. Closer examination of the C5DRY code during this study motivated sensitivity testing to examine an alternative coding of the resistance framework (hereafter as C5DRY-fw). The revised framework considers vegetated and nonvegetated parallel pathways. Rather than the snow pathway being considered parallel to the vegetated and nonvegetated pathways, the ground resistance in the revised framework is treated as parallel pathways of snow covered and bare ground. The snow covered surfaces are treated as before, being split into wet and dry snow, and the bare ground resistances are as in the original model with wet and dry soil pathways. Cold, wet soil is treated as frozen ground. The change in the resistance framework caused a large change in the predicted deposition velocities as seen in Figure 3 and improved the correlation with the observed values (Table 2). Overall, none of the modeling results showed a strong correlation with the observed values, indicating that there is still substantial model development required to adequately model deposition over snow.

Given the variability in V_d values calculated by the five models, it would be challenging to recommend a single value for use in deposition assessments. Instead, an ensemble value might be more appropriate. Therefore, an ensemble averaging of V_d was derived from the five models (using results of ZHANG-SD, Noah-GEM-SD, C5DRY-fw, WESELY, and MLM), as shown in Figure 3 and Table 2. The ensemble model results agreed well in magnitude with the observed V_d for O₃ in winter but still underestimated V_d for O₃ in summer and SO₂ in summer and winter. Correlation between the ensemble results and the observed V_d for O₃ (R = 0.65) was higher than that for each model (the highest R = 0.60). For V_d (SO₂), the correlation coefficient for the ensemble results (R = 0.40) was within the range of that for each model (R = 0.15–0.50).

While the purpose of our analysis is to understand the differences in V_d across models, the ultimate application of the air-surface exchange model is to provide an estimate of chemical flux to the ecosystem. For that reason, it is informative to quantify the impact of differences in V_d on the resulting flux at the annual scale. Table 3 presents the annual cumulative fluxes (F) of O₃ and SO₂ from the observations and models. To obtain the annual fluxes, hourly fluxes were first calculated using hourly V_d and concentrations, which were then aggregated into daily, monthly, and annual fluxes by weighting the missing data periods. Similar to V_d, all the models underestimated the fluxes on annual basis as well. The mean modeled annual fluxes followed the order of Noah-GEM-SD > ZHANG-SD > WESELY > Ensemble > C5DRY-fw > MLM for F (O₃) and ZHANG-SD > C5DRY-fw > Noah-GEM-SD > Ensemble > WESELY > MLM for F (SO₂). Relative differences between the model ensemble and observed means are larger for annual fluxes than for V_d, particularly for SO₂, reflecting the importance of model underestimation of V_d when concentrations are higher (i.e., day versus night; summer versus winter O₃ concentration; and winter versus summer SO₂ concentration; Wu et al., 2016). With respect to fluxes, the ensemble reflects the average bias of the models taking into account the relationships between concentration and V_d. Models perform differently for O₃ and SO₂ relative to the observations, but as with V_d, the ensemble approach provides mean values among all the models, which can avoid too much overestimation or underestimation.

Table 3.

The Mean and Standard Deviation of the Observed and Modeled Annual Cumulative Fluxes of O₃ and SO₂ (g·m⁻²·year⁻¹)

	Observation	ZHANG-SD	Noah-GEM-SD	C5DRY-fw	WESELY	MLM	Ensemble
F (O3)	8.563 ± 1.314	6.669 ± 1.040	6.909 ± 1.103	4.745 ± 0.969	6.380 ± 0.998	4.012 ± 0.819	5.743 ± 0.971
F (SO2)	0.566 ±0.198	0.360 ± 0.134	0.355 ± 0.141	0.356 ± 0.129	0.229 ± 0.080	0.175 ± 0.071	0.295 ± 0.109

4.3. Impact of Meteorological Input on Modeled V_d

As shown in section 4.2, V_d values for O₃ and SO₂ from MLM (the algorithm used in CASTNET) were 30–40% lower than those from ZHANG (the algorithm used in CAPMoN) on an annual basis when the two algorithms were driven by the same meteorological inputs. Due to the lack of on-site meteorological measurements at CAPMoN sites, the archived meteorological forecast data produced by the Canadian weather forecast model were used to drive the ZHANG model to produce V_d, an approach previously described in Brook et al. (1999). Hourly meteorological forecast data at the surface and the first model layer (typically at 40–50-m height) are extracted from the archived model forecasts for the model grids containing the measurement sites. At CASTNET sites, continuous on-site meteorological measurements are taken at 10-m towers and ground-based sensors. Therefore, besides the different algorithms deployed in the monitoring networks (such as CASTNET and CAPMoN), differences in meteorological inputs are another source contributing to the Vd differences. The effects of different meteorological inputs on the calculated V_d were examined below.

Table 4 shows the statistical results of the observed and modeled meteorological variables. On average, the forecasted mean temperature at the surface was close to the measurement mean with a mean bias of only −0.1°C while, at the reference height, the modeled mean was 0.7°C lower than the observed value. The forecasted and measured temperatures are correlated well, with a correlation coefficient of 0.98. Differences between the forecast and observed relative humidity were very small (2.2%). The forecasted daytime solar radiation was about 10% lower than measured. The friction velocity calculated in the forecast model was almost twice that of the observed. The forecast model poorly captured the precipitation amount and its temporal variation. Large differences (>50%) also existed in the snow depth between the forecasted and measured values, but the correlation was reasonably good (R = 0.64).

Table 4.

Statistic Results of the Observed and Modeled Meteorological Variables

		Mean
Meteorological variables	Number	Obs	Sim	Bias	MAE	RMSE	R
Temperature at reference height (°C)	15677	11.3	10.6	−0.7	1.6	2.0	0.98
Surface temperature (°C)	15677	9.7	9.6	−0.1	1.8	2.4	0.98
Relative humidity (%)	15677	69.1	71.3	2.2	8.5	11.1	0.80
Daytime solar radiation (W/m2)	8109	308.4	275.1	−33.3	91.0	129.4	0.89
Friction velocity (cm/s)	15677	47.2	81.3	34.1	38.4	48.3	0.74
Precipitation rate (0.1 mm/hr)	15677	0.57	0.01	−0.56	0.58	4.51	0.17
Surface pressure (hPa)	15677	989.8	987.0	−2.8	2.8	2.9	0.99
Winter snow depth (cm)	5746	15.2	7.2	8.0	9.0	16.6	0.64

Note. Note that Obs is observation, Sim is simulation, MAE is mean absolute error, RMSE is root-mean-square error, R is the correlation coefficient between observation and model simulation, daytime is 0600–1800 (LST), and winter is November–April. Equations for the statistic parameters are shown in equations (S1–S4). LST = local standard time.

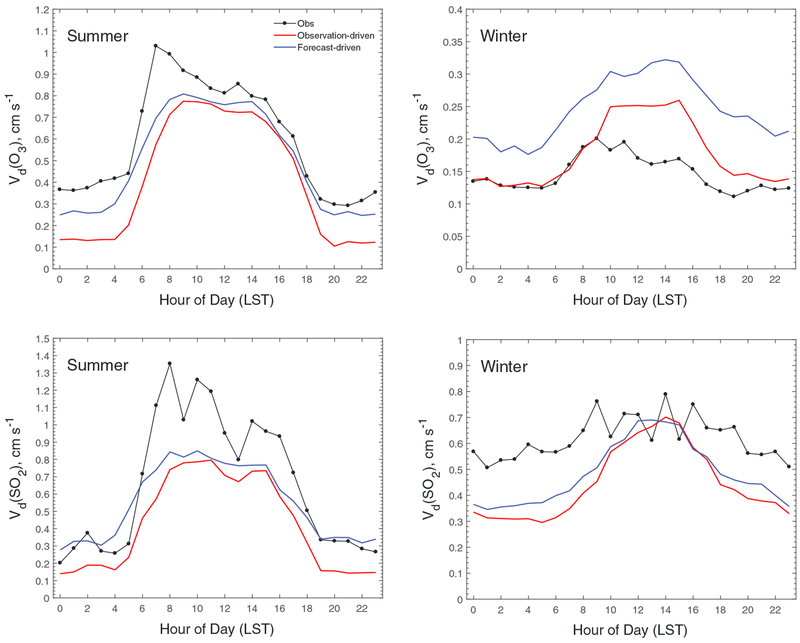
The ZHANG model was applied at Borden Forest using the forecasted meteorology mentioned above, as is done routinely at the CAPMoN sites (hereafter referred to as forecast driven). The parameter configuration used here is the same as in ZHANG-SD since this version showed the best agreement in V_d of O₃ and SO₂ with the observations at Borden Forest. The forecast-driven V_d values were generally 30% larger than the observation-driven values (i.e., ZHANG-SD; Figure 6) and with slightly lower correlations (Table 2). These differences between forecast-driven V_d and observation-driven V_d were solely caused by the different meteorological inputs.

Figure 6.

Comparison of averaged diel cycles of observed and modeled dry deposition velocities (V_d) of O₃ and SO₂ by the ZHANG scheme using on-site observed and model forecasted meteorological forcing. LST = local standard time.

To identify the dominant meteorological variables responsible for the V_d differences, a number of tests were conducted by replacing every observed meteorological variable in ZHANG-SD with the forecast model values. The relative differences in V_d for O₃ and SO₂ are shown in Table 5. The use of the model-based u_* resulted in a 33.6% and 44.6% increase of V_d (O₃) and V_d (SO₂), respectively, as the modeled u_* values were about twice those from the observations (Table 4) and the nonstomatal parameterization depends on u_* (Table 1). The change of V_d due to snow depth was about 10% in winter and expectedly smaller on an annual basis. The impacts of the other meteorological variables were negligible (typically <3%) because those variables were forecasted reasonably accurately, and the dry deposition model is much less sensitive to these variables than to u_*. A similar test was conducted by using the forecasted meteorology to drive the WESELY scheme, in which the surface resistance is parameterized without including u_*. The results (Figure S16 and Table 2) show that the impact of meteorological inputs on WESELY V_d for O₃ and SO₂ was small. The mean relative differences between the forecast-driven and observation-driven V_d values were about 5%. Schwede et al. (2001) calculated V_d (O₃) by MLM using on-site meteorology as well as the output of two meteorological models (MM5 and Eta) and found that the average bias in V_d from using modeled meteorology ranged from −0.001 to 0.106 cm/s, which is within the error of the dry deposition model. Discussions above suggest that, when on-site meteorological data are not available, forecasted meteorology data can be used as a surrogate, such as the approach used in CAPMoN, to drive dry deposition models. Uncertainties in dry deposition estimates from using forecasted meteorology are much smaller than those from using different dry deposition models for the majority of chemical species.

Table 5.

Relative Change of Dry Deposition Velocities (V_d) of O₃ and SO₂ Due to Change in Input Meteorological Forcing

Relative change (%)	Temperature at reference height	Surface temperature	Relative humidity	Solar radiation	Friction velocity	Precipitation rate	Surface pressure	Snow depth
Vd (O3)	0.1	−1.1	0.8	−1.3	33.6	−0.04	0.1	2.6
Vd (SO2)	−0.1	−3.1	1.3	−0.5	44.6	−0.9	−0.05	−6.1

Note. Note that a relative change is defined as $\left(\overline{V_{\text{d,s}}}-\overline{V_{\text{d,c}}}\right)/\overline{V_{\text{d,c}}}\times 100\%,$, where $\overline{V_{\text{d,c}}}$ is the mean V_d in the control experiment that uses the on-site meteorology, and $\overline{V_{\text{d,s}}}$ is the mean V_d in the sensitivity experiment that is the same as the control experiment except that the specified meteorological forcing is from the model simulations instead of the on-site observations.

5. Conclusions and Recommendations

Five commonly used dry deposition algorithms in North America were compared to each other and to a 5-year V_d database of O₃ and SO₂. Considerable differences were found in the estimated V_d values of O₃ and SO₂ between the five algorithms, which were attributed mainly to differences in the models’ surface resistance parameterizations for both stomatal and nonstomatal uptake pathways. Although the effects of R_a and R_b on V_d of O₃ and SO₂ were small in four of the five formulations, their effects were considerably larger in MLM, which has potentially large implications for fast-depositing chemical species (e.g., HNO₃). Due to the large uncertainties in historical dry deposition flux measurements, the five dry deposition algorithms developed and evaluated using these flux data showed similar magnitudes of uncertainties. The uncertainty in prescribed minimum stomatal resistance (R_s,min) dominates the errors in estimated stomatal uptakes of the Jarvis-type stomatal resistance submodules. Several key biological (LAI) and meteorological variables (solar radiation, temperature, humidity, and soil moisture) should be included in parameterizing stomatal uptake. The nonstomatal uptake parameterization including the effects of biological (LAI), meteorological (friction velocity and humidity), and external surface (wetness) conditions performed better than those without such considerations, as demonstrated by the better correlations with the observed V_d. This suggests the necessity for additional measurements of in-canopy processes in order to better understand nonstomatal pathways to improve current parameterizations. It is worth to note that, in general, model development relies on a rather limited availability of field flux measurements, which often contain significant uncertainties themselves. Models parameterized from data sets collected in a specific ecosystem, phenological period, atmospheric chemistry regime, etc. will perform better under conditions reflective of the underlying data from which a parameterization was developed. Some models may therefore perform better than others in one scenario (land use, season, etc.) but may be worse in a different scenario.

For CTM applications, it is recommended to choose an algorithm as base case that can produce mean or median V_d values among all of the available algorithms, and thus likely causing minimum bias. Alternative formulations could then be used for assessments of uncertainty in model output, a practice that has been employed in WRF-Chem in the United States and is also under development in Global Environmental Multiscale - Modelling Air quality and CHemistry (GEM-MACH) in Canada. Ensemble averaging of results from multiple algorithms is also affordable in network operations such as in CASTNET and CAPMoN, an approach that has been used in air quality model simulations (Kioutsioukis & Galmarini, 2014). The ensemble will not always minimize bias relative to observations, as is the case shown in the present study. This may be due to a systematic error (bias) in the observations or a missing process in the models. The ensemble may minimize bias when the models yield estimates that scatter around an unbiased average observation, a case that may suggest that the models are generally capturing the most important processes. Much progress is still needed to develop more mechanistic models of nonstomatal processes, and thus the use of an ensemble approach is warranted. It should be noted that, although the ensemble approach does not necessarily perform better than all of the individual models based on statistical results at this site, it can avoid too much overestimation or underestimation, as has seen in some individual models. Future work will further explore the utility of an ensemble V_d approach in the development of total deposition budgets, and estimates of their uncertainty, used for critical loads and other applications.

Key Points:

• Differences in mean V_d values of O₃ and SO₂ between models were on the order of a factor of 2

• Model differences were mainly due to different surface resistance parameterizations for stomatal and nonstomatal uptake pathways

• Ensemble averaging of results from multiple dry deposition algorithms is recommended