Development of Vibrational Frequency Maps for Nucleobases

Abstract

Vibrational spectroscopy provides a powerful tool to probe the structure and dynamics of nucleic acids because specific normal modes, in particular the base carbonyl stretch modes, are highly sensitive to the hydrogen bonding patterns and stacking configurations in these biomolecules. In this work, we develop vibrational frequency maps for the C=O and C=C stretches in nucleobases that allow the calculations of their site frequencies directly from molecular dynamics simulations. We assess the frequency maps by applying them to nucleobase derivatives in aqueous solutions and nucleosides in organic solvents, and demonstrate that the predicted infrared spectra are in good agreement with experimental measurements. The frequency maps can be readily used to model the linear and non-linear vibrational spectroscopy of nucleic acids and elucidate the molecular origin of the experimentally observed spectral features.

Graphical Abstract

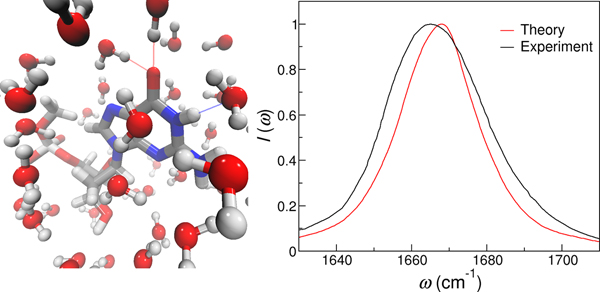
Introduction

Knowledge of the three-dimensional architecture and conformational dynamics of DNA and RNA is essential to a molecular understanding of how these biological macromolecules transmit and faithfully maintain the integrity of genetic information. As such, numerous experimental techniques have been explored to detect the secondary and tertiary structures of nucleic acids, characterize their dynamical transformations and uncover their interactions with proteins and ligands.^1–7 For example, X-ray diffraction has led to the breakthrough discovery of the DNA double helix,⁸ while nuclear magnetic resonance spectroscopy has revealed the structures and internal motions of nucleic acids at atomic resolution.^4,7,9,10

Vibrational spectroscopy, such as infrared (IR) and Raman spectroscopy, provides a complementary and versatile tool to probe the structures and dynamics of nucleic acids ranging from small oligonucleotides to native DNA and RNA in real time in situ.^11–14 These experiments often focus on the absorption bands in the 1600 – 1800 cm⁻¹ region that originate from the in-plane vibrations of double bonds in nucleobases,^11,14,15 and are typically performed in D₂O to avoid the interference of the water bending modes (∼ 1640 cm⁻¹). A particularly widely used chromophore is the base carbonyl stretch mode, as illustrated in Figure 1. The carbonyl stretches exhibit distinct spectral features for different base pairing and stacking motifs, and hence have been utilized to distinguish between the A, B and Z forms of DNA double helices and follow the association between DNA and RNA oligonucleotides.^12,14,16 Moreover, pioneering developments in non-linear vibrational spectroscopy have enabled direct measurements of interactions between chromophores and detection of nucleic acid dynamics with sub-picosecond time resolution. In particular, two-dimensional IR (2D IR) spectroscopy spreads the absorption information over two frequency axes and significantly enhances the spectral and structural resolution, which has been used to reveal the interactions between hydrogen bonded base pairs and elucidate the thermal dissociation mechanism of DNA oligonucleotides with base-pair-specific resolution.^17–21 Vibrational sum-frequency generation spectroscopy, a second-order non-linear technique that is intrinsically surface and interface sensitive, has enabled label-free detection of the conformations, orientations and hybridization dynamics of DNA oligonucleotides and aptamers at solid/liquid interfaces and on membrane surfaces.^22–27

Figure 1:

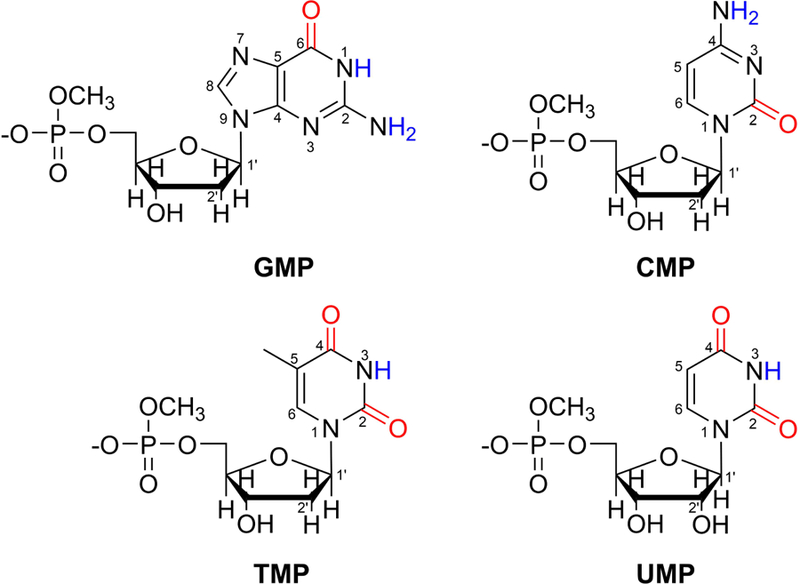
Chemical structures of NMPs with the base carbonyl groups highlighted in red. The labile hydrogens are shown in blue and the ring atoms are numbered. To mimic the phosphodiester linkage at the 5′ end of each NMP, a methoxy group is added to cap the molecule.

Despite the importance of the linear and non-linear vibrational spectroscopy techniques, it is exceedingly difficult to directly assign the complex spectral features to the underlying structures of nucleic acids, which undergo constant fluctuations as the biomolecules interact with the heterogeneous environment. Complications arise mainly from three aspects. First, multiple secondary structures in DNA or RNA can produce a series of overlapping bands and result in an overall spectrum that is broad and featureless. Second, the C=O groups interact with each other to create highly delocalized normal vibrational modes, making it difficult to attribute the observed IR absorption peaks to individual chromophores. Furthermore, the in-plane vibrations of the C=O and C=C groups are interdependent in the pyrimidine bases and further complicate the linear and 2D IR spectra.¹⁵ While electronic structure methods have provided crucial insight into the origin of the IR absorption peaks for mono- and oligonucleotides,^14,28–33 these calculations do not incorporate dynamical effects in describing the IR line shapes and their applications to large biomolecules in the condensed phase are computationally prohibitive. Therefore, it is desirable to develop a theoretical strategy that efficiently disentangles how the IR spectra of nucleic acids arise from the electrostatic environment, base pairing configurations and conformational dynamics of nucleic acids.

One such approach is to combine molecular dynamics (MD) simulations and the mixed quantum/classical treatment of the line shape theory to model the vibrational spectra of nucleic acids. In this approach, we define a vibrational subspace that comprises all the base C=O stretches in a DNA or RNA molecule and treat it quantum mechanically. As the C=O and C=C vibrations are strongly coupled in cytosine, thymine and uracil,^14,15 we also incorporate the C=C stretches in the quantum mechanical region when considering pyrimidine bases. We then perform MD simulations to evolve the lower-frequency degrees of freedom in the nucleic acid, which act as a classical bath to interact with the vibrational subspace. Within this mixed quantum/classical approximation, the central quantity is the Hamiltonian in the vibrational subspace, whose diagonal elements are the site frequencies of the C=O and C=C stretches and the off-diagonal elements are their coupling constants. To describe the diagonal component of the vibrational Hamiltonian, we exploit the fact that the site frequencies of the chromophores are strongly influenced by their surrounding nucleotides, solvent molecules, ligands and ions. These frequency modulations have been shown, in aqueous and biological systems, to be well represented by the electrostatic potentials or fields on the chromophore atoms from the condensed phase environment. This has led to the development of frequency maps for a variety of vibrational modes, including the O–H stretches in liquid water, the amide I and II modes in proteins and the phosphate vibrations in DNA.^34–51

In this work, we invoke a combined MD simulations/electronic structure calculations method to develop the first vibrational frequency maps for nucleic acids in the base carbonyl stretch region. Considering that adenine is the only nucleobase that doesn’t contain a carbonyl group, we use deoxyguanosine, deoxycytidine, deoxythymidine and uridine 5′-monophosphates as model systems to mimic the building blocks of DNA and RNA. We will refer to them as GMP, CMP, TMP and UMP, respectively (Figure 1). From MD simulations of these nucleoside 5′-monophosphates (NMPs) in aqueous solutions, we extract NMP-water clusters that adopt various solvation geometries, evaluate their C=O stretch frequencies using density functional theory (DFT) methods and design C=O frequency maps that correlate their site frequencies with the local electric fields. To account for the strong interactions between the C=O and C=C modes in pyrimidine bases, we also develop a C=C frequency map and obtain the average coupling constants between the chromophores. To validate the frequency maps, we apply them to model the IR spectra of nucleobase derivatives in aqueous solutions and nucleosides in organic solvents and show that the theoretical line shapes are in good agreement with the experimental measurements.

Theoretical and Simulation Methods

Line shape theory

When a molecule interacts with an excitation light that is polarized in the $\widehat{\epsilon }$ direction, its absorption line shape is given by the Fourier transform of the quantum dipole time correlation function,⁵²

$$I(\omega )~\mathrm{Re}{\int }_0^{\infty }dt\hspace{0.17em}{e}^{-i\omega t}\langle \widehat{\epsilon }\cdot \overrightarrow{\mu }(0)\widehat{\epsilon }\cdot \overrightarrow{\mu }(t)\rangle .$$ (1)

Here $\overrightarrow{\mu }(t)$ is the quantum dipole moment operator of the molecule at time t. The angle brackets represent a quantum equilibrium statistical mechanical average, which is very difficult to evaluate for a large DNA or RNA molecule in the condensed phase.

In this work, we are interested in the base carbonyl stretching modes of nucleic acids, which can interact with the C=C vibrations in pyrimidine bases but are relatively separated from other modes. We hence consider the C=O groups as chromophores for purine bases and the C=O and C=C stretching modes as chromophores for pyrimidine bases, and take the mixed quantum/classical approximation. specifically, we treat the vibrational subspace consisting of all the chromophores quantum mechanically, ignore other high-frequency modes and treat all the low-frequency degrees of freedom classically. Within this approximation, the vibrational Hamiltonian (divided by $\hslash$) of a multi-chromophore system is

$${\kappa }_{ab}(t)={\omega }_a(t){\delta }_{ab}+{\omega }_{ab}(t)(1-{\delta }_{ab}),$$ (2)

where a and b index the chromophores in the system, ω_a is the site frequency of chromophore a and ω_ab is the coupling between chromophores a and b. Eq. 1 becomes

$$I(\omega )~\mathrm{Re}{\int }_0^{\infty }dt\hspace{0.17em}{e}^{-i\omega t}\sum _{ab}\langle m_a(0)F_{ab}(t)m_b(t)\rangle e^{-t/2T_1}.$$ (3)

Now the brackets represent classical equilibrium statistical mechanical average, which can be obtained from MD simulations. $m_a={\overrightarrow{m}}_a\cdot \widehat{\epsilon }$, where ${\overrightarrow{m}}_a$ is the transition dipole moment of the a^th chromophore between the ground vibrational state and the first excited state. T₁ is the lifetime of the first excited state of the chromophore, and the term $e^{-t/2T_1}$ is added phenomenologically to include the lifetime broadening effect. In this work, we use a T₁ of 649 fs, which is measured for GMP in D₂O at room temperature using a waiting time series of 2D IR experiments (more details are provided in the Supporting Information). The matrix F (t) describes the time evolution of the vibrational Hamiltonian,

$$\dot{F}(t)=iF(t)\kappa (t),$$ (4)

with the initial condition of F_ab(0) = δ_ab.

When a nucleobase or its derivative contains a single chromophore, Eq. 3 is simplified to

$$I(\omega )~\mathrm{Re}{\int }_0^{\infty }dt\hspace{0.17em}{\text{e}}^{-i\omega t}\langle m(0)m(t)e^{i{\int }_0^t\omega (t\prime )\text{d}t\prime }\rangle e^{-t/2T_1},$$ (5)

where ω(t) is the vibrational frequency of the chromophore at time t.

Constructing the vibrational Hamiltonian

The purine base guanine contains a single carbonyl group (Figure 1) and its vibrational frequency is separated from the C=C stretching mode by over 80 cm⁻¹.^14,15 As such, GMP and its derivatives can be effectively treated as one-chromophore systems and their IR spectra are calculated using Eq. 5. In contrast, the carbonyl vibrations in the pyrimidine bases cytosine, thymine and uracil are strongly coupled with the C=C stretching mode,¹⁵ and hence we include the C₅=C₆ stretch in the vibrational subspace when considering CMP, TMP, UMP and the pyrimidine derivatives. For example, κ is a 2×2 matrix for CMP and a 3×3 matrix for TMP and UMP as they contain varying numbers of C=O and C=C groups (Figure 1). In these cases, we calculate their κ matrices using the Hessian matrix reconstruction (HMR) method, which has been developed for the modeling of the amide I band of proteins.^53,54

From the vibrational Hamiltonian κ (Eq. 2), one can apply matrix diagonalization and obtain the vibrational normal modes of the nucleobase,

$$\mathrm{\Omega }=U^{-1}\kappa U.$$ (6)

The diagonal matrix Ω comprises the frequencies of the normal modes, and the matrix U contains the corresponding eigenvectors. The HMR method takes the reverse approach and allows one to calculate κ from its eigenvalues and eigenvectors,^53–55

$$\kappa =U\mathrm{\Omega }{U}^{-1}.$$ (7)

We compute the elements of Ω and U for CMP, TMP and UMP from DFT calculations. The frequencies of the normal modes and hence the Ω matrix are directly obtained from the IR frequency calculations of the NMP molecules. The eigenvector matrix U is computed by displacing the nucleobase structures using the normal mode coordinates.^53–55 Specifically, we carry out geometry optimizations of the NMP molecules to get the unit vector of each normal mode and the equilibrium bond length of the n^th chromophore (C=O or C=C group),$r_n^0$. We then distort the structure of the nucleobase along a normal mode, from which the length of the n^th chromophore of the i^th normal mode becomes r_ni. We assume the corresponding element of U is proportional to the change in bond length,^53–55

$$U_{ni}\propto r_{ni}-r_n^0.$$ (8)

Note that as the displacements provided in the vibrational analysis are normalized and dimensionless, we multiply them with the amplitude of each normal mode, $\sqrt{\frac{\hslash }{2M\omega }}$,⁴⁰ when moving the atoms. Here M and ω are the reduced mass and frequency of the corresponding normal mode, respectively, and $\hslash$ is the reduced Planck constant. From Eq. 8, the i^th column of the matrix U represents the i^th normal mode, and we determine the elements of U by normalizing and orthogonalizing the matrix.

We carry out these calculations for a total of 1200 CMP-, TMP- and UMP-water clusters extracted from MD simulations. Using Eq. 7, we acquire the site frequencies of the C=O and C=C groups and the couplings between them for each configuration. The site frequencies are used to develop the frequency maps and the average couplings are used in the IR spectra calculations.

MD simulations

MD simulations were performed for GMP, CMP, TMP and UMP in aqueous solutions using the Amber 2016 software package.⁵⁶ The deoxyribonucleotides GMP, CMP and TMP were modeled using the PARMBSC1 force field⁵⁷ and the ribonucleotide UMP was described using the χOL3 force field.^58,59 To mimic the 5′-end phosphodiester linkage in nucleic acids, we added a methoxy cap to each NMP, as shown in Figure 1. The partial charges of the H atoms in the methoxy group were modified from the MOC residue in the PARMBSC1 force fields to ensure a total charge of −1 for each molecule.

Each NMP was solvated in a truncated octahedron box of H₂O, described using the TIP3P model,⁶⁰ with a minimal distance of 20 Å from any face of the solvent box. Here we used H₂O, rather than D₂O, but the solvent effect on the calculated IR spectra are expected to be small because the two molecules share the same potential energy functions and similar dynamics. To neutralize the total charge of each system, a potassium ion was added using the monovalent ion parameters implemented in Amber 2016.⁶¹ The SHAKE algorithm was applied to constrain all the hydrogen-containing bonds⁶² and the particle mesh Ewald method was implemented to treat long-range Coulomb interactions.^63,64 Each system was first equilibrated at a constant temperature of 293 K for 20 ps, and then under the NPT condition at 293 K and 1 atm for 3 ns, using the Langevin thermostat and Berendsen barostat.^65,66 After equilibration, we carried out production runs of 10 ns and collected NMP-water clusters every 25 ps, yielding a total of 400 snapshots for each NMP for the frequency map development. We then performed a production run of 2 ns and saved the configurations every 10 fs for the calculation of the IR spectra. All simulations were performed with a time step of 2 fs. From the MD production runs, we analyzed the hydrogen bonds formed between the base C=O and N-H groups and the solvent molecules, where we considered a $\text{D}-\text{H}\cdots \text{A}$ pair to be hydrogen bonded if the donor-acceptor distance, $d_{DA}\le 3\hspace{0.17em}\mathrm{\AA }$, and the D–H–A angle, ${\theta }_{DHA}\ge 135°$.

To test the frequency maps, we carried out MD simulations of inosine 5′-monophosphate, N⁶,N⁶,9-trimethylisoguanine, caffeine and 4-thiouridine in aqueous solutions, as well as deoxyguanosine in DMSO and uridine in CHCl₃. The nucleobase derivatives and the DMSO solvent were described using the generalized Amber force field (GAFF),^67,68 and CHCl₃ was embedded in Amber 2016.⁶⁹ As inosine-5′-monophosphate had a net charge of −2, we added 2 sodium ions to neutralize the system.⁷⁰ We used identical parameters in these simulations as those in the NMP simulations, except that the temperature of each system was set according to their experimental conditions. Here the simulation temperature for inosine-5′-monophosphate, N⁶,N⁶,9-trimethylisoguanine, 4-thiouridine and uridine was 298 K.^70–73 The temperature for caffeine and deoxyguanosine was 293 and 294 K, respectively.^18,74 We performed production runs of 2 ns for each system and saved the configurations every 10 fs to calculate the IR spectra.

Note that for deoxyguanosine and uridine in organic solvents, our simulated systems were slightly different from their experimental measurements. Specifically, the experiments were performed on a guanine base in DMSO¹⁸ and a modified uridine, where the hydroxyl groups on the ribose were replaced with tertbutyldimethylsilyl groups to increase the solubility of the compound, in CDCl₃.⁷³ In our MD simulations, the solutes were the corresponding nucleosides because their parameters are readily available from the PARMBSC1 and χOL3 force fields^57–59 and because the groups that are covalently linked to the nucleobases are expected to have minor influences on the IR spectra in the 1600 1800 cm⁻¹ region.

DFT calculations

We performed DFT calculations on the NMP-water clusters to obtain the base C=O and C=C stretching frequencies. As D₂O is commonly used as solvents in the IR spectroscopy experiments, we replaced all H₂O molecules with D₂O and changed all labile H atoms in the NMP molecules by D (Figure 1). In addition, we replaced GMP, CMP, TMP and UMP with 9-methylguanine (mG), 1-methylcytosine (mC), 1-methylthymine (mT) and 1-methyluracil (mU), respectively, as previous DFT calculations identified that the sugar and phosphate groups had minor impact on the base carbonyl vibrational properties.³⁰ We used DFT calculations to obtain the vibrational frequencies of the NMP-water cluster with all the water molecules fixed at their positions as sampled from the MD simulations. The electronic structures were described using the B3LYP functional,⁷⁵ the D3 dispersion corrections⁷⁶ and the 6-311G(d,p) basis set. The basis set was chosen to balance the accuracy and efficiency of the geometry optimizations and frequency analyses. To test its performance, we repeated the calculations on two CMP-water clusters with the 6-311++G(d,p) basis set and found that the differences in the carbonyl stretching frequencies were within 6 cm⁻¹, suggesting that the 6-311G(d,p) basis set was sufficient for the frequency predictions.

As the NMP-water clusters contained 144–229 atoms, we carried out initial geometry optimizations using the GPU-accelerated TeraChem software package.^77,78 We then utilized the Gaussian 16 program⁷⁹ to further optimize the structures and perform frequency analyses. A scale factor of 0.9679 was applied to correct the systematic errors of the frequency calculations.⁸⁰ Using the same electronic structure methods, we optimized the structures of mG and mT in vacuum to calculate the vibrational frequencies and transition dipoles of the C=O and C=C modes.

RESULTS AND DISCUSSION

Extracting representative NMP-water clusters from MD simulations

As a first step in the development of the vibrational frequency maps, we perform MD simulations of the NMP molecules in aqueous solutions and collect NMP-water clusters by implementing a spherical cutoff around the solute. To optimize the cutoff distance, R_cut, we consider GMP and compare its C=O stretching frequencies in vacuum and in GMP-water clusters. For this purpose, we carry out DFT calculations of deuterated mG, which shares the same base structure and almost identical carbonyl stretching properties as GMP.^15,30 Our calculation predicts that mG has a C=O vibrational frequency of 1746 cm⁻¹ in vacuum, in good agreement with the experimental value of 1738 cm⁻¹ when the molecule is isolated in N₂ matrix.⁸¹ This absorption peak shifts to 1692 cm⁻¹ when the C=O group forms a single hydrogen bond with a surrounding D₂O molecule, demonstrating the prominent solvochromatic effect and necessitates the sampling of NMP-water clusters that are representative of the solvation environment around the solute.

From the MD simulations of GMP, we calculate the O–O radial distribution function between the guanine base and the solvent molecules. As shown in Figure 2a, the first and second solvation shells of GMP occur at O–O distances of 3.2 and 5.2 Å, respectively. Water molecules in the first solvation shell directly interact with GMP, and on average, they form 1.5 hydrogen bonds with the C=O group and 0.4 hydrogen bonds with the adjacent N₁–H group in the guanine base. As such, we set an initial R_cut of 3.2 Å and include all the water molecules that are within R_cut of any atom in the guanine base, the C_1′ and C_2′ atoms in the sugar ring as well as the O and H atoms that are covalently linked to C_1′ in GMP (Figure 1). We then pick a GMP-water cluster and evaluate its vibrational frequencies using DFT calculations. This cluster contains 18 first-shell water molecules that form 2 hydrogen bonds with the C=O group and 1 hydrogen bond with the N₁-H group of the guanine base, as illustrated in Figure 3. The GMP-water cluster exhibits a C=O stretching frequency of 1678 cm⁻¹, suggesting that the presence of the first solvation shell decreases the absorption frequency of GMP by 68 cm⁻¹ as compared to the gas phase.

Figure 2:

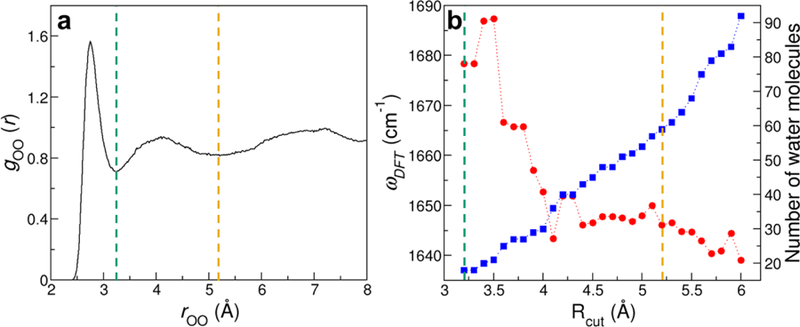
Determination of R_cut for the extraction of NMP-water clusters. (a) Radial distribution function between the O atom in the base of GMP and the O atom in the water molecules. (b) Carbonyl stretch frequencies of a GMP-water cluster as predicted from DFT calculations (red) and the number of water molecules (blue) as a function of R_cut. The green and yellow vertical lines indicate the first and second solvation shells of the guanine base, respectively.

Figure 3:

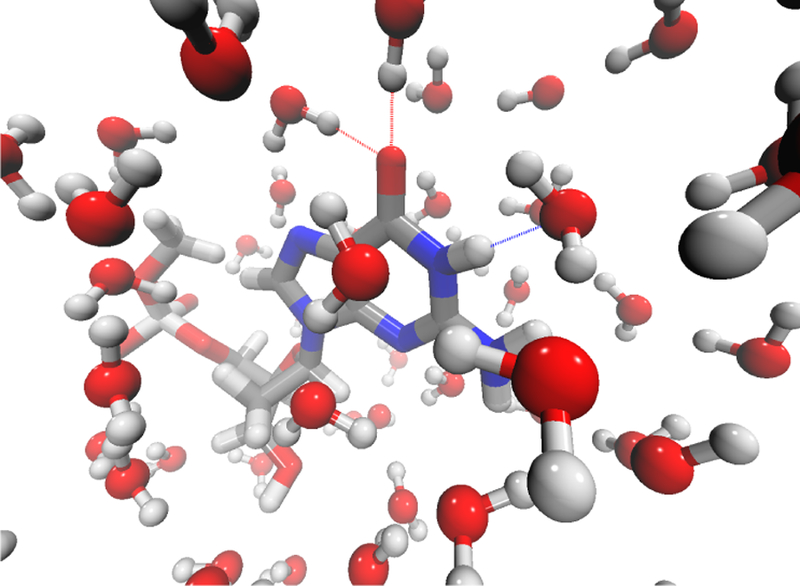
A snapshot of GMP in two solvation layers of H₂O molecules. Silver, red, blue and white represent C, O, N and H atoms, respectively. The dotted lines represent hydrogen bonds between GMP and water.

To assess the influence of solvent molecules beyond the first shell, we take the same snapshot of GMP from MD simulations and gradually increase the R_cut value with a step of 0.1 Å. We then repeat the DFT calculations to evaluate the carbonyl stretching frequencies in the GMP-water clusters. As demonstrated in Figure 2b, the frequencies fluctuate considerably as the cluster size grows larger, and reach a plateau when R_cut ≥ 5.2 Å. Notably, as R_cut increases from 3.2 to 5.2 Å, the C=O absorption peak shifts by 32 cm⁻¹ to the red side, indicating that both the first and second solvation shells are essential in determining the solvochromatic effect on GMP. Accompanying the frequency changes, the number of solvent molecules in the GMP-water cluster increases almost linearly with the cutoff distance. As demonstrated in Figure 3, the cluster contains 59 water molecules when R_cut is 5.2 Å. To balance the accuracy and efficiency of the DFT calculations, we set R_cut = 5.2 Å and extract 400 clusters from each NMP simulation. As we incorporate all solvent molecules that are within R_cut of the bases, the resulting NMP-water configurations comprise 43 – 70 water molecules.

Vibrational frequency maps for the nucleobase C=O stretches

From the NMP-water clusters, we carry out DFT calculations to evaluate the base C=O stretching frequencies and use them as benchmark data to develop the C=O vibrational frequency maps. To reduce the computational cost of the DFT calculations, we replace GMP, CMP, TMP and UMP with mG, mC, mT and mU because the sugar and phosphate groups have minor influences on the base carbonyl frequencies.^15,30 All the molecules in the NMP-water cluster are deuterated to mimic the D₂O solvent used in the IR experiments.¹⁵

To determine which atoms are essential in the normal mode of the base carbonyl stretch, we consider deuterated mG in vacuum and examine its absorption peak at 1746 cm⁻¹. We find that 89% of the vibrational amplitude comes from C=O stretching and 4% from N-D bending, in agreement with the findings in previous calculations.^14,15,30 Therefore, we incorporate the C, O and N atoms in the development of the frequency maps and use their local electric fields as collective coordinates to represent the solvation environment around a nucleobase,

$${\omega }_{map}={\omega }_0+\sum _{i\alpha }{c}_{i\alpha }{E}_{i\alpha }.$$ (9)

Here i indexes C, O and N atoms and α runs over x, y and z. E_iα is the electric field, in atomic unit, on atom i in direction α. In the parameterization of the frequency maps, we consider the electric fields on the chromophore atoms as exerted by all the solvent molecules in the NMP-water cluster, and the partial charges of the O and H atoms are set according to the TIP3P model.⁶⁰ Since the clusters obtained from MD simulations have different orientations, we exploit a coordinate system as shown in Figure 4a. Within each cluster, the C, O and N atoms in the NMP molecule define the xy plane: the y axis is along the $\overrightarrow{CO}$ direction, while the x axis takes an orthogonal direction and points towards the N atom. The z axis is perpendicular to the C-O-N plane.

Figure 4:

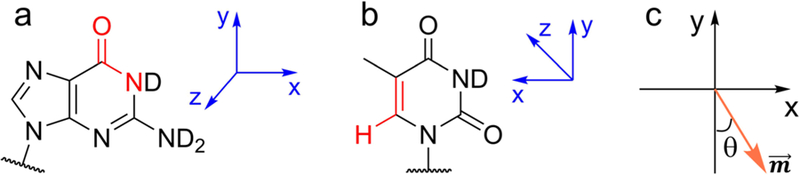
Coordinate system used in the development of the frequency maps for (a) the base C=O stretch mode and (b) the base C=C stretch mode. Atoms used to define the axes are highlighted in red. (c) Coordinate system used in the calculations of the transition dipoles $\overrightarrow{m}$ of the C=O and C=C vibrational modes.

In Eq. 9, the intercept ω₀ and the coefficients c_iα are determined by invoking the Fletcher-Reeves-Polak-Ribiere method⁸² and minimizing the differences in frequencies as predicted using the frequency map and DFT calculations for the NMP-water clusters, ${\mathrm{\Delta }}^2=\sum _j{\left({\omega }_{j,\text{map}}-{\omega }_{j,\text{DET}}\right)}^2$. Note that CMP, TMP and UMP all contain C=O and C=C groups, and their ω_DFT are calculated from the HMR method. Since ω₀ is the C=O stretch frequency in the absence of an external electric field, it can be analyzed by putting the nucleobases in a non-polar solvent. For this purpose, we perform DFT calculations of deuterated mG, mC, mT and mU in octane using the continuum solvation model and identify that the chromophores of the nucleobases can be categories into two types. The first type comprises the C=O group in mG and the C₂=O groups in mT and mU, which have relatively high site frequencies of 1722, 1709 and 1714 cm⁻¹, respectively. In contrast, the C=O group in mC and the C₄=O groups in mT and mU belong to the second type with lower site frequencies of 1686, 1686 and 1700 cm⁻¹, respectively. In all cases, the carbonyl stretch frequencies of the methylated nucleobases are about 20 cm⁻¹ lower than their corresponding gas-phase values. This suggests that ω₀ is strongly influenced by intermolecular interactions such as polarization and dispersion, which are not electrostatic in nature, in the condensed phase.

Due to the observed differences in the C=O frequencies, we treat the two types of chromophores separately and develop frequency maps for each of them. We refer to the two types as GT₂U₂ and CT₄U₄ and determine their ω₀ and c_iα by globally fitting the DFT frequencies of the 3 chromophores in each group. Parameters of the resulting GT₂U₂ and CT₄U₄ frequency maps are provided in Table 1. Note that the C₂=O groups in CMP, TMP and UMP are adjacent to two N atoms (Figure 1), and we use N₃ in the frequency maps because these atoms are capable of forming hydrogen bonds with the surrounding water molecules and influencing the C=O vibrational frequencies.

Table 1:

Parameters of the carbonyl stretch frequency maps. ω₀ are in cm⁻¹. The coefficients for the electric fields, c_iα, are in cm⁻¹/a.u..

Map	ω0	cCx	cCy	cCz	cOx	cOy	cOz	cNx	cNy	cNz
GT2U2	1716	1275	5658	339	−180	−385	−13	−853	−1026	−263
CT4U4	1691	426	5444	−31	−62	−451	21	−1257	315	−60

From Table 1, ω₀ in the GT₂U₂ frequency map is 25 cm⁻¹ larger than that in the CT₄U₄ map, hence properly capturing the trend that is observed when the two types of chromophores are solvated in octane and validating our parameterization procedures based on the NMP-water clusters. As for the coefficients c_iα, the largest contribution in both frequency maps come from the C atom along the $\overrightarrow{CO}$ direction, consistent with the fact that the normal mode is mainly composed of the C=O stretching vibration. Moreover, E_cy is negative since the hydrogen bonding interactions between the base C=O and the water –OH groups are highly directional, and hence the terms +5658E_Cy and +5444E_Cy in the frequency maps correspond to a redshift in the C=O site frequencies upon hydrogen bond formation. Apart from c_Cy, the coefficients for the O and N atoms in the xy plane also have considerable magnitudes. However, as the nucleobases have planar structures, contributions from the electric fields in the z direction are small.

To assess the performance of the combined MD simulations/DFT calculations approach, we plot the carbonyl frequencies predicted from the GT₂U₂ and CT₄U₄ frequency maps (ω_map) against those from DFT calculations (ω_DFT ). As shown in Figure 5, the 1600 NMP-water clusters extracted from MD simulations effectively sample a wide variety of chemical environments around the solute, as evident from the fact that their ω_DFT span a broad range of 1550–1750 cm⁻¹. From Figure 5a, ω_DFT for the C=O group in mG and the C2=O groups in mT and mU have similar distributions with the average values of 1669, 1676 and 1682 cm⁻¹, respectively. Likewise, the C=O group in mC and the C₄=O groups in mT and mU exhibit similar trends with the average ω_DFT of 1634, 1643 and 1655 cm⁻¹, respectively (Figure 5b). These observations justify our choices of developing two frequency maps to describe the vibrational behavior of different chromophore types. From Figure 5, ω_map have an excellent linear relation with ω_DFT in the whole spectral range, demonstrating that the frequency maps are capable of capturing the impact of the heterogeneous solvation conditions on the C=O vibrational frequencies of the NMP molecules. The average ω_map for all the carbonyl stretches are within 4 cm⁻¹ of the corresponding average ω_DFT, and the root-mean-square deviation for all the data points are 12.2 cm⁻¹ for both maps.

Figure 5:

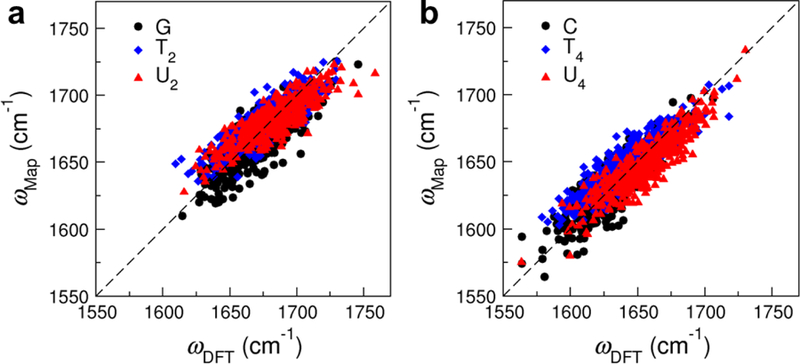
Correlation plots between the carbonyl stretch frequencies predicted from DFT calculations and (a) the GT₂U₂ frequency map for the C=O stretch in GMP and the C₂=O stretch in TMP and UMP, and (b) the CT₄U₄ frequency map for the C=O stretch in CMP and the C₄=O stretch in TMP and UMP. Each plot consists of 1200 data points from the NMP-water clusters. The root-mean-square deviations are 12.2 cm⁻¹ in both plots.

Vibrational frequency map for the nucleobase C=C stretch mode

In the pyrimidine bases cytosine, thymine and uracil (Figure 1), the stretch modes of the C=O and C₅=C₆ groups are highly coupled. In particular, the IR spectrum of TMP in D₂O exhibits three overlapping bands with absorption peaks at 1690 cm⁻¹, 1663 cm⁻¹ and 1629 cm⁻¹, which arise from the coupled C₂=O, C₄=O and C₅=C₆ vibrations.¹⁵ As such, along with the carbonyl stretch frequency maps, we will develop a frequency map to model the C₅=C₆ vibration and fully describe the IR absorption of CMP, TMP and UMP in the spectral region of 1600–1800 cm⁻¹.

We take TMP as a model system and design a C=C frequency map that takes the form of Eq. 9 and incorporates the electric fields on the C₅ and C₆ atoms. As the C=C stretching mode also involves some contributions from the C₆–H bending motion,¹⁵ we define the coordinate system such that the y axis is along the $\overrightarrow{C_6{C}_5}$ direction, the x axis is in the C–C–H plane and points towards the H atom, and the z axis is perpendicular to the C–C–H plane, as shown in Figure 4b. From DFT calculations of the 400 TMP-water clusters, we determine the parameters ω₀ and c_iα in the frequency map by minimizing ${\mathrm{\Delta }}^2=\sum _{j=1}^{400}{\left({\omega }_{j,\text{map}}-{\omega }_{j,\text{DET}}\right)}^2$. Here ω_DFT of the C=C stretches in TMP are obtained using the HMR method.

The parameters for the C=C vibrational frequency map are listed in Table 2. The zero-field intercept ω₀ is 1638 cm⁻¹, in good agreement with the C=C vibrational frequency of 1642 cm⁻¹ from our calculations of deuterated mT in octane. The coefficients c_iα for the C₅ and C₆ atoms have similar magnitude but different signs, as the C=C bond is formed from two identical atoms and they move in opposite directions in a stretching motion. In addition, contributions from the two C atoms in the z direction are small because the C=C stretching mode is mainly within the plane of the nucleobase.

Table 2:

Parameters for the C=C vibrational frequency map. ω₀ is in cm⁻¹ and c_iα are in cm⁻¹/a.u.

Map	ω0	$c_{C_{5}x}$	$c_{C_{5}y}$	$c_{C_{5}z}$	$c_{C_{6}x}$	$c_{C_{6}y}$	$c_{C_{6}z}$
C=C	1638	−1952	−426	−210	1101	1521	62

Compared to the C=O frequency maps in Table 1, c_iα in the C=C frequency map are much smaller in magnitude, indicating that the C=C vibration is less sensitive to the solvent electrostatic environment. To further assess this lack of sensitivity, we construct the correlation plot in Figure 6 for the C=C stretch frequencies obtained from the map and from DFT calculations. While we use the same 1200 snapshots of CMP-, TMP- and UMP-water clusters to compute the frequencies of the C=C and C=O stretches, ω_DFT of the C=C vibration only span a spectral range of 60 cm⁻¹, much narrower than those observed in Figure 5. Moreover, as compared to the C=O stretches, there is a weaker correlation between ω_map and ω_DFT for the C=C vibration, suggesting that the electric fields on the C₅ and C₆ atoms are not the ideal collective coordinates to represent the condensed phase environment. However, we will still use the C=C frequency map for spectra calculations because it provides an efficient way to incorporate the C=C vibrations in the modeling of the pyrimidine bases.

Figure 6:

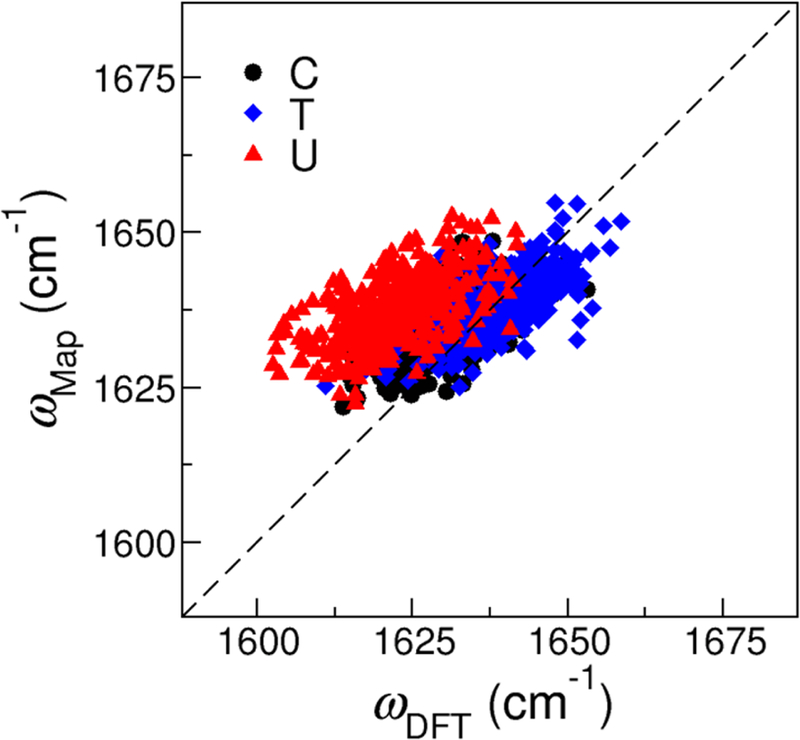
Correlation plot between the C=C stretch frequencies predicted from the frequency map (ω_map) and from DFT calculations (ω_DFT ) for CMP, TMP and UMP. The plot contains 1200 data points from the corresponding NMP-water clusters. The root-mean-square deviation is 10.8 cm⁻¹.

Transition dipoles of the nucleobase C=O and C=C stretches

From Eqs. 3 and 5, we also need the transition dipole moments of the chromophores to model the IR spectra of NMPs. For this purpose, we use deuterated mG and mT, respectively, as model systems to determine the transition dipoles of the C=O and C=C stretches. As the two modes are parameterized using the same procedure, we will discuss the C=O stretch in the following to demonstrate the process. In the first step, we carry out DFT geometry optimizations of deuterated mG in vacuum and use the resulting configuration to define the coordinate system for the C=O vibration, as shown in Figure 4a. Similarly, when we consider the C=C stretch, we use the minimum energy structure of mT to define the coordinate system as shown in Figure 4b. Next, from the optimized geometry of mG, we displace the C and O atoms along y and -y directions, respectively, with equal amount such that the C=O bond is extended or compressed by 0.001 Å. This step is then repeated to change the C=O bond lengthy by ±0.002 Å. At each C=O distance, l, we perform constrained geometry optimization of mG by holding l constant and obtain the total dipole moment, $\overrightarrow{\mu }$, of the molecule. Finally, we assume the change in the molecular dipole arises entirely from the displacement of the C=O bond, and plot the dipole moment in the x, y and z directions as a function of l. Using a linear regression algorithm, we compute the dipole derivatives in the three directions, $\frac{\partial {\mu }_x}{\partial l}$, $\frac{\partial {\mu }_y}{\partial l}$ and $\frac{\partial {\mu }_z}{\partial l}$.

To obtain the magnitude of the transition dipole $\mathrm{\left|}\overrightarrow{m}\mathrm{\right|}$ of the C=O or C=C vibration, we use the following relation,

$$\mathrm{\left|}\overrightarrow{m}\mathrm{\right|}=\frac{1}{\sqrt{M}}\mathrm{\left|}\frac{\partial \overrightarrow{\mu }}{\partial l}\mathrm{\right|}=\sqrt{\frac{1}{M}\left[{\left(\frac{\partial {\mu }_x}{\partial l}\right)}^2+{\left(\frac{\partial {\mu }_y}{\partial l}\right)}^2+{\left(\frac{\partial {\mu }_z}{\partial l}\right)}^2\right]}.$$ (10)

Here M is the reduced mass of the C=O or C=C normal mode, which we acquire from the DFT vibrational analyses of mG and mT, respectively. The values of M, the dipole derivatives and $\left|\overrightarrow{m}\right|$ for the two modes are shown in Table 3.

Table 3:

Magnitudes and directions of the C=O and C=C transition dipoles. The reduced mass M of a vibrational mode is in atomic mass unit (u), and the dipole derivatives $\partial {\mu }_{\text{x}}/\partial l$, $\partial {\mu }_{\text{y}}/\partial l$ and $\partial {\mu }_z/\partial l$ are in D Å⁻¹. The magnitude of the transition dipole is in D Å⁻¹u^−1/2 and the angle θ is in degrees.

Mode	M	$\partial {\mu }_x/\partial l$	$\partial {\mu }_y/\partial l$	$\partial {\mu }_z/\partial l$	$\mathrm{\left|}\overrightarrow{m}\mathrm{\right|}$	θ
C=O	12.49	0.58	−9.08	0	2.57	3.65
C=C	6.19	0	−3.58	0	1.44	0

Stretches of the C=O and C=C groups are in the plane of the purine or pyrimidine rings, resulting in a value of 0 for $\frac{\partial {\mu }_z}{\partial l}$ in both modes. As such, we only focus on the xy plane to determine the orientation of the transition dipoles. As illustrated in Figure 4c, we define θ to be the angle between $\overrightarrow{m}$ and the y axis, and use the relation that $\tan \theta =\mathrm{\left|}\frac{\partial {\mu }_{\text{x}}/\partial l}{\partial {\mu }_{\text{y}}/\partial l}\mathrm{\right|}$ to obtain their values. From Table 3, $\overrightarrow{m}$ of the carbonyl group points from O to C with a slight tilt of θ =3.65°, and $\overrightarrow{m}$ of the C=C group is along the chemical bond pointing from C₅ to C₆. The small θ values are consistent with the fact that the C=O and C=C normal modes are dominated by the stretches of the two groups along the y direction.

Modeling the IR absorption spectra of NMPs in aqueous solutions

To evaluate the performance of the theoretical vibrational frequency maps and transition dipole models, we apply them to calculate the IR spectra of NMPs in aqueous solutions in the 1600–1800 cm⁻¹ region. Note that in CMP, TMP and UMP, the C=O and C=C vibrations are coupled to each other. Considering that these interactions depend on the distances and relative orientations of the chromophores, which have only minor changes in the MD simulations due to the constraint of the ring structures of the pyrimidine bases, the coupling constants remain relatively stable throughout the simulations. Therefore, we calculate the coupling constants for the CMP-, TMP- and UMP-water clusters, each of which contain 400 configurations, using the HMR method^53–55 and take their average values in the IR spectra calculations. The coupling constants are presented in Table 4.

Table 4:

Coupling constants for the C=O and C=C groups in the nucleobases, calculated from the average value of 400 snapshots for CMP-, TMP- and UMP-water clusters. All coupling constants are in cm⁻¹.

Nucleobase	C2=O/C4=O	C2=O/C5=C6	C4=O/C5=C6
Cytosine	–	−10.57	–
Thymine	17.27	−8.16	6.26
Uracil	18.55	−9.35	16.20

To calculate the theoretical IR spectra, we treat GMP as a single-chromophore system. In contrast, CMP, TMP and UMP all contain C=O and C=C groups and we use their site frequencies and couplings to model these multi-chromophore systems. Specifically, we take the following procedure to calculate the IR absorption line shapes of the NMP molecules.

1. From the MD simulations, we calculate the electric fields on the C, O and N atoms for the C=O vibrations in NMP. For CMP, TMP and UMP, we also calculate the electric fields on the C₅ and C₆ atoms for the C=C stretch. The electric fields come from all the solvent molecules and ions whose geometric centers are within 20 Å of the corresponding chromophore atoms, and we exclude the contributions from any atoms that are part of the NMP molecule.

2. The site frequencies of the C=O stretches are obtained using the C=O frequency maps in Table 1. The GT₂U₂ map is used when we consider C=O in GMP or C₂=O in TMP and UMP, and the CT₄U₄ map is implemented when we treat C=O in CMP or C₄=O in TMP and UMP. To compute the site frequencies for the C=C vibrations in CMP, TMP and UMP, we invoke the C=C frequency map in Table 2. These site frequencies constitute the diagonal terms of the vibrational Hamiltonian in Eq. 2.

3. To account for the interactions between chromophores in CMP, TMP and UMP, we take the average coupling constants as listed in Table 4 to construct the off-diagonal terms of the vibrational Hamiltonian.

4. The transition dipoles of the C=O and C=C vibrations are calculated from the instantaneous structures of the NMP molecules in the MD simulations. The coordinate systems are shown in Figure 4 and the magnitude and directions of the transition dipoles are provided in Table 3.

5. The IR spectra of the GMP molecule, which contains only one chromophore, is calculated using Eq. 5. The absorption IR line shapes of CMP, TMP and UMP are obtained by implementing Eq. 3. Here T₁ is set to be 649 fs as determined experimentally for the carbonyl stretching mode of GMP (Supporting Information), and we ignore the differences between the T₁ values of the C=O and C=C stretches.

The theoretical IR spectra of the NMP molecules are shown in Figure 7, which are in good agreement with the experimental measurements.¹⁵ To better compare the results, we summarize the peak positions observed in the theoretical and experimental spectra in Table 5. As shown in Figure 7a, our calculations correctly predict that there is a single absorption band for GMP in the 1600–1800 cm⁻¹ region originating from the C=O stretch vibration. The theoretical absorption peak is at 1668 cm⁻¹ and the full-width-half-max (FWHM) of the spectrum is 24 cm⁻¹, which well reproduce the experimentally observed peak position of 1665 cm⁻¹ and width of 31 cm⁻¹.¹⁵ The other 3 NMPs have more complex spectral features due to coupled vibrations of the C=O and C=C modes. For example, from our MD simulations, the C=O group in CMP has an average frequency of 1635 cm⁻¹ and a standard deviation of 20 cm⁻¹, and the C5=C6 group has an average frequency of 1638 cm⁻¹ and a much narrower distribution of 5 cm⁻¹. While the two modes in CMP show significant overlap in their site frequencies, the large coupling constant of −10.57 cm⁻¹ between them (Table 4) results in two absorption peaks at 1648 and 1624 cm⁻¹ for the molecule, in excellent agreement with the experimental observations.¹⁵

Figure 7:

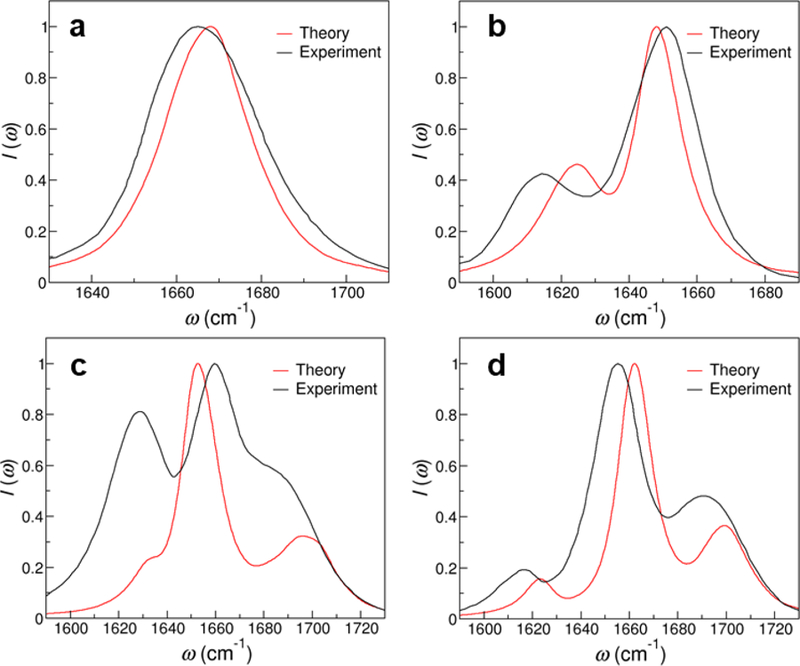
Theoretical and experimental¹⁵ IR spectra of (a) GMP (b) CMP (c) TMP and (d) UMP in aqueous solutions. The IR signals are normalized by the intensities of the highest peak.

Table 5:

Positions of the theoretical and experimental IR absorption peaks for the nucleotides and their derivatives. The frequencies are in cm⁻¹ and ω₁ through ω₃ are arranged from higher to lower frequencies.

Molecule	ω1 (theory)	ω1 (exp)	ω2 (theory)	ω2 (exp)	ω3 (theory)	ω3 (exp)
GMP15	1668	1665	-	-	-	-
CMP15	1648	1651	1624	1614	-	-
TMP15	1696	1690	1653	1663	1633	1629
UMP15	1699	1693	1662	1655	1623	1617
IMP70	1663	1670	-	-	-	-
m3-isoG71	1643	1645	-	-	-	-
caffeine74	1687	1695	1643	1642	-	-
4-thiouridine72	1674	1690	1634	1616	-	-
dGuo/DMSO18	1686	1693	-	-	-	-
Uridine/CHCl3 73	1720	1716	1677	1688	1628	1637

The IR spectra of TMP and UMP both comprise 3 peaks, as shown in Figure 7c and d. To elucidate the origin of the absorption bands, we first consider TMP and find the average frequencies of its C₂=O, C₄=O and C₅=C₆ modes to be 1687, 1654 and 1642 cm⁻¹, respectively. As each of the two C=O groups forms an average of 1.4 hydrogen bonds with the surrounding water molecules, their fluctuating frequencies have a standard deviation of 18 cm⁻¹. In contrast, the C=C vibration is less influenced by the solvent environment and has a distribution of 4 cm⁻¹. By using the C₂=O, C₄=O and C₅=C₆ modes as basis to represent the vibrational subspace of TMP and taking the coupling constants from Table 4, we construct the average vibrational Hamiltonian

$$\kappa =\left(\begin{array}{ccc}1687& 17.27& -8.16\\ 17.27& 1654& 6.26\\ -8.16& 6.26& 1642\end{array}\right).$$

We then diagonalize κ to obtain the normal frequency and normal mode matrices,

$$\mathrm{\Omega }=\left(\begin{array}{ccc}1695& 0& 0\\ 0& 1653& 0\\ 0& 0& 1635\end{array}\right)\text{and}\hspace{0.17em}U=\left(\begin{array}{ccc}0.92& 0.25& 0.30\\ 0.37& -0.76& -0.53\\ -0.10& -0.60& 0.80\end{array}\right).$$

The diagonal matrix Ω contains 3 components, which correspond to the 3 absorption peaks in the TMP spectrum and their values are in quantitative agreement with the peak positions of the TMP molecule as observed experimentally (Table 5). Due to the large couplings between the 3 modes, none of the absorption peaks in TMP can be attributed to the vibration of a single chromophore. For example, the normal-mode matrix U demonstrates that the strongest peak at 1653 cm⁻¹ is composed of the C₂=O, C₄=O and C₅=C₆ vibrations with their contributions being 6%, 58% and 36%, respectively.

UMP shares similar properties with TMP. The average frequencies of its C₂=O, C₄=O and C₅=C₆ modes are 1691, 1654 and 1641 cm⁻¹, respectively. However, due to the lack of a methyl group at the C₅ position (Figure 1), UMP has a much larger coupling constant between the C₄=O and C₅=C₆ modes compared to that in TMP,¹⁵ as shown in Table 4. This can be rationalized using the normal mode components of deuterated mU in vacuum. From DFT calculations, the H atom covalently bonded to C₅ accounts for 8% of the normal mode magnitude for both the C₄=O and C₅=C₆ stretches, and hence serves as a bridge between the two vibrational modes and increases their interactions. Because of the large inter-mode couplings, the 3 absorption bands are more separated from one another in the IR spectrum of UMP as compared that of TMP. Therefore, from analyzing the vibrational Hamiltonian, we uncover that the 3-peak spectral features of TMP and UMP arise both from the distinct site frequencies of their C=O and C=C stretches and the significant couplings between the chromophores.

As Figure 7 and Table 5 show, our theoretical results reproduce the experimental IR line shapes of NMPs very well with the differences in their peak positions all within 10 cm⁻¹. These observations validate our theoretical approach for modeling the IR spectra of nucleobases from three aspects. First, when developing the C=O and C=C vibrational frequency maps, our fitting procedure ensures that the site frequencies predicted by the maps match those from DFT calculations. The excellent agreement in the peak frequencies between the theoretical and experimental spectra therefore reports on the ability of the DFT methods to describe the potential energy surfaces of the C=O and C=C stretches. Second, the inter-chromophore couplings dictate the separation of vibrational normal modes in the IR spectra. The fact that the predicted peak positions and their separations in the spectra of CMP, TMP and UMP properly reproduce the experimental measurements validates our methods of obtaining the coupling constants. Moreover, the FWHM and the line shapes of the spectra are strongly dependent on the fluctuating NMP configurations and solvent environment. The good comparison between the theoretical and experimental line shapes hence provides a stringent test on the capability of MD simulations to correctly capture the dynamics of NMPs in the condensed phase.

Note that we use different magnitude for the C=O and C=C transition dipoles (Table 3) when modeling CMP, TMP and UMP. As shown in Figure 7, this method correctly captures the relative peak intensities in the IR spectra of CMP and UMP. For TMP, however, it significantly underestimates the peak at 1633 cm⁻¹ (T3) as the ratio between its intensity and that of the strongest peak (T2) is 0.24 from our calculations, as compared to 0.81 from the experiment measurements.¹⁵ This phenomenon occurs likely because we obtain the transition dipoles of the C=O and C=C stretches from gas-phase calculations, while the solvation environment has been shown to influence their orientations.¹⁵ To further analyze the effect, we examine the DFT calculations and find that the T3/T2 ratio is 0.06 in vacuum, and it increases to 0.83 when we average over the 400 TMP-water clusters. Therefore, if one wants to accurately describe the peak intensities in the IR spectrum of TMP, a different transition dipole model for the C=C vibration that account for the aqueous environment is required.

Modeling the IR spectra of nucleobase derivatives in aqueous solutions and nucleosides in organic solvents

We use clusters of GMP, CMP, TMP and UMP with surrounding water molecules as model systems to develop the vibrational frequency maps and transition dipoles for the nucleobase C=O and C=C vibrations. However, we expect the theoretical methods to be generally applicable to purines and pyrimidines that contain carbonyl chromophores and potentially be transferable to other solvents. To further validate the frequency maps, we apply them to a set of nucleobase derivatives in aqueous solutions and to nucleosides in organic solvents.

As shown in Figure 8, we choose the nucleobase derivatives inosine 5′-monophosphate (IMP), N⁶,N⁶,9-trimethylisoguanine (m₃-isoG), caffeine and 4-thiouridine as test cases. These compounds contain minor bases in nucleic acids and are selected to assess different combinations of the C=O and C=C frequency maps. To model their IR absorption spectra in aqueous solutions, we follow similar procedures as discussed in the last section without applying any adjustments in the parameters. The theoretical and experimental line shapes and peak positions are compared in Figure 9 and Table 5, respectively.

Figure 8:

Chemical structures of the nucleobase derivatives with the ring atoms labeled. The labile hydrogens that are highlighted in blue are considered to be deuterated in the IR spectra calculations.

Figure 9:

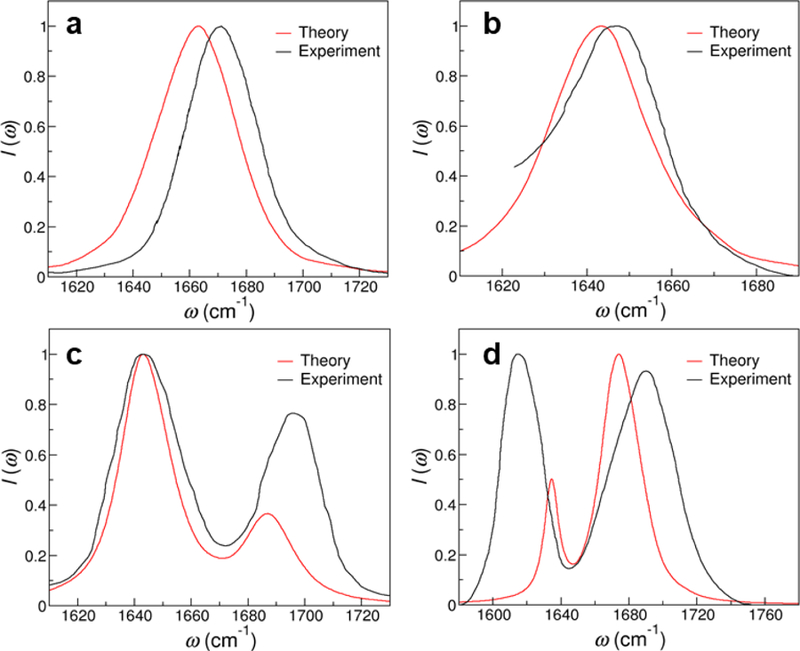
Theoretical and experimental IR spectra of (a) IMP,⁷⁰ (b) m3-isoG,⁷¹ (c) caffeine⁷⁴ and (d) 4-thiouridine.⁷²

We first consider IMP and m₃-isoG because each of them contains only one C=O group. IMP forms from the nucleoside inosine, which can exist in the anticodon of transfer RNAs and form wobble base pairs with other nucleotides.⁸³ Its base hypoxanthine is a spontaneous deamination product of adenine, which differs from guanine by only an amino group at the C₂ position (Figure 8a). We hence apply the GT₂U₂ frequency map to model the C=O stretching mode of IMP and find the theoretical IR spectrum to exhibit a single absorption peak at 1663 cm⁻¹ and a FWHM of 33 cm⁻¹. From Figure 9a, the predicted line shape is in excellent agreement with the experimental measurements, as the peak is 7 cm⁻¹ lower and the FWHM is only 3 cm⁻¹ wider than those in experiments.⁷⁰ Isoguanine is a product from the oxidative damage of DNA^84,85 and here we consider its methylated form m₃-isoG, which has inverted positions for the amino and carbonyl groups as compared to the guanine base (Figure 8b). In m₃-isoG, the single C=O chromophore is adjacent to an amino and an imine group, which mimics the chemical structure of cytosine. Therefore, we invoke the CT₄U₄ frequency map and use the electric fields on the C, O and N₁ atoms to calculate the site frequencies of the chromophore from MD simulations. As demonstrated in Figure 9b, the theoretical spectrum of m₃-isoG has a peak position of 1643 cm⁻¹ and a FWHM of 28 cm⁻¹. It well reproduces the experimental spectrum, in which the absorption peak is at 1645 cm⁻¹ and the width is 32 cm⁻¹.⁷¹

Next, we examine caffeine and 4-thiouridine, which contain multiple chromophores that absorb in the 1600–1800 cm⁻¹ region. Caffeine is a widely consumed central nervous system stimulant⁸⁶ that comprises two C=O groups in the purine ring, as shown in Figure 8c. Considering its structural similarity to thymine, we calculate the electric fields on the corresponding C, O and N₁ atoms and implement the GT₂U₂ and CT₄U₄ frequency maps to obtain the site frequencies of the C₂=O and C₆=O stretches, respectively, from MD simulations. We then take a coupling constant of 17.27 cm⁻¹, which is the average coupling between the C=O groups in thymine (Table 4), to model the interactions between the two chromophores in caffeine. As shown in Figure 9c, the theoretical spectrum has an intense absorption peak at 1643 cm⁻¹ and a second peak at 1687 cm⁻¹, correctly capturing the line shape and peak positions in the experimental spectrum.⁷⁴ The two absorption peaks arise from coupled vibrations of the C₂=O and C₆=O stretches. From the MD simulations, we find that the average frequencies of the two modes are 1677 and 1654 cm⁻¹, respectively, and hence C₂=O has a more significant contribution to the peak at higher frequency, whereas C₆=O contributes more to the peak at lower frequency. As demonstrated in Figure 8d, 4-thiouridine is a minor nucleoside in transfer RNA⁸³ and it has almost identical structure with uridine except that the oxygen atom at position 4 of the pyrimidine ring is replaced by a sulfur atom. We hence apply the GT₂U₂ and the C=C frequency maps to model the C₂=O and C₅=C₆ stretches in 4-thiouridine, which yield average frequencies of 1673 and 1637 cm⁻¹ for the two modes, respectively. To describe their interactions, we take a coupling constant of −9.35 cm⁻¹ as in uracil (Table 4). The theoretical IR spectrum correctly predicts the 2-peak feature as observed in the experimental measurements,⁷² and the absorption bands at 1674 cm⁻¹ and 1634 cm⁻¹ are almost entirely from the C=O and C=C modes, respectively. The predicted peak positions are within 18 cm⁻¹ as compared to the experimental spectrum, although our calculations cannot correctly describe the relative intensities of the two absorption peaks.⁷² These discrepancies appear possibly because exchanging a C=O group to a C=S group results in relatively large perturbations to the corresponding vibrational normal modes.

Finally, we assess the transferability of the frequency maps by applying them to deoxyguanosine (dGuo) in DMSO and uridine in CHCl₃. dGuo and uridine share the same chromophores as GMP and UMP, respectively, and hence we use the same frequency maps and transition dipoles as in the two NMP cases. From Figure 10 and Table 5, the calculated IR line shapes well capture the experimental spectral features, demonstrating that the frequency maps can be used for nucleobases in non-aqueous environment. In particular, dGuo has a single absorption band with a peak position of 1686 cm⁻¹ and a FWHM of 20 cm⁻¹, which are in good agreement with the experimental values of 1693 and 23 cm⁻¹, respectively (Figure 9a).¹⁸ Our calculations also correctly predict that, as compared to the spectrum of GMP in D₂O (Figure 7), dGuo in DMSO has a blue shifted absorption peak and a narrower line width because the organic solvent has a smaller dielectric constant and does not form hydrogen bonds with the base C=O group. Similar to UMP, uridine in CHCl₃ has three absorption bands in the 1600–1800 cm⁻¹ region, and the predicted peak positions are within 11 cm⁻¹ of those in the experimental spectrum (Figure 9b).⁷³ The calculations also capture the trend that, due to the low polarity of CHCl₃, the peaks of uridine are much higher in frequency than those for UMP in D₂O. Note that in Figure 9b, the experimental IR line shape is unexpectedly wide possibly because the uridine molecules dimerize in the nonpolar solvent.⁷³

Figure 10:

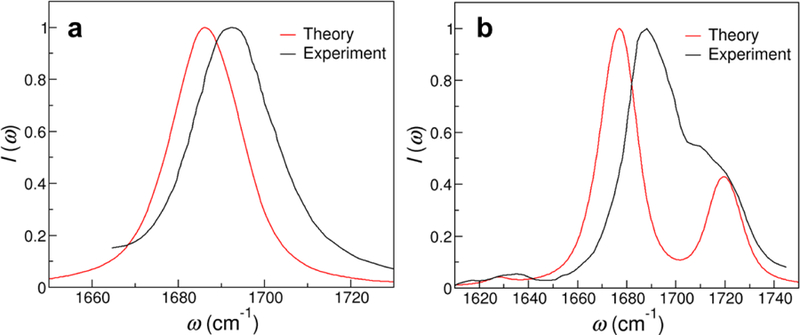
Theoretical and experimental IR spectra of (a) dGuo in DMSO¹⁸ and (b) uridine in CHCl₃.⁷³

CONCLUSIONS

In this work, we combine MD simulations and DFT calculations to develop the first C=O and C=C vibrational frequency maps for nucleobases. By relating the site frequencies to the electric fields from the solvent environment, the frequency maps allow one to calculate the vibrational frequencies of the chromophores directly from MD simulations and effectively incorporate dynamical effects in the modeling of the IR spectra of nucleobases. We then apply the frequency maps, along with the coupling constants and transition dipoles of the C=O and C=C modes, to NMPs and nucleobase derivatives in aqueous solutions as well as nucleosides in organic solvents and demonstrate that the theoretical IR spectra are in good agreement with experimental measurements. In all cases, the predicted peak frequencies are within 18 cm⁻¹ of the peaks in the experimental spectra, validating our theoretical approach. We notice that our theoretical spectra are in general a bit narrower than the corresponding experimental spectra and attribute the errors to the following reasons. First, in the development of the frequency maps, we obtain ω_DFT by optimizing the structure of the solutes, which partially removes the inhomogeneous broadening of the C=O and C=C vibrational frequencies of the NMP molecules. An alternative and more effective approach is to calculate the potential energy surfaces of the bond stretching and compute the vibrational frequencies by numerically solving the Schrödinger equation. Second, Figure 5 shows that the C=O maps slightly overestimate the frequencies on the red side and underestimate them on the blue side as compared to the values of ω_DFT, resulting in a narrowing of the overall IR spectrum. Moreover, the errors might come from the inaccuracy of the classical force field as it determines how solvent molecules and counterions are arranged around the chromophores and the extent to which dynamical effects influence the line widths.

The frequency maps can be readily extended to model non-linear vibrational spectroscopy of oligonucleotides and nucleic acids in the carbonyl stretch region. As they are applicable to nucleobase derivatives and are transferable in different solvents, the maps can also be exploited to study nucleic acids that contain minor bases or in non-aqueous media such as lipid membranes. Moreover, one can combine them with the vibrational frequency map for the phosphate vibrations⁴⁹ to examine different spectral regions and elucidate the interactions between the bases and the backbone of the nucleic acids. These frequency maps bridge vibrational spectroscopy experiments and MD simulations, which provide an essential tool to elucidate how the observed spectral signatures are determined by the structural arrangements of the chromophores, the conformational dynamics of the nucleic acids and the fluctuating solvation environment.