Abstract
Motivation
High-resolution Hi-C data are indispensable for the studies of three-dimensional (3D) genome organization at kilobase level. However, generating high-resolution Hi-C data (e.g. 5 kb) by conducting Hi-C experiments needs millions of mammalian cells, which may eventually generate billions of paired-end reads with a high sequencing cost. Therefore, it will be important and helpful if we can enhance the resolutions of Hi-C data by computational methods.
Results
We developed a new computational method named HiCNN that used a 54-layer very deep convolutional neural network to enhance the resolutions of Hi-C data. The network contains both global and local residual learning with multiple speedup techniques included resulting in fast convergence. We used mean squared errors and Pearson’s correlation coefficients between real high-resolution and computationally predicted high-resolution Hi-C data to evaluate the method. The evaluation results show that HiCNN consistently outperforms HiCPlus, the only existing tool in the literature, when training and testing data are extracted from the same cell type (i.e. GM12878) and from two different cell types in the same or different species (i.e. GM12878 as training with K562 as testing, and GM12878 as training with CH12-LX as testing). We further found that the HiCNN-enhanced high-resolution Hi-C data are more consistent with real experimental high-resolution Hi-C data than HiCPlus-enhanced data in terms of indicating statistically significant interactions. Moreover, HiCNN can efficiently enhance low-resolution Hi-C data, which eventually helps recover two chromatin loops that were confirmed by 3D-FISH.
Availability and implementation
HiCNN is freely available at http://dna.cs.miami.edu/HiCNN/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The Hi-C technique (Lieberman-Aiden et al., 2009) was developed to indicate three-dimensional (3D) conformation of the genome. Compared with previous chromosome conformation capture techniques, including 3C (Dekker et al., 2002), 4C (Zhao et al., 2006) and 5C (Dostie et al., 2006), the main advantage of Hi-C method is that it can capture potential contacts across the entire genome (Lieberman-Aiden et al., 2009), which provides an opportunity to reconstruct the 3D structures of the whole genome (Hu et al., 2013; Varoquaux et al., 2014). Hi-C data have also been applied to the areas of predicting DNA methylation (Wang et al., 2016) and exploring the relationship between Xist lncRNA and 3D genome architecture (Engreitz et al., 2013). By systematically analyzing Hi-C data, researchers have found significant conformational characteristics of the genome including: open and close compartments (Lieberman-Aiden et al., 2009) and their successors six subcompartments (Rao et al., 2014), topologically associating domains (TADs) (Dixon et al., 2012), and Hi-C peaks that indicate chromatin loops (Rao et al., 2014). Low-resolution Hi-C data (e.g. 1 Mb and 500 kb) consist of blurred boundaries of TADs and Hi-C peaks, which makes it difficult to accurately identify the locations of TADs and peaks. Recently, experimental high-resolution Hi-C data are available, such as at 40 kb (Dixon et al., 2012), 10 kb (Rao et al., 2014) and 1 kb (Bonev et al., 2017) resolutions, which makes the identifications of TADs and Hi-C peaks more efficient and accurate. It is apparent that high-resolution Hi-C data are progressively in demand for researchers when they try to explore the complex 3D structures of chromosomes at kilobase resolution.
The publicly available high-resolution Hi-C data are mostly generated from time-consuming Hi-C experiments (Rao et al., 2014), which needs millions of mammalian cells and with a large amount of sequencing cost involved. Therefore, it will be more efficient and economical if we can develop computational methods to enhance the resolutions of Hi-C data. Since the high-resolution Hi-C contact matrices include repeatable patterns (Dixon et al., 2012; Rao et al., 2014), it is feasible to let machine learning algorithms to learn from these patterns and then use the learned models to reveal the patterns that are unobvious in the low-resolution Hi-C data. Zhang et al. (Zhang et al., 2018) developed the state-of-the-art computational method named HiCPlus to enhance the resolutions of Hi-C data, which uses a three-layer convolutional neural network (ConvNet) to learn the mapping between low-resolution and high-resolution Hi-C contact matrices. They first proved that the entries in the Hi-C contact matrices can be reliably predicted from their n × n surrounding matrices and found that when n equals 13 the accuracy reaches a high plateau. HiCPlus outperforms other types of interpolation methods (Zhang et al., 2018) including random forest and Gaussian smoothing. The Pearson’s correlation coefficients between HiCPlus-enhanced and experimental high-resolution Hi-C are even larger than those between two experimental replicates.
There is still room for improvement for HiCPlus. The task of resolution enhancement is analogous to the problem of single image super-resolution (SR) in the field of computer vision. In the past four years, several outstanding ConvNet-based SR methods were developed. SRCNN (Dong et al., 2014) first introduced the deep learning method for image SR, which used a three-layer convolutional neural network to learn an end-to-end mapping between low- and high-resolution images. VDSR (Kim et al., 2016) used a very deep ConvNet (20 layers), first introduced global residual learning for SR, and increased convergence speed by adjustable gradient clipping, which makes it outperform SRCNN. DRRN (Tai et al., 2017) used a further deeper ConvNet (52 layers) and adopted global and local residual learning by introducing recursive learning. Its evaluation results indicate that DRRN outperforms several methods, including VDSR and DRCN (Kim et al., 2016). The architectures of recent published ConvNet-based SR methods [e.g. MemNet (Tai et al., 2017) and CMSC (Hu et al., 2018)] are all based on global and local residual learning. In general, VDSR (Kim et al., 2016) proved that deeper ConvNets and global residual learning are effective to achieve better performance than SRCNN. DRRN (Tai et al., 2017) concluded that local residual learning along with much deeper ConvNets than VDSR can further improve the accuracy.
In this study, we developed a new ConvNet-based computational method named HiCNN for resolution enhancement of Hi-C data. Our method directly learns the mapping function between low-resolution and high-resolution Hi-C contact matrices via a very deep convolutional neural network (54 layers). The first two layers are designed for pattern extraction and representation, which is similar to the first layer in HiCPlus and SRCNN. The following 52 layers are designed to implement global and local residual learning in our ConvNet, because several ConvNet-based SR methods have proved that these two residual learning manners significantly improve the performance of resolution enhancement. The number of layers was predefined to 54 and easy to be altered if needed. Our evaluation results show that HiCNN outperforms HiCPlus in multiple evaluation criteria, which further supports the observation that deeper ConvNets along with global and local residual learning can significantly improve SR performance on Hi-C data.
2 Materials and methods
2.1 Hi-C data preprocessing and contact matrix generation
The high-resolution Hi-C datasets are from GEO GSE63525 in which Rao et al. (Rao et al., 2014) provided high-resolution Hi-C paired-end reads that were mapped to the corresponding reference genomes of eight different cell types. We used three of the eight cell types including GM12878 (human), K562 (human) and CH12-LX (mouse), and downloaded corresponding Hi-C paired-end reads that were uniquely mapped to reference genomes with MAPQ scores from BWA (Li and Durbin 2010) larger than zero. Since Rao et al. (Rao et al., 2014) also released a high-resolution replicate on GM12878, we used four Hi-C datasets in total including GM12878, GM12878 replicate, K562 and CH12-LX. In this way, we can use the Hi-C data from GM12878 replicate to evaluate the enhanced Hi-C data of GM12878 and use Hi-C data from GM12878 and K562 to test if our computational method can effectively enhance Hi-C resolutions of one cell type by using the Hi-C data from another cell type as training data. We can also use Hi-C data from GM12878 and CH12-LX to see if our enhancement method can be applied to different species.
For each of the four datasets, we first looped through all paired-end reads, and then picked up those fallen into the same chromosome. The real high-resolution Hi-C contact matrix of a single chromosome is generated by counting all paired-end reads related to the chromosome. The low-resolution Hi-C contact matrix of a given chromosome is obtained from the following two steps: (i) determining a down sampling ratio and randomly selecting part of the paired-end reads by the ratio; for example, ratio 1/16 means that we randomly select 1/16 of all reads; (ii) generating a low-resolution Hi-C contact matrix using the Hi-C paired-end reads from step 1.
The training data were extracted from low-resolution Hi-C contact matrices (10 kb) of five individual chromosomes including chromosomes 1, 3, 5, 7 and 9 in GM12878 with different down sampling ratios including 1/8, 1/16 and 1/25. The entire big Hi-C contact matrix for each individual chromosome was subdivided into thousands of 40 × 40 small submatrices. We concatenated all the submatrices as the final training data. The generation of target data was the same as the process of generating training data but using the high-resolution Hi-C contact matrices. We used different overlapping size of submatrices to control the size of training datasets. For example, using overlapping size of two columns as increment will result in four times reduction of training data compared with using increment of one column. The validation dataset (containing both low-resolution and corresponding high-resolution Hi-C contact submatrices) was extracted on chromosome 2 in GM12878. We selected chromosome 2 for validation dataset because it has a relatively larger size.
2.2 A very deep convolutional neural network
We built a very deep convolutional neural network (ConvNet) with the number of layers as 54. The details of its architecture are shown in Figure 1. The input of this ConvNet is a set of low-resolution Hi-C contact submatrices with shape equal to (n, 1, 40, 40) where n is the total number of samples (i.e. number of submatrices), ‘1’ corresponds to the input channel size of the first layer, and the last two dimensions (40, 40) are the size of the submatrices. Given a training and target set , where and are the low-resolution and the corresponding high-resolution Hi-C contact submatrices, respectively. The loss function of our ConvNet is
| (1) |
where F is the mapping function from to that we are trying to learn, and Θ denotes the parameter set.
Fig. 1.
The architecture of our convolutional neural network. There are five types of layers, including conv1, conv2, conv3, conv4R and conv5. Edge ‘1’ marks the global residual learning, and Edge ‘2’ marks the local residual learning. The dashed box highlights a building block for local residual learning. ⊕ denotes element-wise addition
There are five different types of layers in our architecture, including conv1, conv2, conv3, conv4R and conv5. The first type (i.e. conv1 in Fig. 1), containing 13 × 13 filters followed by a Rectified Linear Unit (ReLU) (Nair and Hinton, 2010), is designed to extract and represent Hi-C patterns. The second type (i.e. conv2 in Fig. 1), containing a 1 × 1 filter followed by a ReLU, is used to reduce its input channels to one for the afterwards residual learning layers. The shape of the output of conv2 will be (n, 1, 28, 28). The rest part of the architecture after conv2 in Fig. 1 is designed to implement global and local residual learning to make it a deep recursive residual network (DRRN) (Tai et al., 2017). The third type (i.e. conv3 in Fig. 1), containing 3 × 3 filters with zero padding of size 1 (to preserve the size of submatrices), can increase the output channels for the afterwards local residual learning blocks. The fourth type (i.e. conv4R in Fig. 1), containing 3 × 3 filters with zero padding of size 1, is the basic unit of our local residual learning. The fifth type (i.e., conv5 in Fig. 1) is used to reduce the output channel size to match the shape of conv2's output for global residual learning and final prediction output.
We implemented our ConvNet in this study via Pytorch (Paszke et al., 2017). The weight parameters were initialized using the He initialization method with ReLU (He et al., 2015). We used stochastic gradient descent (SGD) with a mini-batch size of 256, a momentum of 0.9, and a weight decay of 0.0001. The learning rate was initially set to 0.1 and was reduced by a factor of 0.1 (i.e. a factor times current learning rate equals new learning rate) when the mean squared error from the validation process has stopped reducing. We used adjustable gradient clipping technique as in (Kim et al., 2016; Tai et al., 2017) with θ equal to 0.01 to increase convergence speed.
2.3 HiCNN pipeline
Our method HiCNN includes three main steps: (i) learning the mapping function by doing training and validation processes to obtain optimal weight parameters; (ii) splitting the big low-resolution Hi-C contact matrix of one individual chromosome into thousands of 40 × 40 input submatrices, and predicting their corresponding high-resolution 28 × 28 output submatrices using the best model we obtained in step 1; (iii) predicting the high-resolution Hi-C contact matrix of the individual chromosome by rearranging the 28 × 28 output submatrices into a new matrix according to their indexes.
Similar to HiCPlus, the size of the output submatrices is smaller compared to the size of input submatrices. For HiCNN, the input submatrices are 40 × 40 and output submatrices 28 × 28. This is because we use the 13 × 13 surrounding values to make prediction for the central entry in the low-resolution big Hi-C matrix, e.g. the Hi-C map for an entire chromosome (every time a submatrix is input into the ConvNet). Therefore, predictions for some values in the input big matrix are not made, named as margin values, e.g. the first six values in the first row. In these cases, zero will be put in the output big matrix as placeholders, which makes the input (low-resolution) big matrix and the output (predicted high-resolution) big matrix having the same numbers of rows and columns.
Notice that the goal of this research is not to increase the number of rows and columns of the low-resolution big matrix. Instead, our HiCNN, and also HiCPlus, are designed to make the zero-inflated or sparse matrix to contain more meaningful values. For example, in order to increase the resolution of the Hi-C matrix of chromosome 1 from 40 into 5 kb, we first convert the 40 kb Hi-C matrix into a 5 kb matrix that usually is very sparse. After that, HiCNN will be executed to predict new values in the matrix while maintaining the same number of rows and columns as the 5 kb sparse matrix.
In order to still be able to make predictions for most of the margin values, we overlap the input submatrices. For example, if a low-resolution submatrix covers the rows of [1, 40] and columns of [1, 40] in the input big matrix. It corresponds to the rows and columns of [7, 34] and [7, 34] in the high-resolution big matrix. To fill up the gaps caused by the shrinking of size for the output submatrix, we make the next input submatrix at rows [1, 40] and columns [29, 68], which leads to rows and columns of [7, 34] and [35, 62] in the output matrix. In this way, the margin values on the right of the first input submatrix will be covered and have values predicted.
2.4 Evaluation methods
In addition to Pearson’s correlation coefficient that HiCPlus used to evaluate its predictions, we also used a more constringent evaluation measure, mean squared error (MSE). MSE is used to measure the average of the squared errors between computational enhanced high-resolution Hi-C data and experimental (i.e. real) high-resolution Hi-C data in terms of genomic distance. Since we represent Hi-C data as a n-by-n bin-based contact matrix, genomic distances in this context mean bin separations where the size of a bin is the resolution of interest. A smaller MSE indicates that on average the predicted Hi-C contacts are more similar to the real ones. Pearson’s correlation coefficient is used to measure the linear correlation between computationally predicted and experimental high-resolution Hi-C data, which is also in terms of genomic distances. A higher Pearson’s correlation indicates that the predicted Hi-C data better match the real Hi-C data.
3 Results
3.1 Training of the very deep convolutional neural network
We used all of the training examples to train HiCPlus, but only used 1/14 of the training data to train our HiCNN. However, we find that we still achieve better performance compared to HiCPlus (details will be discussed in Sections 3.2–3.6). Moreover, the speedup techniques we used made our ConvNet to be able to converge earlier with less epochs. Our training process can be converged in about 200 epochs with no overfitting being observed (Supplementary Fig. S1). Training the very deep ConvNet of our HiCNN (200 epochs needed for convergence) took about 12 h on a NVIDIA V100 GPU with 16 Gb memory, whereas training the ConvNet of HiCPlus (≥2000 epochs needed for better convergence) took about 28 h on the same GPU. Therefore, even though our ConvNet is much deeper than the one of HiCPlus, our training process is much faster.
The input/output channels for the five types of layers (i.e. conv1, conv2, conv3, conv4R and conv5) are 1/8, 8/1, 1/128, 128/128 and 128/1, respectively. We tested several other configurations by increasing channels (increasing all 8 channels to 16 and increasing all 128 channels to 256) but did not obtain noticeable improvement in performance. We have tested different numbers of layers (i.e. 14, 24, 44, 54, 64, 74 and 104 layers) by changing the number of local residual learning blocks and found that (i) ConvNet with the number of layers larger than 14 performs noticeably better than the ConvNet with 14 layers; (ii) the performance of ConvNet is not sensitive to the number of layers when it is larger than 24 (see Supplementary Fig. S2).
3.2 Resolution enhancement in one cell type using different down sampling ratios
The evaluations in this section were performed on one cell type, that is, GM12878. Since we used Hi-C contact matrices of chromosomes 1, 3, 5, 7 and 9 to extract training data and Hi-C contact matrix of chromosome 2 to extract validation data, we randomly chose two other chromosomes 6 and 12 to extract blind test data. We first tested down sampling ratio 1/16; and the results shown in Figure 2 are the mean squared errors (MSEs) and Pearson’s correlation coefficients between the real high-resolution Hi-C data and each of the following four Hi-C datasets on GM12878: low-resolution, HiCNN-enhanced, HiCPlus-enhanced and high-resolution biological replicate. It can be found that for both of the two chromosomes (i.e. 6 and 12) HiCNN outperforms HiCPlus, and both HiCNN and HiCPlus perform better than low-resolution Hi-C and high-resolution Hi-C replicate. We can draw the same conclusions if we set the down sampling ratio to 1/8 (see Supplementary Fig. S3) and to 1/25 (see Supplementary Fig. S4).
Fig. 2.
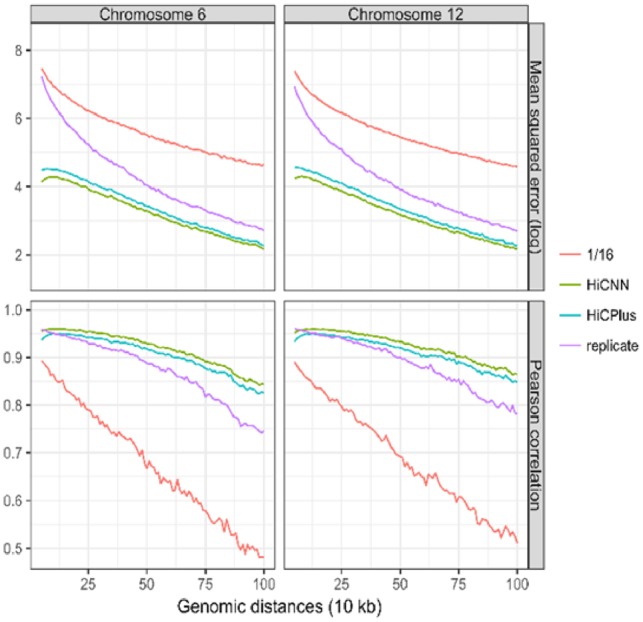
The evaluation results (i.e. mean squared error and Pearson correlation) on one cell type GM12878 between experimental high-resolution Hi-C and each of the four Hi-C datasets, including low-resolution from down sampling ratio equal to 1/16, HiCNN-enhanced, HiCPlus-enhanced and biologically experimental replicate
3.3 Resolution enhancement between two different cell types and two different species
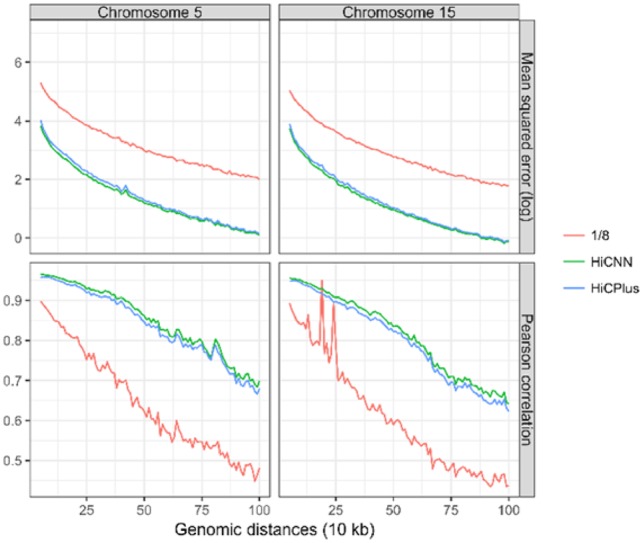
We conducted more experiments to test whether (i) our convolutional model trained on one cell type can be directly used to enhance the Hi-C matrices of another cell type with the same species; (ii) our convolutional model trained on one species can be directly used on enhancing the Hi-C matrices of another species. We used the model trained on GM12878 (human) with down sampling ratio equal to 1/8. We first used this model to enhance the Hi-C matrices of K562 (human), specifically on two randomly selected chromosomes (i.e. 5 and 15). The results are shown in Figure 3, indicating that HiCPlus and HiCNN can both efficiently enhance resolutions of Hi-C data of K562 but HiCNN performs consistently better than HiCPlus in terms of all genomic distances. We next used the same model to enhance the Hi-C resolutions of CH12-LX (mouse). We also used two chromosomes 5 and 15 in CH12-LX to create blind test data. The results are shown in Figure 4. The same conclusions can be drawn as in the previous evaluations conducted on K562.
Fig. 3.

The evaluation results (i.e. mean squared error and Pearson correlation) on K562 in human between experimental high-resolution Hi-C and each of the three Hi-C datasets, including low-resolution from down sampling ratio equal to 1/8, HiCNN-enhanced, and HiCPlus-enhanced. The models HiCNN and HiCPlus use to predict are trained on dataset from GM12878 in human
Fig. 4.
The evaluation results (i.e. mean squared error and Pearson correlation) on CH12-LX in mouse between experimental high-resolution Hi-C and each of the three Hi-C datasets, including low-resolution from down sampling ratio equal to 1/8, HiCNN-enhanced, and HiCPlus-enhanced. The models HiCNN and HiCPlus use to predict are trained on dataset from GM12878 in human
3.4 Resolution enhancement from real low-resolution Hi-C data
We evaluated HiCNN on two sets of real low-resolution Hi-C data compared with the previous low-resolution Hi-C data generated from down sampling. The first real low-resolution dataset is from GEO GSM1551620 (HIC071) on K562 (Rao et al., 2014). Since the high-resolution data in (Rao et al., 2014) are built by combining multiple independent in situ Hi-C samples, we consider each of the Hi-C samples as data generated from a low-resolution experiment. We used the ConvNet model trained on GM12878 with down sampling ratio 1/16 to enhance the low-resolution K562 data. The evaluation results on chromosomes 5 and 15 are shown in Supplementary Figure S5, indicating that HiCNN outperforms HiCPlus.
The second real low-resolution Hi-C dataset is from GEO GSE35156 (Dixon et al., 2012) with the HindIII restriction enzyme in mouse embryonic stem (ES) cells, which can reach a 40 kb resolution. We used the ConvNet trained on GM12878 with down sampling ratio 1/8 to enhance the resolution to 5 kb. We used the ultrahigh-resolution Hi-C data from GEO GSE96107 (Bonev et al., 2017) with the Mbol restriction enzyme to evaluate our predictions. Since the two Hi-C datasets are generated from two different restriction enzymes (i.e. HindIII and Mbol), we used Spearman’s rank correlation coefficient instead of MSE as the evaluation measure (different enzymes result in different scales for the number of Hi-C contacts making MSE not an ideal measure). The evaluation results are shown in Supplementary Figure S6, indicating that both HiCNN and HiCPlus can noticeably improve the real low-resolution Hi-C data and HiCNN outperforms HiCPlus in terms of Spearman’s rank correlation.
3.5 Evaluating HiCNN in terms of the abilities to help recover significant interactions and indicate chromatin states
We used Fit-Hi-C (Ay et al., 2014) to call statistically significant interactions (q-value < 1 × 10-6) in low-resolution, HiCPlus-enhanced, HiCNN-enhanced, and real high-resolution Hi-C contact matrices. We conducted the evaluations on the chromosome 12 of GM12878 within the genomic distances from 50 kb to 2 Mb and with down sampling ratio 1/16. In total, Fit-Hi-C detected 67, 729, 1324, 1421 significant interaction pairs in low-resolution, HiCPlus-enhanced, HiCNN-enhanced, and experimental high-resolution Hi-C contact matrices, respectively. The low-resolution, HiCPlus-enhanced, and HiCNN-enhanced Hi-C contact matrices have 22, 660, 1116 common significant interaction pairs with the interaction pairs detected from real high-resolution Hi-C, respectively (Supplementary Fig. S7). HiCNN performs significantly better than HiCPlus. Specifically, the Hi-C contact matrices enhanced by HiCNN lead to 1116 out of 1421 (79%) significant interactions, which is 30% higher than from the Hi-C contact matrices enhanced by HiCPlus, although both are higher than the number of interactions detected from low-resolution Hi-C. We also conducted the same analysis on chromosome 6 (Supplementary Fig. S8) and can draw the same conclusions as we did on chromosome 12.
We found that the chromatin loops (Hi-C peaks) reported in Rao et al. (2014), which are called by HiCCUPS, highly overlap with the significant interactions called by Fit-Hi-C. As shown in Supplementary Table S1, HiCCUPS detects 434 peaks on chromosome 12 in GM12878. With q-value <1 ×10-6 Fit-Hi-C can successfully detect 300 out of 434 peaks on real high-resolution Hi-C data. HiCNN (266 out of 434) outperforms HiCPlus (218 out of 434) and low-resolution (114 out of 434). When we increase the q-value, the size of the mutual set between the Hi-C peaks called by HiCCUPS and the significant interactions called by Fit-Hi-C increase. HiCNN and HiCPlus perform almost equally well on chromosome 6; and more common peaks are found in both HiCNN-enhanced and HiCPlus-enhanced Hi-C data compared to the common peaks found from the low-resolution Hi-C data.
We compared the CTCF-mediated interactions ensured by ChIA-PET (Tang et al., 2015) with the significant interactions detected from the following Hi-C datasets: low-resolution with down sampling ratio 1/16, real high-resolution, HiCPlus-enhanced, and HiCNN-enhanced. These four Hi-C datasets have 36, 77, 70 and 70 interactions in common with the 5, 600 CTCF interacting pairs on chromosome 6 in GM12878. HiCNN and HiCPlus perform equally better than low-resolution. We did the same analysis on chromosome 12 in GM12878; and the four numbers are 46, 48, 40 and 45 of the 5, 135 CTCF interacting pairs, indicating that HiCNN outperforms HiCPlus.
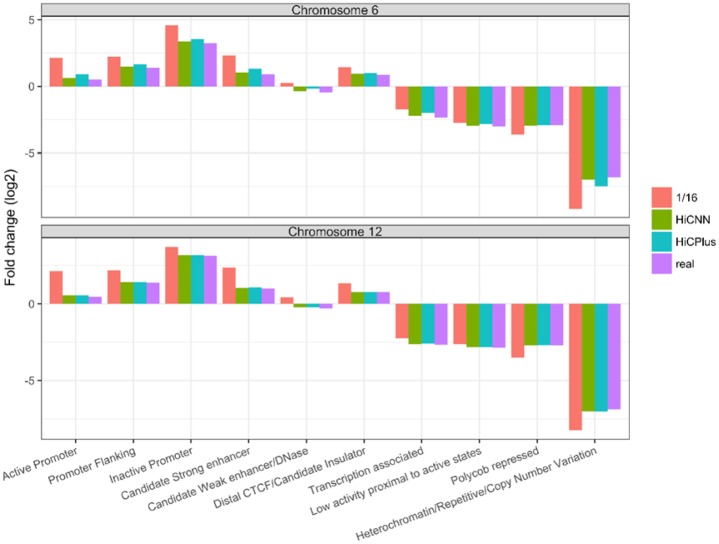
We conducted evaluations from the perspective of chromatin states. The definitions of chromatin states of GM12878 were downloaded from http://rohsdb.cmb.usc.edu/GBshape/cgi-bin/hgFileUi? db=hg19&g=wgEncodeAwgSegmentation, which was generated by the software ChromHMM (Ernst and Kellis, 2012) based on ENCODE data. Using Fit-Hi-C, we detected significant interactions based on real high-resolution Hi-C data. The chromatin segments where the significant interactions locate were gathered in a pool. ChromHMM was then executed on the pool of chromatin segments to call 10 types of chromatin states. In this way, an enrichment profile (indicated by the value of fold enrichment in Fig. 5) of the 10 chromatin states was generated for the interactions detected on real high-resolution Hi-C data. We performed the same procedures on low-resolution (down sampling ratio 1/16), HiCPlus-enhanced, and our HiCNN-enhanced Hi-C data. Figure 5 shows that the enrichment pattern related to HiCNN-enhanced Hi-C data is more similar to the enrichment pattern related to real high-resolution Hi-C data particularly on chromosome 6. This shows that our HiCNN can better enhance the low-resolution Hi-C data so that the interactions detected on the enhanced Hi-C data better fit the real high-resolution Hi-C data in terms of chromatin states.
Fig. 5.
The evaluation results (i.e. fold enrichment of 10 states) for segments that significant interactions residue in. We did the analysis on two chromosomes 6 and 12 in GM12878 for Fit-Hi-C-detected significant interactions from four Hi-C datasets, including real high-resolution, low-resolution from down sampling ratio equal to 1/16, HiCNN-enhanced, and HiCPlus-enhanced
3.6 Cross-validation with 3D fluorescence in situ hybridization
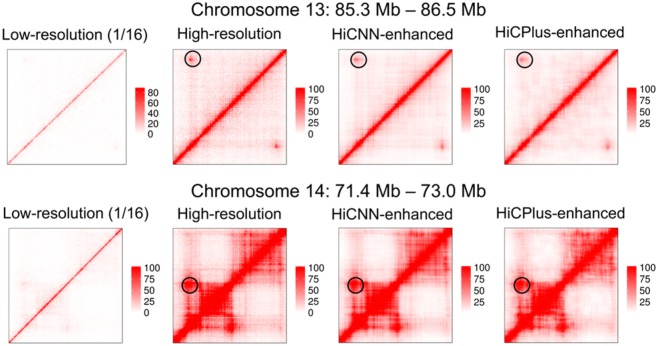
The Hi-C detected interactions can be evaluated by cross-validation with 3D fluorescence in situ hybridization (FISH) (Dixon et al., 2012; Rao et al., 2014). Rao et al. (Rao et al., 2014) conducted 3D-FISH experiments to validate four loops that were indicated by Hi-C peaks. Two of the four loops were selected here, on which we could barely observe the existence of the peaks from their low-resolution (down sampling ratio equal to 1/16) Hi-C heatmaps. We used HiCPlus and HiCNN to enhance the resolutions of chromosomes 13 and 14 where the two loops locate and plotted the Hi-C heatmaps of low-resolution (1/16), real high-resolution, HiCNN-enhanced, and HiCPlus-enhanced data. It can be found that both HiCNN and HiCPlus can successfully help reveal the two peaks by enhancing low-resolution Hi-C data. This example indicates that computational methods for enhancing Hi-C resolutions can be used to call Hi-C peaks and explore the properties of these peaks (Fig. 6).
Fig. 6.
The Hi-C heat maps of chromosomes 13 (85.3–86.5 Mb) and 14 (71.4–73.0 Mb) from four Hi-C datasets, including low-resolution with down sampling ratio equal to 1/16, real high-resolution, HiCNN-enhanced, and HiCPlus-enhanced. HiCNN and HiCPlus can successfully recover the two Hi-C Peaks on the two chromosomes in GM12878
4 Conclusions
In this study, we developed a new computational method HiCNN to better enhance the resolutions of Hi-C contact matrices. We designed a very deep convolutional neural network to learn the mapping function between low-resolution and high-resolution Hi-C contact matrices. The number of layers we used in our ConvNet is 54 and easy to go deeper by increasing the number of local residual learning blocks. Because we used multiple speedup techniques, the training process is much faster than HiCPlus. We compared our method HiCNN with the state-of-the-art method (HiCPlus) and found that HiCNN consistently outperforms HiCPlus and a high-resolution replicate Hi-C dataset. We may conclude that a well-trained ConvNet model can be used on different cell types and in different species (human and mouse), and the mapping function between low- and high-resolution Hi-C contact matrices may be shared across different cell types and species.
Funding
This work was supported by the National Institutes of Health R15GM120650 to Z.W. and start-up funding from the University of Miami to Z.W.
Conflict of Interest: none declared.
Supplementary Material
References
- Ay F. et al. (2014) Statistical confidence estimation for Hi-C data reveals regulatory chromatin contacts. Genome Res., 24, 999–1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonev B. et al. (2017) Multiscale 3D genome rewiring during mouse neural development. Cell, 171, 557–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekker J. et al. (2002) Capturing chromosome conformation. Science, 295, 1306–1311. [DOI] [PubMed] [Google Scholar]
- Dixon J.R. et al. (2012) Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature, 485, 376–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong C. et al. (2014) Learning a deep convolutional network for image super-resolution. In: European Conference on Computer Vision, 2014. pp. 184–199. Springer. [Google Scholar]
- Dostie J. et al. (2006) Chromosome conformation capture carbon copy (5C): a massively parallel solution for mapping interactions between genomic elements. Genome Res., 16, 1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engreitz J.M. et al. (2013) The Xist lncRNA exploits three-dimensional genome architecture to spread across the X chromosome. Science, 341, 1237973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst J., Kellis M. (2012) ChromHMM: automating chromatin-state discovery and characterization. Nat. Methods, 9, 215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K. et al. (2015) Delving deep into rectifiers: surpassing human-level performance on imagenet classification. In: Proceedings of the IEEE International Conference on Computer Vision, 2015. pp. 1026–1034.
- Hu M. et al. (2013) Bayesian inference of spatial organizations of chromosomes. PLoS Comput. Biol., 9, e1002893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y. et al. (2018) Single image super-resolution via cascaded multi-scale cross network. preprint arXiv: 1802.08808.
- Kim J. et al. (2016) Accurate image super-resolution using very deep convolutional networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016. pp. 1646–1654.
- Kim J. et al. (2016) Deeply-recursive convolutional network for image super-resolution. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016. pp. 1637–1645.
- Li H., Durbin R. (2010) Fast and accurate long-read alignment with Burrows–Wheeler transform. Bioinformatics, 26, 589–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E. et al. (2009) Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science, 326, 289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair V., Hinton G.E. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th International Conference on Machine Learning (ICML-10), 2010. pp. 807–814.
- Paszke A. et al. (2017) Automatic differentiation in pytorch. In: NIPS 2017 Autodiff Workshop: The Future of Gradient-based Machine Learning Software and Techniques, 2017.
- Rao S.S. et al. (2014) A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell, 159, 1665–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tai Y. et al. Image super-resolution via deep recursive residual network. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017. p. 5.
- Tai Y. et al. Memnet: a persistent memory network for image restoration. In: Proceedings of the IEEE International Conference on Computer Vision 2017. pp. 4539–4547.
- Tang Z. et al. (2015) CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell, 163, 1611–1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varoquaux N. et al. (2014) A statistical approach for inferring the 3D structure of the genome. Bioinformatics, 30, i26–i33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. et al. (2016) Predicting DNA methylation state of CpG dinucleotide using genome topological features and deep networks. Sci. Rep., 6, 19598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. et al. (2018) Enhancing Hi-C data resolution with deep convolutional neural network HiCPlus. Nat. Commun., 9, 750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Z. et al. (2006) Circular chromosome conformation capture (4C) uncovers extensive networks of epigenetically regulated intra-and interchromosomal interactions. Nat. Genet., 38, 1341–1347. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.