Oligomer Model of PB1 Domain of p62/SQSTM1 Based on Crystal Structure of Homo-Dimer and Calculation of Helical Characteristics

Abstract

Autophagy is an important process for protein recycling. Oligomerization of p62/SQSTM1 is an essential step in this process and is achieved in two steps. Phox and Bem1p (PB1) domains can oligomerize through both basic and acidic surfaces in each molecule. The ZZ-type zinc finger (ZZ) domain binds to target proteins and promotes higher-oligomerization of p62. This mechanism is an important step in routing target proteins to the autophagosome. Here, we determined the crystal structure of the PB1 homo-dimer and modeled the p62 PB1 oligomers. These oligomer models were represented by a cylindrical helix and were compared with the previously determined electron microscopic map of a PB1 oligomer. To accurately compare, we mathematically calculated the lead length and radius of the helical oligomers. Our PB1 oligomer model fits the electron microscopy map and is both bendable and stretchable as a flexible helical filament.

INTRODUCTION

Autophagy is one of the major degradation pathways targeting diverse cellular materials. In particular, autophagy plays an important role in protein recycling. Within this complex process, p62/SQSTM1 is an essential component that selectively recognizes target proteins to form the sequestosome, which comprises a group of adaptor proteins that interact with ubiquitin (Bitto et al., 2014; Klionsky and Emr, 2000; Lin et al., 2013; Nakatogawa et al., 2009; Nam et al., 2017; Varshavsky, 2017). Subsequently, these protein cargos are labeled with p62 and transported into the autophagosome. The aggregation mechanism of p62 is important for the formation of the sequestosome. p62 is multi-modular adaptor protein and consists of several domains and motifs including Phox and Bem1p (PB1), ZZ-type zinc finger (ZZ), TRAF6 binding (TB), LC3-interacting region (LIR), Keap1-interacting region (KIR), and ubiquitin associated domain (UBA). The PB1, ZZ, and UBA domains are involved in the aggregation mechanism (Johansen and Lamark, 2011; Katsuragi et al., 2015; Knaevelsrud and Simonsen, 2010; Lin et al., 2013; Lippai and Low, 2014). The PB1 domain of p62 interacts with PB1 domains of other proteins, such as PKCζ, and can induce self-oligomerization by interacting with the PB1 domains of other p62 molecules (Ciuffa et al., 2015; Lamark et al., 2003; Ren et al., 2014; Saio et al., 2010). The ZZ domain of p62 selectively binds to the target protein with cysteine residues from the p62 PB1 and ZZ domains to form disulfide bonds with additional p62 molecules. The formation of these disulfide bonds enables p62 to form higher oligomers (Cha-Molstad et al., 2015; Kwon et al., 2018). Additionally, the UBA domain of p62 interacts with ubiquitin-tagged proteins and induces the formation of large p62 aggregates (Lin et al., 2013; Rogov et al., 2014).

In order to understand the aggregation mechanism of p62 it is important to understand how PB1 domains self-oligomerize and how disulfide bond formation is induced by the interaction of the ZZ domain with its ligand. Structural studies of the ZZ domain with ligands were recently reported (Kwon et al., 2018; Zhang et al., 2018). However, the mechanism of disulfide bond formation is still unclear. The mechanism of PB1 oligomerization has been studied in various ways. Electron microscopy (EM) studies have shown that the PB1 oligomer is a flexible helical filament, and the dimer interface of the PB1 domains was elucidated by pseudo-contact shift (PCS)-based nuclear magnetic resonance (NMR) (Ciuffa et al., 2015; Saio et al., 2010).

In this study, we introduced mutations within the acidic and basic regions of the PB1 domain to produce a PB1 homo-dimer (Lamark et al., 2003; Saio et al., 2010). We crystallized this homo-dimer to obtain more accurate structural information than that obtained in previous studies. The crystal had two PB1 homo-dimers in the asymmetric unit with the solved structure exhibiting stronger interactions between the PB1 domains than those in the structure determined by the PCS-based NMR method. We also modeled an oligomer (20-mers) of the PB1 domains based on each chain of the crystal structure. These oligomer models had similar helical filaments to those observed in the previous EM study. Using a mathematical approach, we calculated the lead length and radius of these helical oligomer models using the coordinate information from the Protein Data Bank (PDB) file. These helical characteristics were analyzed with the map of the helical filament from the EM study.

MATERIALS AND METHODS

Cloning and purification of the PB1 dimer

The PB1 dimer of the human p62 protein was prepared and crystallized as previously described (Shin et al., 2018). Briefly, two constructs, PB1^DADR and PB1^RA, were expressed in Escherichia coli BL21(DE3)-RIL. Bacteria expressing the mutant constructs were mixed and sonicated. The supernatant containing the his-tagged green fluorescent protein fusion protein was loaded onto Ni-NTA resin (Qiagen, Germany) and eluted with 200 mM imidazole. The supernatant containing the his-tagged GST fusion protein was loaded onto glutathione (GST) resin and cleaved by Tobacco Etch Virus protease (TEV) on the gel. The TEV-cleaved protein was further purified through Ni-affinity chromatography and size exclusion chromatography (HiLoad^TM 25/600 Superdex^TM 75 pg column; GE Healthcare, USA).

Isothermal titration calorimetry (ITC)

Purified samples using GST resin were dialyzed against the solution containing 50 mM Tris-HCl (pH 7.5) and 200 mM NaCl, and centrifuged to remove any residual material. ITC measurement was performed at 25°C°C on a VP-ITC microcalorimetry system (MicroCal; Malvern Panalytical, UK).

Crystallization, X-ray diffraction, and structure determination

The crystallization of the PB1 dimer was performed as previously described (Shin et al., 2018). Briefly, the initial crystals were grown in 2.1 M DL-Malic acid (pH 7.0). The optimized crystallization condition was 1.8 M DL-Malic acid (pH 7.0) and 0.1 M Tris-HCl (pH 7.0). X-ray diffraction data were collected on beamline 11C at the Pohang Accelerator Laboratory (PAL, Korea) and processed using the HKL2000 program (Minor et al., 2006). The collected data was processed and refined to determine the structure by molecular replacement using PHENIX, as summarized in Supplementary Table S1 (Adams et al., 2010). The NMR structure of the PB1 domain homo-dimer (PDB ID: 2KKC) was used as a reference model for molecular replacement (Saio et al., 2009).

Oligomer modeling, measurement, and map fitting

Oligomer modeling was performed using PyMol and Coot (Emsley et al., 2010; Schrodinger, 2010). The measurement of distances and angles was performed using PyMol. Oligomer models were fit to the EM map using Chimera, which is a visualization program for both PDB and electron density map files (Pettersen et al., 2004).

Data and software availability

The coordinates and structure factors for the reported crystal structure in this paper have been deposited in Protein Data Bank. The accession number is PDB: 6JM4.

RESULTS

Crystal structure determination of the PB1 homo-dimer

We introduced several mutations in the PB1 domain of p62 in order to make a PB1 homo-dimer. The PB1 domain of human p62 has three cysteine residues. Cys26 and Cys44 are conserved only in mammals, while Cys27 is not conserved and is replaced by phenylalanine in most other species. We tested three mutations: C26S, C27F, and C44S. C26S and C27F improved protein properties, while C44S decreased the stability of the PB1 monomer.

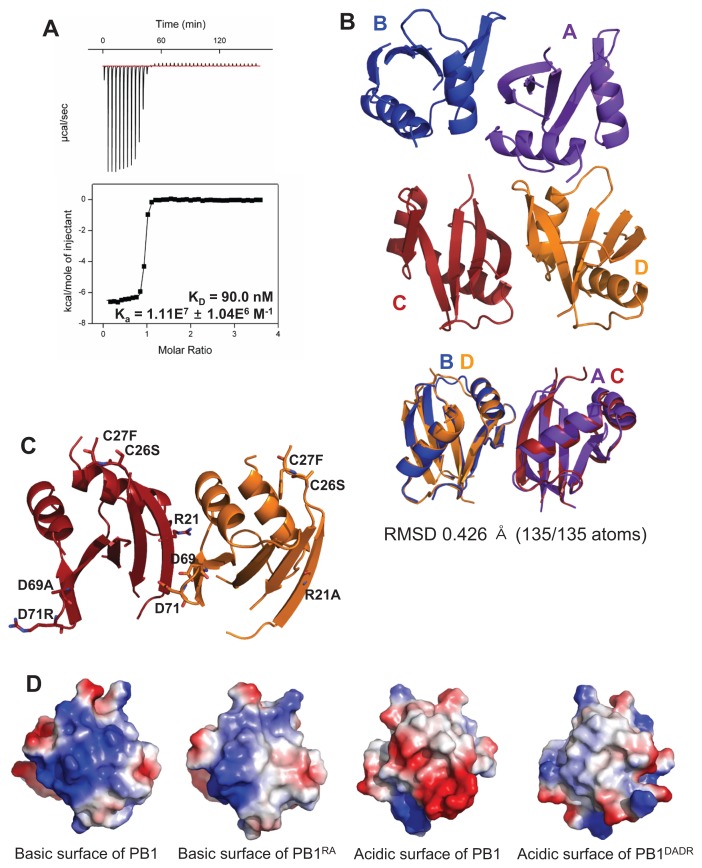
The PB1 domain of p62 has two binding sites and forms higher oligomers in a front-to-back manner (Lamark et al., 2003; Ren et al., 2014; Saio et al., 2010). To disturb this oligomerization and to promote homo-dimer formation, we made two constructs, PB1^RA and PB1^DADR, with mutations on the basic surface and the acidic surface (OPCA motif), respectively (Lamark et al., 2003). PB1^RA contains three mutations (R21A, C26S, and C27F), while PB1^DADR contains four mutations (C26S, C27F, D69A, and D71R). These mutants were expressed and purified as a homo-dimer. The dissociation constant (K_D) of this homo-dimer was 90.0 nM as determined by ITC (Fig. 1A).

Fig. 1. Structural analysis of the crystal structure of the PB1 homo-dimer.

(A) The binding affinity between PB1^RA and PB1^DADR was measured by ITC. (B) The overall crystal structure of the PB1 domain has four chains as two dimers in the asymmetric unit. These two dimers are superposed. (C) The mutated residues are presented as stick and these mutations were located on surface of PB1 homo-dimer. (D) The basic and acidic surfaces of C and D chains are presented by vacuum electrostatics models. The mutated surfaces have less color than the wild type.

The PB1 homo-dimer crystallized in malic acid conditions. We determined the crystal structure at a resolution of 3.2 Å with the asymmetric unit containing four PB1 molecules as two homo-dimers (Supplementary Table S1). Two dimers (A–B chains and C–D chains) were superposed and the calculated root mean square deviation (RMSD) was 0.426 Å (Fig. 1B). Introduced mutations were presented on the exposed surface of PB1 homo-dimer, not on the interface (Fig. 1C). These mutations changed surface charges of the basic surface and the acidic surface to near neutral and induced loss of function as dimerization surfaces (Fig. 1D).

Comparison between the PB1 homo-dimer of p62 and the PB1 hetero-dimer of p62 and PKCζ

Several proteins have PB1 domains that can interact with each other through basic and acidic surfaces. Most PB1 domains have only one binding site, either a basic or an acidic surface for hetero-dimer formation, while the PB1 domain of p62 has both a basic and an acidic surface for homo-oligomerization. The structure of the p62 PB1 and PKCζ PB1 hetero-dimer was previously reported (PDB ID: 4MJS) (Ren et al., 2014). Mutations on the acidic surface of the p62 PB1 domain prevented self-oligomerization, while PKCζ PB1 contains only an acidic surface (Hirano et al., 2005; Lamark et al., 2003; Ren et al., 2014). The basic surface of mutated p62 PB1 interacts with PKCζ PB1 to make a hetero-dimer. We compared the interface of the p62 PB1 homo-dimer with the interface of the hetero-dimer. The residues on the basic surfaces of p62 PB1 were found to be almost identical, with the same orientation and position (Fig. 2A). We also found that the positions of the residues on the acidic surfaces (OPCA motif) of the p62 PB1 and the PKCζ PB1 were consistent with a previous alignment study (Lamark et al., 2003) (Figs. 2B and 2C). Most of the interface residues were in the same positions with the exception of three residues of PKCζ PB1 and three residues of p62 PB1 (Fig. 2B, denoted by red circles).

Fig. 2. Comparison between the PB1 homo-dimer of p62 and the PB1 hetero-dimer of p62 and PKCζ.

(A) The basic surfaces of the p62 PB1 domains from the PB1 homo-dimer and the PB1 hetero-dimer of p62 and PKCζ are superposed. (B) The acidic surfaces (OPCA motif) of p62 PB1 and PKCζ PB1 are superposed. The red circles indicate the differing residues between PB1 domains of p62 and PKCζ. (C) The sequence alignment shows that the interface residues on the OPCA motifs are well conserved. The red letters are differing residues between the PB1 domains of p62 and PKCζ.

Comparison between the PB1 homo-dimer crystal structure and the PB1 homo-dimer determined by PCS-based NMR

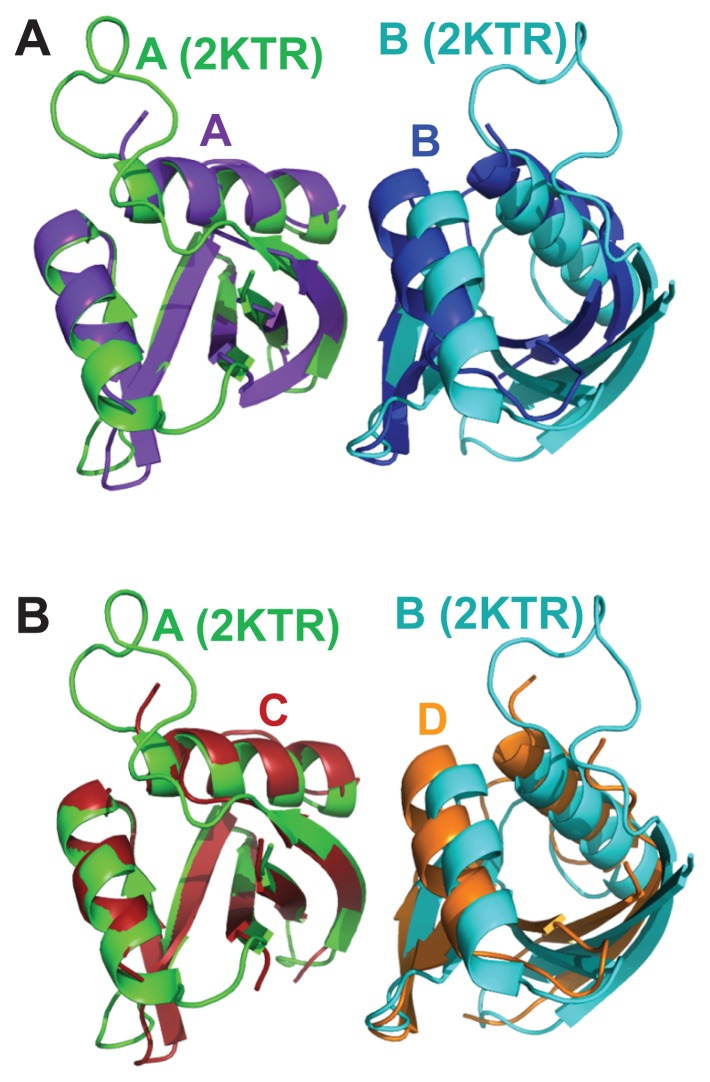
The structure of the PB1 homo-dimer of p62 was previously determined by PCS-based NMR (PDB ID: 2KTR) (Saio et al., 2010). The authors analyzed the interactions of residues at the interface using NMR to produce a model of the homo-dimer of the p62 PB1 domain. Ten structures of the PB1 homo-dimer with the lowest energies calculated by a rigid body docking method were described. We superposed these 10 structures with our crystal structure. The NMR structure with the lowest calculated RMSD (1.530 Å, data not shown) was then compared with the crystal structure (Fig. 3). The overall structure was almost identical but the orientation between the PB1 domains was a little different. Residues that interacted within 4.5 Å were analyzed for a more accurate comparison. Additional interactions between residues at the interface were observed in the crystal structure of the PB1 homo-dimer, which were not seen in the NMR structure (Supplementary Table S2). Five residues had previously been shown to be important for dimer formation (K7, R21, and R22 of the basic surface, and D69 and D71 of the acidic surface) (Lamark et al., 2003) and so we further analyzed these (Table 1). Interactions between K7 and D71, R22 and E82, and R22 and M85 were observed in the crystal structure. In addition, the surface area was calculated using the PISA server (Krissinel and Henrick, 2007). The surface area of the NMR structure was 379.2 Ų, while the surface areas of each chain of the crystal structure were 508.7 Ų and 489.6 Ų (Table 2). These results showed that the homo-dimer from the crystal structure exhibits a stronger self-interaction than the homo-dimer from the NMR structure.

Fig. 3. Comparison between the PB1 homo-dimer crystal structure and the PB1 homo-dimer determined by PCS-based NMR.

(A) The A chain of the PB1 homo-dimer from the crystal structure is superposed with the A chain of the PB1 homo-dimer determined by the PCS-based NMR method. The distance between A and B chains of the NMR structure is longer than that of the crystal structure. (B) The C chain of the PB1 homo-dimer is superposed with the NMR structure.

Table 1.

Key residues interacting within 4.5 Å

Crystal structure (PDB ID: 6JM4)				NMR structure (PDB ID: 2KTR)
A	B	C	D	A	B
K7	D69	K7	D69	K7	D67
K7	D71	K7	D71	K7	D69
K7	D73	K7	D73
R21	Q64	R21	Q64
R21	V75	R21	V75	R21	V73
R21	A76	R21	A76	R21	A74
R21	F77	R21	F77	R21	F75
R21	S78	R21	S78	R21	S76
R21	S77
R21	E82	R21	E82	R21	E80
R22	Y67	R22	Y67	R22	Y65
R22	D69	R22	D69	R22	D67
R22	A70	R22	E68
R22	V75	R22	V75	R22	V73
R22	E82	R22	E82
R22	M85	R22	M85
R22	Y89	R22	Y89	R22	Y87
I92	D69
R96	D71	R94	D69

Table 2.

Surface area of the interface between two chains

Crystal structure (PDB ID: 6JM4)		NMR (PDB ID: 2KTR)
A–B chain	C–D chain	A–B chain
508.7 Å2	489.6 Å2	379.2 Å2

Calculation of tilted angles between PB1 molecules of dimer structures

p62 is a multi-modular adaptor protein that functions as an oligomer and this oligomerization is an important feature for autophagy. In order to understand the characteristics of the p62 oligomer, it is essential to study the PB1 homo-dimer as a primary unit. Thus, we compared the PB1 dimer structures. For more accurate comparisons, the tilted angles between the subunits of the PB1 dimers were calculated using Cα atoms of two residues, F77 (points A and A′) of human p62 (F75 of mouse p62 and V70 of human PKCζ) and R21 (points B and B′) of p62 PB1 (I28 of human PKCζ). These two residues are relatively apart from each other and have low B-factors (Supplementary Fig. S1).

The vectors, $\overrightarrow{\text{AB}}$ and $\overrightarrow{{\text{A}}^{\prime }{\text{B}}^{\prime }}$, of each subunit and the angles between $\overrightarrow{\text{AB}}$ and $\overrightarrow{{\text{A}}^{\prime }{\text{B}}^{\prime }}$ were calculated based on the coordinates from the PDB files. These angles represent tilted angles of each dimer. The angle of A–B dimer was 12.9°, C–D dimer was 16.6°, and PB1-PKCz was 18.2°. The deposited NMR structure of PB1 homo-dimer of p62 has 10 docking models. The tilted angles of these models were calculated as 16.6° to 21.8°.

These vectors and tilted angles only provide information of the relative position between subunits of dimer because the coordinate of origin from PDB file can change. To analyze the characteristics of oligomer, we modeled oligomers from dimer structures.

Oligomer model of PB1 domains

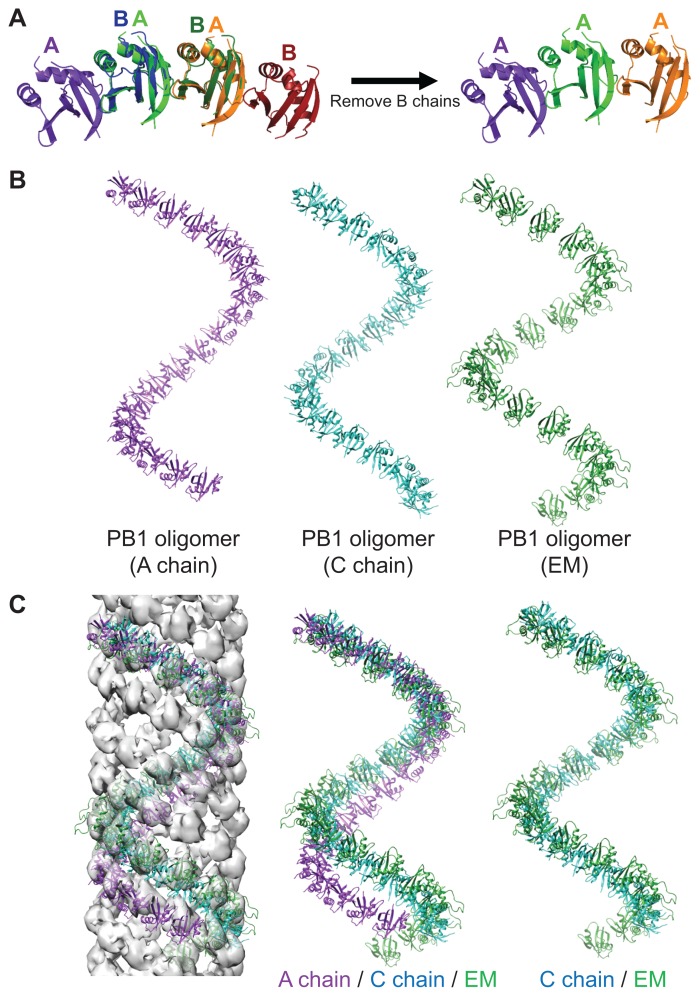
We modeled the oligomers of the A, B, C, and D chains of the crystal structure in a way that superposed several chains (Fig. 4A). These oligomer models were represented by a cylindrical helix as previously reported in an EM study (Fig. 4B) (Ciuffa et al., 2015). As the oligomers of the A and B chains, and the C and D chains were almost identical helical structures, we showed the oligomers of chain A and chain C as representative structures.

Fig. 4. Oligomer modeling and comparison of oligomer models.

(A) The oligomer models were constructed by superposing several dimers and leaving only one kind of chains. (B) Three oligomer models are presented. (C) The oligomer models are fit to the EM map and compared.

The oligomer models were also fit on the EM map (PDB ID: 4UF8) using Chimera (Fig. 4C) (Pettersen et al., 2004). The distance between the subunits of the EM model was longer than the distance between the PB1 domains from the crystal structure. That is, the number of molecules per one turn of the oligomer of the crystal structure was larger than that of the EM model. EM examination revealed that four oligomers of PB1 domains make a helical filament in the EM map. Our oligomer models also feature a helical filament. The oligomers of the C and D chains can make a helical filament with four oligomer models similar to the EM model, but the oligomers of the A and B chains make a helical filament with five oligomer models (data not shown). When comparing the four oligomer models, the oligomers of the C and D chains had the most similar lead length and radius to the EM map. However, the lead length of the oligomers of the A and B chains was longer than the EM model. This difference between lead lengths accounts for the difference in the number of oligomers constituting the filaments. Overall, the C and D chains fit better in the EM map than the A and B chains.

Mathematical functions to calculate helical features

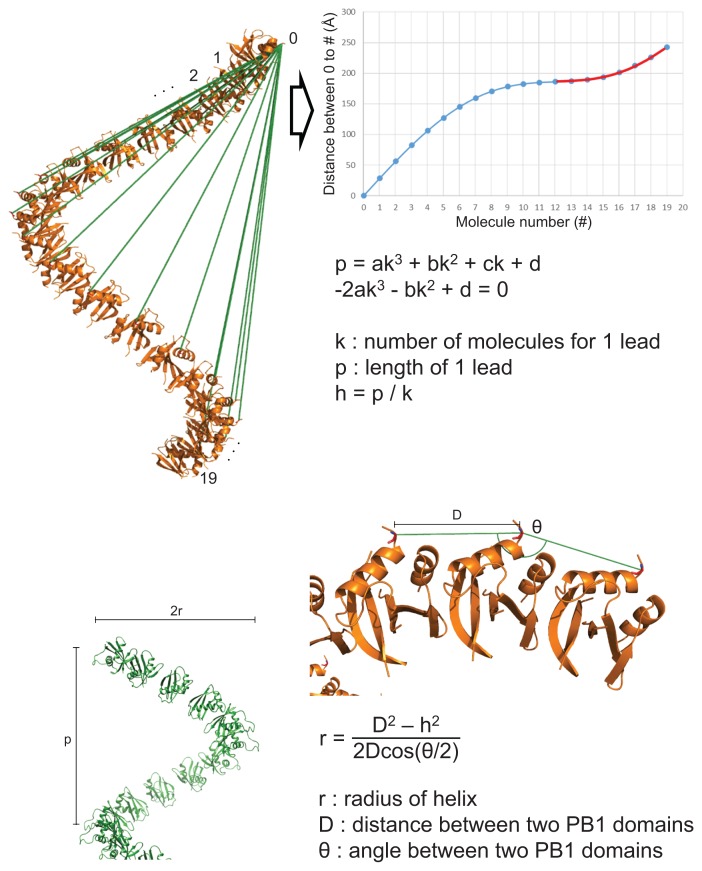
We wanted to accurately calculate helical features of the oligomer models using mathematical functions. A cylindrical helix can be explained in many ways, but can also be explained in terms of lead length and radius. However, the lead length and radius of the helix cannot be calculated accurately from PDB files as only the distance and angle among coordinates can be calculated. Therefore, the exact axis of the helix cannot be defined. To solve this problem, we devised a new formula.

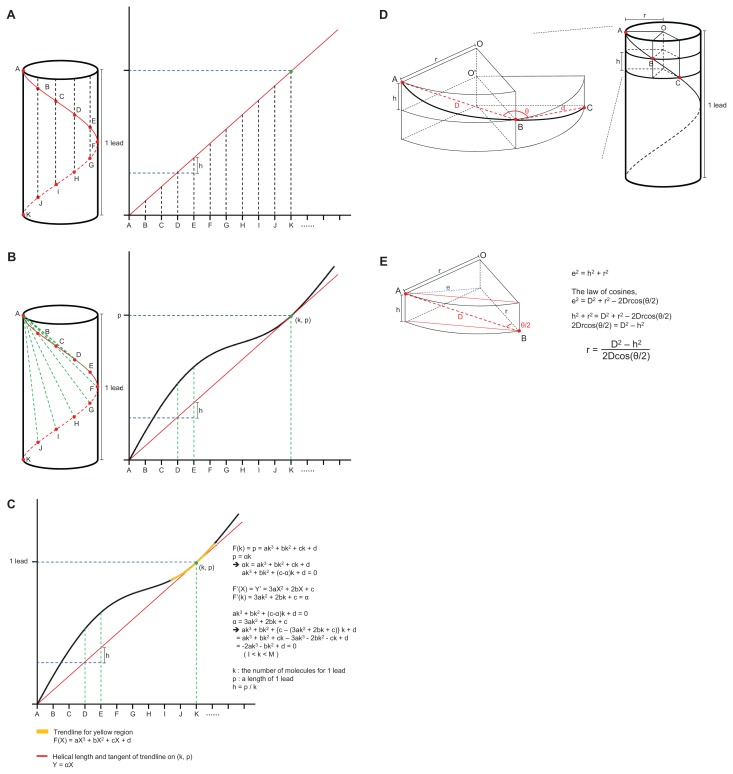
The subunits of the PB1 oligomer model were identical. Therefore, the distances and angles between the same two points of adjacent molecules were identical. When the cylindrical helix was unfolded on the two-dimensional plane it could be seen that identical points (A–K) existed at equal intervals on the slope of the line of the helix (Fig. 5A, red lines). The distance from the start point (A) of the helix to the same point on the next molecule (B) was longer than h (= 1 lead / K). The distances between the points, A to B, A to C, ..., and A to K, were plotted as a wave curve (Fig. 5B). Here, since the K point was the end of one turn, the distance from A to K was one lead and from the next point (L, M, ...) was again above the slope. The function of the slope of the line was Y = αX, and the coordinate (k, p) was the contact point of this line (red line) and the curve (black line).

Fig. 5. Derivation of the formulae for calculating helical characteristics using only the distance and angles between points on the helix.

(A) The cylindrical helix is unfolded and becomes a sloped line on the two-dimensional plane (red line). The identical points (A to K) exist at equal intervals on the sloped line of the helix. (B) The graph of distances from the start point A to the other points, B to K is plotted as a wave curve (black line) and is always above the sloped line (red line). The p of the contact point (k, p) between two lines is equal to one lead length. (C) To simplify a formula, a cubic function of the trend line can be obtained within the range from I to M (yellow line). The process of deriving the formulae is detailed on the right. (D) The cylinder of a helix and segments of disks with height ‘h’ when the cylinder is cut vertically to the axis at point B and C. (E) The sector shaped post is simplified as a trigonal prism. The process of deriving the formulae to calculate the radius (r) is detailed on the right.

Since we only calculated the distances and angles between coordinates in the PDB file, we were only able to draw the curve. To find the tangent line (Y = αX) and contact point (k, p) of this curve, it was necessary to simplify the curve (Fig. 5C). A cubic function could be obtained for the curve by plotting the trend line only within the range, I < X < M (Fig. 5C, yellow line).

Function of a trend line is

$$\text{F}(\text{X})={\text{aX}}^3+{\text{bX}}^2+\text{cX}+\text{d},$$

Tangent line is:

$$\text{Y}=\mathrm{\alpha }\text{X},$$

Contact point is (k, p). Substituting (k, p) for F(X),

$$\text{p}={\text{ak}}^3+{\text{bk}}^2+\text{ck}+\text{d}$$

Substituting (k, p) for tangent line,

$$\text{p}=\mathrm{\alpha }\text{k}$$

Therefore,

$${\text{ak}}^3+{\text{bk}}^2+\text{ck}+\text{d}=\mathrm{\alpha }\text{k}$$

Rearranging,

$${\text{ak}}^3+{\text{bk}}^2+(\text{c}-\mathrm{\alpha })\hspace{0.17em}\text{k}+\text{d}=0$$ (1)

In addition, the slope function of F(X) is F’(X) and,

$${\text{F}}^{’}(\text{X})=3{\text{aX}}^2+2\text{bX}+\text{c}$$

and the slope of the tangent line at (k, p) is α. Therefore, when X is k,

$${\text{F}}^{’}(\text{k})=3{\text{ak}}^2+2\text{bk}+\text{c}=\mathrm{\alpha }$$ (2)

Substituting the α of (1) to (2),

$${\text{ak}}^3+{\text{bk}}^2+\{\text{c}-(3{\text{ak}}^2+2\text{bk}+\text{c})\}\hspace{0.17em}\text{k}+\text{d}=0\hspace{0.17em}\text{for\hspace{0.17em}}(\text{I}<\text{k}<\text{M})$$

Rearranging,

$$-2{\text{ak}}^3-{\text{bk}}^2+\text{d}=0\hspace{0.17em}(\text{I}<\text{k}<\text{M})$$ (3)

The solution to (3) is the number of molecules for one lead (k). F(k) is p (a length of one lead) and h is p/k (Fig. 5C).

The helix cylinder becomes a disk of height ‘h’ when the cylinder is cut vertically to the axis at point B (Fig. 5D). The distance ($\overline{\text{AB}}=\text{D}$) between point A and B and the angle among point A, B, and C (∠ABC′ = θ) can be measured in the PDB file. Since the points A, B, C, and O′ are on one plane and the length of $\overline{\text{A}{\text{O}}^{\prime }}$ and $\overline{{\text{O}}^{\prime }\text{C}}$, and $\overline{\text{AB}}$ and $\overline{\text{BC}}$ are equal $(\overline{\text{A}{\text{O}}^{\prime }})=\overline{{\text{O}}^{\prime }\text{C}},\overline{\text{AB}}=\overline{\text{BC}}$), the angle among ABO' is a half of θ (∠ABO′ = θ/2). Using the length of $\overline{\text{A}{\text{O}}^{\prime }}$ (e) and ($\overline{\text{AB}}$) (D), and the angle of ∠ABO′ (θ/2), r can be calculated (Fig. 5E and Supplementary Fig. S2).

According to the law of cosines and Pythagoras’ theorem,

$$\begin{array}{l}{\text{e}}^2={\text{D}}^2+{\text{r}}^2-2\text{Drcos}(\mathrm{\theta }/2)\\ {\text{e}}^2={\text{h}}^2+{\text{r}}^2\end{array}$$

Therefore,

$${\text{h}}^2+{\text{r}}^2={\text{D}}^2+{\text{r}}^2-2\text{Drcos}(\mathrm{\theta }/2)$$

In summary, the radius (r) is,

$$\text{r}=\frac{{\text{D}}^2-{\text{h}}^2}{2\text{D}\hspace{0.17em}\text{cos}(\mathrm{\theta }/2)}$$

In this way, the lead (p), radius (r), and the number of molecules for one lead (k) of a helical oligomer could now be calculated using the coordinates in the PDB file.

Calculating the features of the oligomer models

These formulae were applied to calculate the inner and outer radius, the lead lengths, and the number of molecules for one lead of the PB1 oligomers based on the Cα atoms of D15 (inner) and G42 (outer), which are the innermost and the outermost residues that exhibit little change of position (Fig. 6 and Table 3). The distances from the first Cα atom of the residue (D15 or G42) to all others and the angles among Cα atoms of three adjacent subunits were measured in PyMol (Supplementary Fig. S3). These distances were presented graphically and trend lines were calculated (Supplementary Fig. S4). The inner radius was calculated as 29.0 to 40.6 Å, and the outer radius was calculated as 57.6 to 69.5 Å. The differences in inner and outer radii were about 10 Å, but this difference was less when compared to the diameter of the PB1 domain, which was 27.3 to 28.9 Å. The calculated lead varied according to the chain. The lead of the A and B chain was 212.2 Å, C and D chain was 169.8 Å, and the EM chain was 153.2 Å. The C, D, and EM chains had almost the same lead, but the lead of A and B chains was longer than the others. The length difference of C and the EM chain was 16.6 Å, while the length difference of A and the EM chain was 59.0 Å. Since one filament of PB1 had four oligomers in the EM map, the pitch of oligomer was 38.3 to 53.1 Å (Supplementary Fig. S5). If the filament models of A and B chains have five oligomers, the pitch will be 42.4 Å. As one pitch of C and D oligomers was 42.5 Å the filament models of A and B chains will have five oligomers. These results showed that the C, D, and EM chains had nearly identical characteristics, while the lead in the A and B chains was one pitch longer than the EM chain. The number of molecules for one lead of each chain was quite different. In one turn, the A and B chains had 17.0 molecules, the C and D chains had 13.5 molecules, and the EM model had 11.8 molecules. The difference in the oligomer models of the crystal structure was due to differences in the lead length. The oligomer model from EM had fewer molecules than the oligomer models from the crystal structure because the distance between the PB1 molecules in the EM model was longer than the crystal structure of the PB1 homo-dimer.

Fig. 6. Application of the formulae to the oligomer models.

Distances and angles between identical points are measured using PyMol and are plotted as a wave curve. The function of a trend line is derived and our formulae are applied to calculate k, p, h, and r.

Table 3.

Calculated characteristics of the modeled helical oligomers

	k	p (Å)	r (Å)
			Inner	Outer
A chain	17.0	212.2 ± 0.0	40.6	69.5
B chain	17.0	212.1 ± 0.1	-	69.9
C chain	13.5	169.8 ± 0.1	-	57.8
D chain	13.5	169.8 ± 0.1	29.0	57.6
Electron microscopy	11.8	153.2 ± 0.3	37.1	64.4

Values are presented as mean only or mean ± SD.

To verify these formulae, the extended oligomer (39-mer) of A chain was modeled and the point of two leads was calculated (Supplementary Fig. S6). The length between 0 and 2k was 424.0 Å and oligomer had 33.9 molecules as twice of one turn. This means the points of multiple k (k, 2k, ... , and nk) are on one line and that our formulae are accurate.

DISCUSSION

Structural analysis of the PB1 dimers and oligomer models

We determined the crystal structure of the p62 PB1 homo-dimer. The basic surfaces of the PB1 domains from the previously determined structure of the PKCζ PB1 and p62 PB1 hetero-dimer (PDB ID: 4MJS) and our p62 PB1 homo-dimeric crystal structure were identical. The acidic surfaces of PKCζ PB1 and p62 PB1 contained different amino acid residues but their positioning’s were consistent with previous alignment studies of the OPCA motif (Lamark et al., 2003).

The overall architecture of the crystal structure and the NMR structure (PDB ID: 2KTR) was almost identical, except that the interaction between the two molecules in the crystal structure was stronger than that of the NMR structure and the intermolecular tilting was slightly different. In turn, these differences affected the radius and the lead length of the oligomer models.

Oligomers were modeled using the crystal structure of the p62 PB1 homo-dimer and these models were subsequently fit to the EM map. For an accurate comparison with EM models, we calculated the radius and the lead length of the oligomer models. The oligomer models consisting of C and D chains had almost the same radius and lead length compared to the EM map, but those consisting of A and B chains were one pitch longer. In the previous EM study the authors measured the features of a helical filament. The radius was approximately 75 Å, lead length was 156 ± 7 Å, and the range of the number of molecules for one lead was 11 to 16. In this study, we calculated the features of the helical oligomer model of the PB1 crystal structure. The outer radius was 57.6 to 69.5 Å, the range of the lead length was 169.8 to 212.2 Å, and the range of the number of molecules for one lead was 13.5 to 17.0 (Ciuffa et al., 2015). These calculated characteristics were similar to those from the EM map and the C–D dimer may be more similar to the actual homo-dimer conformation.

Calculation of the features of a cylindrical helix

The protein structure is recorded in a PDB file, but only the coordinate information of each point is known from the PDB file. It is difficult to identify the geometric characteristics of higher oligomers using only the coordinate information. Additionally, the characteristics of the cylindrical helix cannot be calculated exactly because the exact axis of this oligomer is unknown. Therefore, we devised formulae whereby the exact characteristics of a helical oligomer could be calculated.

When the distances between the first point and the other points on a helix are plotted on a plane the distance between the first point and the point that is exactly one turn ahead is one lead length, and the distances between the first point and the other points are longer than the helical slope. Focusing on this point, the formulae were built using the relationship between the length of one lead, a tangent line, and a contact point. The length of one lead (p) and the number of molecules for one lead (k) can be calculated with these formulae. In addition, the formula for a radius (r) was made using the symmetric properties of the identical points of three adjacent molecules.

We could calculate the exact characteristics of the helix by applying these formulae to the oligomer models. Various helical filaments such as microtubules and actin have been discovered in cells. The characteristics of these helical filaments can now be calculated accurately using our formulae.