$G_{\text{ST}}^{\prime }$, Jost’s D, and $F_{\text{ST}}$ are similarly constrained by allele frequencies: A mathematical, simulation, and empirical study

Abstract

Statistics $G_{\text{ST}}^{\prime }$ and Jost’s D have been proposed for replacing $F_{\text{ST}}$ as measures of genetic differentiation. A principal argument in favour of these statistics is the independence of their maximal values with respect to the subpopulation heterozygosity H_S, a property not shared by $F_{\text{ST}}$. Nevertheless, it has been unclear if these alternative differentiation measures are constrained by other aspects of the allele frequencies. Here, for biallelic markers, we study the mathematical properties of the maximal values of $G_{\text{ST}}^{\prime }$ and D, comparing them to those of $F_{\text{ST}}$. We show that $G_{\text{ST}}^{\prime }$ and D exhibit the same peculiar frequency-dependence phenomena as $F_{\text{ST}}$, including a maximal value as a function of the frequency of the most frequent allele that lies well below one. Although the functions describing $G_{\text{ST}}^{\prime }$, D, and $F_{\text{ST}}$ in terms of the frequency of the most frequent allele are different, the allele frequencies that maximize them are identical. Moreover, we show using coalescent simulations that when taking into account the specific maximal values of the three statistics, their behaviours become similar across a large range of migration rates. We use our results to explain two empirical patterns: the similar values of the three statistics among North American wolves, and the low D values compared to $G_{\text{ST}}^{\prime }$ and $F_{\text{ST}}$ in Atlantic salmon. The results suggest that the three statistics are often predictably similar, so that they can make quite similar contributions to data analysis. When they are not similar, the difference can be understood in relation to features of genetic diversity.

1. INTRODUCTION

Assessing the level of genetic differentiation among subpopulations is a fundamental topic in population genetics, molecular ecology, and conservation genetics. Genetic differentiation is used, for example, to detect genes under natural selection in different subpopulations (Lewontin & Krakauer, 1973), to quantify effects of gene flow and hybridization (Slatkin, 1993), and to detect effects of population fragmentation and to provide conservation recommendations (Frankham, Ballou, & Briscoe, 2002).

For decades, genetic differentiation has been measured most often using Wright’s fixation index $F_{\text{ST}}$ (Wright, 1951). In an informative framework provided by Nei (1973), an additive partition divides the total heterozygosity H_T into a within-subpopulation component, H_S, and an among-subpopulation component, D_ST:

$$H_{\text{T}}=H_{\text{S}}+D_{\text{ST}}.$$

From D_ST, Nei derived the measure of differentiation

$$F_{\text{ST}}=\frac{D_{\text{ST}}}{H_{\text{T}}}.$$ (1)

Because the Wahlund effect (Wahlund, 1928) mathematically ensures that H_T ≥ H_S (as a consequence of the Cauchy-Schwarz inequality, Rosenberg & Calabrese, 2004), $F_{\text{ST}}$ is restricted to lie in the unit interval from 0 to 1. Consequently, $F_{\text{ST}}$ values are often interpreted using a scale from 0 to 1; for example, Wright (1978, p. 85) described the range 0.15–0.25 as indicating “moderately great differentiation,” and the range 0.25–1 as indicating “very great differentiation.”

Many studies, however, challenge this common interpretation of $F_{\text{ST}}$. It has been shown that the maximal $F_{\text{ST}}$ for a specific locus is not always one, but a smaller value that varies with aspects of the genetic diversity at a locus, as measured by H_S (Balloux, Brunner, Lugon-Moulin, Hausser, & Goudet, 2000; Hedrick, 1999, 2005; Hedrick & Kalinowski, 2000; Jost, 2008; Long & Kittles, 2003; Maruki, Kumar, & Kim, 2012), H_T (Edge & Rosenberg, 2014; Jakobsson, Edge, & Rosenberg, 2013), or other allele frequency statistics (Alcala & Rosenberg, 2017; Rosenberg, Li, Ward, & Pritchard, 2003). Consequently, interpreting $F_{\text{ST}}$ values requires consideration of the value of H_S or other summary statistics rather than a fixed scale.

Some have proposed ways of addressing this perceived flaw of $F_{\text{ST}}$. Wang (2015) suggested assessing if $F_{\text{ST}}$ values at a set of loci are influenced by H_S by testing for a significant correlation between the two statistics. A significant correlation is interpreted as indicating that $F_{\text{ST}}$ is constrained by H_S values rather than reflecting the level of genetic differentiation among populations. Although this test is promising for avoiding misinterpretations of $F_{\text{ST}}$ (Whitlock, 2015), frameworks are still needed for interpretation of $F_{\text{ST}}$ in cases with a significant correlation between $F_{\text{ST}}$ and H_S.

Others have proposed replacing $F_{\text{ST}}$ by an alternative genetic differentiation measure whose maximal value does not depend on H_S. Hedrick (2005) proposed standardizing $F_{\text{ST}}$ by its maximum value given the observed value of H_S and the number of subpopulations F_ST,max = [(K − 1)(1 − H_S)]/(K − 1 + H_S). The resulting measure, denoted $G_{\text{ST}}^{\prime }$, is defined as:

$$G_{\text{ST}}^{\prime }=\frac{F_{\text{ST}}}{F_{\text{ST},\text{max}}}.$$ (2)

In a provocative and influential paper, Jost (2008) proposed another measure of genetic differentiation, relying on alternative measures of genetic diversity, the “effective numbers of alleles” within and among populations, denoted respectively by Δ_S = 1/(1 − H_S) and Δ_T = 1/(1 – H_T), rather than within- and among-population heterozygosities H_S and H_T. He also advocated the use of a multiplicative partition of genetic diversity,

$${\mathrm{\Delta }}_{\text{T}}={\mathrm{\Delta }}_{\text{S}}{\mathrm{\Delta }}_{\text{ST}},$$

rather than the additive partitioning used in the derivation of $F_{\text{ST}}$. Considering a context applicable for any value for the number of distinct alleles, though proposed primarily for multiallelic markers, Jost then derived a new differentiation measure, denoted D, by normalizing 1/Δ_ST to lie between 0 and 1:

$$D=\left(\frac{K}{K-1}\right)\left(1-\frac{1}{{\mathrm{\Delta }}_{\text{ST}}}\right).$$

Jost’s D can also be expressed using heterozygosities:

$$D=\left(\frac{K}{K-1}\right)\left(\frac{H_{\text{T}}-H_{\text{S}}}{1-H_{\text{S}}}\right).$$ (3)

For convenience, we henceforth use D to indicate Jost’s D as in Equation 3.

$G_{\text{ST}}^{\prime }$ and D are statistics whose maxima are not constrained by H_S in the sense that irrespective of the value of H_S, they can range from 0 to 1. This property, however, does not ensure that they are unconstrained by other aspects of allele frequencies. In particular, recent studies have highlighted a dependence of the maximal $F_{\text{ST}}$ on the frequency M of the most frequent allele in the total population at a locus.

Rosenberg et al. (2003, Equation 8) showed that for biallelic markers and two subpopulations, the maximum $F_{\text{ST}}$ decreases monotonically from 1 to 0 as a function of M (see also Maruki et al., 2012). Jakobsson et al. (2013) showed that for a value of M chosen uniformly between 0 and 1, the mean maximum $F_{\text{ST}}$ is approximately 0.3585; this maximum can be even lower if the number of alleles at the locus is specified (Edge & Rosenberg, 2014). For biallelic loci, Alcala and Rosenberg (2017) generalized these results to the case of an arbitrary number of subpopulations K. We showed that $F_{\text{ST}}$ continues to have a maximum less than 1 irrespective of the value of M, with exceptions only at finitely many choices for M.

Here, we show that despite the emphasis of the derivations of $G_{\text{ST}}^{\prime }$ and D on eliminating the dependence of maximal values on H_S, both quantities, like $F_{\text{ST}}$, have maxima less than 1 when considered as functions of M. We derive the maximum and minimum values of $G_{\text{ST}}^{\prime }$ and D in terms of M, for a biallelic marker and an arbitrary number of subpopulations K. We then compare the mathematical constraints on $G_{\text{ST}}^{\prime }$ and D with analogous constraints on $F_{\text{ST}}$ from Alcala and Rosenberg (2017), as functions of the number of subpopulations K. We simulate the joint distributions of M and $G_{\text{ST}}^{\prime }$ and of M and D, describing how $G_{\text{ST}}^{\prime }$ and D values are distributed between their minimum and maximum values as functions of the migration rate and the number of subpopulations in an island migration model. We apply our results to show how they explain discrepancies among $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in two empirical examples: the population structure of wild North American wolves and that of Atlantic salmon. We use our results to provide recommendations on the use of the three statistics.

2. MATERIALS AND METHODS

Our goal is to derive the minimum and maximum values $G_{\text{ST}}^{\prime }$ and D can take as functions of the frequency M of the most frequent allele for a biallelic marker, when the number of subpopulations K is a fixed finite value greater than or equal to 2. Following similar derivations for $F_{\text{ST}}$ (Alcala & Rosenberg, 2017), we consider a polymorphic locus with two alleles, A and a, segregating in a total population subdivided into K subpopulations that all contribute equally to the total. We denote the frequency of allele A in subpopulation k by p_k. The frequency of allele a in subpopulation k is 1 - p_k. Each allele frequency p_k lies in the interval [0,1].

The mean frequency of allele A across the subpopulations is $M=(1/K){\sum }_{k=1}^K{p}_k,$, and the mean frequency of allele a is 1 - M.

We assume that allele A is the more frequent allele in the total population, so that M ≥ 1/2 ≥ 1 − M. Because by assumption the locus is polymorphic, M ≄ 1. We denote the mean squared frequency of allele A across the subpopulations by $S=(1/K){\sum }_{k=1}^K{p}_k^2.$We assume that the allele frequencies M and p_k are parametric allele frequencies of the total population and subpopulations, and not estimated values computed from data. In addition, we adopt an interpretation of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D as “statistics” that provide mathematical descriptions of the apportionment of alleles among subpopulations, rather than as “parameters” of an implicit or explicit population-genetic model (Nei, 1986). For this study, the “statistic” interpretation of differentiation measures is favored because it enables descriptions of the relationships of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D with other “statistics” such as the frequency M of the most frequent allele. It also permits evaluation of the relative impact on resulting values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D of mathematical relationships between statistics–which we interpret as mathematical “constraints”–separately from the impact of population-genetic models.

3. RESULTS

3.1. Mathematical constraints on $F_{\text{ST}}$, $G_{\text{ST}}^{\prime },$, and D

3.1.1. $F_{\text{ST}}$, $G_{\text{ST}}^{\prime },$, and D as functions of M

Equations 2 and 3 express $G_{\text{ST}}^{\prime }$ and D as functions of the within- and among-subpopulation heterozygosities H_S and H_T. We express $G_{\text{ST}}^{\prime }$ and D as functions of allele frequencies by substituting into Equations 2 and 3 the expressions for H_S and H_T (Nei, 1973):

$$H_{\text{S}}=1-\frac{1}{K}\sum _{k=1}^K{p}_k^2-\frac{1}{K}\sum _{k=1}^K{\left(1-p_k\right)}^2,$$ (4)

$$H_{\text{T}}=1-M^2-{(1-M)}^2.$$ (5)

H_S simplifies to H_S = 2(M − S), and H_T to H_T = 2M(1 − M). Because we assume a polymorphic locus, 0 ≤ H_S < 1 and 0 < H_T < 1. We obtain:

$$F_{\text{ST}}=\frac{S-M^2}{M(1-M)},$$ (6)

$$G_{\text{ST}}^{\prime }=\frac{(K-1-2S+2M)\left(S-M^2\right)}{(K-1)(1+2S-2M)M(1-M)},$$ (7)

$$D=\frac{2K\left(S-M^2\right)}{(K-1)(1+2S-2M)}.$$ (8)

For a given value of M, we search for the values of p₁, p₂, …, p_K that minimize and maximize $G_{\text{ST}}^{\prime }$ and D across all possible sets of allele frequencies that produce mean frequency M for its most frequent allele. The minimal and maximal $F_{\text{ST}}$ as functions of M are known from Alcala and Rosenberg (2017). We show in Appendix A that the minimal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime },$, and D all equal 0 irrespective of M, for any value of the number of subpopulations K, and that this minimum is reached when alleles have the same frequency in all subpopulations: p₁ = p₂= … = p_K = M.

3.1.2. Maximal values of F_ST, $G_{\text{ST}}^{\prime },$, and D

From Alcala and Rosenberg (2017, Equation 5), letting $\lfloor x\rfloor$ denote the greatest integer less than or equal to x and writing $\left\{x\right\}=x-\lfloor x\rfloor ,$, the maximum of $F_{\text{ST}}$ in terms of M is:

$$F_{\text{ST}}\le \frac{\lfloor KM\rfloor +{\left\{KM\right\}}^2-K{M}^2}{KM(1-M)}.$$ (9)

The derivations of the maxima of $G_{\text{ST}}^{\prime }$ and D in terms of M proceed in three steps. (a) We show in Appendix B that $G_{\text{ST}}^{\prime }$ and D are increasing functions of S. (b) We employ Theorem 1 from Alcala and Rosenberg (2017), which provided the maximal S in terms of M used to obtain the maximal $F_{\text{ST}}$ in terms of M (Alcala & Rosenberg, 2017, Equation 6). This theorem shows that $S\le \left(\lfloor KM\rfloor +{\left\{KM\right\}}^2\right)/K,$, with equality requiring the most frequent allele to have frequency 1 or 0 in all subpopulations except at most one. (c) From (a) and (b), the maximal $G_{\text{ST}}^{\prime }$ and D in terms of M are obtained by substituting the maximal S into Equations 7 and 8:

$$G_{\text{ST}}^{\prime }\le \frac{[K(K-1)+2\{KM\}(1-\left\{KM\right\})]\left(\lfloor KM\rfloor +{\left\{KM\right\}}^2-K{M}^2\right)}{K(K-1)[K-2\{KM\}(1-\left\{KM\right\})]M(1-M)},$$ (10)

$$D\le \frac{2K\left(\lfloor KM\rfloor +{\left\{KM\right\}}^2-K{M}^2\right)}{(K-1)[K-2\{KM\}(1-\left\{KM\right\})]}.$$ (11)

Interestingly, this derivation implies that for fixed M, $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are maximal under the same conditions: when the most frequent allele has frequency 1 or 0 in all except possibly one subpopulation, so that the locus is polymorphic in at most a single subpopulation. Thus, $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are all maximal when fixation is achieved in as many subpopulations as possible.

3.1.3. Comparison of the maximal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime },$, and D

Figure 1 shows the maximal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in terms of M for various values of K. These maximal values have shared properties. $F_{\text{ST}}$ (Alcala & Rosenberg, 2017, p. 1583), $G_{\text{ST}}^{\prime }$ (Supporting Information File S1.1), and D (Supporting Information File S1.2–S1.4) all have peaks at values i/K, where i is an integer ranging in $\left[\lceil \frac{K}{2}\rceil ,K-1\right],$ where it is possible for the allele to be fixed in all K subpopulations. The maximum, treated as a function of M, is not a differentiable function at the peaks i/K (Supporting Information File S1.5); it is smooth and strictly below one between them (Supporting Information File S1.1 and S1.2). If K is even, then the maximal value has a local maximum at M = 1/2, whereas if K is odd, then M = 1/2 is a local minimum (Supporting Information File S1.3).

FIGURE 1.

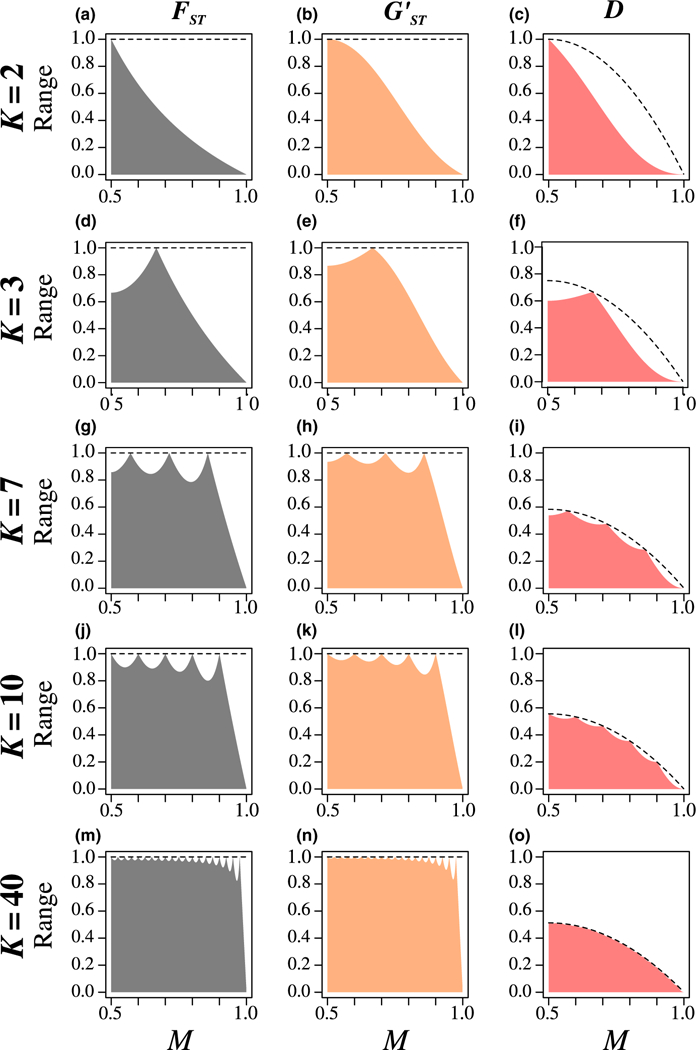
Range of possible values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D as functions of the frequency M of the most frequent allele, for different numbers of subpopulations K. The shaded region represents the space between the minimal and maximal values. The maximal $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are computed from Equations 9–11, respectively. The dashed line represents 1 for $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$, and 2KM(1 − M)/(K − 1) for D (Equation S1.4 in Supporting Information File S1); the maximum value touches the dashed line when M = i/K for integers i in $\left[\lceil \frac{K}{2}\rceil ,K-1\right].$ For $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D, for each K, the minimum value is 0 for all values of M

The maximal values for the three statistics also have distinct properties. From Alcala and Rosenberg (2017, p. 1583), the peaks of the maximal $F_{\text{ST}}$ reach one; the peaks of the maximal $G_{\text{ST}}^{\prime }$ also reach one (Supporting Information File S1.1), whereas the peaks of the maximal D are lower than 1, except if K = 2 (Supporting Information File S1.2). These peaks reach KH_T/(K − 1) = 2KM(1 − M)/(K − 1) (Supporting Information File S1.4). Consequently, $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ are only unconstrained within the unit interval for finitely many values of the frequency M of the most frequent allele, and D is only unconstrained for a single combination of values of K and M, namely (K, M) = (2, 1/2).

For K = 2, the maximal $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values are similar (Figure 1a–c): the maximum is 1 at M = 1/2, decreasing monotonically to 0 at M = 1. The maximal $G_{\text{ST}}^{\prime }$ is the highest of the statistics for all M (Appendix C); as a result, $G_{\text{ST}}^{\prime }$ is the least constrained measure. The maximal D exceeds the maximal $F_{\text{ST}}$ for M < 3/4 and is lower for M > 3/4 (Appendix C). Hence, D is less constrained than $F_{\text{ST}}$ for lower M but more constrained for higher M.

The number of subpopulations K has different effects on the maximum values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D. The maximum of $G_{\text{ST}}^{\prime }$ tends to 1 when K → ∞ (Figure 1b,e,h,k,n and Supporting Information File S1.2), similarly to that of $F_{\text{ST}}$ (Figure 1a,d,g,j,m; Alcala & Rosenberg, 2017); thus, constraints of M on the values of $G_{\text{ST}}^{\prime }$ disappear as K increases. By contrast, the maximal value of D tends to 2M(1 − M) = H_T when K → ∞ (Figure 1c,f,i,l,o, and Supporting Information File S1.7): thus, constraints imposed by M on the values of D remain strong for all K.

3.1.4. Comparison of the range of possible values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D

We can summarize how much M constrains the range of $G_{\text{ST}}^{\prime }$ and D compared to $F_{\text{ST}}$ by computing as functions of the number of subpopulations A_G(K) and A_D(K), the mean maximal $G_{\text{ST}}^{\prime }$ and D across all possible values of M. A_G(K) gives the area between the minimal and maximal values of $G_{\text{ST}}^{\prime }$ as a function of M divided by the length of the domain of possible M values, 1/2. This quantity is useful for comparing results with previous work on the constraints of $F_{\text{ST}}$ (Alcala & Rosenberg, 2017; Edge & Rosenberg, 2014; Jakobsson et al., 2013). Values of A_G(K) near one indicate that $G_{\text{ST}}^{\prime }$ can range between 0 and 1 for most values of M, whereas small values indicate that $G_{\text{ST}}^{\prime }$ values are constrained to a small interval. A_D(K) and A_F(K) describe corresponding computations for D and $F_{\text{ST}}$.

From Alcala and Rosenberg (2017, Equation 8), A_F is:

$$A_F(K)=1-K+2(K+1)\ln K-\frac{4}{K}\sum _{i=2}^{K}i\ln i.$$ (12)

We compute A_G(K) and A_D(K) from the upper bounds derived in the previous sections. Because the lower bound on $G_{\text{ST}}^{\prime }$ and D is 0 for all M between 1/2 and 1, A_G(K) and A_D(K) correspond to the areas under their respective maximal values divided by 1/2, or twice the integrals of Equations 10 and 11 over M. We compute A_G(K) in Supporting Information File S2.1 and A_D(K) in Supporting Information File S2.3:

$$A_G(K)=1-\sum _{i=1}^{K-1}{h}_1(K,i)\arctan \left(\frac{1}{\sqrt{2K-1}}\right)+\sum _{i=1}^{K-1}{h}_2(K,i)\log \left(\frac{i}{i+1}\right)$$ (13)

$$A_D(K)=1-\frac{2\sqrt{2K-1}}{3}\arctan \left(\frac{1}{\sqrt{2K-1}}\right),$$ (14)

where functions h₁ and h₂ follow Equations S2.6 and S2.7 in Supporting Information File S2.

In Figure 2, we compare A_G(K) and A_D(K) to the area between the minimal and maximal $F_{\text{ST}}$ as functions of M (Alcala & Rosenberg, 2017, Equation 9), denoted A_F. We can see in the figure that A_G is greater than A_F for all K, particularly when K is small, whereas A_F and A_G are similar for large K. Thus, $G_{\text{ST}}^{\prime }$ is less constrained than $F_{\text{ST}}$ by M when the number of subpopulations is small, and $G_{\text{ST}}^{\prime }$ and $F_{\text{ST}}$ are comparably constrained when it is large. A_D is seen to be lower than both A_F (except at K = 2) and A_G, and thus, D is more constrained than the other two measures.

FIGURE 2.

The means A_F, A_G, and A_D of the maximal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D, respectively, over the interval M ∈ [1/2, 1), as functions of the number of subpopulations K. A_F(K) is computed from Equation 12, A_G(K) from Equation 13, and A_D(K) from Equation 14. The x-axis is plotted on a logarithmic scale

The pattern of change in A_D(K) as a function of K is distinct from those of A_F(K) and A_G(K). A_D(K) decreases with K (Supporting Information File S2.4), whereas A_F(K) increases with K for all K ≥ 2 (Alcala & Rosenberg, 2017, Theorem 3), and A_G(K) increases with K at least for K ranging from 2 to 10,000 (Supporting Information File S2.2). As K becomes large, A_D tends to 1/3, whereas A_F approaches 1 (Alcala & Rosenberg, 2017, Equation 9), as does A_G (Supporting Information File S2.2). Thus, unlike $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$, D does not have a mean range extending over the whole unit interval when K is large. On the other hand, of the three statistics, A_D(K) has the least change as a function of K, decreasing from $(9-\pi \sqrt{3})/9\approx 0.39540$ to 1/3 (Figure 2), whereas A_F(K) increases from 2 log 2 − 1 ≈ 0.38629 to 1 and A_G(K) increases from (3–2 log 2)/3 ≈ 0.53790 to 1. Thus, the constraint imposed by M on D is more consistent across values of K than are the constraints on the other two measures.

3.2. Simulation-based distributions of $F_{\text{ST}}$, ${\text{G}}_{\text{ST}}^{\prime },$ and D

To illustrate the mathematical properties of differentiation measures $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in the context of evolutionary models, we simulated the joint distribution of each quantity with M under an island migration model, and we compared the distribution to the mathematical minima and maxima of the statistics. This analysis considers allele frequency distributions generated by evolutionary models, rather than treating M as uniformly distributed in [1/2,1).

We simulated independent single-nucleotide polymorphisms (SNPs) under the coalescent using the protocol of Alcala and Rosenberg (2017). Using the software ms (Hudson, 2002), we simulated a population of total size KN diploid individuals subdivided into K subpopulations of equal size N, with migration following the finite island model (Maruyama, 1970; Wakeley, 1998) with migration rate m in each direction between each pair of subpopulations. We examined three K values (2, 7, 40) and three 4Nm values (0.1, 1, 10). We simulated conditional on producing one segregating site in each simulation. For each parameter pair (K,4Nm), we performed 100,000 replicate simulations, sampling 100 lineages per subpopulation (corresponding to 50 diploid individuals) in each replicate. MS commands appear in Supporting Information File S3. Because we do not investigate estimation of allele frequencies from data, $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values were computed assuming that the empirical allele frequencies were parametric allele frequencies.

3.2.1. Weak migration for K = 2

As shown by Alcala and Rosenberg (2017), and seen here in Figure 3a, for K = 2, under weak migration (4Nm = 0.1), the joint density of M and $F_{\text{ST}}$ is greatest near the maximum of $F_{\text{ST}}$ as a function of M. We can see in Figure 3b,c that the joint densities of M and $G_{\text{ST}}^{\prime }$ and of M and D are also highest near their respective maxima as functions of M. For the three statistics, most loci have M near 1/2, indicating that one allele is fixed in one subpopulation and the other is fixed in the second subpopulation, and $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are near 1 (orange areas in Figure 3a–c). The mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values in sliding windows for M (red dashed lines in Figure 3a–c) closely follow their respective maxima. Because the maximal values of the three statistics are similar for K = 2, the joint densities are also similar.

FIGURE 3.

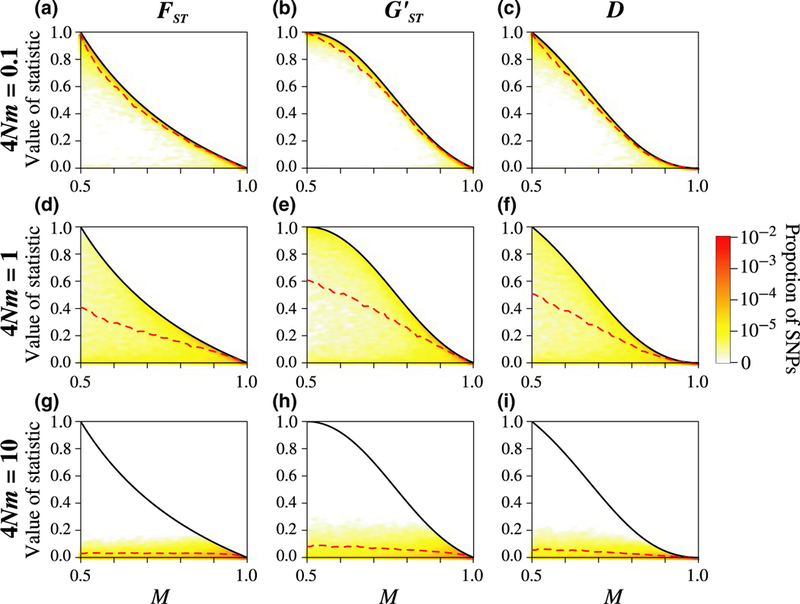
Joint density of the frequency M of the most frequent allele and statistics $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D, for different scaled migration rates 4Nm, considering K = 2 subpopulations. The black solid line represents the maximum value of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, or D in terms of M (Equations 9–11); the red dashed line represents the mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in sliding windows of M of size 0.02 (plotted from 0.51 to 0.99). Colours represent the density of loci, estimated using a Gaussian kernel density estimate with a bandwidth of 0.007, with density set to 0 outside the minimum and maximum values. Loci are simulated using coalescent software MS, assuming an island model of migration and conditioning on one segregating site. Each panel considers 100,000 replicate simulations, with 100 lineages sampled per subpopulation

The conditions under which the maximal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are reached provide an explanation of these observations. We showed that the maximal values of the three statistics are reached under the same condition–when alleles are fixed in one or sometimes both subpopulations. Under weak migration, we expect the derived allele to be trapped in its subpopulation of origin, and the ancestral allele to be fixed in the other subpopulation. This situation matches the conditions under which $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D reach their maximal values as functions of M.

3.2.2. Intermediate migration for K = 2

For K = 2, under intermediate migration (4Nm = 1), the joint densities of M and $F_{\text{ST}}$, M and $G_{\text{ST}}^{\prime }$, and M and D are the highest between their respective minimum and maximum values as functions of M (Figure 3d–f). The mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values in sliding windows for M are almost equidistant from the minimal and maximal values, approaching closer to the maximum when M nears 1 (red dashed line in Figure 3d–f).

Under intermediate migration, we expect the derived allele to segregate into the two subpopulations, but to still be at higher frequency in its subpopulation of origin. Consequently, the condition under which $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D reach their maximum as a function of M is not attained. The condition under which the statistics reach their minimum–equal allele frequencies in all subpopulations–is not expected to be attained either, resulting in $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D between their minimum and maximum values.

3.2.3. Strong migration for K = 2

Continuing with K = 2, under strong migration (4Nm = 10), the three joint densities are the highest near their respective minima as functions of M (Figure 3g–i). The mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in sliding windows for M are near their minimal values (red dashed line in Figure 3g–i).

Under strong migration, we expect the derived allele to segregate into the two subpopulations approximately at the same frequency. Consequently, the condition under which $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D reach their minima as functions of M–equal allele frequencies in all subpopulations–is attained.

3.2.4. Weak, intermediate, and strong migration for K > 2

For K = 7, the joint densities of M and $F_{\text{ST}}$, M and $G_{\text{ST}}^{\prime }$, and M and D follow a similar pattern to that seen for K = 2: the densities lie near the maximal value of their statistics under weak migration, between the minimum and maximum under intermediate migration, and near the minimum under strong migration (Figure 4). Under weak migration, most loci have M near 4/7, 5/7, or 6/7, indicating allele fixation in all subpopulations. Nevertheless, because the maximal values of the three statistics differ greatly, their values under weak migration are quite different: most loci have $F_{\text{ST}}$ ≈ 1 and $G_{\text{ST}}^{\prime }$ ≈ 1, but D < 0.5.

FIGURE 4.

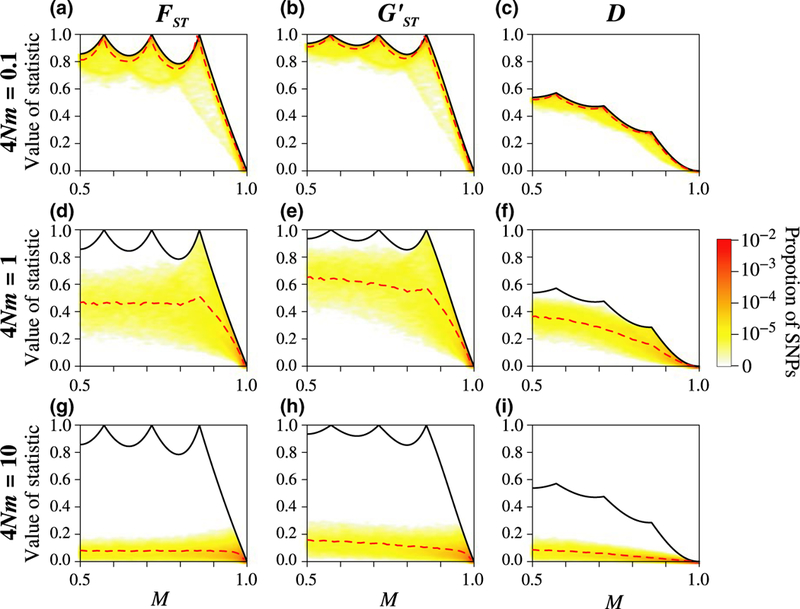
Joint density of the frequency M of the most frequent allele and statistics $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D, for different scaled migration rates 4Nm, considering K = 7 subpopulations. The simulation procedure and figure design follow Figure 3

For K = 40, the joint densities also lie near the maximum under weak migration, between the minimum and maximum under intermediate migration, and near the minimum under strong migration (Supporting Information Figure S1). Under weak migration, loci have M values that range from 1/2 to 1. Because the maxima of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ are similar, their values under weak migration are also similar: most loci have $F_{\text{ST}}$ ≈ 1 and $G_{\text{ST}}^{\prime }$ ≈ 1. By contrast, D < 0.5.

Interestingly, comparing the densities of M and D under weak migration as a function of K, we can see that the values of D are more weakly influenced by K (Figures 3c, 4c, and Supporting Information Figure S1C). By contrast, the values of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ are more strongly influenced by K (Figures 3a, 4a, and Supporting Information Figure S1a and Figures 3b, 4b, and Supporting Information Figure S1b).

3.2.5. Proximity of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D to their maximum values

To measure the impact of evolutionary processes on $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values and to summarize Figures 3 and 4 and Supporting Information Figure S1, we quantified the proximity of the joint densities of M and $F_{\text{ST}}$, M and $G_{\text{ST}}^{\prime }$, and M and D to their maximum value as a function of M across a range of migration rates and numbers of subpopulations.

We denote by ${\overline{F}}_{\text{ST}},{\overline{G}}_{\text{ST}}^{\prime },\text{and}\overline{D}$, and $\overline{D}$ the mean values of FST, $F_{\text{ST}},G_{\text{ST}}^{\prime }$, and D across a set of Z loci, respectively. To be precise, these means are obtained by computing F_z, G’_z, and D_z–the values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D for biallelic loci z—for each z from 1 to Z, and averaging F_z, $F_z,G_z^{\prime },$ and D_z across the Z loci (Equations D1 and D2 in Appendix D). The corresponding mean maximal $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D across the Z loci are denoted ${\overline{F}}_{\max },{\overline{G}}_{\max }^{\prime },\text{and}{\overline{D}}_{\text{max}}$. They are computed by substituting the observed frequency M_z of the most frequent allele at loci z = 1, 2, …, Z into the expression for the maximal $F_{\text{ST}}$ (Equation 9), $G_{\text{ST}}^{\prime }$ (Equation 10), and D (Equation 11), and averaging the values over the Z loci (Equations D3 and D4 in Appendix D). We computed ${\overline{F}}_{\text{ST}}/{\overline{F}}_{\max },{\overline{G}}_{\text{ST}}^{\prime }/{\overline{G}}_{\text{max}}^{\prime },$, and $\overline{D}/{\overline{D}}_{\max },$, which we describe as normalized statistics, across a range of values of K (2, 10, and 100) and scaled migration rates (0.01–100; Figure 5).

FIGURE 5.

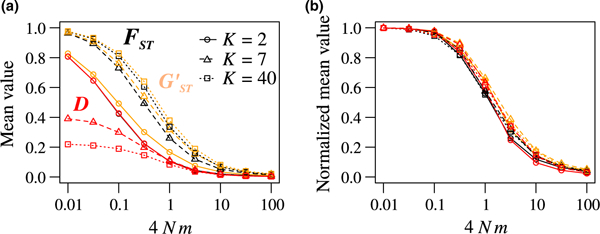
Mean ${\overline{F}}_{\text{ST}},{\overline{G}}_{\text{ST}}^{\prime },$ and D across biallelic loci. (a) Unnormalized means ${\overline{F}}_{\text{ST}},{\overline{G}}_{\text{ST}}^{\prime },$ and D. (b) Normalized means ${\overline{F}}_{\text{ST}}/{\overline{F}}_{\max },{\overline{G}}_{\text{ST}}^{\prime }/{\overline{G}}_{\max }^{\prime }$ and $\overline{D}/{\overline{D}}_{\max },$ the ratio of the mean value to the mean maximal value given the observed frequency M of the most frequent allele. Both plots show quantities as functions of the number of subpopulations K and the scaled migration rate 4Nm. Colours represent the different statistics. Line types represent values of K: 2 (solid), 7 (dashed), and 40 (dotted). Values are computed from coalescent simulations using software ms as in Figure 3, with 1,000 replicate biallelic loci and 100 lineages per subpopulation. ${\overline{F}}_{\max },{\overline{G}}_{\max }^{\prime }$ and < ${\overline{D}}_{\max }$ are respectively computed from equation 11 of Alcala and Rosenberg (2017) and Equations D3 and D4 in Appendix D

Interestingly, for a fixed 4Nm, ratios are similar for the three measures across all values of K (Figure 5b). The largest difference between $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ values is 0.07 and is reached when 4Nm = 1; the largest difference between D and $G_{\text{ST}}^{\prime }$ is 0.06, also when 4Nm = 1. Thus, all three measures provide similar information once their mathematical constraints are taken into account.

3.3. Application to data

We now use two SNP data sets to illustrate how our findings can explain patterns in genomic data.

3.3.1. K = 2: wolf and dog

The first data set (Cronin, Cánovas, Bannasch, Oberbauer, & Medrano, 2015) consists of samples from 305 North American wild wolves (Canis lupus) and 91 dogs (Canis familiaris; 36 mixed-breed dogs, 53 poodles, one Australian shepherd, and one Border collie). The wolves and dogs are typed at 123,801 biallelic loci. This example illustrates the dependence of the constraints of the differentiation measures on M when performing pairwise comparisons.

The joint densities of M and $F_{\text{ST}}$, M and $G_{\text{ST}}^{\prime }$, and M and D appear in Figure 6a–c. Most loci have relatively large values of M, for which the differentiation statistics are tightly constrained. As we saw using coalescent simulations (Figure 3), values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are globally close; $G_{\text{ST}}^{\prime }$ values are the largest of the three measures for all M, D exceeds $F_{\text{ST}}$ for intermediate M, and $F_{\text{ST}}$ exceeds D for high M.

FIGURE 6.

Joint density of the frequency M of the most frequent allele and three differentiation measures ($F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D), and unnormalized and normalized mean values of the differentiation measures across loci, for 305 wolves and 91 dogs from North America, using 123,801 SNPs. (a) M and $F_{\text{ST}}$. (b) M and $G_{\text{ST}}^{\prime }.$ (c) M and D. (d) Unnormalized mean values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D across SNPs, and the mean values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D across SNPs normalized by the mean of their maximal values. In (a-c), the figure design follows Figure 3. In (d), ${\overline{F}}_{\max },{\overline{G}}_{\max }^{\prime },$ and ${\overline{D}}_{\max }$ are respectively computed from equation 11 of Alcala and Rosenberg (2017) and Equations D3 and D4 in Appendix D

In addition, we can see in Figure 6D that normalizing the mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D increases their values considerably. As we observed in the simulations (Figure 5), $G_{\text{ST}}^{\prime }$ values are slightly closer to their maxima than are $F_{\text{ST}}$ and D values.

3.3.2. K > 2: Atlantic salmon

The second data set consists of 900 Atlantic salmon (Salmo salar) sampled from 26 populations (Bourret et al., 2013) and typed at 1,335 biallelic loci. This example illustrates the constraints of the measures when many subpopulations are considered.

The joint densities of M with $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D appear in Figure 7a– c. As was seen in coalescent simulations (Figure 4), values of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ are close, with larger $G_{\text{ST}}^{\prime }$ ; D values are lower than both $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ for all M.

FIGURE 7.

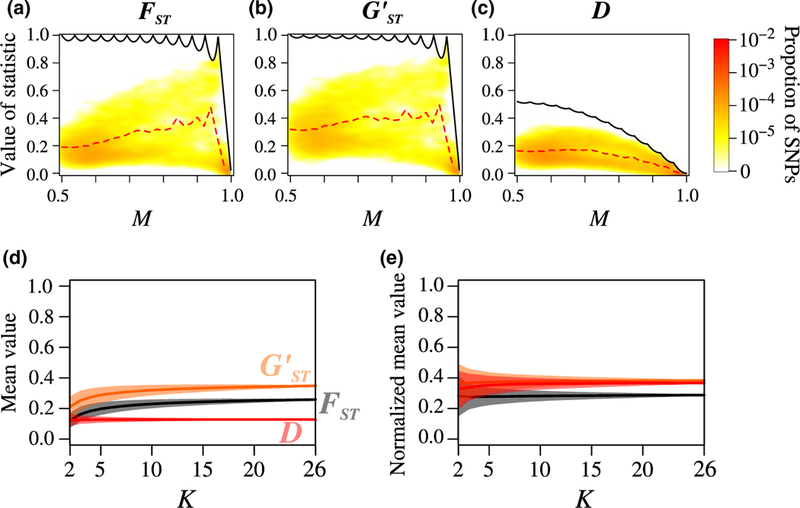
Joint density of the frequency M of the most frequent allele and three differentiation measures ($F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D), and unnormalized and normalized mean values of the differentiation measures across loci, for 900 Atlantic salmon from 26 populations, using 1,335 SNPs. Sample sizes range from 25 to 40 per population. (a) M and $F_{\text{ST}}$. (b) M and $G_{\text{ST}}^{\prime }$. (c) M and D. (d) Mean values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime },$ and D across SNPs, for sets of geographic regions as a function of K, the number of regions considered. (e) Ratio of mean values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D across SNPs to their maximal mean values as functions of K. In (a-c), the figure design follows Figure 3. Coloured bars in (d) and (e) represent 2.5 and 97.5 quantiles of distributions of values across sets of size K. In (e), ${\overline{F}}_{\max },{\overline{G}}_{\max }^{\prime },\text{and}{\overline{D}}_{\max }$ are respectively computed from equation 11 of Alcala and Rosenberg (2017) and Equations D3 and D4 in Appendix D

Figure 7d,e illustrate the impact of the number of subpopulations on values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D. The figure represents the mean $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values across loci for sets of K salmon subpopulations among the 26 subpopulations, for K ranging from 2 to 26. For computational simplicity, when the number of possible sets exceeded 10,000, we randomly chose without replacement 10,000 sets to compute the three measures. We can see in Figure 7d that the values of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ depend more strongly on the value of K, whereas the values of D are weakly affected by K. In addition, we can see in Figure 7e that even though the mean values of D are smaller than those of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$, they are comparably close to the maximum value as the means of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$. Also, as we showed with coalescent simulations (Figure 5), $G_{\text{ST}}^{\prime }$ values are slightly closer to their associated maximal values than are D and $F_{\text{ST}}$.

4. DISCUSSION

We have shown that for biallelic markers and arbitrary numbers of subpopulations K, the maximal values of $G_{\text{ST}}^{\prime }$ and D are both lower than 1 for most frequencies M of the most frequent allele. We have described the properties of the maximal values of $G_{\text{ST}}^{\prime }$ and D as functions of M, and compared them with that of $F_{\text{ST}}$. We have shown that $G_{\text{ST}}^{\prime }$ is the least constrained by M, and that D is the most constrained. Despite these differences, the allele frequencies that minimize and maximize $G_{\text{ST}}^{\prime }$ and D are the same. Using coalescent simulations and two data examples, we have shown that values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D normalized by their respective maxima given M are more similar to each other than are their unnormalized counterparts.

Contrary to the claim of Jost (2008), D does not eliminate all counterintuitive phenomena observed with $F_{\text{ST}}$: we exhibit domains of M under which the maximal D is well below 1. One possible explanation of this discrepancy is that examples in Jost (2008) focused on cases with either many alleles or K = 2 subpopulations, whereas we find strong constraints on D in the case of a biallelic marker and K > 2. Moreover, despite the strong arguments of Jost (2008) about the importance of “mathematical misconceptions” underlying the construction of $F_{\text{ST}}$, we find that $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D have similar behaviour once we account for their respective maximal values as functions of M. Note that because H_T = 2M(1 − M) for biallelic markers, M uniquely specifies H_T and H_T uniquely specifies M; thus, our results describing constraints on $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D as functions of M can also be viewed as constraints as functions of H_T.

Although $G_{\text{ST}}^{\prime }$ and D are not constrained by the value of the within-subpopulation heterozygosity H_S, we have shown that both statistics are constrained by allele frequencies in other ways. It does not follow that a measure that has no constraints in terms of H_S has no constraints at all; the differentiation measures that have been proposed to supplant $F_{\text{ST}}$ present some degree of constraint in terms of M or H_T and are thus subject to analogous criticism. Possibly, any differentiation measure would possess some constraint. This result accords with the conclusion of Meirmans and Hedrick (2011) that a summary statistic unconstrained in relation to all aspects of allele frequencies probably does not exist.

Focusing on the frequency M of the most frequent allele enables a coalescent interpretation of constraints on differentiation statistics. In a coalescent framework, for a locus at which alleles arise as unique mutations, fixing M corresponds to fixing the number of sampled lineages containing an allele, inducing a distribution of the time depth at which a mutation arose. Genetic differentiation statistics conditional on different values of M can then be viewed as examining constraints on differentiation for loci whose alleles have originated at different times. In this coalescent interpretation, normalization by the maximum value given M enables comparisons of the values of the statistics irrespective of the depth at which a mutation appeared in the gene tree. Thus, both the values of differentiation statistics conditionally on M and the values of those statistics normalized by their maxima given M are potentially useful in disentangling the relative impacts of ancient and recent evolutionary events on patterns of polymorphism. Note that this perspective is distinct from the usual coalescent-based interpretation of Slatkin (1991), in which $F_{\text{ST}}$ statistics are computed in sequence regions rather than pointwise and have a more direct interpretation in relation to coalescence times.

We found that the three differentiation measures have similar values when comparing pairs of subpopulations (K = 2) using biallelic loci. Indeed, both the mathematical constraints and the distributions generated by common biological processes produce similar values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D. Consequently, it appears that choosing one measure among the three is not very important when considering biallelic loci and performing pairwise population comparisons. This result contrasts with that of Table 1 of Jost (2008), which showed that $F_{\text{ST}}$ and D can give very different results when K = 2, but considering multiallelic loci. Extending our results to the case of K = 2 and multiallelic loci using the framework laid out in Jakobsson et al. (2013) and Edge & Rosenberg (2014) could potentially solve this apparent discrepancy that the statistics are similar when considering a biallelic locus and K = 2 but different when considering a multiallelic locus and K = 2.

We highlight a trade-off in the properties of differentiation statistics based on biallelic loci: D values are the least sensitive to the effect of the number of subpopulations K, but the most strongly constrained. Knowing this trade-off can potentially help users choose among statistics. For example, if the goal is to compare differentiation among species with various distinct numbers of subpopulations, then D could be the most useful, whereas $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ could be more suitable for providing a wider range of values in comparisons with the same value of K.

Modified $F_{\text{ST}}$ statistics that incorporate the number of subpopulations have previously been suggested. In Supporting Information File S4, we examine two alternative statistics, $G_{\text{ST,Nei}}^{\prime }$, due to Nei (1987) and $G_{\text{ST}}^{″}$ due to Meirmans and Hedrick (2011), designed as modified versions of $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$, respectively, and both incorporating a factor dependent on the number of subpopulations. We show that $G_{\text{ST}}^{\prime }$ and $G_{\text{ST}}^{\prime \prime }$. are constrained by the value of M similarly to $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$, respectively, but to a slightly lesser degree (Supporting Information Figures S3–S5). These constraints are stronger if K = 2, decreasing as K increases (Supporting Information Figure S2). Along with computations by Alcala and Rosenberg (2017) showing constraints on the Weir-Cockerham estimator θ (Weir & Cockerham, 1984) as a function of M, these results suggest that mathematical constraints on $F_{\text{ST}}$-related statistics are pervasive, rather than features of particular formulations of the measure.

As a first step in analyzing a dataset, similarly to the proposal from Wang (2015), we suggest evaluating $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D in relation to another statistic dependent on allele frequencies. This exploratory step ensures that dependencies among statistics are identified. In addition, we suggest displaying the maximal values of the statistics (Equations 9–11). Indeed, we showed that when correcting for the mathematical maximum in terms of M, all measures provide similar information. This result accords with that of Heller and Siegismund (2009), who found a strong correlation among empirically reported $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values. Meirmans and Hedrick (2011) further highlighted theoretical connections among them, showing that ${\lim }_{K\to \infty }\left(G_{\text{ST}}^{\prime }/F_{\text{ST}}\right)=1/\left(1-H_S\right).$ In agreement with their result, we found that maximal $F_{\text{ST}}$ and $G_{\text{ST}}^{\prime }$ values are particularly close when K is large and when an allele is fixed in each subpopulation–producing H_S = 0. Meirmans and Hedrick (2011) also showed that ${\lim }_{K\to \infty }\left(D/G_{\text{ST}}^{\prime }\right)=H_T,$, which accords with our result that the maximal D approaches H_T when K is large, and the maximal $G_{\text{ST}}^{\prime }$ approaches 1.

$F_{\text{ST}}$ and other genetic differentiation statistics are often used to search for loci responsible for local adaptation. Following from the initial approach of Lewontin and Krakauer (1973), many tests compute the distribution of $F_{\text{ST}}$ in a set of genotyped loci and consider loci with $F_{\text{ST}}$ values above a threshold as candidates for local adaptation (see e.g., OutFLANK, Whitlock & Lotterhos, 2015 for a modern implementation). $F_{\text{ST}}$ bounds in terms of M demonstrate that if such methods do not account for the frequency of the most frequent allele, certain loci will be undetectable even if they contribute to local adaptation: irrespective of the threshold chosen, there exist large M values for which the upper bound on $F_{\text{ST}}$ lies below the threshold.

Some outlier studies of adaptation eliminate loci from consideration based on a cutoff such as M = 0.95 (Whitlock & Lotterhos, 2015). Because the value of M above which associated $F_{\text{ST}}$ values necessary lie below a threshold F_threshold depends on F_threshold’ depending on the threshold and the cutoff for M, filtering loci according to a cutoff for M could either eliminate loci for which $F_{\text{ST}}$ outliers could potentially be detected or retain loci for which $F_{\text{ST}}$ outliers could never be detected. Importantly, because of their similar behavior in relation to M, $G_{\text{ST}}^{\prime }$ and D would have the same limitation.

In this context, normalizing the differentiation statistic of interest by its maximum given M could produce a measure that does not have the limitation that some loci would be undetectable by outlier tests. However, because the variability of the statistic across locidepends on M, such a normalization would inflate the variance of the statistic, potentially interfering with the ability of outlier tests to identify the loci of greatest interest. By contrast, methods that consider the joint distribution of differentiation statistics such as $F_{\text{ST}}$ and other variables, such as heterozygosity statistics (Beaumont & Nichols, 1996), potentially avoid this concern.

The process by which we assess the position of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D values between their minimal and maximal values–computing the ratio of the values of each differentiation measure to a maximum value given a variable (here M)–is similar to the derivation of standardized differentiation statistics (Hedrick, 1999, 2005; Meirmans, 2006). This result shows that we can perform other kinds of standardizations, by the maximum value of the statistics given M rather than by the maximum given H_S. Our work refines the classification of differentiation statistics from Meirmans and Hedrick (2011), which included three classes–F statistics, standardized statistics such as $G_{\text{ST}}^{\prime }$, and D-like statistics–making standardized statistics based on H_S a subclass among a plethora of other possible standardizations, each of which would lead to specific behaviours. Because summary statistics unconstrained in relation to all potentially interesting aspects of allele frequencies probably do not exist, however, we caution that sequentially multiplying normalizations might not be the best approach to understand genetic differentiation. Rather, plotting observations of a genetic differentiation statistic as a function of a variable of interest such as M, as in Figures 3–7, while highlighting the maximal values of the statistic, enables an enlightened interpretation. If a normalization is desired, performing a normalization of $F_{\text{ST}}$ by its maximum value given M provides results similar to those obtained by normalizing $G_{\text{ST}}^{\prime }$, which is already normalized by its maximum value given H_S.

We used normalization to show that taking into account the maximal values of the three statistics, they are similarly affected by migration. Under the island model of migration and considering a multiallelic locus with an infinite alleles mutation model, Whitlock (2011) and Alcala, Goudet, and Vuilleumier (2014) found that for a fixed value of the migration rate, unnormalized values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D can be very different. We confirmed these results under the same migration model but using a biallelic infinite sites mutation model. Nevertheless, we showed that normalized statistics are strikingly similarly affected by migration. Finding such strong similarities rather than differences among the three statistics is a first step to reconcile their results, emphasizing that the different measures have more features in common than might be apparent from the existence of strong arguments in favour of one or another among them.

APPENDIX A. The minimal values of $G_{\text{ST}}^{\prime }$ and D

In this appendix, we show that the only allelic configuration for which $G_{\text{ST}}^{\prime }=0$ is p₁ = p₂ = … = p_K = M. This configuration is also the only configuration for which D = 0.

From Equation 7, $G_{\text{ST}}^{\prime }=0$ if and only if either K − 1 + H_S = K − 1 − 2S + 2M = 0 or K(S - M²) = 0. Because H_S ≥ 0 and K > 1, K − 1 + H_S ≥ K − 1 > 0. From Alcala and Rosenberg (2017, “Lower bound” subsection), K(S − M²) = 0 if and only if p_k = M in all subpopulations k. Similarly, from Equation 8, D = 0 if and only if K(S − M²) = 0.

Consequently, p₁ = p₂ = … = p_K = M is the only allele frequency vector that yields $G_{\text{ST}}^{\prime }=0$ and the only vector that yields D = 0; this configuration can be reached for all M ∈ [1/2, 1). Because from Alcala and Rosenberg (2017, “Lower bound” subsection), p₁ = p₂ = … = p_K = M is also the only configuration that yields $F_{\text{ST}}$ = 0, we can conclude that the minimal values of $F_{\text{ST}}$, $G_{\text{ST}}^{\prime }$, and D are the same and equal to 0 irrespective of M, for any value of the number of subpopulations K.

APPENDIX B. $G_{\text{ST}}^{\prime }$ and D as functions of S

In this appendix, we show that both $G_{\text{ST}}^{\prime }$ (Equation 2) and D (Equation 3) are increasing functions of $S=\frac{1}{K}{\sum }_{k=1}^K{p}_k^2,$, with $p_k\in [0,1]$ for all k.

We take the derivatives of Equations 7 and 8 with respect to S:

$$\frac{d{G}_{\text{ST}}^{\prime }}{dS}=\frac{K[1-2M(1-M)]-{(1+2S-2M)}^2}{(K-1)M(1-M){(1+2S-2M)}^2},$$ (B1)

$$\frac{dD}{dS}=\frac{2K[1-2M(1-M)]}{(K-1){(1+2S-2M)}^2}.$$ (B2)

The denominator in Equation B1 is positive because 1 + 2S − 2M = 1 − H_S > 0 (using Equation 4). The sign of $d{G}_{\text{ST}}^{\prime }/dS$ is therefore determined by the sign of its numerator. Because from Equation 5, H_T = 2M(1 − M), the numerator of Equation B1 is

$$\begin{array}{l}K[1-2M(1-M)]-{(1+2S-2M)}^2\\ =K\left(1-H_T\right)-{\left(1-H_S\right)}^2\\ =K\left(1-H_T\right)-\left(1-H_S\right)+H_S\left(1-H_S\right).\end{array}$$ (B3)

From Hedrick (2005, p. 1634), H_T ≤ (H_S + K − 1)/K and hence 1 − H_T ≥ (1 − H_S)/K, equality requiring that each allele be present only in a single subpopulation. Thus, K(1 − H_T) ≥ 1 − H_S. Because 0 ≤ H_S < 1, we also have H_S(1 − H_S) ≥ 0, equality requiring H_S = 0. Consequently, Equation B3 is nonnegative, as is the numerator of $d{G}_{\text{ST}}^{\prime }/dS$ We conclude that dG’_ST/dS is nonnegative, with equality possible only at the point S = M, and that $G_{\text{ST}}^{\prime }$ is an increasing function of S.

The denominator in Equation B2 is also positive, so the sign of dD/dS is determined by the sign of its numerator. The numerator equals 2K(1 − H_T) and hence is positive, as 0 < H_T < 1 for polymorphic loci. Consequently, dD/dS is positive, and we conclude that D is an increasing function of S.

APPENDIX C. Upper bounds for the case of K = 2

In the case of K = 2, because 1/2 ≤ M < 1, $\lfloor KM\rfloor =1,$ and {KM} = KM − $\lfloor KM\rfloor =2M-1$. Equations 9–11 then simplify:

$$F_{\text{ST}}\le \frac{1-M}{M}$$ (C1)

$$G_{\text{ST}}\le \frac{(1-M)\left(-4M^2+6M-1\right)}{M\left(4M^2-6M+3\right)}$$ (C2)

$$D\le \frac{4{(1-M)}^2}{4M^2-6M+3}.$$ (C3)

Denoting the upper bounds in Equations 9–11 by F*(M), G*(M), and D*(M), respectively, for the case of K = 2, Equations C1–C3 give

$$G^{*}(M)-F^{*}(M)=\frac{4{(1-M)}^2(2M-1)}{M\left(4M^2-6M+3\right)}$$ (C4)

$$F^{*}(M)-D^{*}(M)=\frac{(1-M)(2M-1)(4M-3)}{M\left(4M^2-6M+3\right)}$$ (C5)

$$G^{*}(M)-D^{*}(M)=\frac{(1-M)(2M-1)}{M\left(4M^2-6M+3\right)}.$$ (C6)

The denominator in Equations C4–C6 is positive in the permissible range for M, as 4M² − 6M + 3 has no real roots. We can then observe that G*(M) ≥ F*(M) and G*(M) ≥ D*(M), with equality in both cases if and only if M = 1/2. We also have F*(M) < D*(M) for 1/2 < M < 3/4, F*(M) > D*(M) for 3/4 < M < 1, and F*(M) = D*(M) for M = 1/2 and M = 3/4.

APPENDIX D. Normalized mean $G_{\text{ST}}^{\prime }$ and D

This appendix provides the formulas to compute the normalized means, ${\overline{G}}_{\text{ST}}^{\prime }/{\overline{G}}_{\text{max}}^{\prime }$ and $\overline{D}/{\overline{D}}_{\max },$, used in Figures 5–7.

Given a set of Z loci, we denote by $G_z^{\prime },D_z,$ D_z, and M_z the values of $G_{\text{ST}}^{\prime },$ D, and M at locus z. The mean $G_{\text{ST}}^{\prime }$ and D for the set, denoted by and $\overline{D},$ are

$${\overline{G}}_{\text{ST}}^{\prime }=\frac{1}{Z}\sum _{z=1}^Z{G}_z^{\prime }$$ (D1)

$$\overline{D}=\frac{1}{Z}\sum _{z=1}^Z{D}_z.$$ (D2)

From Equations 10 and 11, the corresponding mean maximal values given the observed M_z at the Z loci are denoted by $\overline{G}{\text{'}}_{\max }$ and ${\overline{D}}_{\max }:$

$$\overline{G}{\text{'}}_{\max }=\frac{1}{Z}\sum _{z=1}^Z\left[\frac{\left[K(K-1)+2\left\{K{M}_z\right\}\left(1-\left\{K{M}_z\right\}\right)\right]}{K(K-1)\left[K-2\left\{K{M}_z\right\}\left(1-\left\{K{M}_z\right\}\right)\right]}\times \frac{(\lfloor K{M}_z\rfloor +{\left\{K{M}_z\right\}}^2-K{M}_z^2)}{M_z\left(1-M_z\right)}\right]$$ (D3)

$${\overline{D}}_{\max }=\frac{1}{Z}\sum _{z=1}^z\frac{2K\left(\lfloor K{M}_z\rfloor +{\left\{K{M}_z\right\}}^2-K{M}_z^2\right)}{(K-1)\left[K-2\left\{K{M}_z\right\}\left(1-\left\{K{M}_z\right\}\right)\right]}.$$ (D4)