Pharmaceutical-based entrainment of circadian phase via nonlinear model predictive control

Abstract

The widespread adoption of closed-loop control in systems biology has resulted from improvements in sensors, computing, actuation, and the discovery of alternative sites of targeted drug delivery. Most control algorithms for circadian phase resetting exploit light inputs. However, recently identified small-molecule pharmaceuticals offer advantages in terms of invasiveness and potency of actuation. Herein, we develop a systematic method to control the phase of biological oscillations motivated by the recently identified small molecule circadian pharmaceutical KL001. The model-based control architecture exploits an infinitesimal parametric phase response curve (ipPRC) that is used to predict the effect of control inputs on future phase trajectories of the oscillator. The continuous time optimal control policy is first derived for phase resetting, based on the ipPRC and Pontryagin’s maximum principle. Owing to practical challenges in implementing a continuous time optimal control policy, we investigate the effect of implementing the continuous time policy in a sampled time format. Specifically, we provide bounds on the errors incurred by the physiologically tractable sampled time control law. We use these results to select directions of resetting (i.e. phase advance or delay), sampling intervals, and prediction horizons for a nonlinear model predictive control (MPC) algorithm for phase resetting. The potential of this ipPRC-informed pharmaceutical nonlinear MPC is then demonstrated in silico using real-world scenarios of jet lag or rotating shift work.

1. Introduction

A coalescing of control engineering and systems biology has resulted in widespread use of open-loop and feedback control approaches in biological and biomedical applications [1, 2]. These include identifying and modulating cellular behavior [3–5], treating diseases [6, 7], constructing synthetic biological circuits [8, 9], optimizing biomanufacturing productivity [10, 11], and formulating targeted drug delivery systems [12–15]. Unlike open-loop systems that require manual intervention at critical times to prevent deleterious outcomes, closed-loop drug delivery systems enable effective regulation of targeted biological pathways by leveraging control-relevant models, systematic prediction, or decision-making based on clinical targets. Therefore, these approaches have found use in manufacturing and medical devices. Additional improvements in the quality of closed-loop drug delivery and adherence within society has been fueled by the invention of wearable sensors [16], minimally invasive actuators, and embedded decision-making platforms [17], along with novel drug delivery mechanisms [18] or input-output pairs [19]. This paper demonstrates how selecting control input (from light-based methods to small-molecule pharmaceuticals) or controller design parameters plays an essential role in resetting the phase of mammalian circadian rhythms.

Circadian rhythms are endogenous daily oscillations in gene expression or metabolism driving temporal adaptations in most organisms. In mammals, these oscillations are generated by genetic feedback loops within each cell of the organism [20]. Since environmental signals (such as ambient light) set the time of this biological clock, mistimed environmental cues may result in adverse changes to these rhythms, and consequently, a loss of temporal regulation of the genetic architecture, and psychological and physiological pathologies [21]. In recent years, small-molecule pharmaceuticals have gained significant interest as a path toward modulating the circadian clock to reduce the effects of circadian disturbances [22, 23]. Small-molecule pharmaceuticals present critical benefits over the use of light for clock resetting including avoiding the day-time “dead-zone” where light evokes a minimal phase response, and reducing the impractical and burdensome challenge of attempting to tightly control one’s light environment. For example, light-based regulation would necessitate sustained periods of time wearing low-transmission glasses or light visors [24]. Most importantly, light dosing strategies typically take several days to reset circadian rhythms: hence the prevalence of sustained jet lag following long trips across time zones. Even state-of-the-art optimal control policies involving light necessitate as much as eight days to complete a phase resetting when allowing for regular sleep timing [25].

Pharmaceuticals are expected to enable direct manipulation of sensitive control targets within the clock, allowing more rapid clock resetting [26]. The complex nature of the circadian oscillator necessitates a control approach toward dosing strategies for these drugs, as identical stimuli applied at different times of the day may have drastically disparate effects on the clock. Modeling approaches such as those described in [27] have been employed to identify the underlying mechanistic action of these drugs. Such models may, in turn, be used to inform advanced model-based control strategies such as model predictive control (MPC) for circadian regulation.

Prior studies employing models of circadian dynamics have independently investigated optimal control-based approaches for manipulating the circadian clock. For example, nonlinear MPC and multi-target MPC for light-resetting a Drosophila circadian clock model was demonstrated in [26, 28], and complementary phase response curves (PRCs) were leveraged to identify potential control targets. Other studies using nonlinear Drosophila clock models [29, 30] proposed more efficient procedures to obtain light-based optimal control trajectories by relaxing the nonlinear control problem into a mixed-integer formulation. Recent work has extended the concept of using light-based feedback control to investigate re-entrainment of clocks in humans. Attempts have been made to pose this complex problem as a scheduling problem to obtain the best bang-off-bang strategy [24] for light inputs. Recently, the authors in [31] used lower harmonics to formulate an approximate model of the circadian oscillations in humans, and exploited the structure of the co-state equation to propose an efficient line-search algorithm to obtain optimal control sequences. Although these methods are elegant and have been demonstrated to be effective via numerous simulation studies, a significant drawback of optimal control approaches is that they are rarely immune to measurement inaccuracies, exogenous noise, or plant-model mismatch (i.e. discrepancies between the system under control and the model describing it). Further-more, without model approximation, deriving optimal control sequences remain computationally prohibitive, if not intractable, for complex high-dimensional nonlinear models [30].

The use of feedback in circadian entrainment remains a relatively unexplored problem. A notable exception is [32], where the authors developed a framework for control of circadian rhythms using short-duration pulses to shift the phase, via proportional-integral-derivative (PID) control by exploiting a low-dimensional approximate predictive model of the phase dynamics, known as a phase response curve (PRC). This low-dimensional representation of pertinent phase information and the predictive power of a ipPRC enables the construction of MPC algorithms that are well-known to be inherently robust to noise and plant-model mismatch. A prominent recent study derived a feedback control law for circadian entrainment using lookup tables from the optimal control [33]. This study focused on a light input which may be switched on and off at will, and although highly effective for light, pharmaceutical delivery under this policy would incur errors. More importantly, the main result proven herein bounds the nearness of their feedback control approach to their optimal control law. A preliminary investigation of the potential of MPC in circadian control with pharmaceuticals was undertaken in [34, 35], which demonstrated MPC of mammalian circadian rhythms via KL001, a small-molecule pharmaceutical that was recently used to manipulate (in vivo) the circadian clock in mammals [22, 23]. Although previous investigations have revealed the importance of carefully selecting prediction horizon and controller sampling time of the MPC to reset the circadian oscillator, no systematic method of selecting these design variables has been derived.

This study seeks to answer three fundamental questions:

1. What does the optimal control policy for pharmaceutical-driven circadian phase resetting look like?

2. What design considerations should be made in implementing feedback control of circadian phase? More specifically, how does the selection of sampling or switching times and the prediction horizon affect the optimality of the applied control?

3. How can these design considerations shape our selection of circadian therapeutics?

In answering these questions, this study presents a systematic framework for constructing ipPRC-based nonlinear MPC formalisms capable of manipulating mammalian clocks using small-molecule pharmaceuticals.

2. Phase-Reduced Model and Optimal Phase Shifting

First, the circadian oscillator model and its accompanying notation are presented.

2.1. Circadian oscillator model

Circadian dynamics are most commonly represented by limit-cycle oscillators. These oscillators are generally modeled using a class of smooth nonlinear dynamical systems of the form

$$\frac{dx}{dt}\text{=}f\left(x,p,u\right),$$ (1)

where $x\left(t\right)\in {ℝ}^{\text{n}}$ denote states such as mRNA or protein concentrations, $\text{p}\in {ℝ}^m$ denote kinetic parameters, and $\text{u}\left(t\right)\in {ℝ}^{\text{ℓ}}$ denote control inputs. The zero-input system $ẋ=f\left(x,p,\text{0}\right)$ comprises an exponentially-attractive limit cycle $\Gamma \subset {ℝ}^{\text{n}}$ that satisfies

$$\underset{t\to \infty }{\text{lim}}\left[x\left(t\right)-x\left(t-T\right)\right]=\text{0,}$$ (2)

with period T and angular frequency ω = 2π/T. A two-dimensional limit cycle with states x = [x₁, x₂] is visualized in Fig. 1A.

Figure 1:

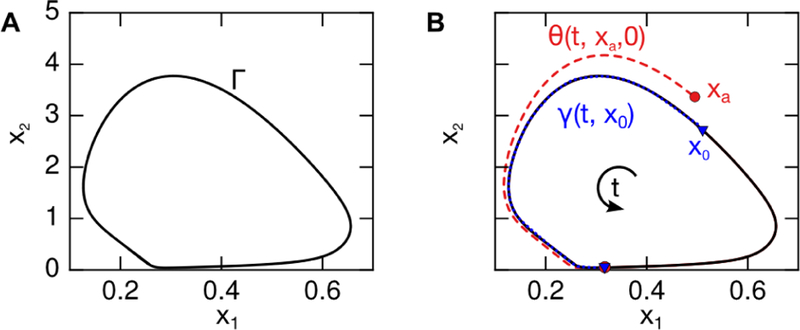
Schematic of limit cycle dynamics for arbitrary states x₁ and x₂. (A) The limit cycle Г in state space. (B) Schematic of trajectories γ and θ These points may be assigned identical phases (ϕ_a = ϕ₀), as the trajectories originating at these points converge asymptotically.

This study is concerned with dynamics of the phase of oscillation, and so we first map every unique point on the limit cycle $x_{\text{0}}\in \Gamma$ to a unique scalar phase ${\varphi }_{\text{0}}\in {\mathbb{S}}^{\text{1}}=\left[\text{0},\text{2}\pi \right)$. Phase is defined such that for an oscillator on the limit cycle, phase advances linearly with time. Let ${\Phi }_{\Gamma }:\Gamma \to {\mathbb{S}}^{\text{1}}$ denote the corresponding map relating x₀ to oscillator phase ${\varphi }_{\text{0}}={\Phi }_{\Gamma }\left(x_{\text{0}}\right)$.

Let γ(t; x₀) denote the solution of system (1) with initial condition $x\left(\text{0}\right)=x_{\text{0}}\in \Gamma$. Thus a time-dependent phase variable

$${\varphi }_{\Gamma }\left(t\right)={\Phi }_{\Gamma }\left[\gamma \left(t,x_{\text{0}}\right)\right]$$ (3)

may be established. Considering that the unperturbed oscillator traverses the limit cycle at the constant rate ω, the system phase evolves in time according to:

$${\varphi }_{\Gamma }\left(t\right)=\omega t\text{+}{\varphi }_{\text{0}}\mathrm{mod}\text{2}\pi .$$ (4)

The application of an exogenous input (such as a control action) will divert the state of an oscillatory system away from the limit cycle Г. In order to ascertain the phase shift incurred by such an input, we must assign a phase to points on ${ℝ}^{\text{n}}\backslash \Gamma$ that are not on the limit cycle Г, that are exponentially attracted to Г. This can be done by assigning them the phase of the trajectory to which they ultimately converge. The trajectory denoted θ(t; x_a, u) is the time evolution of point x_a ∉ Г, with dynamics given by (1) and control input u. For the zero-input case (u = 0), the state x_a may be assigned the phase of the initial condition of the trajectory γ(t; x₀) to which the trajectory θ(t; x_a, 0) ultimately converges. The asymptotic phase of x_a, denoted ϕ_a, is equal to the phase ϕ₀ of point x₀ ∈ Г, subject to

$$\text{0}=\underset{t\to \infty }{\lim }\parallel \theta \left(t,x_{\text{a}},\text{0}\right)-\gamma \left(t,x_{\text{0}}\right)\parallel .$$ (5)

This relationship yields the asymptotic phase map ϕ_a = Φ(x_a). The asymptotic phase map may be used to formulate a time-dependent asymptotic phase variable

$$\varphi \left(t,\text{0}\right)=\Phi \left[\theta \left(t,x_{\text{a}},\text{0}\right)\right]$$ (6)

for the zero-input case. The trajectories γ and θ with identical phase, and their asymptotic convergence, are shown schematically in Fig. 1B.

This formulation yields phase dynamics identical to the case for ϕ, with particular solutions of the form ϕ(t; 0) = ωt + ϕ₀ with initial phase ϕ₀. The following subsection describes how the concept of an asymptotic phase variable can be extended for the more challenging and useful case of non-zero control input u.

2.2. Infinitesimal parametric phase response curves and the phase-reduced model

For an oscillator in the neighborhood of Г, the phase dynamics resulting from a control input may be derived by the chain rule:

$$\frac{d\varphi \left(t,\text{u}\right)}{dt}=\omega \text{+}\frac{\partial }{\partial t}\frac{\partial \Phi \left[\gamma \left(t,x_{\text{0}}\right)\right]}{\partial \text{u}}u\left(t\right)$$ (7)

which yields a first-order approximation of phase dynamics for a nonzero control input.

Pharmaceutical manipulations of the clock are generally considered to be mediated by temporary changes in one or more parameter values (e.g. increased degradation of a protein, or decreased transcriptional rate) [23, 36]. Input u(t) is incorporated into the ODE model as a time-dependent modification of parameters p

$$p\left(t\right)=p_{\text{0}}\text{+}u\left(t\right).$$ (8)

Substituting this into (7) yields

$$\frac{d\varphi }{dt}=\omega \text{+}\frac{\partial }{\partial t}\frac{\partial \Phi \left[\gamma \left(t,x_{\text{0}}\right)\right]}{\partial p}u\left(t\right),$$ (9)

where $\frac{\partial }{\partial t}\frac{\partial \Phi \left[\gamma \right]}{\partial p}$ is the infinitesimal parametric PRC (ipPRC) for the oscillator on the limit cycle [37]. The formulation (9) is valid up to the first-order approximation in both duration and magnitude of the control, and is referred to as the phase-reduced model.

The one-dimensional phase equation is therefore given by:

$$\frac{d\varphi }{dt}=\omega \text{+}B\left(t,\varphi \right)\cdot u\left(t\right),$$ (10)

where B(t; ϕ) is the ipPRC and u(t) is the parametric perturbation.

Assumption 1.

The ipPRC B(·) is fully known and dependent only on the asymptotic phase ϕ(t).

The ipPRC can be calculated numerically from mechanistic models of the clock for a known control input as above, or alternately could be characterized experimentally [37, 38]. Since the ipPRC is generated from a clock model, it may exhibit minor differences with the ipPRC of the mammalian circadian system. This contributed to our decision to later apply control via MPC, as it is inherently robust to plant-model mismatch. The ipPRC may be quantified directly via impulse response tests, though these experiments are challenging to perform.

A prior method of formulating asymptotic phase dynamics assumed short pulses of control inputs that relax completely to the limit cycle after each pulse [32], and thus the phase sensitivity on the limit cycle may be used. Assumption 1, rather, implies that the phase response dynamics are constant along isochrons (state-space regions of constant phase). This assumption is violated as the oscillator becomes more distant from its limit cycle, or closer to the fixed point at the center of the limit cycle. Identifying violations of this assumption may be studied in the future, and in these cases, the model should be simulated in full. This assumption has been used in prior studies as well [25, 33]. Our assumption yields a few practical advantages when implementing pharmaceutical inputs. Short pulses are less able to evoke significant phase shifts, as the realized phase shift is determined by integration of the ipPRC. Thus, the ipPRC must be of extreme magnitude to yield appreciable shifts for short pulses. Pharmaceutical inputs to the clock are not likely to have the extremely rapid pharmacokinetics needed to be approximated as short pulses.

Assumption 2.

The ipPRC map is continuous on [0, 2π] and has exactly two zero crosses in that interval; the derivatives of the ipPRC at the zero crosses have opposite sign.

This PRC form is readily found in the literature, and for stimuli of a finite duration is commonly referred to as a type 1 phase response [38, 39]. Methods for calculation of the ipPRC using limit-cycle oscillator models are described elsewhere [37]. The other phase response observed (solely) for finite-duration stimuli, a type 0 phase response, contains a discontinuity. This form is associated with a strong and extended stimulus or multiple stimuli over several days, and therefore does not correspond to the ipPRC [38–40]. Furthermore, a type 0 phase response may be generated from an ipPRC that conforms to Assumption 2 by applying a long-duration stimulus.

2.3. The phase resetting problem and optimal phase resetting via Pontryagin’s maximum principle

The phase-resetting problem involves tracking a reference oscillator with phase given by ϕ_r(t) ϵ [0, 2π), with the oscillator ϕ(t; u) which obeys (10), and with control input bounded by u ϵ [u_min, u_max]. The phase of the reference oscillator is given by:

$${\varphi }_{\text{r}}\left(t\right)={\omega }_{\text{r}}t\text{+}{\varphi }_{\text{r}}\left(\text{0}\right)\mathrm{mod}2\pi .$$

Assumption 3.

The reference angular velocity is identical to the angular velocity of the oscillator, that is, ω ≡ ω_r.

Assumption 4.

The oscillator is not perturbed by exogenous inputs (e.g. light, metabolic changes) other than control actions.

Through these assumptions we seek to achieve a phase shift rather than entrain to a dynamic phase angle or an environment that also perturbs the system under control. Future studies may approach the more complicated case in which small differences between the day length and human circadian periods (see [41]), and dynamic light input, are accounted for. This simple case of achieving a static phase shift more simply yields optimal control policies that are sufficient to provide understanding for feedback controller design.

The phase difference between the reference oscillator and the oscillator under control is:

$$\chi \left(t\right)=\varphi \left(t\right)-{\varphi }_{\text{r}}\left(t\right)\mathrm{mod}2\pi .$$

The total desired phase shift is such that χ(t_f ) = 0 where t_f is the time at which the control action is finished, and therefore

$$\Delta {\varphi }_{\text{f}}=-\chi \left(\text{0}\right)\mathrm{mod}2\pi .$$

In an ideal case where pharmaceutical inputs can be continuously dosed, one can derive an optimal control trajectory for entrainment via Pontryagin’s Maximum/Minimum Principle [42]. The optimal control problem may be formulated with state dynamics

$$\dot{\varphi }=\omega \text{+}B\left(\varphi \right)\cdot u\left(t\right)$$ (11)

$$\varphi \left(\text{0}\right)={\varphi }_{\text{0}},$$

and cost functional

$$J\left[u\left(t\right)\right]={\int }_{\text{0}}^{t_{\text{f}}}1dt,$$ (12)

for minimum-time entrainment. This cost functional does not include a penalty for introducing a drug which may have side effects or be otherwise undesirable. If the drug selected elicits dose-dependent off-target effects, the cost functional could be modified to penalize dose as well, and the performance between cases could be compared.

This yields a free-time fixed-endpoint problem, which can be solved using standard optimal control approaches [33, 42]. The Hamiltonian

$$\text{H}\left(\varphi ,\lambda ,u\right)=\left(\omega +B\left(\varphi \right)\cdot u\right)\cdot \lambda \text{+}\text{1}$$ (13)

is formulated with λ is the dynamic costate with terminal condition λ(t_f) = 0. Using Pontryagin’s Maximum Principle with constrained control inputs in the range [u_min, u_max] we can write

$$\begin{gathered} \underset{u}{\text{max}}\text{H}\left(\varphi ,\lambda ,u\right)=\underset{u_{\text{min}}\le u\le u_{\text{min}}}{\text{max}}\left\{\left(\omega \text{+}B\left(\varphi \right)\cdot u\right)\cdot \lambda \text{+}\text{1}\right\} \\ =\omega \cdot \lambda \text{+}\text{1}\text{+}\underset{u_{\text{min}}\le u\le u_{\text{min}}}{\text{max}}\left\{B\left(\varphi \right)\cdot u\cdot \lambda \right\} \end{gathered}$$

which yields the optimal “bang-bang” control policy

$${\text{u}}^{\star }\left(\text{t}\right)\hspace{0.17em}\hspace{0.17em}=\left\{\begin{array}{cc}{u}_{\text{max}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}\cdot \hspace{0.17em}\hspace{0.17em}\lambda >\text{0}\hfill \\ u_{\text{min}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}\cdot \hspace{0.17em}\hspace{0.17em}\lambda \le \text{0}\hfill \end{array}\right..$$ (14)

Here, the terminal condition of the costate, λ(t_f ) = 0, forces the costate to be either positive or negative for any given initial condition for all time, and so for a specific initial condition the control input depends exclusively on the sign of B(ϕ), c.f. [33].

This implies that the oscillator should be shifted in only either the negative or positive direction toward its final phase shift, but not both. For an oscillator with desired phase shift Δϕf and initial phase ϕ₀, the optimal control input u^⋆ is one of two admissible trajectories: either that for achieving the positive phase shift

$${\text{u}}_{+}^{*}\left(\text{t}\right)\hspace{0.17em}\hspace{0.17em}=\left\{\begin{array}{ll}{u}_{\text{max}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}>\text{0}\hfill \\ u_{\text{min}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}\le \text{0}\hfill \end{array}\right..$$ (15)

or the negative phase shift

$${\text{u}}_{-}^{*}\left(\text{t}\right)\hspace{0.17em}\hspace{0.17em}=\left\{\begin{array}{ll}{u}_{\text{min}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}\ge \text{0}\hfill \\ u_{\text{min}}\hfill & \text{if}B\left(\varphi \right)\hspace{0.17em}\hspace{0.17em}<\text{0}\hfill \end{array}\right..$$ (16)

Which of these two trajectories is optimal depends upon which reaches ∆ϕ_f more rapidly, where ∆ϕ accumulates over time according to

$$\Delta \varphi ={\int }_{\text{0}}^{t}B\left(\varphi \left(\text{t'}\right)\right)\cdot u\left(\text{t'}\right)dt\text{'}\text{mod}\text{2}\pi .$$ (17)

A decision boundary between advances and delays is denoted ∆ϕ_b (i.e., ∆ϕ_f > ∆ϕ_b indicates that delays are preferable, and ∆ϕ_f < ∆ϕ_b indicates that advances are preferable). Correspondingly, that boundary for the continuous time optimal control is denoted $\Delta {\varphi }_B^{\star }$. Thus, the two admissible trajectories may be calculated and compared to determine optimality.

This concept is illustrated for the small-molecule pharmaceutical KL001 input in Fig. 3. For KL001 drug action, u_max = 0:06 to reflect a 60% decrease in degradation rate, and u_min = 0 to reflect that decreasing the degradation rate cannot result in the synthesis of new biomolecules. The ipPRC is shown in Fig. 2 Here, we visualize the two admissible trajectories as two oscillators ϕ⁺(t) and ϕ⁻(t) receiving control inputs $u_{\text{+}}^{\star }\left(t\right)$ and $u_{-}^{\star }\left(t\right)$, respectively, causing the accumulation of phase shifts ∆ϕ⁺(t) and ∆ϕ⁻(t) moving in opposite directions around the circle of all phase shifts ∆ϕ ϵ [0, 2π) starting at ∆ϕ = 0. The time $t_B^{\star }$ at which these oscillators meet therefore achieves any phase shift on [0, 2π). This time may be found for any initial phase ϕ₀ by solving the coupled equations (10) and (17) for inputs $u_{\text{+}}^{\star }\left(t\right)$ and $u_{-}^{\star }\left(t\right)$, with the terminal condition of ∆ϕ⁺(t^⋆) = ∆ϕ⁻(t^⋆).

Figure 3:

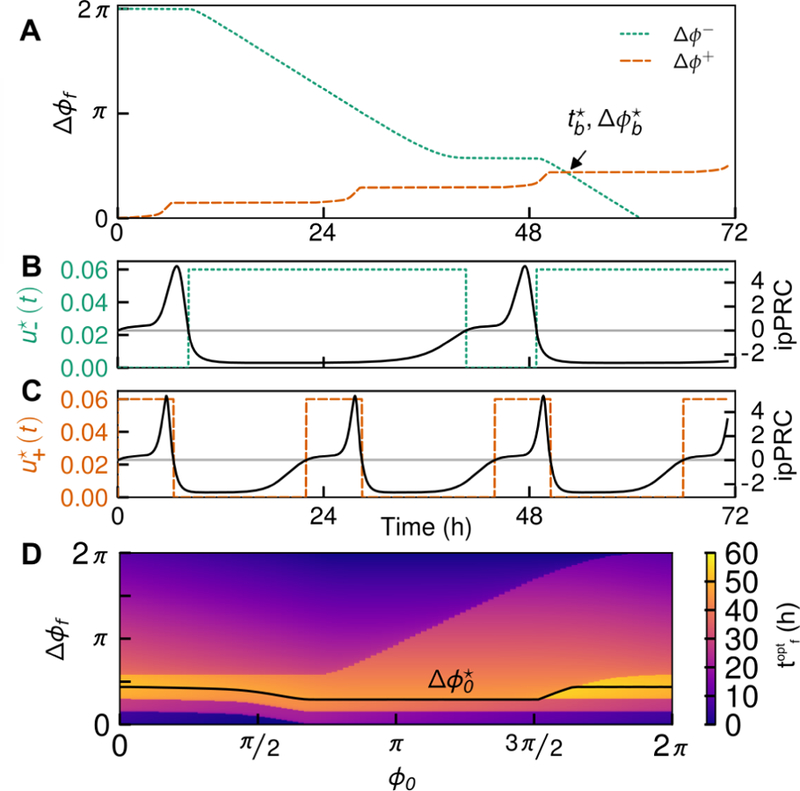
Optimal control of the circadian clock by use of the ipPRC shown in Fig. 2B. (A) Maximal phase advances $\Delta {\varphi }_{\text{+}}^{\star }\left(t\right)$ and delays $\Delta {\varphi }_{-}^{\star }\left(t\right)$ for the ipPRC, with ϕ₀ = 0 and u_max = 0:06, u_min = 0:00. The respective maximal phase shifts meet at time $t_B^{\star }$ and phase shift $\Delta {\varphi }_B^{\star }$ as marked on the graph. All phase shifts may be achieved in time less than or equal to $t_B^{\star }$. Note that $t_f^{\text{opt}}\left(\text{0},\Delta {\varphi }_f\right)$ can be found on this plot by seeking the minimum time at which the oscillator crosses the desired ∆ϕ_f (for example, $t_f^{\text{opt}}\left(\text{0},3\pi /2\right)\approx 20\text{h},$ and is achieved by a phase delay). (B,C) Plot of optimal inputs $u_{-}^{\star }\left(t\right)$ and $u_{\text{+}}^{\star }\left(t\right)$, respectively, for the phase delay and advance shown in A. (D) Heatmap of optimal time to reset the clock $t_f^{\text{opt}}$ as a function of initial phase as desired shift. Note that $\Delta {\varphi }_B^{\star }$, the boundary between advances and delays, is dependent on ϕ₀.

Figure 2:

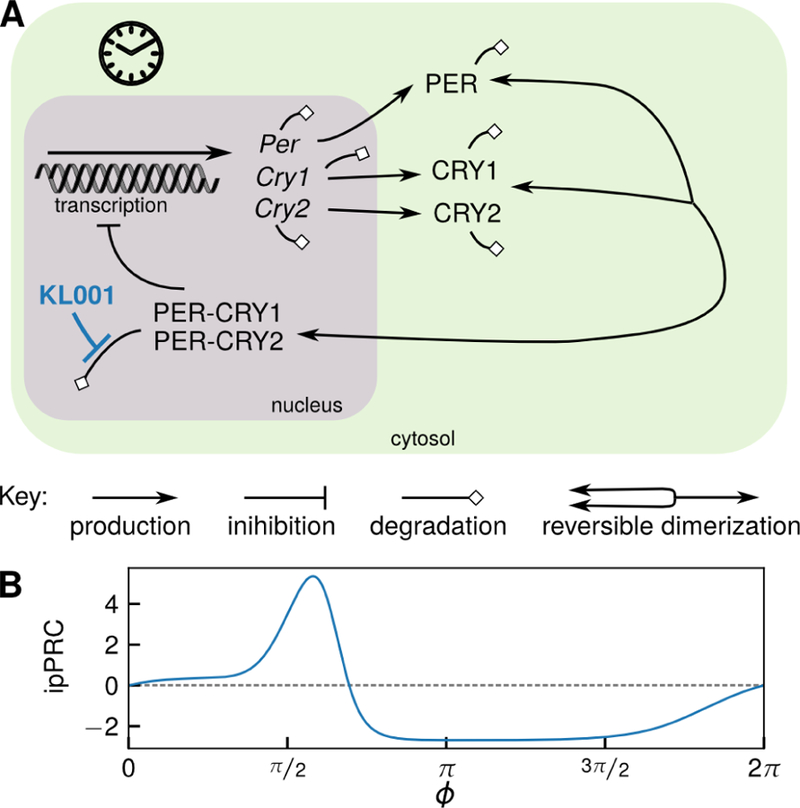
Schematic of the core circadian gene regulatory network and effect of small molecule KL001. (A) The core circadian negative feedback loop. KL001 stabilizes nuclear CRY by reducing its degradation rate, as shown in blue. (B) Infinitesimal parametric phase response curve (ipPRC) for KL001-mediated stabilization of nuclear CRYs.

Thus, $\Delta {\varphi }_b^{\star }\left({\varphi }_{\text{0}}\right)$ is defined as the phase shift at which ϕ⁻(t) and ϕ⁺(t) meet. The maximum time to achieve any phase shift starting from ϕ₀ is given by $t_b^{*}\left({\varphi }_0\right)$, and $\Delta {\varphi }_b^{*}\left({\varphi }_0\right)$ (depicted as a solid black line in Fig. 3D) yields the boundary between where a positive shift and negative shift are optimal to reach a desired ∆ϕ_f from phase ϕ₀. The optimal control input for a given ϕ₀ and ∆ϕ_f is therefore defined as:

$$u^{\star }\left(t\right)=\left\{{}_{u_{-}^{\star }\left(t\right)\text{if}\Delta {\varphi }_f\ge \Delta {\varphi }_b^{\star }\left({\varphi }_{\text{0}}\right)}^{u_{+}^{\star }\left(t\right)\text{if}\Delta {\varphi }_f<\Delta {\varphi }_b^{\star }\left({\varphi }_{\text{0}}\right)}\right.\cdot$$ (18)

Therefore the optimal shift time $t_{\text{f}}^{\text{opt}}\left({\varphi }_{\text{0}},\Delta {\varphi }_{\text{f}}\right)$ may be calculated by applying this continuous time optimal control until ∆ϕ = ∆ϕ_f One can formally write $t_b^{\star }$ as

$$t_b^{\star }\left({\varphi }_{\text{0}}\right)=\underset{\Delta {\varphi }_f}{\text{sup}}{t}_f^{\text{opt}}\left({\varphi }_{\text{0}},\Delta {\varphi }_{\text{f}}\right).$$ (19)

Remark. A bang-bang optimal control policy for light entrainment was shown previously in [24] and [31]. Applying these solutions, however, necessitated either a line search or a search for switching times due to the nonlinear temporal relationship between light input and driving force on the oscillator. Because pharmaceutical control of the clock can be parameterized directly within the limit cycle model, this formulation provides a simple way to compute the theoretical optimal phase resetting policy. Therefore, this provides a means for determining the relative efficacy of any applied control policy.

3. Closing the loop: designing an ipPRC-based nonlinear MPC

3.1. Motivation

Model predictive control is generally implemented by solving a finite-horizon optimal control problem at discrete sampling times, that is, for t = 0, τ, 2τ, , where τ is the sampling time. This section will demonstrate that time discretization causes a loss of optimal control in regions where the step includes a zero cross of the ipPRC, as the input cannot be adjusted during the step and the continuous-time optimal control policy will be violated (visualized in Fig. 5). Additionally, care must be taken to ensure that a controller selects the optimal direction of phase shifting (e.g., 8h advance vs. 16h delay) when only observing a finite portion of the future ipPRC. For the continuous time optimal control, that boundary is known to be $\Delta {\varphi }_b^{\star }$, however, this is unlikely to be the correct boundary for the sampled-time case. Further, there is no guarantee that this boundary will appear from simply solving the finite-horizon optimal control.

Figure 5:

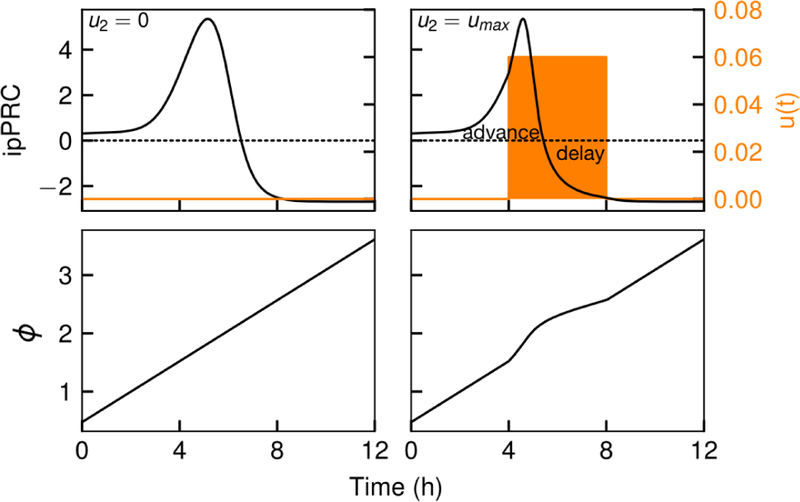
Error in applying the optimal control policy occurs at the zero-crosses of the ipPRC. For a sampling time of 4 h, the zero-cross occurs in the second step t₁ < t⁰ < t₂, and so u₂ will necessarily violate the continuous-time optimal control law. For the cases shown here, Δϕ₂(u_max) = Δϕ₂(u_min) = 0, and the resulting phase at the end of step 2 is identical due to cancellation of the advance by the delay. Finally, it is noteworthy that this single pathological step consumes most of the positive region of the ipPRC, suggesting that τ = 4 h is a poor choice for sampling time if phase advances are desirable.

This section explores how the formulation of the finite-horizon optimal control problem for MPC affects our ability to control the clock. For example, consider an ipPRC with a small positive region. A large sampling time in this case may result in a controller unable to access the positive ipPRC region due to the surrounding negative region being included in each step, and the inadvertent delays canceling the desired advance. This would force such a controller to use phase delays to achieve even small positive phase shifts.

It is therefore useful to compare the performance of a controller with piecewise constant control and uniformly spaced steps in sampling and switching time (the sampling-time control) to the continuous-time optimal control case to identify where inefficiency accumulates. This technique can be used to find a balance between high performance and the computational cost and physical impracticality of frequently updating the algorithm via measurement of physiological phase markers.

Additionally, the controller design will inform the suitability of a specific pharmaceutical for use. For example, a drug with a small positive ipPRC region will not be an appropriate choice for achieving large phase advances if an alternative drug with a larger positive ipPRC region exists. Alternately, the drug with the larger positive ipPRC region may be unsuitable if its pharmacokinetics are slow, such that sampling times must be very long to allow drug clearance between adjusting the dose.

3.2. Exploiting the ipPRC to choose MPC sampling time

Consider the more practical scenario of implementing control inputs parameterized as piecewise constant signals with equispaced time intervals between the knots (i.e., the switching times) of the control parameterization trajectory. This is commonly done when solving and applying MPC in continuous-time. The control input is defined as constant across time steps of uniform duration in a finite horizon, as commonly done for MPC:

$$u\left(t\right)=u_{\text{i}}\text{for}t\in \left[t_{\text{i}-\text{1}},t_{\text{i}}\right),$$ (20)

where t_i are the discrete sampling times, with i = 1, … , N_p where N_p is the number of steps in the prediction horizon (and control horizon, in this paper). Then, u_i ϵ [u_min, u_max] is a scalar constant, and τ = t_i − t_i−1 is the sampling time for the controller.

Next, we are interested in quantifying the error incurred due to piecewise constant control actions at discrete sampling times. To better understand this error, we derive bounds on two metrics: the residual phase error, and the number of additional cycles to complete reset. Definitions for and proofs of bounds on these metrics follow.

Definition 1. The residual phase error $\left({\text{E}}_{\tau }^{\varphi }\right)$ is the phase error remaining at sampling time t_k, the first sampling time for which the continuous-time optimal control would have first completed the reset.

Recall that $t_{\text{f}}^{\text{opt}}$ is the time at which χ(t) = 0 under the optimal control and so

$$\text{k}=\text{arg}\underset{i\in \mathbb{N}}{\text{min}}i\text{subject}\text{to:}{t}_i\ge t_{\text{f}}^{\text{opt}}.$$ (21)

Based on Definition 1, the residual phase error is given by

$${\text{E}}_{\tau }^{\varphi }=\chi \left(t_{\text{k}}\right).$$ (22)

First, we provide bounds on ${\text{E}}_{\tau }^{\varphi }$ and demonstrate that these bounds are solely dependent on the sampling time τ and the ipPRC specific to the pharmaceutical being used. To do so, let n_cyc be the number of 2π cycles required to achieve the continuous time optimal control resetting using the optimal control policy (18). Furthermore, we denote ${\text{E}}_{\tau }^{\text{0,}-}$,${\text{E}}_{\tau }^{\text{0,}\text{+}}$, and E^s to be the errors incurred at the step including the negative zero cross, the step including the positive zero cross, and a correction for phase advance cases, respectively.

Theorem 1 (Bounding of ${\text{E}}_{\tau }^{\varphi }$). Suppose Assumptions 1–4 hold. The residual phase error incurred by the sampled- time control (20) satisfies

$${\text{E}}_{\tau }^{\varphi }\hspace{0.17em}\hspace{0.17em}\le \hspace{0.17em}\hspace{0.17em}\left({\text{n}}_{\text{cyc}}+\text{1}\right)\hspace{0.17em}\left({\text{E}}_{\tau }^{\text{0},-}\text{+}\hspace{0.17em}\hspace{0.17em}{\text{E}}_{\tau }^{\text{0,+}}\hspace{0.17em}\hspace{0.17em}\text{+}\hspace{0.17em}\hspace{0.17em}{\text{E}}^s\right).$$

Proof. Note that the sampling-time control is able to identically track the continuous-time optimal control except where consecutive sampling times occur on either side of a zero-cross of the ipPRC.

By Assumption 2, the ipPRC has two zero-crosses in each [0, 2π) cycle and so this occurs at most twice per cycle. A zero cross occurs at t = t⁰ (where t_i−1 < t⁰ < t_i). The phase shift accumulated for a single step of the controller from t_i−1 to t_i is given by

$$\Delta {\varphi }_i\left(u_i\right)={\int }_{t_{i-\text{1}}}^{t_i}B\left(\varphi \left(\text{t'}\right)\right)\cdot u_{i}dt\text{'},$$ (23)

which must be solved numerically with (10) to provide ϕ(t^′). Based on the arguments made in the previous section using Pontryagin’s principle, we know that the optimal control policy selects either u_max or u_min until the zero-cross, then the opposite following it. Thus, the maximal loss of phase advance or delay is incurred if the switching times are positioned such that the shift incurred over that time step Δϕ_i(u_i) = 0 for the maximal input case, as this indicates that phase advances and delays cancel. The worst-case loss is therefore incurred where the controller takes no action on either side of the zero-cross, as the maximal action would also incur no shift (as shown in Fig. 5).

The maximal loss in phase shift is of equal magnitude in the positive and negative directions because competing advances and delays of identical magnitudes cancel. The maximal error incurred at a given zero-cross is

$${\text{E}}_{\tau }^{\text{0}}=\underset{t_{i-\text{1,}u}}{\text{max}}\left|{\int }_{t_{i-\text{1}}}^{t^{\text{0}}}B\left(\varphi \left(\text{t'}\right)\right)\cdot udt\text{'}\right|$$ (24)

and the error for the positive or negative zero-cross is denoted ${\text{E}}_{\tau }^{\text{0,+}}$ or ${\text{E}}_{\tau }^{\text{0},-}$, respectively. The maximal phase error incurred for each cycle is the sum of the maximal error from each zero-cross, all other steps are identical to the continuous-time optimal control. A demonstration of the phase-shift cancellation by competing advances and delays is shown in Fig. 5.

For phase advances, additional error is incurred by phase advances accumulating less due to the zero crosses, thus, the oscillator phase will reach the next positive ipPRC region later than it would if it could achieve the full phase advance. The additional error accumulated is equal to the maximal shift that could be achieved in the extra time that it takes to reach the positive region. The time lost per cycle for phase advances is:

$$t_E\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\frac{T}{2\pi }\hspace{0.17em}\hspace{0.17em}\cdot \hspace{0.17em}\hspace{0.17em}\left(E_{\tau }^{\text{0,+}}\hspace{0.17em}\hspace{0.17em}\text{+}\hspace{0.17em}{E}_{\tau }^{\text{0},-}\right)$$ (25)

where T is the oscillatory period. This results in an additional residual phase error per cycle of

$$E^s=\left\{\begin{array}{ll}\underset{0\le t\le T}{\text{max}}{\int }_t^{\text{t}+\hspace{0.17em}\hspace{0.17em}{\text{t}}_E}B\left(\varphi \left(t\text{'}\right)\right)dt\text{'}\hfill & \text{if}\Delta {\varphi }_f<\Delta {\varphi }_b\hfill \\ 0\hfill & \text{if}\Delta {\varphi }_f\ge \Delta {\varphi }_b\hfill \end{array}\right.$$ (26)

where ∆ϕ_b is the decision boundary between phase advances and delays. In the case of phase delays, this quantity is 0, since the oscillator phase will reach the next negative region more rapidly due to achieving less phase delay.

These errors $\left(E_{\tau }^{\text{0},-}\text{+}{E}_{\tau }^{\text{0,+}},\text{and}{E}^{\text{s}}\right)$ are caused by deviations from the optimal control policy at ipPRC zero crosses, and the sampling-time optimal control otherwise exactly follows the continuous time optimal control. Each of these errors occurs at a rate of once per cycle. Thus, we can bound the residual time phase error

$$E_{\tau }^{\varphi }\le \left(n_{\text{cyc}}\left(\Delta {\varphi }_f,{\varphi }_{\text{0}}\right)\text{+}\text{1}\right)\left(E_{\tau }^{\text{0},-}\text{+}{E}_{\tau }^{\text{0,+}}\text{+}{E}^s\right)$$ (27)

for a given τ, which concludes the proof.

The bound $E_{\tau }^{\varphi }$ may be thought of as the maximal value of χ(t_k) for optimal control with sampling time τ.

Remark. At first glance, it may seem that this bound is loose for the case of arbitrarily large n_cyc, the number of cycles to achieve any reset is bounded by the finite scalar

$${\text{n}}_{\text{cyc}}^{\text{max}}=\underset{\Delta {\varphi }_f,{\varphi }_{\text{0}}}{\text{max}}{n}_{\text{cyc}}\left(\Delta {\varphi }_f,{\varphi }_{\text{0}}\right)$$

the maximum number of number of cycles to achieve any continuous time optimal reset. Applying this value in (27), we may bound the residual time phase error for any sampling-time optimal reset.

Fig. 6 shows how the residual phase error bounds evolve over time for phase advances or delays, ϕ₀ = 0, and τ = 2 h. This corresponds to the actual residual phase error incurred, by numerically calculating the optimal control. Although the error bound increased identically for each cycle, the actual residual phase error varies each cycle, depending upon how each zero-cross aligns with the sampling times.

Figure 6:

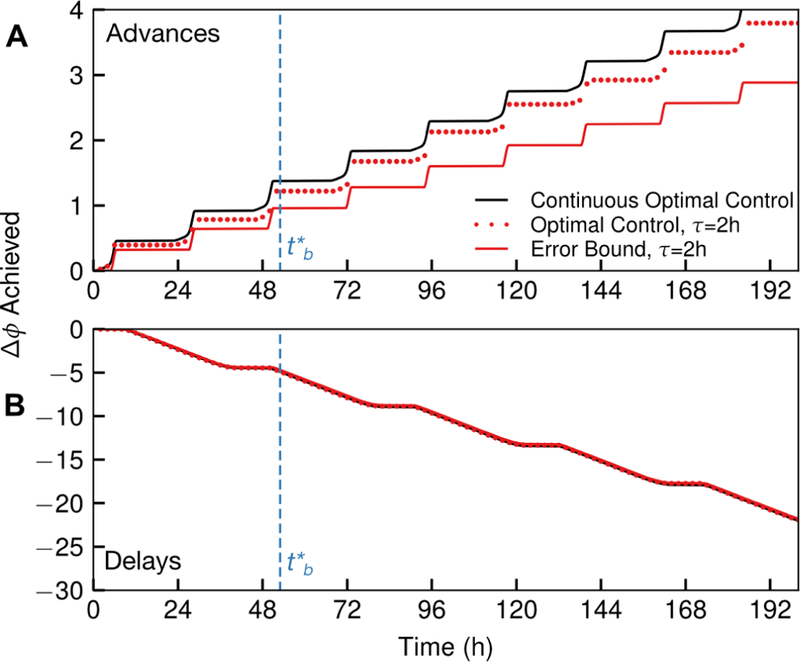
The phase shift accumulated in the continuous-time optimal control (black line) plotted as a function of time, in comparison to the lower bound on phase shift accumulated (red line) and the actual discrete-time phase shift accumulated (red dots), for τ = 2 h and ϕ₀ = 0. The residual phase error is the difference between the continuous time optimal control and the actual discrete-time control. Phase advances (A) and delays (B) are shown explicitly. The bound deviates further from the optimal control at each completed cycle, however, only the shifts that occur before $t_B^{\star }$ (dashed line) are attempted under the optimal control policy. Additionally, the error is more severe for phase advances, due to the relatively smaller positive region of the ipPRC, the fact that phase advances incur zero crosses more rapidly due to shortening the period, and the proximity of that positive region to a large negative region. For panel (B), these lines are nearly on top of one another. The numerically-calculated optimal control for τ = 2 h indeed obeys the bounds derived in Theorem 1 from the continuous time optimal control.

Fig. 7A-B demonstrates this bound for KL001 under τ = 1, 2, 4 h, for ϕ₀ = 0. The number of cycles to achieve each reset for phase advances or delays ∆ϕ_f ϵ [−2π, 2π] (to explicitly show advances and delays) and ϕ₀ = 0 under the continuous-time optimal control for KL001 is shown in Fig. 7A. The region of this plot that corresponds to the phase resetting directions selected by the continuous-time optimal control (advances for $\Delta {\varphi }_f<\Delta {\varphi }_B^{\star },$ delays for $\Delta {\varphi }_f\ge \Delta {\varphi }_B^{\star }$) are denoted between the dashed lines. Notably, the number of cycles to achieve phase advances accumulates more rapidly due to the smaller positive region of the ipPRC, and as such, error will incur more quickly in phase advance regions. Fig. 7B shows the bounds on the residual phase error for τ = 1, 2, 4 h, and the actual residual phase error incurred for numerically calculating the optimal control for each shift and sampling time. As observed, the calculated residual phase errors fall within the computed bounds.

Figure 7:

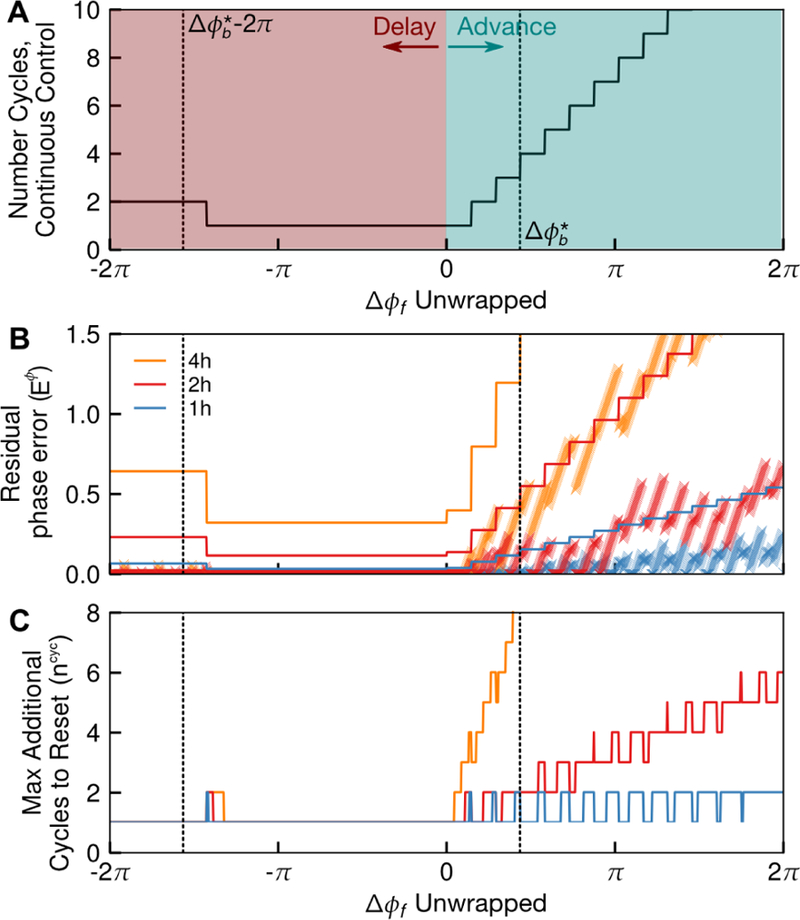
Sampling time τ affects circadian phase resetting for optimal control with evenly-spaced switching times, a common feature of feedback control and MPC. (A) Plot of number of cycles required to achieve each phase advance or delay under continuous-time optimal control. Errors due to switching timing occurs where the ipPRC crosses 0, and thus is residual phase error is a function of the number of cycles required for continuous-time optimal control. (B) A bound on $E_{\tau }^{\varphi }$, the distance to the nal phase that will remain at $t=t_f^{\text{opt}}$ under optimal control with a constant sampling time is derived from the continuous optimal control trajectory. Here, the derived bound is shown as a line, and the $E_{\tau }^{\varphi }$ for numerically calculated optimal control solutions are shown as x markers for each τ (plotted as discrete points for ease of visualization). The residual phase error in each case indeed obeys the theoretical bounds. (C) A bound on ${\text{n}}_{\text{cyc}}^{\text{add}}$ is also derived. For this example, 1 h and 2 h shifts yield similar residual phase error and allow a complete reset in at most two additional cycles, under ∆ϕ_b = ∆ϕ^⋆. Thus, either is a reasonable choice for sampling time, though a 2 h sampling time will reduce the cost of sampling by half. Alternately, if this drug were used only to achieve phase delays, a 4 h sampling rate would be similarly suitable.

In addition to the residual phase error, it is useful to determine how much additional time it would take to reach a complete reset. Effectively, we aim to nd t^add for $\chi \left(t_f^{\text{opt}}\text{+}{t}^{\text{add}}\right)=\text{0.}$ Finding or bounding t^add is complicated, as it necessitates knowledge of the entire discrete-time optimal control trajectory for each ϕ₀ and ∆ϕ_f How-ever, the most additional time to reset is incurred when a

phase advance requires waiting through the negative ipPRC region (or the inverse case, a phase delay forcing a wait through the positive ipPRC region) to complete the resetting. Conveniently, we may bound the number of additional cycles to complete a phase reset without explicit knowledge of the full discrete-time optimal control.

Definition 2.The number of additional cycles to complete reset $\left({\text{n}}_{\tau }^{\text{add}}\in \mathbb{N}\right)$ is a positive scalar that enforces the constraint

$$\chi \left(t_f\text{+}{\text{n}}_{\text{cyc}}^{\text{add}}{T}^{\text{+},-}\right)=\text{0}$$

where T ^+,− is the accelerated/decelerated period of the oscillator induced by a phase advance/delay, respectively.

Remark. We note that T ⁺ < T < T ⁻, and by virtue of being on a limit cycle yields

$$\underset{t\to \infty }{\text{lim}}\left[x\left(t,p\text{,}{u}_{\text{+}}\right)-x\left(t-t^{\text{+}}\text{,}p\text{,}{u}_{\text{+}}\right)\right]=\text{0}$$

and

$$\underset{t\to \infty }{\text{lim}}\left[x\left(t,p\text{,}{u}_{-}\right)-x\left(t-t^{-}\text{,}p\text{,}{u}_{-}\right)\right]=\text{0}$$

which hold true for any T ⁺-periodic control input u₊ that phase advances the oscillator and shortens the period, or T ⁻-periodic control input u₋ that phase delays the oscillator and lengthens the period. In sum, phase advances result in transient shortening of the period, and phase delays result in a transient lengthening of the period.

The following upper bound is proposed on the number of additional cycles to complete reset.

Theorem 2 (Bounding of ${\text{n}}_{\text{cyc}}^{\text{add}}$).

Let $\Delta {\varphi }_{g,\tau }^{-}$ and $\Delta {\varphi }_{g,\tau }^{\text{+}}$ be the maximum phase delay and advance that is guaranteed to be achievable in a cycle of 2 respectively. Recall that ∆ϕ_b is the decision boundary between phase advances or delays. The number of additional cycles to correct for the residual phase error incurred by the sampled-time control (20) is bounded above by

$$n_{\text{cyc}}^{\text{add}}\le \left\{{}_{⌊E_{\tau }^{\varphi }/\Delta {\varphi }_{g,\tau }^{-}⌋\text{+}\text{1}if\Delta {\varphi }_f\le \Delta {\varphi }_b}^{⌊E_{\tau }^{\varphi }/\Delta {\varphi }_{g,\tau }^{\text{+}}⌋\text{+}\text{1}if\Delta {\varphi }_f\le \Delta {\varphi }_b}\right.,$$ (28)

where ⌊ · ⌋ denotes the floor function.

Proof. Let $\Delta {\varphi }_{\text{g,}\tau }^{\text{+}}$ denote the phase advance that are guaranteed to be achievable in a single cycle. This is more simply thought of as the maximum total phase advance or delay achievable in a cycle minus the worst-case zero-cross error. For advances, the maximum phase advance achieved in a cycle is achieved by the continuous time optimal control policy for advances:

$$\Delta {\varphi }_{\text{cyc}}^{\text{+}}={\int }_{\text{0}}^{T^{\text{+}}}B\left(\varphi \left(t\text{'}\right)\right)\cdot u_{-}^{\ast }\left(\text{t'}\right)dt\text{'}\text{.}$$ (29)

The phase shift that is guaranteed to be achievable for each cycle for a step size of τ is therefore

$$\Delta {\varphi }_{\text{g,}\tau }^{\text{+}}=\Delta {\varphi }_{\text{cyc}}^{\text{+}}-E_{\tau }^{\text{0},\text{+}}-E_{\tau }^{\text{0},-},$$ (30)

and an equivalent method can be used to calculate $\Delta {\varphi }_{\text{g,}\tau }^{\text{+}}$.

The bound may be calculated by dividing the remaining error $E_{\tau }^{\varphi }$ by the advance or delay that is guaranteed to be achieved each cycle for a sampling time of τ This implies (28).

This bound is plotted for the use of KL001 and τ = 1, 2, 4 h in Fig. 7C. For sampling times of 1 or 2 h, the residual phase error may corrected in 1–2 cycles, with the vast majority of cases needing only an additional cycle. Furthermore, because this method assumes the worst possible alignment of the control switching times for every cycle, it is unlikely that the full two additional cycles will be needed. Alternately, the 4 h sampling time potentially results in many additional cycles needed to achieve a complete reset. This is because, as shown in Fig. 5, a 4 h step could be aligned such that nearly the entire phase advance region of the ipPRC is lost. Correspondingly, $\Delta {\varphi }_{\text{g,}\tau }^{\text{+}}$ is small in value. Thus, we may conclude that a sampling time of 2 h is approximately as effective as 1 h, and provides a 50% reduction in computational and sampling costs over 1 h sampling times, given our assumptions. Our controller designed in Section 4 therefore uses τ = 2 h. However, if a controller was designed to only produce phase delays, a 4 h sampling time is sufficiently near to the optimal control. This metric is therefore useful in designing controllers for a given problem and potential pharmaceutical given its ipPRC.

For these plots, dashed lines bound the phase shifts that are performed by the continuous-time optimal control to achieve complete coverage of phase shifts from 0 to 2π This implicitly assumes that the direction of optimal phase shifting is known for our choice of τ and is identical to the continuous time optimal control bound ∆ϕ^⋆. The following subsection addresses the choice of resetting direction (given ∆ϕ^⋆ for the continuous optimal case).

While numerical calculation of the in finite-horizon optimal control may seem advantageous, the optimizations involved are costly, as the selection of each step affects the region of the ipPRC available in the ensuing steps. Rather, we propose to formulate the MPC problem using the bounds derived from the optimal control as guidelines, and perform phase shifts by repeatedly solving the finite-horizon optimal control. It must be emphasized that because the bound we have derived is for the maximum residual phase error incurred at each zero-cross, a controller need not solve the in finite-time optimal sampling time control to be governed by the bound. Solving a finite-horizon optimal control problem is sufficient for these bounds on accumulated error to apply.

3.3. On MPC formulation and the selection of a prediction and control horizon

MPC involves repeatedly solving a finite horizon optimal control problem. For the continuous-time optimal control (in Section 2.3) the direction of phase shifting was determined by calculation of the equal-time phase shift boundary ∆ϕ^⋆. That boundary may differ for the discrete-time optimal control for a given step size. However, in MPC, whether the oscillator should advance or delay is implicitly solved in the finite horizon optimization. This subsection demonstrates via simulations that the finite-horizon optimal control in MPC is dependent on the number of steps. Because the finite-horizon optimal phase shifting direction can differ from the true optimal direction, we propose a multi-staged optimization for solving the finite-horizon optimal control.

The MPC problem is formulated in a similar fashion as [34], where the prediction and control horizons are set to be identical. The prediction horizon consists of N_p steps with sampling time τ For an oscillator at t = t_k this yields:

$$U\triangleq {\left[u\left(t_{\text{k}}\text{+}\tau \right)\cdot \cdot \cdot u\left(t_{\text{k}}\text{+}{N}_p\tau \right)\right]}^{\top }$$ (31)

as the knots of the control trajectory defined at each of the N_p steps. Eqn. (10) is used as the MPC predictor, which estimates the oscillator phase at the end of each of $\mathcal{l}\in \left[1,\cdot \cdot \cdot ,{\text{N}}_p\right]$ steps. The predictor formulation of (10) is

$$\widehat{\varphi }\left(t_i\text{+}\ell \tau \right)=\varphi \left(t_i\right)\text{+}\omega \tau \text{+}\sum _{k=1}^{\mathcal{l}}{\int }_{t_i+\left(k-1\right)\tau }^{t_i+k\tau }B\left(\varphi \right)\cdot u_{k}dt.$$ (32)

Here, i is the index of the applied control steps, and k is the index of the predictor. The predicted phase error $\widehat{\chi }\left(t\right)$ is de ned as the magnitude of the phase difference between the predicted phase $\widehat{\varphi }$ and the environmental phase:

$$\widehat{\chi }\left(t\right)\triangleq \widehat{\varphi }\left(t\right)-{\varphi }_{\text{r}}\left(t\right)\text{mod}\text{2}\pi$$ (33)

We want the phase error to reflect the absolute phase distance between reference and controlled oscillators, and so we define

$$h_{\varphi }\left(t\right)=\text{min}\left|\left(\widehat{\chi }\left(t\right),2\pi -\widehat{\chi }\left(t\right)\right)\right|$$

To avoid overcorrecting to for small amounts of noise in the phase estimate, we ignore phase error below a constant δ_ϕ:

$$g_{\varphi }\left(t\right)\triangleq \left\{{}_{h_{\varphi }\left(t\right)\text{otherwise}}^{0\text{if}{h}_{\varphi }\left(t\right)<{\delta }_{\varphi }}\right.$$ (34)

so that imprecisions in calculating phase do not result in controller action (similar to the zone-MPC approach of [7]). Thus, the finite-horizon optimal control problem at each time t_i may be solved for the optimal trajectory $u_{\text{MPC}}^{\star }$:

$$u_{\text{MPC}}^{\star }=\text{arg}\underset{U}{\text{min}}{\text{Σ}}_{l=1}^{N_p}{\omega }^{\varphi }{\text{g}}_{\varphi }^2\left(t_i\text{+}\ell \tau \right)\text{+}{\omega }^u{u}_{\ell }^2$$ (35)

Subject to: Eqn. (32) Eqn. (33)

$$u_{\text{min}}\le u_{\ell }\le u_{\text{max}},$$

for all ℓ = 1, , N_p, where w^ϕ and w^u are positive weighting scalars evaluated at the end of the time step and start of the time step, respectively, as phase error is calculated after the control is applied for that step. Weights w_u are nominal so that the control input is 0 when input would incur no phase shift. After identifying the optimal piecewise control trajectory u^⋆, the initial step $u_1^{\star }$ is applied to the system (in this case the full 8-state ODE model) for t ϵ (t_i, t_i + τ] as is standard in model predictive control.

For the ensuing simulations, a sampling time of τ = 2 h was used, as described in the prior section. Additionally, weights w^ϕ = 10 and w^u = 1, so that no control is delivered for marginal gains in phase shifting, and δ_ϕ = 0.1 as in [35].

Simulations demonstrate that the optimization step in the MPC is susceptible to errors induced by choosing the slower direction to achieve a phase reset. The example in Fig. 8 shows how the finite horizon optimal control $u_{\text{MPC}}^{\star }$ calculated for ∆ϕ_f = π, ϕ₀ = 0 varies with N_p. For short prediction horizons, the controller applies a phase advance, because more of the positive ipPRC region is immediately visible to the predictor, suggesting that this will achieve most rapid reset. By extending the prediction horizon to N_p = 10 (20 h), more of the negative region of the ipPRC is available, and so the controller targets phase delays, consistent with the in finite-time optimal control for τ = 2 h. In some cases, performing the optimization with both advances and delays available results in an “indecisive” controller that changes directions during the phase shifting, causing excessive lags to reset.

Figure 8:

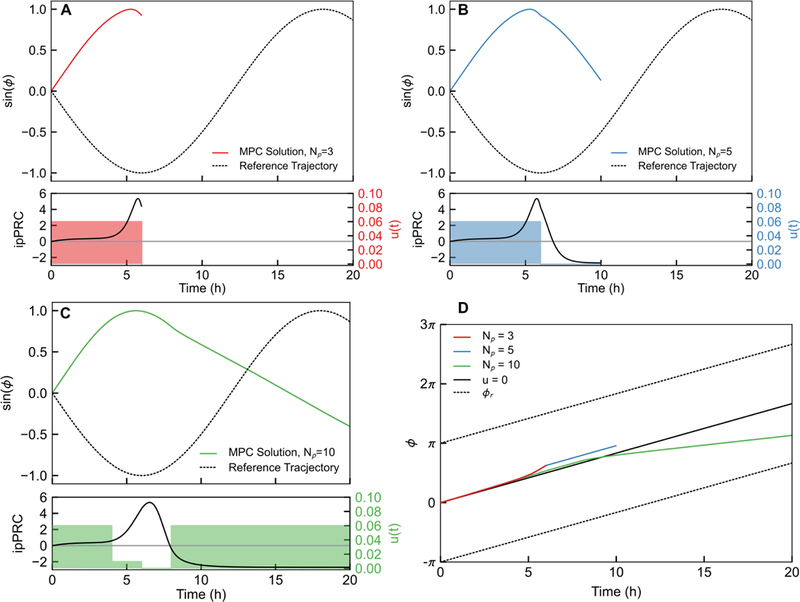
Changes in the prediction horizon affect the finite-horizon optimal control trajectory based on the observable ipPRC. This is demonstrated by computing the first finite-horizon optimal control trajectory and varying that horizon. (A-C) Finite-horizon optimal control trajectories for N_p = 3, 5, and 10, respectively. In all cases, τ = 2h, ∆ϕ_f = and ϕ₀ = 0. Note that not only do the finite horizon optimal controls computed by the MPC differ, they seek to achieve the same shift by either advances (A,B) or delays (C). The in finite-horizon optimal control is achieved via delays (∆ϕ_f > ∆ϕ^⋆), and so A or B would lead to excessively-long resetting by either selecting advances to achieve the shift, or first selecting advances then later choosing delays as in C. (D) This result is visualized by plotting the phase progression for each MPC case and for the 0-input case. Phase advances evidently yield slower progress toward the reference phase, and thus short prediction horizons choose ineffectively. This complication in MPC problem formulation may be circumvented by providing the controller with the optimal resetting direction a priori.

One solution to the problem of inconsistent finite-horizon optimal control policies is to extend the prediction horizon such that it always observes the entirety of the reset, to guarantee that the finite-horizon optimal control calculated during MPC is equal to the in finite-horizon optimal control, that is: $u_{\text{MPC}}^{\star }=u_{\tau }^{\star }$ However, this leads to excessive computational costs, especially for small sampling times. Furthermore, the optimization formulation itself poses challenges. Minimizing the time to complete the reset is challenging, as there is no gradient along which to move unless the reset is completed during the prediction horizon, leading to cases with an in finite cost. Minimizing phase error at each step may be suboptimal as well: the fastest reset achievable may involve temporarily increasing χ(t) for cases where ∆ϕ_f < π and ∆ϕ_f >$\Delta {\varphi }_{\tau }^{\star }$.

An alternate approach, which is employed in the following section, is to use a two-stage optimization, where the direction of the reset (advance or delay) is chosen first using a pre-selected bound ∆ϕ_b. Furthermore, we propose using ∆ϕ_b = ∆ϕ^⋆, as this will ensure that the bounds on residual phase error and additional cycles to reset hold, as derived in the prior section, and thus provide guarantees on controller performance in the absence of plant-model mismatch or noise. One further important consideration is that a controller with N_p = 1 will be unable to avoid ac-cumulating error at the zero-crosses, whereas a controller with a larger N_p provides exibility to adjust the control inputs preceding a zero-cross to minimize the accumulated error. For this reason, the design parameters were set to N_p = 5 and ∆ϕ_b = ∆ϕ^⋆ for our controller. We note, however, that the derived bounds hold even for N_p = 1.

4. In silico application of designed MPC controller for phase resetting

To demonstrate the efficacy of this control approach, this section presents two control scenarios in our in silico circadian simulator (shown schematically in Fig. 4). We note here that the predictor in our MPC formulation was the phase only model, but the system that we applied the control input to is the full 8-state ODE model. Thus, we are testing Assumption 1, since control inputs will perturb the system from the limit cycle, and control will only be viable if the phase-only model reduction accurately describes phase dynamics in state space. We parameterized the controller with τ = 2h, N_p = 5, and ∆ϕ_b = ∆ϕ^⋆, as prescribed by the design considerations in the prior sections.

Figure 4:

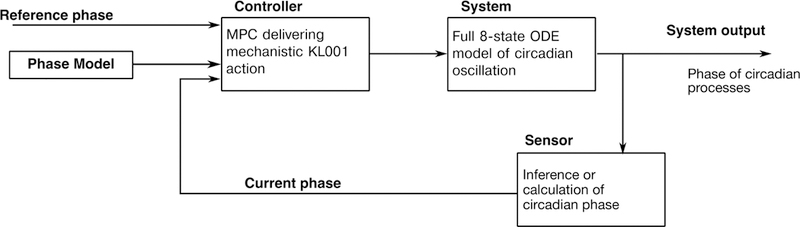
In silico scheme for MPC of circadian rhythms. In experimental or clinical application, a human, organism, or cell culture would replace the 8-state ODE model as the system under control, and phase would be estimated rather than calculated.

The first scenario (Fig. 9) is an example of extreme jet lag, in which the environment undergoes a 5 h phase advance, followed three days later by a phase delay of 11 h This is the equivalent of a flight from Boston to London, then London to Honolulu. Here, the controller first waits for a positive region of the ipPRC rather than immediately attempting a delay, as ∆ϕ_f < ∆ϕ_b. Thus, it completes this phase advance in approximately 30 h. The 11 h delay occurs during a region where B(ϕ) < 0, and thus control input is provided immediately. This shift is completed in a total of two continuous doses, in approximately 36 h. Without a control approach, light input alone achieves a shift of 2–3h per day at most, thus, this represents a significant speed up in phase resetting. If light is delivered under optimal control, these shifts are predicted to take several days [24], thus demonstrating the potential for improvement by a pharmaceutical input.

Figure 9:

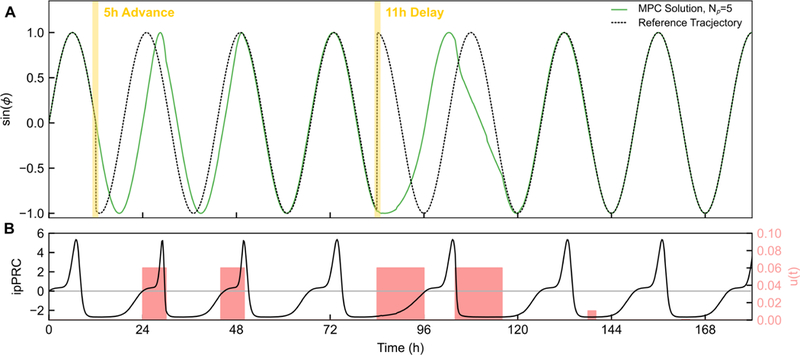
Demonstration of MPC for phase resetting in response to jet lag. This scenario involves a 5h (0.417π rad) phase advance followed by a 11h (0.917π rad) phase delay, the equivalent of flying from Boston to London, then London to Honolulu three days later. (A) Phase of oscillator under MPC compared to reference phase (local time) for the jet lag problem. For this problem, τ = 2h and N_p = 5. (B) Timing of control inputs and ipPRC throughout the simulation. In both cases, the reset is completely achieved in less than 48h, a drastic speedup in comparison to the untreated case or the light-input case [33]. For simplicity, no light input to the clock was assumed in this case, though it may be incorporated as an additional disturbance input to the phase model, or applied as part of multi-input control.

The second scenario (Fig. 10) involves the delivery of KL001 to align an individual working on a rotating shift pattern, from [43]. Here, the time on the x-axis is local time, and the phase of the oscillator is initialized for an individual entrained to a normal light-dark cycle. In this protocol, the individual works two days of morning shift, followed by two days of evening shift, followed by two days of night shift (work shifts denoted by gray boxes. This perpetually phase-delaying schedule is easily tracked by KL001 input, as KL001 more easily achieves phase delays. Notably, by taking one large dose after the conclusion of each pair of shifts, the individual rapidly shifts to the new work phase. Each shift worked in this protocol occurs while the individual is exactly phase-aligned with their work environment. This scenario exclusively involves phase delays, and so under the analysis of Section 3 a larger sampling time of τ = 4 h (or possibly even larger) would be similarly effective.

Figure 10:

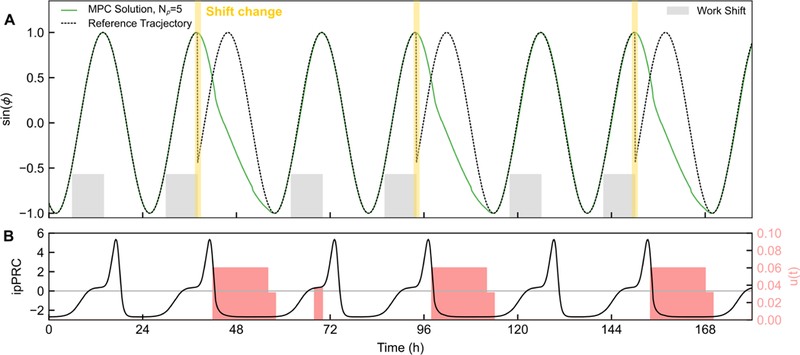
Demonstration of MPC for phase resetting in response to a weeklong rotating shift work schedule, described in [43]. This scenario involves 8h phase delays every two days when rotating from morning (06:00–14:00), to evening (14:00–22:00) to night (22:00–06:00) shifts, followed by days off. (A) Phase of oscillator under MPC compared to reference phase for the shift work problem. In this example, time corresponds to clock time, such that Per expression in an individual entrained for morning work will occur near dusk. The reference phase was adjusted to the next rotating shift following the last work cycle of the prior rotating shift. For this problem, τ = 2h and N_p = 5. (B) Timing of control inputs and ipPRC throughout the simulation. Because all shifts are achieved by delays, a slower sampling rate (longer duration between dosage changes) would have a similar efficacy. For simplicity, no light input to the clock was assumed in this case, though it may be incorporated as an additional disturbance input to the phase model, or applied as part of multi-input control.

Importantly, the possibly competing effects of light was neglected in these scenarios. This could be achieved simply by restricting light input during the phase-shifting steps, or treating light as a complementary control input, using an approach such as [25]. This is a possible topic for future study.

5. Conclusion

This paper presents tools for designing feedback control of circadian rhythms based upon an optimal control policy. Importantly, this paper provides a bound on the errors incurred by discrete sampling and update times during pharmaceutical control of circadian oscillation. These results may then be applied to compare against the efficacy of a light-based approach; see, for example, [33]. Thus, we implicitly considered the non-instantaneous pharmacokinetics of circadian pharmaceuticals. The optimal control problem in the case of known pharmacokinetics will likely necessitate computational, rather than analytic, solutions. In our simpler discrete-time formulation, one may think of the time step of each input as an approximation of the pharmacokinetics by a square wave. While this approximation is clearly non-physiological, it yields analytic solutions that can guide the search for viable pharmaceutical actuators. The principle that imprecision in following the optimal control policy is incurred when drug action occurs during ipPRC zero-crosses points indicates, for example, that a drug with slow pharmacokinetics and a short ipPRC positive region will be inefficient at achieving phase advances. Future studies will directly incorporate pharmacokinetics, which may be easily added to an MPC formulation, and then MPC solutions may be compared to performance under the optimal control policy. Further-more, we have shown the advantages provided by pharmacological actuation, as any phase reset is predicted to be achievable in under 60 h. Uniquely, we propose a formulation of the nonlinear MPC based on the bounds derived from the optimal control problem.

Since drug discovery for the manipulation of circadian rhythms is ongoing, this paper presents a perspective on which pharmaceuticals will enable control. Specifically, an ideal circadian pharmaceutical will have (i) large-magnitude positive and negative ipPRC regions, to enable bidirectional phase resetting, and (ii) rapid pharmacokinetics, to enable precise timing of its effect and minimal losses during ipPRC zero-crosses. This is in contrast to traditional pharmaceutical approaches that select for a long drug half-life to ensure its effect is sustained. Future studies should explicitly incorporate simple pharmacokinetic profiles, rather than piecewise-constant control. However, achieving closed-form solutions or error bounds for these problems is challenging.

While this study has approached control of circadian phase, circadian amplitude has been also been recognized as an important physiological parameter. Previous studies have predicted that light resetting of the clock is associated with diminished amplitudes [24, 44]. Changes in amplitude of circadian parameters may be due to deviation from the limit cycle within individual cells, or due to desynchrony among cellular oscillators during phase shifting [45]. Deviation from the limit cycle may be predicted through amplitude response curves (ARCs), and changes in synchrony may be predicted by judicious use of the ipPRC. Elsewhere, we have begun the development of MPC that maintains circadian synchrony through phase shifting [46] Future studies of circadian control may explicitly include control of circadian amplitudes in addition to phase.

Finally, the remaining link in achieving closed-loop circadian control is the development of a noninvasive circadian phase sensor. While phase may be assessed relatively simply from cellular bioluminescent reporters, noninvasive in vivo phase inference in mammals is an open challenge. Recent work in assessing phase from ambulatory monitoring has shown promise and reasonably accurate predictions [47], however, the propagation of measurement errors through such a control algorithm also remains an open question. An ideal phase sensor would rely on simple data such as solely actigraphy, rather than additional biophysical sensors (e.g. skin temperature, salivary melatonin), and remains in development. The abilities of phase inference methods and controller robustness will be of consequence for the implementation of any form of circadian feedback control mentioned herein.

Biographies

John H. Abel is a Postdoctoral Research Fellow in the Department of Anesthesiology, Critical Care and Pain Medicine at Massachusetts General Hospital, and an affiliated researcher at the Picower Institute for Learning and Memory at the Massachusetts Institute of Technology (MIT). He received the B.S. degree in Chemical Engineering from Tufts University (2013), the M.S. degree in Chemical Engineering from the University of California, Santa Barbara (2015), and the Ph.D. degree in Systems Biology from Harvard University (2018). His research interests are in the application of dynamical systems and control theory to neuroscience, systems biology of circadian rhythms, and physiological closed-loop control.

Ankush Chakrabarty received a B.E. with first-class honors from Jadavpur University, India (2011), and a Ph.D. from Purdue University, West Lafayette, USA (2016), both in Electrical Engineering. Since 2018, he is a Visiting Research Scientist in the Control and Dynamical Systems Group at Mitsubishi Electric Research Laboratories (MERL), prior to which he was a Postdoctoral Fellow at Harvard University. His work leverages artificial intelligence and approximation/relaxation methods to provide computationally efficient and provably safe solutions to challenging problems arising in control and estimation, with special emphasis on model predictive control and unknown input estimation.

Elizabeth B. Klerman is an Associate Professor of Medicine at Harvard Medical School, and a Physician in the Department of Medicine at the Brigham and Women's Hospital. She received the B.S. in Interdisciplinary Science from the Massachusetts Institute of Technology (MIT), and the PhD in Physiology and M.D. degrees from Harvard University. She is a member of the Sleep Research Society, the Society for Research in Biological Rhythms, the Association for Clinical and Translational Science, and the International Academy of Astronautics. She was received Phi Beta Kappa for her undergraduate work and a NASA JSC Director’s Innovation Award as member of International Space Station Flexible Lighting Team. Dr. Klerman's current research focuses on the interaction of endocrine, circadian and sleep rhythms in normal and pathological states; and mathematical modeling of the sleep and circadian system and markers of its function.

Francis J. Doyle III is the John A. Paulson Dean of the Harvard John A. Paulson School of Engineering and Applied Sciences at Harvard University, where he also is the John A. & Elizabeth S. Armstrong Professor. He received a B.S.E. degree from Princeton, C.P.G.S. from Cambridge, and Ph.D. from Caltech, all in Chemical Engineering. He has held faculty appointments at Purdue University, the University of Delaware, and UCSB. In addition he has held visiting positions at DuPont, Weyerhaeuser, and Stuttgart University. He has been recognized as a Fellow of multiple professional organizations including: IEEE, IFAC, AIMBE, and the AAAS. He was the President for the IEEE Control Systems Society in 2015, and was the Vice President of the International Federation of Automatic Control from 2014 to 2017. In 2005, he was awarded the Computing in Chemical Engineering Award from the AIChE for his innovative work in systems biology, and in 2015 received the Control Engineering Practice Award from the American Automatic Control Council for his development of the artificial pancreas. In 2016, he was inducted as a Fellow into the National Academy of Medicine for his work on biomedical control. His research interests are in systems biology, network science, modeling and analysis of circadian rhythms, and drug delivery for diabetes.