Energetics of angstrom-scale conformational changes in an RCK domain of the MthK K⁺ channel

Summary

Allosteric proteins transition among different conformational states in a ligand-dependent manner. Upon resolution of a protein's individual states, one can determine the probabilities of these states, thereby dissecting the energetic mechanisms underlying their conformational changes. Here we examine individual RCK domains that form the regulatory module of the Ca²⁺-activated MthK channel. Each domain adopts multiple conformational states differing on an angstrom scale. The probabilities of these different states of the domain, assessed in different Ca²⁺ concentrations, allowed us to fully determine a six-state model that is minimally required to account for the energetic characteristics of the Ca²⁺-dependent conformational changes of an RCK domain. From the energetics of this domain we deduced, in the framework of statistical mechanics, an analytic model that quantitatively predicts the experimentally observed Ca²⁺ dependence of the channel's open probability.

Introduction

The Ca²⁺-activated MthK K⁺ channel consists of a transmembrane pore module and a cytoplasmic regulatory module¹. The regulatory module is formed by eight RCK (regulator of conductance to K⁺) domains. Three conformational states, S₁, S₂ and S₃^{1, 2} (PDBs 1LNQ, 2FY8 and 4RO0) of the RCK domain have been captured crystallographically (all notations and abbreviations are listed in the Supplementary Note 1). One Ca²⁺-binding site was initially identified in each RCK domain, and a subsequent study revealed two additional sites^{1, 3} (Supplementary Fig. 1). Thus, a total of 24 Ca²⁺-binding sites are present in the regulatory module. Electrophysiology studies have shown that Ca²⁺ binding to the regulatory module increases the channel’s open probability (p_o) by about four orders of magnitude, with a measured Hill coefficient⁴ as high as ~20 and an average value of ~10^{5, 6}. These behaviors could be explained using a modified version of the Monod-Wyman-Changeux (MWC) model⁷, which involves a series of cooperative binding of numerous Ca²⁺ ions^{5, 6} (modified MWC models were also used in earlier studies of other types of channels^{8, 9}). To a large degree, the apparent strong cooperative Ca²⁺ binding reflects cooperative interactions among RCK domains during channel activation.

To understand the gating mechanism of the MthK channel, it is necessary to examine directly the regulatory module itself, a task that cannot be accomplished with single-channel-current-recording techniques^{10, 11}. Here, we use a polarization-microscope-based method¹² to investigate the Ca²⁺-dependent conformational changes of a single, fluorescently labeled RCK domain within an isolated regulatory module of the MthK channel. Based on the probabilities of individual conformational states determined here, we set out to establish a model that quantitatively accounts for the Ca²⁺-dependent regulation of RCK's conformational changes, and to obtain, in the framework of statistical mechanics, an analytic solution that can predict the experimentally observed channel's p_o over a wide range of Ca²⁺ concentrations ([Ca²⁺]).

Results

Ca²⁺-dependent conformational changes in RCK

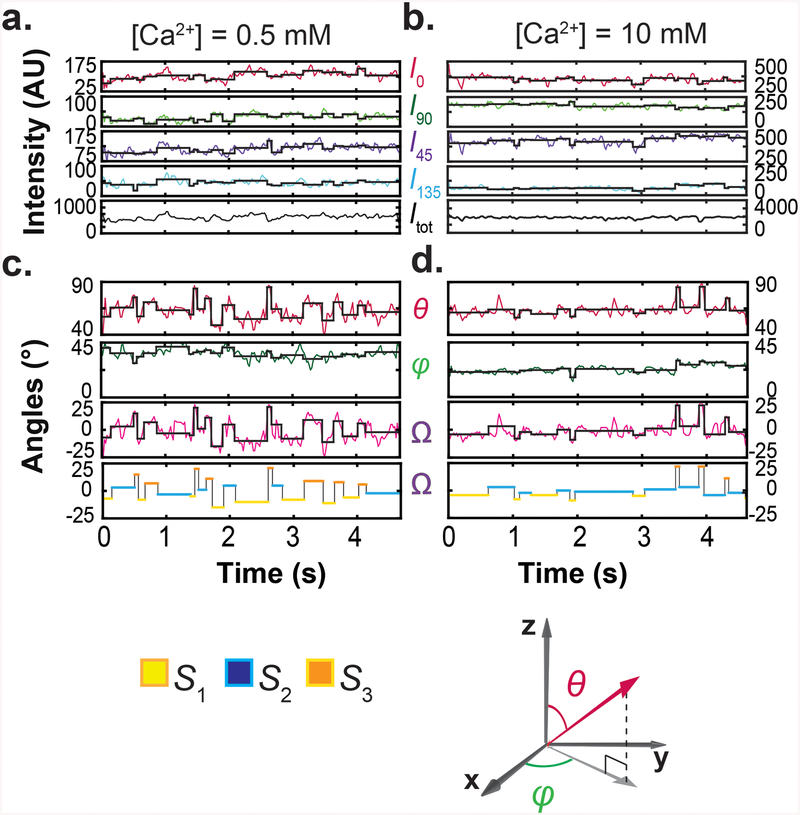
As described in a companion paper¹², we examined the spatial orientation changes of helix αB in the RCK domain, which is located closest to the channel's gate and adopts a unique orientation in each of the three conformational states identified crystallographically^{1, 2}. In one of the eight RCK domains within the regulatory module, this α-helix was labeled with a bifunctional rhodamine molecule via two mutant cysteine residues. Individual labeled regulatory modules (without the pore module) were attached to a coverslip via a four-fold attachment, so that their central axis would be aligned with the optical (z) axis¹². We collected fluorescence intensities from individual particles via four polarization channels in different Ca²⁺ concentrations (Fig 1a,b), from which we calculated the total emitted intensity (I_tot), and inclination (θ) and rotation (φ) angles of the fluorophore's dipole and thus of the α-helix (Fig 1c,d). We also calculated the angle change between two conformations in the actual rotation plane (Ω), which is a function of θ and φ. The state S₂, with an intermediate θ value, was chosen as reference and, consequently, Ω₂₂ values were thus distributed around zero. The black traces superimposed on the experimental intensity and calculated angle traces were generated by setting the amplitude of a given event uniformly to the average of the observed values within that event, a procedure that increased the effective signal-to-noise ratio (SNR) and thus angle resolution of individual events. Starting and end points of individual events were statistically determined from the concurrent changes in all four intensity traces.

Figure 1.

Polarized-fluorescence intensities and calculated I_tot, θ, φ and Ω at two Ca²⁺ concentrations. a, b. Four intensity components (I₀, I₄₅, I₉₀ and I₁₃₅) of single particles recorded over ~5 seconds in 0.5 mM (a) and 10 mM (b) Ca²⁺, and I_tot calculated from I₀, I₄₅, I₉₀ and I₁₃₅. c, d. Values of θ and φ calculated from the four intensity components and values of Ω calculated relative to S₂. Transition points of the black traces superimposed on the experimental intensity and angle traces were determined by a changepoint analysis whereas the constant values between the transitioning points are means of the observed data. For easy visualization, a colored-for-conformational-state version of the black trace for Ω is shown below. For reference, coordinate systems are shown at the lower right corner.

We identified individual conformational states on a particle-by-particle basis to eliminate the inter-particle variability, and on the basis of both its θ and φ angles, to increase resolution and reliability. As θ is unique for each of the three crystallographically identified conformational states, we used it to identify the corresponding states¹². To achieve greater accuracy, we estimated the θ value of each state from the distribution of mean θ values of individual particles analyzed separately (Fig. 2a). For each of the three states, the values of either θ or Ω were similar across all examined Ca²⁺ concentrations. Furthermore, across these concentrations, the mean θ values of the three states and the mean Ω values among them were comparable to those values predicted from the crystal structures^{1, 2} (Fig. 2b).

Figure 2.

Comparison of θ and Ω angles determined from single-molecule fluorescence polarization measurements with those from existing crystal structures. a. θ and Ω values (mean ± σ; n = 110–1589) of the labeled helix in the three conformational states, determined over a range of Ca²⁺ concentrations in the fluorescence study and analyzed on a particle-by-particle basis. b. θ and Ω values deduced from the three crystal structural states^{1, 2} compared with mean θ and Ω values determined from fluorescence measurements. These mean values and their associated σ values of θ and Ω are calculated from their respective arithmetic means of individual analyzed particles, examined over the entire Ca²⁺ range shown in a.

Ca²⁺ dependence of state probabilities of RCK

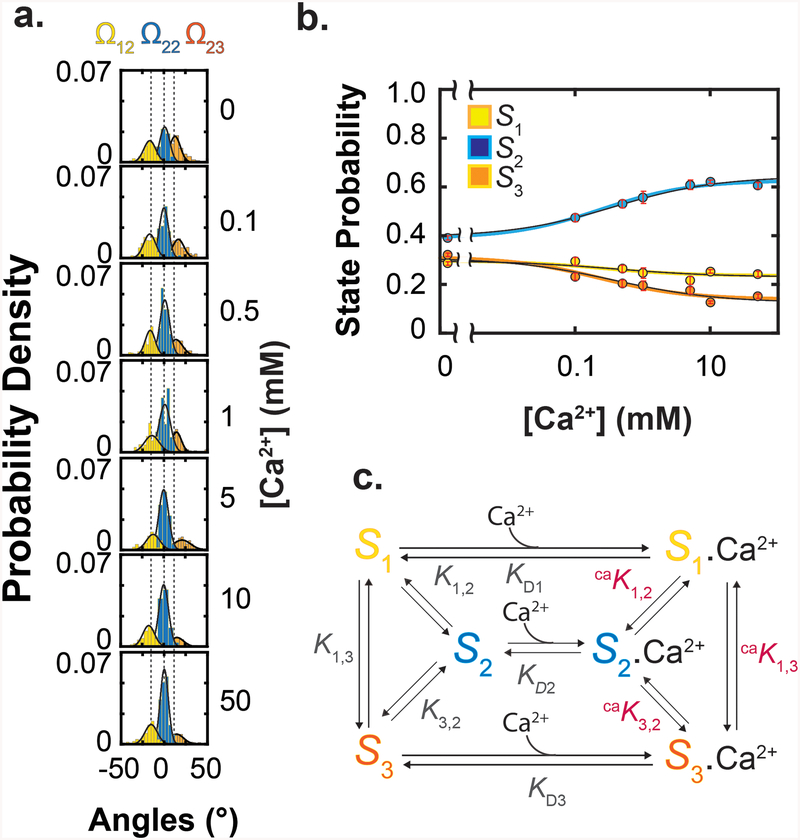
We built distributions of the three states in various Ca²⁺ concentrations from the events identified in each Ω trace through particle-by-particle analysis (Fig 3a). From these distributions, we generated the plot of the state probabilities versus the Ca²⁺ concentration (Fig. 3b), showing that all three states were substantially present in the absence or the presence of Ca²⁺, a defining feature of the MWC model⁷. Consistent with the open-state structure of MthK, in which all RCK domains are in the S₂ state bound with Ca²⁺, the relative population of S₂ increased with Ca²⁺ concentration, whereas those of S₁ and S₃ decreased (Fig. 3a, b). Thus, RCK can bind Ca²⁺ not only in S₂ but also in S₁ and S₃, although the relative distribution of these states varied with the Ca²⁺ concentration.

Figure 3.

Ca²⁺ dependence of state probabilities and state diagram of an energetic model of RCK. a. Distributions of Ω angle values at various Ca²⁺ concentrations obtained from total 980 particles. For illustration, the curves were calculated from the values of the mean and standard deviation σ. b. Probabilities (mean ± s.e.m.; n = 110 – 1589) of a RCK to adopt the three conformational states, calculated from the data shown in a and plotted against Ca²⁺ concentrations. The state-color-coded curves superimposed on the data correspond to a global fit of Eq. 3 to the three plots in Fig. 3b alone, whereas the thin black curves correspond to a global fit of Eq. 15 to all of the plots in Fig. 3b and Fig, 5b together. c. A six-state model of RCK where it exists in three conformations with or without Ca²⁺ bound.

The observed Ca²⁺ dependence of RCK conformations strongly implies the existence of minimally six states: three conformations without Ca²⁺ (S₁, S₂ and S₃) and three with n₁ number of Ca²⁺ bound $\left(S_1\cdot {\text{Ca}}_{{\text{n}}_1}^{2+},S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\text{ and }{S}_3\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right)$ (Fig. 3c). Given that in the open-state structure¹ all RCK domains adopt S_2, we chose that state as a reference for other states (i), to define the following equilibrium constants:

$$K_{\text{i},2}=\frac{\left[S_{\text{i}}\right]}{\left[S_2\right]};{}^{\text{ca}}K{}_{\text{i},2}=\frac{\left[S_{\text{i}}\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}{\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]};K_{D\text{i}}=\frac{\left[S_{\text{i}}\right]{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{\left[S_{\text{i}}\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}i=1,2,3$$ (1)

K_i,2 and ^caK_i,2 could be calculated directly from the state populations under zero and saturating Ca²⁺ conditions, respectively, and K_Di could be independently determined from the “midpoint” positions of the population curves (Fig. 3b). Together, these constants would fully define the model quantitatively.

The Ca²⁺ dependence of the probability (p_i) of a labeled RCK domain to adopt a given conformation i should reveal its relationship with other RCK domains within the regulatory module. On the one hand, if RCK domains were independent of each other and Ca²⁺ effectively bound to only one site in a RCK domain, the Ca²⁺ dependence of p_i would follow an equation describing the Ca²⁺ and RCK interaction in a one-to-one stoichiometry. On the other hand, if there were a high degree of positive cooperativity among Ca²⁺ sites located within a RCK or among RCK domains, as is the case with the full channel^{5, 6}, the exponent n₁ of the Ca²⁺-concentration term in Eq. 1 would be much greater than one.

The observed concentration of RCK in all six conformational states [^obsS], i.e., three without and three with n₁ number of Ca²⁺ bound, is given by:

$$\left[{}^{\text{obs}}S\right]=\left[S_1\right]+\left[S_2\right]+\left[S_3\right]+\left[S_1\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]+\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]+\left[S_3\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]$$ (2)

Under an equilibrium condition, out of the nine equilibrium constants, only five constants (in certain combinations) would be independent parameters in the model (Eq. 1; Fig. 3c). We chose to use and K_D2, K_1,2, K_3,2, ^caK_1,2 ^caK_3,2 in the following expressions. The probability p_i for RCK with and without Ca²⁺ bound is defined by:

$$p_{\text{i}}=\frac{\left[S_{\text{i}}\right]+\left[S_{\text{i}}\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}{[{}_{}{}^{\text{obs}}S]}=\frac{K_{\text{i},2}{+}^{\text{ca}}{K}_{\text{i},2}\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{Di}}}{(K+1)+{(}^{\text{ca}}K+1)\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D\text{i}}}}$$ (3)

where K and ^caK are the ratios of the “decreasing” species (S₁ and S₃) relative to the “increasing” species (S₂) for the cases with and without Ca²⁺ bound, respectively:

$$K=\frac{\left[S_1\right]+\left[S_3\right]}{\left[S_2\right]}=K_{1,2}+K_{3,2};{}^{\text{ca}}K=\frac{\left[S_1\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]+\left[S_3\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}{\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}={}^{\text{ca}}{K}_{1,2}+{}_{}{}^{\text{ca}}K{}_{3,2}$$ (4)

We fit Eq. 3 globally to the three relations between state probabilities and Ca²⁺ concentrations (Fig. 3b). The resulting values of all equilibrium constants are presented in Supplementary Table 1. The fitted n₁ value was 0.643, consistent with the scenario that Ca²⁺ binding primarily to one site in individual RCK domains promotes the Ca²⁺-dependent redistribution among the three conformational states. The observed value of less than one may reflect errors of measurements or a modest negative cooperative interaction from another site. In any case, the shallow Ca²⁺ dependence indicates that, in the isolated regulatory module, RCK domains did not exhibit the level of positive cooperativity expected from the steep Ca²⁺ dependence of MthK-channel activation^{5, 6}, and appeared to undergo the observed conformational changes largely independently.

If individual RCK domains undergo conformational changes independently, then the spontaneous p_o of a MthK channel under a Ca²⁺-free condition should be related to the probability that individual RCK domains adopt the conformation underlying the channel's open state. The observations that all eight RCK domains adopted S₂ in the open-state structure^{1, 3}, and that Ca²⁺, which activates the channel, favored S₂ over other conformations (Fig. 3b) are consistent with the notion that all RCK domains primarily adopt S₂ (dubbed all-S₂) in the open state. Furthermore, the probability of all-S₂ in the absence of Ca²⁺, given by $p_2^8=5.1\times {10}^{-4}$, is comparable to the experimentally determined spontaneous p_o (2.6 × 10⁻⁴) of the MthK channel⁶ (Supplementary Table 2).

Deducing an energetic model of the MthK channel

If the RCK domain acts as the basic functional unit of the regulatory module, then establishing an energetic model for the whole MthK channel only requires further deducing the energetics of the gate, plus those of additional unobserved configurations and Ca²⁺-RCK interactions that occur in the regulatory module of a whole channel. Below, we develop a model to quantitatively predict the energetic hallmark of regulation of the MthK channel by Ca²⁺, in the form of the p₀ –[Ca²⁺] relationship. Detailed statistical mechanics-based derivations are presented in Supplementary Notes 2–4.

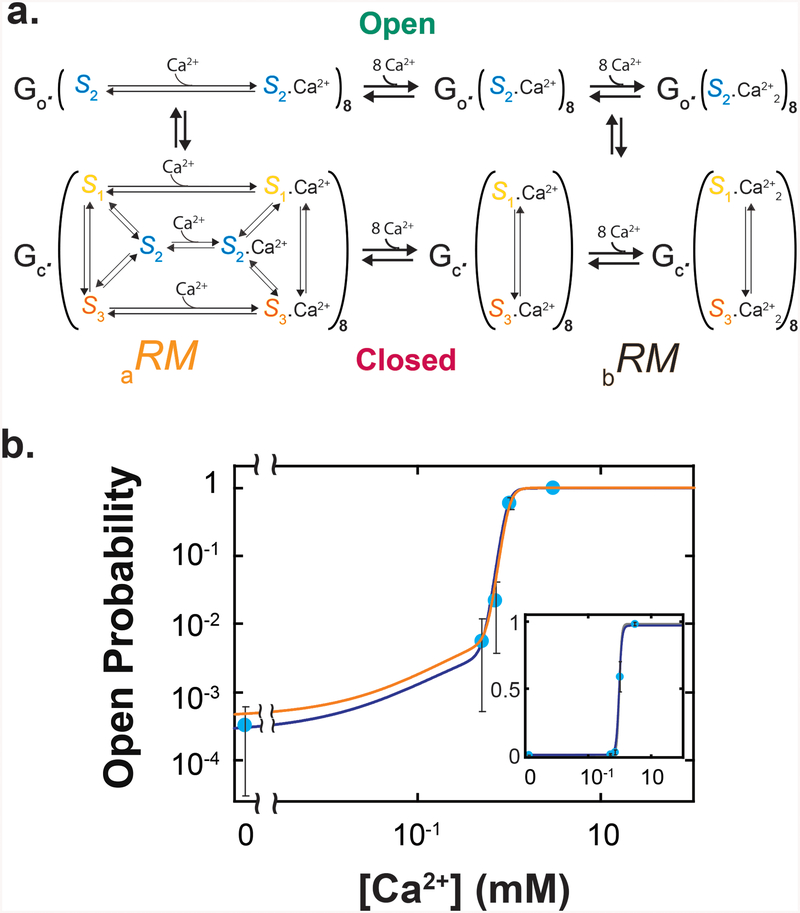
In an isolated regulatory module, eight independent RCK domains, each of which can adopt three conformations, giving rise to 3⁸ = 6561 possible permutations. Of those 6561 permutations, if only the all-S₂ species underlies the open state of the regulatory module (RM_o), then the remaining permutations would represent a closed-state configuration (a), denoted by _aRM_c (Fig. 4a). As such, individual RCK domains in _aRM_c would independently adopt any conformations, with or without Ca²⁺ bound. The concentration of _aRM_c would be given by:

$$\left[{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{c}}\right]={\left[{}^{\text{obs}}S\right]}^{\text{m}}-{\left(\left[S_2\right]+\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]\right)}^{\text{m}}$$ (5)

where [^obsS] is already defined in Eq. 2; and m is 8, the number of the RCK domain.

Figure 4.

Model of the regulatory module in two configurations. a. State diagram of _aRM where in closed states, eight RCKs can independently adopt any of the three conformations, whereas in open states, all RCKs are in S₂, regardless of whether they are bound with Ca²⁺. All-S₂ species with or without Ca²⁺ bound should be excluded from the closed state of the regulatory module in _aRM, but it was not explicitly done for graphic simplicity. b. State diagram of _bRM where in closed states, individual RCKs can adopt S₁ or S₃ but not S₂, whereas in the open state, all RCKs are in S₂. c. Predicted open probabilities of _aRM (orange, left) and _bRM (black, right) plotted against the Ca²⁺ concentration. The vertical dashed lines indicate the EC₅₀ value of the experimental p_o−[Ca²⁺] relation of the MthK channel⁶.

We also considered a previously proposed configuration (b) of the closed state, denoted by _bRM_c, where RCK domains would adopt only S₁ or S₃¹³. Thus, in our model, during the transition from _aRM_c to _bRM_c, S₂ would be excluded from all closed species (Fig 4b). The coexistence of Ca²⁺-free S₁ and S₃ has been observed crystallographically². We further stipulate that _bRM_c would exist with or without Ca²⁺ bound⁷. Without explicitly invoking any additional distinct intermediate species, a transition from _aRM_o (open state, all RCK domains in S₂) to _bRM_c(closed state, S₂ excluded) would be perceived as a cooperative transition, because all eight RCK domains must transition to S₁ or S₃. As such, we modeled the binding of Ca²⁺ to individual RCK domains in _bRM as being cooperative⁴ (Fig. 4b). The concentration of _bRM_c should then be expressed as:

$$\left[{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{c}}\right]={\left(\left[S_1\right]+\left[S_3\right]\right)}^{\text{m}}+{\left(\left[S_1\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]+\left[S_3\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]\right)}^{\text{m}}$$ (6)

Regarding the open state, we treated the all-S₂ species alone as the open state (RM_o). The observed concentration of all-S₂ in configuration _aRM or _bRM (with and without Ca²⁺ bound) would be given by Eq. 7 or Eq. 8.

$$\left[{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{o}}\right]={\left(\left[S_2\right]+\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]\right)}^{\text{m}}$$ (7)

$$\left[{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{o}}\right]={\left[S_2\right]}^{\text{m}}+{\left[S_2\cdot {\text{Ca}}_{{\text{n}}_1}^{2+}\right]}^{\text{m}}$$ (8)

Given that _bRM would have far fewer states than _aRM, it should have higher energy. Implicitly, the binding of Ca²⁺ to at least one additional site (denoted by n₂) in individual RCK domains would be required to lower the free energy of _bRM. Operationally, Ca²⁺ binding to the n₂ site would regulate the relative distribution between _aRM and _bRM, whereas Ca²⁺ binding to the n₂ site would regulate the relative distribution among the RCK conformations. However, what is denoted by n₁ may not necessarily be the same physical site in _aRM and in _bRM. Below, we examine first the p_o predicted on the basis of _aRM or _bRM alone, and then the energetic characteristics of the n₂ site.

Substituting Eqs. 4–8 into the following defining relation:

$$p_{\text{o}}=\frac{[O]}{[O]+[C]}$$ (9)

where [O] and [C] denote the concentrations of the open and closed states, we obtained the expressions for the regulatory module’s p_o in _aRM and _bRM:

$${}_{\text{a}}{}^{\text{obs}}p{}_{\text{o}}=\frac{\left[{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{o}}\right]}{\left[{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{c}}\right]+\left[{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{o}}\right]}=\frac{{\left(1+\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}}{{\left(K+1+\left({}^{\text{ca}}K+1\right)\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}}$$ (10)

$${}_{\text{b}}{}^{\text{obs}}p{}_{\text{o}}=\frac{\left[{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{o}}\right]}{\left[{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{c}}\right]+\left[{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{o}}\right]}=\frac{1+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}}{1+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}+K{}^{\text{m}}+{\left({}^{\text{ca}}K\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}}$$ (11)

The p_o-[Ca²⁺] curves calculated with Eqs. 10 and 11 (Fig. 4c) exhibited the following features (all parameters in this paragraph are tabulated in Supplementary Table 2). First, the predicted EC₅₀ value of 1.6 mM for _aRM is comparable to the 0.97 mM value estimated from the fit of a version of the Hill-equation⁴ (Eq. 58, Supplementary Note 4) to a previously observed channel's p_o−[Ca²⁺] relationship⁶. Second, as already mentioned above, the predicted minimal _ap_o of _aRM is close to the observed channel's minimal p_o in the absence of Ca²⁺ (_chp_o). Third, the predicted maximal ${}_{\text{b}}{}^{\text{ca}}p{}_{\text{o}}$ of _bRM is 0.98, which is the same as the observed channel's maximal $p_{\text{o}}\left({}_{\text{ch}}{}^{\text{ca}}p{}_{\text{o}}\right)$ of 0.98.⁶ Finally, the end point of the curve for _aRM practically matches the starting point of the curve for _bRM. Thus, combining Eqs. 10 and 11, which underlie the two curves in Fig. 4c, would adequately account for the full range of the observed p_o of the channel $\left({}_{\text{ch}}{}^{\text{obs}}p{}_{\text{o}}\right)$.

A channel model that contains configurations a and b is shown in Figure 5a. In configuration a, Ca²⁺ binding to all sites n₁ in a regulatory module leads to ${}_{\text{a}}RM\cdot {\left({\text{Ca}}_{{\text{n}}_1}^{2+}\right)}_{\text{m}}$, whereas in configuration b, Ca²⁺ binding to all sites n₂ in a regulatory module leads to ${}_{\text{b}}RM\cdot {\left({\text{Ca}}_{{\text{n}}_2}^{2+}\right)}_{\text{m}}$. In all three RCK conformations, Ca²⁺ would bind to site n₂ with the same unknown K_D (dubbed K_Dn2), but it would bind to site n₁ with three different K_Di values, all of which were properly scaled and expressed in the form of K_D2 in the above equations. Equalizing the average free energy of ${}_{\text{a}}RM\cdot {\left({\text{Ca}}_{{\text{n}}_1}^{2+}\right)}_{\text{m}}$ and that of ${}_{\text{b}}RM\cdot {\left({\text{Ca}}_{{\text{n}}_2}^{2+}\right)}_{\text{m}}$ requires that the overall apparent K_D for Ca²⁺ binding to site n₁ (K_Dn1) be the same as K_Dn2. Thus, we could deduce the value of K_Dn2 from that of K_Dn1 in accordance with the relation (Supplementary Note 4):

$$K_{Dn2}=K_{Dn1}=\frac{K+1}{{}_{}{}^{ca}K+1}{K}_{D2}$$ (12)

which yields 0.38 mM. With an explicit inclusion of the n₂ site, the total open species in _aRM and _bRM (RM_o, Eqs. 5 and 6) and the total closed species(RM_c, Eqs. 7 and 8) would be defined as:

$$\left[\begin{array}{c}{}_{\text{ch}}{}^{\text{obs}}R{M}_{\text{o}}\end{array}\right]=\left[\begin{array}{c}{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{o}}\end{array}\right]+\left[\begin{array}{c}{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{o}}\cdot {\left({\text{Ca}}_{{\text{n}}_2}^{2+}\right)}_{\text{m}}\end{array}\right]$$ (13)

$$\left[\begin{array}{c}{}_{\text{ch}}{}^{\text{obs}}R{M}_{\text{c}}\end{array}\right]=\left[\begin{array}{c}{}_{\text{a}}{}^{\text{obs}}R{M}_{\text{c}}\end{array}\right]+\left[\begin{array}{c}{}_{\text{b}}{}^{\text{obs}}R{M}_{\text{c}}\cdot {\left({\text{Ca}}_{{\text{n}}_2}^{2+}\right)}_{\text{m}}\end{array}\right]$$ (14)

Substituting Eqs. 13 and 14 (in the form of energetic constants) into Eq. 9 yielded the p_o−[Ca²⁺] relation for the whole channel:

$${}_{\text{ch}}{}^{\text{obs}}p{}_{\text{o}}={\left(1+\frac{{\left[\text{C}{\text{a}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_2}}{K_{Dn2}}\right)}^{\text{m}}\left(1+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}\right){\left(1+\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}\left(1-{}_{g}K\right)+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_2}}{K_{D\text{n}2}}\right)}^{\text{m}}\left(1+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}\right)+\left({\left(K+1+({}^{\text{ca}}K+1)\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}+{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_2}}{K_{D\text{n}2}}\right)}^{\text{m}}\left(K^{\text{m}}+{\left({}^{\text{ca}}K\frac{{\left[{\text{Ca}}^{2+}\right]}^{{\text{n}}_1}}{K_{D2}}\right)}^{\text{m}}\right)\right){}_{\text{g}}K$$ (15)

where _gK is the apparent equilibrium constant of the gate, as defined in Supplementary Note 4; K describes the relative distribution between “[S₁] + [S₃]” (unbound closed species in configuration b) and [S₂](open species); and ^caK describes the relative distribution between the corresponding Ca²⁺-bound closed and open species (Eq. 4). In an ideal case where the total amount of energy related to this fully reversible conformation redistribution equals that derived from Ca²⁺ binding, K^m should equal to ^caK^−m. We noted that fitted K (1.576) is slightly smaller than ^caK⁻¹ (1.686)(Supplementary Table 1). The small “excess” Ca²⁺-binding energy defined by $kT\text{ln}{\left(K^{\text{ca}}{K}^{-1}\right)}^{\frac{m}{2}}$ could, in principle, help to energetically equalize the open and closed states of the channel gate itself. ${\left(K^{\text{ca}}{K}^{-1}\right)}^{\frac{m}{2}}$ yields a value of 1.3; within experimental errors, a _gK of 1.3 (slightly favoring the closed state) would be sufficient to close the small gap between the observed minimal p_o and that predicted by the model for the regulatory module alone (i.e., Eq. 15 where _gK is set to 1).

Figure 5.

Model for the whole MthK channel. a. State diagram of an energetic model for the whole channel. The gate (G) and the regulatory module (RM) both are either in an open state (o) or in a closed (c) state; RM can exist in _aRM (left) or _bRM (right). All-S₂ species with or without Ca²⁺ bound in _aRM should be excluded from the closed state of the regulatory module, but it was not explicitly done for graphic simplicity. b. The calculated (orange) and fitted (blue) p_o−[Ca²⁺] curves of the whole channel model (Eq. 15), plotted along the electrophysiological data previously obtained at pH 8.1 (mean ± s.e.m.)⁶, where both p_o and the Ca²⁺ concentration are plotted on logarithmic scales; shown in the inset are the same curves and data where p_o is plotted on a linear scale. The calculation and fit are performed as described in the text. The spontaneous _chp_o was estimated from a linear fit of the plot of observed _chp_o in the absence of Ca²⁺ versus pH⁶.

To test the predictability of our model, we calculated a p_o−[Ca²⁺] curve with Eq. 15, using the parameters determined from fluorescence polarization measurements (Fig. 3c; Supplementary Table 1; _gK = 1.3, K_Dn2 = 0.38 mM, and n₂= 1). The calculated curve matches the p_o−[Ca²⁺] relationship previously determined by electrophysiology⁶, within the experimental errors (Fig. 5b, data points colored light blue and the curve colored orange). It is noteworthy that when explicitly expressed, Eq. 15 would be fully defined by a total of ten parameters: K_1,2, K_3,2 (expressed together as K), ^caK_1,2 and ^caK_3,2 (expressed as ^caK), n₁ and K_D2, all determined from studying RCK; m determined by crystallography; n₂, K_Dn2 and _gK can be deduced as described above. This large number of parameters cannot be extracted by fitting the p_o−[Ca²⁺] curve with a Hill equation⁴.

For comparison, we estimated _gK and K_Dn2 by fully constraining them with experimental measurements. First, we used Eq. 59 (Supplementary Note 4) to directly calculate _gK from the constant K (Eq. 4; Supplementary Table 1) and minimal _chp_o of the channel (Supplementary Table 2; reference⁶), obtaining a slightly larger value of 1.7. We then determined K_Dn2 through a global fit of Eq. 15 to the experimental p_o−[Ca²⁺] relationship of the channel⁶ (Fig. 5b, blue curve) and the three plots regarding Ca²⁺-dependence of RCK conformations in the isolated regulatory module (Fig. 3b, black curves; all resulting parameters are tabulated in Supplementary Table 1). The fit yielded a K_Dn2 value of 0.39 mM, nearly the same as the deduced 0.38 mM. In the fit, _gK was set at 1.7, instead of 1.3 and, consequently, the calculated (orange) and fitted (blue) curves diverged slightly and can be recognized. The inferences are that given the rather small _gK, the observed channel's operational energy primarily reflects that of the regulatory module, and that the present model (Eq. 15; Fig. 5) quantitatively predicts the experimental MthK's p_o−[Ca²⁺] relationship.

Discussion

The regulatory module of the MthK channel harvests the so-called gating energy from the binding of Ca²⁺ to its eight RCK domains. In the model described here, each RCK in _aRM may independently adopt three conformations, with or without Ca²⁺ bound. Even considering only a single Ca²⁺ site per RCK, eight independent RCK domains could generate 6⁸ (~1.7 million) possible permutations or 3⁸ (6561) in the absence of Ca²⁺. If among this large number of permutations, only all-S₂ is associated with the open conformation of the channel, the spontaneous p_o would be primarily determined by entropic energy, given the vastly different numbers of the accessible open versus closed species. The large number of closed species should be depopulated toward the limiting case of effectively one state by Ca²⁺ binding, and the collective probability of all closed species in saturating Ca²⁺ concentrations should be much smaller than the probability of the open species, such that the channel’s p_o would rise from the minimum towards 1. Indeed, electrophysiology studies have shown that Ca²⁺ regulation of the MthK channel occurs primarily while the gate is closed^{5, 6}.

A proposal that a MthK channel can open from the all-S₁ state has been put forward, on the basis of the following observations¹³. First, an all-S₁ form of the isolated regulatory module was captured crystallographically, with Ba²⁺ present at multiple sites within individual RCK domains. Second, Ba²⁺ can activate the MthK channel, albeit with lower efficacy and potency than Ca²⁺. Third, a mutation at a putative Ba²⁺ binding site eliminates the ability of Ba²⁺ to activate the channel. Thus far, there is no structural evidence to link all-S₁ to the open state of the channel yet. In any case, the probability of all-S₁ species predicted from our measurements is low, and thus the p_o−[Ca²⁺] curves calculated from two compared models, in which either only all-S₂ or all-S₂ and all-S₁ are open species, are visually indistinguishable, even on double logarithmic plots (Supplementary Fig. 2). Should Ba²⁺ act differently than Ca²⁺, such that Ba²⁺ binding to RCK would populate S₁ instead of S₂, modeling all-S₁ species as an open state could in principle accommodate the observed channel activation by Ba²⁺. Here we considered only all-S₂ as the open species for the following reasons. First, only all-S₂ was observed in an open-state structure of the MthK channel. Second, we intended to account for the Ca²⁺-dependent regulation, for which all-S₂ being the open species is sufficient. Third, we do not have the quantitative information regarding Ba²⁺-bound RCK to express the all-S₁ species in the analytic model. In any case, the present model could be expanded to include additional open and closed species to account for other features of the channel.

As mentioned, one defining feature of the MWC model is that a protein may adopt one of two (or more) alternative states (R or T) with or without ligand bound⁷. A second defining feature is that all protomers in the protein must be in the same state. In our model, ~1.7 million species form a grand canonical ensemble in terms of statistical mechanics, and given its thermodynamic nature, the model does not concern the paths between any pair of states, regardless of whether they exist in the same or between coexisting configurations a and b (here divided merely for a conceptual purpose). In the vast majority of closed states of either configuration, RCK domains in different conformations coexist. Thus, our model does not satisfy that the second defining feature of the MWC model.

As a special case of the MWC model, the Hill equation⁴ would be defined here by minimal and maximal P_o, EC₅₀ and the Hill coefficient (Eq. 58, Supplementary Note 4). In our model, the minimal or maximal P_o each is defined by three parameters $\left({\left[\left(K_{1,2}+K_{3,2}+1\right){}_{}{}^m{}_g{}^{}K\right]}^{-1}\text{\hspace{0.17em}or}{\left[\left({}_{}{}^{\text{ca}}K{}_{1,2}+{}_{}{}^{\text{ca}}K{}_{3,2}\right){}_{}{}^m{}_g{}^{}K\right]}^{-1}\right)$. The EC₅₀ depends on all independent parameters in a complex manner, and the analytic expression of the Hill coefficient would be even more complex, if it is reachable. Thus, extracting four parameters from the p_o−[Ca²⁺] relationship of the MthK channel using the Hill equation could lead to an empirical quantitative description of observed Ca²⁺-dependent redistribution between the total open species and the total closed species, but would not reveal the energetic mechanism underlying Ca²⁺-dependent gating conformational changes that occur in the regulatory module.

Thus, examining the behaviors of individual RCK domains is necessary to understand the energetic mechanism of the MthK channel. The channel model deduced here on the basis of energetics of the RCK domain well predicts the observed p_o−[Ca²⁺] relationship⁶, in which the binding of Ca²⁺ increases the channel's p_o by two distinct mechanisms. First, independent, non-cooperative binding of Ca²⁺ to individual RCK domains populates S₂ over S₁ or S₃, enhancing the probability of individual RCKs to adopt S₂ and thereby fine tuning p_o. Second, cooperative Ca²⁺ binding would populate _bRM over _aRM, of which the former has fewer closed states. These tuning and configuration-switching mechanisms primarily underlie the shallow and steep phases of the p_o−[Ca²⁺] relationship, respectively. The good agreement between our data obtained with the isolated regulatory module and previous electrophysiology data with the whole channel validates our approach. The present energetic study serves as a foundation for a subsequent study¹⁴, where we use the present method to examine the multi-state conformational dynamics of RCK, and demonstrate how the resulting dynamic information can be used as a temporal template to link its existing structures.

Online Methods

Sample preparation and data recording

As described in reference¹², a recombinant protein of the MthK channel's regulatory module, which contained a N-terminal recognition sequence for biotin ligase, a C-terminal His-tag with a preceding specific-protease-cutting sequence, and the double E146C and L153C mutation in helix αB, was produced using the bacterial BL-21 expression system. The protein was labeled with bifunctional rhodamine (Bis-((N-Iodoacetyl)-Piperazinyl)-Sulfonerhodamine; Invitrogen B10621) via the two mutant cysteine residues and attached to a coverslip conjugated with streptavidin (Arrayit) via biotinylated N-termini. Polarized emissions from individual bi-functional rhodamine labels, excited in the evanescent field created at the surface of the sample coverslip by circularly polarized laser beam (532 nm), were collected via a fluorescence microscope with four polarization emission channels onto an electron-multiplying charge-coupled device camera, while the sample protein was immersed in a solution containing 200 mM KCl, Ca²⁺ of various concentrations, and 10 mM HEPES titrated to pH 8.0, where 1 mM EGTA was used as a buffer in the nominal Ca²⁺-free and low (0.1 mM) Ca²⁺ solutions.

Data analysis

Also as described in reference¹², each intensity of the four emission components collected from a given fluorophore was a direct summation of individual pixels. I_tot, θ, φ, and Ω were calculated using Eqs. 62, 63, 61, and 70 in the Supplementary Note 3 and 6 in the above reference, respectively. Conformational transitions and states were identified in two separate steps. A changepoint algorithm was applied to the intensity traces to detect the transitions between conformational events, whereas a k-means-cluster-based algorithm was applied to identify the conformational states of individual events based on both θ and φ.

Data availability

Data and materials described here will be made available upon reasonable request.