Summary
Allosteric proteins transition among different conformational states in a ligand-dependent manner. Upon resolution of a protein's individual states, one can determine the probabilities of these states, thereby dissecting the energetic mechanisms underlying their conformational changes. Here we examine individual RCK domains that form the regulatory module of the Ca2+-activated MthK channel. Each domain adopts multiple conformational states differing on an angstrom scale. The probabilities of these different states of the domain, assessed in different Ca2+ concentrations, allowed us to fully determine a six-state model that is minimally required to account for the energetic characteristics of the Ca2+-dependent conformational changes of an RCK domain. From the energetics of this domain we deduced, in the framework of statistical mechanics, an analytic model that quantitatively predicts the experimentally observed Ca2+ dependence of the channel's open probability.
Introduction
The Ca2+-activated MthK K+ channel consists of a transmembrane pore module and a cytoplasmic regulatory module1. The regulatory module is formed by eight RCK (regulator of conductance to K+) domains. Three conformational states, S1, S2 and S31, 2 (PDBs 1LNQ, 2FY8 and 4RO0) of the RCK domain have been captured crystallographically (all notations and abbreviations are listed in the Supplementary Note 1). One Ca2+-binding site was initially identified in each RCK domain, and a subsequent study revealed two additional sites1, 3 (Supplementary Fig. 1). Thus, a total of 24 Ca2+-binding sites are present in the regulatory module. Electrophysiology studies have shown that Ca2+ binding to the regulatory module increases the channel’s open probability (po) by about four orders of magnitude, with a measured Hill coefficient4 as high as ~20 and an average value of ~105, 6. These behaviors could be explained using a modified version of the Monod-Wyman-Changeux (MWC) model7, which involves a series of cooperative binding of numerous Ca2+ ions5, 6 (modified MWC models were also used in earlier studies of other types of channels8, 9). To a large degree, the apparent strong cooperative Ca2+ binding reflects cooperative interactions among RCK domains during channel activation.
To understand the gating mechanism of the MthK channel, it is necessary to examine directly the regulatory module itself, a task that cannot be accomplished with single-channel-current-recording techniques10, 11. Here, we use a polarization-microscope-based method12 to investigate the Ca2+-dependent conformational changes of a single, fluorescently labeled RCK domain within an isolated regulatory module of the MthK channel. Based on the probabilities of individual conformational states determined here, we set out to establish a model that quantitatively accounts for the Ca2+-dependent regulation of RCK's conformational changes, and to obtain, in the framework of statistical mechanics, an analytic solution that can predict the experimentally observed channel's po over a wide range of Ca2+ concentrations ([Ca2+]).
Results
Ca2+-dependent conformational changes in RCK
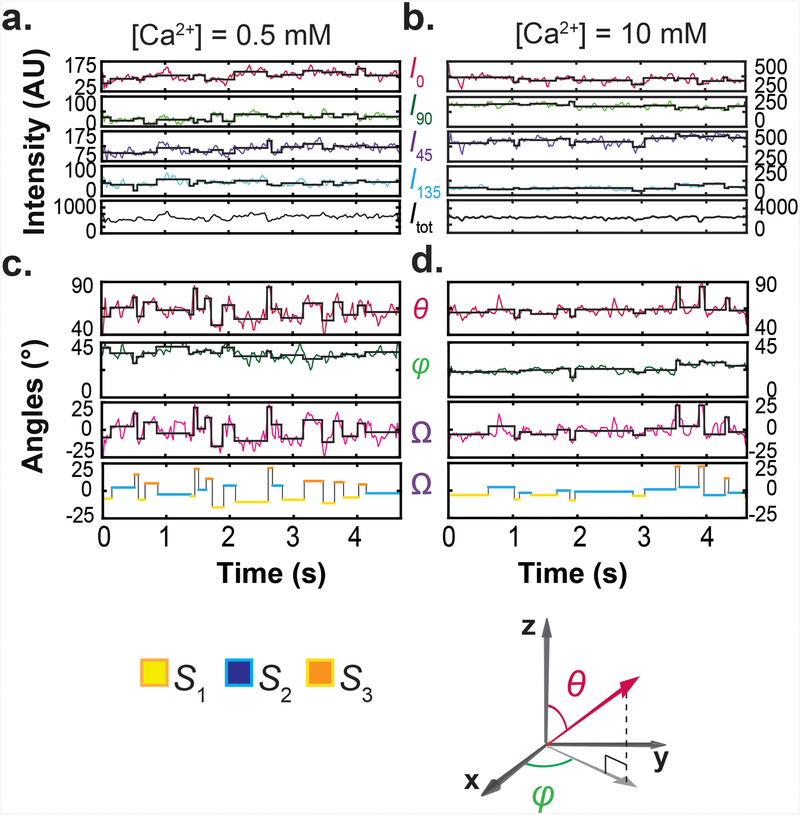
As described in a companion paper12, we examined the spatial orientation changes of helix αB in the RCK domain, which is located closest to the channel's gate and adopts a unique orientation in each of the three conformational states identified crystallographically1, 2. In one of the eight RCK domains within the regulatory module, this α-helix was labeled with a bifunctional rhodamine molecule via two mutant cysteine residues. Individual labeled regulatory modules (without the pore module) were attached to a coverslip via a four-fold attachment, so that their central axis would be aligned with the optical (z) axis12. We collected fluorescence intensities from individual particles via four polarization channels in different Ca2+ concentrations (Fig 1a,b), from which we calculated the total emitted intensity (Itot), and inclination (θ) and rotation (φ) angles of the fluorophore's dipole and thus of the α-helix (Fig 1c,d). We also calculated the angle change between two conformations in the actual rotation plane (Ω), which is a function of θ and φ. The state S2, with an intermediate θ value, was chosen as reference and, consequently, Ω22 values were thus distributed around zero. The black traces superimposed on the experimental intensity and calculated angle traces were generated by setting the amplitude of a given event uniformly to the average of the observed values within that event, a procedure that increased the effective signal-to-noise ratio (SNR) and thus angle resolution of individual events. Starting and end points of individual events were statistically determined from the concurrent changes in all four intensity traces.
Figure 1.
Polarized-fluorescence intensities and calculated Itot, θ, φ and Ω at two Ca2+ concentrations. a, b. Four intensity components (I0, I45, I90 and I135) of single particles recorded over ~5 seconds in 0.5 mM (a) and 10 mM (b) Ca2+, and Itot calculated from I0, I45, I90 and I135. c, d. Values of θ and φ calculated from the four intensity components and values of Ω calculated relative to S2. Transition points of the black traces superimposed on the experimental intensity and angle traces were determined by a changepoint analysis whereas the constant values between the transitioning points are means of the observed data. For easy visualization, a colored-for-conformational-state version of the black trace for Ω is shown below. For reference, coordinate systems are shown at the lower right corner.
We identified individual conformational states on a particle-by-particle basis to eliminate the inter-particle variability, and on the basis of both its θ and φ angles, to increase resolution and reliability. As θ is unique for each of the three crystallographically identified conformational states, we used it to identify the corresponding states12. To achieve greater accuracy, we estimated the θ value of each state from the distribution of mean θ values of individual particles analyzed separately (Fig. 2a). For each of the three states, the values of either θ or Ω were similar across all examined Ca2+ concentrations. Furthermore, across these concentrations, the mean θ values of the three states and the mean Ω values among them were comparable to those values predicted from the crystal structures1, 2 (Fig. 2b).
Figure 2.
Comparison of θ and Ω angles determined from single-molecule fluorescence polarization measurements with those from existing crystal structures. a. θ and Ω values (mean ± σ; n = 110–1589) of the labeled helix in the three conformational states, determined over a range of Ca2+ concentrations in the fluorescence study and analyzed on a particle-by-particle basis. b. θ and Ω values deduced from the three crystal structural states1, 2 compared with mean θ and Ω values determined from fluorescence measurements. These mean values and their associated σ values of θ and Ω are calculated from their respective arithmetic means of individual analyzed particles, examined over the entire Ca2+ range shown in a.
Ca2+ dependence of state probabilities of RCK
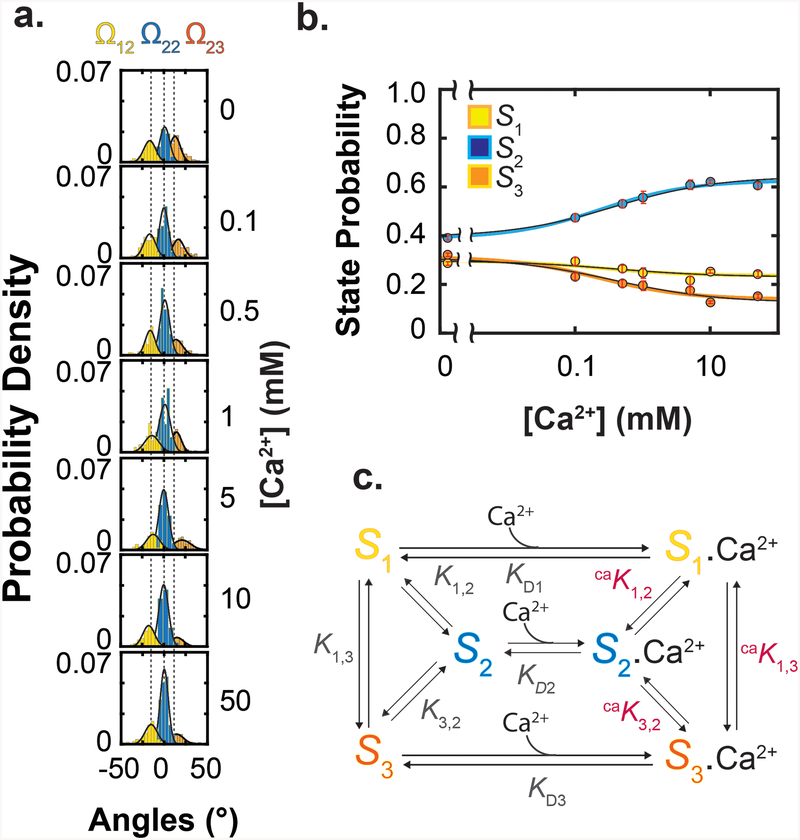
We built distributions of the three states in various Ca2+ concentrations from the events identified in each Ω trace through particle-by-particle analysis (Fig 3a). From these distributions, we generated the plot of the state probabilities versus the Ca2+ concentration (Fig. 3b), showing that all three states were substantially present in the absence or the presence of Ca2+, a defining feature of the MWC model7. Consistent with the open-state structure of MthK, in which all RCK domains are in the S2 state bound with Ca2+, the relative population of S2 increased with Ca2+ concentration, whereas those of S1 and S3 decreased (Fig. 3a, b). Thus, RCK can bind Ca2+ not only in S2 but also in S1 and S3, although the relative distribution of these states varied with the Ca2+ concentration.
Figure 3.
Ca2+ dependence of state probabilities and state diagram of an energetic model of RCK. a. Distributions of Ω angle values at various Ca2+ concentrations obtained from total 980 particles. For illustration, the curves were calculated from the values of the mean and standard deviation σ. b. Probabilities (mean ± s.e.m.; n = 110 – 1589) of a RCK to adopt the three conformational states, calculated from the data shown in a and plotted against Ca2+ concentrations. The state-color-coded curves superimposed on the data correspond to a global fit of Eq. 3 to the three plots in Fig. 3b alone, whereas the thin black curves correspond to a global fit of Eq. 15 to all of the plots in Fig. 3b and Fig, 5b together. c. A six-state model of RCK where it exists in three conformations with or without Ca2+ bound.
The observed Ca2+ dependence of RCK conformations strongly implies the existence of minimally six states: three conformations without Ca2+ (S1, S2 and S3) and three with n1 number of Ca2+ bound (Fig. 3c). Given that in the open-state structure1 all RCK domains adopt S2, we chose that state as a reference for other states (i), to define the following equilibrium constants:
| (1) |
Ki,2 and caKi,2 could be calculated directly from the state populations under zero and saturating Ca2+ conditions, respectively, and KDi could be independently determined from the “midpoint” positions of the population curves (Fig. 3b). Together, these constants would fully define the model quantitatively.
The Ca2+ dependence of the probability (pi) of a labeled RCK domain to adopt a given conformation i should reveal its relationship with other RCK domains within the regulatory module. On the one hand, if RCK domains were independent of each other and Ca2+ effectively bound to only one site in a RCK domain, the Ca2+ dependence of pi would follow an equation describing the Ca2+ and RCK interaction in a one-to-one stoichiometry. On the other hand, if there were a high degree of positive cooperativity among Ca2+ sites located within a RCK or among RCK domains, as is the case with the full channel5, 6, the exponent n1 of the Ca2+-concentration term in Eq. 1 would be much greater than one.
The observed concentration of RCK in all six conformational states [obsS], i.e., three without and three with n1 number of Ca2+ bound, is given by:
| (2) |
Under an equilibrium condition, out of the nine equilibrium constants, only five constants (in certain combinations) would be independent parameters in the model (Eq. 1; Fig. 3c). We chose to use and KD2, K1,2, K3,2, caK1,2 caK3,2 in the following expressions. The probability pi for RCK with and without Ca2+ bound is defined by:
| (3) |
where K and caK are the ratios of the “decreasing” species (S1 and S3) relative to the “increasing” species (S2) for the cases with and without Ca2+ bound, respectively:
| (4) |
We fit Eq. 3 globally to the three relations between state probabilities and Ca2+ concentrations (Fig. 3b). The resulting values of all equilibrium constants are presented in Supplementary Table 1. The fitted n1 value was 0.643, consistent with the scenario that Ca2+ binding primarily to one site in individual RCK domains promotes the Ca2+-dependent redistribution among the three conformational states. The observed value of less than one may reflect errors of measurements or a modest negative cooperative interaction from another site. In any case, the shallow Ca2+ dependence indicates that, in the isolated regulatory module, RCK domains did not exhibit the level of positive cooperativity expected from the steep Ca2+ dependence of MthK-channel activation5, 6, and appeared to undergo the observed conformational changes largely independently.
If individual RCK domains undergo conformational changes independently, then the spontaneous po of a MthK channel under a Ca2+-free condition should be related to the probability that individual RCK domains adopt the conformation underlying the channel's open state. The observations that all eight RCK domains adopted S2 in the open-state structure1, 3, and that Ca2+, which activates the channel, favored S2 over other conformations (Fig. 3b) are consistent with the notion that all RCK domains primarily adopt S2 (dubbed all-S2) in the open state. Furthermore, the probability of all-S2 in the absence of Ca2+, given by , is comparable to the experimentally determined spontaneous po (2.6 × 10−4) of the MthK channel6 (Supplementary Table 2).
Deducing an energetic model of the MthK channel
If the RCK domain acts as the basic functional unit of the regulatory module, then establishing an energetic model for the whole MthK channel only requires further deducing the energetics of the gate, plus those of additional unobserved configurations and Ca2+-RCK interactions that occur in the regulatory module of a whole channel. Below, we develop a model to quantitatively predict the energetic hallmark of regulation of the MthK channel by Ca2+, in the form of the p0 –[Ca2+] relationship. Detailed statistical mechanics-based derivations are presented in Supplementary Notes 2–4.
In an isolated regulatory module, eight independent RCK domains, each of which can adopt three conformations, giving rise to 38 = 6561 possible permutations. Of those 6561 permutations, if only the all-S2 species underlies the open state of the regulatory module (RMo), then the remaining permutations would represent a closed-state configuration (a), denoted by aRMc (Fig. 4a). As such, individual RCK domains in aRMc would independently adopt any conformations, with or without Ca2+ bound. The concentration of aRMc would be given by:
| (5) |
where [obsS] is already defined in Eq. 2; and m is 8, the number of the RCK domain.
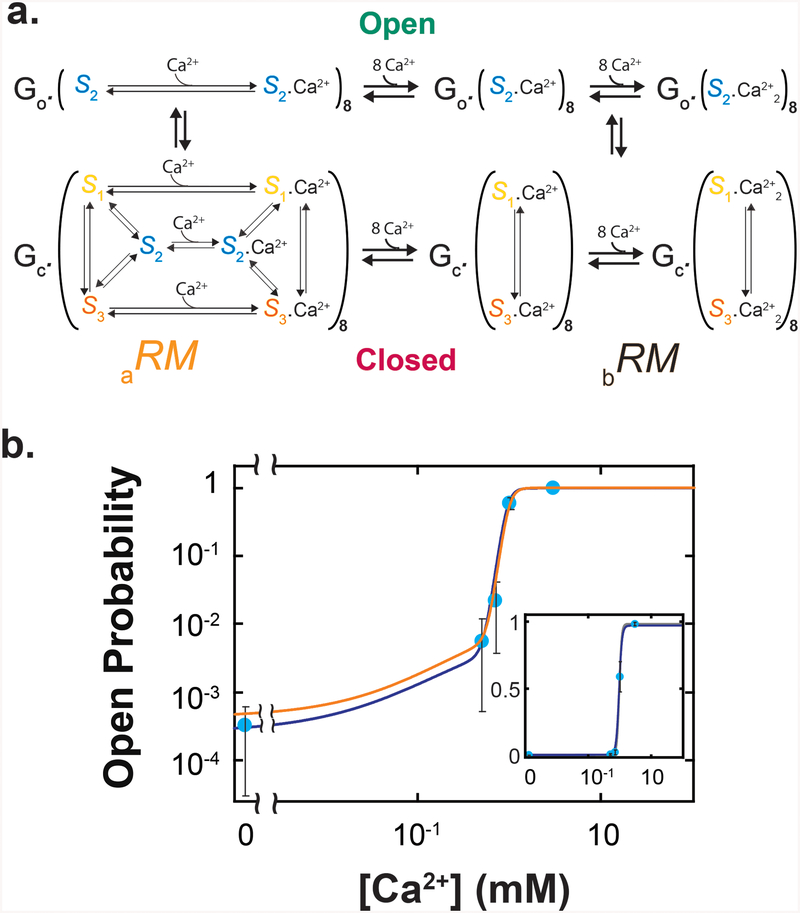
Figure 4.
Model of the regulatory module in two configurations. a. State diagram of aRM where in closed states, eight RCKs can independently adopt any of the three conformations, whereas in open states, all RCKs are in S2, regardless of whether they are bound with Ca2+. All-S2 species with or without Ca2+ bound should be excluded from the closed state of the regulatory module in aRM, but it was not explicitly done for graphic simplicity. b. State diagram of bRM where in closed states, individual RCKs can adopt S1 or S3 but not S2, whereas in the open state, all RCKs are in S2. c. Predicted open probabilities of aRM (orange, left) and bRM (black, right) plotted against the Ca2+ concentration. The vertical dashed lines indicate the EC50 value of the experimental po−[Ca2+] relation of the MthK channel6.
We also considered a previously proposed configuration (b) of the closed state, denoted by bRMc, where RCK domains would adopt only S1 or S313. Thus, in our model, during the transition from aRMc to bRMc, S2 would be excluded from all closed species (Fig 4b). The coexistence of Ca2+-free S1 and S3 has been observed crystallographically2. We further stipulate that bRMc would exist with or without Ca2+ bound7. Without explicitly invoking any additional distinct intermediate species, a transition from aRMo (open state, all RCK domains in S2) to bRMc(closed state, S2 excluded) would be perceived as a cooperative transition, because all eight RCK domains must transition to S1 or S3. As such, we modeled the binding of Ca2+ to individual RCK domains in bRM as being cooperative4 (Fig. 4b). The concentration of bRMc should then be expressed as:
| (6) |
Regarding the open state, we treated the all-S2 species alone as the open state (RMo). The observed concentration of all-S2 in configuration aRM or bRM (with and without Ca2+ bound) would be given by Eq. 7 or Eq. 8.
| (7) |
| (8) |
Given that bRM would have far fewer states than aRM, it should have higher energy. Implicitly, the binding of Ca2+ to at least one additional site (denoted by n2) in individual RCK domains would be required to lower the free energy of bRM. Operationally, Ca2+ binding to the n2 site would regulate the relative distribution between aRM and bRM, whereas Ca2+ binding to the n2 site would regulate the relative distribution among the RCK conformations. However, what is denoted by n1 may not necessarily be the same physical site in aRM and in bRM. Below, we examine first the po predicted on the basis of aRM or bRM alone, and then the energetic characteristics of the n2 site.
Substituting Eqs. 4–8 into the following defining relation:
| (9) |
where [O] and [C] denote the concentrations of the open and closed states, we obtained the expressions for the regulatory module’s po in aRM and bRM:
| (10) |
| (11) |
The po-[Ca2+] curves calculated with Eqs. 10 and 11 (Fig. 4c) exhibited the following features (all parameters in this paragraph are tabulated in Supplementary Table 2). First, the predicted EC50 value of 1.6 mM for aRM is comparable to the 0.97 mM value estimated from the fit of a version of the Hill-equation4 (Eq. 58, Supplementary Note 4) to a previously observed channel's po−[Ca2+] relationship6. Second, as already mentioned above, the predicted minimal apo of aRM is close to the observed channel's minimal po in the absence of Ca2+ (chpo). Third, the predicted maximal of bRM is 0.98, which is the same as the observed channel's maximal of 0.98.6 Finally, the end point of the curve for aRM practically matches the starting point of the curve for bRM. Thus, combining Eqs. 10 and 11, which underlie the two curves in Fig. 4c, would adequately account for the full range of the observed po of the channel .
A channel model that contains configurations a and b is shown in Figure 5a. In configuration a, Ca2+ binding to all sites n1 in a regulatory module leads to , whereas in configuration b, Ca2+ binding to all sites n2 in a regulatory module leads to . In all three RCK conformations, Ca2+ would bind to site n2 with the same unknown KD (dubbed KDn2), but it would bind to site n1 with three different KDi values, all of which were properly scaled and expressed in the form of KD2 in the above equations. Equalizing the average free energy of and that of requires that the overall apparent KD for Ca2+ binding to site n1 (KDn1) be the same as KDn2. Thus, we could deduce the value of KDn2 from that of KDn1 in accordance with the relation (Supplementary Note 4):
| (12) |
which yields 0.38 mM. With an explicit inclusion of the n2 site, the total open species in aRM and bRM (RMo, Eqs. 5 and 6) and the total closed species(RMc, Eqs. 7 and 8) would be defined as:
| (13) |
| (14) |
Substituting Eqs. 13 and 14 (in the form of energetic constants) into Eq. 9 yielded the po−[Ca2+] relation for the whole channel:
| (15) |
where gK is the apparent equilibrium constant of the gate, as defined in Supplementary Note 4; K describes the relative distribution between “[S1] + [S3]” (unbound closed species in configuration b) and [S2](open species); and caK describes the relative distribution between the corresponding Ca2+-bound closed and open species (Eq. 4). In an ideal case where the total amount of energy related to this fully reversible conformation redistribution equals that derived from Ca2+ binding, Km should equal to caK−m. We noted that fitted K (1.576) is slightly smaller than caK−1 (1.686)(Supplementary Table 1). The small “excess” Ca2+-binding energy defined by could, in principle, help to energetically equalize the open and closed states of the channel gate itself. yields a value of 1.3; within experimental errors, a gK of 1.3 (slightly favoring the closed state) would be sufficient to close the small gap between the observed minimal po and that predicted by the model for the regulatory module alone (i.e., Eq. 15 where gK is set to 1).
Figure 5.
Model for the whole MthK channel. a. State diagram of an energetic model for the whole channel. The gate (G) and the regulatory module (RM) both are either in an open state (o) or in a closed (c) state; RM can exist in aRM (left) or bRM (right). All-S2 species with or without Ca2+ bound in aRM should be excluded from the closed state of the regulatory module, but it was not explicitly done for graphic simplicity. b. The calculated (orange) and fitted (blue) po−[Ca2+] curves of the whole channel model (Eq. 15), plotted along the electrophysiological data previously obtained at pH 8.1 (mean ± s.e.m.)6, where both po and the Ca2+ concentration are plotted on logarithmic scales; shown in the inset are the same curves and data where po is plotted on a linear scale. The calculation and fit are performed as described in the text. The spontaneous chpo was estimated from a linear fit of the plot of observed chpo in the absence of Ca2+ versus pH6.
To test the predictability of our model, we calculated a po−[Ca2+] curve with Eq. 15, using the parameters determined from fluorescence polarization measurements (Fig. 3c; Supplementary Table 1; gK = 1.3, KDn2 = 0.38 mM, and n2= 1). The calculated curve matches the po−[Ca2+] relationship previously determined by electrophysiology6, within the experimental errors (Fig. 5b, data points colored light blue and the curve colored orange). It is noteworthy that when explicitly expressed, Eq. 15 would be fully defined by a total of ten parameters: K1,2, K3,2 (expressed together as K), caK1,2 and caK3,2 (expressed as caK), n1 and KD2, all determined from studying RCK; m determined by crystallography; n2, KDn2 and gK can be deduced as described above. This large number of parameters cannot be extracted by fitting the po−[Ca2+] curve with a Hill equation4.
For comparison, we estimated gK and KDn2 by fully constraining them with experimental measurements. First, we used Eq. 59 (Supplementary Note 4) to directly calculate gK from the constant K (Eq. 4; Supplementary Table 1) and minimal chpo of the channel (Supplementary Table 2; reference6), obtaining a slightly larger value of 1.7. We then determined KDn2 through a global fit of Eq. 15 to the experimental po−[Ca2+] relationship of the channel6 (Fig. 5b, blue curve) and the three plots regarding Ca2+-dependence of RCK conformations in the isolated regulatory module (Fig. 3b, black curves; all resulting parameters are tabulated in Supplementary Table 1). The fit yielded a KDn2 value of 0.39 mM, nearly the same as the deduced 0.38 mM. In the fit, gK was set at 1.7, instead of 1.3 and, consequently, the calculated (orange) and fitted (blue) curves diverged slightly and can be recognized. The inferences are that given the rather small gK, the observed channel's operational energy primarily reflects that of the regulatory module, and that the present model (Eq. 15; Fig. 5) quantitatively predicts the experimental MthK's po−[Ca2+] relationship.
Discussion
The regulatory module of the MthK channel harvests the so-called gating energy from the binding of Ca2+ to its eight RCK domains. In the model described here, each RCK in aRM may independently adopt three conformations, with or without Ca2+ bound. Even considering only a single Ca2+ site per RCK, eight independent RCK domains could generate 68 (~1.7 million) possible permutations or 38 (6561) in the absence of Ca2+. If among this large number of permutations, only all-S2 is associated with the open conformation of the channel, the spontaneous po would be primarily determined by entropic energy, given the vastly different numbers of the accessible open versus closed species. The large number of closed species should be depopulated toward the limiting case of effectively one state by Ca2+ binding, and the collective probability of all closed species in saturating Ca2+ concentrations should be much smaller than the probability of the open species, such that the channel’s po would rise from the minimum towards 1. Indeed, electrophysiology studies have shown that Ca2+ regulation of the MthK channel occurs primarily while the gate is closed5, 6.
A proposal that a MthK channel can open from the all-S1 state has been put forward, on the basis of the following observations13. First, an all-S1 form of the isolated regulatory module was captured crystallographically, with Ba2+ present at multiple sites within individual RCK domains. Second, Ba2+ can activate the MthK channel, albeit with lower efficacy and potency than Ca2+. Third, a mutation at a putative Ba2+ binding site eliminates the ability of Ba2+ to activate the channel. Thus far, there is no structural evidence to link all-S1 to the open state of the channel yet. In any case, the probability of all-S1 species predicted from our measurements is low, and thus the po−[Ca2+] curves calculated from two compared models, in which either only all-S2 or all-S2 and all-S1 are open species, are visually indistinguishable, even on double logarithmic plots (Supplementary Fig. 2). Should Ba2+ act differently than Ca2+, such that Ba2+ binding to RCK would populate S1 instead of S2, modeling all-S1 species as an open state could in principle accommodate the observed channel activation by Ba2+. Here we considered only all-S2 as the open species for the following reasons. First, only all-S2 was observed in an open-state structure of the MthK channel. Second, we intended to account for the Ca2+-dependent regulation, for which all-S2 being the open species is sufficient. Third, we do not have the quantitative information regarding Ba2+-bound RCK to express the all-S1 species in the analytic model. In any case, the present model could be expanded to include additional open and closed species to account for other features of the channel.
As mentioned, one defining feature of the MWC model is that a protein may adopt one of two (or more) alternative states (R or T) with or without ligand bound7. A second defining feature is that all protomers in the protein must be in the same state. In our model, ~1.7 million species form a grand canonical ensemble in terms of statistical mechanics, and given its thermodynamic nature, the model does not concern the paths between any pair of states, regardless of whether they exist in the same or between coexisting configurations a and b (here divided merely for a conceptual purpose). In the vast majority of closed states of either configuration, RCK domains in different conformations coexist. Thus, our model does not satisfy that the second defining feature of the MWC model.
As a special case of the MWC model, the Hill equation4 would be defined here by minimal and maximal Po, EC50 and the Hill coefficient (Eq. 58, Supplementary Note 4). In our model, the minimal or maximal Po each is defined by three parameters . The EC50 depends on all independent parameters in a complex manner, and the analytic expression of the Hill coefficient would be even more complex, if it is reachable. Thus, extracting four parameters from the po−[Ca2+] relationship of the MthK channel using the Hill equation could lead to an empirical quantitative description of observed Ca2+-dependent redistribution between the total open species and the total closed species, but would not reveal the energetic mechanism underlying Ca2+-dependent gating conformational changes that occur in the regulatory module.
Thus, examining the behaviors of individual RCK domains is necessary to understand the energetic mechanism of the MthK channel. The channel model deduced here on the basis of energetics of the RCK domain well predicts the observed po−[Ca2+] relationship6, in which the binding of Ca2+ increases the channel's po by two distinct mechanisms. First, independent, non-cooperative binding of Ca2+ to individual RCK domains populates S2 over S1 or S3, enhancing the probability of individual RCKs to adopt S2 and thereby fine tuning po. Second, cooperative Ca2+ binding would populate bRM over aRM, of which the former has fewer closed states. These tuning and configuration-switching mechanisms primarily underlie the shallow and steep phases of the po−[Ca2+] relationship, respectively. The good agreement between our data obtained with the isolated regulatory module and previous electrophysiology data with the whole channel validates our approach. The present energetic study serves as a foundation for a subsequent study14, where we use the present method to examine the multi-state conformational dynamics of RCK, and demonstrate how the resulting dynamic information can be used as a temporal template to link its existing structures.
Online Methods
Sample preparation and data recording
As described in reference12, a recombinant protein of the MthK channel's regulatory module, which contained a N-terminal recognition sequence for biotin ligase, a C-terminal His-tag with a preceding specific-protease-cutting sequence, and the double E146C and L153C mutation in helix αB, was produced using the bacterial BL-21 expression system. The protein was labeled with bifunctional rhodamine (Bis-((N-Iodoacetyl)-Piperazinyl)-Sulfonerhodamine; Invitrogen B10621) via the two mutant cysteine residues and attached to a coverslip conjugated with streptavidin (Arrayit) via biotinylated N-termini. Polarized emissions from individual bi-functional rhodamine labels, excited in the evanescent field created at the surface of the sample coverslip by circularly polarized laser beam (532 nm), were collected via a fluorescence microscope with four polarization emission channels onto an electron-multiplying charge-coupled device camera, while the sample protein was immersed in a solution containing 200 mM KCl, Ca2+ of various concentrations, and 10 mM HEPES titrated to pH 8.0, where 1 mM EGTA was used as a buffer in the nominal Ca2+-free and low (0.1 mM) Ca2+ solutions.
Data analysis
Also as described in reference12, each intensity of the four emission components collected from a given fluorophore was a direct summation of individual pixels. Itot, θ, φ, and Ω were calculated using Eqs. 62, 63, 61, and 70 in the Supplementary Note 3 and 6 in the above reference, respectively. Conformational transitions and states were identified in two separate steps. A changepoint algorithm was applied to the intensity traces to detect the transitions between conformational events, whereas a k-means-cluster-based algorithm was applied to identify the conformational states of individual events based on both θ and φ.
Data availability
Data and materials described here will be made available upon reasonable request.
Supplementary Material
Acknowledgments
We thank Y. Zhou for technical support; Y. Jiang and R. MacKinnon for providing the cDNA of MthK; V. Pau and B. Rothberg for sharing their published data for comparison; and P. De Weer, T. Hoshi, and B. Salzberg for critiques of our manuscript at different stages of its development. This study was supported by the grant GM055560 from the National Institute of General Medical Sciences of the National Institutes of Health to Z.L.
Footnotes
Competing Interests
There are no competing interests.
References
- 1.Jiang Y et al. Crystal structure and mechanism of a calcium-gated potassium channel. Nature 417, 515–522 (2002). [DOI] [PubMed] [Google Scholar]
- 2.Ye S, Li Y, Chen L, & Jiang Y Crystal structures of a ligand-free MthK gating ring: insights into the ligand gating mechanism of K+ channels. Cell 126, 1161–1173 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Pau VP et al. Structure and function of multiple Ca2+-binding sites in a K+ channel regulator of K+ conductance (RCK) domain. Proc. Natl. Acad. Sci. U. S. A 108, 17684–17689 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hill AV The possible effects of the aggregation of the molcules of hemoglobin on its dissociation cruves. The Journal of Physiology XL, iv–vii (1910). [Google Scholar]
- 5.Zadek B & Nimigean CM Calcium-dependent gating of MthK, a prokaryotic potassium channel. J. Gen. Physiol 127, 673–685 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pau VP, Barca-Heidemann K, & Rothberg BS Allosteric mechanism of Ca2+ activation and H+-inhibited gating of the MthK K+ channel. J. Gen. Physiol 135, 509–526 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Monod J, Wyman J, & Changeux JP On the nature of allosteric transitions: a plausible model. J. Mol. Biol 12, 88–118 (1965). [DOI] [PubMed] [Google Scholar]
- 8.Marks TN & Jones SW Calcium currents in the A7r5 smooth muscle-derived cell line. An allosteric model for calcium channel activation and dihydropyridine agonist action. J. Gen. Physiol 99, 367–390 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zagotta WN, Hoshi T, & Aldrich RW Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J Gen. Physiol 103, 321–362 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sakmann B & Neher E Single-Channel Recording (Plenum Press,1995). [Google Scholar]
- 11.Miller C Ion channel reconstitution (Plenum, New York, 1986). [Google Scholar]
- 12.Lewis JH & Lu Z Resolving angstrom-scale protein-conformational changes by analyzing fluorescence anisotropy. Nat. Struct. Mol. Biol 26, 802–807 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Smith FJ, Pau VP, Cingolani G, & Rothberg BS Crystal structure of a Ba2+-bound gating ring reveals elementary steps in RCK domain activation. Structure 20, 2038–2047 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lewis JH & Lu Z Integrating spatiotemporal features of a ligand-regulated, multi-state allosteric protein. Nat. Struct. Mol. Biol 26, 816–822 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and materials described here will be made available upon reasonable request.