Evaluation of Statistical Techniques to Normalize Mass Spectrometry-Based Urinary Metabolomics Data

Abstract

Human urine recently became a popular medium for metabolomics biomarker discovery because its collection is non-invasive. Sometimes renal dilution of urine can be problematic in this type of urinary biomarker analysis. Currently, various normalization techniques such as creatinine ratio, osmolality, specific gravity, dry mass, urine volume, and area under the curve are used to account for the renal dilution. However, these normalization techniques have their own drawbacks. In this project, mass spectrometry-based urinary metabolomic data obtained from prostate cancer (n=56), bladder cancer (n=57) and control (n=69) groups were analyzed using statistical normalization techniques. The normalization techniques investigated in this study are Creatinine Ratio, Log Value, Linear Baseline, Cyclic Loess, Quantile, Probabilistic Quotient, Auto Scaling, Pareto Scaling, and Variance Stabilizing Normalization. The appropriate summary statistics for comparison of normalization techniques were created using variances, coefficients of variation, and boxplots. For each normalization technique, a principal component analysis was performed to identify clusters based on cancer type. In addition, hypothesis tests were conducted to determine if the normalized biomarkers could be used to differentiate between the cancer types. The results indicate that the determination of statistical significance can be dependent upon which normalization method is utilized. Therefore, careful consideration should go into choosing an appropriate normalization technique as no method had universally superior performance.

1. Introduction

Urinary metabolomics is a valuable source in the early disease diagnosis process. It was reported in many studies that certain metabolites are differentially expressed in the presence of diseases like cancer [1-3]. Therefore it is a valuable source in the early disease diagnosis process. Normally, patients are hesitant to damage their organs and tissues to give samples during the disease diagnosis process. Human urine recently became a popular medium for metabolomics biomarker discovery because its collection is non-invasive. Usually, these metabolomic markers are not specific for a particular disease and there are variations in experimental designs and individual’s physiology. Therefore, a thorough statistical interpretation is necessary to evaluate their significance as disease markers [1, 3].

Depending on the amount of water a particular patient drinks, sometimes renal dilution of urine can be problematic in this type of urinary biomarker analysis [1, 3]. Currently, various normalization techniques such as creatinine ratio, osmolality, specific gravity, dry mass, urine volume, and area under the curve are used to account for the renal dilution [4]. However, these normalization techniques have their drawbacks. For example, most widely used conventional creatinine-based corrections are affected by a multitude of patient factors such as age, race, physical activity, muscle mass, gender and normal physiological functions such as menstrual cycle. The specific gravity normalization is strongly influenced by both the number of particles in the solution and their size. Normalization of urinary metabolites using specific gravity is problematic when large molecules are present in urine [5].

Due to variation in experimental designs and individual physiology, metabolomic data often need to undergo extensive preprocessing techniques before any conclusions can be made. A variety of methods have been proposed to normalize urinary metabolites before data analysis, but the statistical properties of these methods are largely unexplored [5]. Therefore, an urgent need exists in urinary metabolomics filed for reliable normalization techniques to account for the renal dilution and other variations [1].

In recent years, there has been an increasing amount of attention given to the evaluation of normalization methods. Much work has focused on the development and comparison of different data-driven normalization techniques that utilize advanced statistical methods [2, 6-9]. Others have explored strategies relying primarily on biological values such as creatinine and osmolality for normalization [5, 10-13]. In addition, there is a large variety in the types of analyses presented in normalization evaluations. For example, the metabolomics study might be targeted or untargeted, might explore a small or larger number of metabolites, and might present an inconsistent variety of statistical results [10]. These factors make it difficult to complete a truly comprehensive evaluation of the currently available normalization techniques. To date, there is a deficiency in the amount of research that simultaneously examines both biological and data-driven normalization methods with a comprehensive set of statistical procedures. The work of Kohl et al. [14] is a notable exception to this as they compare creatinine normalized values with ten more advanced statistical normalization procedures. However, their data sets were generated using nuclear magnetic resonance (NMR) spectroscopy. In this study, a liquid chromatography tandem mass spectrometry (LC/MS/MS) urinary metabolomic data obtained from prostate cancer, bladder cancer, and control groups were analyzed using eight different normalization techniques. The normalization methods chosen include both biological and data-driven techniques, and the statistical results presented cover the initial stages of data analysis with summary statistics through hypothesis testing, principal component analysis, and classification.

2. Materials and Methods

2.1. Metabolomics Data Set

In our previous study, the levels of Proline (Pro), Kynurenine (Kyn), Uracil (Ura), Creatinine (Cre) and Glycerol-3-phosphate (G3P) in 113 patients with genitourinary malignancies were analyzed using a validated LC/MS/MS method and compared with no evidence of malignancy urine samples [3]. The original experimental procedures and sample collections were approved by the Missouri University of Science and Technology, Institutional Review Board (IRB). The validated LC/MS/MS method parameters are listed in Table 1. The data set selected for this project from the above LC/MS/MS study were composed of Prostate cancer (PCa) (n=56) and Bladder cancer (BCa) (n=57) that were obtained from the Central Missouri Urology Clinic (Rolla, MO, USA) [3]. The no evidence of malignancy (NEM) urine samples (n=68) were collected from healthy volunteers from Rolla, MO, USA [3]. The demographic distribution of cancer patients and normal subjects were mainly from nearby cities. The age distribution of cancer patients was from 53-94 y, and the range for normal subjects was 18-87 y. More information about the samples, sample preparations and the LC/MS/MS method conditions can be found in Gamagedara et al. [3].

Table 1.

LC/MS/MS method information for four metabolites, creatinine, and glutamine (IS)

	Glycerol-3- phosphate	Proline	Kynurenine	Uracil	Creatinine	Glutamine (IS)
Q1	173.0	116.0	209.1	112.9	114.0	148.0
Q2	99.0	70.1	192.1	70	44.1	130.0
Confirmation Ion Pairs	173/155.1	116/88.1	209.1/94.1	112.9/78	114/86	148/121.1
LOD (nM)	2	2	0.05	0.4	3	0.4
R2	0.995	0.999	0.999	0.999	0.995	N/A
Retention Time (min)	5.3	3.2	9.6	5.1	2.3	2.1

2.2. Normalization Techniques

A total of eight different normalization techniques were employed in the analysis. Seven of the methods are statistical in nature, while the eighth is biological. The seven data-driven techniques represent a combination of methods that are designed to remove extraneous sample-to-sample variation and those aiming to reduce the variation within each metabolite. Specifically, the statistical techniques used were: Auto Scaling, Cyclic Loess (Loess), Linear Baseline Scaling, Pareto Scaling, Probabilistic Quotient Normalization (PQN), Quantile Normalization, and Variance Stabilization Normalization (VSN). Auto Scaling and Pareto Scaling are nearly identical in their implementation. Auto Scaling uses the standard deviation as a scaling factor while Pareto Scaling uses the square root of the standard deviation [15, 16]. Cyclic Loess has roots in MA plots from genomic data, which are modified Bland-Altman plots displaying the intensity log-ratio (M) and the mean log intensity (A), and performs normalization by iteratively fitting non-linear local regression models to adjust the intensities [17]. Linear Baseline Scaling assumes linearity between metabolites and uses a scaling factor that is calculated from the median intensity [18]. PQN is like Linear Baseline Scaling in that it uses a baseline value, often derived from median intensities, in order to construct a reference metabolite that is then used for scaling [19]. Quantile Normalization seeks to transform the data in such a way that the distributions of intensities for each metabolite are the same. This is achieved by equating quantile values [18]. VSN uses non-linear transformations to produce a constant variance in the data [20]. Finally, Creatinine Normalization, the biological technique, was calculated by taking the ratio of the concentration of each metabolite to the observed level of creatinine [1, 3, 21, 22]. More comprehensive details on the aforementioned normalization techniques, along with descriptions of several others, can be found in Ejigu et al. [6], Kohl et al. [14], Li et al. [8], Li et al. [9], and Wu and Li [4].

Another consideration for normalization and data preprocessing is the use of logarithms. Some authors and online normalization software creators consider a logarithm transformation to be an independent normalization technique [9, 23]. This approach, however, is not universal. Ejigu et al. [6] for example, carry out additional normalization methods after transforming the data by taking logarithms. The log-transformed data is therefore treated as the baseline. Here, we follow Ejigu et al. [6] by first taking a base 2 logarithm of the concentrations and then proceed with the seven data-driven normalization methods. Creatinine normalization is the exception to this as the logarithm transformation is calculated after taking the metabolite/creatinine ratios.

Each of the normalization techniques is implemented in the statistical computing language R [24], and all of the subsequent data analysis steps are performed using the R software version 3.5.2. Several R packages are available to aid in the analysis of metabolomic data including MetaboDiff [25] and MetNorm [26]. In addition, a number of online applications with web-based interfaces have been created for the same purpose. Examples of these include [23] and NOREVA [9]. Here, R code taken from Ejigu et al. [6] and Kohl et al. [14] was used to create the normalized data.

2.3. Evaluation Metrics

Several quantitative and visual approaches were utilized in order to evaluate the resulting normalized values. First, box plots of the normalized concentrations were created for each metabolite. These plots can be used as a rough, initial comparison of the distributions of the normalized concentrations, and enables the visualization of the amount of variation that remains within each metabolite for each of the different normalization techniques. The box plots display the first, second, and third quartiles of the normalized values shows outliers and gives a rough estimate of the spread of the data. These values are all commonly included as summary statistics in an initial exploratory data analysis. Next, the amount of variation for each metabolite is also quantified by calculating the coefficient of variation and median absolute deviation for each normalization method. The coefficient of variation (CV) is defined as the ratio of the standard deviation and the mean of the concentrations. If x_ij is the concentration of the ith metabolite from the jth observation, ${\overline{x}}_i$ is the mean concentration of the ith metabolite, and s_i is the standard deviation of the ith metabolite concentrations, then CV is defined as

$$CV=\frac{S_i}{{\overline{x}}_i}$$

The median absolute deviation (MAD) is calculated by finding the median of the absolute values of the differences of each concentration with the median concentration. MAD is defined as

$$MAD=\mathit{median}(\mid x_{ij}-{\tilde{x}}_i\mid )$$

where ${\overline{x}}_i$ is the median concentration of the ith metabolite. Calculating CV and MAD enables a more specific quantitative comparison of the variation in the normalized data that is not possible by examination of box plots alone.

One of the main goals of this type of metabolic analysis is to determine whether the metabolites under investigation show a statistically significant difference between some biological outcomes. Another goal is to assess whether these metabolites can then have practically significant use in diagnosing or differentiating between the biological outcomes. Therefore, in addition to the basic visualization and summary statistic calculations described above, the results of a number of additional statistical procedures were also calculated and compared for each normalization technique. First, the results of hypothesis tests examining a difference in mean metabolite concentration levels between each cancer group and NEM are compared. Then, a principal component analysis is conducted in order to determine if the metabolites can be used to identify clusters of individuals with cancer and those with NEM. Finally, the results of a random forest classification model are used to see whether any of the normalization techniques can be used to accurately classify an individual into one of the cancer groups or NEM using the normalized metabolite concentrations.

3. Results and Discussion

3.1. Visualization and Variation

As outlined in Section 2.3, the first stage of the analysis consists of creating box plots of the resulting normalized intensities for each metabolite. The four corresponding box plots are in Figure 1. The results are somewhat similar across each of the four metabolites. There appear to be two separate groups in terms of location of the median concentration. Auto Scaling, Pareto Scaling, and VSN produced normalized concentrations with medians close to zero. Many of the normalized concentrations for these techniques are also negative. All of the other normalization methods produced results with medians that were significantly larger than those in this first group of techniques. There is some fluctuation in the resulting variation of the concentrations. Creatinine and VSN produced values with the largest interquartile ranges for each metabolite. PQN, Linear Baseline, and the standard logarithm transformed data produced normalized concentrations with interquartile ranges that overall tended to be the narrowest. There was some change in the resulting variability among the four metabolites as each normalization technique produced values with relatively larger variances for Ura.

Figure 1.

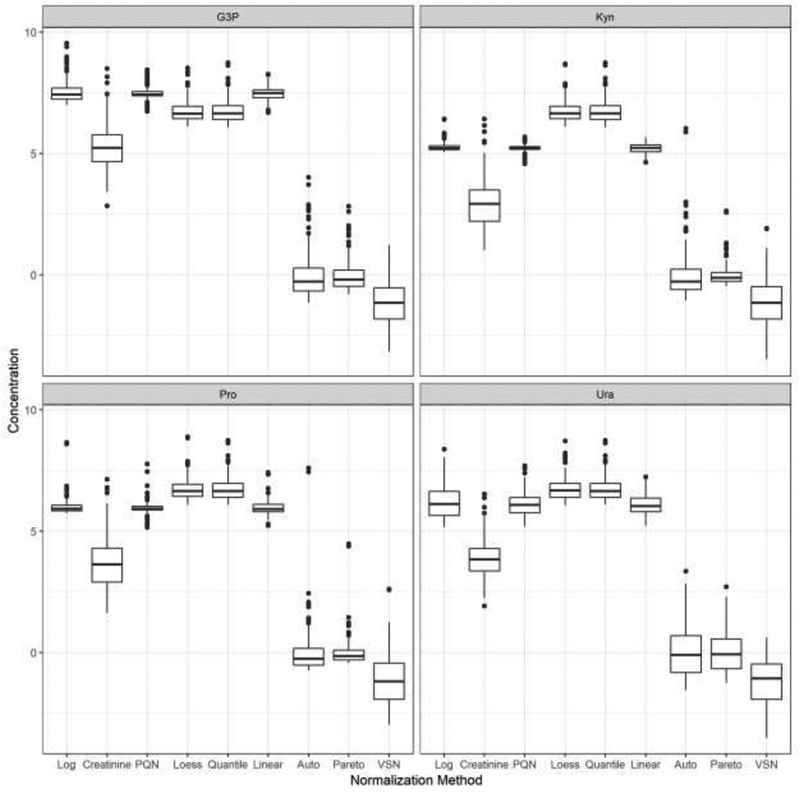
Box plots showing distributions of normalized concentrations for each metabolite. The vertical axis represents values of the normalized metabolite concentrations and the horizontal axis displays the different normalization techniques. The panels summarize G3P in the upper left, Kyn in the upper right, Pro in the bottom left, and Ura in the bottom right. The box plots display the three quartiles and any potential outliers.

The results for the coefficients of variation and the median absolute deviations are in Table 2 and Table 3, respectively. It is important to note that the coefficients of variation for Auto Scaling and Pareto Scaling are omitted from the results. Auto Scaling produces a data set where the standard deviation of the concentrations of each metabolite is equal to one. This will cause the value of the coefficient of variation to become significantly inflated if the mean concentration is close to zero, which is the case here. Pareto Scaling suffers from a similar issue. Therefore, it is not useful to compare values for these two methods.

Table 2.

Coefficients of variation for normalized concentrations of each metabolite.

	G3P	Pro	Kyn	Ura
Log	0.07	0.06	0.04	0.11
Creatinine	0.17	0.29	0.35	0.20
PQN	0.04	0.05	0.03	0.08
Loess	0.07	0.07	0.07	0.07
Quantile	0.07	0.07	0.07	0.07
Linear Baseline	0.04	0.05	0.04	0.07
VSN	−0.86	−0.93	−0.91	−0.76

Table 3.

Median absolute deviations for normalized concentrations of each metabolite.

	G3P	Pro	Kyn	Ura
Log	0.24	0.10	0.08	0.49
Creatinine	0.56	0.70	0.64	0.47
PQN	0.09	0.09	0.06	0.32
Loess	0.26	0.25	0.26	0.29
Quantile	0.29	0.29	0.29	0.29
Linear Baseline	0.17	0.16	0.12	0.28
Auto Scaling	0.49	0.30	0.41	0.75
Pareto Scaling	0.34	0.17	0.18	0.61
VSN	0.65	0.75	0.67	0.69

In accordance with Ejigu et al. [6] we will consider normalization methods that produce smaller values of CV and MAD to be better performing. Based on these criteria, PQN and Linear Baseline performed the best for CV, with Loess, Quantile, and the rudimentary logarithm transformation close behind. VSN had the largest CV and thus performed the worst. For MAD, the results were quite similar with PQN and Linear Baseline performing the best while VSN had the poorest performance.

3.2. Hypothesis Testing

For each of the four metabolites and both cancer types, Welch's t test for two independent samples was conducted to compare the mean metabolite concentrations for cancer versus NEM. This procedure was repeated for each of the 8 normalization methods as well as the baseline log-transformed data. The resulting p-values can be found in Table 4 and Table 5. Since the primary focus of this analysis is to compare the different normalization procedures, and not to identify significant metabolites, the p-values have not been corrected for multiple comparisons.

Table 4.

Prostate cancer vs. NEM p-values for testing a difference in mean concentrations.

	G3P	Pro	Kyn	Ura
Log	0.99	0.43	0.19	0.67
Creatinine	0.52	0.42	0.78	0.71
PQN	0.27	0.09	0.74	0.98
Loess	0.89	0.81	0.44	0.66
Quantile	0.92	0.98	0.15	0.56
Linear Baseline	0.60	0.24	0.44	0.73
Auto Scaling	0.99	0.43	0.19	0.67
Pareto Scaling	0.99	0.43	0.19	0.67
VSN	0.62	0.83	0.08	0.79

Table 5.

Bladder cancer vs. NEM p-values for testing a difference in mean concentrations.

	G3P	Pro	Kyn	Ura
Log	0.03	0.25	0.40	< 0.01
Creatinine	0.55	0.31	0.18	0.83
PQN	0.10	0.99	0.15	< 0.01
Loess	0.02	0.13	0.07	< 0.01
Quantile	0.05	0.43	0.47	< 0.01
Linear Baseline	0.83	0.27	0.01	0.01
Auto Scaling	0.03	0.25	0.40	< 0.01
Pareto Scaling	0.03	0.25	0.40	< 0.01
VSN	0.13	0.49	0.67	0.01

It is clear from the tables that the results of the hypothesis tests vary significantly. There are large differences in the results across the normalization methods, the metabolites, and the cancer types. For prostate cancer, none of the normalization methods would result in a conclusion of a significant difference between cancer versus NEM for any of the metabolites at a 5% significance level. Looking closer at each of the metabolites individually for prostate cancer, G3P had a very large range of p-values. PQN produced the smallest p-value while Auto Scaling, Pareto Scaling, and the log transformed data had the largest p-values. For Pro, PQN again produced the smallest p-value at 0.09, which would be marginally significant at the 5% level of significance. The largest p-value for Pro came from Quantile normalization at 0.98. The results for Kyn essentially flipped for these two methods - Quantile had the second lowest p-value and PQN had one of the largest. One normalization method, VSN, produced a p-value that would be marginally significant for the Kyn metabolite. Results for Ura displayed no significance across all of the normalization methods, but this metabolite did have a smaller range of p-values.

The hypothesis tests for bladder cancer produced a number of conflicting results. The range of p-values for G3P again was quite large extending from 0.03 to 0.83, but here there were several normalization methods that produced significant p-values. There is an approximately even split between methods with showing statistically significant results and those with insignificant results. The results for Ura are also quite interesting. All of the data-driven normalization techniques, along with the logarithm baseline, showed statistically significant results with all of the p-values being at or below 0.01. Creatinine, on the other hand, had a p-value of 0.83.

3.3. Principal Component Analysis

The first step in evaluating the principal component analysis results involved calculating and comparing the percentage of variance that is explained by the first two principal components for each normalization method. It is desirable to have the principal components capture as much of the variation in the original normalized values as possible. Consequently, larger values are preferred for the percentage of variance explained with the caveat that the percentage of variance explained is not guaranteed to be strongly associated with the disease outcome. The first two principal components were chosen because the original analysis showed that the first two principal components accounted for over 96% of the variance in the metabolite concentrations [3]. As can be seen in Table 6, these results are fairly similar for the majority of the normalization data sets with all methods except Auto Scaling explaining at least 80% of the variance in the concentrations. Creatinine normalization performed the best accounting for 96% of the variance and was the only method to explain over 90% of the variance. The range of values for the percentages of variation explained spanned nearly 20%, which is quite larger. Clearly the quality of the resulting principal components, in terms of accounting for the variation in the original data, is highly dependent on the normalization technique.

Table 6.

Percentage of variance explained by the first two principal components for each normalization technique.

	Explained
Log	0.87
Creatinine	0.96
PQN	0.82
Loess	0.88
Quantile	0.82
Linear Baseline	0.85
Auto Scaling	0.78
Pareto Scaling	0.82
VSN	0.83

In addition to examining the percentage of variance explained, it is also useful to plot the principal component scores in order to check for clustering. Figure 2 shows the PCA plots for each of the normalization procedures. None of the plots exhibit any clustering for the three groups, but there are still interesting differences in the results among the normalization methods. Notably, Auto Scaling, Pareto Scaling, VSN, and Creatinine normalization all generated plots with principal component scores that were much more spread out that the other methods. In contrast, Linear Baseline, Loess, PQN, Quantile, and the Log baseline all resulted in plots that are clumped closely together. This difference could influence the ability to detect clustering, if any had been present, with the different normalization techniques.

Figure 2.

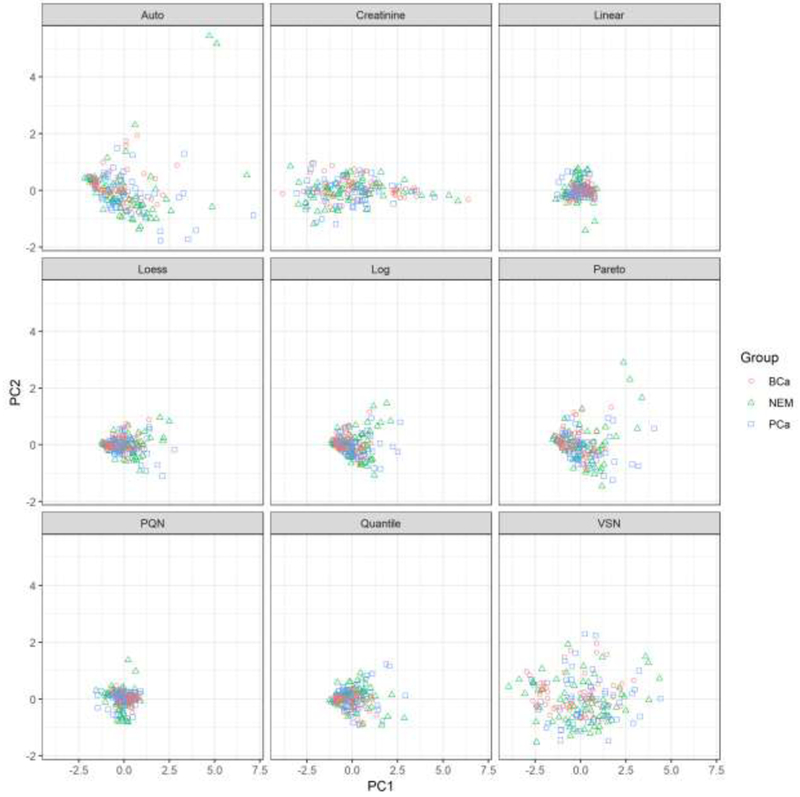
Plot of the first two principal component scores for each normalized data set. The horizontal axis represents scores for the first principal component and the vertical axis has the corresponding scores for the second principal component. Each pane displays the principal component scores for a different normalization method. Patients with bladder cancer are represented by red circles, patients with prostate cancer are represented with blue squares, and patients showing no evidence of malignancy are shown with green triangles.

3.4. Classification

Two random forest classification models were created in order to classify prostate cancer vs. NEM and bladder cancer vs. NEM. A random forest is a collection of decision trees constructed by bootstrap aggregation [27]. Each individual tree is grown using a bootstrap sample of the original data. Observations that are not included in the bootstrap sample are referred to as out-of-bag (OOB). The prediction accuracy of a random forest classifier can be measured by predicting values for the OOB data and then comparing these predictions with the true values. A better performing model will minimize the error rate for prediction the OOB data. Table 7 shows the OOB error rates for predicting the two cancer types.

Table 7.

OOB error rates for random forest classification.

	Prostate	Bladder
Log	0.51	0.45
Creatinine	0.55	0.42
PQN	0.55	0.47
Loess	0.49	0.41
Quantile	0.45	0.42
Linear Baseline	0.44	0.47
Auto Scaling	0.50	0.40
Pareto Scaling	0.50	0.44
VSN	0.49	0.37

The error rates are far from promising for both cancer types with values sometimes surpassing 50%. Predictions for bladder cancer tend to be marginally better than those for prostate cancer. Moreover, each of the normalization methods generally performed poorly. Nevertheless, there were still noticeable differences in performance between the normalization techniques. Linear Baseline had the lowest error rate for prediction of prostate cancer while VSN most accurately predicted bladder cancer. The difference between the best and worst performers for predicting both cancer types was at least 10%. Such a large discrepancy in error rates implies that the choice of the normalization method would greatly influence any conclusions drawn about the predictive accuracy of using normalized metabolite concentrations to classify cancer type.

In addition to examining the prediction error rate, receiver operating characteristic (ROC) curves were created for each classification procedure. These plots enable one to examine additional classification metrics such as sensitivity (true positive rate) and specificity (true negative rate). Figure 3 shows the ROC curve for predicting prostate cancer and Figure 4 displays the results for bladder cancer.

Figure 3.

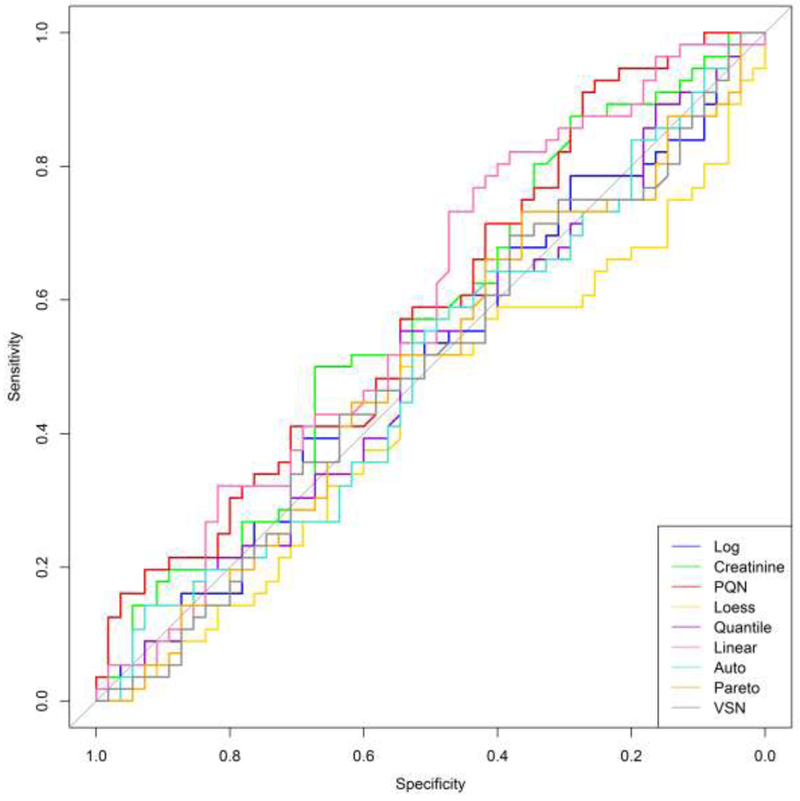
Prostate cancer ROC curves for each normalized data set. The horizontal axis displays the specificity (true negative rate) while the vertical axis represents the sensitivity (true positive rate). ROC curves for each normalization technique are shown with different colors.

Figure 4.

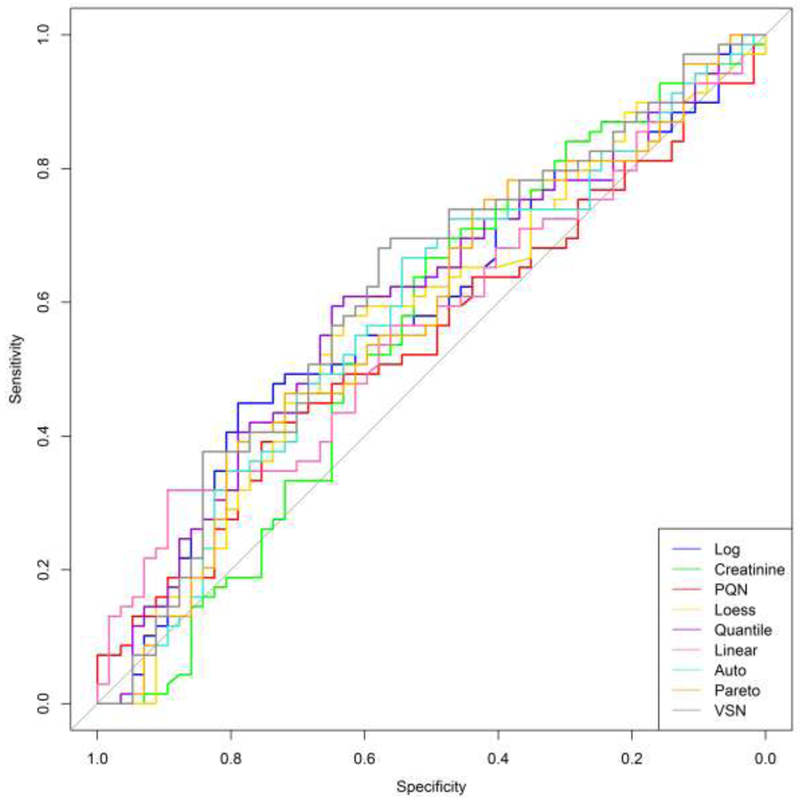
Bladder cancer ROC curves for each normalized data set. The horizontal axis displays the specificity (true negative rate) while the vertical axis represents the sensitivity (true positive rate). ROC curves for each normalization technique are shown with different colors.

Ideally, the ROC curves would hug the upper-left corner. This signifies an accurate classifier and produces a larger area under the curve (AUC). A weak classifier will result in a ROC curve that closely follows the diagonal of the plot and will have a smaller AUC. For both cancer types, the ROC curves tend to be very close to the diagonal through the middle of the plot. This is true for all of the normalization techniques and signals unsatisfactory classification results. The ROC curves for bladder cancer are marginally improved over the prostate cancer results, but each normalization technique still had difficulty in accurately predicting bladder cancer. The ROC curves show significant variability in the performance of the different normalization techniques. This, again, indicates that the specific interpretations of these results are dependent on which method was used to normalize the data.

4. Conclusions

This project investigated a number of competing normalization techniques applied to urinary metabolomic data analyzed via LC/MS/MS. A wide range of statistical procedures were conducted in order to evaluate any potential differences in the results obtained using the different normalization methods. Here, it was clear that the conclusions drawn from the statistical analyses can vary significantly based on the chosen normalization technique. In particular, box plots, measures of variation, and hypothesis test results showed considerable variation between the different normalized data sets. Especially concerning is the wide range of p-values produced for testing differences in mean metabolite concentrations between cancer groups and NEM. Moreover, results can be inconsistent within a particular normalization method as there were instances where techniques, relative to the other methods, had lower p-values for one metabolite but larger p-values for another metabolite. These results indicate that the determination of statistical significance can be dependent upon which normalization method is utilized.

Ideally, it is desirable to develop a specific recommendation for researchers to use when making data preprocessing and normalization decisions during the analysis of urinary metabolic data using LC/MS/MS. However, the results of this project indicate that such a goal is difficult to achieve as no normalization technique under study demonstrated universally superior performance, and there was no clear winner between the biological normalization technique and the data-driven techniques. In addition, the discrepancy in hypothesis testing results is particularly concerning as it is conceivable to abuse the choice of normalization technique for data dredging and p-hacking. Therefore, careful consideration should be given to the planning of the entire statistical analysis prior to the examination of the data, and the choice of the normalization method should correspond to the specific challenges of the data.

Many questions still remain regarding the development of best practices for the normalization of urinary metabolomic data. The majority of studies evaluating normalization techniques rely on analyzing existing data where the true metabolite concentrations are unknown. Designing an experiment specifically to evaluate current normalization methods where the true concentrations are known could be one potentially beneficial avenue for future research. In addition, several of the advanced normalization techniques, such as Cyclic Loess, rely on tuning parameters, and in-depth statistical evaluations on the influence of these parameters are currently lacking.

Highlights.

• This study compares the biological and statistical normalization methods for urinary metabolomics data.

• The choice of normalization technique significantly influenced conclusions during each stage of data analysis.

• No normalization method showed universally superior performance.

• Data processing should be carefully planned prior to analysis to ensure valid results.