Generalization of the time-to-event continual reassessment method to bivariate outcomes

Abstract

This article considers the problem of designing Phase I-II clinical trials with delayed toxicity and efficacy outcomes. The proposed design is motivated by a Phase I-II study evaluating all-trans retinoic acid (ATRA) in combination with a fixed dose of daratumumab in the treatment of relapsed or refractory multiple myeloma. The primary objective of the study is to identify a dose that maximizes efficacy and has an acceptable level of toxicity. The toxicity endpoint is observed in one cycle of therapy (i.e., 4 weeks) while the efficacy endpoint is assessed after 8 weeks of treatment. The difference in endpoint observation windows causes logistical challenges in conducting the trial, since it is not practical to wait until both outcomes for each patient have been fully observed before sequentially assigning the dose of a newly eligible patient. In order to avoid delays in treatment for newly enrolled patients and to accelerate trial progress, we generalize the time-to-event continual reassessment method (TITE-CRM) to bivariate outcomes. Simulation studies are conducted to evaluate the proposed method, and we found that the proposed design is able to accurately select doses that maximize efficacy and have acceptable toxicity, while using all available information in allocating patients at the time of dose assignment. We compare the proposed methodology to two existing methods in the area.

1. Introduction

Historically, the primary objective of Phase I clinical trials is to identify the maximum tolerated dose (MTD) of the agent or agents being investigated. In the subsequent Phase II trial, the agent is often evaluated for efficacy, at the recommended dose (MTD). In oncology trials of cytotoxic agents, identification of the MTD is usually determined by considering dose-limiting toxicity (DLT) information only, with the assumption that the MTD is the highest dose that satisfies some safety requirement, so that it provides the most promising outlook for efficacy. In general, the design of Phase I trials is driven by the assumption of monotone increasing dose-toxicity and dose-efficacy relationships. In the current landscape of oncology drug development, the classic assumptions imposed by cytotoxic agents may no longer be applicable, requiring new strategies for dose selection and trial design.

By contrast, many biological agents are assumed safe overall and higher doses do not necessarily produce greater efficacious response. However, we must still monitor for the unexpected and account for safety. Conditional on safety, other outcomes may serve as the primary endpoint in determining which dose to carry forward. Examples include an early measure of efficacy (i.e. clinical response), pharmacokinetic/pharmacodynamics, and biological targets (i.e. immune response). Dose-efficacy relationships for these agents may exhibit non-monotone increasing patterns, such as increasing at low doses and plateauing at higher levels, or peaking at an intermediate dose. For example, molecules with anti-angiogenic activity often appear to exhibit hormesis, i.e., bell-shaped dose-response curves (Reynolds 2010). A review of 24 Phase I targeted therapy trials show that patients receiving lower doses do not necessarily fare worse (Jain et al. 2010). A lower dose than the MTD may exhibit as much activity as higher doses, and beyond this dose we are merely adding toxicity. If the dose-efficacy relationship is monotone increasing, the MTD is the most efficacious dose with an acceptable risk of toxicity. In this case, we would want a dose-finding method to be able identify the MTD. However, if the dose-efficacy relationship plateaus or peaks at a dose lower than the MTD, we would want to recommend a lower dose and the goal of the trial shifts to identifying a dose with acceptable toxicity that maximizes efficacious response. In recent years, there have been several new methods proposed for locating such a dose in Phase I-II trials of biological agents, including Zhang et al. (2006), Braun (2002), Thall & Cook (2004), Wages & Tait (2015), among many others. A comprehensive overview of Bayesian designs for Phase I-II clinical trials is provided by Yuan et al. (2016).

Most existing Phase I-II methods, in their current form, are most appropriate when both binary toxicity and binary efficacy endpoints can be observed in a reasonably similar and short time-frame. Yuan & Yin (2009) and Yin et al. (2013) note that in some practical situations, this may not be possible due to the fact that efficacy may occur much later than toxicity. If this delay is expected, then most Phase I-II methods are not optimal because the trial would have to either pause before each patient is enrolled in order to fully observe the efficacy responses or to assign doses base on less efficacy data than toxicity data. If the delay is particularly long, then it will cause the duration of the trial to be much too long and wastes resources (Yuan & Yin 2009). The are several existing phase I-II methods that are able to handle delayed outcomes, including Yuan & Yin (2009), Jin et al. (2014), Liu & Johnson (2016), and Riviere et al. (2018). While there are similarities between the methodology we propose and that described in Riviere et al. (2018), the main differences are that their methods rely upon a set of multi-parameter logistic models and that their methods only model efficacy as a time-to-event outcome. Our method models both toxicity and efficacy as time-to-event outcomes, governed by a class of single parameter continual reassessment method (CRM; O’Quigley et al. (1990)) models. In our simulation studies in Section 3, we provide a comparison to two methods described in Riviere et al. (2018).

1.1. Motivating application

This work is motivated by a Phase I-II clinical trial studying the dosing of all-trans retinoic acid (ATRA) (Schenk et al. 2014) in combination with a fixed dose of daratumumab (Lonial et al. 2015) in the treatment of relapsed or refractory multiple myeloma. The trial was designed to find a dose that is safe and that maximizes efficacy, from among three dose levels of ATRA {15, 30, 45 mg/m²} and a fixed dose of daratumumab {16 mg/kg}. The decision endpoints are dose-limiting toxicities (DLTs), based on protocol-specific adverse event definitions, in one cycle (i.e., 28 days) of therapy, and early measures of efficacy, defined by best overall response (CR or PR) at 8 weeks of treatment. To address the problem of delayed efficacy presented by this example, we propose a time-to-event (TITE) extension to the method of Wages & Tait (2015), which assumed completely observed bivariate binary outcomes that were obtainable in a reasonably similar time frame.

1.2. Study objective

In general, consider a trial aimed at selecting a safe dose that maximizes efficacy, denoted ν, from a set of I pre-defined dose levels $\mathcal{D}=\{d_1\mathrm{,}{d}_2\mathrm{,}\dots \mathrm{,}{d}_I\}$. Using the terminology of Riviere et al. (2018), we term ν a correct dose. Denote the probability of DLT at each dose level by π_T(d_i), and the efficacy probability at each dose level by π_E(d_i). Based on a pre-specified maximum DLT rate ξ, we want to exclude overly toxic doses, defining a set of acceptable (safe) doses as $\mathbb{A}=\{d_i:{\pi }_T(d_i)<\xi \}$. The primary objective of the study is to identify a dose ν such that:

$$\nu =\text{arg\hspace{0.05em}}\underset{d_i\in \mathbb{A}}{\text{max}}({\pi }_E(d_i))\mathrm{.}$$ (1)

The primary objective at the conclusion of the study is to locate ν. The goal within the trial is to allocate as many patients as possible at and around ν, while some patients are still under observation for toxicity and efficacy responses.

2. Proposed methods

We lean upon the strategy of the TITE-CRM (Cheung & Chappell 2000) to propose a time-to-event extension to the Wages & Tait (2015) method. At the time a dosing decision is to be made, we utilize data from patients who have only been observed for a portion of the observation window associated with either endpoint, in addition to those who have been completely followed for the entire toxicity and efficacy evaluation period.

2.1. Models and inference for toxicity

Toxicity is modeled using TITE-CRM, introduced by Cheung & Chappell (2000), as a way to utilize information from partially observed subjects throughout the trial. In the absence of DLT, each accrued patient is assigned a weight that is a function of the portion of the DLT evaluation window that he or she has been followed. A patient that has been observed for the entire DLT observation window or experienced a DLT within that window provides complete information and is fully weighted. Like the CRM, the TITE-CRM assumes a working dose-toxicity model ψ(d_i, θ) that is monotonic in both dose level, d_i, and the parameter, θ. A common choice is the power model $\psi (d_i\mathrm{,}\theta )=p_i^{\text{exp}(\theta )}$, where 0 < p₁ < ⋯ < p_I < 1 are pre-specified constants, often referred to as the skeleton of the model. At the time each dosing decision is to be made, given the observed DLT data accrued up to the first n patients, the weighted likelihood of the model parameter θ is given by

$$L_n(\theta ;w)=\prod _{j=1}^n{(w_{j\mathrm{,}n+1}\psi (x_j\mathrm{,}\theta ))}^{y_{j\mathrm{,}n+1}}{(1-w_{j\mathrm{,}n+1}\psi (x_j\mathrm{,}\theta ))}^{1-y_{j\mathrm{,}n+1}}\mathrm{,}$$ (2)

Where x_j ∈ {d₁,…,d_I} is the dose administered to patient j, y_j,n+1 is the DLT indicator for patient j prior to the enrollment of patient n+1, and w_j,n+1 is the toxicity weight assigned to the observation just prior to the entry of patient n+1. As patient n+1 is accrued to the study, based on a prior distribution f(θ), the model parameter θ can be estimated via the posterior mean in a Bayesian framework by computing

$${\widehat{\theta }}_n^w=\frac{\int \theta L_n(\theta ;w)f(\theta )d\theta }{\int L_n(\theta ;w)f(\theta )d\theta }\mathrm{,}$$

whereby estimates of the DLT probabilities at each dose level can be computed as ${\widehat{\pi }}_T(d_i)=\psi (d_i\mathrm{,}{\widehat{\theta }}_n^w)$. These estimates will be used in estimating an acceptable set of safe doses by evaluating which doses have estimated probabilities less than a maximum acceptable DLT rate ξ so that $\tilde{\mathbb{A}}=\{d_i:{\widehat{\pi }}_T(d_i)<\xi \}$.

The weight function represents the amount of information available from a patient when a new patient is to be enrolled in the study. Denote the length of time that defines the protocol-specific DLT evaluation window as λ_T. Cheung & Chappell (2000) evaluated the impact of various weight functions, and their simulation results point towards the adequacy of a linear weight function in many cases. That is, suppose a patient has been followed for time u_T. A weight proportional to the length of follow-up λ_T is given by

$$w(u_T;{\lambda }_T\mathrm{,}{x}_j)=\text{min}(u_T/{\lambda }_T\mathrm{,1})\mathrm{,}$$ (3)

with patients who have completed the full DLT evaluation period, as well as those who have experienced a DLT at any time, receiving a weight of 1.

2.2. Models and inference for efficacy

As for toxicity, the modeling framework for efficacy uses partially observed efficacy data from patients who have not yet completed a full efficacy observation period. In the absence of an efficacious response, each accrued patient is assigned a weight that is a function of the portion of the efficacy evaluation window that he or she has been followed. A patient that has been observed for the entire efficacy observation window or experienced an efficacious response within that window provides complete information and is fully weighted. As in the original Phase I-II design proposed by Wages & Tait (2015), efficacy is modeled by constructing multiple working models for efficacy and utilizing model selection techniques to allow for the uncertainty in the shape of the dose-response curve. Both unimodal and plateau skeletons for a total of L = 2I − 1 working models are included in the set of possible models, where I is number of pre-defined doses levels. For example, if I = 6, then we can construct a set of 11 working models as specified below in equation (10). We model the probability of efficacy at dose d_i via a class of working models ${\varphi }_{\mathcal{l}}(d_i;{\beta }_{\mathcal{l}})=q_{i\mathcal{l}}^{\text{exp}({\beta }_{\mathcal{l}})}$, where ${\beta }_{\mathcal{l}}$ is a scalar parameter and $0<q_{1\mathcal{l}}<\cdots <q_{I\mathcal{l}}<1$ are the skeleton values under working model $\mathcal{l}$. Given the observed efficacy data accrued up to the first n patients into the study, the weighted likelihood under working model $\mathcal{l}$ of the model parameter ${\beta }_{\mathcal{l}}$ is given by

$$L_{\mathcal{l}\mathrm{,}n}({\beta }_{\mathcal{l}};v)=\prod _{j=1}^n{(v_{j\mathrm{,}n+1}{\varphi }_{\mathcal{l}}(x_j\mathrm{,}{\beta }_{\mathcal{l}}))}^{z_{j\mathrm{,}n+1}}{(1-v_{j\mathrm{,}n+1}{\varphi }_{\mathcal{l}}(x_j\mathrm{,}{\beta }_{\mathcal{l}}))}^{1-z_{j\mathrm{,}n+1}}\mathrm{,}$$ (4)

where x_j ∈ {d₁,…,d_I} is the dose administered to patient j, z_j,n+1 is the efficacy indicator for patient j prior to the enrollment of patient n+1, and v_j,n+1 is the efficacy weight assigned to the observation just prior to the entry of patient n+1. Like toxicity, a linear weight function can be utilized in specifying patient efficacy weights. Suppose a patient has been followed for time u_E. The weight function proportional to the length of follow-up λ_E is given by v(u_E;λ_E,x_j)=min(u_E/λ_E,1), with patients who have completed the full efficacy evaluation period, as well as those who have experienced a efficacy at any time, receiving a weight of 1.

We denote a set of prior model probabilities as h={h(1),…,h(L)} and, for each model, a prior distribution on ${\beta }_{\mathcal{l}}$ as $g_{\mathcal{l}}({\beta }_{\mathcal{l}})$. One option is to set $h\left(\mathcal{l}\right)=1/L$ for all $\mathcal{l}$ so that every model is equally likely at the beginning of the trial, although this structure could place larger prior probabilities on some models and smaller probabilities on other models if reliable prior information is available. Based on these priors and the likelihood under each model, after the accrual of n patents, the posterior model probability for model $\mathcal{l}$ is given by:

$${\tau }_n(\mathcal{l})=\frac{h(\mathcal{l})\int L_{\mathcal{l}\mathrm{,}n}({\beta }_{\mathcal{l}};v)g_{\mathcal{l}}({\beta }_{\mathcal{l}})d{\beta }_{\mathcal{l}}}{\sum _{\mathcal{l}=1}^{L}h(\mathcal{l})\int L_{\mathcal{l}\mathrm{,}n}({\beta }_{\mathcal{l}};v)g_{\mathcal{l}}({\beta }_{\mathcal{l}})d{\beta }_{\mathcal{l}}}\mathrm{.}$$ (5)

Each time a new patient is accrued to the study, all candidate models will be evaluated by their likelihood of representing the true dose-efficacy relationship. We appeal to sequential Bayesian model choice by choosing a model m ∈ {1,…,L} with the largest posterior probability such that $m=\text{arg}{\text{max}}_{\mathcal{l}}({\tau }_n(\mathcal{l}))$ and estimate the probabilities of efficacy at each dose by computing

$${\widehat{\pi }}_E(d_i)={\varphi }_m(d_i\mathrm{,}{\widehat{\beta }}_{m\mathrm{,}n}^v);{\widehat{\beta }}_{m\mathrm{,}n}^v=\frac{\int {\beta }_m{L}_{m\mathrm{,}n}({\beta }_m;v)g_m({\beta }_m)d{\beta }_m}{\int {\beta }_m{L}_{m\mathrm{,}n}({\beta }_m;v)g_m({\beta }_m)d{\beta }_m}\mathrm{.}$$

In the original Wages & Tait (2015) method, patients were assigned to the dose with highest estimated efficacy probability within the estimated set of acceptable doses $\mathbb{A}$. Early in the trial, when sample size was very small, patients were randomized within the safe range $\mathbb{A}$, with randomization probabilities weighted according to the estimated efficacy probabilities. Randomization of the first n_AR patients was referred to as the adaptive randomization stage, and n_AR was a specification that was calibrated at the design stage in order to yield good operating characteristics.

Yan et al. (2019) showed that an alternative randomization strategy tends to perform better regarding the accuracy of correct dose selection and patient allocation to correct doses. This alternative randomization strategy also eliminates the need of specifying n_AR at the design stage. Therefore, for our proposed method, we choose to use the following randomization strategy. The estimated correct dose from each candidate model can be given as

$$\mathcal{S}\left(\mathcal{l}\right)=\text{min}\left(\text{arg}\underset{d_i\in \mathbb{A}}{\text{max}}\left({\varphi }_{\mathcal{l}}\left(d_i,{\widehat{\beta }}_{\mathcal{l}\mathrm{,}n}^v\right)\right)\right).$$ (6)

Therefore we can adaptively randomize patients based on the likelihood of each model and its corresponding best dose $\mathcal{S}\left(\mathcal{l}\right)$. The randomization probability is calculated as

$$R_i^{*}=\frac{R_i^{**}}{\sum _{i=1}^I{R}_i^{**}}\mathrm{,}\text{where\hspace{0.17em}}{R}_i^{**}=\sum _{\mathcal{l}=1}^{2I-1}{\tau }_n(\mathcal{l})I(d_i=\mathcal{S}\left(\mathcal{l}\right)\text{\hspace{0.17em}and\hspace{0.17em}}{\tau }_n(\mathcal{l})\ge {\tau }_{(L-L^{\prime }+1)})\mathrm{.}$$ (7)

where I(·) is an indicator function and τ₍₁₎ ≤…≤ τ_(L) denote the ordered posterior model probability ${\tau }_n(\mathcal{l})$. L is the total number of candidate models and $L^{\prime }$ is the number of models being considered in the calculation of randomization probabilities. Equation (7) considers the recommended dose from $L^{\prime }$ best-fit models and weights the recommendations of each model by ${\tau }_n(\mathcal{l})$. Initially, there are L = 2I − 1 candidate models. Instead of considering all candidate models at each sequential dosing decision, we reduce the number of models being considered based on the observed sample size relative to the maximum total sample size N:

$$L^{\prime }=\lceil {\left(\frac{N-n}{N}\right)}^{\delta }L\rceil \mathrm{,}$$ (8)

where δ is a pre-specified constant and ⌈ ⌉ denotes the ceiling function, yielding the least integer that is greater than or equal to ${\left(\frac{N-n}{N}\right)}^{\delta }L$. Yan et al. (2019) recommends the use δ = 2 or δ = 3 when total sample size is between 32 and 64. This allows the method to drop candidate models with fewer observations early in the trial, but more data are required to exclude a model towards the end.

2.3. Dose-finding algorithm

Starting the Trial:

In order to get the trial underway, we will choose the efficacy skeleton with the largest prior probability, $h(\mathcal{l})$, among the orders being considered. If several, or all, of the models have the same maximum prior probability, then there are several options to assign the dose for the first patient. One may choose to start at the lowest dose level or the prior-estimated MTD. Another option is to determine the acceptable range $\mathbb{A}$ from the toxicity skeleton and the first patient will be randomized with probability $R_i^{*}$ assuming ${\tau }_0(\mathcal{l})=h(\mathcal{l})$. For the purpose of this study, we choose to start from the lowest study dose level.

Conducting the Trial:

After the first patient, we update the data and re-fit the model each time another subject is enrolled into the study. Throughout the trial, all patients will be randomized based on equation (7). Our method ensures that all patients are only randomized within the estimated safe range $\mathbb{A}$. Early in the trial, patients are randomized to a wide range of dose levels. However, the range of randomization is expected to converge to correct doses as data accumulates.

Ending the Trial:

The trial ends typically when a pre-defined maximum sample size N is reached. As in Wages & Tait (2015), we may also close the trial early for safety concerns or futility based on exact binomial confidence intervals, although we do not study such rules in this current work.

3. Numerical studies

3.1. Application to motivating example

The motivating example studies escalating doses of ATRA in combination with a fixed dose of daratumumab in the treatment of relapsed or refractory multiple myeloma. The trial aims at selecting a correct dose from three candidate dose levels of ATRA, {15,30,45 mg/m²}, denoted by d₁,d₂,d₃. To design a study using the proposed method, we assume dose-toxicity is monotonic and choose toxicity prior skeleton p = (0.15,0.25,0.35). For this study, we only included skeletons that reflect dose-efficacy curves that plateau because we do not expect efficacy to decrease at higher doses. A class of L = 3 efficacy skeletons Q can be constructed as

$$Q=\left(\begin{array}{ccc}0.2& 0.3& 0.4\\ 0.3& 0.4& 0.4\\ 0.4& 0.4& 0.4\end{array}\right)\mathrm{.}$$

For all model parameters, for both toxicity and efficacy, we used N(0,1.34) prior distributions. The DLT observation window is λ_T = 4 weeks and the efficacy observation window is λ_E = 8 weeks. If we waited until each patient is fully observed for efficacy before we enrolled the next patient, a trial of 35 patients would be impractically long. However, if we can enroll a patient every two weeks, our proposed method can shorten the trial duration to approximately 19 months by using partial information obtained from the patients who are still under observation.

We simulated DLT and efficacy outcomes under probability Scenario 2 in Table 1. The entire simulated trial of 35 patients is provided in Figure 1. Suppose the trial starts with the first patient receiving d₁, and no DLT or efficacy responses are observed by the time the second patient is enrolled 2 weeks later. The weight of the toxicity outcome from the first patient is given by w(u_T;λ_T,x_j) = min(2/4,1) = 0.5 and the weight of efficacy outcome is v(u_E;λ_E,x_j) = min(2/8,1) = 0.25. Applying the TITE CRM, we can estimate the probability of DLT from the lowest dose to the highest dose, that is (0.11,0.20,0.29). With the likelihood function (4), we can calculate the posterior model probabilities for each $\mathcal{l}$ according to equation (5). For $\mathcal{l}=\mathrm{1,}\dots \mathrm{,3}$, ${\tau }_1(\mathcal{l})=\mathrm{0.327,0.333,}$ and 0.339, respectively. The posterior model probabilities are very close to each other because we only have one observation. According to equation (6), the implied best dose for each model $\mathcal{l}=\mathrm{1,2,3}$ is dose level d₃,d₂,d₁, respectively.

Table 1:

Toxicity and efficacy probability scenarios and simulation results for the motivating example. The table reports the true toxicity probability at each dose, the true efficacy probability at each dose, the percentage of trials in which each dose was selected as the dose to carry forward at the end of the trial, and the average trial duration. The maximum sample size is N = 35 patients.

	True (toxicity, efficacy) probability			Duration
Scenario 1	(0.05, 0.15)	(0.10, 0.30)	(0.20,0.45)	(months)
Tox-U, Eff-U	9.7	25.9	64.4	19.01
Tox-U, Eff-W	9.7	29.7	60.9	19.01
Tox-W, Eff-W	9.2	25.2	65.6	19.06
Tox-W, Eff-U	8.2	24.6	67.2	19.00
Scenario 2	(0.05, 0.15)	(0.10, 0.35)	(0.20, 0.35)
Tox-U, Eff-U	10.2	48.0	41.8	18.92
Tox-U, Eff-W	10.6	49.1	40.3	18.88
Tox-W, Eff-W	9.9	48.6	41.5	18.94
Tox-W, Eff-U	10.2	47.0	42.8	19.02
Scenario 3	(0.05, 0.30)	(0.10, 0.30)	(0.20, 0.30)
Tox-U, Eff-U	44.5	30.9	24.3	19.01
Tox-U, Eff-W	46.3	29.3	24.4	19.00
Tox-W, Eff-W	45.0	29.9	25.1	19.00
Tox-W, Eff-U	43.5	30.6	25.9	18.88
Scenario 4	(0.15, 0.15)	(0.30, 0.30)	(0.40, 0.30)
Tox-U, Eff-U	35.5	51.8	12.7	19.14
Tox-U, Eff-W	36.2	51.8	12	18.91
Tox-W, Eff-W	36.5	51.8	11.7	19.01
Tox-W, Eff-U	39	48.9	12.1	18.93

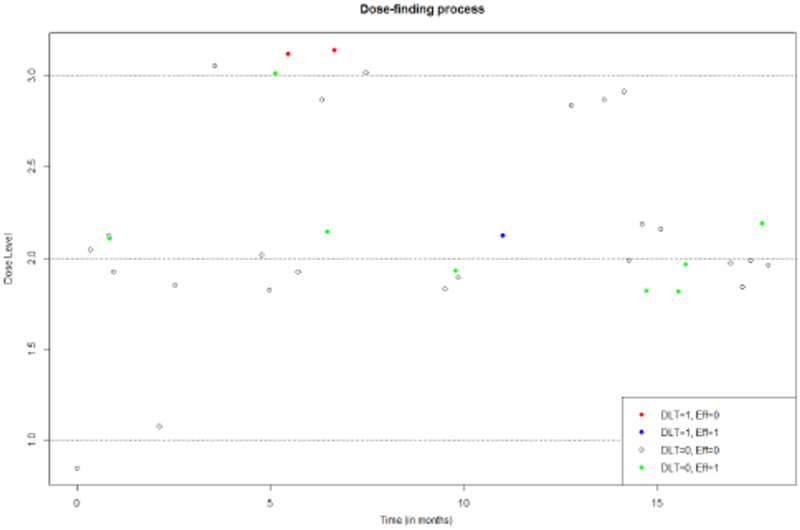
Figure 1:

Simulated trial using the proposed TITE-B design under Scenario 2 in Table 1.

The second patient will be randomized, and the dose assigning probability calculated using equation (7). The randomization probability of each dose is 0.327,0.333, and 0.339. The second patient will have approximately the same probability of receiving each of the candidate doses. This is intuitively appropriate as we currently do not have enough information to favor one dose over another and rely mostly on the model skeletons. All three dose levels have positive probabilities to be assigned because the toxicity skeletons and observed data suggest that the estimated risk of DLT at the highest dose is smaller than the pre-specified threshold ξ = 0.33. For the second patient, all 3 models are included in the calculation of dose assigning probabilities since the sample is currently very small. As the sample size increases, we gradually reduce the number of models included in the calculation. The number of models used in probability calculation can be obtained from equation (8). This process continues until the maximum sample size is reached. Overall three DLTs are observed, two at d₃ and one at d₂. At d₃, only 1/9=11% of patients had an efficacious response. At d₂, 8/24=33% had an efficacious response. The correct dose is ultimately identified as dose level 2 with a true DLT probability of 0.10 and a true efficacy probability of 0.35.

For the motivating example, we ran simulations in R to demonstrate the operating characteristics under various true dose-outcome scenarios with a sample size of 35 patients accrued in cohorts of size 1. We detail the simulation scenarios and results in Table 1. Patient accrual is assumed to follow a Poisson distribution with rate = 0.5 per week. The time to event distribution for toxicity or efficacy response is assumed to follow either a conditional uniform distribution or a Weibull distribution. For a conditional uniform distribution, the time-to-event would be randomly generated on the interval (0,4) for toxicity and (0,8) for efficacy. For the Weibull model the shape parameter was fixed at a value of 4 and the scale parameters were chosen so that the cumulative distribution function at times λ_T and λ_E would be the probability of toxicity and efficacy, respectively, at each dose level. Both of these time-to-event models were used in Cheung & Chappell (2000). Therefore, for each scenario, we investigated four different specifications:

1. Tox-U, Eff-U: the patients time-to-event for both toxicity and efficacy were generated under a conditionally uniform model.

2. Tox-U, Eff-W: the patients time-to-toxicity were generated under a conditionally uniform model; the patients time-to-efficacy were generated under a Weibull model.

3. Tox-W, Eff-W: the patients time-to-event for both toxicity and efficacy were generated under a Weibull model.

4. Tox-W, Eff-U: the patients time-to-toxicity were generated under a Weibull model; the patients time-to-efficacy were generated under a conditionally uniform model.

For each scenario considered in Table 1, 1000 simulated trials were run. The results report the true toxicity probability at each dose, the true efficacy probability at each dose, the percentage of trials in which each dose was selected as the dose to carry forward at the end of the trial, and the average trial duration. Trial duration is calculated as the time from the treatment of the first patient to the time the last patient completed follow-up. It is clear from examining the results in Table 1 that the proposed methodology is performing well in terms of recommending correct doses in a high percentage of trials. In Scenario 1, there is a single dose d₃ that is safe and maximizes efficacy, and our method selects this dose in more than 60% of trials of 35 patients. In Scenarios 2 and 3, there are multiple doses that are safe and maximize efficacy and the method tends to select these doses in a very high percentage of trials. In Scenario 4, there is one unsafe dose and our method selects this dose in a low percentage of simulated trials. In supplemental material accompanying this article, we have provided additional simulation results over a broad range of scenarios with different assessment windows for the endpoints, patient accrual rates, and time-to-event distributions. In the following section, we provide a comparison to an alternative method in the area.

3.2. Operating characteristics

We performed extensive computer simulations in order to examine the operating characteristics of the proposed methodology and compare it to an alternative method in the area. We compared our method, termed TITE-B, to the results provided in Riviere et al. (2018) for two different methods described in their paper, termed MTA-RA and MTA-PM, in terms of the ability of each method to locate correct doses and the optimal dose, as well as to allocate patients to these doses. Using the definitions of Riviere et al. (2018), a correct dose is defined as a dose that maximizes efficacy and has an acceptable risk of toxicity and the optimal dose is defined as the lowest safe dose that achieves the highest efficacy. Note that in the case of plateau dose-efficacy probability scenarios, the definition of a correct dose may be met by more than one dose level, while the optimal dose is a single dose level. In the case of unimodal dose-efficacy probability scenarios, the optimal dose and the correct dose will coincide with one another as a single dose.

We generated operating characteristics over eight scenarios of I = 6 dose levels and four scenarios of I = 4 dose levels that appear in Riviere et al. (2018), with 2000 trials simulated under each scenario. In each scenario in Table 2, correct doses are indicated in bold type, and the optimal dose is underlined. The maximum sample size for each simulated trial was N = 60 patients and the toxicity upper bound used to define safe doses was ξ = 0.35. Because we are using results provided in Riviere et al. (2018) as a comparator, the MTA-RA and MTA-PM methods use a cohort size of 3 patients, whereas we recommend a cohort size of 1 for our method and use it throughout the conduct of TITE-B. We assumed that the patient accrual followed a Poisson process with a rate of 0.28 patients per week; i.e., approximately one patient every 3.5 weeks. The Riviere et al. (2018) methods assume that toxicity is quickly observable and thus treat the DLT endpoint as a binary endpoint that is fully observed at the time of each dosing decision. TITE111-B treats toxicity as a time-to-event outcome with the DLT evaluation window of λ_T = 4 weeks. Both methods model efficacy as a time-to-event endpoint using an efficacy evaluation period of λ_E = 7 weeks. In order to provide a justifiable comparison to Riviere et al. (2018), we assumed that at each dose level, the time-to-efficacy followed an exponential distribution exp(ζ), with the parameter ζ chosen such that at the end of follow-up, the efficacy rate at each dose matched those displayed in Table 2. That is,

$${\zeta }_i=\frac{-\text{log}(1-{\pi }_E(d_i))}{{\lambda }_E};i=\mathrm{1,}\dots \mathrm{,}I$$ (9)

so that ζ varies across the dose levels. For TITE-B, time-to-toxicity is also generated using an exponential distribution similar to equation (9), based on λ_T and π_T(d_i).

Table 2:

True probability scenarios (S1–S12) taken from Riviere et al. (2018). In each scenario, correct doses, defined as doses that maximizes efficacy and have an acceptable risk of toxicity, are indicated in bold type. The optimal dose, defined as the lowest safe dose that achieves the highest efficacy, is underlined.

		Dose level
Scenario		1	2	3	4	5	6
S1	Toxicity	0.005	0.01	0.02	0.05	0.10	0.15
	Efficacy	0.01	0.10	0.30	0.50	0.80	0.80
S2	Toxicity	0.01	0.05	0.10	0.25	0.50	0.70
	Efficacy	0.40	0.40	0.40	0.40	0.40	0.40
S3	Toxicity	0.01	0.02	0.05	0.10	0.20	0.30
	Efficacy	0.25	0.45	0.65	0.65	0.65	0.65
S4	Toxicity	0.01	0.02	0.05	0.10	0.25	0.50
	Efficacy	0.05	0.45	0.70	0.70	0.70	0.70
S5	Toxicity	0.01	0.05	0.15	0.20	0.45	0.60
	Efficacy	0.10	0.35	0.60	0.60	0.60	0.60
S6	Toxicity	0.01	0.05	0.10	0.20	0.30	0.50
	Efficacy	0.05	0.10	0.20	0.35	0.55	0.55
S7	Toxicity	0.02	0.07	0.13	0.17	0.25	0.30
	Efficacy	0.30	0.50	0.70	0.73	0.76	0.77
S8	Toxicity	0.03	0.06	0.10	0.20	0.40	0.50
	Efficacy	0.30	0.50	0.52	0.54	0.55	0.55
S9	Toxicity	0.01	0.05	0.15	0.25
	Efficacy	0.10	0.35	0.60	0.30
S10	Toxicity	0.10	0.20	0.03	0.50
	Efficacy	0.50	0.70	0.60	0.40
S11	Toxicity	0.05	0.10	0.16	0.22
	Efficacy	0.02	0.28	0.50	0.80
S12	Toxicity	0.05	0.10	0.16	0.22
	Efficacy	0.80	0.50	0.28	0.02

All design specifications used for MTA-RA and MTA-PM are provided in Riviere et al. (2018). In Scenarios 1–8, for TITE-B, we used a toxicity skeleton of (p₁,…,p₆) = (0.02,0.06,0.12,0.20,0.30,0.40) and L = 11 possible efficacy skeletons of:

$$Q=\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\\ q_4\\ q_5\\ q_6\\ q_7\\ q_8\\ q_9\\ q_{10}\\ q_{11}\end{array}\right)=\left(\begin{array}{c}0.59\mathrm{,0.50,0.40,0.30,0.20,0.12}\\ \mathrm{0.50,}0.59\mathrm{,0.50,0.40,0.30,0.20}\\ \mathrm{0.40,0.50,}0.59\mathrm{,0.50,0.40,0.30}\\ \mathrm{0.30,0.40,0.50,}0.59\mathrm{,0.50,0.40}\\ \mathrm{0.20,0.30,0.40,0.50,}0.59\mathrm{,0.50}\\ \mathrm{0.12,0.20,0.30,0.40,0.50,}0.59\\ \mathrm{0.20,0.30,0.40,0.50,}0.59\mathrm{,}0.59\\ \mathrm{0.30,0.40,0.50,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ \mathrm{0.40,0.50,}0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ \mathrm{0.50,}0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ 0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ \end{array}\right)\mathrm{.}$$ (10)

q₁ through q₆ represent scenarios where the dose-efficacy peaked at dose d₁ through d₆, respectively; q₇ through q₁₁ are scenarios when dose-efficacy plateaus after the optimal dose. In Scenarios 9–12, we used a toxicity skeleton of p = (0.02,0.06,0.12,0.20) and L = 7 possible efficacy skeletons of:

$$Q=\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\\ q_4\\ q_5\\ q_6\\ q_7\end{array}\right)=\left(\begin{array}{c}0.59\mathrm{,0.50,0.40,0.30}\\ \mathrm{0.50,}0.59\mathrm{,0.50,0.40}\\ \mathrm{0.40,0.50,}0.59\mathrm{,0.50}\\ \mathrm{0.30,0.40,0.50,}0.59\\ \mathrm{0.40,0.50,}0.59\mathrm{,}0.59\\ \mathrm{0.50,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ 0.59\mathrm{,}0.59\mathrm{,}0.59\mathrm{,}0.59\\ \end{array}\right)\mathrm{.}$$ (11)

In all scenarios, we assume no existing knowledge about the candidate models and set $h(\mathcal{l})=1/L\text{\hspace{0.17em}for\hspace{0.17em}}\mathcal{l}=\mathrm{1,2,}\dots \mathrm{,}L$. For all model parameters, we used N(0,1.34) prior distributions.

3.3. Results

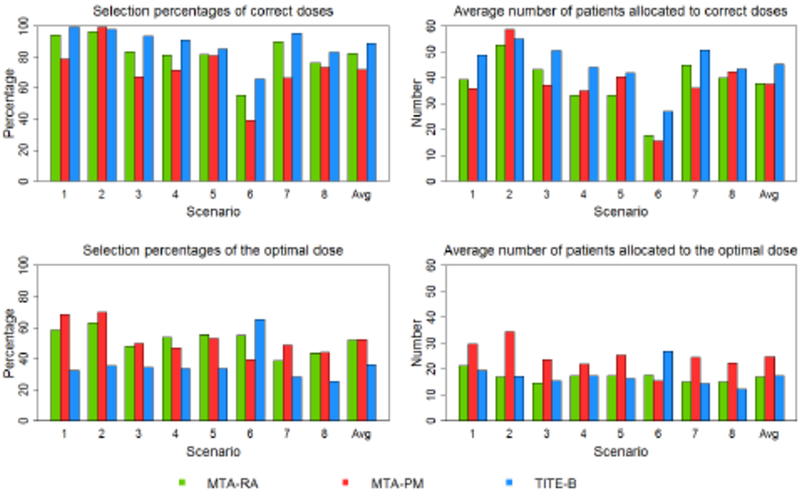
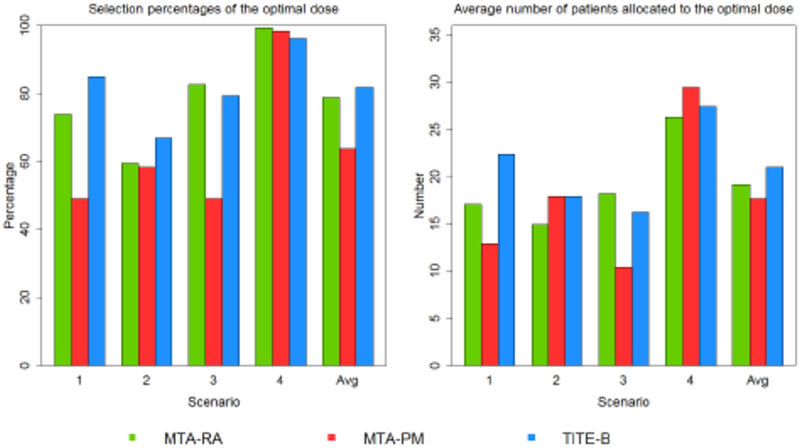
Figures 2 and 3 examine the operating characteristics of the proposed method regarding its ability to correctly select correct and optimal doses, as well as the number of patients treated at these doses. In Scenarios 1–8, most scenarios have multiple correct doses along the flat part of the dose-efficacy curves. In Scenarios 9–12, in the case of unimodal dose-efficacy curves, there is only one correct dose, which of course is also the optimal dose. In Scenario 7 and 8, efficacy does not exactly plateau, but rather increases slightly beginning at dose levels 2 and 3, respectively. In these scenarios, we take the optimal and correct doses to be the same as those reported in Riviere et al. (2018), even though it could be argued that the optimal doses are levels 6 and 4, rather levels 2 and 3, in Scenarios 7 and 8, respectively. Figures 1 and 2 report the percentage of trials that each method selected and treated patients at optimal and correct doses according to the definition of those doses in Riviere et al. (2018) in order to provide a justifiable comparison. Overall, the TITE-B selects correct doses in a higher percentage of simulated trials in nine scenarios of the twelve scenarios considered. On average across all scenarios, the TITE-B selects correct doses in 86.6% of simulated trials, the MTA-RA does so in 81.2% of trials, and MTA-PM does so in 69.4% of trials. In terms of patient allocation, the TITE-B treats 37.1 of 60 patients on average at correct doses, the MTA-RA treats an average of 31.7 patients at correct doses, and the MTA-PM treats 31.0 patients on average at correct doses.

Figure 2:

Simulated results under Scenarios 1–8.

Figure 3:

Simulated results under Scenarios 9–12.

With regards to selecting and treating patients at the optimal dose, the MTA-RA and MTA-PM methods tended to do a better job of locating the lowest dose with maximum efficacy when the dose-efficacy curve plateaus and there are multiple safe doses along the plateau (Scenarios 1–5). Dose-efficacy models in Riviere et al. (2018) are governed by a plateau parameter that is intended to accurately locate the dose at which the dose-efficacy curve begins to level off. However, if the beginning of the plateau occurs at a dose close to the boundary of acceptable (safe) doses (Scenario 6), or the dose-efficacy curve peaks at an intermediate dose and then begins to decline (Scenarios 9–12), then the TITE-B method tended to do better. Throughout Scenarios 1–8, the MTA-RA and MTA-PM methods performed better than the TITE-B method in terms of selecting the optimal dose, with the exception of Scenario 6 (66.6% for TITE-B; 55.2% for MTA-RA; 39.5% for MTA-PM). In terms of allocating patients to the optimal dose in Scenarios 1–8, the MTA-PM method performed the best of the three methods, allocating 24.8 patients on average to the optimal dose. The MTA-RA and TITE-B methods performed similarly on this metric, allocating 16.96 and 17.5 patients, respectively, to the optimal dose in these scenarios.

It is difficult to know what impact the differences in these methods have on their various performances. For instance, the MTA-RA and MTA-PM methods do not model toxicity as a time-to-event endpoint, while the TITE-B method does. Also, the cohort size is larger for the MTA-RA and MTA-PM methods which could also contribute to differences in operating characteristics. These results provide a general comparison between the three methods, with the main take home message being that the TITE-B is better at identifying correct doses in a broad range of scenarios and that the modeling framework in Riviere et al. (2018) enables it to better locate the lowest safe dose with maximum efficacy in the case of dose-efficacy curves that plateau beyond an intermediate dose. The limitations of this comparison include that we did not compare stopping rules for the various methods and that Riviere et al. (2018) does not report overall trial duration so it is difficult to know how much time is saved by modeling both endpoints as time-to-event outcomes when compared to their method.

4. Discussion

In this article, we answered the question posed in the Wages & Tait (2015) article about extending their method to situations efficacy outcomes may be delayed. We outlined a phase I-II method that accounts for varying degrees of delayed outcomes for both toxicity and efficacy endpoints in locating a correct dose, defined as a safe dose that maximizes efficacy. Through extensive simulations, we demonstrated the method’s ability to accurately select correct doses while ensuring all available information is used in assigning doses to participating patients. We also showed the robustness of the proposed method against various toxicity and efficacy probability scenarios, time-to-event distributions, and patient accrual rates.

Although faster patient enrollment may not diminish the accuracy of correct dose selection selection, it may decrease the number of patients receiving the correct dose (supplemental material). Therefore, when enrollment is very fast, the proposed method, as well as other methods, may face logistical implementation challenges. A solution is to temporarily pause enrollment to accumulate data from the existing patients. It requires further research to find and test appropriate enrollment restrictions. Another potential direction for future study is early termination rules. In our study, the trial continued until the maximum sample size was reached. Early termination rules, either for futility or safety, may further reduce expected trial duration and save resources.

The methodology proposed in this article differs from suggested methods in this area in several ways. The methods of Yuan & Yin (2009) and Jin et al. (2014) are based on different dose selection criteria than that described in Section 1.2. The method of Yuan & Yin (2009) is based upon locating the dose that maximizes the ratio of the areas under the survival curves (AUSC) of toxicity and efficacy as a trade-off, with a higher value of AUSC indicating a more desirable dose. The method of Jin et al. (2014) is driven by the definition of efficacy-toxicity (eff-tox) probability trade-off contours Thall2004. Both of these methods utilize a more complex modeling framework, whereas the method we proposed builds upon the under-parameterized TITE-CRM (Cheung & Chappell 2000). Comparison between our method and these methods would have been difficult since the primary objectives of the study may differ in that each method may be attempting to identify different doses within the same scenario. The method of Liu & Johnson (2016) assumes that efficacy probabilities are monotone increasing and does not account for plateau or unimodal relationships, so our method has more flexibility in being able to accommodate a more broad range of dose-response curves. Finally, this paper only studied situations in which dosing decisions were guided by DLT’s that occurred in cycle 1 of treatment, which is generally 28 days. However, acute toxicity may not provide a complete representation of tolerability for targeted and immune therapies. These new agents are being administered over extended periods of time, which can result in relevant DLTs occurring outside of a short-term evaluation window. Although not studied in this work, our method has the flexibility to accommodate various DLT assessment window lengths. An R package for the simulation and implementation of this work is currently under construction.