Abstract
The preejection period (PEP) is a valid index of myocardial contractility and beta-adrenergic sympathetic control of the heart defined as the time between electrical systole (ECG Q wave) to the initial opening of the aortic valve, estimated as the B point on the impedance cardiogram (ICG). B-point detection accuracy can be severely impacted if ICG cardiac cycles corrupted by motion artifact, noise, or electrode displacement, are included in the analyses. Here, we developed new algorithms to detect and exclude corrupted ICG cycles by analyzing their level of activity. PEP was then estimated and analyzed on ensemble averaged clean ICG cycles using an automatic algorithm previously developed by the authors for the detection of B point in awake individuals (Forouzanfar, et al., 2018). We investigated the algorithms’ performance relative to expert visual scoring on long-duration data collected from 20 participants during overnight recordings, where the quality of ICG could be highly affected by movement artifacts and electrode displacements, and the signal could also vary according to sleep stage and time of night.
The artifact rejection algorithm achieved a high accuracy of 87% in detection of expert-identified corrupted ICG cycles, including those with normal amplitude as well as out-of-range values, and was robust to different types and levels of artifact. Intraclass correlations for concurrent validity of the B-point detection algorithm in different sleep stages and in-bed wakefulness exceeded 0.98, indicating excellent agreement with the expert. The algorithms show promise toward sleep applications requiring accurate and reliable automatic measurement of cardiac hemodynamic parameters.
1. Introduction
Preejection period (PEP) is a hemodynamic measure of myocardial contractility which is widely used by psychophysiologists as a valid index of sympathetic beta-adrenergic influences upon the heart (Bagley & El-Sheikh, 2014; Cacioppo, et al., 1994; Gatzke-Kopp & Ram, 2018; Giuliano, et al., 2018; Schächinger, Weinbacher, Kiss, Ritz, & Langewitz, 2001; Sherwood, Allen, Obrist, & Langer, 1986).
PEP is defined as the time between the onset of ventricular depolarization (electrical systole) to the initial point of ejection of blood from the left ventricle (mechanical opening of the aortic valve) and can be noninvasively estimated as the time difference between the electrocardiogram (ECG) Q wave and the impedance cardiogram (ICG) B point (Pinheiro, Postolache, & Girão, 2013; Sherwood, et al., 1990; Tavakolian, 2016; Visser, Mook, van der Wall, & Zijlstra, 1993).
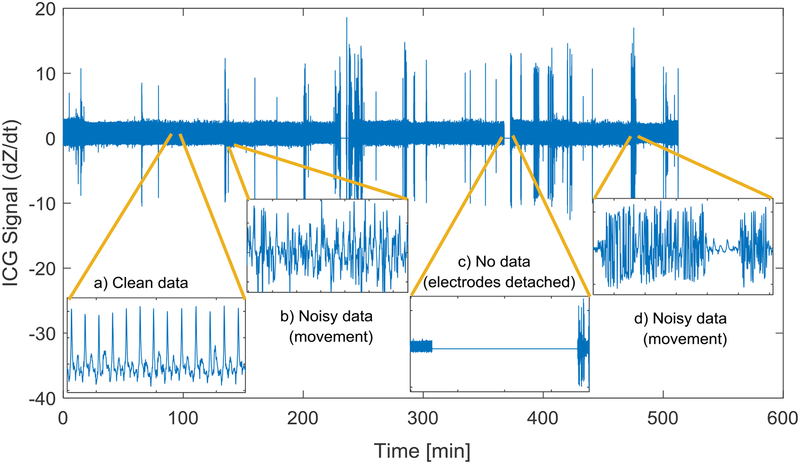
The reliability of PEP measurements depends on the accurate detection of B point on ICG signal (Árbol, et al., 2017; Cieslak, et al., 2017; Debski, et al., 1991; Debski, Zhang, Jennings, & Kamarck, 1993; Ermishkin, Kolesnikov, & Lukoshkova, 2014; Lozano, et al., 2007; Miller & Horvath, 1978; Sherwood, et al., 1990; Stern, Wolf, & Belz, 1985; van Lien, Schutte, Meijer, & de Geus, 2013). However, the detection of B point, defined as a reversal, inflection, or rapid slope change on the ICG signal rise, can be challenging as it can be easily affected by noise and artifacts mainly caused by body movements and electrode displacements. The problem can be even more critical in long-duration measurements such as during overnight recordings when subject movements are not controlled and electrodes could be easily displaced or lose contact (see Figure 1) (Altshuler & Brebbia, 1967). Such data usually need to be visually inspected by an expert and the portions of data that contain no valid information discarded from further analysis (Debski, et al., 1991; Sherwood, Allen, Obrist, & Langer, 1986; van Lien, Schutte, Meijer, & de Geus, 2013). Visual inspection is however time consuming and inefficient when analyzing data collected over extended time periods.
Figure 1.
Example of ICG signal recorded overnight (~8 hours). Examples of clean and corrupted segments of the data are shown in the insets.
Automatic algorithms based on ensemble averaging (Cieslak, et al., 2015; Kelsey & Guethlein, 1990; Muzi, et al., 1985; Qu, Zhang, Webster, & Tompkins, 1986; Riese, et al., 2003; Shoemaker, Appel, Kram, Nathan, & Thompson, 1988) and digital filtering (Bagal, Pandey, Naidu, & Hardas, 2018; Chabchoub, Mansouri, & Salah, 2016; Nagel, et al., 1989; Wang, Sun, & Van de Water, 1995; Yamamoto, et al., 1988) have been used to reduce the effect of noise and artifacts on the ICG signal. However, such algorithms are only applicable at moderate levels of noise and artifacts when valid ICG cycles still exist and are recoverable. Automatic algorithms based on post-hoc outlier detection from estimated hemodynamic parameters such as PEP, ejection time, or beat-to-beat time interval have been used for identifying artifacts (Berntson, Quigley, Jang, & Boysen, 1990; Cybulski, et al., 2017; Forouzanfar, et al., 2018). However, the hemodynamic parameters that show within-range values could still be invalid if estimated from highly corrupted ICG cycles. For long datasets, automatic algorithms are therefore needed to identify highly corrupted portions of data and exclude them before application of any algorithm to detect the B point. Here, we therefore aimed to develop automatic algorithms for the detection and exclusion of corrupted ICG cardiac cycles prior to B-point detection. Following the application of these algorithms, we investigated the performance of our newly-proposed algorithm for the detection of B point, which was previously shown to be robust to ICG signal morphology variations and noise and artifacts in short-duration data (~2 minutes) in awake individuals, at rest and post-exercise (Forouzanfar, et al., 2018). We hypothesized that the algorithm should be valid even for prolonged datasets. Thus, in the current work, we evaluated its performance on overnight datasets that were several hours in duration. Since PEP can vary according to wake or sleep stage and time of night (Burgess, Penev, Schneider, & Van Cauter, 2004; de Zambotti, et al., 2014; de Zambotti, et al., 2012; de Zambotti, et al., 2013; Trinder, et al., 2001), we also considered the performance of the algorithm in different sleep states and times.
2. Method
2.1. Experimental Design
Twenty healthy adults were recruited from the San Francisco Bay Area and underwent standard polysomnography (PSG) recordings at the SRI Human Sleep Research Laboratory, as part of a study investigating the acute effect of alcohol on sleep and the cardiovascular system. Only data from non-alcohol nights were used in this study. Participants had no current mental or medical conditions, and were not taking medication affecting sleep or cardiovascular functioning. The study was reviewed and approved by the SRI International Institutional Review Board, and all participants provided written informed consent. Participants characteristics are provided in Table 1.
Table 1.
Characteristics of participants and resting-state cardiovascular measures.
| 20 (10 females) | |
| Caucasian, No. | 18 |
| 46.2 (8.4) | |
| 24.9 (3.8) | |
| 108 (12) | |
| 73 (5) | |
| 71 (14) |
Participants arrived about 4 hours before their desired bedtime to allow electrode attachment and routine lab procedures. They self-selected lights-off and lights-on times. They slept in sound attenuated and temperature-controlled rooms.
Standard PSG was performed using EEG (F3, F4, C3, C4, 01, 02, referenced to the contralateral mastoid; 256 Hz sampled and 0.3–35 Hz filtered), bilateral EOG and submental EMG recordings using Compumedics amplifiers (Compumedics, Abbotsford, Victoria, Australia), following the American Academy of Sleep Medicine (AASM) guidelines (Iber, Ancoli-Israel, Chesson, & Quan, 2007). Sleep stages (wake, N1, N2, N3, and REM sleep) were visually scored in 30-s epochs by experts following the AASM rules.
ECG signal was collected via a dedicated channel in the PSG system. ECG was recorded in modified D2 Einthoven configuration via Ag/AgCl Meditrace surface spot electrodes and sampled at 512Hz. ICG dZ/dt signal, representing the rate of change in the impedance waveform on a given beat, was recorded via HIC-4000 Bioelectric impedance cardiography (Bio-Impedance Technology, Inc., Chapel Hill, NC). The dZ/dt output signal was interfaced and acquired within the PSG recording system. ICG was recorded using a 4-lead 8-point connection arrangement in which a 4mA AC 100 kHz was transmitted in the outer electrodes and the output voltage recorded by the inner electrodes.
2.2. Preprocessing
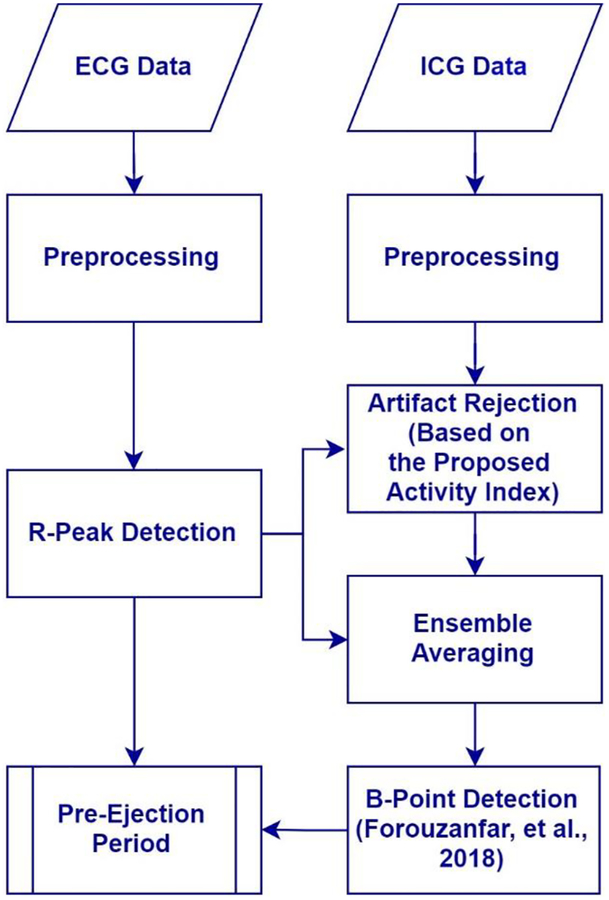
A block diagram representation of the processing of the data and application of algorithms is presented in Figure 2. Simultaneously recorded ICG and ECG signals were digitally filtered with a 4th-order Butterworth bandpass filter to remove the high frequency noise and artifacts and low-frequency drift. The lower and upper cutoff frequencies were set to 0.5 Hz and 35 Hz, and 0.5 and 25 Hz for ECG and ICG, respectively. The ICG bandpass filter cutoff frequencies are commonly used in the literature to remove respiration and low-frequency movement artifacts (Raza, Patterson, & Wang, 1992), and power-line and high frequency noise (de Geus & van Doornen, 1996; Debski, et al., 1991; Hu, et al., 2014a; Shi, Heinig, & Kanoun, 2011) while leaving ICG distinct features (B, Z, and X point) unaltered. The filter was applied in both forward and backward directions to avoid any phase shift.
Figure 2.
Block diagram representation of the flow of data handling and algorithms applied.
2.3. R-peak Detection
ECG signal samples with a value more than ten standard deviations away from the mean were identified as outliers and were replaced by interpolating the remainder of ECG samples. Average R-R interval was then estimated using power spectral analysis. An automatic peak detection algorithm available in MATLAB R2018a software was adopted to detect the ECG R peaks using half of the average R-R interval as the minimum distance criterion between two successive peaks. To intensify the R peaks and minimize the effect of T waves with amplitudes higher than normal, the automatic peak detection algorithm was applied on the ECG signal derivative. R-R intervals with a value more than ten standard deviations away from their mean were identified as outliers. The out-of-range R-R intervals are mainly due to inaccurate R-peak detection caused by noise and artifacts corrupting the ECG signal. Those cardiac cycles that happen to have an out-of-range ECG signal level or R-R value were excluded from further analysis.
2.4. ICG Artifact Rejection
Noise and movement artifacts usually affect the ICG signal by increasing its variations in time (see Figure 1, insets b and d). On the other hand, high-level movements may loosen the electrodes contact, resulting in an almost constant signal mainly carrying noise (see Figure 1, inset c). These artifacts lead to an imprecise detection of B point and inaccurate measurement of PEP. Having a measure of ICG signal activity, corrupted ICG cycles can be identified and excluded from further analysis.
ICG cardiac cycles were identified using the ECG R peaks as the reference. Every portion of the ICG signal located between two successive ECG R peaks was marked as an ICG cardiac cycle. Data collected from three individuals (not included in the rest of the analysis) that contained different artifact types including movement and electrode displacement were used to design the algorithms and find their parameters.
An activity index (AI) was defined to measure the ICG signal variations over each cardiac cycle, as follows:
| (1) |
Where
| (2) |
and
| (3) |
AIi is the i-th ICG cardiac cycle activity index, dZ(j)/dt is the j-th ICG cycle sample, Ni is the total number of ICG signal samples over i-th cardiac cycle, and M is the total number of ICG cycles. The activity index is in fact the standard deviation of normalized ICG signal in each cardiac cycle. To obtain a valid activity index robust to signal level variations between and within individuals, ICG signal variations over each cardiac cycle were normalized by the median of the ICG cycles amplitude. The ICG cycle amplitude was defined as the difference between the ICG maximum (Z point) and minimum (X point) over each cardiac cycle.
In order to obtain a reliable measure of the normalizing factor C, the unnormalized activity index, i.e. equation (1) with C = 1, was first calculated. Two low sensitivity thresholds, set at 0.02 and 2, were applied to detect and reject those ICG cycles with too low (such as no data segments where the electrodes are detached) or too high (such as sharp spikes due to rapid movements) activity, respectively. This step is required to obtain a reliable estimate of the normalizing factor in cases where majority of the ICG cycles are corrupted.
Having excluded the highly corrupted ICG cycles, the normalizing factor was calculated according to equation (3). The activity index was then calculated and two higher sensitivity thresholds, set at 0.1 and 0.4, were applied to detect and reject those ICG cycles with low or high activity, respectively.
An outlier detection algorithm was then developed to remove any further ICG cycles that appear to be inconsistent with the remainder of cycles. Outliers were defined as those ICG cycles with an activity index of more than four scaled median absolute deviation (MADN) away from the median, as follows:
| (4) |
where
| (5) |
The proposed artifact rejection algorithm based on the defined activity index can be summarized as follows:
2.5. Ensemble averaging
The artifact free ICG cycles were ensemble averaged over 30-sec time intervals corresponding to the scored PSG. ECG R peaks were used as the time markers for ensemble averaging.
2.6. B-point Detection Algorithm
A B-point detection algorithm was developed in (Forouzanfar, et al., 2018) that was robust to the variations of ICG signal and outperformed the conventional algorithms. The algorithm was customized for B-point detection from individual ensemble averaged ICG cycles in the current dataset as follows:
Detect the main ICG peak (C-point).
Find the main local minimum (A-point) between the first ICG cycle sample (R-peak location) and the C-point.
Calculate the ICG height (H) as the amplitude difference between the detected A-point and C-point.
Find all the monotonically increasing segments between A-point and C-point and select the one with the highest height that starts from at least ⅔ of the C-point amplitude and reaches at least 3/4 of C-point amplitude. If no such segment is found, relax the second condition to 1/2 of C-point amplitude. If no such segment is found, select the last monotonically increasing segment.
Find all the d3Z/dt3 zero-crossings over the first ⅔ of the most prominent monotonically increasing segment and discard those with dZ/dt slope (d2Z/dt2) of greater 6 × H/fs.
Find all the d3Z/dt3 local maximums over the first ⅔ of the most prominent monotonically increasing segment and discard those with d3Z/dt3 value of less than 0.002 × H/fs.
Label the last zero-crossing or local maximum of d3Z/dt3 as the B-point. If no zero-crossing or local maximum exists, label the first point of the segment as B-point.
2.7. Data Analysis
In order to evaluate the performance of the ICG artifact rejection algorithm, 2000 ICG cardiac cycles (100 per individual) were randomly selected and visually scored by an expert (MdZ), blinded to the algorithm scoring, as either corrupted or clean cycles. Clean cycles were selected as those cycles that followed the general pattern of the ICG signal with B, Z, and X points uncontaminated by artifacts (Sherwood, et al., 1990). In order to study the performance of the algorithm at different levels of ICG signal amplitude, the expert-detected corrupted cycles were divided into three groups: below normal, normal, and above normal amplitude. Normal amplitude cycles for each subject were defined as those with an amplitude of >0.5 or <2 times of the median amplitude of the clean cycles. Each cycle’s amplitude was defined as the difference between its maximum and minimum values.
In order to evaluate the performance of the algorithm on different artifact types and levels, three categories of artifacts including electrode detachment, low-level movement, and high-level movement were selected by the expert based on the shape of ICG cycles and their pattern variations over time. The accuracy of the artifact rejection algorithm was then analyzed on each artifact category.
True positive (TP), false positive (FP), false negative (FN), and true negative (TN) rates were calculated according to the expert scores. The performance of the algorithm was evaluated in terms of the overall accuracy: (TP+TN)/(TP+TN+FP+FN), overall error: (FP+FN)/(TP+TN+FP+FN), sensitivity: TP/(TP+FN), specificity: TN/(FP+TN), positive predictive value: TP/(TP+FP), and negative predictive value: TN/(TN+FN).
The proposed artifact rejection algorithm was run on all individual ICG cardiac cycles and the detected corrupted cycles were excluded from further study. The algorithm-detected clean ICG cycles were then ensemble averaged over 30-sec time intervals. The performance of B-point detection algorithm was evaluated on 20% of the ensemble averaged ICG cycles randomly selected for each participant in each sleep stage across the night. The location of B point was visually marked by an expert (MdZ), blinded to the algorithm scoring. Expert had the option to refuse to score those ICG cycles that did not have a clear B point. The 20% selection rule resulted in a total of 14745 ensemble averaged ICG cycles out of which 929 were in N1, 7494 were in N2, 2103 were in N3, 2722 were in REM, and 1497 were in wake stages.
PEP was calculated as the time difference between the ICG B point and the ECG Q-wave onset. The Q wave onset was approximated as the ECG R peak time minus a constant set to 35 ms (Seery, Kondrak, Streamer, Saltsman, & Lamarche, 2016). PEP was averaged across all cardiac cycles for each participant.
Concurrent validity was assessed in different sleep stages using intraclass correlation coefficients (ICCs) based on a random effects model (Model 2) in (Shrout & Fleiss, 1979). ICCs based on a random effects model provide a single index that captures both the rank order consistency and the extent of agreement between the proposed algorithm and the expert (Kelsey, Ornduff, & Alpert, 2007; Kelsey, et al., 1998). Mean and standard deviation of PEP measured by the proposed method and the expert were also calculated.
Box and whisker plots were drawn to analyze the distribution and variability of PEP estimates and their differences, and Bland-Altman plots were used to compare the differences between the algorithm and expert estimated PEPs and analyze their potential agreement at different PEP values across individuals.
Variations in PEP across the night were obtained by averaging the algorithm-estimated PEP over 1-hour time intervals. Mean and standard error were then calculated each hour for the 20 individuals.
3. Results
A total of 454 out of 2000 ICG cycles were scored by the expert as corrupted cycles among which 333 were correctly detected by the proposed algorithm (TP). The algorithm also detected 149 cycles that were not scored by the expert as corrupted (FP). The proposed algorithm achieved an overall accuracy of 87%, overall error of 13%, sensitivity of 73%, specificity of 90%, positive predictive value of 69%, and negative predictive value of 92%, which shows close agreement with the expert (see Table 2).
Table 2.
Confusion table summarizing the performance of the artifact rejection algorithm versus expert.
| Expert | |||
|---|---|---|---|
| N = 2000 | Corrupted cycle | Clean cycle | |
| Algorithm | Corrupted cycle | 333 (TP) | 149 (FP) |
| Clean cycle | 121 (FN) | 1397 (TN) | |
Among the expert-selected corrupted ICG cycles, 9% were classified as below-normal, 54% as normal, and 37% as above-normal amplitude. The artifact rejection algorithm detected 90%, 74%, and 100% of the corrupted cycles with amplitudes below normal, normal, and above normal, respectively, which shows its high accuracy at different levels of ICG signal amplitude.
The proposed artifact rejection algorithm detected 100% of the electrode detachment cases, 90% of high-level movement artifacts, and 71% of the-low level movement artifacts which shows its robustness to different types and levels of artifact.
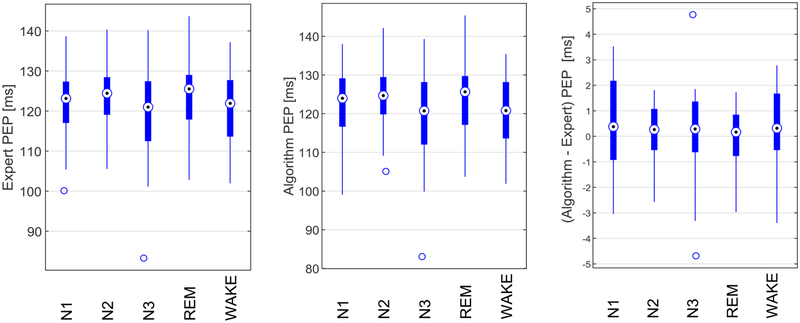
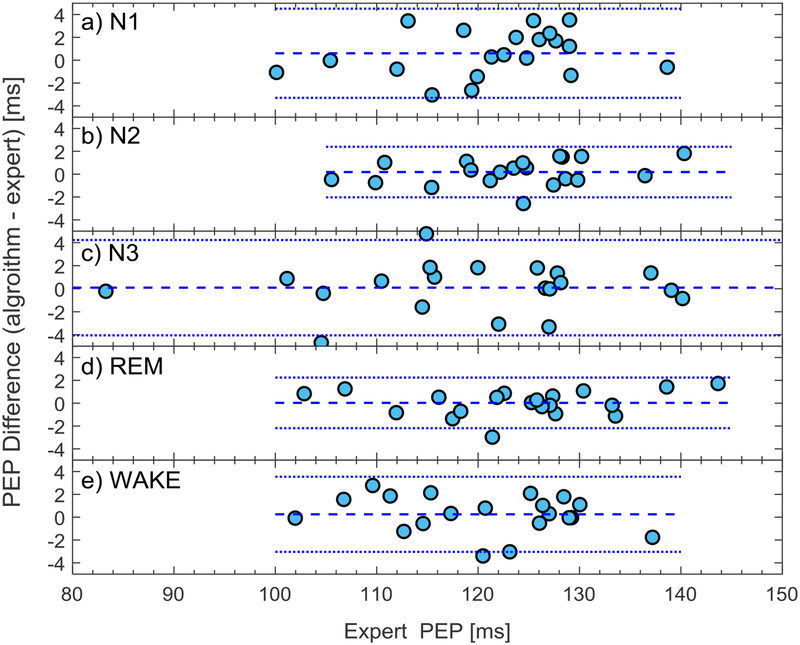
Results of the application of the PEP detection algorithm to the clean ensemble averaged ICG cycles are displayed in Table 3 and Figure 3. The intraclass correlation coefficients were uniformly high, ranging from 0.976 to 0.994, indicating excellent agreement between the proposed algorithm and the expert for clean cycles in each sleep stage, and during in-bed wakefulness (see Table 3). The box plots indicated that the highest variation in both expert and algorithm estimated PEP occurred in N3 sleep stage (see Figure 3). However, the highest variations in the estimation error occurred in N1 and wake stages following by N3. Bland Altman plots show close agreement between the algorithm and the expert at different PEP values across individuals (see Figure 4).
Table 3.
Statistical comparison between the algorithm and expert-determined PEP values across sleep stages and wakefulness in 20 healthy participants.
| Sleep Stage | PEP | Mean (ms) | SD (ms) | ICC* |
|---|---|---|---|---|
| N1 | Expert | 121.42 | 8.93 | 0.976 |
| Algorithm | 122.03 | 9.64 | ||
| N2 | Expert | 123.48 | 8.60 | 0.992 |
| Algorithm | 123.66 | 8.99 | ||
| N3 | Expert | 119.26 | 14.00 | 0.989 |
| Algorithm | 119.36 | 14.29 | ||
| REM | Expert | 123.91 | 10.00 | 0.994 |
| Algorithm | 123.94 | 10.23 | ||
| WAKE | Expert | 120.62 | 9.14 | 0.983 |
| Algorithm | 120.87 | 8.91 |
intraclass correlation coefficient
Figure 3.
Box plot of the expert and algorithm estimated PEPs and their differences. The central circles indicate the median, and the bottom and top edges of the boxes indicate the 25th and 75th percentiles, respectively. The whiskers extend the most extreme data points not considered outliers, and the outliers are plotted individually by the ‘ס’ symbol.
Figure 4.
Bland-Altman plot of the algorithm and expert PEP estimates plotted as the difference against expert in (a) N1, (b) N2, (c) N3, (d) REM, and (e) wake stages. The horizontal dotted lines show the limits of agreement, and the horizontal dashed line shows the bias.
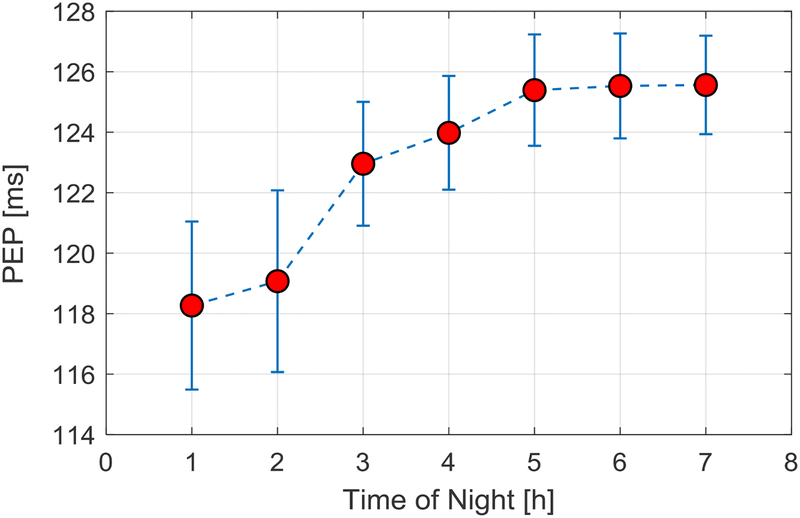
Finally, Figure 5 shows PEP values plotted hourly across the night for the group. As is clearly evident, PEP increases, reflecting reduced sympathetic nervous system activity, across the night.
Figure 5.
PEP values (average ± SEM) plotted for each hour of the night in 20 participants, showing a pattern of increasing PEP across the night.
4. Discussion
Impedance cardiography is an important noninvasive technique for the evaluation of cardiac hemodynamic parameters such as PEP. However, the intrinsic ICG pattern variability between and within individuals and the high sensitivity of the technique to noise and movement artifacts may significantly degrade its accuracy and reliability, especially during prolonged recordings.
A number of automatic algorithms have been developed for the detection and correction of B point on the ICG signal and the estimation of the PEP. However, no fully automatic algorithm exists that can process the simultaneously recorded ECG and ICG signals collected in uncontrolled conditions over extended time periods to obtain a reliable measure of PEP. Visual inspection of data is always necessary before analysis of data collected over extended time periods to identify the corrupted portions of data and exclude them from further analysis.
In this paper, we developed a new ICG artifact rejection technique to detect the ICG corrupted cycles. The algorithm was applied on sleep data to remove the corrupted ICG cycles and was found to closely match the expert visual inspection.
The developed artifact rejection algorithm worked based on measuring the activity (variations) of the ICG signal within each cardiac cycle, where those cycles with lower or higher than normal activity were marked as corrupted cycles. The activity was defined as the standard deviation of normalized ICG cycles where the normalization was performed according to the median ICG signal height. A limitation of the proposed technique is that it does not consider the shape of the ICG signal over each cardiac cycle, and therefore cycles with corrupted shapes that do not have an out-of-range activity index cannot be detected. Defining an index that quantifies the pattern similarity between the ICG cycles and a reference template can solve such issues, and will be addressed in a future work.
Unlike artifact reduction techniques based on ensemble averaging (Cieslak, et al., 2015; Kelsey & Guethlein, 1990; Muzi, et al., 1985; Qu, Zhang, Webster, & Tompkins, 1986; Riese, et al., 2003; Shoemaker, Appel, Kram, Nathan, & Thompson, 1988) and digital filtering (Bagal, Pandey, Naidu, & Hardas, 2018; Chabchoub, Mansouri, & Salah, 2016; Wang, Sun, & Van de Water, 1995) that are based on the assumption that a valid ICG signal always exists and is only affected by noise and artifacts to a certain extent, our proposed artifact rejection algorithm provided a reliable measure of the level of noise and artifacts that can be used for the detection and exclusion of highly corrupted ICG cycles that cannot be recovered. Invalid ICG data such as those due to electrode detachment (see Figure 1, inset c) or high levels of movement (see Figure 1, insets b and d) cannot be recovered by any artifact reduction algorithm. Digital filtering techniques are also not very effective in suppressing artifacts that have spectral overlap with the ICG signal. A possible solution to overcome the limitations of conventional digital filters, is the application of adaptive filters (Barros, Yoshizawa, & Yasuda, 1995; Hu, et al., 2014a; Mallam & Rao, 2016; Ono, et al., 2004; Pandey & Pandey, 2005). However, adaptive filters require an independent signal or noise reference which is not easy to obtain. An accelerometer attached to the body may provide a reference of body movements, however, further study is required to identify if the measured movements are correlated with the movement artifacts induced on ICG signal.
Unlike those artifact detection methods that are based on identifying corrupted cardiac cycles as those with out-of-range parameter values (after detecting signal fiducial points in each cardiac cycle and estimating hemodynamic parameters) (Berntson, Quigley, Jang, & Boysen, 1990; Cybulski, et al., 2017; Forouzanfar, et al., 2018), our proposed artifact rejection method analyzes each ICG cardiac cycle level of noise and artifacts and rejects corrupted cycles prior to fiducial point detection and hemodynamic parameter estimation. Methods based on the detection of hemodynamic parameter outliers can only identify those corrupted cycles that have out-of-range parameter values disregarding those corrupted cycles with within-range but potentially invalid values.
It was found that half of the expert-detected corrupted ICG cycles have normal amplitudes within the clean cycles’ amplitude range. Therefore, using simple thresholding techniques based on the amplitude of the ICG cycles are not effective in detecting corrupted cycles. Though the accuracy of the proposed technique was higher in detecting corrupted cycles with out-of-range values (90% in detecting below-normal and 100% in detecting above-normal cycles), it still achieved high accuracy in detecting corrupted cycles with normal amplitude (74% accuracy). The artifact rejection algorithm also showed high accuracy in detecting different types and levels of artifacts: it detected all the electrode detachment cases and achieved an excellent accuracy of 90% in detecting artifacts caused by high-level movements. The performance of the algorithm slightly reduced to 71% for low-level movement artifacts. The reduction in accuracy for low-level artifacts is naturally expected given that the criterion used to define artifacts (activity index AI) is based on measuring the cycle variations, which has close to normal-range values at lower-level artifacts.
We previously showed that our B-point detection algorithm performed well on short-duration data (~2 minutes) collected from participants sitting quietly (Forouzanfar, et al., 2018). Here, we showed that the algorithm also performed well even when applied on long-duration data collected overnight (~8 hours), during different sleep stages and wakefulness, when it is expected that PEP will vary (Burgess, Penev, Schneider, & Van Cauter, 2004; de Zambotti, et al., 2014; de Zambotti, et al., 2012; de Zambotti, et al., 2013; Trinder, et al., 2001). The algorithm performed well in all sleep stages with small errors and high ICCs against expert visual scoring (Table 3). The Bland-Altman and Box plot analyses confirmed the close agreement between the algorithm and the expert.
There was some variability in the estimation error according to sleep stage, as shown in the box plots, being highest in N1 and wakefulness, which could be associated with the more unstable state of these stages. The smaller number of ICG cycles in N1 and wakefulness datasets (due to the expected lower amount of time spent by participants in these stages across the night) compared to the other sleep stages could also lead to a higher error variation.
The estimated PEP patterns of variation were consistent with those previously reported across stages of sleep (de Zambotti, et al., 2014; de Zambotti, et al., 2012; de Zambotti, et al., 2013) and as a function of time of night (Covassin, de Zambotti, Cellini, Sarlo, & Stegagno, 2012; Trinder, et al., 2001). As is evident from our data, the variation in PEP across the night is greater than variation across stages of sleep. There is a progressive lengthening of PEP with hours of sleep, reflecting a reduction in sympathetic activity, as also shown by others (Covassin, de Zambotti, Cellini, Sarlo, & Stegagno, 2012; Trinder, et al., 2001). This time of night dependency of PEP probably masks sleep stage-related variation in sympathetic activity. For example, it should be noted that PEP was lower during slow-wave sleep (N3) than REM (see Table 3), which reflects the greater prevalence of slow-wave sleep in the first part of the night compared to a greater distribution of REM sleep in the latter part of the night.
A future application of our algorithms in the context of sleep could be to analyze changes in PEP across the sleep onset process, across sleep stage transitions, and across the night in individuals with and without trouble sleeping to investigate possible anomalies in sympathetic withdrawal across sleep-wake transitions and as well as according to time of night. It should be noted that there are other issues with the interpretation of PEP, regardless of accuracy of measurement, such as the influence of the afterload on PEP independent of beta-adrenergic control (Newlin & Levenson, 1979), which needs to be accounted for (Trinder, et al., 2001).
This study was limited to 20 healthy individuals with no history of cardiovascular disease. Further research is needed to validate the performance of algorithms on a larger number of healthy subjects as well as patients with different cardiovascular diseases. Also, in this study, the ICG data were recorded using a 4-lead 8-point electrode connection arrangement and filtered at fixed cutoff frequencies. Further research is needed to verify the performance of the algorithms in other electrode configurations such as band electrodes and at different filter cutoff frequencies. In such settings, the proposed method core components remain the same, but its parameter values may need to be tuned to account for signal and noise variations. It should be noted that the main focus of this paper was on the rejection of noise and artifacts affecting the ICG signal. Given that ECG signal is, in general, more robust to noise and artifacts compared to the ICG signal, and the R peak, even in a noisy ECG signal, is usually easy to detect (compared to the B point on ICG signal which could be very challenging to detect), the main challenge in measuring PEP is the accurate detection of B point.
Based on the Center for Disease Control and Prevention (CDC’s) definition of overweight and obesity in adults, 35% of participants were overweight/obese (BMI > 25 kg m−2). None of them was in the underweight range (BMI < 18.5 kg m−2). An exploratory analysis was performed to assess the performance of the B-point detection algorithm according to BMI categories (normal weight vs overweight/obese). The intraclass correlation of coefficient between the algorithm and the expert was 0.997 for the normal group and 0.991 for the overweight/obese group, showing excellent agreement between the algorithm and expert in both weight categories.
With the advancement in sensing technology, portable wearable solutions for impedance cardiography are quickly growing (Hafid, et al., 2018; Hu, et al., 2014b; Pinheiro, Postolache, & Girão, 2013; Ulbrich, et al., 2014; Weyer, Menden, Leicht, Leonhardt, & Wartzek, 2015; Yazdanian, Mahnam, Edrisi, & Esfahani, 2016). The opportunity to collect continuous information about electromechanical parameters of the cardiovascular system in naturalistic settings needs automatic processing and analysis of noisy data collected over extended time periods without the need for expert inspection and visual scoring. Our proposed algorithms performed well in the analysis sleep data corrupted by movement artifacts and electrode displacements. Future work will involve evaluating the performance of the proposed algorithms in monitoring of PEP in other noisy settings such as full-day routine activities.
Acknowledgments
This research was partly supported by the National Institute on Alcohol Abuse and Alcoholism (NIAAA) R21AA024841 (IMC and MdZ), and by the National Heart, Lung, and Blood Institute (NHLBI) R01HL139652 (MdZ).
References
- Altshuler KZ, & Brebbia R (1967). Body movement artifact as a contaminant in psychophysiological studies of sleep. Psychophysiology, 3, 327–335. doi: 10.1111/j.1469-8986.1967.tb02716.x [DOI] [PubMed] [Google Scholar]
- Árbol JR, Perakakis P, Garrido A, Mata JL, Fernández-Santaella MC, & Vila J (2017). Mathematical detection of aortic valve opening (B point) in impedance cardiography A comparison of three popular algorithms. Psychophysiology, 54(3), 350–357. doi: 10.1111/psyp.12799 [DOI] [PubMed] [Google Scholar]
- Bagal UR, Pandey PC, Naidu SMM, & Hardas SP (2018). Detection of opening and closing of the aortic valve using impedance cardiography and its validation by echocardiography. Biomedical Physics & Engineering Express, 4, 1–12. doi: 10.1088/2057-1976/aa8bf5 [DOI] [Google Scholar]
- Bagley EJ, & El-Sheikh M (2014). Relations between daytime pre-ejection period reactivity and sleep in late childhood. Journal of Sleep Research, 23, 337–340. doi: 10.1111/jsr.12117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barros AK, Yoshizawa M, & Yasuda Y (1995). Filtering noncorrelated noise in impedance cardiography. IEEE Transactions on Biomedical Engineering, 42(3), 324–327. doi: 10.1109/10.364522 [DOI] [PubMed] [Google Scholar]
- Berntson GG, Quigley KS, Jang JF, & Boysen ST (1990). An approach to artifact identification: application to heart period data. Psychophysiology, 27(5), 586–598. doi: 10.1111/j.1469-8986.1990.tb01982.x [DOI] [PubMed] [Google Scholar]
- Burgess HJ, Penev PD, Schneider R, & Van Cauter E (2004). Estimating cardiac autonomic activity during sleep: impedance cardiography, spectral analysis, and Poincare plots. Clinical Neurophysiology, 115(1), 19–28. doi: 10.1016/S1388-2457(03)00312-2 [DOI] [PubMed] [Google Scholar]
- Cacioppo JT, Berntson GG, Binkley PF, Quigley KS, Uchino BN, & Fieldstone A (1994). Autonomic cardiac control. II. Noninvasive indices and basal response as revealed by autonomic blockades. Psychophysiology, 31(6), 586–598. doi: 10.1111/j.1469-8986.1994.tb02351.x [DOI] [PubMed] [Google Scholar]
- Chabchoub S, Mansouri S, & Salah RB (2016). Impedance cardiography signal denoising using discrete wavelet transform. Australasian Physical and Engineering Science in Medicine, 39, 655–663. doi: 10.1007/s13246-016-0460-z [DOI] [PubMed] [Google Scholar]
- Cieslak M, Ryan WS, Babenko V, Erro H, Rathbun ZM, Meiring W, Kelsey RM, Blascovich J, & Grafton ST (2017). Quantifying rapid changes in cardiovascular state with a moving ensemble average. Psychophysiology. doi: 10.1111/psyp.13018 [DOI] [PubMed] [Google Scholar]
- Cieslak M, Ryan WS, Macy A, Kelsey RM, Cornick JE, Verket M, Blascovich J, & Grafton S (2015). Simultaneous acquisition of functional magnetic resonance images and impedance cardiography. Psychophysiology, 52(4), 481–488. doi: 10.1111/psyp.12385 [DOI] [PubMed] [Google Scholar]
- Covassin N, de Zambotti M, Cellini N, Sarlo M, & Stegagno L (2012). Nocturnal cardiovascular activity in essential hypotension: evidence of differential autonomic regulation. Psychosomatic Medicine, 74(9), 952–960. doi: 10.1097/PSY.0b013e318272db69 [DOI] [PubMed] [Google Scholar]
- Cybulski G, Młyńczak M, Zyliński M, Strasz A, Gąsiorowska A, & Niewiadomski W (2017). The Quality of Automatic Artifact Identification in Ambulatory Impedance Cardiography Monitoring In Eskola H, Väisänen O, Viik J, & Hyttinen J (Eds.), IFMBE Proceedings (Vol. 65, pp. 165–168). Singapore: Springer.doi: 10.1007/978-981-10-5122-7_42 [DOI] [Google Scholar]
- de Geus EJC, & van Doornen LJP (1996). Ambulatory assessment of parasympathetic/sympathetic balance by impedance cardiography In Fahrenberg J & Myrtek M (Eds.), Ambulatory assessment: Computer-assisted psychological and psychophysiological methods in monitoring and field studies (pp. 141–163). Ashland, OH, US: Hogrefe & Huber Publishers. [Google Scholar]
- de Zambotti M, Cellini N, Baker FC, Colrain IM, Sarlo M, & Stegagno L (2014). Nocturnal cardiac autonomic profile in young primary insomniacs and good sleepers. International Journal of Psychophysiology, 93(3), 332–339. doi: 10.1016/j.ijpsycho.2014.06.014 [DOI] [PubMed] [Google Scholar]
- de Zambotti M, Covassin N, Cellini N, Sarlo M, Torre J, & Stegagno L (2012). Hemodynamic and autonomic modifications during sleep stages in young hypotensive women. Biological Psychology, 91(1), 22–27. doi: 10.1016/j.biopsycho.2012.05.009 [DOI] [PubMed] [Google Scholar]
- de Zambotti M, Covassin N, Sarlo M, De Min Tona G, Trinder J, & Stegagno L (2013). Nighttime cardiac sympathetic hyper-activation in young primary insomniacs. Clinical Autonomic Research, 23(1), 49–56. doi: 10.1007/s10286-012-0178-2 [DOI] [PubMed] [Google Scholar]
- Debski TT, Kamarck TW, Jennings JR, Young LW, Eddy MJ, & Zhang YX (1991). A computerized test battery for the assessment of cardiovascular reactivity. International Journal of Bio-Medical Computing, 27(3–4), 277–289. doi: 10.1016/0020-7101(91)90068-P [DOI] [PubMed] [Google Scholar]
- Debski TT, Zhang Y, Jennings JR, & Kamarck TW (1993). Stability of cardiac impedance measures: aortic opening (B-point) detection and scoring. Biological Psychology, 36(1–2), 63–74. doi: 10.1016/0301-0511(93)90081-I [DOI] [PubMed] [Google Scholar]
- Ermishkin VV, Kolesnikov VA, & Lukoshkova EV (2014). Age-dependent and pathologic changes in ICG waveforms resulting from superposition of pre-ejection and ejection waves. Physiological Measurement, 35, 943–963. doi: 10.1088/0967-3334/35/6/943 [DOI] [PubMed] [Google Scholar]
- Forouzanfar M, Baker FC, de Zambotti M, McCall C, Giovangrandi L, & Kovacs GTA (2018). Toward a better noninvasive assessment of preejection period: A novel automatic algorithm for B-point detection and correction on thoracic impedance cardiogram. Psychophysiology, 55(8), e13072. doi: 10.1111/psyp.13072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatzke-Kopp L, & Ram N (2018). Developmental dynamics of autonomic function in childhood. Psychophysiology, 55(11), e13218. doi: 10.1111/psyp.13218 [DOI] [PubMed] [Google Scholar]
- Giuliano RJ, Karns CM, Bell TA, Petersen S, Skowron EA, Neville HJ, & Pakulak E (2018). Parasympathetic and sympathetic activity are associated with individual differences in neural indices of selective attention in adults. Psychophysiology, 55(8), e13079. doi: 10.1111/psyp.13079 [DOI] [PubMed] [Google Scholar]
- Hafid A, Benouar S, Kedir–Talha M, Abtahi F, Attari M, & Seoane F (2018). Full Impedance Cardiography Measurement Device Using Raspberry PI3 and System-on-Chip Biomedical Instrumentation Solutions. IEEE Journal of Biomedical and Health Informatics, 22(6), 1883–1894. [DOI] [PubMed] [Google Scholar]
- Hu X, Chen X, Ren R, Zhou B, Qian Y, Li H, & Xia S (2014a). Adaptive Filtering and Characteristics Extraction for Impedance Cardiography. Journal of Fiber Bioengineering and Informatics, 7, 81–90. doi: 10.3993/jfbi03201407 [DOI] [Google Scholar]
- Hu X, Chen X, Ren R, Zhou B, Qian Y, Li H, & Xia S (2014b). Portable Health Monitoring Device for Electrocardiogram and Impedance Cardiography Based on Bluetooth Low Energy. Journal of Fiber Bioengineering and Informatics, 7(3), 397–408. doi: 10.3993/jfbi09201409 [DOI] [Google Scholar]
- Iber C, Ancoli-Israel S, Chesson A, & Quan S (2007). The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specification. Westchester, IL: American Academy of Sleep Medicine. [Google Scholar]
- Kelsey RM, & Guethlein W (1990). An evaluation of the ensemble averaged impedance cardiogram. Psychophysiology, 27(1), 24–33. doi: 10.1111/j.1469-8986.1990.tb02173.x [DOI] [PubMed] [Google Scholar]
- Kelsey RM, Ornduff SR, & Alpert BS (2007). Reliability of cardiovascular reactivity to stress: internal consistency. Psychophysiology, 44(2), 216–225. doi: 10.1111/j.1469-8986.2007.00499.x [DOI] [PubMed] [Google Scholar]
- Kelsey RM, Reiff S, Wiens S, Schneider TR, Mezzacappa ES, & Guethlein W (1998). The ensemble-averaged impedance cardiogram: an evaluation of scoring methods and interrater reliability. Psychophysiology, 35(3), 337–340. doi: 10.1037/e526132012-264 [DOI] [PubMed] [Google Scholar]
- Lozano DL, Norman G, Knox D, Wood BL, Miller BD, Emery CF, & Berntson GG (2007). Where to B in dZ/dt. Psychophysiology, 44(1), 113–119. doi: 10.1111/j.1469-8986.2006.00468.x [DOI] [PubMed] [Google Scholar]
- Mallam M, & Rao KCB (2016). Efficient reference‑free adaptive artifact cancellers for impedance cardiography based remote health care monitoring systems. Springerplus, 770(5), 1–17. doi: 10.1186/s40064-016-2461-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JC, & Horvath SM (1978). Impedance Cardiography. Psychophysiology, 15, 80–91. doi: 10.1111/j.1469-8986.1978.tb01340.x [DOI] [PubMed] [Google Scholar]
- Muzi M, Ebert TJ, Tristani FE, Jeutter DC, Barney JA, & Smith JJ (1985). Determination of cardiac output using ensemble-averaged impedance cardiograms. Journal of Applied Physiology, 58, 200–205. doi: 10.1152/jappl.1985.58.1.200 [DOI] [PubMed] [Google Scholar]
- Nagel JH, Shyu LY, Reddy SP, Hurwitz BE, McCabe PM, & Schneiderman N (1989). New signal processing techniques for improved precision of noninvasive impedance cardiography. Annals of Biomedical Engineering, 17(5), 517–534. doi: 10.1007/BF02368071 [DOI] [PubMed] [Google Scholar]
- Newlin D, & Levenson R (1979). Pre-ejection period: measuring beta-adrenergic influences upon the heart. Psychophysiology, 16(6), 546–553. doi: 10.1111/j.1469-8986.1979.tb01519.x [DOI] [PubMed] [Google Scholar]
- Ono T, Miyamura M, Yasuda Y, Ito T, Saito T, Ishiguro T, Yoshizawa M, & Yambe T (2004). Beat-to-Beat Evaluation of Systolic Time Intervals during Bicycle Exercise Using Impedance Cardiography. Tohoku Journal of Experimental Medicine, 203, 17–29. doi: 10.1620/tjem.203.17 [DOI] [PubMed] [Google Scholar]
- Pandey VK, & Pandey PC (2005). Cancellation of Respiratory Artifact in Impedance Cardiography IEEE Engineering in Medicine and Biology 27th Annual Conference (pp. 5503–5507). Shanghai, China: IEEE. doi: 10.1109/ICDSP.2007.4288551 [DOI] [PubMed] [Google Scholar]
- Pinheiro E, Postolache O, & Girão P (2013). Contactless Impedance Cardiography Using Embedded Sensors. Measurement Science Review, 13(3), 157–164. doi: 10.2478/msr-2013-0025 [DOI] [Google Scholar]
- Qu MH, Zhang YJ, Webster JG, & Tompkins WJ (1986). Motion artifact from spot and band electrodes during impedance cardiography. IEEE Transactions on Biomedical Engineering, 33(11), 1029–1036. doi: 10.1109/TBME.1986.325869 [DOI] [PubMed] [Google Scholar]
- Raza SB, Patterson RP, & Wang L (1992). Filtering respiration and low-frequency movement artefaces from cardiogenic electrical impedance signal. Medical and Biological Engineering and Computing, 30, 557–561. doi: 10.1007/BF02457837 [DOI] [PubMed] [Google Scholar]
- Riese H, Groot PF, van den Berg M, Kupper NH, Magnee EH, Rohaan EJ, Vrijkotte TG, Willemsen G, & de Geus EJ (2003). Large-scale ensemble averaging of ambulatory impedance cardiograms. Behavior Research Methods, Instruments, & Computers, 35(3), 467–477. doi: 10.3758/bf03195525 [DOI] [PubMed] [Google Scholar]
- Schächinger H, Weinbacher M, Kiss A, Ritz R, & Langewitz W (2001). Cardiovascular indices of peripheral and central sympathetic activation. Psychosomatic Medicine, 63(5), 788–796. doi: 10.1097/00006842-200109000-00012 [DOI] [PubMed] [Google Scholar]
- Seery MD, Kondrak CL, Streamer L, Saltsman T, & Lamarche VM (2016). Preejection period can be calculated using R peak instead of Q. Psychophysiology, 53(8), 1232–1240. doi: 10.1111/psyp.12657 [DOI] [PubMed] [Google Scholar]
- Sherwood A, Allen MT, Fahrenberg J, Kelsey RM, Lovallo WR, & Doornen LJP (1990). Methodological Guidelines for Impedance Cardiography. Psychophysiology, 27(1), 1–23. doi: 10.1111/j.1469-8986.1990.tb02171.x [DOI] [PubMed] [Google Scholar]
- Sherwood A, Allen MT, Obrist PA, & Langer AW (1986). Evaluation of Beta-Adrenergic Influences on Cardiovascular and Metabolic Adjustments to Physical and Psychological Stress. Psychophysiology, 23(1), 89–104. doi: 10.1111/j.1469-8986.1986.tb00602.x [DOI] [PubMed] [Google Scholar]
- Shi Q, Heinig A, & Kanoun O (2011). Design and Evaluation of a Portable Device for the Measurement of Bio-impedance- Cardiograph In Kanoun O (Ed.), Lecture Notes on Impedance Spectroscopy: Measurement, Modeling and Applications (pp. 65–72). London, UK.: Taylor & Francis.doi: 10.1201/9781482266894 [DOI] [Google Scholar]
- Shoemaker WC, Appel PL, Kram HB, Nathan RC, & Thompson JL (1988). Multicomponent noninvasive physiologic monitoring of circulatory function. Critical Care Medicine, 16(5). doi: 10.1097/00003246-198805000-00004 [DOI] [PubMed] [Google Scholar]
- Shrout PE, & Fleiss JL (1979). Intraclass correlations: uses in assessing rater reliability. Psychological Bulletin, 86(2), 420–428. doi: 10.1037/0033-2909.86.2.420 [DOI] [PubMed] [Google Scholar]
- Stern HC, Wolf GK, & Belz GG (1985). Comparative measurements of left ventricular ejection time by mechano-, echo- and electrical impedance cardiography. Arzneimittel-Forschung, 35(10), 1582–1586. [PubMed] [Google Scholar]
- Tavakolian K (2016). Systolic Time Intervals and New Measurement Methods. Cardiovascular Engineering and Technology, 7(2), 118–125. doi: 10.1007/s13239-016-0262-1 [DOI] [PubMed] [Google Scholar]
- Trinder J, Kleiman J, Carrington M, Smith S, Breen S, Tan N, & Kim Y (2001). Autonomic activity during human sleep as a function of time and sleep stage. Journal of Sleep Research, 10, 253–264. doi: 10.1046/j.1365-2869.2001.00263.x [DOI] [PubMed] [Google Scholar]
- Ulbrich M, Muhlsteff J, Sipila A, Kamppi M, Koskela A, Myry M, Wan T, Leonhardt S, & Walter M (2014). The IMPACT shirt: textile integrated and portable impedance cardiography. Physiological Measurement, 35(6), 1181–1196. doi: 10.1088/0967-3334/35/6/1181 [DOI] [PubMed] [Google Scholar]
- van Lien R, Schutte NM, Meijer JH, & de Geus EJ (2013). Estimated preejection period (PEP) based on the detection of the R-wave and dZ/dt-min peaks does not adequately reflect the actual PEP across a wide range of laboratory and ambulatory conditions. International Journal of Psychophysiology, 87(1), 60–69. doi: 10.1016/j.ijpsycho.2012.11.001 [DOI] [PubMed] [Google Scholar]
- Visser KR, Mook GA, van der Wall E, & Zijlstra WG (1993). Theory of the determination of systolic time intervals by impedance cardiography. Biological Psychology, 36(1–2), 43–50. doi: 10.1016/0301-0511(93)90079-n [DOI] [PubMed] [Google Scholar]
- Wang X, Sun HH, & Van de Water JM (1995). An advanced signal processing technique for impedance cardiography. IEEE Transactions on Biomedical Engineering, 42(2), 224–230. doi: 10.1109/10.341836 [DOI] [PubMed] [Google Scholar]
- Weyer S, Menden T, Leicht L, Leonhardt S, & Wartzek T (2015). Development of a wearable multi-frequency impedance cardiography device. Journal of Medical Engineering and Technology, 39(2), 131–137. doi: 10.3109/03091902.2014.990161 [DOI] [PubMed] [Google Scholar]
- Yamamoto Y, Mokushi K, Tamura S, Mutoh Y, Miyashita M, & Hamamoto H (1988). Design and implementation of a digital filter for beat-by-beat impedance cardiography. IEEE Transactions on Biomedical Engineering, 35(12), 1086–1090. doi: 10.1109/10.8694 [DOI] [PubMed] [Google Scholar]
- Yazdanian H, Mahnam A, Edrisi M, & Esfahani MA (2016). Design and Implementation of a Portable Impedance Cardiography System for Noninvasive Stroke Volume Monitoring. J Med Signals Sens, 6(1), 47–56. [PMC free article] [PubMed] [Google Scholar]