SPHERICAL U-NET FOR INFANT CORTICAL SURFACE PARCELLATION

Abstract

In human brain MRI studies, it is of great importance to accurately parcellate cortical surfaces into anatomically and functionally meaningful regions. In this paper, we propose a novel end-to-end deep learning method by formulating surface parcellation as a semantic segmentation task on the sphere. To extend the convolutional neural networks (CNNs) to the spherical space, corresponding operations of surface convolution, pooling and upsampling are first developed to deal with data representation on spherical surface meshes, and then spherical CNNs are constructed accordingly. Specifically, the U-Net and SegNet architectures are transformed to the spherical representation for neonatal cortical surface parcellation. Experimental results on 90 neonates indicate the effectiveness and efficiency of our proposed spherical U-Net, in comparison with the spherical SegNet and the previous patch-wise classification method.

1. INTRODUCTION

In human brain MRI studies, it is of great importance to accurately parcellate the convoluted cerebral cortex into anatomically and functionally meaningful regions. Although many methods have been proposed [1–8], they require accurate cortical surface registration and designing of hand-crafted features. Recently, motivated by the powerful feature learning capability of deep learning methods, Wu et al. [9] partially addressed these issues by leveraging a conventional CNN architecture. Specifically, they first mapped the convoluted cortical surface onto a sphere to project intrinsic surface patches into 2D image patches, and then classified these image patches with the conventional CNN. However, this type of patch-wise classification methods for segmentation is usually criticized for two main reasons: 1) It treats each patch independently, thus leading to lots of redundancy due to patch overlapping; 2) There is a trade-off between localization accuracy and spatial contextual information. That is, larger patches require more pooling layers that reduce the localization accuracy, while small patches make the network see only little context [10].

To address these issues, we consider cortical surface parcellation as a vertex-wise labeling task, where fully convolutional networks (FCNs) have shown excellent performance [10–12]. Generally, a FCN is composed of an encoder and a decoder. The encoder is mainly composed of convolution and pooling layers to produce high-level low-resolution feature representation, while the decoder upsamples and increases the resolution by successive layers. This architecture enables an efficient end-to-end training without any pre- or post-processing. Among FCNs, U-Net [10] has been proved to be an effective architecture for biomedical image segmentation [13, 14], due to its superior generalization ability for small training datasets. Thus, we are motivated to extend U-Net for cortical surface parcellation of infants. We also extend the SegNet [11], another popular FCN architecture, for comparison.

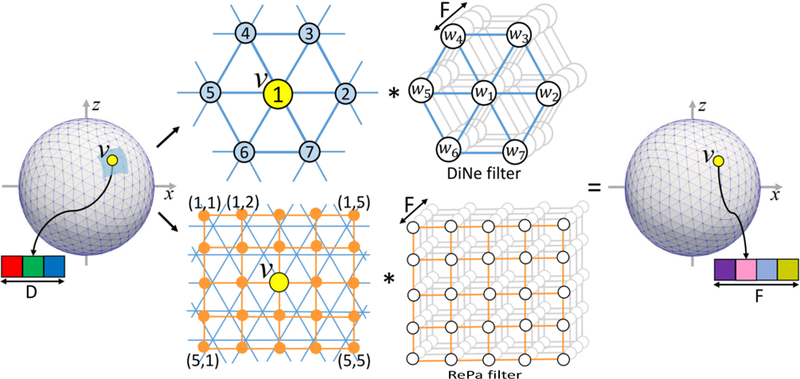
However, these conventional CNNs are not directly applicable to cortical surface meshes, since there is no consistent definition of neighborhood on the surface meshes [15–17]. Seong et al. [18] have attempted to solve this problem by designing filters on the spherical surface for sex classification. Specifically, a rectangular filter samples points in rectangular patches and then rearranges the sampled data for convolution operation, referred as Rectangular Patch (RePa) convolution (bottom row in Fig. 2). However, both methods [9, 18] require a patch extraction step in order to utilize available toolboxes. This patch extraction step has two inherent drawbacks: 1) It involves the re-interpolation process and thus complicates the network and increases computational burden; 2) It also brings feature distortion into the network inevitably.

Fig. 2.

Up: Our proposed DiNe convolution. Down: the RePa convolution in [18]. Both convolutions transfer the input feature map with D channels to the output feature map with F channels.

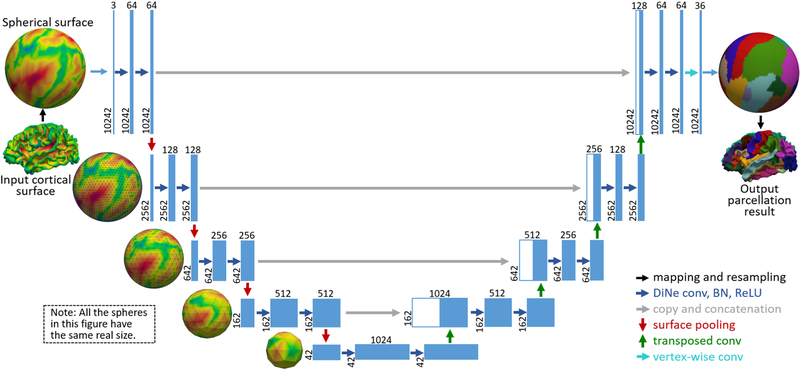
Inspired by the consistent structure of the standard spherical surface meshes, we first developed the spherical surface convolution, pooling and transposed convolution, which are free of patch extraction and interpolation, and thus are much faster and more efficient. Accordingly, we extend the U-Net from image domains to spherical surface domains. Our spherical U-Net architecture (Fig. 1) has been validated on cortical surfaces of 90 infants, achieving higher accuracy and faster speed than other comparison methods.

Fig. 1.

Spherical U-Net architecture for infant cortical surface parcellation. Blue boxes represent feature maps. The number of features is denoted above the box, while the number of vertices is provided at the lower left edge of the box.

2. METHOD

2.1. Convolution and Pooling on Spherical Surface

As shown in Fig. 2, we define a new convolution filter, termed Direct Neighbor (DiNe) filter on the sphere. Since a standard sphere for surface cortical representation is hierarchically generated from icosahedron by adding a new vertex to the center of each edge in each triangle, the number of vertices on the surface are increased from 12 to 42, 162, 642, 2562, 10242, and so on. Hence, each sphere is composed of two types of vertices: 1) 12 vertices with only 5 direct neighbors and 2) remaining vertices with 6 direct neighbors. For the vertices with 6 neighbors, DiNe assigns index 1 to the center vertex and 2–7 to its neighbors sequentially according to the angle between the vector of center vertex to neighboring vertex and the x-axis in the tangent plane. For the 12 vertices with 5 neighbors, DiNe assigns both 1 and 2 to the center vertex, and 3–7 to the neighbors in the same way as vertices with 6 neighbors.

We implement the DiNe convolution using a data reshaping method to formulate the convolution operation as a simple filter weighting process. For each vertex v, on a standard spherical surface with N vertices, at a certain convolution layer with input feature number D and output feature number F, feature data I_v (7×D) from the direct neighbors are first extracted and reshaped into a row vector I v’ (1×7D). Then, iterating over all vertices, we can obtain the full-node filter matrix I (N×7D). By multiplying I with the convolution layer’s filter weight W (7D×F), the output surface O (N×F) with F features can be obtained.

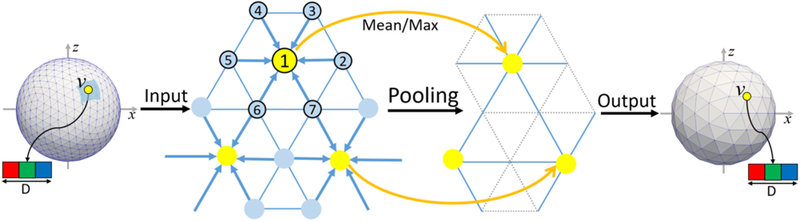
The pooling operation on the spherical surface is performed in the reverse order of the icosahedron expansion process. As shown in Fig. 3, in a pooling layer, for each center vertex v, all feature data I_v (7×D) aggregated from itself and its neighbors are averaged or maximized, and then a refined feature I_v’ (1×D) can be obtained. Meanwhile, the number of vertices is decreased to (N+6)/4.

Fig. 3.

Illustration of the spherical surface pooling operation.

2.2. Upsampling on Spherical Surface

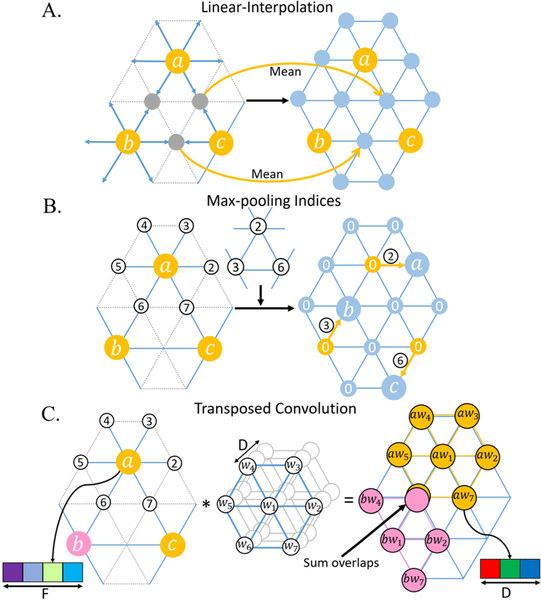
We develop three corresponding upsampling methods by analogy with conventional image upsampling methods.

Linear-Interpolation:

Linear-Interpolation follows the rule of icosahedron expansion, which is the exact opposite of mean-pooling operation. For each new vertex generated from the edge’s center, its feature is linearly interpolated by the two parent vertices of this edge (Fig. 4A).

Fig. 4.

Illustration of three upsampling methods.

Max-pooling Indices:

Max-pooling Indices, introduced by SegNet [11], uses the memorized pooling indices computed in the max-pooling step of the encoder to perform nonlinear upsampling at the corresponding decoder. We transform this method to spherical surface as shown in Fig. 4B. For example, max-pooling indices 2, 3, and 6 are first stored for vertices a, b, and c, respectively. Then at the corresponding upsampling layer, the 2-nd neighbor of a, 3-rd neighbor of a, and 6-th neighbor of c are restored with a, b and c’s value, respectively, and other vertices are set as 0.

Transposed Convolution:

Transposed convolution is also known as fractionally-strided convolution, deconvolution or up-convolution in U-Net [10]. From the perspective of image transformation, transposed convolution restores pixels around every center pixel by sliding-window filtering over all original pixels, then sums where output overlaps. Inspired by this concept, we restore a spherical surface I (N×D, where N denotes the number of vertices, and D denotes the number of features) using DiNe filter to do transposed convolution with every vertex on the pooled surface O (N’×F, N’=(N+6)/4)) and then summing overlap vertices, as shown in Fig. 4C.

2.3. Spherical U-Net Architecture

The proposed spherical U-Net architecture is illustrated in Fig. 1. It has an encoder path and a decoder path each with five resolution steps. Different from the standard U-Net, we replace all 3×3 convolutions with our DiNe convolution, 2×2 up-convolution with our surface transposed convolution, and 2×2 max pooling with our surface mean-pooling. At the final layer, 1×1 convolution is replaced by simple vertex-wise filter weighting to map 64-component feature vector to the desired number of classes. Note that we do not need any tiling strategy in the original U-Net [10] to allow a seamless output segmentation map, because the data flow in our network is on a closed spherical surface.

As RePa convolution is very memory-intensive for a full spherical U-Net experiment, we create a smaller variant UNet18-RePa. It is different from our spherical U-Net in three points: 1) It only consists of three pooling and three transposed convolution layers, thus including only 18 convolution layers; 2) It replaces all DiNe convolution with RePa convolution; 3) The feature number is halved at each corresponding layer. Meanwhile, for a fair comparison, we create a U-Net18-DiNe by replacing all RePa convolution with DiNe convolution in U-Net18-RePa. Moreover, we design a baseline architecture Naive-DiNe with 16 DiNe convolution blocks (DiNe (64 convolution filters), BN, ReLU) and without any pooling and upsampling layers. In addition to the above variants, we study upsampling using Max-pooling Indices (SegNet-Basic) and Linear-Interpolation (SegNet-Inter). Both of them require no learning for upsampling and thus are created in a SegNet style. They are different from our spherical U-Net in two points: 1) There is no copy and concatenation path in both models; 2) For upsampling, SegNet-Basic uses Max-pooling Indices and SegNet-Inter uses Linear-Interpolation.

3. EXPERIMENTS

3.1. Dataset and Image Processing

In experiments, we used the infant brain MRI dataset in [9, 19], with 90 term-born neonates. All images were processed using a standard infant-specific pipeline [20]. Each vertex on the cortical surface was coded with 3 shape attributes, i.e., the mean curvature, sulcal depth, and average convexity. Our aim is to parcellate these vertices into 36 regions for each hemisphere. To utilize the proposed method, each inner cortical surface was mapped onto a standard sphere [21]. To have a uniform spherical representation, we resampled each spherical surface using 10,242 vertices without any surface registration [22]. Each cortical shape attribute was normalized between −1 and 1. Same as in Wu et al. [9], a 3-fold cross-validation was adopted and Dice ratio was used to measure the overlap between the manual parcellation and the automatic parcellation.

3.2. Training

We trained all the variants using mini-batch (1 surface per batch) stochastic gradient descent (SGD) with initial learning rate 0.1 and momentum 0.99 with weight decay 0.0001. Given different network architectures, we used a self-adaption strategy for updating learning rate, which reduces the learning rate by a factor of 5 once training Dice stagnates for 2 epochs. This strategy allowed us to achieve a gain in Dice ratio around 3% for most architectures. We used the cross-entropy loss as the objective function for training. The other hyper-parameters were empirically set by babysitting the training process at the first-fold cross-validation and the optimal parameters were reused for other two-fold cross-validation. We also augmented the training data by randomly rotating each sphere to generate more training surfaces.

3.3. Results

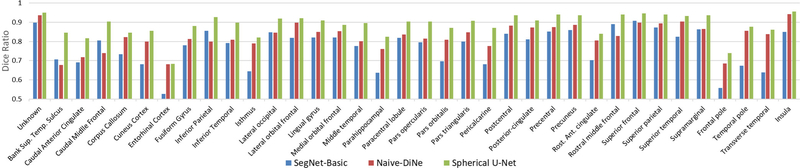
We report the means and standard deviations of Dice ratios, as well as the number of parameters, memory storage and time for one inference on a NVIDIA Geforce GTX1060 GPU, in Table 1. Fig. 5 further provides a quantitative comparison of Dice ratios for each of the 36 cortical ROIs.

Table 1.

Comparison of different network architectures.

Architectures	Params (MB)	Storage (MB)	Infer time (ms)	Dice (%)
Learning for upsampling
U-Net	26.9	1635	18.3	88.87+2.43
U-Netl8-DiNe	1.7	955	8.9	88.05+2.46
U-Netl8-RePa	5.2	5047	64.5	88.28+2.50
No learning for upsampling
Naive-DiNe	0.4	1499	15.8	81.74+4.96
SegNet-Basic	14.5	1341	113.5	78.31+4.62
SegNet-Inter	22.0	1533	20.1	75.12+8.39
Results reported in Wu et al. [9]
Multi-atlas with majority voting				84.54+0.08
DCNN without graph cuts				86.18+0.06
DCNN with graph cuts				87.06+0.06

Fig. 5.

Quantitative comparison of different models for each cortical ROI.

Table 1 shows the three spherical U-Net architectures consistently achieve better results than other methods, indicating that the spherical U-Net has strong ability to capture fine-grained features from the concatenation path and learnable upsampling method. On the contrary, without pooling and upsampling layers, Naive-DiNe can only see maximum 16 hops from the center vertex, of which the receptive filed is too small to capture key information for vertex’s labeling. RePa convolution is obviously more time-consuming and memory-intensive, while our proposed DiNe convolution is 7 times faster than RePa, 5 times smaller on memory storage and 3 times lighter on model size. When comparing U-Net with SegNet, the Dice difference is likely caused by the different information passed from the encoder path to the decoder path, which means feature map concatenation may be more important in spherical surface data than Max-pooling Indices.

Fig. 6 provides a visual comparison between parcellation results using different models. We can see that the results of the spherical U-Net show high consistency with the manual parcellations without isolated noisy labels. As in [9], we also incorporate the graph cuts method for post-processing the output of our spherical U-Net, but this step has no improvement in quantitative results. This may indicate that our spherical U-Net is capable of learning spatially-consistent information in an end-to-end way without postprocessing.

Fig. 6.

Visual comparison of cortical parcellation results using different methods. (a) Manual parcellation; (b) SegNet-Basic; (c) Naive-DiNe; (d) Spherical U-Net.

4. CONCLUSION

In this paper, we transformed the conventional CNNs into the spherical CNNs by developing respective methods for surface convolution, pooling, and upsampling. We designed a spherical U-Net architecture using DiNe convolution and transposed convolution based on the spherical cortical representation and successfully applied it to infant cortical surface parcellation. Comparisons with several architecture variants have validated the accuracy and speed of the proposed method. We will release the PyTorch [23] implementation of our spherical U-Net soon.