Abstract
Understanding chemical mechanisms requires estimating dynamical statistics such as expected hitting times, reaction rates, and committors. Here, we present a general framework for calculating these dynamical quantities by approximating boundary value problems using dynamical operators with a Galerkin expansion. A specific choice of basis set in the expansion corresponds to the estimation of dynamical quantities using a Markov state model. More generally, the boundary conditions impose restrictions on the choice of basis sets. We demonstrate how an alternative basis can be constructed using ideas from diffusion maps. In our numerical experiments, this basis gives results of comparable or better accuracy to Markov state models. Additionally, we show that delay embedding can reduce the information lost when projecting the system’s dynamics for model construction; this improves estimates of dynamical statistics considerably over the standard practice of increasing the lag time.
I. INTRODUCTION
Molecular dynamics simulations allow chemical mechanisms to be studied in atomistic detail. By averaging over trajectories, one can estimate dynamical statistics such as mean first-passage times or committors. These quantities are integral to chemical rate theories.1–3 However, events of interest often occur on time scales several orders of magnitude longer than the time scales of microscopic fluctuations. In such cases, collecting chemical-kinetic statistics by integrating the system’s equations of motion and directly computing averages (sample means) requires prohibitively large amounts of computational resources.
The traditional way to address this separation in time scales was through theories of activated processes.2,4 By assuming that the kinetics are dominated by passage through a single transition state, researchers were able to obtain approximate analytical forms for reaction rates and related quantities. These expressions can be connected with microscopic simulations by evaluating contributing statistics, such as the potential of mean force and the diffusion tensor.5–7 However, many processes involve multiple reaction pathways, such as the folding of larger proteins.8,9 In these cases, it may not be possible in practice, or even in principle, to represent the system in a way that the assumptions underlying theories of activated processes are reasonable.
More recently, transition path sampling algorithms, which focus sampling on the pathways connecting metastable states, have been used to estimate rates.10,11 Given such trajectories, dynamical statistics, such as committors, can be learned.12,13 Short trajectories reaching the metastable states can be harvested efficiently, but sampling long trajectories, especially those including multiple intermediates, becomes difficult.14,15 Another approach is to use splitting schemes, which aim to efficiently direct sampling by intelligently splitting and reweighting short trajectory segments.16–25 Some of these methods can yield results that are exact up to statistical precision, with minimal assumptions about the dynamics.20–25 However, the efficiency of these schemes is generally dependent on a reasonable choice of low-dimensional collective variable (CV) space: a projection of the system’s phase space. Not only can this choice be nonobvious,12 but it can also be statistic specific. Moreover, starting and stopping the molecular dynamics many times based on the values of the CVs may be impractical depending on the implementation of the molecular dynamics engine and the overhead associated with computational communication.
A third approach is the construction of Markov state models (MSMs).26–28 Here, the dynamics of the system are modeled as a discrete-state Markov chain with state-to-state transition probabilities estimated from previously sampled data. Projecting the dynamics onto a finite-dimensional model introduces a systematic bias, although this bias goes to zero in an appropriate limit of infinitely many states.29 While MSMs were initially developed as a technique for approximating the slowest eigenmodes of a system’s dynamics,26 MSMs can also be used to calculate dynamical statistics for the study of kinetics.30–32 Since MSM construction only requires time pairs separated by a single lag time, one has more freedom in how one generates the molecular dynamics data. In particular, if the lag time is sufficiently short, MSMs can be used to estimate rates even in the absence of full reactive trajectories. Constructing an efficient MSM requires projection onto CVs, and the systematic error in the resulting estimates can depend strongly on how they are defined. However, the CV space can generally be higher dimensional since it is only used to define Markov states.
It has been shown that calculating the system’s eigenmodes with MSMs can be generalized to a basis expansion of the eigenmodes using an arbitrary basis set.29,33,34 In this paper, we show that a similar generalization is possible for other dynamical statistics. Rather than solving eigenproblems, these quantities solve linear boundary value problems. This raises additional challenges: not only do the solutions obey specific boundary conditions, but the resulting approximations are also sensitive to the choice of lag time. We provide numerical schemes to address these difficulties.
We organize our work as follows. In Sec. II, we give background on the transition operator and review both MSMs and more general schemes for data-driven analysis of the spectrum of dynamical operators. We then continue our review with the connection between operator equations and chemical kinetics in Sec. III. In Sec. IV, we present our formalism. We discuss the choice of basis set in Sec. V and introduce a new algorithm for constructing basis sets that obey the boundary conditions our formalism requires. In Sec. VI, we show that delay embedding can recover information lost in projecting the system’s dynamics onto a few degrees of freedom, negating the need for increasing the scheme’s lag time to enforce Markovianity. We then demonstrate our algorithm on a collection of long trajectories of the Fip35 WW domain dataset in Sec. VII and conclude in Sec. VIII.
II. BACKGROUND
Many key quantities in chemical kinetics can be expressed through solutions to linear operator equations. Key to this formalism is the transition operator. We begin by assuming that the system’s dynamics are given by a Markov process ξ(t) that is time-homogeneous, i.e., that the dynamics are time-independent. We do not put any restrictions on the nature of the system’s state space. For example, if ξ is a diffusion process, the state space could be the space of real coordinates, . Similarly, for a finite-state Markov chain, it would be a finite set of configurations. We also do not assume that the dynamics are reversible or that the system is in a stationary state unless specifically noted.
The transition operator at a lag time of s is defined as
| (1) |
where f is a function on the state space and E denotes expectation. Note that due to time-homogeneity, we could just as easily have defined the transition operator with the time pair in place of . Depending on the context in question, may also be referred to as the Markov or Koopman operator.35,36 We use the term transition operator as it is well established in the mathematical literature and stresses the notion that is the generalization of the transition matrix for finite-state Markov processes. For instance, the requirement that the rows of a transition matrix sum to one generalizes to
| (2) |
Studying the transition operator provides, in principle, a route to analyzing the system’s dynamics. Unfortunately, is often either unknown or too complicated to be studied directly. This has motivated research into data-driven approaches that instead treat indirectly by analyzing sampled trajectories.
A. Markov state modeling
One approach to studying chemical dynamics through the transition operator is the construction of Markov state models.26–28 In this technique, one constructs a Markov chain on a finite state space to model the true dynamics of the system. The transition matrix of this Markov chain is then taken as a model for the true transition operator.
To construct an MSM from trajectory data, we partition the system’s state space into M nonoverlapping sets. We refer to these sets as Markov states and denote them as Si. Now, let μ be an arbitrary probability measure. If the system is initially distributed according to μ, the probability of transitioning from a set Si to Sj after a time s is given by
| (3) |
where is the indicator function
| (4) |
Here, ∫ f(x)μ(dx) is the expectation with respect to the probability measure μ.37 When μ has a probability density function, this integral is the same as the integral against the density, and in a finite state space, it would be a weighted average over states. This formalism lets us treat both continuous and discrete state spaces with one notation.
Because the sets Si partition the state space, a simple calculation shows that the elements in each row of Pij sum to one. Pij therefore defines a transition matrix for a finite-state Markov process, where state i corresponds to the set Si. The dynamics of this process are a model for the true dynamics, and Pij is a model for the transition operator.
To build this model, we construct an estimate of Pij from sampled data. A simple approach is to collect a dataset consisting of N time pairs, (Xn, Yn). Here, the initial point Xn is drawn from μ, and Yn is collected by starting at Xn and propagating the dynamics for time s. Note that since the choice of μ in (3) is relatively arbitrary, it can be defined implicitly through the sampling procedure. For instance, one can construct a dataset by extracting all pairs of points separated by the lag time s from a collection of trajectories; since we have assumed the dynamics are time-homogeneous, the actual physical time at which Xn was collected does not matter. We then define μ to be the measure from which our initial points were sampled. With this dataset, Pij is now approximated as
| (5) |
Like Pij, (5) defines a valid transition matrix. This is not the only approach for constructing estimates of Pij. One commonly used approach modifies this procedure to ensure that gives reversible dynamics. In this approach, one adds a self-consistent iteration that seeks to find the reversible transition matrix with the maximum likelihood given the data.38,39
The MSM approach has many attractive features. Since Pij defines a valid transition matrix, the MSM defines a Markov chain that can be used as a general model for the dynamics. This model can then be simplified by merging the Markov sets to improve interpretability.28,40,41 MSMs can also be used to estimate spectral information associated with the transition operator, such as its eigenvalues and eigenvectors, as we discuss in further detail in Sec. II B.26,27,29,39 Finally, MSMs can be used to calculate a wide class of dynamical quantities, including committors, reaction rates, and expected hitting times.30–32 Importantly, as constructing MSMs only requires datapoints separated by a short lag time, these long-time dynamical quantities can be evaluated using a collection of short trajectories.42 In this paper, we focus exclusively on the latter application and consider MSMs as a technique for calculating the dynamical quantities required in rate theories.
The accuracy with which Pij approximates depends strongly on the choice of the sets Si, and choosing good sets is a nontrivial problem in high-dimensional state spaces.43–47 To address this issue, states are generally constructed by projecting the system’s state space onto a CV space. Sets are then defined by either gridding the CV space or clustering sampled configurations based on the values of their CVs. Unfortunately, when gridding, the number of states grows exponentially with the dimension of the CV space. This is not necessarily the case for partitioning schemes based on data clustering, and the recent work in this direction appears promising.39,48–52 In particular, recent approaches have used variational principles associated with the spectrum of to give a quantitative notion of approximation quality across clustering procedures.34,53–57 However, effectively clustering high-dimensional data is a nontrivial problem,58,59 and constructing an MSM that accurately reflects the dynamics may still require knowledge of a good, relatively low-dimensional CV space.43,44,60
B. Data-driven solutions to eigenfunctions of dynamical operators
A related approach to characterizing chemical systems is to estimate the eigenfunctions and eigenvalues of operators associated with the system’s dynamics from sampled data.36 These separate the dynamics by time scale: eigenfunctions with larger eigenvalues correlate with the system’s slower degrees of freedom. These eigenfunctions and eigenvalues can often be approximated from trajectory data, even when the transition operator is unknown. Multiple schemes that attempt this have been proposed, often independently, in different fields.26,33,34,61–67 We refer to the family of these techniques using the umbrella term Dynamical Operator Eigenfunction Analysis (DOEA) for brevity and convenience. In this subsection, we summarize a simple DOEA scheme for the transition operator for the reader’s convenience, largely following Ref. 63. We refer the reader to Ref. 36 for a discussion of other schemes.
Here, we consider the solution to the eigenproblem
| (6) |
We approximate ψl as a sum of basis functions ϕj with unknown coefficients aj,
| (7) |
This is an example of the Galerkin approximation of (6),26 a formalism we cover more closely in Sec. IV.
We now assume our data take the form discussed in Sec. II A. Substituting the basis expansion into (6), multiplying by ϕi(x), and taking the expectation against μ, we obtain the matrix equation
| (8) |
where Kij and Sij are defined as
| (9) |
| (10) |
respectively. The matrix elements can be approximated as
| (11) |
| (12) |
We substitute these approximations into (8) and solve for estimates of ai and λl. Equation (7) can then be used to give an approximation for ψl.
DOEA schemes are closely linked to MSMs. Using the indicator functions from Sec. II A is mathematically equivalent to solving for the eigenfunctions of Pij. Indeed, one of the first uses for MSMs was for approximating the eigenfunctions and eigenvalues of the transition operator.26,29
The use of more general basis sets in DOEA allows information to be more easily extracted from high-dimensional CV spaces and gives added flexibility in algorithm design.43,44,61,68,69 For instance, time-lagged independent component analysis (TICA) corresponds to a basis of linear functions and is commonly applied as a preprocessing step to generate CVs for MSM construction.43,44,61 Alternatively, variational principles can be exploited to obtain the eigenfunctions of for reversible dynamics (variational approach of conformation dynamics, VAC)34 and, more generally, for the singular value decomposition of (the variational approach for Markov processes, VAMP).54,55 These principles suggest cost functions that can be used to assess how well a basis recapitulates the spectral properties of .34,55,70 Furthermore, by directly minimizing these cost functions, one can construct nonlinear basis sets using machine learning approaches such as tensor-product algorithms or neural networks.54,71
While attempts have been made to define a theory of chemical dynamics purely in terms of the transition operator’s eigenfunctions and eigenvalues,53 most chemical theories require dynamical quantities, such as committors and mean first-passage times. In this work, we show that it is possible to construct estimates of these quantities using a general basis expansion. Just as DOEA schemes extend MSM estimates of spectral properties to general basis functions, our formalism generalizes the MSM estimation of the quantities used in rate theory.
III. THE GENERATOR AND CHEMICAL KINETICS
Many key quantities in chemical kinetics solve operator equations acting on functions of the state space. Below, we give a quick review of this formalism, detailing a few examples of chemically relevant quantities that can be expressed in this manner. These include statistics such as the mean first-passage time, forward and backward committors, and autocorrelation times. In particular, many of these operator equations are examples of Feynman-Kac formulas. For an in-depth treatment of this formalism, we refer the reader to Refs. 72 and 73.
In this work, we focus on analyzing data gathered from experiments or simulations. We expect the data to consist of a series of measurements collected at a fixed time interval. Therefore, rather than considering the dynamics of ξ(t), we will consider the dynamics of a discrete-time process Ξ(t) constructed by recording ξ every Δt units of time. If Δt is sufficiently small, this should not appreciably change any kinetic quantities.
In the discussion that follows, we choose to work with the generator of Ξ(t), defined as
| (13) |
instead of the transition operator. This makes no mathematical difference, but using simplifies the presentation. We also stress that, with the exception of (24), the equations that follow hold only for a lag-time of s = Δt. For larger lag times, i.e., s > Δt, these equations only hold approximately. This is discussed further in Sec. VI.
A. Equations using the generator
We begin by considering the mean first-passage time and forward committor, two central quantities in chemical kinetics.2,74,75 Let A and B be disjoint subsets of state space and let τA be the first time the system enters A,
| (14) |
The mean first-passage time is the expectation of τA, conditioned on the dynamics starting at x,
| (15) |
Note that 1/mA(x) is a commonly used definition of the rate.2 The forward committor is defined as the probability of entering B before A, conditioned on starting at x,
| (16) |
Both of these quantities solve operator equations using the generator. The mean first-passage obeys the operator equation
| (17) |
Here, Ac denotes the set of all state space configurations not in A. Equation (17) can be derived by conditioning on the first step of the dynamics. For all x in Ac, we have
where the second line follows from the time-homogeneity of Ξ. Rearranging then gives (17).
We can show that the forward committor obeys
| (18) |
by similar arguments. We introduce the random variable
| (19) |
For all x outside A and B, we can then write
which gives (18) on rearranging.
B. Expressions using adjoints of the generator
Additional quantities can be characterized using adjoints of the generator. We reintroduce the sampling measure μ from Sec. II and define the inner product
| (20) |
Equipped with this inner product, the space of all functions that are square-integrable against μ forms a Hilbert space that we denote as . The unweighted adjoint of is the operator such that for all u and in the Hilbert space,
| (21) |
We now assume that the system has a unique stationary measure. The change of measure from μ to the stationary measure is defined as the function π such that
| (22) |
or equivalently,
| (23) |
holds for all functions f. As an example, if the dynamics are stationary at thermal equilibrium, we might have
where H(x) is the system’s Hamiltonian, T is the system’s temperature, and kB is the Boltzmann constant. However, this relation is not necessarily true for general state spaces or for nonequilibrium stationary states.
The change of measure to the stationary measure can be written as the solution to an expression with . Interpreting (23) as an inner product, the definition of the adjoint implies
for all f, or equivalently,
| (24) |
The other equations may use weighted adjoints of . Let p be the change of measure from μ to another, currently unspecified measure. The p-weighted adjoint of is the operator such that
| (25) |
A few manipulations show that the weighted adjoint can be expressed as
| (26) |
This reduces to the unweighted adjoint when p(x) = 1.
One example of a formula that uses a weighted adjoint is a relation for the backward committor. The backward committor is the probability that, if the system is observed at configuration x and the system is in the stationary state, the system exited state A more recently than state B. It satisfies the equation
| (27) |
Finally, we note that some quantities in chemical dynamics require the solution to multiple operator equations. For instance, in transition path theory3 the total reactive current and reaction rate between A and B require evaluating the backward committor and the forward committor, followed by another application of the generator. The total reactive current from B to A is given by
| (28) |
Here, C is a set that contains B but not A. The reaction rate constant is then given by
| (29) |
We derive these expressions in Sec. S3 of the supplementary material through arguments very similar to those presented in Ref. 76.
Evaluating the integrated autocorrelation time (IAT) of a function requires estimating π, as well as solving an equation using the generator. For a function with ∫ f(x)π(x)μ(dx) = 0, the IAT is the sum over the correlation function
| (30) |
and, using the Neumann series representation77 of the appropriate pseudoinverse of , can be expressed as
| (31) |
where ω is the solution to the equation
| (32) |
constrained to have ∫ ω(x)π(x)μ(dx) = 0.
Note that although the quantities mentioned above give us information about the long-time behavior of the system, the formalism introduced here only requires information over short time intervals. This suggests that solving these equations directly could lead to a numerical strategy for estimating these long-time statistics from short-time data.
IV. DYNAMICAL GALERKIN APPROXIMATION
Inspired by the theory behind DOEA and MSMs, we seek to solve the equations in Sec. III in a data-driven manner. We first note that the equations follow the general form
| (33) |
or
| (34) |
Here, D is a set in state space that constitutes the domain, g is the unknown solution, and h and b are known functions. If b is zero everywhere or Dc is empty, we say the problem has homogeneous boundary conditions.
If the generator and its adjoints are known, these equations can, in principle, be solved numerically.78–80 However, this is generally not the case, and even if the operators are known, the dimension of the full state space is often too high to allow numerical solution. In our approach, we use approximations similar to (11) and (12) to estimate these quantities from trajectory data. This procedure only requires collections of short trajectories of the system and works when the dynamical operators are not known explicitly.
We explicitly derive the scheme for operator equations using the generator; the required modifications for equations using an adjoint require only slight modification, and are discussed at the end of Secs. IV B and IV C. We construct an approximation of the operator equation through the following steps:
-
1.
Homogenize boundary conditions: If necessary, rewrite (33) as a problem with homogeneous boundary conditions using a guess for g.
-
2.
Construct a Galerkin scheme: Approximate the solution as a sum of basis functions and convert the result of step 1 into a matrix equation.
-
3.
Approximate inner products with trajectory averages: Approximate the terms in the Galerkin scheme using trajectory averages and solve for an estimate of g.
Since we use dynamical data to estimate the terms in a Galerkin approximation, we refer to our scheme as Dynamical Galerkin Approximation (DGA).
A. Homogenizing the boundary conditions
First, we rewrite (33) as a problem with homogeneous boundary conditions. This allows us to enforce the boundary conditions in step 2 by working within a vector space where every function vanishes at the boundary of the domain. If the boundary conditions are already homogeneous, either because b is explicitly zero or because D includes all of state space, this step can be skipped. We introduce a guess function r that is equal to b on Dc. We then rewrite (33) in terms of the difference between the guess and the true solution
| (35) |
This converts (33) into a problem with homogeneous boundary conditions
| (36) |
| (37) |
A naive guess can always be constructed as
| (38) |
but if possible, one should attempt to choose r so that γ can be efficiently expressed using the basis functions introduced in step 2.
B. Constructing the Galerkin scheme
We now approximate the solution of (36) and (37) via basis expansion using the formalism of the Galerkin approximation. Equation (36) implies that
| (39) |
holds for all u in the Hilbert space . This is known as the weak formulation of (36).81
The space is typically infinite dimensional. Consequently, we cannot expect to ensure that (39) holds for every function in . We therefore attempt to solve (39) only on a finite-dimensional subspace of . To do this, we introduce a set of M linearly independent functions denoted as that obey the homogeneous boundary conditions; we refer to these as the basis functions. The space of all linear combinations of the basis functions forms a subspace in which we call the Galerkin subspace, G. By construction, every function in G obeys the homogeneous boundary conditions. We now project (39) onto this subspace, giving the approximate equation
| (40) |
for all ũ in G. Here, is an element of G approximating γ. Constructing G using a linear combination of basis functions that obey the homogeneous boundary conditions ensures that obeys the homogeneous boundary conditions as well. If we had constructed G using arbitrary basis functions, this would not be true. As we increase the dimensionality of G, we expect the error between γ and to become arbitrarily small.
Since ũ is in G, it can be written as a linear combination of basis functions. Consequently, if
holds for all ϕi, then (40) holds for all ũ. Moreover, the construction of G implies that there exist unique coefficients aj such that
| (41) |
enabling us to write
| (42) |
where
| (43) |
| (44) |
| (45) |
If the terms in (43)–(45) are known, (42) can be solved for the coefficients aj, and an estimate of g can be constructed as
| (46) |
Since is zero on Dc and r obeys the inhomogeneous boundary conditions by construction,
| (47) |
Consequently, our estimate of g obeys the boundary conditions.
A similar scheme can be constructed for equations with a weighted adjoint by adding one additional step to the procedure. After homogenizing the boundary conditions, we multiply both sides of (36) by p. We then proceed as before and obtain (42) with terms defined as
| (48) |
| (49) |
| (50) |
C. Approximating inner products through Monte Carlo
Solving for aj in (41) requires estimates of the other terms in (42). In general, these terms cannot be evaluated directly, due to the complexity of the dynamical operators and the high dimensionality of these integrals. However, we can estimate these terms using trajectory averages, in the style of the estimates in (11). Let ρΔt be the joint probability measure of Ξ(0) and Ξ(Δt), such that for two sets X and Y in state space,
| (51) |
We observe that
| (52) |
We now assume that we have a dataset of the form described in Sec. II A, with a lag time of Δt. Since each pair is a draw from ρΔt, (52) can be approximated using the Monte Carlo estimate
| (53) |
Similarly, inner products of the form can be estimated as
| (54) |
If the Galerkin scheme arose from an equation with a weighted adjoint, evaluating the expectations in (48) and (50) may require p to be known a priori. However, if p = π, one can construct an estimate of π by applying the DGA framework to Eq. (24).
D. Pseudocode
The DGA procedure can thus be summarized as follows:
-
1.
Sample N pairs of configurations , where Yn is the configuration resulting from propagating the system forward from Xn for time Δt.
-
2.
Construct a set of M basis functions ϕi obeying the homogeneous boundary conditions and, if needed, the guess function r.
-
3.
Estimate the terms in (42) using the expressions in Sec. IV C.
-
4.
Solve the resulting matrix equations for the coefficients and substitute them into (46) to construct an estimate of the function of interest.
Some DGA estimates may require additional manipulation to ensure physical meaning. For instance, changes of measure and expected hitting times are nonnegative, and committors are constrained to be between zero and one. These bounds are not guaranteed to hold for estimates constructed through DGA. To correct this, we apply a simple postprocessing step and round the DGA estimate to the nearest value in the range. Alternatively, constraints on the mean of the solution [e.g., that for ω below (32)] can be applied by subtracting a constant from the estimate.
Finally, many dynamical quantities require the evaluation of additional inner products. For instance, to estimate the autocorrelation time, tf, one must construct approximations to ω and π and set ω to have zero mean against π(x)μ(dx). One would then evaluate the numerator and denominator of (31) using (54).
To aid the reader in constructing estimates using this framework, we have written a Python package for creating DGA estimates.82 This package also contains code for constructing the basis set we introduce in Sec. V. As part of the documentation, we have included Jupyter notebooks to aid the reader in reproducing the calculations in this work.
E. Connection with other schemes
As we have previously discussed, the DGA formalism is closely related to DOEA. Rather than considering the solution for a linear system, we could construct a Galerkin scheme for the eigenfunctions of . Since and have the same eigenfunctions, in the limit of infinite sampling and an arbitrarily good basis, this would give equivalent results to the scheme in Sec. II B. DOEA techniques have also been extended to solve (24).83 A similar algorithm for addressing boundary conditions has also been suggested in the context of the data-driven study of partial differential equations and fluid flows.84
Our scheme is also closely related to Markov state modeling. Let ϕi be a basis set of indicator functions on disjoint sets Si covering the state space. Under minor restrictions, applying DGA with this basis is equivalent to estimating the quantities in Sec. III with an MSM. We give a more thorough treatment in Sec. S1 of the supplementary material; here, we quickly motivate this connection by examining (43) for this particular choice of basis. We note that we can divide both sides of (42) by without changing the solution. For this choice of basis, we would then have
| (55) |
where P is the MSM transition matrix defined in (3) and I is the identity matrix. Because of this similarity, we refer to a basis set constructed in this manner as an “MSM” basis.
V. BASIS CONSTRUCTION USING DIFFUSION MAPS
One natural route to improving the accuracy of DGA schemes is to improve the set of basis functions ϕi, thus reducing the error caused by projecting the operator equation onto the finite-dimensional subspace. Various approaches have been used to construct basis sets for describing dynamics in DOEA schemes.43,44,61,68,69 However, if Dc is nonempty, these functions cannot be used in DGA. In particular, the linear basis in TICA cannot be used. Here, we provide a simple method for constructing basis functions with homogeneous boundary conditions based on the technique of diffusion maps.85,86
Diffusion maps are a technique shown to have success in finding global descriptions of molecular systems from high-dimensional input data.87–92 A simple implementation proceeds by constructing the transition matrix
| (56) |
where Kε is a kernel function. This function decays exponentially with the distance between datapoints xm and xn at a rate set by ε. Multiple choices of Kε exist; we give the algorithm used to construct the kernel in Sec. S2 of the supplementary material. The eigenvectors of PDMAP with M highest positive eigenvalues were historically used to define a new coordinate system for dimensionality reduction. They can also be used as a basis set for DOEA and similar analyses.66,68,93 Here, we extend this line of research, showing that diffusion maps can also be used to construct basis functions that obey homogeneous boundary conditions on arbitrary sets as required for use in DGA. We note that the diffusion process represented by PDMAP is not intended as an approximation of the dynamics, but rather as a tool for building the basis functions ϕi. In particular, while the PDMAP matrix is typically reversible, this imposes no reversibility constraint in the DGA scheme using the basis derived from PDMAP.
To construct a basis set that obeys nontrivial boundary conditions, we first take the submatrix of PDMAP such that xm, xn ∈ D. We then calculate the eigenvectors φi of this submatrix that have the M highest positive eigenvalues and take as our basis
| (57) |
In addition to allowing us to define a basis set, PDMAP gives a natural way of constructing guess functions that obey the boundary conditions. Since (56) is a transition matrix, it corresponds to a discrete Markov chain on the data. Therefore, we can construct guesses by solving analogs to (33) using the dynamics specified by the diffusion map. For equations using the generator, we solve the problem
| (58) |
| (59) |
where I is the identity matrix. Here, the sum runs over all datapoints, not just those in D. The resulting estimate obeys the boundary conditions for all datapoints sampled in Dc.
Equation (58) can also be used to construct guesses for equations using weighted adjoints. In principle, one could replace PDMAP with its weighted adjoint against p and solve the corresponding equation. However, rn still obeys the boundary conditions irrespective of the weighted adjoint used. We therefore take the adjoint of PDMAP with respect to its stationary measure. Since the Markov chain associated with the diffusion map is reversible,85 PDMAP is self-adjoint with respect to its stationary measure and we again solve (58). We discuss how to perform out-of-sample extension on the basis and the guess functions in Sec. S2 of the supplementary material.
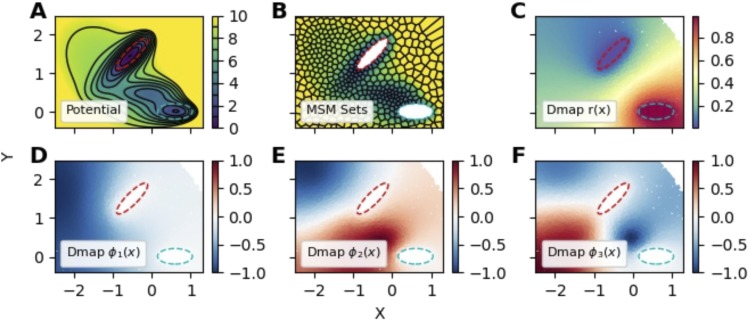
To help the reader visualize a diffusion-map basis, we analyze a collection of datapoints sampled from the Müller-Brown potential,94 scaled by 20 so that the barrier height is about 7 energy units; we set kBT = 1. This potential is sampled using a Brownian particle with an isotropic diffusion coefficient of 0.1 using the BAOAB integrator for overdamped dynamics with a time step of 0.01 time units.95 Trajectories are initialized out of the stationary measure by uniformly picking 10 000 starting locations on the interval . Initial points with potential energies larger than 100 are rejected and resampled to avoid numerical artifacts. Each trajectory is then constructed by simulating the dynamics for 500 steps, saving the position every 100 steps. We then define two states A and B (red and cyan dashed contours in Fig. 1, respectively) and construct the basis and guess functions required for the committor. The results, plotted in Fig. 1, demonstrate that the diffusion-map basis functions are smoothly varying with global support.
FIG. 1.
Example basis and guess functions constructed by the diffusion-map basis on the scaled Müller-Brown potential. (a) The potential energy surface. Black contour lines indicate the potential energy in units of kBT; red and cyan dotted contours indicate the boundaries of states A and B, respectively. (b) An MSM clustering with 500 sets on the domain; the color scale is the same as in (a). Each MSM basis function is one inside a cell and zero otherwise. Sets inside states A and B are not shown to emphasize the boundary conditions. (c) Scatter plot of the guess function for the committor for hitting B before A, constructed using (58). [(d)–(f)] Scatter plots of the first three basis functions constructed according to (57).
A. Basis set performance in high-dimensional CV spaces
We now test the effect of dimension on the performance of the basis set by attempting to calculate the forward committor and total reactive flux for a series of toy systems based on the model mentioned above. To be able to vary the dimensionality of the system, we add up to 18 harmonic “nuisance” degrees of freedom. Specifically,
| (60) |
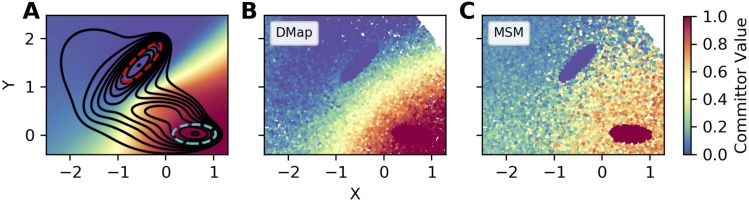
where UMB is the scaled Müller-Brown potential discussed above. We compare our results with references computed by a grid-based scheme described in the supplementary material. Our reference for the committor is plotted in Fig. 3(a). We initialize the x and y dimensions as discussed above; the initial values of the nuisance coordinates were drawn from their marginal distributions at equilibrium. We then sampled the system using the same procedure as before.
FIG. 3.
Example forward committors calculated using the diffusion-map and MSM bases on a high-dimensional toy problem. The system is the same as in Fig. 1, with 18 additional nuisance dimensions. (a) Forward committor function calculated using an accurate grid-based scheme. The black lines indicate the contours of free energy in the x and y coordinates, and the red and cyan dashed contours indicate the two states. Every subsequent dimension has a harmonic potential with a force constant of 2. [(b) and (c)] Estimated forward committor constructed using the diffusion map and MSM bases, respectively.
Throughout this section and all subsequent numerical comparisons, we compare the diffusion-map basis with a basis of indicator functions. Since, with minor restrictions, using a basis of indicator functions is equivalent to calculating the same dynamical quantities using a MSM, we estimate committors, mean first-passage times, and stationary distributions by constructing a MSM in PyEMMA and using established formulas.31,32,76 In general, it is not our intention to compare an optimal diffusion-map basis to an optimal MSM basis. Multiple diffusion-map and clustering schemes exist, and performing an exhaustive comparison would require comparison over multiple methods and hyperparameters. We leave such a comparison for future work and only seek to present reasonable examples of both schemes.
MSM clusters are constructed using k-means, as implemented in PyEMMA.60 While MSMs are generally constructed by clustering points globally, this does not guarantee that a given clustering satisfies a specific set of boundary conditions. Consequently, we modify the set definition procedure slightly.
We first construct M clusters on the domain D and then cluster Dc separately. The number of states inside Dc is chosen so that states inside Dc have approximately the same number of samples on average as states in the domain. For the current calculation, this corresponded to approximately one state inside set A or B for every five states inside the domain; we round to a ratio of 1/5 for numerical simplicity. We note that clustering on the interior of Dc does not affect calculated committors or mean first-passage times. We use 500 basis functions for both the MSM and diffusion-map basis sets. Plots supporting this choice can be found in Sec. S5 of the supplementary material.
In modern Markov state modeling, one commonly constructs the transition matrix only over a well-connected subset of states named the active set.39,96 We have followed this practice and excluded points outside the active set from any error analyses of the resulting MSMs. We believe this gives the MSM basis an advantage over the diffusion-map basis in our comparisons, as we are explicitly ignoring points where it fails to provide an answer and would presumably give poor results.
It is also common to ensure that the resulting matrix obeys detailed balance through a maximum likelihood procedure.38,39 We choose not to do this because we do not wish to assume reversibility in our formalism. Moreover, our calculations have also shown that enforcing reversibility can introduce a statistical bias that dominates the error in any estimates. We give numerical examples of this phenomenon in Sec. S6 of the supplementary material.
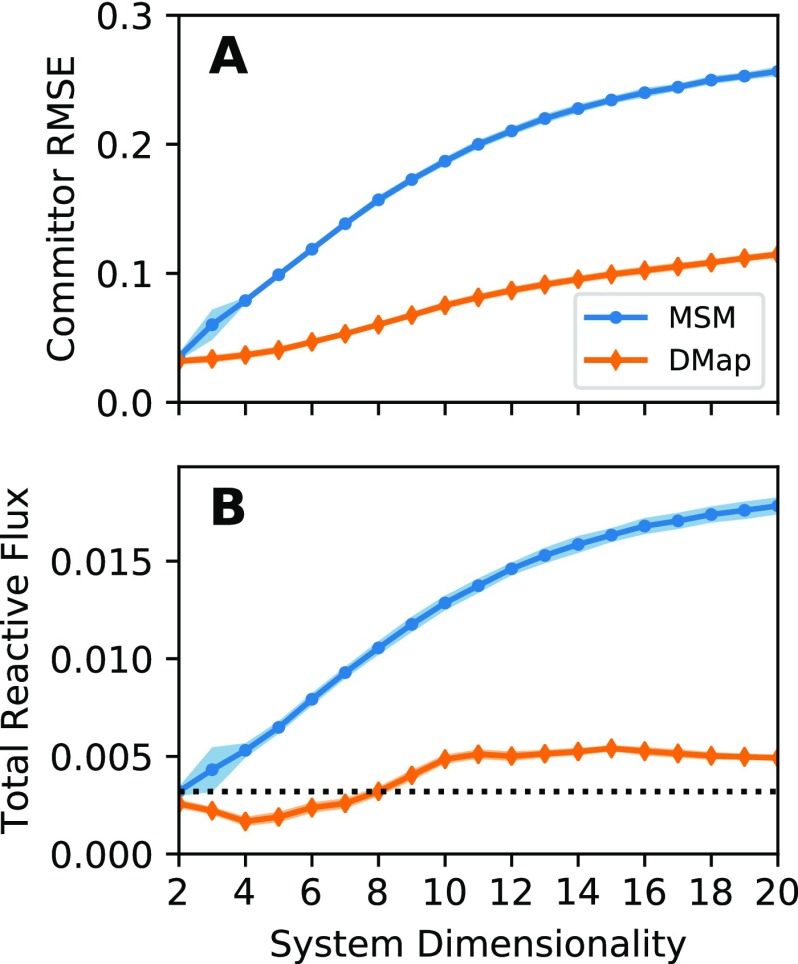
In Fig. 2(a), we plot root-mean-square error (RMSE) between the estimated and reference forward committors as a function of the number of nuisance degrees of freedom. While for low-dimensional systems, the MSM and the diffusion-map basis give comparable results, as we increase the dimensionality, the MSM gives increasingly worse answers. To aid in understanding these results, we plot example forward committor estimates for the 20-dimensional system in Fig. 3. We see that the diffusion-map basis manages to capture the general trends in the reference in Fig. 3(a). In contrast, the MSM basis gives considerably noisier results.
FIG. 2.
Comparison of basis performance as the dimensionality of the toy system increases. (a) The average error in the forward committor between states B and A in Fig. 3 for both the MSM and the diffusion-map basis function, as a function of the number of nuisance degrees of freedom. (b) Estimated reactive flux using both the MSM and the diffusion-map basis function as a function of the same. In both plots, shading indicates the standard deviation over 30 datasets. The dotted line in (b) is the reactive flux as calculated by an accurate reference scheme.
We also estimate the total reactive flux across the same dataset, setting C and Cc in (28) to be the sets on either side of the calculated isocommittor one-half surface [Fig. 2(b)]. The large errors that we observe in the reactive flux occur due to the nature of the dataset. If data were collected from a long equilibrium trajectory, it would not be necessary to estimate π(x) separately, and we could set π(x) = 1. In that case, provided the number of MSM states was sufficient, the MSM reactive flux reverts to the direct estimation of the number of reactive trajectories per unit time. This would give an accurate reactive flux regardless of the quality of the estimated forward or backward committors.
VI. ADDRESSING PROJECTION ERROR THROUGH DELAY EMBEDDING
Our results suggest that improving basis set choice can yield DGA schemes with better accuracy in higher-dimensional CV spaces. However, even large CV spaces are considerably lower-dimensional than the system’s full state space. Consequently, they may still omit key degrees of freedom needed to describe the long-time dynamics. In both MSMs and DOEA, this projection error is often addressed by increasing the lag time of the transition operator.39,54,71,97 In the long-lag-time limit, bounds on the approximation error for DOEA show that the scheme gives the correct equilibrium averages up to projection.29,98 However, MSMs and DOEA cannot resolve dynamics on time scales shorter than the lag time. This is reflected in existing DOEA error bounds on the relative error of the estimate of the subdominant eigenvalue, which do not vanish with increasing lag time.98 Moreover, whereas changing the lag time does not affect the eigenfunctions in (6), the equations in Sec. III hold only for a lag time of Δt. Using a longer time is effectively making the approximation
| (61) |
This causes a systematic bias in the estimates of the dynamical quantities discussed in Sec. III. While for small lag times this bias is likely negligible, it may become large as the lag time increases. For instance, estimates of the mean first-passage time grow linearly with s as the lag time goes to infinity.97
Here, we propose an alternative strategy for dealing with projection error. Rather than looking at larger time lags, we use past configurations in CV space to account for contributions from the removed degrees of freedom. This idea is central to the Mori-Zwanzig formalism.99 Here, we use delay embedding to include history information. Let ζ(t) be the projection of Ξ(t) at time t. We define the delay-embedded process with d delays as
| (62) |
Delay embedding has a long history in the study of deterministic, finite-dimensional systems, where it has been shown that delay embedding can recapture attractor manifolds up to diffeomorphism.100,101 Weaker mathematical results have been extended to stochastic systems,102,103 although these are not sufficient to guarantee its effectiveness in all cases.
Delay embedding has been used previously with dimensionality reduction on both experimental104 and simulated chemical systems105,106 and has also been used in applications of DOEA in geophysics.66 In Refs. 66 and 107, it was argued that delay embedding can improve statistical accuracy for noise-corrupted and time-uncertain data. Other methods of augmenting the dynamical process with history information have been used in the construction of MSMs. In Ref. 108, each trajectory was augmented with a labeling variable indicating its origin state. In Ref. 97, it was suggested to write transition probabilities as a function of both the current and the preceding MSM state. This corresponds to a specific choice of basis on a delay embedded process.
Here, we show that delay embedding can be used to improve dynamical estimates in DGA. To apply DGA to the delay-embedded process, we must extend the functions h and b in (33) and (34) to the delay-embedded space. We do this by using the value of the function on the central time point,
| (63) |
where denotes rounding down to the nearest integer. The states D and Dc in the delay-embedded space are extended similarly. One can easily show that this preserves dynamical quantities such as mean first-passage times and committors. The basis set is then constructed directly on θ, and the DGA formalism is applied as before.
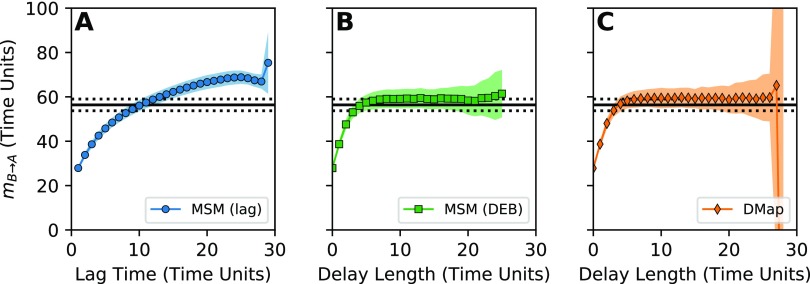
We test the effect of delay embedding in the presence of projection error by constructing DGA schemes on the same system as in Sec. V and taking as our CV space only the y-coordinate. For this study, we revise our dataset to include 2000 trajectories, each sampled for 3000 time steps. While using longer trajectories changes the density such that it is closer to equilibrium, it allows us to test longer lag times and delay lengths. To ensure that our states are well-defined in this new CV space, we redefine state A to be the set {y > 1.15}, and state B to be the set {y < 0.15}. We then estimate the mean first-passage time into state A, conditioned on starting in state B at equilibrium,
We construct estimates using an MSM basis with varying lag time, an MSM basis with delay embedding, and a diffusion-map basis with delay embedding. In Fig. 4, we plot the average mean first-passage time as a function of the lag time and the trajectory length used in the delay embedding. We compare the resulting estimates with an estimate of the mean first-passage time constructed using our grid-based scheme. In addition, an implied time scale analysis for the two MSM schemes is given in Sec. S7 of the supplementary material.
FIG. 4.
Comparison of methods for dealing with the projection error in an incomplete CV space. In all subplots, we estimate the mean first-passage time from state to state using a DGA scheme on only the y coordinate of the Müller-Brown potential. (a) Estimate constructed using an MSM basis with increasing lag time in (61), as a function of the lag time. (b) Estimate constructed using an MSM basis, but applying delay embedding rather than increasing the lag time, as a function of the delay length. (c) Estimate constructed using the diffusion-map basis with delay embedding, as a function of the delay length. In each plot, the symbols show the mean over 30 identically constructed trajectories, and the shading indicates the standard deviation across trajectories. The black solid line is an estimate of the mean first-passage time calculated using the reference scheme in the supplementary material, and the dashed error bars represent the standard deviation of the mean first-passage time over state B.
The mean first-passage time estimated from the MSM basis with the lag time steadily increases as the lag time becomes longer [Fig. 4(a)], as predicted in Ref. 97. In contrast, the estimates obtained from delay embedding both converge as the delay length increases, albeit to a value slightly larger than the reference. We believe this small error is because we treat the dynamics as having a discrete time step, while the reference curve approximates the mean first-passage time for a continuous-time Brownian dynamics. In particular, the latter includes events in which the system enters and exits the target state within the duration of a discrete-time step, but such events are missing from the discrete-time dynamics.
In all three schemes, we see anomalous behavior as the length of the lag time or delay length increases. This is due to an increase in statistical error when the delay length or lag time becomes close to the length of the trajectory. If each trajectory has N datapoints, performing a delay-embedding with d delays means that each trajectory only gives N − d samples. When N and d are of the same order of magnitude, this leads to increased statistical error in the estimates in Sec. IV C, to the point of making the resulting linear algebra problem ill-posed. The diffusion-map basis fluctuates to unreasonable values at long delay lengths, and the MSM basis fails completely, truncating the curve in Figs. 4(b) and 4(c). Similarly, the lagged MSM has an anomalous downturn in the average mean first-passage time near 26 time units. We give additional plots supporting this interpretation in Sec. S7 of the supplementary material.
Finally, we observe that the delay length required for the estimate to converge is substantially smaller than the mean first-passage time. This suggests that delay embedding can be effectively used on short trajectories to get estimates of long-time quantities.
VII. APPLICATION TO THE Fip35 WW DOMAIN
To further assess our methods, we now apply them to molecular dynamics data and seek to evaluate committors and mean first-passage times. In contrast to the simulations mentioned above, we do not have accurate reference values and cannot directly calculate the error in our estimates. Instead, we observe that both the mean first-passage time and forward committor are conditional expectations and obey the following relations:109
This suggests a scheme for assessing the quality of our estimates. If we have access to long trajectories, each point in the trajectory has an associated sample of τA and . We define the two empirical cost functions
| (64) |
| (65) |
Here, xn is a collection of samples from a long trajectory, τA,n is the time from xn to A, and is one if the sampled trajectory next reaches B and zero if it next reaches A. The numerical estimates of the mean first-passage time and committor are written as and , respectively. In the limit of N → ∞, the true mean first-passage time and committor would minimize (64) and (65). We consequently expect lower values of our cost functions to indicate improved estimates. For a perfect estimate, however, these cost functions would not go to zero. Rather, in the limit of infinite sampling, (64) and (65) would converge to the variances of τA and . For the procedure to be valid, it is important that the cost estimates are not constructed using the same dataset used to build the dynamical estimates. This avoids spurious correlations between the dynamical estimate and the estimated cost.
We applied our methods to the Fip35 WW domain trajectories described by D. E. Shaw Research in Refs. 110 and 111. The dataset consists of six trajectories, each of length 100 000 ns with frames output every 0.2 ns. Each trajectory has multiple folding and unfolding events, allowing us to evaluate the empirical cost functions. To avoid correlations between the DGA estimate and the calculated cost, we perform a test/train split and divide the data into two halves. We choose three trajectories to construct our estimate and use the other three to approximate the expectations in (64) and (65). Repeating this for each possible choice of trajectories creates a total of 20 unique test/train splits.
To reduce the memory requirements in constructing the diffusion map kernel matrix, we subsampled the trajectories, keeping every 100th frame. This allowed us to test the scheme over a broad range of hyperparameters. We expect that in practical applications a finer time resolution would be used, and any additional computational expense could be offset by using landmark diffusion maps.112
To define the folded and unfolded states, we follow Ref. 48 and calculate rβ1 and rβ1, the minimum root-mean-square-displacement for each of the two β hairpins, defined as amino acids 7–23 and 18–29, respectively.48 We define the folded configuration as having both rβ1 < 0.2 nm and rβ2 < 0.13 nm and the unfolded configuration as having 0.4 nm < rβ1 < 1.0 nm and 0.3 nm < rβ2 < 0.75 nm. For convenience, we refer to these states as A and B throughout this section. We then attempt to estimate the forward committor between the two states and the mean first-passage time into A using the same methods as in Sec. VI.
We take as our CVs the pairwise distances between every other α-carbon, leading to a 153-dimensional space. In previous studies, dimensionality-reduction schemes such as TICA have been applied prior to MSM construction. We choose not to do this, as we are interested in the performance of the schemes in large CV spaces. This also helps control the number of hyperparameters and algorithm design choices. Indeed, our tests suggest that, while using TICA with well-chosen hyperparameters can lead to improvements for both basis sets, the qualitative trends in our results remain unchanged. However, we think the interaction between dimensionality-reduction schemes and families of basis sets merits future investigation.
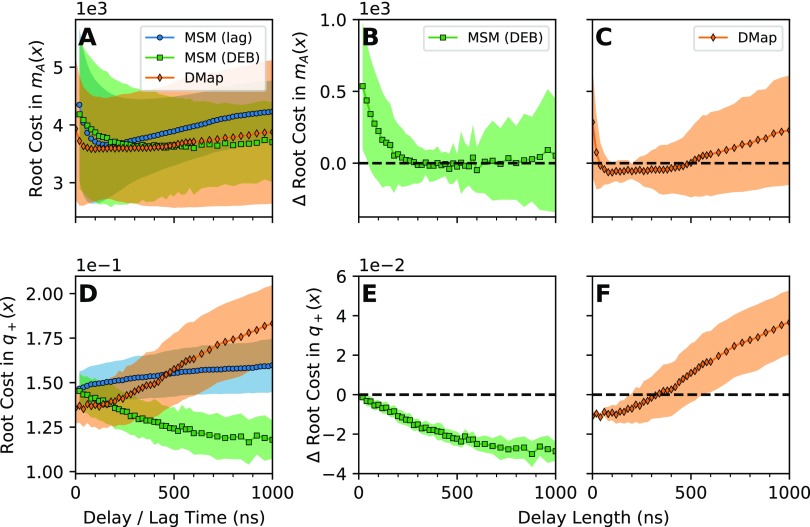
Our results are given in Fig. 5. In Figs. 5(a) and 5(b), we give the mean value of the cost for the mean first-passage time and forward committor over all test/train splits, as calculated using 200 basis functions for each algorithm. The number of basis functions was chosen to give the best result for the MSM scheme with increasing lag over any lag time, although we see only very minor differences in behavior for larger basis sets. The large standard deviations primarily reflect variation in the cost across different test/train splits, rather than any difference between the methods. This suggests the presence of large numerical noise in our results.
FIG. 5.
Results from a DGA calculation on a dataset of six long folding and unfolding trajectories of the Fip35 WW domain. [(a) and (d)] The root cost in the mean first-passage time and forward committor, respectively, calculated using an MSM basis with increasing lag time, an MSM basis with delay embedding, and diffusion map basis with delay embedding, averaged over all test/train splits. [(b), (c), (e), and (f)] Difference in root cost relative to the best parameter choice for the estimate constructed using the MSM basis with increasing lag time. Negative values are better. (b) Difference in cost for the mean first-passage time estimated with an MSM basis with delay embedding. (c) The same as in (b) but with the diffusion map basis instead. (e) Difference in cost for the committor estimated with an MSM basis with delay embedding. (f) The same as in (e) but with the diffusion map basis instead. In all plots, the symbols are the average over test/train splits, and the shading indicates the standard deviation across test/train splits.
To get a more accurate comparison, we instead look at the expected improvement in cost between schemes for a given test/train split. To quantify whether an improvement occurs, we first determine the best parameter choice for the MSM basis with increasing lag. We estimate the cost for the MSM basis with delay embedding and for the diffusion-map basis, and calculate the difference in cost vs the lagged MSM scheme for each test/train split. We then average and calculate the standard deviation over pairs, and plot the results in Figs. 5(c)–5(f). As the difference is calculated against the best parameter choice for the lagged MSM scheme, they are intrinsically conservative: in practice, one should not expect to have the optimal lagged MSM parameters.
In our numerical experiments, we see that the diffusion map seems to give the best results for relatively short delay lengths. However, the diffusion-map basis performs progressively worse as the delay length increases. The mechanism causing this loss in accuracy requires further analysis. This tentatively suggests the use of the diffusion-map basis for datasets consisting of very short trajectories, where using long delays may be infeasible. In contrast, our results with the delay-embedded MSM basis are more ambiguous. For the mean first-passage time, we do not see significant improvement over the results from the lagged MSM results. We do see noticeable improvement in the estimated forward committor probability as the delay length increases. However, we observe that the delay lengths required to improve upon the diffusion map result are comparable in magnitude to the average time required for the trajectory to reach either the A or B states. Indeed, we only see an improvement over the diffusion-map result at a delay length of 180 ns, and we observe that the longest the trajectory spends outside of both state A and state B is 223 ns. This negates any advantage of using datasets of short trajectories.
Caution is warranted in interpreting these results. We see large variances between different test/train splits, suggesting that despite having 300 μs of data in each training dataset, we are still in a relatively data-poor regime. Similarly, we cannot make an authoritative recommendation for any particular scheme for calculating dynamical quantities without further research. Such a study would not only require more simulation data but also a comparison of multiple clustering and diffusion map schemes across several hyperparameters and their interaction with various dimensionality-reduction schemes. We leave this task for future work. However, our initial results are promising, suggesting that further development of DGA schemes and basis sets is warranted.
VIII. CONCLUSIONS
In this paper, we introduce a new framework for estimating dynamical statistics from trajectory data. We express the quantity of interest as the solution to an operator equation using the generator or one of its adjoints. We then apply a Galerkin approximation, projecting the unknown function onto a finite-dimensional basis set. This allows us to approximate the problem as a system of linear equations, whose matrix elements we approximate using Monte Carlo integration on dynamical data. We refer to this framework as Dynamical Galerkin Approximation (DGA). These estimates can be constructed using collections of short trajectories initialized from relatively arbitrary distributions. Using a basis set of indicator functions on nonoverlapping sets recovers MSM estimates of dynamical quantities. Our work is closely related to existing work on estimating the eigenfunctions of dynamical operators in a data-driven manner.
To demonstrate the utility of alternative basis sets, we introduce a new method for constructing basis functions based on diffusion maps. Results on a toy system show that this basis has the potential to give improved results in high-dimensional CV spaces. We also combine our formalism with delay-embedding, a technique for recovering degrees of freedom omitted in constructing a CV space. Applying it to an incomplete, one-dimensional projection of our test system, we see that delay embedding can improve on the current practice of increasing the lag time of the dynamical operator.
We then applied the method to long folding trajectories of the Fip35 WW domain to study the performance of the schemes in a large CV space on a nontrivial biomolecule. Our results suggest that the diffusion-map basis gives the best performance for short delay times, giving results that are as good or better than the best time-lagged MSM parameter choice. Moreover, our results suggest that combining the MSM basis with delay embedding gives promising results, particularly, for long delay lengths. However, long delay lengths are required to see an improvement over the diffusion-map basis, potentially negating any computational advantage in using short trajectories to estimate committors and mean first-passage times.
We believe our work raises new theoretical and algorithmic questions. Most immediately, we hope our preliminary numerical results motivate the need for new approaches to building basis sets and guess functions obeying the necessary boundary conditions. Further theoretical work is also required to assess the validity of using delay embedding in our schemes. Finally, we believe it is worth searching for connections between our work, VAC and VAMP theory,34,54,55,70,71 and earlier approaches for learning dynamical statistics.12,13,89 In particular, a variational reformulation of the DGA scheme would allow substantially more flexible representation of solutions. With these further developments, we believe DGA schemes have the potential to give further improved estimates of dynamical quantities for difficult molecular problems.
SUPPLEMENTARY MATERIAL
Additional theoretical and numerical support for our arguments is given in the supplementary material. We first show how MSM estimates of dynamical quantities can be derived using DGA. We then detail the specific procedure used to construct the diffusion map kernel and describe our out-of-sample extension procedure. This is followed by an adaptation of the reactive flux and transition path theory rate to discrete-time Markov chains. We then describe how we compute the reference values for dynamical quantities on the Müller-Brown potential. We next give additional plots justifying our MSM hyperparameter choices in Sec. V: we explain our choice for the number of MSM states and show that enforcing reversibility can cause substantial statistical bias in the estimates of dynamical quantities. Finally, we give additional plots examining the convergence of the delay embedded estimates in Sec. VI.
ACKNOWLEDGMENTS
This work was supported by the National Institutes of Health Award R01 GM109455 and by the Molecular Software Sciences Institute (MolSSI) Software Fellows program. Computing resources where provided by the University of Chicago Research Computing Center (RCC). The Fip35 WW domain data were provided by D.E. Shaw Research. Most of this work was completed while J.W. was a member of the Statistics Department and the James Franck Institute at the University of Chicago. We thank Charles Matthews, Justin Finkel, and Benoit Roux for helpful discussions, as well as Fabian Paul, Frank Noé, and the anonymous reviewers for their constructive feedback on earlier versions of the manuscript.
Note: This article is part of the Special Topic “Markov Models of Molecular Kinetics” in J. Chem. Phys.
Contributor Information
Erik H. Thiede, Email: .
Dimitrios Giannakis, Email: .
Aaron R. Dinner, Email: .
Jonathan Weare, Email: .
REFERENCES
- 1.Kramers H. A., Physica 7, 284 (1940). 10.1016/s0031-8914(40)90098-2 [DOI] [Google Scholar]
- 2.Hänggi P., Talkner P., and Borkovec M., Rev. Mod. Phys. 62, 251 (1990). 10.1103/revmodphys.62.251 [DOI] [Google Scholar]
- 3.Vanden-Eijnden E., Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology (Springer, 2006), Vol. 1, pp. 453–493. [Google Scholar]
- 4.Berezhkovskii A. M., Szabo A., Greives N., and Zhou H.-X., J. Chem. Phys. 141, 204106 (2014). 10.1063/1.4902243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ma A., Nag A., and Dinner A. R., J. Chem. Phys. 124, 144911 (2006). 10.1063/1.2183768 [DOI] [PubMed] [Google Scholar]
- 6.Ovchinnikov V., Nam K., and Karplus M., J. Phys. Chem. B 120, 8457 (2016). 10.1021/acs.jpcb.6b02139 [DOI] [PubMed] [Google Scholar]
- 7.Ghysels A., Venable R. M., Pastor R. W., and Hummer G., J. Chem. Theory Comput. 13, 2962 (2017). 10.1021/acs.jctc.7b00039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dinner A. R. and Karplus M., J. Phys. Chem. B 103, 7976 (1999). 10.1021/jp990851x [DOI] [Google Scholar]
- 9.Dinner A. R., Šali A., Smith L. J., Dobson C. M., and Karplus M., Trends Biochem. Sci. 25, 331 (2000). 10.1016/s0968-0004(00)01610-8 [DOI] [PubMed] [Google Scholar]
- 10.Dellago C., Bolhuis P. G., Csajka F. S., and Chandler D., J. Chem. Phys. 108, 1964 (1998). 10.1063/1.475562 [DOI] [Google Scholar]
- 11.Bolhuis P. G., Chandler D., Dellago C., and Geissler P. L., Annu. Rev. Phys. Chem. 53, 291 (2002). 10.1146/annurev.physchem.53.082301.113146 [DOI] [PubMed] [Google Scholar]
- 12.Ma A. and Dinner A. R., J. Phys. Chem. B 109, 6769 (2005). 10.1021/jp045546c [DOI] [PubMed] [Google Scholar]
- 13.Hu J., Ma A., and Dinner A. R., Proc. Natl. Acad. Sci. U. S. A. 105, 4615 (2008). 10.1073/pnas.0708058105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Grünwald M., Dellago C., and Geissler P. L., J. Chem. Phys. 129, 194101 (2008). 10.1063/1.2978000 [DOI] [PubMed] [Google Scholar]
- 15.Gingrich T. R. and Geissler P. L., J. Chem. Phys. 142, 234104 (2015). 10.1063/1.4922343 [DOI] [PubMed] [Google Scholar]
- 16.Huber G. A. and Kim S., Biophys. J. 70, 97 (1996). 10.1016/s0006-3495(96)79552-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.van Erp T. S., Moroni D., and Bolhuis P. G., J. Chem. Phys. 118, 7762 (2003). 10.1063/1.1562614 [DOI] [PubMed] [Google Scholar]
- 18.Faradjian A. K. and Elber R., J. Chem. Phys. 120, 10880 (2004). 10.1063/1.1738640 [DOI] [PubMed] [Google Scholar]
- 19.Allen R. J., Frenkel D., and ten Wolde P. R., J. Chem. Phys. 124, 024102 (2006). 10.1063/1.2140273 [DOI] [PubMed] [Google Scholar]
- 20.Warmflash A., Bhimalapuram P., and Dinner A. R., J. Chem. Phys. 127, 154112 (2007). 10.1063/1.2784118 [DOI] [PubMed] [Google Scholar]
- 21.Vanden-Eijnden E. and Venturoli M., J. Chem. Phys. 131, 044120 (2009). 10.1063/1.3180821 [DOI] [PubMed] [Google Scholar]
- 22.Dickson A., Warmflash A., and Dinner A. R., J. Chem. Phys. 131, 154104 (2009). 10.1063/1.3244561 [DOI] [PubMed] [Google Scholar]
- 23.Guttenberg N., Dinner A. R., and Weare J., J. Chem. Phys. 136, 234103 (2012). 10.1063/1.4724301 [DOI] [PubMed] [Google Scholar]
- 24.Bello-Rivas J. M. and Elber R., J. Chem. Phys. 142, 094102 (2015). 10.1063/1.4913399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dinner A. R., Mattingly J. C., Tempkin J. O., Koten B. V., and Weare J., SIAM Rev. 60, 909 (2018). 10.1137/16m1104329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schütte C., Fischer A., Huisinga W., and Deuflhard P., J. Comput. Phys. 151, 146 (1999). 10.1006/jcph.1999.6231 [DOI] [Google Scholar]
- 27.Swope W. C., Pitera J. W., and Suits F., J. Phys. Chem. B 108, 6571 (2004). 10.1021/jp037421y [DOI] [Google Scholar]
- 28.Pande V. S., Beauchamp K., and Bowman G. R., Methods 52, 99 (2010). 10.1016/j.ymeth.2010.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sarich M., Noé F., and Schütte C., Multiscale Model. Simul. 8, 1154 (2010). 10.1137/090764049 [DOI] [Google Scholar]
- 30.Noé F. and Fischer S., Curr. Opin. Struct. Biol. 18, 154 (2008). 10.1016/j.sbi.2008.01.008 [DOI] [PubMed] [Google Scholar]
- 31.Noé F. and Prinz J.-H., in An Introduction to Markov State Models and their Application to Long Timescale Molecular Simulation, Advances in Experimental Medicine and Biology, edited by Bowman G. R., Pande V. S., and Noé F. (Springer, 2014), Vol. 797, Chap. 6. [Google Scholar]
- 32.Keller B. G., Aleksic S., and Donati L., in Biomolecular Simulations in Drug Discovery, edited by Gervasio F. L. and Spiwok V. (Wiley-VCH, 2019), Chap. 4. [Google Scholar]
- 33.Weber M., “Meshless methods in conformation dynamics,” Ph.D. thesis, Freie Universität Berlin, 2006. [Google Scholar]
- 34.Noé F. and Nüske F., Multiscale Model. Simul. 11, 635 (2013). 10.1137/110858616 [DOI] [Google Scholar]
- 35.Eisner T., Farkas B., Haase M., and Nagel R., Operator Theoretic Aspects of Ergodic Theory (Springer, 2015), Vol. 272. [Google Scholar]
- 36.Klus S., Nüske F., Koltai P., Wu H., Kevrekidis I., Schütte C., and Noé F., J. Nonlinear Sci. 28, 985 (2018). 10.1007/s00332-017-9437-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Billingsley P., Probability and Measure (John Wiley & Sons, 2008). [Google Scholar]
- 38.Bowman G. R., Beauchamp K. A., Boxer G., and Pande V. S., J. Chem. Phys. 131, 124101 (2009). 10.1063/1.3216567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Prinz J.-H., Wu H., Sarich M., Keller B., Senne M., Held M., Chodera J. D., Schütte C., and Noé F., J. Chem. Phys. 134, 174105 (2011). 10.1063/1.3565032 [DOI] [PubMed] [Google Scholar]
- 40.Deuflhard P., Huisinga W., Fischer A., and Schütte C., Linear Algebra Appl. 315, 39 (2000). 10.1016/s0024-3795(00)00095-1 [DOI] [Google Scholar]
- 41.Röblitz S. and Weber M., Adv. Data Anal. Classif. 7, 147 (2013). 10.1007/s11634-013-0134-6 [DOI] [Google Scholar]
- 42.Noé F., Schütte C., Vanden-Eijnden E., Reich L., and Weikl T. R., Proc. Natl. Acad. Sci. U. S. A. 106, 19011 (2009). 10.1073/pnas.0905466106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schwantes C. R. and Pande V. S., J. Chem. Theory Comput. 9, 2000 (2013). 10.1021/ct300878a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pérez-Hernández G., Paul F., Giorgino T., De Fabritiis G., and Noé F., J. Chem. Phys. 139, 015102 (2013). 10.1063/1.4811489 [DOI] [PubMed] [Google Scholar]
- 45.Schwantes C. R., McGibbon R. T., and Pande V. S., J. Chem. Phys. 141, 090901 (2014). 10.1063/1.4895044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schütte C. and Sarich M., Eur. Phys. J.: Spec. Top. 224, 2445 (2015). 10.1140/epjst/e2015-02421-0 [DOI] [Google Scholar]
- 47.Shukla D., Hernández C. X., Weber J. K., and Pande V. S., Acc. Chem. Res. 48, 414 (2015). 10.1021/ar5002999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Berezovska G., Prada-Gracia D., and Rao F., J. Chem. Phys. 139, 035102 (2013). 10.1063/1.4812837 [DOI] [PubMed] [Google Scholar]
- 49.Sheong F. K., Silva D.-A., Meng L., Zhao Y., and Huang X., J. Chem. Theory Comput. 11, 17 (2014). 10.1021/ct5007168 [DOI] [PubMed] [Google Scholar]
- 50.Li Y. and Dong Z., J. Chem. Inf. Model. 56, 1205 (2016). 10.1021/acs.jcim.6b00181 [DOI] [PubMed] [Google Scholar]
- 51.Husic B. E. and Pande V. S., J. Chem. Theory Comput. 13, 963 (2017). 10.1021/acs.jctc.6b01238 [DOI] [PubMed] [Google Scholar]
- 52.Husic B. E., McKiernan K. A., Wayment-Steele H. K., Sultan M. M., and Pande V. S., J. Chem. Theory Comput. 14, 1071 (2018). 10.1021/acs.jctc.7b01004 [DOI] [PubMed] [Google Scholar]
- 53.Prinz J.-H., Chodera J. D., and Noé F., Phys. Rev. X 4, 011020 (2014). 10.1103/physrevx.4.011020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mardt A., Pasquali L., Wu H., and Noé F., Nat. Commun. 9, 5 (2018). 10.1038/s41467-017-02388-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wu H. and Noé F., preprint arXiv:1707.04659 (2017).
- 56.Wang W., Cao S., Zhu L., and Huang X., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 8, e1343 (2018). 10.1002/wcms.1343 [DOI] [Google Scholar]
- 57.Husic B. E. and Pande V. S., J. Am. Chem. Soc. 140, 2386 (2018). 10.1021/jacs.7b12191 [DOI] [PubMed] [Google Scholar]
- 58.Steinbach M., Ertöz L., and Kumar V., New Directions in Statistical Physics (Springer, 2004), pp. 273–309. [Google Scholar]
- 59.Kriegel H.-P., Kröger P., and Zimek A., ACM Trans. Knowl. Discovery Data 3, 1 (2009). 10.1145/1497577.1497578 [DOI] [Google Scholar]
- 60.Scherer M. K., Trendelkamp-Schroer B., Paul F., Pérez-Hernández G., Hoffmann M., Plattner N., Wehmeyer C., Prinz J.-H., and Noé F., J. Chem. Theory Comput. 11, 5525 (2015). 10.1021/acs.jctc.5b00743 [DOI] [PubMed] [Google Scholar]
- 61.Molgedey L. and Schuster H. G., Phys. Rev. Lett. 72, 3634 (1994). 10.1103/physrevlett.72.3634 [DOI] [PubMed] [Google Scholar]
- 62.Takano H. and Miyashita S., J. Phys. Soc. Jpn. 64, 3688 (1995). 10.1143/jpsj.64.3688 [DOI] [Google Scholar]
- 63.Hirao H., Koseki S., and Takano H., J. Phys. Soc. Jpn. 66, 3399 (1997). 10.1143/jpsj.66.3399 [DOI] [Google Scholar]
- 64.Schütte C., Noé F., Lu J., Sarich M., and Vanden-Eijnden E., J. Chem. Phys. 134, 204105 (2011). 10.1063/1.3590108 [DOI] [PubMed] [Google Scholar]
- 65.Giannakis D., Slawinska J., and Zhao Z., Feature Extraction: Modern Questions and Challenges (2015), pp. 103–115. [Google Scholar]
- 66.Giannakis D., “Data-driven spectral decomposition and forecasting of ergodic dynamical systems,” Appl. Comput. Harmonic Anal. (in press). 10.1016/j.acha.2017.09.001 [DOI] [Google Scholar]
- 67.Williams M. O., Kevrekidis I. G., and Rowley C. W., J. Nonlinear Sci. 25, 1307 (2015). 10.1007/s00332-015-9258-5 [DOI] [Google Scholar]
- 68.Boninsegna L., Gobbo G., Noé F., and Clementi C., J. Chem. Theory Comput. 11, 5947 (2015). 10.1021/acs.jctc.5b00749 [DOI] [PubMed] [Google Scholar]
- 69.Vitalini F., Noé F., and Keller B., J. Chem. Theory Comput. 11, 3992 (2015). 10.1021/acs.jctc.5b00498 [DOI] [PubMed] [Google Scholar]
- 70.Nüske F., Keller B. G., Pérez-Hernández G., Mey A. S., and Noé F., J. Chem. Theory Comput. 10, 1739 (2014). 10.1021/ct4009156 [DOI] [PubMed] [Google Scholar]
- 71.Nüske F., Schneider R., Vitalini F., and Noé F., J. Chem. Phys. 144, 054105 (2016). 10.1063/1.4940774 [DOI] [PubMed] [Google Scholar]
- 72.Del Moral P., Feynman-Kac Formulae (Springer, 2004). [Google Scholar]
- 73.Karatzas I. and Shreve S., Brownian Motion and Stochastic Calculus (Springer Science & Business Media, 2012), Vol. 113. [Google Scholar]
- 74.Du R., Pande V. S., Grosberg A. Y., Tanaka T., and Shakhnovich E. S., J. Chem. Phys. 108, 334 (1998). 10.1063/1.475393 [DOI] [Google Scholar]
- 75.Bolhuis P. G., Dellago C., and Chandler D., Proc. Natl. Acad. Sci. U. S. A. 97, 5877 (2000). 10.1073/pnas.100127697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Metzner P., Schütte C., and Vanden-Eijnden E., Multiscale Model. Simul. 7, 1192 (2009). 10.1137/070699500 [DOI] [Google Scholar]
- 77.Yosida K., Functional Analysis (Springer-Verlag, New York, Berlin, 1971). [Google Scholar]
- 78.Lapelosa M. and Abrams C. F., Comput. Phys. Commun. 184, 2310 (2013). 10.1016/j.cpc.2013.05.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lai R. and Lu J., Multiscale Model. Simul. 16, 710 (2018). 10.1137/17m1123018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Khoo Y., Lu J., and Ying L., Res. Math. Sci. 6, 1 (2018). 10.1007/s40687-018-0160-2 [DOI] [Google Scholar]
- 81.Evans L., Partial Differential Equations (Orient Longman, 1998). [Google Scholar]
- 82.Thiede E., PyEDGAR, https://github.com/ehthiede/PyEDGAR/, 2018.
- 83.Wu H., Nüske F., Paul F., Klus S., Koltai P., and Noé F., J. Chem. Phys. 146, 154104 (2017). 10.1063/1.4979344 [DOI] [PubMed] [Google Scholar]
- 84.Chen K. K., Tu J. H., and Rowley C. W., J. Nonlinear Sci. 22, 887 (2012). 10.1007/s00332-012-9130-9 [DOI] [Google Scholar]
- 85.Coifman R. R. and Lafon S., Appl. Comput. Harmonic Anal. 21, 5 (2006). 10.1016/j.acha.2006.04.006 [DOI] [Google Scholar]
- 86.Berry T. and Harlim J., Appl. Comput. Harmonic Anal. 40, 68 (2016). 10.1016/j.acha.2015.01.001 [DOI] [Google Scholar]
- 87.Ferguson A. L., Panagiotopoulos A. Z., Debenedetti P. G., and Kevrekidis I. G., Proc. Natl. Acad. Sci. U. S. A. 107, 13597 (2010). 10.1073/pnas.1003293107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Rohrdanz M. A., Zheng W., Maggioni M., and Clementi C., J. Chem. Phys. 134, 124116 (2011). 10.1063/1.3569857 [DOI] [PubMed] [Google Scholar]
- 89.Zheng W., Qi B., Rohrdanz M. A., Caflisch A., Dinner A. R., and Clementi C., J. Phys. Chem. B 115, 13065 (2011). 10.1021/jp2076935 [DOI] [PubMed] [Google Scholar]
- 90.Ferguson A. L., Panagiotopoulos A. Z., Kevrekidis I. G., and Debenedetti P. G., Chem. Phys. Lett. 509, 1 (2011). 10.1016/j.cplett.2011.04.066 [DOI] [PubMed] [Google Scholar]
- 91.Long A. W. and Ferguson A. L., J. Phys. Chem. B 118, 4228 (2014). 10.1021/jp500350b [DOI] [PubMed] [Google Scholar]
- 92.Kim S. B., Dsilva C. J., Kevrekidis I. G., and Debenedetti P. G., J. Chem. Phys. 142, 085101 (2015). 10.1063/1.4913322 [DOI] [PubMed] [Google Scholar]
- 93.Berry T., Giannakis D., and Harlim J., Phys. Rev. E 91, 032915 (2015). 10.1103/physreve.91.032915 [DOI] [PubMed] [Google Scholar]
- 94.Müller K. and Brown L. D., Theor. Chim. Acta 53, 75 (1979). 10.1007/bf00547608 [DOI] [Google Scholar]
- 95.Leimkuhler B. and Matthews C., Appl. Math. Res. Express 2013, 34 (2012). 10.1093/amrx/abs010 [DOI] [Google Scholar]
- 96.Beauchamp K. A., Bowman G. R., Lane T. J., Maibaum L., Haque I. S., and Pande V. S., J. Chem. Theory Comput. 7, 3412 (2011). 10.1021/ct200463m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Suárez E., Adelman J. L., and Zuckerman D. M., J. Chem. Theory Comput. 12, 3473 (2016). 10.1021/acs.jctc.6b00339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Djurdjevac N., Sarich M., and Schütte C., Multiscale Model. Simul. 10, 61 (2012). 10.1137/100798910 [DOI] [Google Scholar]
- 99.Zwanzig R., Nonequilibrium Statistical Mechanics (Oxford University Press, 2001). [Google Scholar]
- 100.Takens F., Lect. Notes Math. 898, 366 (1981). 10.1007/bfb0091924 [DOI] [Google Scholar]
- 101.Aeyels D., SIAM J. Control Optim. 19, 595 (1981). 10.1137/0319037 [DOI] [Google Scholar]
- 102.Muldoon M. R., Broomhead D. S., Huke J. P., and Hegger R., Dyn. Stab. Syst. 13, 175 (1998). 10.1080/02681119808806259 [DOI] [Google Scholar]
- 103.Stark J., Broomhead D., Davies M., and Huke J., Nonlinear Anal.: Theory, Methods Appl. 30, 5303 (1997). 10.1016/s0362-546x(96)00149-6 [DOI] [Google Scholar]
- 104.Berry T., Cressman J. R., Greguric-Ferencek Z., and Sauer T., SIAM J. Appl. Dyn. Syst. 12, 618 (2013). 10.1137/12088183x [DOI] [Google Scholar]
- 105.Wang J. and Ferguson A. L., Phys. Rev. E 93, 032412 (2016). 10.1103/physreve.93.032412 [DOI] [PubMed] [Google Scholar]
- 106.Wang J. and Ferguson A. L., J. Phys. Chem. B 122, 11931 (2018). 10.1021/acs.jpcb.8b08800 [DOI] [PubMed] [Google Scholar]
- 107.Fung R., Hanna A. M., Vendrell O., Ramakrishna S., Seideman T., Santra R., and Ourmazd A., Nature 532, 471 (2016). 10.1038/nature17627 [DOI] [PubMed] [Google Scholar]
- 108.Suarez E., Lettieri S., Zwier M. C., Stringer C. A., Subramanian S. R., Chong L. T., and Zuckerman D. M., J. Chem. Theory Comput. 10, 2658 (2014). 10.1021/ct401065r [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Durrett R., Probability: Theory and Examples (Cambridge University Press, 2010). [Google Scholar]
- 110.Shaw D. E., Maragakis P., Lindorff-Larsen K., Piana S., Dror R. O., Eastwood M. P., Bank J. A., Jumper J. M., Salmon J. K., Shan Y., and Wriggers W., Science 330, 341 (2010). 10.1126/science.1187409 [DOI] [PubMed] [Google Scholar]
- 111.Piana S., Sarkar K., Lindorff-Larsen K., Guo M., Gruebele M., and Shaw D. E., J. Mol. Biol. 405, 43 (2011). 10.1016/j.jmb.2010.10.023 [DOI] [PubMed] [Google Scholar]
- 112.Long A. W. and Ferguson A. L., Appl. Comput. Harmonic Anal. 47, 190 (2019). 10.1016/j.acha.2017.08.004 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional theoretical and numerical support for our arguments is given in the supplementary material. We first show how MSM estimates of dynamical quantities can be derived using DGA. We then detail the specific procedure used to construct the diffusion map kernel and describe our out-of-sample extension procedure. This is followed by an adaptation of the reactive flux and transition path theory rate to discrete-time Markov chains. We then describe how we compute the reference values for dynamical quantities on the Müller-Brown potential. We next give additional plots justifying our MSM hyperparameter choices in Sec. V: we explain our choice for the number of MSM states and show that enforcing reversibility can cause substantial statistical bias in the estimates of dynamical quantities. Finally, we give additional plots examining the convergence of the delay embedded estimates in Sec. VI.