Natural image and receptive field statistics predict saccade sizes

Abstract

Humans and other primates sample the visual environment using saccadic eye movements that shift a high-resolution fovea towards regions of interest to create a clear perception of a scene across fixations. Many mammals, however, like mice, lack a fovea, which raises the question of why they make saccades. Here, we describe and test the hypothesis that saccades work with the adaptive properties of neural networks. Specifically, we determined the minimum amplitude of saccades in natural scenes necessary to provide uncorrelated inputs to model neural populations for a wide range of receptive field (RF) sizes. This analysis predicts the distributions of observed saccade sizes during passive viewing for non-human primates, cats, and mice. Furthermore, disrupting the development of RF properties by monocular deprivation changes saccade sizes consistent with this hypothesis. Therefore, natural scene statistics and the neural representation of natural images appear to be critical factors guiding saccadic eye movements.

Introduction

The human visual system is characterized by an uneven distribution of sensors: in the fovea, densely packed cone photoreceptors provide high-resolution visual signals, whereas in the periphery, a low density of cone photoreceptors provides low-resolution signals. Because the density of cones in the periphery is approximately a factor of 30 lower than in the middle of the fovea¹, humans construct a detailed perception of a scene by making fast saccadic eye movements that are typically larger than the fovea^2–4, focusing the fovea on salient and task-dependent locations in the visual scene^3,5–7. Several afoveate animals, however, including mice^8,9, also make saccadic eye and head movements with similar dynamics^10,11. Mouse saccadic eye movements are typically on the order of 10° in magnitude^12,13, which are small relative to their large visual field of about 280°¹⁴. Therefore, it seems unlikely that salient or task-dependent features within the visible scene are typically guiding where mice direct their saccades.

We propose a new hypothesis about why afoveate mammals, like the mouse, make saccades that also has implications for human saccades. Saccades provide many individual visual neurons with new input regardless of the presence of a fovea. When a mouse makes a saccade, the resolution of the neural representation of the visual scene at each location does not change, but which specific neurons are stimulated does change. Visual neurons are sensitive to such changes, which often lead to large transient responses^15–17. Indeed, neurons quickly adjust to constant and unchanging stimuli by reducing their responsiveness¹⁸ and this effect is more than fast enough to have consequences following each saccade¹⁹. Using a combination of analytical and computational models, we quantify the relationship between response gain and the impact of shifting versus maintaining gaze. Shifting gaze results in increased spike rate across the neuronal population. Furthermore, the increases in spike rate are largest for saccades that move RFs into regions of the scene that are uncorrelated with previous regions.

We tested our hypothesis by measuring the minimal gaze shift required for RFs of varying size to receive novel information in natural scenes. We find that these distances are able to predict both the range and shape of saccade size distributions during passive viewing for several mammals. Additionally, when mice were deprived of visual input to one eye during early development, spatial acuity was reduced for the deprived eye and saccade sizes for these animals increased compared to non-deprived animals as predicted by our hypothesis. Our results suggest a general strategy used by a variety of animals that calibrates the magnitude of saccadic eye movements to sample the environment efficiently for visual processing.

Results

Similarities between mouse and human saccadic eye movements

To test our hypothesis about saccadic eye movements, we first examined the saccades of an afoveate mammal, the mouse. We wanted to determine whether the saccadic behaviour of mice shared characteristics with the saccadic behaviour of humans. We conducted a version of a human saccade study² where we measured eye movements while displaying a random sample of small and large natural images in front of head-fixed mice running on a floating track ball (Fig. S1a). The mice were free to run and look, whenever and wherever they wanted while we used two cameras to track the position of both eyes and detect saccades (Fig. S1b).

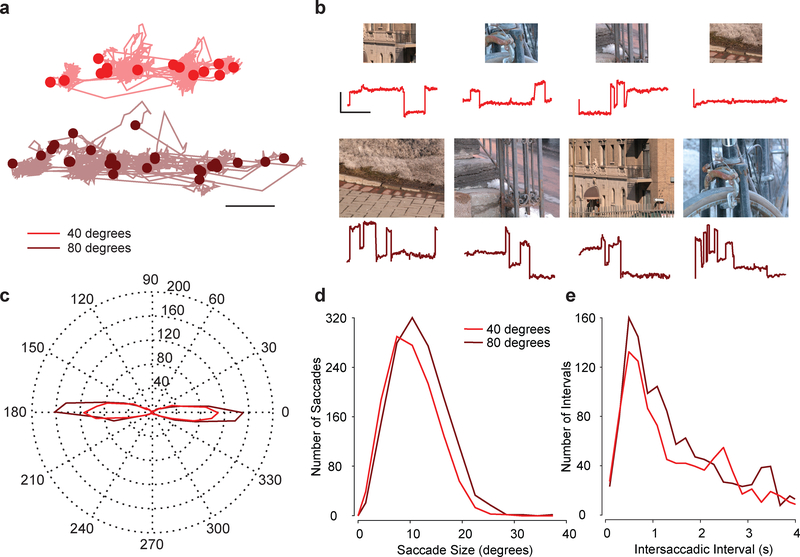
Mice made eye movements that reflect an active exploration of visual scenes. These eye movements were almost exclusively horizontal (Fig. 1a), and their amplitude and frequency varied with image size (Fig. 1a–b). To examine how systematic these trends are, we measured the distribution of saccade directions. Mouse saccades were strongly biased along the horizontal axis (Fig. 1c), such that 84% of all saccades were within 20° from horizontal. In addition, the amplitudes of those saccades were larger and more frequent for large compared to small images (Fig. 1d). Both the horizontal bias and size dependence of saccades are comparable with what is observed in humans². Saccades often occurred in short bursts followed by long periods without a saccade, resulting in a skewed distribution of fixation lengths, which is also observed in humans² (Fig. 1e). Often, bursts of saccades coincided with periods when the mouse was running, but regardless of whether mice were running or not, the relationship between saccade properties and image size remained consistent (see Online Methods). Overall, our data demonstrate that mice, like humans, actively sample larger scenes with larger and more frequent saccades. This result suggests that afoveate mammals, like humans, make saccadic eye movements in order to facilitate acquisition of information from the visual scene.

Figure 1.

Saccade size and frequency increase with increasing image size. a, Example of eye traces in response to presentations of four small (red, 80° × 64°) and large (maroon, 40° × 32°) images. Scale bar is 5°. These are representative examples from a total of 144 images shown to six mice. b, Corresponding horizontal eye position over time to the four small and large images. Scale bar is 10 s by 10°. c, A histogram of saccade directions for both sized images for all six mice. d, Histogram of saccade sizes for large (n = 1355 saccades) and small (n = 1145 saccades) images for all six mice. The median saccade amplitude for large images was 11.25°, bootstrapped 95% confidence interval = [10.85, 11.54]. The median saccade amplitude for small images was 9.99°, bootstrapped 95% confidence interval = [9.70, 10.30]. e, Histogram of intersaccadic intervals for small and large images for all six mice (data asymptotes beyond 4 seconds and is not shown). The large image median saccade interval (n =1322 intervals) was 1.53 s with bootstrapped 95% CI = [1.40, 1.67], while the small image median saccade interval (n = 1138 intervals) was 1.67 s with bootstrapped 95% CI = [1.48, 1.83]. The large image median saccade rate per image was 0.30 saccades/s with bootstrapped 95% CI = [0.23, 0.33], while the small image median saccade rate per image was 0.23 saccades/s with bootstrapped 95% CI = [0.17, 0.32]. Each set of data was resampled 1000 times allowing repeats to produce surrogate datasets of the same size.

Effect of saccades on the adaptive responses of neural populations

The shared saccadic behaviour of foveate and afoveate mammals suggests that some common processes exist to generate saccades. Here we propose that a possible common process is one that sets the average saccade size to maximize the population response. We will demonstrate that saccades that are large enough to decorrelate incoming input increase the population response.

Our hypothesis depends on the assumption that local adaptation during a fixation results in a total spike response in the population that is larger immediately after a saccadic eye movement than if the eye had remained in the same position or received similar visual input. The most commonly studied adaptation in the nervous system is a divisive change in gain²⁰, but it is not obvious that such adaptation will cause the total responses in a population to increase after a saccade. Whether the response of any given neuron will increase or decrease after a saccade depends on the RF stimulus before the saccade, the level of gain adaptation produced by that RF stimulus, and the RF stimulus after the saccade.

We first consider an arbitrary neuron whose RF jumps from one location to another after some fixation interval (e.g., 300 ms). During this fixation interval, some gain adaptation occurs. Let the input signal during the fixation interval be a, and the input signal for the next fixation after the saccade be b, and let the probability of this arbitrary pair of levels be p(a,b). To be concrete, one can think of these levels as, for example, a local luminance or the value obtained from applying a spatial RF to the stimulus without gain adaptation. We assume that by the end of the fixation interval the response gain is given by:

$$g_a=\frac{k}{k+a}$$ (1),

where k is an arbitrary positive constant. Note that the gain is between 0 and 1 and declines with increasing input level a. For simplicity, we assume that the response of the neuron at the end of the fixation interval is the input signal times the gain:

$$r_a=a\frac{k}{k+a}$$ (2)

If the eyes do not move after the fixation interval or view similar information after a saccade, then the response immediately after that interval will remain the same. If the eyes move to the new location, then the response immediately after the saccade will be:

$$r_b=b\frac{k}{k+a}$$ (3)

Because saccades are not planned based on any given visual neuron’s response, it is safe to assume that the probability of the two levels falling on the RF only depends on the endpoints of the saccade and not their order: p(a,b) = p(b,a). Therefore, we can determine the average effect of saccades for any arbitrary pair of endpoint levels by considering a pair of identical neurons, one with input level a and one with input level b, where either the levels stay the same after the fixation interval, or the levels are swapped after the fixation interval. We now show that for any pair of levels and for any value of the adaptation constant k, the total response from the two neurons when the levels are swapped is larger than when the levels remain the same.

The total response just after the end of the fixation interval when the levels stay the same is given by:

$$same=a\frac{k}{k+a}+b\frac{k}{k+b}$$ (4),

and the total response immediately after the levels are swapped is given by:

$$novel=b\frac{k}{k+a}+a\frac{k}{k+b}$$ (5)

Thus, the difference in response is:

$$novel-same=b\frac{k}{k+a}+a\frac{k}{k+b}-a\frac{k}{k+a}-b\frac{k}{k+b}$$ (6)

Combining terms (by finding the common denominator) and then simplifying shows that:

$$novel-same=\frac{k{(b-a)}^2}{(k+a)(k+b)}$$ (7),

which is greater than or equal to zero for arbitrary positive values of a, b and k, and when a and b are different. Thus, for an arbitrary population of RFs, the total response after a saccade will be larger than if the eyes remained in the same position. Under the assumption that the variance of the spike rate increases in proportion to mean spike rate²¹, or more generally that the variance increases as a power function of the mean spike rate with an exponent less than 2, then the average signal-noise-ratio (SNR) of the total spiking activity in a population will increase immediately after a saccade.

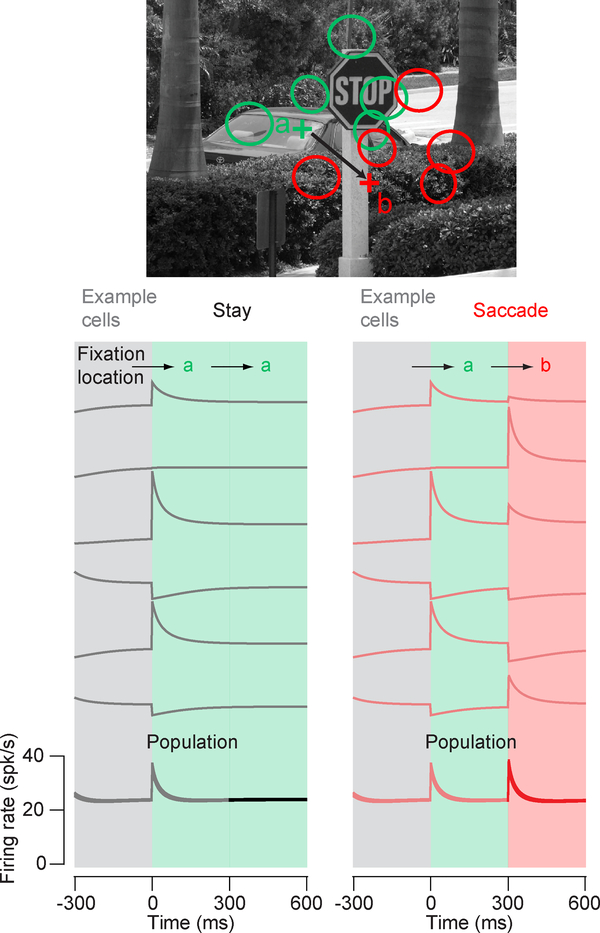
To check the logic of this analysis, we also ran simulations demonstrating this effect across a population of 500 neurons (Fig. 2). The input for each neuron was randomly switched at each saccade and underwent gain adaptation (equation 1) with a time constant equal to half of the fixation duration (300 ms). Saccades cause large changes in response amplitude that slowly adapt to the current input. Importantly, using this simulation we can test the effect across the population of making a saccadic eye movement or staying in a fixation location. As described above, staying in the same location does not change the population response amplitude (black trace), but making a saccade causes an average increase in the population firing rate (red trace).

Figure 2.

Saccades increase the average response of cells with adaptive changes in gain. Responses were simulated for n = 500 neurons with randomly placed RFs (green circles) where the eyes either remained at the starting fixation location (a, green cross) or moved to a new fixation location (b, red cross). Remaining at the same location does not change the adapted responses (left, black) while moving the RFs to a new location (red circles) does change adapted responses (right, red). Although the new inputs to the RFs can lead to smaller or larger responses for a random selection of example cells (right versus left column “Example Cells”), overall, there is a net increase in response as a result of the new input (right versus left column “Population”).

Quantifying novel receptive field information in natural scenes

Considering that saccades increase the average response of a population of neurons by changing RF inputs, we then wanted to know how large saccades would need to be to maximize those changes for natural scenes. Despite saccade behaviour being similar between mice and humans, our observed saccade amplitudes in mice are larger than those found in humans^2–4. This difference in saccade amplitude may reflect a difference in neuronal RF sizes between these species. Mouse visual cortex²² is characterized by RFs that are much larger than those in primate visual cortex²³. Therefore, mouse RFs may require relatively large saccades to provide uncorrelated inputs, while primate RFs may require only relatively small saccades.

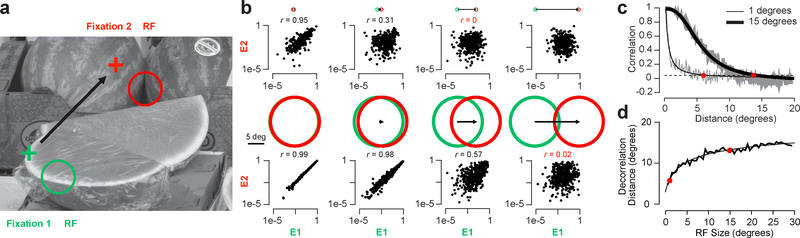
We examined how RF size impacts input decorrelation quantitatively by analysing the saccade distance required to provide novel information to RFs of varying size in natural images²⁴. Since an abundant amount of RF information is readily available for the primary visual cortex (V1) in several mammals²⁵, we based our initial analysis on V1 simple and complex cell RFs, though we explored other RF configurations as well. We measured the impact of saccades by passing the inputs representing two successive fixation points (e.g., Fig. 3a, green and red crosses) through V1 simple and complex cell model RF filters²⁶ of a specific size that were normalized for local luminance and contrast^24,27. For each image, we simulated several million randomly directed saccades ranging in size from 0.1° to 50° starting from randomly-placed RF locations with RF sizes ranging from 0.5° to 30° and RF orientations of 0, 45, 90, and 135°. For each RF size and orientation, we measured the correlation for a population of neurons based on model responses of V1 simple and complex cells. For example, we used normalized energy model responses for complex cells, E₁ and E₂, from the beginning (green) to the end (red) of a saccade as a function of saccade sizes (Fig. 3b, distances between fixation locations). The top row in Fig. 3b illustrates an example of how correlation varies for 1° RFs (typical for primates) as saccade size increases. For these small RFs, responses before and after a saccade are not clearly uncorrelated until distances are greater than 5° (third column). The bottom row in Fig. 3b illustrates an example of how correlation declines with distance for larger RFs, 15°, typical for mice. These larger RFs require greater distances to decorrelate the model responses (Fig. 3c). We define the “decorrelation distance” as the point when the correlation between the RF responses before and after a saccade is less than a decorrelation threshold (Fig. 3c, dashed line). For the image shown in Fig. 3a, there is a systematic increase in decorrelation distance with RF size (Fig. 3d). We find that decorrelation distance generally starts at a point larger than the smallest RF size, followed by increases that eventually saturate as RF size increases (Fig. S2).

Figure 3.

Measuring decorrelation distance in natural images. a, Example image from a total of n = 392 images with a pair of RFs (RF) from the beginning (green circle) and end (red circle) of a saccade (black arrow). b, Scatter plots of the complex cell “energy” responses (E) for all pairs of RFs that have the same distance between them (n = 400 response pairs). The top row is data for RFs that are 1° in diameter and the bottom row is data for RFs that are 15° in diameter. The green and red circles indicate the RF size and the black arrow indicates the distance between RFs. Correlation values that fell below the decorrelation threshold are noted in red. c, Correlation measurements for all distances between RFs for the same two sizes (data from b are represented as single points in c). Gray lines are individual correlation measurements for each distance and the black lines are fits based on equation 16 in Online Methods. d, Decorrelation distances for all RF sizes (where data from c cross below the dashed line). The measured distances are plotted along with a fit based on equation 17 in Online Methods.

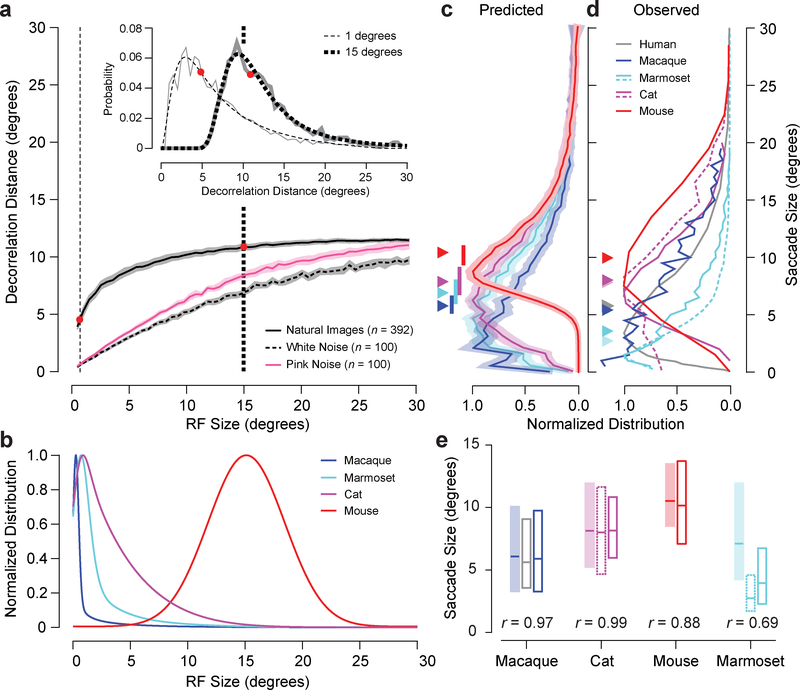
To incorporate the diversity of natural scene statistics we computed the decorrelation distance relative to RF size for V1 simple and complex cells from 392 natural images (median and 95% confidence interval is shown in Fig. 4a). Note that the underlying decorrelation distance distributions are skewed with long tails (Fig. 4a, inset, and Fig. S3). The features that are correlated across space in natural images are captured by our V1 RFs^28,29. In contrast to natural images, applying our procedure to white noise and pink noise (1/frequency power spectrum) yields a decorrelation distance (Fig. 4a) that is determined solely by the RF size and overlap.

Figure 4.

Decorrelation distance and RF size predict saccade size. a, Median and 95% confidence interval of decorrelation distance versus RF size for natural, white noise, and pink noise images. The inset shows the entire distribution of decorrelation distances for two RF sizes indicated by the corresponding vertical dashed lines. Gray lines are individual probability measurements for each distance and the black lines are fits based on equation 18 in Online Methods. b, Distributions of RF sizes for macaques, marmosets, cats, and mice (see Online Methods for details). c, RF sizes were transformed into decorrelation distances or predicted saccade sizes using the data represented in a. The mean and shaded bootstrapped 95% confidence band represent the distribution of all predicted saccade sizes. Each set of data was resampled 1000 times allowing repeats to produce surrogate datasets of the same size. Median predicted saccade sizes are indicated by a triangle. A correspondingly coloured vertical bar represents the range of median predicted saccade sizes when using RFs that are halved to doubled in size. d, Observed saccade sizes for humans and macaques, cats, mice, and marmosets (dashed versus solid lines represent different sets of data: see Online Methods for details). Median observed saccade sizes are indicated by triangles. e, Comparison of predicted (shaded) and observed (white) saccade size box plots of distributions (range: 25th and 75th quartiles, centre: median). Solid and dashed outlined boxes correspond to solid and dashed lines in d. The correlation between the entire predicted and average observed saccade size distributions is displayed at the bottom of each set of box plots.

Predicting saccades sizes from natural scene statistics

If the goal of saccades is to find novel information in natural scenes, the function in Fig. 4a suggests that animals with small RFs would employ a distinct strategy from animals with large RFs. Primates, with their fine vision, would make saccades larger than their RF sizes to decorrelate incoming inputs (e.g., 5° for a 1° RF), whereas mice, with large RFs, would make saccades smaller than their RF sizes (e.g., 11° for a 15° RF). To quantitatively test whether this prediction holds, we examined saccadic behaviour of animals with varying RF sizes. We extracted RF sizes for macaques, marmosets, cats and mice from existing databases, taking into consideration RF variance with eccentricity (Fig. 4b, see details in Online Methods and Fig. S4). We passed each distribution through the decorrelation distance function to construct predictions of saccade size for each species (Fig. 4c). The decorrelation function compresses the predicted saccade size distributions together with much more overlap (Fig. 4c) compared to the RF size distributions (Fig. 4b) and produces skewed saccade size distributions that correspond to the natural scene statistics (Fig. 4a, inset). Importantly, these predicted saccade size distributions are comparable to observed saccade sizes (Fig. 4d). While macaques and mice have RF profiles that are widely distinct (Fig. 4b), their saccadic behaviour overlaps substantially (Fig. 4d). The cat, with intermediate RF sizes, exhibits saccadic behaviour between the mouse and macaque (Fig. 4d). All three animals have saccade size distributions with shapes matching a skewed Gaussian, which corresponds very closely with what we observe for our predicted saccade size distributions. The predicted and observed distributions are highly correlated with aligned medians and quartiles (Fig. 4e). Because these mammals represent a diverse sample, our predictions are robust to RF size variations within each species due to measurement differences or RFs in different visual areas contributing to saccade sizes. The triangles in Fig. 4c–d represent median predicted and observed saccade sizes and the bars below the triangles in Fig. 4c represent the ranges of predictions for medians if we use RF sizes that are half to double in size compared to V1 RF sizes. For macaques, cats, and mice, each observed median overlaps with the middle of the range of predicted medians, while there is little to no overlap between predicted median ranges across animals.

While the decorrelation model accurately predicts the amplitudes of saccades made by macaques, cats, and mice, marmosets make notably smaller saccades than we predicted (Fig. 4e). All mammals use head movements for very large shifts in gaze but marmosets, in particular, use head movements that are as fast as eye movements for even modest shifts in gaze³⁰. Including head movements in gaze shifts would therefore move the observed gaze sizes of marmosets toward the larger amplitudes predicted by the decorrelation analysis. Some species use head movements exclusively to shift gaze in the same manner as saccades^10,11, and there is even one case where a human compensated for the loss of saccadic eye movements with head movements³¹.

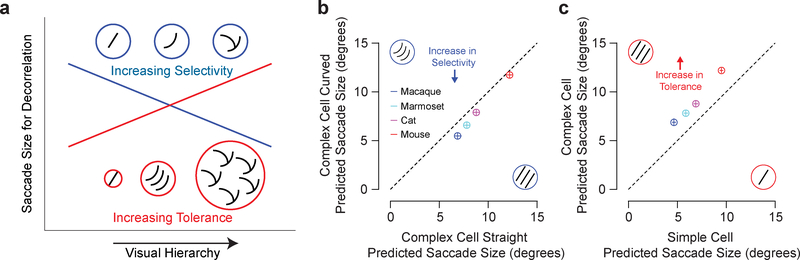
Our analysis shows how RF size influences saccade size predictions, but other RF properties also affect our predictions. For example, selectivity and tolerance, which both increase along the visual hierarchy³² change predicted saccade sizes systematically in different ways (Fig. 5a). To demonstrate how selectivity changes saccade size predictions, we added a subtle amount of curvature (23° bend in the centre) to the sinusoidal component of our V1 complex cell RF and compared saccade size predictions using this model to our original model with a standard V1 complex cell RF. This new RF is more selective than our original RF because curved contours occur less often than straight contours in natural scenes³³. The model based on curved complex cell RFs indeed consistently predicts smaller saccade sizes than our original model based on a standard V1 complex cell RF (Fig. 5b). Other features of our model that increase or decrease selectivity, such as surround suppression¹⁵ (Fig. S5a) and a cardinal orientation bias³⁴ (Fig. S5b), also decrease and increase predicted saccade sizes, respectively. Similarly, RFs that detect progressively less selective features such as non-oriented RMS contrast and luminance, require progressively greater saccade sizes because these features correlate over greater distances than oriented features²⁹. To demonstrate how tolerance changes saccade side predictions, we separated our saccade size predictions for V1 simple and complex cells. Simple cells detect luminance contrast features at a particular orientation and spatial frequency and the phase and polarity must match the RF. Complex cells detect luminance contrast features at a particular orientation and spatial frequency regardless of the phase and polarity of the feature and are therefore more tolerant than simple cells. As expected, a model based on complex cells consistently predicts larger saccades than simple cells (Fig. 5c). Overall, selectivity and tolerance tend to cancel out their influence on saccade sizes, and although there may be subtle changes to predicted saccade sizes with specific model variations, the ordering, separation, and shape of the distributions in Fig. 4 persists with these manipulations. Our model has one free parameter (decorrelation threshold) that can be optimized with changes to RF models to best align predictions with behavioural data (Fig. S6).

Figure 5.

Selectivity and tolerance decrease and increase saccade sizes necessary for decorrelation, respectively. a, Selectivity and tolerance both increase along the visual hierarchy, but have opposite effects on optimal saccade sizes. For decorrelation, saccade sizes need to be smaller with greater selectivity (blue) and larger for greater tolerance (red). b, Predicted median saccade sizes are smaller for RFs that detect curved contours compared to RFs that detect straight contours. c, Predicted median saccade sizes are larger for complex cell RFs compared to simple cell RFs. For b and c, vertical and horizontal lines in the circles represent 95% confidence intervals of the median (n = 392 images).

Decreasing spatial acuity increases saccade sizes

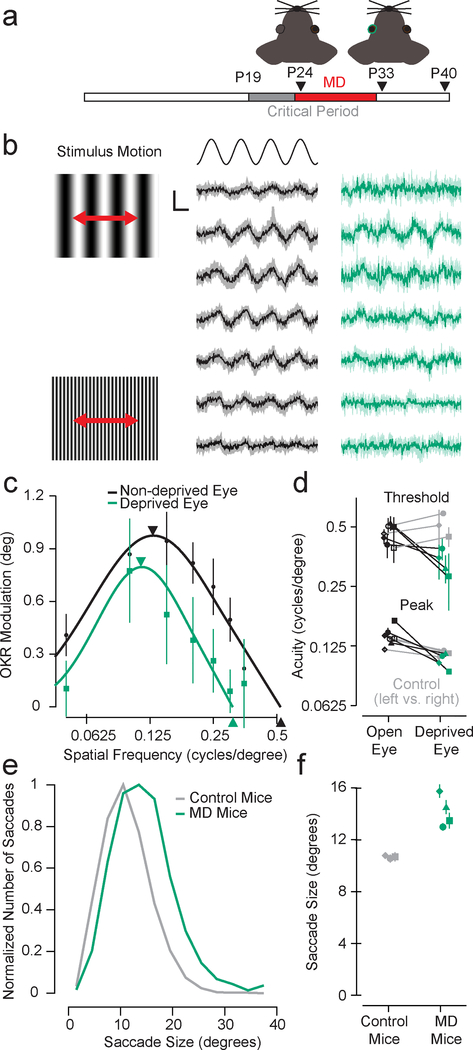
If saccade sizes depend on the acuity of our visual system, or RF size, as we demonstrated in Fig. 4, then we should be able to increase saccade sizes directly by reducing visual acuity. One way we can disrupt acuity is to close one eye during the developmental critical period, which leads to a loss of spatial acuity for that eye³⁵. We directly tested our hypothesis by using this monocular deprivation (MD) paradigm to reduce spatial acuity in a sample of four mice and measured the impact on saccade sizes compared to control mice of the same age with normal visual development.

We performed MD during the visual critical period³⁶ and allowed the deprived eye to reopen at the end of the critical period at P33 (Fig. 6a). After the mice reached an age of visual maturity at P40³⁷, we measured their spatial acuity using the optokinetic reflex (OKR)³⁸. The OKR was triggered by a large luminance sinusoidal grating slowly moving horizontally back and forth as a sinusoidal function of time (Fig. 6b). The eye tracks this movement to maintain gaze stability and the effectiveness of this tracking varies as a function of spatial frequency (Fig. 6b and 6c), providing an estimate of visual acuity.

Figure 6.

Decreasing acuity with monocular deprivation (MD) increases saccade sizes. a, Timeline of monocular deprivation (P24-P33) and acuity and saccade measurements (P40). b, A sinusoidal luminance grating (left) was moved back and forth horizontally ±6° at 0.5 Hz to induce an optokinetic reflex (OKR). The eye movements for an example mouse at varying spatial frequencies (low-to-high for top-to-bottom) are shown for the non-deprived (black) and deprived (green) eyes. Shaded error bands are 95% confidence intervals of the median (n = 20 stimulus repeats for all mice). Vertical scale bar is 2° and horizontal scale bar is 0.5 s. c, Corresponding OKR modulation varies as a function of spatial frequency. The peak spatial frequency and high spatial frequency threshold are lower for the deprived versus non-deprived eye. Arrows are median peak and threshold estimates. Error bars are 95% confidence intervals of the median. d, This reduction in acuity was consistent across four mice (see also Fig. S7a). Three control mice (grey) had similar acuity for both eyes that matched the acuity of the non-deprived eye of the MD mice. Error bars are standard error of the median. e, Saccade sizes were larger for MD mice versus control mice (MD: median = 13.91°, n = 1448 saccades, bootstrapped 95% confidence interval = [13.46, 14.37]; control: median = 10.73°, n = 1586 saccades, bootstrapped 95% confidence interval = [10.52, 10.94]). f, This was consistent for all MD mice (n = 668, 256, 226, and 298 saccades) compared to all control mice (n = 896, 344, and 346 saccades). Each data point is the median and error bars are standard error of the median.

For all MD mice, the visual acuity was significantly diminished in the deprived compared to the non-deprived eye as determined by the high spatial frequency threshold or the peak spatial frequency (Fig. 6d, green versus black; see also Fig. S7a), consistent with a previous MD study in mice³⁵. The control mice that had normal visual development had acuity for both eyes that was the same as the acuity we observed for the non-deprived eye of MD mice (Fig. 6d, open and grey vs. black data points; see also Fig. S7b), consistent with previous measurements of spatial acuity in mice using multiple methods^35,38,39.

Having established a change in spatial acuity in the MD mice, we then measured saccade sizes in both groups while presenting the same natural images used for the data described in Fig. 1. The saccade sizes for all of the MD mice were consistently and significantly larger than the control mice (Fig 6e and 6f, median saccade size MD: 13.91°; control: 10.73°). Therefore, reducing spatial acuity resulted in increased saccade sizes.

Discussion

We have explored whether saccadic eye movement behaviour across mammals can be described by a common process that provides the individual visual neurons with novel information. While saccades have been associated with the presence of a fovea, we demonstrate a common dependence of saccadic size and frequency on image size in mice and humans, even though mice lack a fovea (Fig. 1). We provided evidence that saccades act to decorrelate inputs by combining decorrelation distance statistics of natural images with cortical RF size distributions to predict saccade sizes for a number of different mammals with varying visual acuity. Those predictions are remarkably well matched to the median and shape of observed saccade size distributions during passive viewing (Fig. 4c–e).

We chose V1 RFs to make our saccade size predictions for a practical reason: V1 is the most widely studied visual area in several species²⁵ and this allowed us to use data that were collected in a similar manner and make fair comparisons across species. Other visual areas, however, might play critical roles in shaping the saccadic eye movement statistics. For example, it may be that decorrelation at the level of the retina or area V2 shapes saccade amplitudes. Those areas exhibit different RF sizes than the V1 sizes we used, but those differences can be reconciled with a single scale factor^40,41. To explore the impact of changing RF size within species, we halved and doubled the measured RF distributions and found that the predicted rank ordering of saccade size across species was preserved (Fig 4c), thus indicating that our hypothesis does not depend on the particular RF sizes of V1. Furthermore, our scene analysis contains a single free parameter (decorrelation threshold) that can be optimized with changes to RF sizes to best align predictions with behavioural data (Fig. S6).

As information flows through the visual system, RFs not only increase in size, but gain greater complexity and selectivity. The increased selectivity of their RF properties may act to reduce the saccade distance necessary for decorrelation (Fig. 5a). For example, using non-oriented RFs that sense luminance or RMS contrast results in larger predicted saccade sizes than the oriented RFs we employ. Further, as RFs increase in selectivity from an oriented contour to an oriented curved contour (Fig. 5b), from centre-only to centre-surround (Fig. S5b), or from a cardinal orientation to an oblique orientation (Fig. S5a), the predicted saccade sizes decline. Regardless of complexity, spatial correlation for features is driven by the Gestalt principles of proximity, continuation, and similarity that are based on the cohesiveness of matter. We therefore predict that more complex RFs would produce similarly shaped predicted saccade size distributions with smaller median sizes. In other words, there is an expected increase in saccade size along the visual hierarchy because RF size increases, but simultaneously a predicted decrease in saccade size because the selectivity of the RFs increases. Thus, these two factors, selectivity and tolerance, may balance each other³², yielding little changes in predicted saccade sizes (Fig. 5a). Therefore, our results should not depend on the specific choice of V1 RFs.

Most research on saccadic eye movements has focused on determining where humans are likely to direct their fovea. The results of this body of work have concluded that the target of a saccade can be predicted based on salience⁵ or the maximization of task-relevant information^3,7. The task dependence of saccadic eye movements was demonstrated very elegantly in the early eye traces of Yarbus⁶, where he had subjects look at images and had them answer different questions about those images. None of these proposals, however, can likely explain why mice make saccadic eye movements. Even considering non-uniformity in the density of their retinal ganglion cells, which form a weak horizontal streak⁴², the horizontal dominance of mouse saccades (Fig. 1c) prevents the higher-density portion from viewing novel information. During a saccade, mice could also be repositioning the binocular region of the retina¹³. No difference in acuity has been reported, however, for V1 neurons in the binocular region relative to the monocular region⁴³. These considerations suggests that an alternative explanation like the one we have presented is required to account for saccadic eye movements. Fixational eye movements, between saccades, have previously been proposed to decorrelate retinal responses^44,45, and microsaccades during prolonged fixation have been shown to prevent image fading, such as the Troxler effect, which reduces responses to entoptic stimuli⁴⁶, but all of these eye movements are substantially smaller than what we are proposing.

An open question is how our proposed saccade strategy develops over time. We can begin to answer that question by perturbing the system by either changing natural scene statistics or RF properties. Previous studies have demonstrated changes in saccades sizes with changes in natural scene statistics. Saccade sizes and frequency decrease for dynamic versus static natural scenes⁴. Dynamic natural scenes provide new visual information to RFs without saccadic eye movements. Another study suggests that saccade sizes can quickly change based on current scene statistics. Larger saccades were observed for images filtered for low spatial frequencies and smaller saccades were observed for images filtered for high spatial frequencies⁴⁷, which is exactly what our hypothesis predicts. Low spatial frequencies require larger distances and high spatial frequencies require smaller distances to decorrelate inputs. Disrupting RF statistics in humans, by long-term conditions such as macular degeneration or short-term occlusion, resulting in a lack of a fovea and reduced spatial acuity, leads to subjects making larger saccades⁴⁸ or changing saccade strategy⁴⁹ consistent with our proposal. Our MD experiment demonstrates that reducing visual acuity leads to increasing saccade sizes in mice as well. Larger saccades were also observed in mice that were dark-reared¹³, which results in both reduced spatial acuity³⁹ and a change in the movement map for saccades in the superior colliculus (SC)¹³. The SC is an attractive target for further examination of our hypothesis because it contains linked sensory and motor maps, although it is unclear how the retinotopic organization in the SC is related to the saccade size distributions we have measured.

Our visual system is confronted with critical bottlenecks that limit performance: limits in the number of sensors, number of nerve fibres, and metabolic energy available for conveying information to and between central areas. Neuronal adaptation has been proposed as one method to decorrelate neural signals, reduce redundancy, reduce energy consumption and hence generally maximize efficiency⁵⁰. We suggest that the motor system co-evolves with these adaptive processes in a way that matches the statistics of the natural world and the processing limitations of our sensory systems. Saccades and other fast gaze shifts allow organisms to sample novel features continually. While the distributions of saccade sizes may often reflect this default sampling strategy that is optimal for passively viewing typical natural scenes, this strategy is undoubtedly overridden by top-down processes when task demands require specific processing of visual scenes^3,6,7. We demonstrate here that the saccadic behaviour of many mammals under free viewing matches this default strategy, indicating that the motor and sensory systems cooperate to efficiently sample and process visual scenes. Active sensation thus reflects constraints imposed by the scene statistics, internal representations and task demands.

Online Methods

Preparation of animals

All procedures were approved by The University of Texas at Austin Institutional Animal Care and Use Committee and are in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Additional details can also be found in the Life Sciences Reporting Summary. We used six adult mice (3 to 12 months): four were C57BL/6 female mice and two were PV-Cre;Ai14 female mice⁵¹ in our experiments. To immobilize mice during experiments, a titanium bar was secured to the skull using dental acrylic under isoflurane anesthesia (1–3%). In addition, we measured natural saccadic eye movements in one female fixation-trained marmoset^30,52. A titanium headpost was fixed to the skull with acrylic under isoflurane anesthesia (1–3%).

Stimuli

We used a DLP LED projector (VPixx Technologies, Inc.) with a refresh rate of 240 Hz and a DepthQ HDs3D2 projector (DepthQ/Lightspeed Design, Inc.) with a refresh rate of 120 Hz to display natural images on a screen placed 22 cm in front of the mice. For natural stimuli, we used up to 36 images for each mouse from the McGill Calibrated Color Image Database⁵³, and we used full images for “large” images (covering 80° × 64° of the visual field) and centre-cropped images for “small” images (covering 40° × 32° of the visual field). Using Psychtoolbox⁵⁴, we displayed images for 30 s with a 2-s grey screen between image presentations. During preliminary experiments, we discovered that mice trained on an unrelated binocular vision task would make saccades much more frequently to the novel stimuli for our free-viewing experiment compared to naïve mice. Additionally, all mice (trained and untrained) would quickly habituate to our experiment within and across sessions, making saccades less and less frequently. Therefore, we collected saccade data on six mice trained for binocular vision tasks (Samonds et al., VSS abstr 62.26, 2016; SFN abstr 493.09, 2017) and only collected data for each mouse for 2–3 sessions, with 8–12 images presented in each session, before or after their behavioural task. Each mouse had to make saccadic eye movements for at least eight large images with at least an average of five saccades per image for each eye or were not included in further analysis. This was to make sure that we had sufficient samples to compare saccade sizes between large and small images for each mouse. For the marmoset, we presented 24 images of only one size (covering 40° × 32° of the visual field) from the same database on a 21” CRT with a refresh rate of 85 Hz, at a distance of 50 cm, for 30 s, and randomly interleaved with unrelated 1-second fixation trials using Maestro software.

Eye and running tracking

We used two infrared security cameras mounted in front of both eyes of each mouse head-fixed and running on a floating track ball⁵⁵. We positioned the cameras so that they were perpendicular to the orbital axis of each eye (Fig. S1a, 50° from frontoparallel and slightly pointed downward). The position of cameras occluded portions of both peripheral monocular visual fields, but the central 80° in front of each mouse, where images were presented (Fig. S1a), remained clear. The cameras collected 800 × 600 pixel images at 20 frames per second for early experiments and 30 frames per second for later experiments. We saved cropped images of 250 × 250 pixels centred over the eye for all experiments and used infrared lighting to minimize shadows (Fig. S1a). Custom Matlab software was used to track the centres and sizes of the pupils (Fig. S1a, white crosshairs) and corneal reflections (Fig. S1a, black crosshairs) offline (see also Supplemental Video 1). The position of the pupil centres were calibrated to degrees of visual angle by placing a 3.25-mm diameter^56,57 artificial eyeball in the same location as the mouse eyeball and rotating it +/−60° and measuring how the tracking position varied systematically. We examined the feasibility of using the same size eyeball for calibration for all mice by normalizing the distributions of saccades sizes for each mouse to have either the same mean or median. In all cases, this only reduced the width of the overall recombined distribution by less than 5% compared to the original distribution suggesting that there was minimal variability between eyeball sizes for our mice.

The running speeds of mice were measured from absolute changes in ball position (sampled at 200 Hz) with an optical mouse placed next to the ball (Fig. S1a). Running speed was smoothed in 200 ms windows and calibrated by rotating the ball for a set distance and duration. Saccade sizes increased with image size regardless of whether the mice were running or not. When the mice were running (≥2 cm/s), saccade sizes for large images were a median of 11.35° (n = 1028 saccades, bootstrapped 95% confidence interval = [10.84, 11.85]) and saccade sizes for small images were a median of 10.03° (n = 919 saccades, bootstrapped 95% confidence interval = [9.66, 10.43]). When the mice were stationary (<2 cm/s), saccade sizes for large images were a median of 10.85° (n = 327 saccades, bootstrapped 95% confidence interval = [10.45, 11.32]) and saccade sizes for small images were a median of 10.32° (n = 226 saccades, bootstrapped 95% confidence interval = [9.34, 10.81]).

For the marmoset, we tracked the position of one eye using the EyeLink 1000 (SR Research) camera and software that detected pupil position at 1000 samples per second. We calibrated position into degrees of visual angle using a fixation task described in detail elsewhere^30,52.

Saccade detection

For mice, saccades were detected by finding peaks in the frame-by-frame change in absolute pupil position (Fig. S1b, velocity) over time. We set a threshold for each eye by examining the peaks in velocity and comparing them to the traces of vertical and horizontal position over time, which was when the velocity typically exceeded 90°/s (Fig. S1b, dashed red line). The beginning (Fig. S1b, green circles) and end (Fig. S1b, red circles) of saccades were then set as the first points in both directions from the peak velocity that went below a second threshold that was 1.5°/s (Fig. S1b, dashed green line). Because we were recording from both eyes and eye movements were conjugate 99% of the time (Samonds et al., VSS abstr 62.26, 2016; SFN abstr 493.09, 2017), we used this redundant information to confirm the presence of saccades. However, we still included saccades that occurred in only one eye once they were verified in the video recordings of the eye movements. Since mice saccade relatively infrequently, we manually checked all traces of horizontal position over time and confirmed and checked any questionable saccades that were detected or missed for both presence and size accuracy using the saved video recordings of the eye movements.

For marmosets, we detected saccades using the same methods, but adjusted the thresholds, since sampling frequency was higher and saccades were substantially smaller. We used a peak threshold where velocity had to exceed 20°/s and the beginning and end of the saccades were the first points when velocity went below 10°/s. This method allowed us to detect clear saccades with sizes less than 0.5°. We rejected any saccades detected with sizes that were less than two times the RMS noise observed during fixation periods (<0.2°). We lastly manually checked traces of vertical and horizontal position over time for detection accuracy.

RF size distributions

Since, macaques, marmosets, and cats have a non-uniform distribution of RF sizes across the primary visual cortex and experiments typically sample neurons with a bias for location (e.g., para-foveal), we had to estimate non-biased distributions of RF sizes for the entire primary visual cortex for each of these animals. First, the average size of RFs increase with increasing eccentricity in the primary visual cortex. For macaques, we used the square root of RF areas of the data points and power function fits from Van Essen et al.²³ (Fig. S4a, blue):

$$RFArea=A*eccentricit{y}^{-B}$$ (8)

For marmosets, we obtained the RF plots from Chaplin et al.⁵⁸, computed the RF area and eccentricity, and then took the square root of the areas. We then fit the data with power functions in the same manner as Van Essen et al.²³ (Fig. S4a, cyan). For cats, we used the RF areas reported by Albus for eccentricities less than 10°⁵⁹ (Fig. S4a, small magenta data points). Then we used the mean and standard errors of RF widths reported for five ranges of eccentricity by Wilson and Sherman⁶⁰. We plotted these as data points at the centre of the ranges (Fig. S4a, large magenta data points with error bars). These values were corrected based on Wilson and Sherman’s fit of underestimation of hand-mapping measurements. With this correction, the means and standard errors match very well with the data with overlapping eccentricities from Albus⁵⁹, and are in the range of what we would expect when compared to the marmoset and macaque data. We again applied power function fits to this data. For all three species, we estimated a distribution of RF size at each eccentricity using a Gaussian with a mean equal to the fit and standard deviation equal to the mean. We chose this after measuring standard deviations on the same order as the mean at several ranges of eccentricities for all three animals.

Second, the visual field is not represented uniformly in the visual cortex. There is an over-representation of the central portion of the visual field. This is typically described as a function of cortical magnification, where the percentage of neurons that represent the visual field at each eccentricity varies. For several non-human primates, this has been thoroughly characterized and we use the same function for macaques and marmosets reported by Chaplin et al.⁵⁸ (Fig. S4b, blue). Cats have an area centralis where the central visual field is not as over-represented as in the fovea of non-human primates. We combined all the data points of cortical magnification in cat area 17 based on area that we could extract from published figures^59–61 and normalized them using a total area of 380 mm^{2 61}. Then we fit a cortical magnification function to those data points using the same modified power function equation described in Chaplin et al.⁵⁸ (Fig. S4b, magenta):

$$Magnification=e^{-A*eccentricity}\frac{B}{eccentricity+C}$$ (9)

The comparison between the cortical magnification functions we used for non-human primates and cats corresponds very closely with a comparison of changes in cone density with eccentricity for these same species⁴¹, which is consistent with the notion that cortical magnification reflects retinal ganglion cell density⁴⁰.

Finally, we combined the size versus eccentricity distributions and cortical magnification results to produce overall estimated RF size distributions for macaques, marmosets, and cats. The distributions of sizes for each eccentricity (Fig. S4a) were multiplied by their corresponding cortical magnifications (Fig. S4b) and the distributions were summed resulting in a total number of RF sizes for all eccentricities. Because cortical magnification is so strong for all three species, the choice of fits (power versus linear) did not strongly influence the overall shape of the RF size distributions. In all cases, the RFs beyond 10° eccentricity (Fig. S4b) have minimal influence on the distributions. For mice, we used a previously reported distribution of RF areas⁶² and fit a Gaussian to the square roots of those areas.

There can be significant differences in RF estimates depending on the methods⁶³. We chose data from each animal that used similar minimum response field measurements of RF area⁶⁴. We also included a diverse enough range of animals so that experimental differences in size estimates would be smaller than RF size differences between animals. Based on spatial frequency preference measurements^22,65–67 and spatial acuity measurements for these animals^68–71, our RF estimates do accurately represent the differences between these animals.

Natural image analysis

We measured decorrelation distances in natural images using the methods described in detail elsewhere²⁴. First, we converted 392 images from the McGill Calibrated Color Image Database⁵³ to grayscale. Then, we chose an energy model-based RF²⁶ that captures the phase invariant properties of complex cell RFs in the visual cortex that represent spatial frequency and orientation. We generated RFs with a two-dimensional (2D) Gabor function:

$$G(x,y)=e^{-\frac{x^2+y^2}{2{\sigma }^2}}\sin ((x\cos (\theta )+y\sin (\theta ))f+\phi )$$ (10),

where x and y are horizontal and vertical position, σ is the standard deviation of the Gaussian envelope, and θ is the orientation, f is the frequency, and φ is the phase shift of the sinusoid. We generated two 2D Gabor filters with 90° differences in phase and the functions were cropped within a circle centred on the function with a diameter of four standard deviations. The period was always 1.5 times this diameter and the bandwidth was just over one octave with diameters ranging from 30° to 0.5° linked with spatial frequencies ranging from 0.05 to 3 cycles/°. We used orientations of 0, 45, 90, and 135°. There is a small difference in our analysis for 0° and 90° compared to 45° and 135° (Fig. S5b), but we combined all data across all four orientations. All of the following steps were repeated for each RF size.

Next, for the simple and complex RF model, we took the dot product of the two 90° out-of-phase filters (G₁(x,y) and G₂(x,y)) with 100 randomly chosen locations within each individual image (I(x,y)). The only restriction was that the location had to allow the RF to fit completely within the image. For the complex RF model, we then squared this result and summed the outputs:

$$E=\sum ({\left(G_1(x,y)\cdot I(x,y)\right)}^2+{\left(G_2(x,y)\cdot I(x,y)\right)}^2)$$ (11)

Simple cell response were represented only as the dot product of the two 90° out-of-phase filters. We used an equal number of simple and complex cells for macaques, marmosets and cats⁷² and twice as many simple cells versus complex cells for mice^22,73. We then normalized all responses by dividing the responses by the local luminance and RMS contrast within the RFs^24,27. Local luminance and contrast were computed under a raised cosine window:

$$w_i=0.5\left(cos\left(\frac{x}{r}\sqrt{{\left(x_i-x_c\right)}^2+{\left(y_i-y_c\right)}^2}\right)+1\right)$$ (12),

where i is the pixel number in the RF, r is the radius of the RF, and x_c and y_c are the centre of the RF. The luminance L was computed as the weighted average of the image intensity in the RF:

$$L=\frac{1}{{\sum }_{i=1}^N{w}_i}{\sum }_{i=1}^N{w}_i{L}_i$$ (13),

where N is the total number of pixels in the RF and L_i is the intensity at pixel i. The RMS contrast was similarly weighted by the cosine function:

$$C_{RMS}=\sqrt{\frac{1}{{\sum }_{i=1}^N{w}_i}{\sum }_{i=1}^N{w}_i\frac{{\left(L_i-L\right)}^2}{L^2}}$$ (14)

Divisive normalization within the receptive field had no impact on decorrelation distance. We tested for the effect of divisive normalization from the surround (surround suppression) on our measurements for RFs up to 10° in size by normalizing the response in the same manner described above, but with a size 3 times the centre RF size based on physiological measurements of the surround size in macaque and mouse V1 cells^63,74,75. Although the surround effectively increases RF size, surround suppression increases the selectivity of a RF¹⁵ and overall reduced decorrelation distances (Fig. S5a). We do not include surround suppression in our saccade size predictions in Fig. 4 because the large size of the surround makes it impossible to sample enough large saccades for large RFs within our images (we had to extrapolate to predict saccade sizes for mice in Fig. S5a). Varying model parameters (Fig. S6) or including RF properties that correlate over larger distances²⁹ could compensate for the reduced decorrelation distance. Lastly, to examine the effect of RF selectivity, we added a circular function to the phase in equation 10 to add curvature to the sinusoid component of the Gabor function:

$${\phi }_{curve}(x,y)=\frac{\sqrt{{(x-r)}^2+y^2}}{2r}$$ (15),

where x and y are RF locations and r is the RF radius. Then we repeated all the same steps that we did to generate V1 complex cell responses. This produced a RF that detects phase invariant curvature and has similar properties that have been documented for RFs in V2⁷⁶.

Next, we chose a second set of 100 random locations within each image all at the same particular distance from our original random locations, ranging from 0.1° to 50°, and measured the correlation between responses for each distance. Again, the RF at these second locations had to fit completely within the image. To prevent noise from influencing threshold crossings, we fit a sigmoid function to correlation versus distance data for each RF size:

$$r=k_1\left(\frac{k_2}{d^{k_3}+k_2}\right)+k_4$$ (16),

where r is the correlation, d is the distance, k₂ determines the horizontal position, k₃ determines the fall-off rate, and k₁ and k₂ determine the vertical position.

Finally, we searched for the smallest distance where the correlation was less than a set threshold. This was defined as the decorrelation distance for each RF size. The threshold is the one free parameter that we use to fit predictions to observed data and the same thresholding was used for all animals. Increasing this threshold reduces decorrelation distances and decreasing this threshold increases decorrelation distances (Fig. S6a). Over a limited range, varying this threshold preserves the separation of predicted saccade sizes between species, but decreases or increases their absolute values, respectively (Fig. S6b). As the threshold becomes larger or smaller outside of this range, the separation becomes wider or narrower between species, respectively (Fig. S6b). We fit a saturating function to decorrelation distance versus RF size (Fig. 3d) to cover all possible RF sizes used:

$$D=\frac{k_{1}d}{d^{k_2}+k_3}+k_4$$ (17),

where D is the decorrelation distance, d is the RF size, k₁ and k₂ determine the slope and curvature, k₃ determines the saturating point, and k₄ determines the initial decorrelation distance. Predicted saccade sizes were computed by summing up the distributions of decorrelation distance for both simple and complex cells and weighting them by V1 RF distributions. The decorrelation distance histograms were then fitted with a skewed Gaussian:

$$P=k_1+k_2\left(e^{\frac{-{\left(D-D_0\right)}^2}{2{\left(\sigma +\gamma \left(D-D_0\right)\right)}^2}}-e^{\frac{-1}{{\gamma }^2}}\right)$$ (18),

where P is the probability of observing a distance, D is the decorrelation distance, D₀ is the Gaussian centre point, σ is the standard deviation, γ is the skew, and k₁ and k₂ determine the offset and amplitude constrained to always be equal to or greater than zero.

Gain-adaptation model

We constructed a simulation of the response time course for 500 neurons with distinct RFs in visual cortex to determine the effect of adaptation and saccades on response sensitivity. The response of each neuron was the product of the RF, stimulus and gain adaptation (equation 1) with a time constant half of the fixation duration. For each neuron, the response time course R(t) is determined by the following equations:

$$R(t)=RF*S(t)*\left(\frac{k}{k+a(t)}\right)$$ (19)

$$a(t)=\left(a(t-1)+RF*S(t)\right)e^{\frac{-dt}{\tau }}$$ (20),

where RF is the receptive field, S is the stimulus which changes with saccades, k is a constant of normalization (30), and τ is the time constant of the response (150 ms).

Saccade size distributions for other animals

Human saccade sizes were measured while they viewed natural images for 30 s that spanned 32° × 24°². The macaque and marmoset saccade sizes were measured while they viewed natural images for 20 s that spanned 44° × 34° of their visual fields³⁰. We also repeated our mouse experiment with the exact same experimental conditions on one marmoset and obtained results as previously reported³⁰. Finally, we include two distributions of cat saccade sizes. The first distribution was measured while cats were free viewing in the dark⁷⁷ and the second similar distribution was measured while cats were viewing a 21-min natural video of unknown size⁷⁸. Our results for mice and Otero-Millan et al.² reveal that saccade size depends on image size and the stimuli shown to different species varied from image sizes ranging from 32° to 44°. However, the changes in saccade size are about 1° for each doubling of image size. Therefore, differences in saccades sizes due to differences in image sizes are likely to be smaller than differences in saccade sizes between species. As noted above, when we did have different sets of data for one species, the differences between studies were indeed smaller than the differences between species. Additionally, humans and macaques had very similar saccade sizes and have nearly identical spatial acuity⁶⁸.

Monocular deprivation (MD)

MD was induced during the critical period as previously described⁷⁹. One eye (2 left, 2 right) in each mouse (PV-Cre;ChR2; 2 females, 2 males) was sutured closed under anesthesia (as described above) at P24 for 9 days (Fig. 6a until the end of the critical period at P33). The sutures were removed and head plates were attached to each mouse as described above. Three age-matched control mice (PV-Cre; 1 female, 2 males) had head plates attached at the same time.

Optokinetic reflex (OKR) measurements

When the MD and control mice reached an age of P40, we measured their acuity and saccade sizes. We generated an OKR moving a 108° × 108° sinusoidal luminance grating (100% Michelson contrast) back and forth (±6°) along the horizontal plane as a sinusoidal function of time (0.5 Hz) in front of the mouse (Fig. 6b). This speed was chosen to produce the maximum amount of eye movement or velocity (1.5 Hz temporal frequency at 0.125 cycles/°) ³⁸. Slower speeds produce higher gains, but result in a smaller change in position. To assess acuity, we varied the spatial frequency (0.05, 0.1, 0.15, 0.2, 0.25, 0.3, and 0.35 cycles/°) and quantified the peak-to-peak modulation of horizontal eye movement. We quantified the modulation as the amplitude parameter of a cosine fit with a matched profile of the stimulus motion. The only other free parameter of the fit was a delay between the stimulus and the eye movement. The median modulation versus spatial frequency was then fit with a Gaussian function of log-spatial frequency (Fig. 6c). We used this function to compute the peak spatial frequency (Fig. 6c and 6d) and the spatial frequency cut-off or threshold was determined using a linear extrapolation to zero modulation using the data on the high end of spatial frequencies (Fig. 6c and 6d).

Statistical analysis

Data collection and analysis were not performed blind to the conditions of the experiments. No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those reported in previous studies^51,74. No assumptions were made about the distributions of data and all confidence intervals and statistical tests were based on bootstrap analysis of the median. Each set of data was resampled 1000 times allowing repeats to produce surrogate datasets of the same size. The 25th and 975th samples of sorted estimates from these datasets were then used as the 95% confidence intervals and the160th and 840th samples were used for the standard error of medians for all results.

Supplementary Material

supplemental figures

Figure S1. Experimental setup. a, Natural images were displayed to mice running on a floating Styrofoam ball, while we tracked eye position with infrared cameras and running speed with an optical mouse. b, Saccades were detected when velocity exceeded an initial threshold (red dashed line), and the beginning (green circle) and end (red circle) of saccades were determined as when the velocity fell below a second threshold in opposite directions (green dashed line).

Figure S2. Examples of decorrelation distances versus RF size estimated for individual images using V1 complex cells. These are representative examples from a sample of n = 392 natural images. The measured distances are plotted along with a fit based on equation 17 in Online Methods.

Figure S3. Entire raw probability distribution of decorrelation distances for n = 392 images for all RF sizes from Fig. 4a.

Figure S4. Receptive size and cortical magnification versus eccentricity. a, RF size (square root of area) versus eccentricity replotted from previous studies (see legend) for macaques (n = 248 RF sizes²³), marmosets (n = 597 RF sizes⁵⁸), and cats (n = 643 RF sizes for individual data points⁵⁹; mean and standard error for n = 178 RF sizes grouped by eccentricity⁶⁰). All fits are based on the same function used in Van Essen et al.²³ b, Cortical magnification versus eccentricity replotted from previous studies (see legend). The large plot only shows the fits and the first 10° of eccentricity with linear axes to emphasize the severity of the fall-off. The inset shows all of the data (n = 82 cortical magnification estimates for cats^59–61). The fit for cat data was based on the same function used in Chaplin et al.⁵⁸ (see Online Methods for details).

Figure S5. More examples of changes in predicted saccade sizes as a result of RF selectivity changing. a, Predicted median saccade sizes are smaller for RFs with a suppressive surround compared to RFs that only have divisive normalization within the classical RF. *Extrapolated surround suppression prediction for the mouse. b, Predicted median saccade sizes are larger for RFs that detect cardinal orientations compared to RFs that detect oblique orientations. For a and b, vertical and horizontal lines in the circles represent 95% confidence intervals of the median (n = 392 images).

Figure S6. The effect of decorrelation threshold on predicted saccade sizes. a, Median decorrelation distances decrease for increasing decorrelation thresholds (n = 392 images). b, Predicted median saccade sizes correspondingly decrease with increasing decorrelation thresholds. Decreasing intensity in colour corresponds to different thresholds defined by the decreasing intensity of black in a. Vertical lines in the circles represent 95% confidence intervals of the median (n = 392 images). Dashed versus solid lines represents different sets of data (see Online Methods for details).

Figure S7. Monocular deprivation (MD) consistently shifts the optokinetic reflex (OKR) spatial frequency curve to lower spatial frequencies for the deprived eye. a, Normalized (by the peak) OKR gain versus spatial frequency data points for all four MD mice. b, OKR gain versus spatial frequency was similar between left and right eyes for three control mice and similar to the non-deprived eye of MD mice. For a and b, data points are medians and error bars are 95% confidence intervals of the median (n = 20 repeats for all mice).