Abstract
Neuron shows distinct dependence of electrical activities on membrane patch temperature, and the mode transition of electrical activity is induced by the patch temperature through modulating the opening and closing rates of ion channels. In this paper, inspired by the physical effect of memristor, the potassium and sodium ion channels embedded in the membrane patch are updated by using memristor-based voltage gate variables, and an external stimulus is applied to detect the variety of mode selection in electrical activities under different patch temperatures. It is found that each ion channel can be regarded as a physical memristor, and the shape of pinched hysteresis loop of memristor is dependent on both input voltage and patch temperature. The pinched hysteresis loops of two ion-channel memristors are dramatically enlarged by increasing patch temperature, and the hysteresis lobe areas are monotonously reduced with the increasing of excitation frequency if the frequency of external stimulus exceeds certain threshold. However, for the memristive potassium channel, the AREA1 corresponding to the threshold frequency is increased with the increasing of patch temperature. The amplitude of conductance for two ion-channel memristors depends on the variation of patch temperature. The results of this paper might provide insights to modulate the neural activities in appropriate temperature condition completely, and involvement of external stimulus enhance the effect of patch temperature.
Keywords: Pinched hysteresis loop, Ion channels, Patch temperature, Memristor
Introduction
In recent decades, many researchers have attempted to study and understand the potential causes of various dynamic properties of neuronal membrane potential, and some models of neuronal electrical activity had been proposed to deal with the generation and propagation of action potentials. For example, the Hindmarsh–Rose (HR) neuron model (Hindmarsh and Rose 1982, 1984) was effective to characterize the main dynamical properties of neural activities. Furthermore, the simplified second order nonlinear FitzHugh–Nagumo (FHN) neuron model (FitzHugh 1961), and the Wilson–Cowan neuron model for mathematical description of cortical column activity (Wilson and Cowan 1972), also confirmed that their reliability in evaluating dynamics of neural activities. These ordinary differential equations (ODEs) based oscillator-like neurons were almost derived from the Hodgkin–Huxley (HH) (1952) model or the simplified version. The HH model is the cornerstone of modern computational neuroscience. It is a system consisting of four-dimensional autonomous differential equations containing messy nonlinear functions for the initiation and propagation of an action potential in squid giant axon membrane.
Different neural dynamic behaviors have been found by investigating these neuron models. The main feature of electrical activity is represented by the sample time series of membrane potentials. By setting appropriate parameters in the neuron model, the membrane potential can present different patterns, such as quiescent, spiking, bursting and even chaotic. For instance, different bifurcation scenarios of firing patterns were observed in different chronic constriction injury models, which were induced by adjusting two physiological parameters (Jia et al. 2017). In biological neurons, the intrinsic time delay should be considered, the response time delay results from delay or transient period when external stimulus is encoded, and the propagation time delay is often generated by intersynaptic signal transmission (Mondal et al. 2019). In fact, the anatomical structure of some inter-neurons confirmed the existence of a time delay in autapse, which enhances the self-adaption of neurons to external stimulus. For example, the bursting activity and electromagnetic radiation on neuron can be suppressed when the autaptic modulation of neuron is activated (Xu et al. 2017). Moreover, extensive investigation confirmed that different kinds of electric field can cause distinct mode transition in electrical activities of neuron (Ma et al. 2019). Information transmission delays in neural networks lead to spatial coherence resonance (Wang et al. 2010), and there was an important relationship between average frequency and phase synchronization (Nordenfelt et al. 2013). The dynamics of voltage-gated ion channels in neurons are intrinsic random, therefore, the spike latency (Ozer et al. 2009) and different discharge patterns under the regulation of electromagnetic field (Xu et al. 2019) were studied in presence of channel noise. Furthermore, the effects of noise on the dynamical response and mode selection in neural activities of neurons and network were also studied extensively (Wang and Jiao 2006; Wang et al. 2018; Yao and Ma 2018). By establishing various neural networks, it is possible to study the collective behaviors such as synchronous transformation (Yao et al. 2017; Ge et al. 2018) and pattern selection (Perc 2007) to understand the potential occurrence mechanism of neuronal disease. Indeed, nonlocal coupling (Tian et al. 2018), and external stimulus (Guo et al. 2017) can affect the dynamic behavior of nervous system. Neural coding and the cognitive mapping have caused widespread concern in the field of neurodynamics (Wang and Zhang 2007). Neural network is a high-dimensional nonlinear complex dynamic system composed of a large number of neurons. However, neural energy may be an effective tool for studying the global behavior of brain activity (Wang and Zhu 2016). Based on the experimental results of signal transmission, an energy coding method is proposed (Wang and Wang 2017; Wang et al. 2015). Inspired by this theory, important research results have been achieved by applying different neural models and energy calculation methods. Such as the transmembrane electrical potential energy is analyzed in detail, and the neuron’s energy consumption minimal during bursting is found (Zhu et al. 2019). This can provide a theoretical basis for understanding the dynamics of neural activities.
In previous studies, the studies (Ma et al. 2012; Xu et al. 2018a, b) of ion channels and biofilms were carried out under the condition of constant temperature, that is, T = 6.3 °C. However, ambient temperature is one of the most important factors affecting neural activity. It regulates the excitability of neurons by regulating the ion channel conductance and gated dynamics. Recent theoretical studies have revealed the functional importance of temperature in modulating neurodynamics. For instance, Szabo et al. (2008) explored the impacts of temperature acclimation on central neural circuit and its behavioral output. Yang and Jia (2005) investigated that the effect of patch temperature as a control parameter on the spontaneous action potential of a finite size of membrane patch. It was found that the mean open rate of sodium and potassium channels of the HH neuron was decreased, and the mean duration of spikes of membrane potential was also decreased, which was qualitatively consistent with previous experimental results of single ion channel. Micheva and Smith (2005) examined the effects of temperature on the presynaptic function of primary cultured hippocampal neurons in rats. The results showed that the circulation of synaptic vesicles varied greatly at different temperatures. Hyun et al. (2011) used Aplysia neurons to research the mechanism of changes in discharge modes caused by temperature change, and they confirmed when the temperature rises, the discharge patterns of neurons could change. Therefore, the dynamic of neuron system is manipulated by the variation of patch temperature.
Memristor (Chua and Kang 1976; Chua et al. 2012) is a specific electric device that the memductance is dependent on the input current, and the magnetic flux is contributed by the exchange of charges. Recent study showed that the dynamic behavior of the memristor nonlinear oscillator is strictly correlated with the initial conditions in the memristor element (Bao et al. 2018). Each synapse can contribute to regulating the activity of other synapses (Maio et al. 2018). When the memristive synapse is activated (Wang and Ma 2018; Wang et al. 2018; Xu et al. 2018a, b; Guo et al. 2018), exponential flux-controlled coupling can lead to synchronization and oscillation death of neuron network (Thottil and Ignatius 2016). The dynamics becomes complex and interesting when memristor is involved into the nonlinear circuits. Based on the great similarity between memristor and biological synapse, and combining memristor network and sparse coding technology, an intelligent sparse coding scheme which can efficiently process massive information is proposed (Ji et al. 2019). The existence of a memristor-based hyperchaotic system with line of equilibrium and with no equilibrium has been studied, and it is proved that the dynamic behavior of memory system is controllable (Prousalis et al. 2017). At the same time, the practical electric circuits are employed to reproduce the properties of memristor systems in many studies (Rajamani et al. 2017; Volkov et al. 2014). Chua (2015) according to the basic circuit theory, the time-varying potassium and sodium conductance in the potassium and sodium ion-channels in the HH model were replaced by time-invariant potassium memristor and sodium channel memristor devices, respectively. From this new perspective, many unsolved anomalies can be explained.
It is well known that the remarkable characteristic of memristor is a hysteresis loop, and the shape of the hysteresis loop is determined by the device attributes and input signals. In particular, the hysteresis loop of memristor depends on the magnitude and frequency of the input signal. In this paper, based on the HH neuron model, the effect of temperature on the membrane potential of HH neurons is first studied. Secondly, the ion channels are updated with memrisitve type which is also related to temperature. Thirdly, the external sinusoidal voltage signal is applied to discuss the mode selection of electrical activity at different membrane temperatures.
Model of memristive ion channels
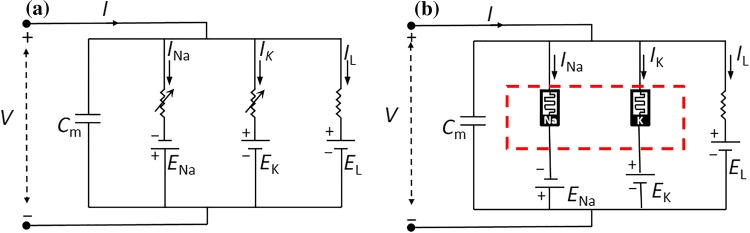
Temperature plays an important role in regulating the activity of memristive ion-channel in HH axon system. The HH model postulated a biological neuron model to deal with the current flow through the surface membrane of a giant nerve fibre in 1952. This model is made up from a line of identical 2-terminal electrical devices in Fig. 1a.
Fig. 1.
Electrical circuit representing membrane aRK and RNa are considered time-varying resistors [Original figure from (Hodgkin and Huxley 1952)]; b Memristive HH model [Original figure from (Chua et al. 2012)], the red dotted boxes indicate that the system is affected by temperature
Here V denotes the membrane potential of neuron, and Cm is the membrane capacitance per unit area. EK, ENa and EL denote the potassium ion battery voltage, the sodium ion battery voltage, and the leakage battery voltage, respectively. Furthermore, IK, INa and IL are the potassium current, the sodium current, and the leakage current, respectively. n, m, and h are the mean ratios of the open gates of the working channels. The factors n4 and m3h are the mean portions of the open ion channels within the membrane patch. RK = 1/gK, RNa = 1/gNa and RL = 1/gL, and RK and RNa represent two resistances which are not constant but vary with time. The dynamics of the neuron is described by the HH model with details as follows:
| 1 |
However, Chua pointed out that the mathematical models of those resistors behaved as the so-called time invariant memristive systems (Chua 2015), and the two elements RK and RNa called memristive devices in Fig. 1b. More specifically, the circuit element RK in the HH model is described as a first-order potassium ion-channel memristor. Similarly, the circuit element RNa is identified as a second-order sodium ion-channel memristor. Memristor has the ability to recall the resistance of the previous current when the current is turned off and will remember the resistance when the current is restored. As an unignorable factor in the systems, temperature is known to modulate the kinetic rates of ion channels. The red dotted boxes indicate the effect of temperature on the system in Fig. 1b.
The memristor is 2-terminal electrical device whose instantaneous terminal current and voltage obey a state-dependent Ohm’s law (Chua et al. 2012). A voltage-controlled generic memristor is defined by i = G(x)v, and G(x) represents the memductance of the memristor, whose unit is in Siemens (S). So the potassium ion-channel is described as follows:
| 2 |
and
| 3 |
| 4 |
where GK(n) represents the memductance of the potassium ion-channel memristor, and n is the mean ration of open potassium ion-channel gates of the working channels. The opening and closing rates of potassium ion-channel are given by
| 5 |
Equations (2), (4) and (5) together define the “first-order memristor” (Chua et al. 2012).
Similarly, let us consider the time-vary conductance of sodium GNa in HH Model related to input voltage vNa and output current iNa, and the sodium ion-channel can be rewritten as:
| 6 |
and
| 7 |
| 8 |
where GNa(m, h) represent the memductance of the sodium ion-channel memristor, and the opening and closing rates of sodium ion-channel are described as follows:
| 9 |
and
| 10 |
Equations (6), (8), (9) and (10) together define the “second-order memristor” (Chua et al. 2012).
The temperature factor ϕ(T) in Eqs. (5), (9) and (10) was given by Hodgkin and Huxley (Hodgkin and Huxley 1952):
| 11 |
When the temperature T is 6.3 °C, the value of the factor ϕ(T) is equal to 1.
In following simulations, we use the following parameters for the neuron model (Guo et al. 2017): gK = 36 mS/cm2, gNa= 120 mS/cm2, gL = 0.3 mS/cm2, EK = −12 mV, ENa = 115 mV, EL = 10 mV, Cm= 1 μF/cm2. The model is integrated using the Euler method with a time step h = 0.0001 ms, and recording data starts after 50 ms.
Results and discussion
It was demonstrated that the patch temperature can modulate the excitability of neurons by regulating the ion channel conductance and gated dynamics. In this section, we firstly discuss the temperature effect on the membrane potential of neurons. Secondly, in order to study the temperature effect on the memristive ion channels, an external stimulus [e.g., the external sinusoidal voltage signal (Chua and Kang 1976; Chua et al. 2012)] is applied to detect a variety of frequency selections in electrical activity at different membrane temperatures.
Temperature effect on the membrane potential of neurons
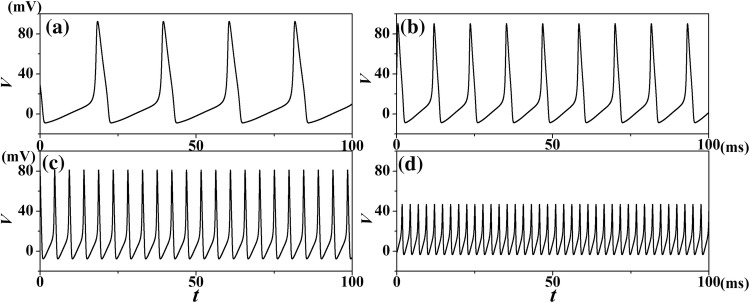
It is concluded that temperature plays an important role in the membrane potential of neurons. To observe the effects of different temperatures on the temporal evolution of neurons, our samples (T = 0.3 °C, 6.3 °C, 16.3 °C and 26.3 °C) were plotted in Fig. 2. When the external current intensity is fixed, the neural activity shows a significant change as the temperature rises from 0.3 to 26.3 °C: the frequency decrease, and the amplitude increases substantially. Previous experiment (Correa et al. 1992) showed that higher temperatures shorten the duration of peak membrane potential. This phenomenon indicates that the membrane potential of neurons is largely caused by changes in temperature, which is consistent with the experiment result.
Fig. 2.
Temporal evolution of transmembrane potentials of HH neuron model Eq. (1) for different temperatures at Iapp= 20.0μA/cm2. aT = 0.3 °C; bT = 6.3 °C; cT = 16.3 °C; dT = 26.3 °C
Moreover, the spike number of neural action potential for varies temperature and external current is plotted in Fig. 3. It is found that the action potential of neurons shows distinct boundary under different external currents and temperatures. There is no spike in black color area, i.e., the membrane potential in this region is in a quiescent state. The discharge state of membrane potential has not a correlation with the temperature when external current is < 7 μA/cm2. When Iapp is increased from 7 to 63 μA/cm2, the threshold external current which change the neuron condition from quiescent state to spiking state will increase nonlinearly with the increasing of temperature. The threshold external current will reduce nonlinearly with the increasing of temperature when Iapp is between 92 and 152 μA/cm2. These phenomena show that neural activities are largely regulated by the variations in temperature.
Fig. 3.
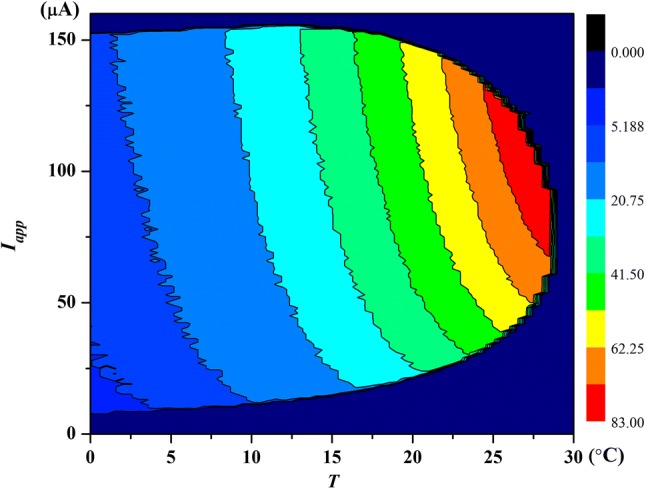
(Color online) The spike number of action potential of neuron within 100 ms
Temperature effect on the first-order memristor of potassium channel
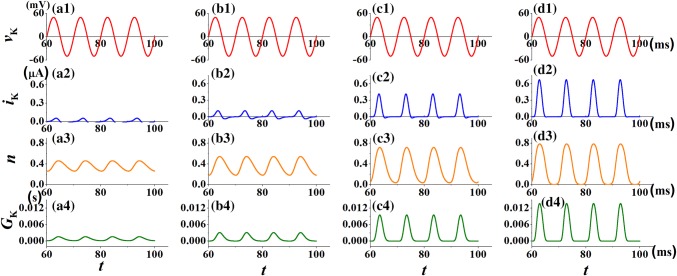
To illustrate the effect of temperature on the shape of pinched hysteresis loop in potassium channel memristor, the sinusoidal voltage, vK = 50sin(2πft) with frequency f = 100 Hz is applied. Figure 4 shows the waveforms of applied sinusoidal voltage vK, output potassium ion current iK(t), the mean rations of open potassium ion-channel gates of the working channels n(t) and the memductance of the potassium ion-channel memristor GK(t) under different temperatures, respectively. When a sinusoidal voltage is applied to the potassium ion-channel memristor system, the output current iK(t) keeps the waveform of the input voltage and begins to oscillate. It means that the potassium ion-channel system has memory function. We observe that the rise of temperature increases the amplitude of response current iK(t), however, the negative part of iK(t) is almost disappear at high temperature T = 26.3 °C (shown in Fig. 4d2). The amplitude of the fraction of open potassium ion-channel and the conductance GK(t) of the potassium ion-channel memristor are also increased with temperature. Compared with the case T = 6.3 °C in Fig. 4b4, the increase of temperature (T = 16.3 °C, 26.3 °C in Fig. 4c4, d4) decreases the width of the peak of the conductance GK(t). It may be because the temperature can also determine the conductance of the memristor.
Fig. 4.
The response current iK(t), the fraction n(t) of open potassium ion-channel and the conductance GK(t) of the potassium ion-channel memristor for different temperature T at vK = 50sin(2πft). The parameter is selected as f = 100 Hz. a1–a4T = 0.3 °C; b1–b4T = 6.3 °C; c1–c4T = 16.3 °C; d1–d4T = 26.3 °C
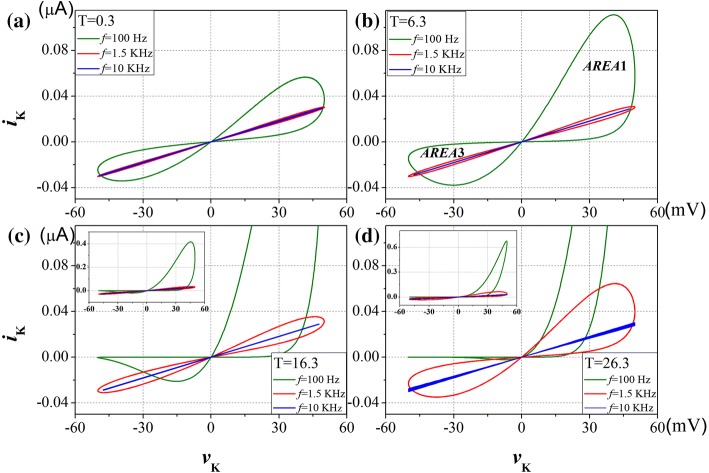
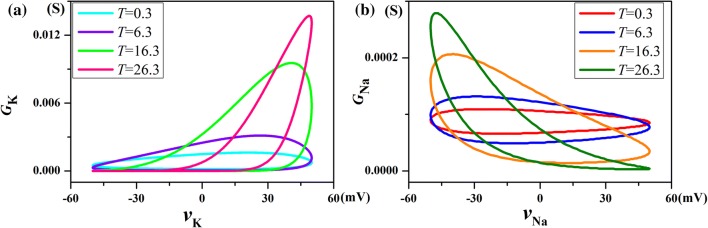
The pinched hysteresis loops of potassium ion-channel with different frequencies and different temperatures are displayed in Fig. 5. Sinusoidal voltage input waveform, vK = Asin(2πft) with amplitude A = 50 mV, and f = 100 Hz, 1.5 kHz and 10 kHz are applied in turn. Although the temperature varies, the shape of the pinched hysteresis loop correspond to a sinusoidal signal is ‘pinched’ at the origin, for any frequency. It’s the first fingerprint of memristor. In addition, with the increase of the input frequency, the pinched hysteresis loop tends to be straight line as frequency is infinity. It’s the second fingerprint of memristor. At low frequencies, memristive system usually behave as non-linear resistors, at intermediate frequencies they exhibit pinched hysteresis loops, and at high frequencies they typically operate as linear resistors. This phenomenon is very similar to that found by Chua et al. (2012). But the shape of the pinched hysteresis loop enlarged dramatically as the temperature was increased from T = 0.3 °C in Fig. 5a to T = 26.3 °C in Fig. 5d. The slope change of the pinched hysteresis loop corresponds to switching between different resistance states. The area in the first quadrant (AREA1) is enlarged more than the area in the third quadrant (AREA3). It implies that the rise of temperature will enhance the memory effect of the response current on the positive part of the input voltage than the negative part.
Fig. 5.
Pinched hysteresis loop of the potassium ion-channel memristor computed at different frequencies and temperatures, for aT = 0.3 °C; bT = 6.3 °C; cT = 16.3 °C; dT = 26.3 °C
Starting from some critical frequencies, it was shown that the hysteretic lobe area should be monotonously reduced with the increase of excitation frequency (Adhikari et al. 2013). The relationship between memristor of hysteresis lobe area and frequency of periodic excitation at different temperatures is also studied here, and the loci (Lissajous figure) of vK(t), iK(t) corresponding to the input voltage and output current are shown in Fig. 5b. The lobe areas in first and third quadrant of ion-channel memristor are defined by the Riemann–Stieltjes integral (Adhikari et al. 2013):
| 12 |
where Θ is the time period of the sinusoidal vK(t).
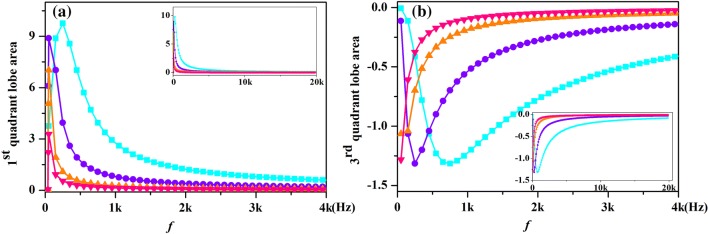
Figure 6 shows that variation in hysteretic lobe area with increasing frequency of potassium ion-channel memristor for varies temperatures. The area of the pinched hysteresis lobe is the origin of the memory effect (Biolek et al. 2012). It is clearly shown in Fig. 6a that the peak values of AREA1 are increased with the increasing of temperature, so does the critical frequencies which correspond to the peak value of AREA1. The peak values of AREA3 are almost the same at different temperatures, as shown in Fig. 6b, but the critical frequencies are increased with the increasing of temperature. Such as in Fig. 6b the critical frequency is 150 Hz for T = 6.3 °C and the critical frequency increased to 750 Hz when the temperature is 26.3 °C. If a device exhibits a compressed hysteresis loop, but the hysteresis lobe region does not shrink with increasing frequency, beyond a certain frequency, then it is not a memristor. The device exhibits a memory effect when the critical frequency is exceeded, and the increase of temperature lead to the increase of the critical frequency. Moreover, the frequency of the input signal that required for the hysteretic lobe area to approach zero increases with the rising temperature. Therefore, when the input signal exceeds the critical frequency, the high temperature corresponds to a large hysteretic lobe area with same input signal. It means that the raise of temperature will increase the memory effect of ion-channel memristor.
Fig. 6.
The lobe area of pinched hysteresis loop of the potassium ion-channel memristor computed at different frequencies and temperatures [T = 0.3 °C (pink downtriangle), T = 6.3 °C (orange uptriangle), T = 16.3 °C (violet circle) and T = 26.3 °C (cyan square)]. a The first quadrant; b The third quadrant. (Color figure online)
Temperature effect on the second-order memristor of sodium channel
The HH model can be divided into four parts: the membrane voltage, the potassium gate activation function, the sodium gate activation function and the leakage current. In order to investigate the effect of temperature on the shape of pinched hysteresis loop in sodium channel memristor, the sinusoidal voltage, vNa = 50sin(2πft) with frequency f = 500 Hz is applied. The waveform of applied sinusoidal voltage vNa, output sodium ion current iNa(t), the mean rations of open sodium ion-channel gates of the working channels m(t) and the memductance of the sodium ion-channel memristor GNa(t) under different temperatures are plotted in Fig. 7. The temperatures are set to T = 0.3 °C, 6.3 °C, 16.3 °C and 26.3 °C in the sodium gate activation function, respectively.
Fig. 7.
The response current iNa(t), the fraction m(t) of open sodium ion-channel and the conductance GNa(t) of the sodium ion-channel memristor for different temperature T at vNa = 50sin(2πft). The parameter is selected as f = 500 Hz. a1–a4T = 0.3 °C; b1–b4T = 6.3 °C; c1–c4T = 16.3 °C; d1–d4T = 26.3 °C
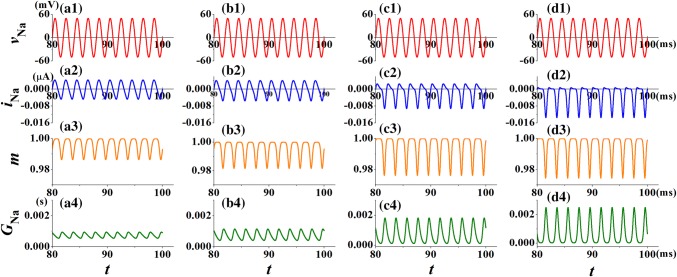
When a sinusoidal voltage is applied to the sodium ion-channel memristor system, Fig. 7a2–d2 show that the output current iNa(t) begins to oscillate, which keeps the memory about the input voltage. It means that the sodium ion-channel system has memory function. The rise of temperature increases the amplitude of response current iNa(t), however, the positive part of iNa(t) almost disappears at high temperature T = 26.3 °C (shown in Fig. 7d2, which is contrary to Fig. 4d2). Obviously, the amplitude of the fraction of open sodium ion-channel and the conductance GNa(t) of sodium ion-channel memristor also increased with temperature. Such as when the value of temperature is 0.3 °C, the oscillation range of the response current is 0.0043 mA to − 0.0047 mA in Fig. 7a2, and the oscillation range of the response current is 0.0006 mA to − 0.0135 mA at the value of temperature is 26.3 °C in Fig. 7d2. Meanwhile, the conductance range of the sodium ion-channel memristor is increased with the rise of temperature. Observe from Fig. 7a4, the oscillation the rage of GNa(t) is from 0.0005 to 0.0009 S when the value of temperature is 0.3 °C. With the increasing of temperature, the oscillation the rage of GNa(t) is 0.00025 S to 0.0024 S at T = 26.3 °C in Fig. 7d4. It may be because the temperature can also determine the conductance of the memristor.
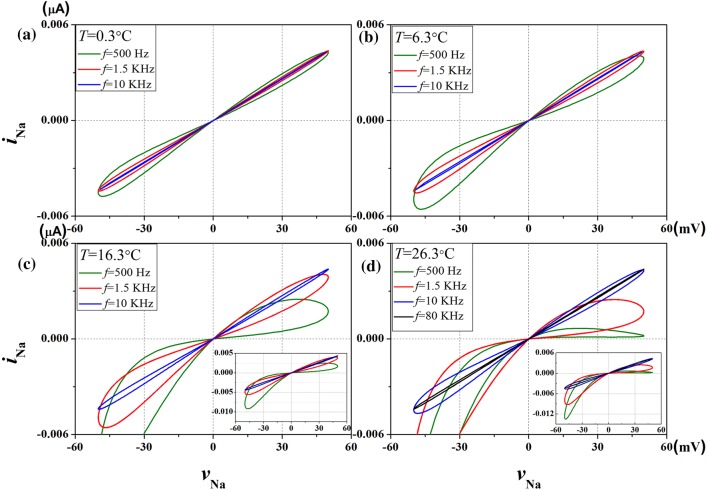
The pinched hysteresis loops of the sodium ion-channel memristor are obtained by applying a sinusoidal voltage input waveform vNa = 50sin (2πft), with amplitude A = 50 mV, and calculating its response current waveform iNa(t) for several temperature values. The parameter is selected as f = 500 Hz, 1.5 kHz, and 10 kHz in turn, and 80 kHz cases have been added in Fig. 8d. The results are similar to that of potassium ion-channel memristor system, despite the temperature changes, for any frequency f, the shape of pinched hysteresis loops correspond to the sinusoidal signal “shrinking” at the origin. It’s the first fingerprint of memristor. In addition, with the increase of the input frequency, the pinched hysteresis loop tends to be straight line as frequency is infinity. That is to say, when the frequency of input voltage is large enough, the change of voltage vNa and current iK(t) is linear. It’s the second fingerprint of memristor. The loop shape depends not only on the amplitude and frequency of the applied sinusoidal single, but also on the temperature of the sodium ion-channel. The pinched hysteresis loops at several of temperatures are calculated in Fig. 8. We found that increasing temperature widens the range of the pinched hysteresis loops. At intermediate frequency, temperatures have significant effect on the pinched hysteresis loop of sodium channel memristor. It’s remarkable that it takes 80 kHz frequency at 26.3 °C to pinched hysteresis loop tends to a straight line in Fig. 8d. The results show that the area of the pinched hysteresis loop in the third quadrant (AREA3) is much smaller than that of the first quadrant (AREA1). This means that the rise of temperature will enhance the memory effect of the response current on the negative part of the input voltage than the positive part.
Fig. 8.
The pinched hysteresis loops of sodium ion-channel memristor computed at different frequencies and temperatures, for aT = 0.3 °C; bT = 6.3 °C; cT = 16.3 °C; dT = 26.3 °C
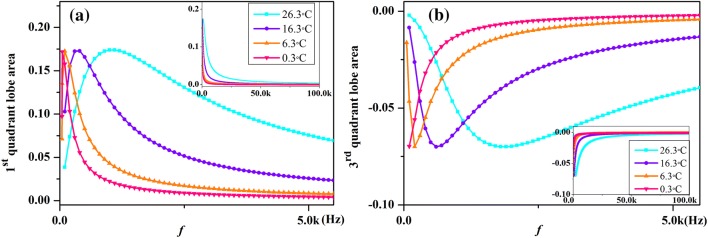
Figure 9 shows that variation in hysteretic lobe area with increasing frequency of sodium ion-channel memristor for varies temperatures. From Fig. 9 we can see that the absolute value of the hysteresis lobe area is inversely proportional to the excitation frequency when the frequency of input signal is beyond a certain critical frequency. The peak values of AREA1 and AREA3 are almost the same at different temperature, but the critical frequencies are increased with the increasing of temperature. In addition, the frequency of the input signal that required for the hysteretic lobe area to approach zero increases with the rising temperature, and these results correspond to Fig. 6. It means that an increase in temperature changes the memory effect of ion-channel memristor, because larger input signal frequencies are needed to obtain the same area of pinched hysteresis loop.
Fig. 9.
The lobe area of pinched hysteresis loop of the sodium ion-channel memristor computed at different frequencies and temperatures [T = 0.3 °C (pink downtriangle), T = 6.3 °C (orange uptriangle), T = 16.3 °C (violet circle) and T = 26.3 °C (cyan square)]. a The first quadrant; b The third quadrant. (Color figure online)
Different effects on the first-order and second-order memristors
Moreover, the properties of memristors are shown in the slope of the pinched hysteresis loops. Figure 10 shows the details of the effects of temperatures on the conductance GK(t) of the potassium ion-channel memristor and the conductance GNa(t) of the sodium ion-channel memristor. From the analysis of Fig. 10, the range of the curve increases with the rise of temperature, that is to say, temperature has a certain influence on electrical conductivity. At temperatures of 0.3 °C and 26.3 °C, the maximum conductance GK(t) is 0.0017 S and 0.013 S, respectively. When the temperature increases from 0.3 to 26.3 °C, the maximum conductance GNa(t) increases from 0.00011 S to 0.00027 S. The ion-channel memristors are completely specified by two scalar functions of three variables, namely, GK(t) and GNa(t). This result indicates that temperature plays an important role in the properties of memristor. It is necessary to consider the effect of temperature on ion-channel memristor. We find it particularly interesting that temperature has a certain effect on the shape of two groups of conductive hysteresis loops, and the shape changes are symmetrical. The results may be related to potassium gate activation function and the sodium gate activation function.
Fig. 10.
The hysteresis loop between conductance and sinusoidal voltage at different temperature, and the amplitude of sinusoidal voltage input waveform is 50 mV, for af = 100 Hz; bf = 500 Hz
Conclusions
In summary, the effects of patch temperature on the membrane potential of neuron and the pinched hysteresis loop of ion channels were investigated. As the temperature increases, the amplitude and frequency of electrical activity change significantly, and it indicates that electrical activity is sensitive to the change of temperature. Moreover, each ion channel can be regarded as a physical memristor whose shape of the pinched hysteresis loop depends on the input voltage and temperature.
The pinched hysteresis loop of ion-channel memristor changes obviously at different temperatures. The hysteresis lobe area decreases monotonously with the increase of excitation frequency if the external stimulus frequency changes from a certain threshold. Although the temperature varies, the shape of the pinched hysteresis loop corresponding to the sinusoidal signal is ‘pinched’ at the origin, and tends to be straight when frequency is infinity. The frequency value of input signal required for the hysteresis lobe area to approach zero increases with the rising temperature. Further investigations revealed that the higher the patch temperature the larger the hysteresis lobe area when the external forcing current exceeds the frequency threshold. That is, the memory effect can be enhanced under higher temperature.
Optimal temperatures of ion-channel have been believed to modulate and enhance signal transmission (Yang and Jia 2005). The functional roles of temperature in promoting the signal transduction for the ion channels related neural information was revealed. Our results confirmed that temperature has an effect on the memory effect of ion-channel memristor. These finding might offer important biological implications, because realistic neurons are often simultaneously affected by varies temperatures (Micheva and Smith 2005; Hyun et al. 2011). It seems feasible to optimize the temporal regulation of neuronal signals by temperature control. We hope that this research can provide verifiable hypotheses for future electrophysiological experiments. The further work of this topic includes studying the influence of noise on ion channels at varies temperatures based on the of memristor model in multilayer neural network (Ge et al. 2019; Lu et al. 2019a, b).
This work was supported by the National Natural Science Foundation of China under Grant under Nos. 11775091 (YJ), 11672122 and 11765011 (JM), and the self-determined research funds of CCNU from the college’s basic research and operation of MOE under Nos. CCNU18QN035 (LY) and CCNU18TS032 (XZ).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ying Xu, Email: xuyingny@mails.ccnu.edu.cn.
Jun Ma, Email: hyperchaos@163.com.
Xuan Zhan, Email: zhanxuan@mail.ccnu.edu.cn.
Lijian Yang, Email: janeyang@mail.ccnu.edu.cn.
Ya Jia, Email: jiay@mail.ccnu.edu.cn.
References
- Adhikari SP, Sah PdM, Kim H, Chua L. Three fingerprints of memristor. IEEE Trans Circuits-I. 2013;60(11):3008–3021. doi: 10.1109/TCSI.2013.2256171. [DOI] [Google Scholar]
- Bao B, Hu A, Bao H, Xu Q, Chen M, Wu H (2018) Three-dimensional memristive Hindmarsh–Rose neuron model with hidden coexisting asymmetric behaviors. Complexity. Article ID 3872573
- Biolek Z, Biolek D, Biolkova V. Computation of the area of memristor pinched hysteresis loop. IEEE Trans Circuits-II. 2012;59(9):670–671. [Google Scholar]
- Chua L. Everything you wish to know about memristor but are afraid to ask. Radioengin. 2015;24(2):319–368. doi: 10.13164/re.2015.0319. [DOI] [Google Scholar]
- Chua L, Kang SM. Memristive devices and systems. Proc IEEE. 1976;64(2):209. doi: 10.1109/PROC.1976.10092. [DOI] [Google Scholar]
- Chua L, Sbitnev V, Kim H. Hodgkin–Huxley axon is made of memristors. Int J Bifurc Chaos. 2012;22(3):1230011. doi: 10.1142/S021812741230011X. [DOI] [Google Scholar]
- Correa AM, Bezanilla F, Latorre R. Gating kinetics of batrachotoxin-modified Na + channels in the squid giant axon voltage and temperature effects. Biophys J. 1992;61(5):1332–1352. doi: 10.1016/S0006-3495(92)81941-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1961;1(6):445. doi: 10.1016/S0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge M, Jia Y, John BK, Xu Y, Shen J, Lu L, Liu Y, Pei Q, Zhan X, Yang L. Propagation of firing rate by synchronization in a feed-forward multilayer Hindmarsh–Rose neural network. Neurocomputing. 2018;320:60–68. doi: 10.1016/j.neucom.2018.09.037. [DOI] [Google Scholar]
- Ge M, Jia Y, Xu Y, Lu L, Wang H, Zhao Y. Wave propagation and synchronization induced by chemical autapse in chain feed-forward Hindmarsh–Rose neural network. Appl Math Comput. 2019;352:136–145. [Google Scholar]
- Guo D, Perc M, Zhang Y. Frequency-difference dependent stochastic resonance in neural systems. Phys Rev E. 2017;96(2):022415. doi: 10.1103/PhysRevE.96.022415. [DOI] [PubMed] [Google Scholar]
- Guo D, Gan J, Tan T, Tian X, Wang G, Tak-Pan Ng K. Neonatal exposure of ketamine inhibited the induction of hippocampal long-term potentiation without impairing the spatial memory of adult rats. Cogn Neurodyn. 2018;12:377–383. doi: 10.1007/s11571-018-9474-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindmarsh JL, Rose RM. A model of the nerve impulse using two first-order differential equations. Nature. 1982;296(5853):162–164. doi: 10.1038/296162a0. [DOI] [PubMed] [Google Scholar]
- Hindmarsh JL, Rose RM. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond B. 1984;221(1222):87–102. doi: 10.1098/rspb.1984.0024. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. The dual effect of membrane potential on sodium conductance in the giant axon of Loligo. J Physiol. 1952;116(4):497–506. doi: 10.1113/jphysiol.1952.sp004719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyun NG, Hyun KH, Hyun KB, Han JH, Lee K, Kaang BK. A computational model of the temperature-dependent changes in firing patterns in aplysia neurons. Korean J Physiol Pharmacol. 2011;15(6):371–382. doi: 10.4196/kjpp.2011.15.6.371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji X, Hu X, Zhou Y, Dong Z, Duan S. Adaptive sparse coding based on memristive neural network with applications. Cogn Neurodyn. 2019 doi: 10.1007/s11571-019-09537-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia B, Gu H, Xue L. A basic bifurcation structure from bursting to spiking of injured nerve fibers in a two-dimensional parameter space. Cogn Neurodyn. 2017;11(2):189–200. doi: 10.1007/s11571-017-9422-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L, Jia Y, Xu Y, Ge M, Pei Q, Yang L. Energy dependence on modes of electric activities of neuron driven by different external mixed signals under electromagnetic induction. Sci China Technol Sci. 2019;62(3):427–440. doi: 10.1007/s11431-017-9217-x. [DOI] [Google Scholar]
- Lu L, Jia Y, Kirunda JB, Xu Y, Ge M, Pei Q, Yang L. Effects of noise and synaptic weight on propagation of subthreshold excitatory postsynaptic current signal in a feed-forward neural network. Nonlinear Dyn. 2019;95(2):1673–1686. doi: 10.1007/s11071-018-4652-9. [DOI] [Google Scholar]
- Ma J, Huang L, Tang J, Ying H, Jin W. Spiral wave death, breakup induced by ion channel poisoning on regular Hodgkin–Huxley neuronal networks. Commun Nonlinear Sci. 2012;17(11):4281–4293. doi: 10.1016/j.cnsns.2012.03.009. [DOI] [Google Scholar]
- Ma J, Zhang G, Hayat T, Ren G. Model electrical activity of neuron under electric field. Nonlinear Dyn. 2019;95:1585–1598. doi: 10.1007/s11071-018-4646-7. [DOI] [Google Scholar]
- Maio VD, Santillo S, Sorgente A, Vanacore P, Ventriglia F. Influence of active synaptic pools on the single synaptic event. Cogn Neurodyn. 2018;12:391–402. doi: 10.1007/s11571-018-9483-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheva KD, Smith SJ. Strong effects of subphysiological temperature on the function and plasticity of mammalian presynaptic terminals. J Neurosci. 2005;25(33):7481–7488. doi: 10.1523/JNEUROSCI.1801-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mondal A, Upadhyay RK, Ma J, Yadav BK, Sharma SK, Mondal A. Bifurcation analysis and diverse firing activities of a modified excitable neuron model. Cogn Neurodyn. 2019 doi: 10.1007/s11571-019-09526-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordenfelt A, Used J, Sanjuán MA. Bursting frequency versus phase synchronization in time-delayed neuron networks. Phys Rev E. 2013;87(5):052903. doi: 10.1103/PhysRevE.87.052903. [DOI] [PubMed] [Google Scholar]
- Ozer M, Uzuntarla M, Perc M, Grahamc LJ. Spike latency and jitter of neuronal membrane patches with stochastic Hodgkin–Huxley channels. J Theor Biol. 2009;261(1):83–92. doi: 10.1016/j.jtbi.2009.07.006. [DOI] [PubMed] [Google Scholar]
- Perc M. Effects of small-world connectivity on noise-induced temporal and spatial order in neural media. Chaos. 2007;31(2):280–291. [Google Scholar]
- Prousalis DA, Volos CK, Stouboulos IN, Kyprianidis IM. Hyperchaotic memristive system with hidden attractors and its adaptive control scheme. Nonlinear Dyn. 2017;90(3):1681–1694. doi: 10.1007/s11071-017-3758-9. [DOI] [Google Scholar]
- Rajamani V, Sah MPD, Mannan ZI, Kim H, Chua L. Third-order memristive Morris–Lecar model of barnacle muscle fiber. Int J Bifurc Chaos. 2017;27(4):1730015. doi: 10.1142/S0218127417300154. [DOI] [Google Scholar]
- Szabo TM, Brookings T, Preuss T, Faber DS. Effects of temperature acclimation on a central neural circuit and its behavioral output. J Neurophysiol. 2008;100(6):2997. doi: 10.1152/jn.91033.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thottil SK, Ignatius RP. Nonlinear feedback coupling in Hindmarsh–Rose neurons. Nonlinear Dyn. 2016;87(3):1879–1899. doi: 10.1007/s11071-016-3160-z. [DOI] [Google Scholar]
- Tian C, Cao L, Bi H, Xu K, Liu Z. Chimera states in neuronal networks with time delay and electromagnetic induction. Nonlinear Dyn. 2018;93(3):1695–1704. doi: 10.1007/s11071-018-4285-z. [DOI] [Google Scholar]
- Volkov AG, Reedus J, Mitchell CM, Tucket C, Forde-Tuckett V, Volkova MI, Markin VS, Chua L. Memristors in the electrical network of Aloe vera L. Plant Signal Behav. 2014;9(7):e29056. doi: 10.4161/psb.29056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Jiao X. Stochastic model and neural coding of large-scale neuronal population with variable coupling strength. Neurocomputing. 2006;69(7–9):778–785. doi: 10.1016/j.neucom.2005.05.010. [DOI] [Google Scholar]
- Wang C, Ma J. A review and guidance for pattern selection in spatiotemporal system. Int J Mod Phys B. 2018;32(6):1830003. doi: 10.1142/S0217979218300037. [DOI] [Google Scholar]
- Wang YH, Wang R. An improved neuronal energy model that better captures of dynamic property of neuronal activity. Nonlinear Dyn. 2017;91(1):319–327. doi: 10.1007/s11071-017-3871-9. [DOI] [Google Scholar]
- Wang R, Zhang Z. Energy coding in biological neural network. Cogn Neurodyn. 2007;1(3):203–212. doi: 10.1007/s11571-007-9015-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Zhu Y. Can the activities of the large scale cortical network be expressed by neural energy? A brief review. Cogn Neurodyn. 2016;10(1):1–5. doi: 10.1007/s11571-015-9354-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Perc M, Duan Z, Chen G. Spatial coherence resonance in delayed in delayed Hodgkin–Huxley neuronal networks. Int J Mod Phys B. 2010;24(09):1201–1213. doi: 10.1142/S0217979210055317. [DOI] [Google Scholar]
- Wang Z, Wang R, Fang R. Energy coding in neural network with inhibitory neurons. Cogn Neurodyn. 2015;9(2):129–144. doi: 10.1007/s11571-014-9311-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Lin Q, Yao Y, Yang K, Tian M, Wang Y. Dynamics of a stochastic system driven by cross-correlated sine-Wiener bounded noises. Nonlinear Dyn. 2018 [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12(1):1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Ying H, Jia Y, Ma J, Hayat T. Autaptic regulation of electrical activities in neuron under electromagnetic induction. Sci Rep. 2017;7:43452. doi: 10.1038/srep43452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Jia Y, Ge M, Lu L, Yang L, Zhan X. Effects of ion channel blocks on electrical activity of stochastic Hodgkin–Huxley neural network under electromagnetic induction. Neurocomputing. 2018;283:196–204. doi: 10.1016/j.neucom.2017.12.036. [DOI] [Google Scholar]
- Xu Y, Jia Y, Kirunda JB, Shen J, Ge M, Lu L, Pei Q (2018b) Dynamic behaviors in coupled neurons system with the excitatory and inhibitory autapse under electromagnetic induction. Complexity 2018:3012743
- Xu Y, Jia Y, Wang HW, Liu Y, Wang P, Zhao Y. Spiking activities in chain neural network driven by channel noise with field coupling. Nonlinear Dyn. 2019;95(4):3237–3247. doi: 10.1007/s11071-018-04752-2. [DOI] [Google Scholar]
- Yang L, Jia Y. Effects of patch temperature on spontaneous action potential train due to channel fluctuations: coherence resonance. Biosystems. 2005;81(3):267–280. doi: 10.1016/j.biosystems.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Yao Y, Ma J. Weak periodic signal detection by sine-Wiener-noise-induced resonance in the FitzHugh–Nagumo neuron. Cogn Neurodyn. 2018;12(3):343–349. doi: 10.1007/s11571-018-9475-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao C, Zhan M, Shuai J, Ma J, Kurths J. Insensitivity of synchronization to network structure in chaotic pendulum systems with time-delay coupling. Chaos. 2017;27:126702. doi: 10.1063/1.5010304. [DOI] [PubMed] [Google Scholar]
- Zhu F, Wang R, Pan X, Zhu Z. Energy expenditure computation of a single bursting neuron. Cogn Neurodyn. 2019;13(1):75–78. doi: 10.1007/s11571-018-9503-3. [DOI] [PMC free article] [PubMed] [Google Scholar]