A cortical model with multi-layers to study visual attentional modulation of neurons at the synaptic level

Abstract

Visual attention is a selective process of visual information and improves perceptual performance by modulating activities of neurons in the visual system. It has been reported that attention increased firing rates of neurons, reduced their response variability and improved reliability of coding relevant stimuli. Recent neurophysiological studies demonstrated that attention also enhanced the synaptic efficacy between neurons mediated through NMDA and AMPA receptors. Majority of computational models of attention usually are based on firing rates, which cannot explain attentional modulations observed at the synaptic level. To understand mechanisms of attentional modulations at the synaptic level, we proposed a neural network consisting of three layers, corresponding to three different brain regions. Each layer has excitatory and inhibitory neurons. Each neuron was modeled by the Hodgkin–Huxley model. The connections between neurons were through excitatory AMPA and NMDA receptors, as well as inhibitory GABA_A receptors. Since the binding process of neurotransmitters with receptors is stochastic in the synapse, it is hypothesized that attention could reduce the variation of the stochastic binding process and increase the fraction of bound receptors in the model. We investigated how attention modulated neurons’ responses at the synaptic level on the basis of this hypothesis. Simulated results demonstrated that attention increased firing rates of neurons and reduced their response variability. The attention-induced effects were stronger in higher regions compared to those in lower regions, and stronger for inhibitory neurons than for excitatory neurons. In addition, AMPA receptor antagonist (CNQX) impaired attention-induced modulations on neurons’ responses, while NMDA receptor antagonist (APV) did not. These results suggest that attention may modulate neuronal activity at the synaptic level.

Introduction

Visual attention is the ability of the brain that improves our perception by selectively enhancing neuronal responses to particular visual stimuli (Carrasco et al. 2004; Posner and Petersen 2012; Reynolds et al. 1999; Sommer 2007; Treue and Maunsell 2005; Parhizi et al. 2018). Many attention tasks were designed to investigate attentional effects on neuronal activity in various brain regions. It was reported that visual attention can increase firing rates and reduce response variability of single neurons (Antonerxleben and Carrasco 2013; Carrasco 2011; Gardner 2015). The attention-modulated activity is stronger in higher visual areas than in lower visual areas (Gazzaniga 2004). Recently, neurophysiological experiments showed that attentional modulation differed between putative interneurons (characterized by narrow spiking waveforms) and putative pyramidal neurons (characterized by broad spiking waveforms). Putative interneurons had stronger attentional modulation on firing rates and response variability than did putative pyramidal neurons (Anderson et al. 2013; Ison et al. 2011; Mitchell et al. 2007; Thiele et al. 2016). These results indicate that attentional effects on neuronal activity are dependent on types of neurons and their located regions in the hierarchical visual system.

A recent study further demonstrated that attentional modulation may exist on the synaptic level (Briggs et al. 2013). Briggs et al. (2013) simultaneously recorded thalamocortical neurons in the lateral geniculate nucleus (LGN) and monosynaptically connected (i.e., postsynaptic) neurons in primary visual cortex (V1) of macaque monkeys performing a spatial attention task, and found that attention significantly improved the probability that presynaptic stimulation evoked a postsynaptic action potential, suggesting that attention enhanced neuronal communication by increasing the efficacy of presynaptic input in driving postsynaptic responses. Another study also reported that reduction of attention-induced variance in macaque V1 was mediated by NMDA and AMPA receptors (Herrero et al. 2013). The NMDA receptor antagonist (APV) or the AMPA receptor antagonist (CNQX) impaired attentional effects on neuronal activities. Taken together, these results suggest that attention may influence the binding process of neurotransmitters with postsynaptic receptors, thereby modulating response properties of different types of neurons in various cortical areas. It is important to understand theoretically how attention modulates neuronal activity at the synaptic level.

Many computational models have been proposed to understand effects of attention on behavioral performance and neuronal spiking activities (Ardid et al. 2010; Buehlmann and Deco 2008; Gravier et al. 2016; Haab et al. 2009, 2011; Lanyon and Denham 2009). The mechanisms of attention in these models can be explained in different levels of implementation detail, such as detailed biophysical neuron models and their microcircuits (Ardid et al. 2007; Buia and Tiesinga 2008; Deco and Thiele 2011; Wagatsuma et al. 2013), abstract spiking neurons (Buia and Tiesinga 2006; Itti and Koch 2000), dynamic rate coded populations (Beuth and Hamker 2015; Deco and Lee 2015) or more abstract mathematical descriptions (Boynton 2009; Reynolds and Heeger 2009). For example, the normalization model of visual attention (Boynton 2009; Reynolds and Heeger 2009) that is characterized as a simple mathematical abstraction with several parameters could reproduce various electrophysiological results on spatial and feature-based modes of attention. The model describes the functions of visual attention at the macroscopic level without specifying the underlying biophysical mechanisms or neural circuitries. Some neural network models of attention have been developed based on the microscopic-level circuit structure in the cortex (Deco and Thiele 2011; Wagatsuma et al. 2013). In these network models, each single neuron was modeled by the conductance-based Hodgkin–Huxley (H–H) model or the integrate-and-fire model. Connection weights among neurons could be described by functional weights (Wagatsuma et al. 2013) or through excitatory or inhibitory channels (Deco and Thiele 2011). These models are also able to simulate attentional modulations on neuronal responses in spatial or feature-based attention tasks. However, these models limit their analysis on studying rate effects of attention, do not account for attentional effects on response variability. It remains unknown whether visual attention modulates neuronal firing rates and its response variability in the same mechanism and whether these phenomena could be explained by the attention-modulated process of information transmission at synapses between neurons.

To investigate these issues, we developed a three-layer network model to study attentional modulations at the synaptic level. Each layer in the model corresponds to a brain region, and consists of excitatory and inhibitory neurons. The connections between neurons have excitatory AMPA and NMDA receptors or inhibitory GABA receptors. Since it is known that transmission of neurotransmitters from the presynaptic to the postsynaptic membranes in the synaptic cleft involves a random process (Gibb 1978; Dobrunz and Stevens 1997; Di Maio et al. 2017), it is reasonable to assume that the binding process of neurotransmitters with postsynaptic receptors is stochastic. According to observations in the recording experiments, attention increases the stability of neuronal responses and enhances the reliability of information coding (Sprague et al. 2015). Therefore, we assume that attention will reduce the randomness during the binding process and increase the fraction of bound receptors in the postsynaptic membrane.

Based on this hypothesis, we set two groups of parameters that controlled the stochastic binding process of AMPA, NMDA or GABA receptors in the model. One group of parameters simulated the attention-attended condition and the other group of parameters simulated the attention-unattended condition. Four main results were achieved in the model: (1) Firing rates of both excitatory and inhibitory neurons increased in the attention-attended condition compared to those in the attention-unattended condition, and the response variability of the two types of neurons became smaller in the former condition. (2) The attentional modulation of neuronal responses was stronger for inhibitory neurons than for excitatory neurons. (3) The attentional modulation was stronger for neurons in higher regions than in lower regions. (4) Attentional gain of neuronal firing rates and reduction of response variability were impaired by the injection of AMPA antagonist (CNQX). These simulated results were consistent with experimental findings, suggesting that the model could explain basic properties of attentional modulations of neuronal activity at the synaptic level.

Methods

The structure of the network model of visual attention

We proposed a functional network model of visual attention, consisting of excitatory and inhibitory neurons. We introduced the structure of the network model, each type of neurons and their connections in the following sections.

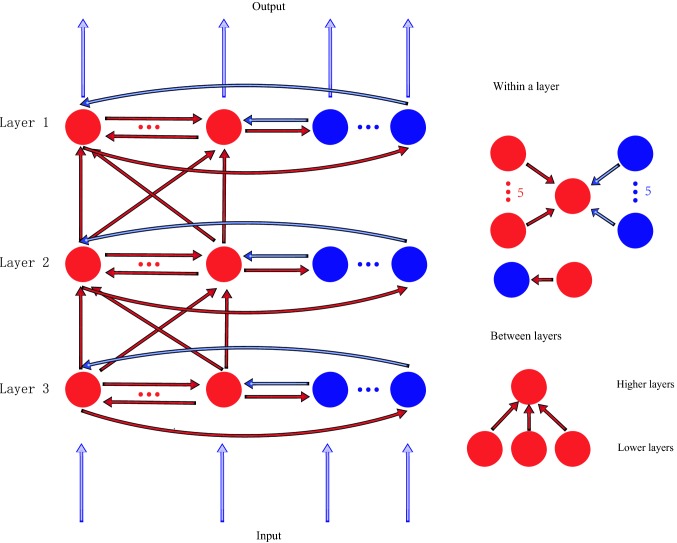
The functional network model is structured in three layers (Fig. 1, labeled as layer 1, layer 2 and layer 3, respectively), and each layer corresponds to a visual region, such as V1, V2, V4 and so on. There are 20 excitatory neurons and 5 inhibitory neurons in each region. Excitatory neurons in the model connect to other neurons through excitatory AMPA and NMDA receptors, and inhibitory neurons connect to other neurons through inhibitory GABA receptors. The connection patterns within a layer and between layers are explained as below (Bazhenov et al. 2004). Within a layer: each excitatory neuron receives inputs from five randomly selected excitatory neurons and five inhibitory neurons; each inhibitory neuron receives inputs from one randomly selected excitatory neuron. Between layers: an excitatory neuron has projections from three excitatory neurons selected randomly in the previous layer. Signals are transmitted only through excitatory neurons between layers. There are no feedback signals from higher layers to lower layers. There are no connections between inhibitory neurons within a layer or between layers. Neurons in layer 1 receive a sustained external current input, and neurons in other layers do not receive the external input directly.

Fig. 1.

The structure of the network model with three layers. Each layer corresponds to a brain region. The red circles represent excitatory neurons, and the blue circles indicate inhibitory neurons. The red arrows indicate excitatory connections and the blue arrows indicate inhibitory connections. The connections within a region and between regions are shown in the right side of the figure

We use the H–H model in this paper (Hodgkin and Huxley 1989), which could characterize response properties and spike waveforms of excitatory and inhibitory neurons, respectively. The H–H model also allows us to add synaptic currents which may be modulated by visual attention into each neuron (Guo et al. 2016a, b). The models of the excitatory and inhibitory neuron are shown as below (Pospischil et al. 2008):

Excitatory neuron: besides internal ion currents, there are two types of excitatory synaptic currents (${\text{I}}_{\text{AMPA}}$, ${\text{I}}_{\text{NMDA}}$) and a type of inhibitory synaptic current (${\text{I}}_{{\text{GABA}}_{\text{A}}}$). The kinetics model of the excitatory neuron is following:

$$\begin{array}{cc}\hfill {\text{C}}^e\frac{{\text{dV}}^e}{\mathrm{dt}}& =-{\text{I}}_{\mathit{Na}}^e\left({\text{V}}^e\right)-{\text{I}}_K^e\left({\text{V}}^e\right)-{\text{I}}_L^e\left({\text{V}}^e\right)-{\text{I}}_M^e\left({\text{V}}^e\right)-{\text{I}}_{\mathrm{AMPA}}\left(V^e,{\text{r}}_{\mathrm{AMPA}}\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}^e,{\text{r}}_{\mathrm{NMDA}}\right)-{\text{I}}_{{\text{GABA}}_{\mathrm{A}}}\left({\text{V}}^e,{\text{r}}_{{\text{GABA}}_{\mathrm{A}}}\right)\hfill \\ \hfill \end{array}$$ 1

where ${\text{V}}^e$ is the membrane potential, ${\text{I}}_L^e$ is the leak current, ${\text{I}}_{\mathit{Na}}^e,{\text{I}}_K^e$ are the sodium and potassium currents responsible for action potentials, ${\text{I}}_M^e$ is a slow voltage-dependent potassium current responsible for spike-frequency adaptation, ${\text{r}}_{\text{AMPA}}$ (${\text{r}}_{\text{NMDA}},{\text{r}}_{{\text{GABA}}_{\text{A}}}$) represents the fraction of bound AMPA (NMDA, ${\text{GABA}}_{\text{A}}$) receptors. ${\text{C}}^e$ is the membrane capacity.

Inhibitory neuron: besides internal ion currents, there are two types of excitatory synaptic currents (${\text{I}}_{\text{AMPA}}$, ${\text{I}}_{\text{NMDA}}$) from connected excitatory neurons. The kinetics model of the inhibitory neuron is following:

$${\text{C}}^i\frac{{\text{dV}}^i}{\mathrm{dt}}=-{\text{I}}_{\mathit{Na}}^i\left({\text{V}}^i\right)-{\text{I}}_K^i\left({\text{V}}^i\right)-{\text{I}}_L^i\left({\text{V}}^i\right)-{\text{I}}_{\text{AMPA}}\left({\text{V}}^i,{\text{r}}_{\text{AMPA}}\right)-{\text{I}}_{\text{NMDA}}\left({\text{V}}^i,{\text{r}}_{\text{NMDA}}\right)$$ 2

where ${\text{V}}^i$ is its membrane potential, ${\text{I}}_L^i$ is the leak current, ${\text{I}}_{\mathit{Na}}^i,{\text{I}}_K^i$ are the sodium and potassium currents responsible for action potentials, other parameters have the same meaning as those for excitatory neurons. The membrane capacity mainly controls the firing rate. The sodium, potassium and voltage-dependent potassium currents influence both the firing rate and spike waveform. In the simulation, values of these parameters listed in Table 1 were different for excitatory and inhibitory neurons. These values were adopted from experimental measurements (Pospischil et al. 2008).

Table 1.

values of the parameters used in the network model

Constant	Value	Unit	Constant	Value	Unit
${\mathit{C}}^{\mathit{e}}$	0.29	$\mathrm{\mu }\text{F}/{\text{cm}}^2$	${\mathit{E}}_{{\mathbf{GABA}}_{\mathit{A}}}$	− 80	mV
${\mathit{C}}^{\mathit{i}}$	0.1	$\mathrm{\mu }\text{F}/{\text{cm}}^2$	${\mathit{\alpha }}_{{\mathbf{GABA}}_{\mathit{A}}}$	5	–
${\mathit{g}}_{\mathit{Na}}^{\mathit{e}}$	50	$\text{ms}/{\text{cm}}^2$	${\mathit{\beta }}_{{\mathbf{GABA}}_{\mathit{A}}}$	0.18	–
${\mathit{V}}_{\mathit{Na}}^{\mathit{e}}$	50	mV	${\text{g}}_{\mathit{AMPA}}$	0.9	$\text{ms}/{\text{cm}}^2$
${\mathit{g}}_{\mathit{Na}}^{\mathit{i}}$	56	$\text{ms}/{\text{cm}}^2$	$E_{\mathit{AMPA}}$	0	mV
${\mathit{V}}_{\mathit{Na}}^{\mathit{e}}$	50	mV	${\alpha }_{\mathit{AMPA}}$	1	–
${\mathit{g}}_{\mathit{K}}^{\mathit{e}}$	5	$\text{ms}/{\text{cm}}^2$	${\beta }_{\mathit{AMPA}}$	0.5	–
${\mathit{V}}_{\mathit{K}}^{\mathit{e}}$	− 90	mV	$V_p$	5	mV
${\mathit{g}}_{\mathit{K}}^{\mathit{i}}$	10	$\text{ms}/{\text{cm}}^2$	$K_p$	2	mV
${\mathit{V}}_{\mathit{K}}^{\mathit{i}}$	− 90	mV	$T_{\mathit{max}}$	1	–
${\mathit{g}}_{\mathit{L}}^{\mathit{e}}$	0.1	$\text{ms}/{\text{cm}}^2$	$g_{\mathit{NMDA}}$	0.9	$\text{ms}/{\text{cm}}^2$
${\mathit{V}}_{\mathit{L}}^{\mathit{e}}$	− 70	mV	$E_{\mathit{NMDA}}$	0	mV
${\mathit{g}}_{\mathit{L}}^{\mathit{i}}$	0.15	$\text{ms}/{\text{cm}}^2$	${\alpha }_{\mathit{NMDA}}$	0.072	–
${\mathit{V}}_{\mathit{L}}^{\mathit{i}}$	− 70	mV	${\beta }_{\mathit{NMDA}}$	0.0067	–
${\mathit{g}}_{\mathit{M}}$	0.07	$\text{ms}/{\text{cm}}^2$	$T_f$	− 25	mV
${\mathit{V}}_{\mathit{T}}$	− 56.2	mV	${\sigma }_f$	12.5	mV
${\mathit{\tau }}_{\mathit{max}}$	608	ms	$\tau$	2.7	ms
${\mathit{g}}_{{\mathbf{GABA}}_{\mathit{A}}}$	1	$\text{ms}/{\text{cm}}^2$

Remark: The values of parameters were listed in the table, which were used in the model. The parameters of excitatory and inhibitory neurons model were adopted from experimental measurements (Pospischil et al. 2008), while the parameters of two excitatory receptors (AMPA, NMDA) and one inhibitory receptor were also chosen from experimental data (Koch 1989)

Synaptic model

Here we briefly introduce postsynaptic mechanisms of information transmission. Conventional synaptic transmission in the central nervous system is mediated by excitatory and inhibitory amino acid neurotransmitters, glutamate and GABA, respectively. Glutamate activates postsynaptic neurons while GABA inhibits postsynaptic neurons (Zhang et al. 2013; Guo et al. 2012).

Excitatory neurotransmitter glutamate activates two kinds of receptors: faster activated AMPA/kainate receptors and slower activated NMDA receptors.

AMPA/kainate receptors

The AMPA current is then given by the following equation (Koch 1989):

$${\text{I}}_{\text{AMPA}}={\text{g}}_{\mathrm{AMPA}}{\text{r}}_{\mathrm{AMPA}}\left(\text{V}-{\mathrm{E}}_{\text{AMPA}}\right)$$ 3

where $g_{\mathit{AMPA}}$ is the maximal conductance, $E_{\mathit{AMPA}}$ is the reversal potential, $r_{\mathit{AMPA}}$ represents the fraction of bound AMPA receptors. V indicates the membrane potential of the postsynaptic neuron.

NMDA receptors

NMDA receptors are also sensitive to glutamate, but they mediate synaptic currents that are substantially slower than AMPA currents. Under normal physiological conditions, NMDA receptor channels are partially blocked by $M{g}^{2+}$. If the postsynaptic neuron is polarized, or the neuron is in a low $M{g}^{2+}$ concentration environment, the blocked $M{g}^{2+}$ can be removed. Therefore, when the postsynaptic neuron is activated, NMDA receptor channels will open and the synaptic current can last for a relatively long time (Phillips and Constantine-Paton 2009).

The NMDA current is given by the following equation (Koch 1989):

$${\text{I}}_{\text{NMDA}}={\text{g}}_{\text{NMDA}}{\mathrm{f}}_{\text{NMDA}}\left(\text{V}\right){\mathrm{r}}_{\text{NMDA}}\left(\text{V}-{\text{E}}_{\text{NMDA}}\right)$$ 4

$${\text{f}}_{\text{NMDA}}\left(\text{V}\right)={\left(1+{\text{e}}^{\frac{-\text{V}+{\text{T}}_{\text{f}}}{{\mathrm{\sigma }}_{\text{f}}}}\right)}^{-1}$$ 5

where $g_{\mathit{NMDA}}$ is the maximal conductance, $E_{\mathit{NMDA}}$ is the reversal potential, $r_{\mathit{NMDA}}$ represents the fraction of bound NMDA receptors, $f_{\mathit{NMDA}}\left(\text{V}\right)$ reflects the slow dynamical process in NMDA receptors. The value of ${\sigma }_f$ is set as 12.5 mV, indicating that ${\text{f}}_{\text{NMDA}}\left(\text{V}\right)$ changes slowly with the membrane potential of V.

GABA_A and GABA_B receptors

GABA is the main inhibitory neurotransmitter in the cortex, and it also activates two classes of receptors, $GAB{A}_A$ receptors which have relatively fast kinetics, and $GAB{A}_B$ receptors which are much slower and involve second messengers. Unlike $GAB{A}_A$ receptors, responses from $GAB{A}_B$ receptors require high levels of presynaptic activity, thus only the $GAB{A}_{\text{A}}$ current is taken into account in the network model. The current is given by the following equation (Koch 1989):

$${\text{I}}_{{\text{GABA}}_{\text{A}}}={\text{g}}_{{\text{GABA}}_{\text{A}}}{\mathrm{r}}_{{\text{GABA}}_{\text{A}}}\left(\text{V}-{\text{E}}_{{\text{GABA}}_{\text{A}}}\right)$$ 6

where $g_{{\text{GABA}}_A}$ is the maximal conductance, $E_{{\text{GABA}}_A}$ is the reversal potential, ${\text{r}}_{{\text{GABA}}_A}$ represents the fraction of bound $GAB{A}_{\text{A}}$ receptors.

The model of the fraction of bound receptors r (${\mathit{r}}_{\mathit{AMPA}},{\mathit{r}}_{\mathit{NMDA}},{\mathbf{r}}_{{\mathbf{GABA}}_{\mathit{A}}}$)

Signals are transmitted between neurons through action potentials. A presynaptic neuron generates an action potential and releases neurotransmitters into the synaptic cleft, and then the neurotransmitters transmit in the cleft and bind with postsynaptic receptors. The kinetic model of this process can be represented as follows:

$$\text{R}+\text{T}\stackrel{\mathrm{\alpha },\mathrm{\beta }}{\leftrightarrow }{\text{TR}}^{\ast }$$

where $\text{R and}T{R}^{\ast }\text{are the}$ bound and unbound form of postsynaptic receptors respectively, $\mathrm{\alpha }\text{and}\mathrm{\beta }$ are the forward and backward rates for neurotransmitter binding. Their values are constant in the network model (listed in Table 1). Letting r represent the fraction of bound receptors, the kinetics is described by a first order differential equation (Destexhe et al. 2008):

$$\frac{{\text{dr}}_i}{\mathrm{dt}}=\mathrm{\alpha }\left[\text{T}\right]\left(1-{\text{r}}_i\right)-\mathrm{\beta }{\text{r}}_i,i=AMPA,NMDA,{\text{GABA}}_A$$ 7

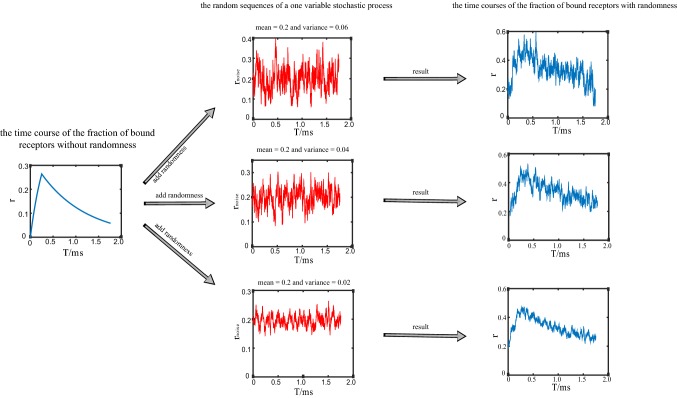
where $\left[T\right]$ is the concentration of neurotransmitters. Considering that the concentration of neurotransmitters in the synaptic cleft rises and falls very rapidly, it is assumed that [T] occurs as a pulse, then solving the Eq. (7) and leading to the following expression. The fraction of bound receptors r rises exponentially during a pulse, and decreases exponentially after a pulse (Fig. 2).

1. During a pulse $\left(t_0<t<t_1\right),\left[\text{T}\right]=T_{\mathit{max}},r$ is given by:

   $$\text{r}\left(\text{t}\right)={\text{r}}_{\infty }+\left(\text{r}\left({\text{t}}_0\right)-{\text{r}}_{\infty }\right)exp\left[-\left(\text{t}-{\text{t}}_0\right)/{\mathrm{\tau }}_{\text{r}}\right)]$$ 8

   where

   $${\text{r}}_{\infty }=\frac{\mathrm{\alpha }{\text{T}}_{\text{max}}}{\mathrm{\alpha }{\text{T}}_{\text{max}}+\mathrm{\beta }}$$ 9

   and

   $${\mathrm{\tau }}_{\text{r}}=\frac{1}{\mathrm{\alpha }{\text{T}}_{\text{max}}+\mathrm{\beta }}$$ 10
2. After a pulse $\left(\text{t}>t_1\right),\left[T\right]=0,r$ is given by:

   $$\text{r}\left(\text{t}\right)=\text{r}\left({\text{t}}_1\right)exp\left[-\mathrm{\beta }\left(\text{t}-{\text{t}}_1\right)\right]$$ 11

Fig. 2.

An example of the time courses of the random binding process in the network model. The left column shows the time course of the fraction of bound receptors without randomness during a spike from presynaptic neuron (calculated by Eqs. (8) and (11)). The middle column shows the random sequences with different variance (0.06, 0.04, 0.02, respectively), while the mean value is the same (0.2) (calculated by Eq. (12)). The right column shows the time courses of the fraction of bound receptors, which are added with different random sequences. During generation of the variable in the stochastic process, we set the mean value of the noise at a relatively high level, while the variance of the noise was set at a relatively small value, so we can guarantee that the fraction of bound receptors with noise (shown in the right column) are always positive in trials

The model of stochastic process of neurotransmitters transmitting and binding with receptors (AMPA, NMDA and ${\mathit{GABA}}_{\mathit{A}}$ receptors)

As we mentioned in the previous section, the process that neurotransmitters transmit in the synaptic cleft and bind with postsynaptic receptors involves randomness. Thus, we introduce a stochastic variable to simulate the randomness in the binding process. A one-variable stochastic process that is controlled by a parameter ${\sigma }_{\text{i}}$ is described by the following equation (Destexhe and Paré 1999; Destexhe et al. 2001):

$$\begin{array}{cc}\hfill \frac{d{r}_{\mathit{noise}}^i\left(\text{t}\right)}{\mathit{dt}}& =-\frac{1}{\tau }\left[r_{\mathit{noise}}^i\left(t\right)-r_{nois{e}_0}^i\right]+\sqrt{\frac{2{\sigma }_i^2}{\tau }}{\chi }_i\left(\text{t}\right)\hfill \\ \hfill & i=AMPA,NMDA,GAB{A}_A\hfill \\ \hfill \end{array}$$ 12

where ${\chi }_i\left(\text{t}\right)$ is the Gaussian white noise of zero mean and unit standard deviation, $r_{nois{e}_0}^i,{\mathrm{\sigma }}_i$ are the mean and standard deviation of the random sequence ($i=AMPA,NMDA,GAB{A}_A$), respectively. $\tau$ is the time constant. The numerical scheme for integration of the stochastic differential equations takes advantage of the fact that these stochastic processes are Gaussian, which leads to an exact update rule:

$$\begin{array}{cc}\hfill r_{\mathit{noise}}^i\left(\text{t}+\text{h}\right)& =r_{nois{e}_0}^i+\left[r_{\mathit{noise}}^i\left(t\right)-r_{nois{e}_0}^i\right]exp\left(-\frac{h}{\tau }\right)+{\text{A}}^i·\text{N}\left(0,1\right)\hfill \\ \hfill {\text{A}}^i& =\sqrt{{\mathrm{\sigma }}_{\text{i}}^2\left[1-exp\left(\frac{-2\text{h}}{\mathrm{\tau }}\right)\right]}\hfill \\ \hfill \end{array}$$ 13

where $\text{N}\left(0,1\right)$ is normal random numbers (zero mean, unit standard deviation) and ${\text{A}}^i$ is the amplitude coefficient which is given above. And h is the iteration step.

In the model, the standard deviation of the stochastic process (12) can be determined by the parameter ${\sigma }_{\text{i}}$ ($i=AMPA,NMDA,GAB{A}_A$). This stochastic process is combined with $r_i$ ($i=AMPA,NMDA,GAB{A}_A$) defined in Eqs. (8) and (11) to simulate the randomness in the binding process of AMPA, NMDA or $GAB{A}_A$ receptors, respectively. Figure 2 shows the time course of the fraction of bound receptors with or without the stochastic variable. It is noted that the parameter ${\sigma }_{\text{i}}$ can easily control the randomness in the binding process. With increasing the value of ${\sigma }_{\text{i}}$, the variation of bound receptors also increases. Based on the assumption that attention reduces randomness in the neurotransmitter binding process, we select two groups of values for ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ to represent the attention attended and unattended conditions, respectively. For simplicity, we do not consider the attentional effect through $GAB{A}_A$ receptors in the current model, so the value of ${\sigma }_{GAB{A}_A}$ is kept constant throughout the following stimulation.

The neural network model

We summarized the equations of excitatory and inhibitory neurons in each layer and their related synaptic currents in the model.

• Layer 1

  Excitatory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^e\frac{{\text{dV}}_{\mathrm{i}}^1}{\mathrm{dt}}& ={\text{I}}_{\mathrm{app}}-{\text{I}}_{\mathit{Na}}^e\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_K^e\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_L^e\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_M^e\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^1,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{W}}_{\mathrm{i},\mathrm{j}}^1{\text{r}}_{\mathrm{AMPAj}}^1\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^1,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{W}}_{\text{i},\mathrm{j}}^1{\text{r}}_{\mathrm{NMDAj}}^1\right)-{\text{I}}_{{\mathrm{GABA}}_{\mathrm{A}}}\left({\text{V}}_{\mathrm{i}}^1,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\text{W}}_{\mathrm{i},\text{j}}^1{\text{r}}_{{\mathrm{GABA}}_{\mathrm{A}}\mathrm{j}}^1\right)\hfill \\ \hfill & i=1,\dots ,20;j=1,\dots ,25\hfill \\ \hfill \end{array}$$ 14
  Inhibitory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^i\frac{{\text{dV}}_{\mathrm{i}}^1}{\text{dt}}& ={\text{I}}_{\mathrm{app}}-{\text{I}}_{\mathit{Na}}^i\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_K^i\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_L^i\left({\text{V}}_{\mathrm{i}}^1\right)-{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^1,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\text{W}}_{\mathrm{i},\mathrm{j}}^1{\text{r}}_{\mathrm{AMPAj}}^1\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^1,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{W}}_{\text{i},\text{j}}^1{\text{r}}_{\mathrm{NMDAj}}^1\right)i=21,\dots ,25;j=1,\dots ,25\hfill \\ \hfill \end{array}$$ 15

• Layer 2

  Excitatory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^e\frac{{\text{dV}}_{\mathrm{i}}^2}{\text{dt}}& =-{\text{I}}_{\mathit{Na}}^e\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_K^e\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_L^e\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_M^e\left({\text{V}}_{\mathrm{i}}^2\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^2,\sum _{\mathrm{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\text{j}}^2{\text{r}}_{\mathrm{AMPAj}}^2+{\text{W}}_{\mathrm{i},\mathrm{j}}^{12}{\text{r}}_{\mathrm{AMPAj}}^1)\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^2,\sum _{\mathrm{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\text{j}}^2{\text{r}}_{\mathrm{NMDAj}}^2+{\text{W}}_{\mathrm{i},\text{j}}^{12}{\text{r}}_{\mathrm{NMDAj}}^1)\right)-{\text{I}}_{{\mathrm{GABA}}_{\text{A}}}\left({\text{V}}_{\mathrm{i}}^2,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\text{W}}_{\mathrm{i},\text{j}}^2{\text{r}}_{{\mathrm{GABA}}_{\text{Aj}}}^2\right)\hfill \\ \hfill & i=1,\dots ,20;j=1,\dots ,25\hfill \\ \hfill \end{array}$$ 16
  Inhibitory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^i\frac{{\text{dV}}_{\mathrm{i}}^2}{\text{dt}}& =-{\text{I}}_{\mathit{Na}}^i\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_K^i\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_L^i\left({\text{V}}_{\mathrm{i}}^2\right)-{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^2,\sum _{\text{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\text{j}}^2{\text{r}}_{\mathrm{AMPAj}}^2+{\text{W}}_{\mathrm{i},\text{j}}^{12}{\text{r}}_{\mathrm{AMPAj}}^1)\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^2,\sum _{\text{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\text{j}}^2{\text{r}}_{\mathrm{NMDAj}}+{\text{W}}_{\mathrm{i},\mathrm{j}}^{12}{\text{r}}_{\mathrm{NMDAj}}^1)\right)i=21,\dots ,25;j=1,\dots ,25\hfill \\ \hfill \end{array}$$ 17

• Layer 3

  Excitatory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^e\frac{{\text{dV}}_{\mathrm{i}}^3}{\text{dt}}& =-{\text{I}}_{\mathit{Na}}^e\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_K^e\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_L^e\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_M^e\left({\text{V}}_{\mathrm{i}}^3\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^3,\sum _{\text{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\text{j}}^3{\text{r}}_{\mathrm{AMPAj}}^3+{\text{W}}_{\mathrm{i},\mathrm{j}}^{23}{\text{r}}_{\mathrm{AMPAj}}^2)\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^3,\sum _{\text{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\mathrm{j}}^3{\text{r}}_{\mathrm{NMDAj}}^3+{\text{W}}_{\mathrm{i},\mathrm{j}}^{23}{\text{r}}_{\mathrm{NMDAj}}^2)\right)\hfill \\ \hfill & -{\text{I}}_{{\mathrm{GABA}}_{\mathrm{A}}}\left({\text{V}}_{\mathrm{i}}^3,\sum _{\mathrm{j}=1}^{\mathrm{m}}{\text{W}}_{\mathrm{i},\text{j}}^3{\text{r}}_{{\mathrm{GABA}}_{\mathrm{A}}\text{j}}^3\right)\text{i}=1,\dots ,20;\text{j}=1,\dots ,25\hfill \\ \hfill \end{array}$$ 18
  Inhibitory neuron:

  $$\begin{array}{cc}\hfill {\text{C}}^i\frac{{\text{dV}}_{\mathrm{i}}^3}{\text{dt}}& =-{\text{I}}_{\mathit{Na}}^i\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_K^i\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_L^i\left({\text{V}}_{\mathrm{i}}^3\right)-{\text{I}}_{\mathrm{AMPA}}\left({\text{V}}_{\mathrm{i}}^3,\sum _{\text{j}=1}^{\text{m}}({\text{W}}_{\mathrm{i},\mathrm{j}}^3{\text{r}}_{\mathrm{AMPAj}}^3+{\text{W}}_{\mathrm{i},\mathrm{j}}^{23}{\text{r}}_{\mathrm{AMPAj}}^2)\right)\hfill \\ \hfill & -{\text{I}}_{\mathrm{NMDA}}\left({\text{V}}_{\mathrm{i}}^3,\sum _{\text{j}=1}^{\mathrm{m}}({\text{W}}_{\mathrm{i},\text{j}}^3{\text{r}}_{\mathrm{NMDAj}}^3+{\text{W}}_{\mathrm{i},\text{j}}^{23}{\text{r}}_{\mathrm{NMDAj}}^2)\right)i=21,\dots ,25;j=1,\dots ,25\hfill \\ \hfill \end{array}$$ 19

where $W^1,W^2,W^3$ are the connection weight matrix within layer 1, layer 2 and layer 3, respectively. $W^{12}$ is the connection weight matrix from layer 1 to layer 2, $W^{23}$ is the connection weight matrix from layer 2 to layer 3. The i and j are neural index, indexes from 1 to 20 represent excitatory neurons, and indexes from 21 to 25 represent inhibitory neurons. In the connection weight matrix: in the same layer, $W_{\text{i},\text{j}}=\frac{1}{12}$ if neuron j is connected to neuron i, and $W_{\text{i},\text{j}}=0$ if neuron j is not connected to neuron i; between layers, ${\text{W}}_{i,j}^{12}=1$ if neuron j is connected to neuron i, and ${\text{W}}_{i,j}^{12}=0$ if neuron j is not connected to neuron i, ${\text{W}}_{i,j}^{23}=0.9$ if neuron j is connected to neuron i, and ${\text{W}}_{i,j}^{23}=0$ if neuron j is not connected to neuron i. We set the weight matrix with these values in order to keep the firing activity of excitatory and inhibitory neurons in a reasonable level, neither too high nor too low. If the connecting weight is too small, no neuronal signals could be transferred from layer to layer. If the connecting weight is too large, all neurons fire in a same pattern with high firing rates. Thus, we simulated the network many times to get the proper range of values of the connection matrix, and select one set of values used in the network model. We did not change these values of the weight matrix through the simulation.

The kinetics of $r_{\mathit{AMPA}},r_{\mathit{NMDA}},r_{GAB{A}_A}$ are given by:

1. During a pulse $\left(t_0<t<t_1\right)$

   $$\left\{\begin{array}{c}{\text{r}}_{\text{AMPA}}\left(\text{t}\right)={\text{r}}_{\infty }+\left({\text{r}}_{\text{AMPA}}\left({\text{t}}_0\right)-{\text{r}}_{\infty }\right)exp\left[-\left(\text{t}-{\text{t}}_0\right)/{\mathrm{\tau }}_{\text{r}}\right)]+{\text{r}}_{\text{noise}}\left({\mathrm{\sigma }}_{\text{AMPA}}\right)\hfill \\ {\text{r}}_{\text{NMDA}}\left(\text{t}\right)={\text{r}}_{\infty }+\left({\text{r}}_{\text{NMDA}}\left({\text{t}}_0\right)-{\text{r}}_{\infty }\right)exp\left[-\left(\text{t}-{\text{t}}_0\right)/{\mathrm{\tau }}_{\text{r}}\right)]+{\text{r}}_{\text{noise}}\left({\mathrm{\sigma }}_{\text{NMDA}}\right)\hfill \\ {\text{r}}_{{\text{GABA}}_{\text{A}}}\left(\text{t}\right)={\text{r}}_{\infty }+\left({\text{r}}_{{\text{GABA}}_{\text{A}}}\left({\text{t}}_0\right)-{\text{r}}_{\infty }\right)exp\left[-\left(\text{t}-{\text{t}}_0\right)/{\mathrm{\tau }}_{\text{r}}\right)]\hfill \end{array}\right)$$ 20
2. After a pulse $\left(t_1<t<t_1+t_{\mathit{DeadTime}}\right)$:

   $$\left\{\begin{array}{c}{\text{r}}_{\text{AMPA}}\left(\text{t}\right)=r\left({\text{t}}_1\right)exp\left[-\beta \left(\text{t}-{\text{t}}_1\right)\right]+{\text{r}}_{\text{noise}}\left({\mathrm{\sigma }}_{\text{AMPA}}\right)\hfill \\ {\text{r}}_{\text{NMDA}}\left(\text{t}\right)=r\left({\text{t}}_1\right)exp\left[-\beta \left(\text{t}-{\text{t}}_1\right)\right]+{\text{r}}_{\text{noise}}\left({\mathrm{\sigma }}_{\text{NMDA}}\right)\hfill \\ {\text{r}}_{{\text{GABA}}_{\text{A}}}\left(\text{t}\right)=r\left({\text{t}}_1\right)exp\left[-\beta \left(\text{t}-{\text{t}}_1\right)\right]\hfill \end{array}\right)$$ 21
3. Other, the receptor channels are closed $\left(t_1+t_{\mathit{DeadTime}}<t<t_{\mathit{nextspike}}\right)$:

   $${\text{r}}_{\text{AMPA}}\left(\text{t}\right)={\text{r}}_{\text{NMDA}}\left(\text{t}\right)={\text{r}}_{{\text{GABA}}_{\text{A}}}\left(\text{t}\right)=0$$ 22

where $r_{\infty }$ is the maximal proportion of bound receptors, $r_{\mathit{noise}}$ is a one-variable stochastic process, the specific formula see (12), (13).

The values of the parameters used in the network model are listed in Table 1. These values are adopted from experimental measurements. During simulation of the network model, values of the most parameters were kept constant. We only changed the values of ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ that control the binding process randomness of AMPA receptors and NMDA receptors to indicate the two attentional conditions. We built our own Matlab codes to make simulation in Windows 7. The Euler method was used to solve the differential equations with an iteration step of 0.002.

Results

During the simulation, a constant external current was inputted to the neurons in layer 1 for 400 ms. This external current evoked the baseline activity of neurons in each layer, and attention would modulate this baseline activity. The network model was calculated for 48 times (trials) using the same set of parameter values. In each trial, the one-variable stochastic process generated a different series even through the variances and means of the series were the same across the trials. The series was added to the proportion of bound AMPA receptors and NMDA receptors. So the firing pattern in each trial was different. We calculated the mean firing rate and response variability of neurons in the model across 48 trials.

Attentional modulation on firing rates through AMPA receptors

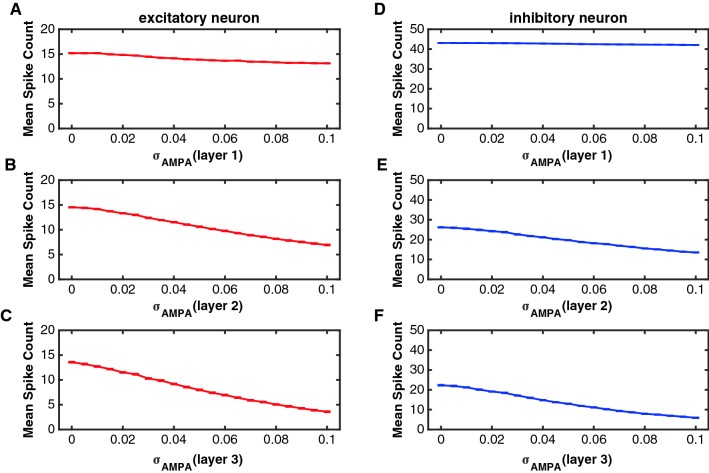
The parameter ${\sigma }_{\mathit{AMPA}}$ can control the randomness in the binding process of AMPA receptors, a smaller value of ${\sigma }_{\mathit{AMPA}}$ indicated less randomness and a higher fraction of bound receptors in the postsynaptic membrane. Figure 3 shows the relation between ${\sigma }_{\mathit{AMPA}}$ and firing rates of excitatory and inhibitory neurons in layer 1, layer 2 and layer 3, respectively. The average number of spikes of excitatory and inhibitory neurons in layer 2 and 3 decreased while ${\sigma }_{\mathit{AMPA}}$ increased. Neurons in layer 1 did not change their firing rates so much with ${\sigma }_{\mathit{AMPA}}$ due to the external current. Firing rates in layer 1 were higher than firing rates in layer 2 and layer 3, indicating spikes were lost during their transmission from one layer to another.

Fig. 3.

The relation between ${\sigma }_{\mathit{AMPA}}$ and the spike count (spike number in 400 ms) of excitatory and inhibitory neurons in the three layers. In this simulation, the value of ${\sigma }_{\mathit{NMDA}}$ was set zero (there was no noise in NMDA receptors). To simulate results in one layer, the value of ${\sigma }_{\mathit{AMPA}}$ changed from 0 to 0.1 in that layer, but was kept a constant value in the other two layers (${\sigma }_{\mathit{AMPA}}$ = 0.08). a–c The function of the mean spike count against ${\sigma }_{\mathit{AMPA}}$ for excitatory neurons in layer 1 (a), layer 2 (b) and layer 3 (c), respectively. d–f The function of the mean spike count against ${\sigma }_{\mathit{AMPA}}$ for inhibitory neurons in layer 1 (d), layer 2 (e) and layer 3 (f), respectively. The red curves indicate the excitatory neurons and the blue curves represent the inhibitory neurons. Error bars indicate s.e.m. The values of s.e.m. are very small in the figures

We selected two groups of different values for ${\sigma }_{\mathit{AMPA}}$ to represent the attention attended and unattended conditions. In synaptic connections between excitatory neurons, ${\sigma }_{\mathit{AMPA}}=0.075$ represented the attention-attended condition while ${\sigma }_{\mathit{AMPA}}=0.08$ indicated the attention-unattended condition. In synaptic connections from excitatory neurons to inhibitory neurons, ${\sigma }_{\mathit{AMPA}}=0.075$ and ${\sigma }_{\mathit{AMPA}}=0.09$ represented the attention attended and unattended conditions, respectively. There were two reasons to select these values. (1) According to the stochastic process defined in Eq. (12), ${\sigma }_{\mathit{AMPA}}$ could not be too large. Otherwise, the fraction of bound receptors could be negative. To avoid this negative situation, we limited the value of ${\sigma }_{\mathit{AMPA}}$ in a range of [0 0.1], a value higher than 0.1 almost shut down firings of neurons in layer 3 (see Fig. 3). (2) According to the simulated results in Fig. 3, the firing rate monotonically decreased with the increment of the value of ${\sigma }_{\mathit{AMPA}}$. If the value of ${\sigma }_{\mathit{AMPA}}$ in the attended condition is smaller than the value in the unattended condition, firing rates of neurons in the model are always higher in the attended than in the unattended conditions. Of cause the increased percentage of firing rates was dependent on the difference between the two values. We optimally chose the two specific values for the attention attended and unattended conditions by simulating the network many times. With these two values, we could calculate the percentage of attention-modulated firing rates in the model to be comparable with experimental observations.

Table 2 shows the attentional effect on firing rates of excitatory and inhibitory neurons in layer 1, layer 2 and layer 3. The attentional modulation in layer 1 was not significant due to the large input of the external current to each neuron (excitatory neurons: P = 0.1068; inhibitory neurons: P = 0.1111, Mann–Whitney U-test). There was a modest but significant increase in the spike count with attention for excitatory neurons in layer 2 (P < 0.01, Mann–Whitney U-test); as for inhibitory neurons in layer 2, attention significantly improved spike counts (P < 0.01, Mann–Whitney U-test); In layer 3, we found that the effect of attention on spike counts was also significant (P < 0.01, Mann–Whitney U-test).

Table 2.

attentional modulation of mean spike counts of excitatory and inhibitory neurons in layer 1, 2 and 3 through AMPA receptors

	Mean spike count Unattended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{AMPA}}=0.08$(excitatory) ${\sigma }_{\mathit{AMPA}}=0.09$(inhibitory)	Mean spike count Attended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{AMPA}}=0.075$(excitatory) ${\sigma }_{\mathit{AMPA}}=0.075$(inhibitory)	Increased percentage $\frac{(R_{att.}-R_{unatt.})}{R_{unatt.}}$ (%)	Significance test between excitatory and inhibitory neurons
Layer 1
Excitatory	$13.33\pm 0.03$	$13.43\pm 0.03$	0.75ns	Absolute increase (ns)
Inhibitory	$42.19\pm 0.01$	$42.32\pm 0.01$	0.31ns	Relative increase (ns)
Layer 2
Excitatory	$8.151\pm 0.06$	$8.57\pm 0.06$	4.83**	Absolute increase (**)
Inhibitory	$14.50\pm 0.09$	$16.32\pm 0.07$	11.15**	Relative increase (**)
Layer 3
Excitatory	$5.05\pm 0.08$	$5.54\pm 0.08$	8.81**	Absolute increase (**)
Inhibitory	$6.95\pm 0.11$	$8.67\pm 0.10$	19.76**	Relative increase (**)

Remark: $R_{att.}$ represents the mean spike count in the attention attended condition and $R_{unatt.}$ represents the activity in the attention unattended condition. The increased percentage indicates attentional modulation of firing rates. Statistical significance between the attention attended and unattended conditions was checked by Mann–Whitney U test (indicated in the column of Increased percentage, ns: p  > 0.05; **: p  < 0.01) for each type of neurons in each layer. Statistical significance of attention-modulated effects were calculated between excitatory and inhibitory neurons from the same layer in Absolute and Relative increases by Mann–Whitney U test (ns p  > 0.05; **p  < 0.01), respectively

We further compared the attentional modulation of excitatory neurons with the attentional modulation of inhibitory neurons. The absolute increase in spike counts between the attention attended and unattended conditions was significantly larger for inhibitory neurons than for excitatory neurons (layer 2: P < 0.01; layer 3: P < 0.01, Mann–Whitney U-test). The relative increase of spike counts (percentage) for inhibitory neurons was also significantly larger than that for excitatory neurons (layer 2: P < 0.01; layer 3: P < 0.01, Mann–Whitney U-test). These results demonstrated that attentional modulation was much stronger for inhibitory neurons compared with excitatory neurons in the network model, which was consistent with findings reported in some experimental studies (Anderson et al. 2013).

Attentional modulation on response variability through AMPA receptors

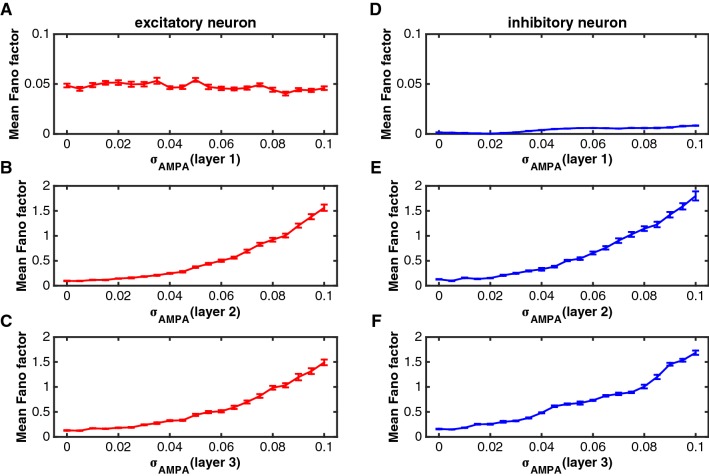
Response variability reflects how reliably information is encoded by neuronal signals. An attention-dependent reduction in response variability could, therefore, enhance sensory processing of behaviorally relevant stimuli. To quantify response variability, we computed the Fano factor, the ratio of the spike count variance to the mean spike count across trials. In the model, we varied ${\sigma }_{\mathit{AMPA}}$ in a range of [0 0.1]. For each ${\sigma }_{\mathit{AMPA}}$ value, we repeated 48 trials to calculate a Fano factor for each neuron and averaged it for each type of neurons (excitatory or inhibitory neurons) in each layer. Figure 4 shows the effect of ${\sigma }_{\mathit{AMPA}}$ on Fano factors of excitatory and inhibitory neurons in layer 1, layer 2 and layer 3, respectively. The Fano factor increased monotonically as ${\sigma }_{\mathit{AMPA}}$ became larger in layer 2 and layer 3, indicating the response variability increased. The Fano factor in layer 1 did not change so much with ${\sigma }_{\mathit{AMPA}}$ and the values were also small.

Fig. 4.

The effect of ${\sigma }_{\mathit{AMPA}}$ on Fano factors of excitatory and inhibitory neurons in the three layers. The parameters were set as the same as those in Fig. 3. a–c The impact of ${\sigma }_{\mathit{AMPA}}$ on the Fano factor of excitatory neurons in layer 1 (a), layer 2 (b) and layer 3 (c). d–f The impact of ${\sigma }_{\mathit{AMPA}}$ on the Fano factor of inhibitory neurons in layer 1 (d), layer 2 (e) and layer 3 (f). The red curves indicate the excitatory neurons and the blue curves represent the inhibitory neurons. Error bars indicate s.e.m

We chose the two groups of same values for ${\sigma }_{\mathit{AMPA}}$ as used in the previous section, and calculated Fano factors in the attention attended and unattended conditions. Table 3 shows the Fano factors of excitatory and inhibitory neurons in layer 1, layer 2, and layer 3. In layer 1, the Fano factor was at a low level because of the large effect of the external current, and attention did not reduce the Fano factor of either excitatory or inhibitory neurons (excitatory neurons: P = 0.1988; inhibitory neurons: P = 0.5476, Mann–Whitney U-test). However, attention significantly reduced Fano factors of excitatory neurons in layer 2 (P < 0.01, Mann–Whitney U-test), but did not significantly reduce Fano factors of inhibitory neurons in layer 2 although attention decreased their values at about 27.75% (P = 0.095, Mann–Whitney U-test). It was also found that each inhibitory neuron in layer 2 consistently decreased its Fano factor by attention. The lack of statistical significance may due to the small number of inhibitory neurons (five neurons). In layer 3, attention significantly reduced Fano factors of both excitatory and inhibitory neurons (excitatory neurons: P = 0.019; inhibitory neurons: P < 0.01; Mann–Whitney U-test).

Table 3.

attentional modulation of mean Fano factors of excitatory and inhibitory neurons in layer 1, 2 and 3 through AMPA receptors

	Mean Fano factor Unattended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{AMPA}}=0.08$ (excitatory) ${\sigma }_{\mathit{AMPA}}=0.09$(inhibitory)	Mean Fano factor Attended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{AMPA}}=0.075$ (excitatory) ${\sigma }_{\mathit{AMPA}}=0.075$ (inhibitory)	Decreased percentage $\frac{(R_{unatt.}-R_{att.})}{R_{unatt.}}$ (%)	Significance test between excitatory and inhibitory neurons
Layer 1
Excitatory	$0.44\pm 2.0\times {10}^{-3}$	$0.49\pm 1.5\times {10}^{-3}$	−  11.09ns	Absolute decrease (ns)
Inhibitory	$6.50\times {10}^{-3}\pm 2.67\times {10}^{-4}$	$5.98\times {10}^{-3}\pm 1.68\times {10}^{-4}$	8.15ns	Relative decrease (ns)
Layer 2
Excitatory	$0.92\pm 0.04$	$0.83\pm 0.03$	9.85**	Absolute decrease (**)
Inhibitory	$1.42\pm 0.05$	$1.03\pm 0.05$	27.75ns	Relative decrease (**)
Layer 3
Excitatory	$0.98\pm 0.04$	$0.82\pm 0.04$	16.82**	Absolute decrease (**)
Inhibitory	$1.46\pm 0.03$	$0.89\pm 0.01$	38.72**	Relative decrease (**)

Remark: $R_{att.}$ represents the mean Fano factor in the attention attended condition and $R_{unatt.}$ represents the Fano factor in the attention unattended condition. The decreased percentage indicates attentional modulation of Fano factors. Statistical significance between the attention attended and unattended conditions was checked by Mann–Whitney U test (indicated in the column of Decreased percentage, ns: p  > 0.05; **: p  < 0.01) for each type of neurons in each layer. Statistical significance of attention-modulated effects were calculated between excitatory and inhibitory neurons from the same layer in Absolute and Relative decreases by Mann–Whitney U test (ns: p  > 0.05; **: p  < 0.01), respectively

We also compared the attentional modulation on Fano factors of inhibitory neurons with that of excitatory neurons, and found that the absolute reduction of Fano factors by attention was significantly stronger for inhibitory neurons than for excitatory neurons (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test). The relative percentage of decrement was also significantly larger for inhibitory neurons in layer 2 and layer 3, respectively (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test), with a mean decrement of 27.75% (layer 2) and 38.72% (layer 3) for inhibitory neurons compared to a mean decrement of 9.85% (layer 2) and 16.82% (layer 3) for excitatory neurons. These results demonstrated that the attentional modulation of Fano factors was stronger for inhibitory neurons than for excitatory neurons.

Attentional modulation on firing rates through NMDA receptors

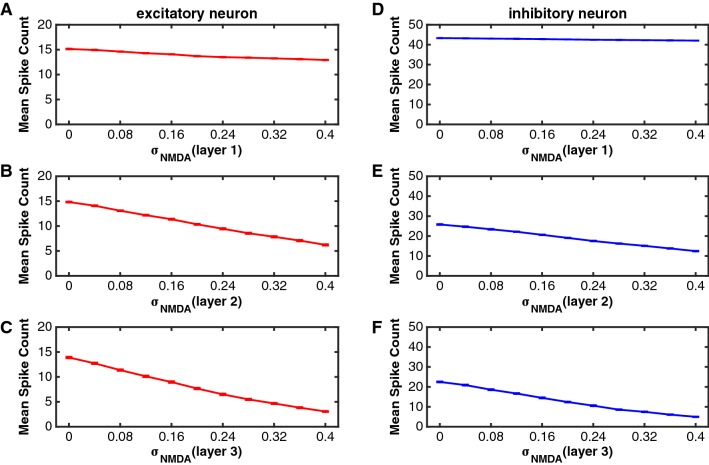
To investigate the effect of ${\sigma }_{\mathit{NMDA}}$ on firing rates, we let the value of ${\sigma }_{\mathit{NMDA}}$ vary in a range of [0 0.4], and computed the mean spike count of each neuron across trials and averaged it across the same type of neurons in each layer. Figure 5 shows the relation between ${\sigma }_{\mathit{NMDA}}$ and the mean spike count of each type of neurons in the three layers, respectively. Overall, neural spike counts decreased as ${\sigma }_{\mathit{NMDA}}$ increased for both excitatory and inhibitory neurons in layer 2 and layer 3. In layer 1, firing rates did not change so much with the value of ${\sigma }_{\mathit{NMDA}}$ either of excitatory or inhibitory neurons.

Fig. 5.

The function of the spike count against ${\sigma }_{\mathit{NMDA}}$ for excitatory and inhibitory neurons in the three layers. In this simulation, the value of ${\sigma }_{\mathit{AMPA}}$ was set zero (there was no noise in AMPA receptors). To simulate results in one layer, the value of ${\sigma }_{\mathit{NMDA}}$ changed from 0 to 0.4 in that layer, but was kept a constant value (${\sigma }_{\mathit{NMDA}}$ = 0.12) for neurons in the other two layers. a–c The relation of the mean spike count with ${\sigma }_{\mathit{NMDA}}$ for excitatory neurons in layer 1 (a), layer 2 (b) and layer 3 (d). d–f The relation of mean spike count with ${\sigma }_{\mathit{NMDA}}$ for inhibitory neurons in layer 1 (d), layer 2 (e) and layer 3 (f). The red curves indicate the excitatory neurons and the blue curves represent the inhibitory neurons. Error bars indicate s.e.m

We also selected two groups of different values for ${\sigma }_{\mathit{NMDA}}$ to simulate the attention attended and unattended conditions, where ${\sigma }_{\mathit{NMDA}}=0.12$ (unattended) and ${\sigma }_{\mathit{NMDA}}=0.04$ (attended) were set for synaptic connections between excitatory neurons, and ${\sigma }_{\mathit{NMDA}}=0.16$ (unattended) and ${\sigma }_{\mathit{NMDA}}=0.04$ (attended) for synaptic connections from excitatory neurons to inhibitory neurons. We had similar two reasons described in the previous section to select these values. Because it decreased monotonically with the increment of ${\sigma }_{\mathit{NMDA}}$ in the network model, the firing rate was higher in the attended than unattended conditions if the value of ${\sigma }_{\mathit{NMDA}}$ was smaller in the former condition. The percentage of firing rate change is dependent on the difference between the two values in the two attention conditions. We chose these values for the attended and unattended conditions, which could generate the percentage of firing rate change in the network model comparable with experimental data.

Table 4 shows the attentional effect on spike counts of excitatory and inhibitory neurons in layer 1, layer 2 and layer 3. In layer 1, there was a modest but significant increase in spike counts in the attention attended condition compared to that in the unattended condition (excitatory neurons: P < 0.01; inhibitory neurons: P < 0.01; Mann–Whitney U-test). In layer 2, attention also significantly increased spike counts of excitatory and inhibitory neurons (excitatory neurons: P < 0.01; inhibitory neurons: P < 0.01; Mann–Whitney U-test). The results in layer 3 was similar to those in layer 2, and the attentional modulation of spike counts was significant for both excitatory and inhibitory neurons (excitatory neurons: P < 0.01; inhibitory neurons: P < 0.01; Mann–Whitney U-test). Moreover, we compared the attentional modulation on spike counts of inhibitory neurons with that of excitatory neurons. The absolute increase of spike counts was significantly larger for inhibitory neurons than for excitatory neurons in layer 2 and layer 3, respectively (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test). Similarly, the relative percentage increase of spike counts was also significantly stronger for inhibitory neurons (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test). These results demonstrated again that the attention (indicated by the decreased value of ${\sigma }_{\mathit{NMDA}}$) increased spike counts of both excitatory and inhibitory neurons and the attention-dependent modulation on spike counts was significantly stronger for inhibitory neurons.

Table 4.

attentional modulation of mean spike counts of excitatory and inhibitory neurons in layer 1,2 and 3 through NMDA receptors

	Mean spike count Unattended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{NMDA}}=0.12$(excitatory) ${\sigma }_{\mathit{NMDA}}=0.16$(inhibitory)	Mean spike count Attended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{NMDA}}=0.04$(excitatory) ${\sigma }_{\mathit{NMDA}}=0.04$(inhibitory)	Increased percentage $\frac{(R_{att.}-R_{unatt.})}{R_{unatt.}}$ (%)	Significance test between excitatory and inhibitory neurons
Region 1
Excitatory	$14.28\pm 0.06$	$14.94\pm 0.06$	4.62**	Absolute increase (ns)
Inhibitory	$42.78\pm 0.02$	$43.16\pm 0.02$	0.89**	Relative increase (ns)
Region 2
Excitatory	$12.18\pm 0.09$	$14.09\pm 0.08$	15.68**	Absolute increase (**)
Inhibitory	$20.61\pm 0.11$	$24.68\pm 0.17$	19.75**	Relative increase (**)
Region 3
Excitatory	$10.12\pm 0.15$	$12.73\pm 0.14$	25.79**	Absolute increase (**)
Inhibitory	$14.48\pm 0.22$	$20.90\pm 0.22$	44.34**	Relative increase (**)

Remark: $R_{att.}$ represents the mean spike count in the attention attended condition and $R_{unatt.}$ represents the activity in the attention unattended condition. The increased percentage indicates attentional modulation of firing rates. Statistical significance between the attention attended and unattended conditions was checked by Mann–Whitney U test (indicated in the column of Increased percentage, ns: p > 0.05; **: p < 0.01) for each type of neurons in each layer. Statistical significance of attention-modulated effects were calculated between excitatory and inhibitory neurons from the same layer in Absolute and Relative increases by Mann–Whitney U test (ns: p > 0.05; **: p < 0.01), respectively

Attentional modulation on response variability through NMDA receptors

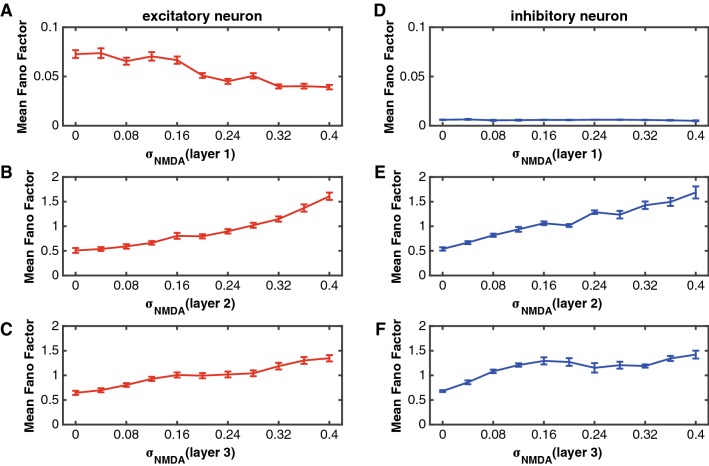
In this section we investigated the relation between the response variability of neurons and the randomness of binding process in NMDA receptors. We varied the value of ${\sigma }_{\mathit{NMDA}}$ in a range of [0 0.4], and calculated Fano factors of neurons in the network. Figure 6 shows the function of Fano factors of excitatory and inhibitory neurons against ${\sigma }_{\mathit{NMDA}}$ in layer 1, layer 2 and layer 3, respectively. It was noted that the Fano factor increased as ${\sigma }_{\mathit{NMDA}}$ became larger (the randomness of NMDA receptors binding process becomes larger), indicating that reducing randomness of binding process in NMDA receptors decreased response variability of neurons in the network. It means that attention can reduce the Fano factor on the basis of the model assumption. We chose the same two groups of parameters used in the “Attentional modulation on firing rates through NMDA receptors” section as the attention attended and unattended conditions, respectively.

Fig. 6.

The influences of ${\sigma }_{\mathit{NMDA}}$ on Fano factors of excitatory and inhibitory neurons in the three layers. The parameters were set as the same as those in Fig. 5. a–c The function of the Fano factor against ${\sigma }_{\mathit{NMDA}}$ for excitatory neurons in layer 1 (a), layer 2 (b) and layer 3 (c). d–f The function of the Fano factor against ${\sigma }_{\mathit{NMDA}}$ for inhibitory neurons in layer 1 (d), layer 2 (e) and layer 3 (f). The red curves indicate the excitatory neurons and the blue curves represent the inhibitory neurons. Error bars indicate s.e.m

Table 5 shows the attentional effect on Fano factors of excitatory and inhibitory neurons in layer 1, layer 2 and layer 3. In layer 1, the Fano factor was at a low level because of the large effect of the external current, indicating that the response variability across trials was small, and attention did not significantly reduce the Fano factor (excitatory neurons: P = 0.5608; inhibitory neurons: P = 0.5476; Mann–Whitney U-test). In layer 2, however, attention significantly reduced Fano factors for both excitatory and inhibitory neurons (excitatory neurons: P < 0.01; inhibitory neurons: P < 0.01; Mann–Whitney U-test). The same results were obtained in layer 3. Attention also significantly reduced Fano factors of both excitatory and inhibitory neurons (excitatory neurons: P < 0.01; inhibitory neurons: P = 0.015; Mann–Whitney U-test). Moreover, we compared the attentional modulation on Fano factors of excitatory neurons with that of inhibitory neurons, and found that the absolute change of Fano factors between the attention attended and unattended conditions was significantly stronger for inhibitory neurons than for excitatory neurons (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test). The relative percentage of decreased Fano factors was also significantly larger for inhibitory neurons (layer 2: P < 0.01; layer 3: P < 0.01; Mann–Whitney U-test), with a mean decreasing Fano factors of 37.03% (layer 2) and 33.60% (layer 3) for inhibitory neurons compared to a mean decreasing Fano factors of 18.86% (layer 2) and 24.80% (layer 3) for excitatory neurons. It suggests that attention (indicated by the decreased value of ${\sigma }_{\mathit{NMDA}}$) made stronger modulation of Fano factors for inhibitory neurons.

Table 5.

attentional modulation of mean Fano factors of excitatory and inhibitory neurons in layer 1, 2 and 3 through NMDA receptors

	Mean Fano factor Unattended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{NMDA}}=0.12$(excitatory) ${\sigma }_{\mathit{NMDA}}=0.16$(inhibitory)	Mean Fano factor Attended (mean $\pm$ s.e.m.) ${\sigma }_{\mathit{NMDA}}=0.04$(excitatory) ${\sigma }_{\mathit{NMDA}}=0.04$(inhibitory)	Decreased percentage $\frac{(R_{unatt.}-R_{att.})}{R_{unatt.}}$ (%)	Significance test between excitatory and inhibitory neurons
Region 1
Excitatory	$0.07\pm 4.30\times {10}^{-3}$	$0.07\pm 4.95\times {10}^{-3}$	−  4.61ns	Absolute decrease (ns)
Inhibitory	$5.95\times {10}^{-3}\pm 2.2\times {10}^{-4}$	$6.45\times {10}^{-3}\pm 4.5\times {10}^{-4}$	−  8.78ns	Relative decrease (ns)
Region 2
Excitatory	$0.66\pm 0.04$	$0.58\pm 0.04$	18.86**	Absolute decrease (**)
Inhibitory	$1.06\pm 0.04$	$0.67\pm 0.03$	37.03*	Relative decrease (**)
Region 3
Excitatory	$0.93\pm 0.04$	$0.70\pm 0.04$	24.80**	Absolute decrease (**)
Inhibitory	$1.29\pm 0.07$	$0.86\pm 0.04$	33.60**	Relative decrease (**)

Remark: $R_{att.}$ represents the mean Fano factor in the attention attended condition and $R_{unatt.}$ represents the Fano factor in the attention unattended condition. The decreased percentage indicates attentional modulation of Fano factors. Statistical significance between the attention attended and unattended conditions was checked by Mann–Whitney U test (indicated in the column of Decreased percentage, ns: p > 0.05; **: p < 0.01) for each type of neurons in each layer. Statistical significance of attention-modulated effects were calculated between excitatory and inhibitory neurons from the same layer in Absolute and Relative decreases by Mann–Whitney U test (ns: p > 0.05; **: p < 0.01), respectively

Comparison of attentional modulations in different layers

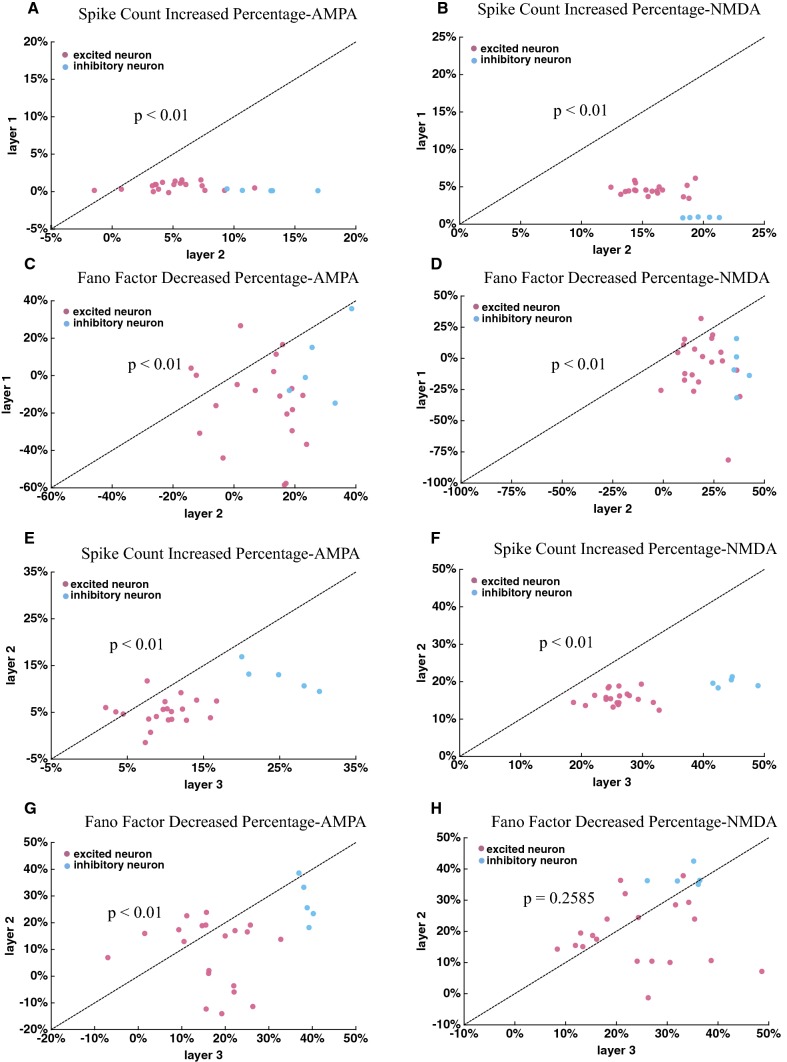
It has been reported that the attention-modulated effect on neuronal activity was stronger in higher visual areas, such as V4, IT, FEF, MT and MST, than in lower visual areas, such as V1 and V2 (Mitchell et al. 2007; Herrero et al. 2013; Treue and Maunsell 2005; Lee and Maunsell 2010). There were three layers in our model. We compared the attention-modulated effect on firing rates and response variability between layers. We calculated the percentage of increased firing rates and the percentage of decreased response variability modulated by attention for each neuron in each layer. Figure 7a–d show the results between layer 1 and layer 2. The percentage of increased firing rates was significantly larger for neurons in layer 2 (Mann–Whitney U-test, increased percentage with AMPA receptors: P < 0.01; increased percentage with NMDA receptors: P < 0.01). The percentage of reduced Fano factors was significantly larger for neurons in layer 2 (Mann–Whitney U-test, decreased percentage with AMPA receptors: P < 0.01; decreased percentage with NMDA receptors: P < 0.01).

Fig. 7.

Comparing attentional effects on firing rates and Fano factors between layers. a–b The attentional effects on the firing rate between layer 1 and layer 2 mediated by ${\sigma }_{\mathit{AMPA}}$ (a) and ${\sigma }_{\mathit{NMDA}}$ (b), respectively. C–D The attentional effects on the Fano factors between layer 1 and layer 2 mediated by ${\sigma }_{\mathit{AMPA}}$ (c) and ${\sigma }_{\mathit{NMDA}}$ (d), respectively. e, f Comparing the attentional effect on the firing rate in layer 2 to that in layer 3 mediated by ${\sigma }_{\mathit{AMPA}}$ (e) and ${\sigma }_{\mathit{NMDA}}$ (f). g, h Comparing the attentional effect on the Fano factors between layer 2 and layer 3 mediated by ${\sigma }_{\mathit{AMPA}}$ (g) and ${\sigma }_{\mathit{NMDA}}$ (h). The statistical significance was examined by Mann–Whitney U test, and its p value was shown in the corresponding figure. The red dots represent the data from excitatory neurons and the blue dots indicate inhibitory neurons

Figure 7e–h show the attention modulated effect on firing rates and Fano factors between layer 2 and layer 3. The percentage of increased firing rates by attention was stronger for neurons in layer 3 (Mann–Whitney U-test, increased percentage with AMPA receptors: P < 0.01; increased percentage with NMDA receptors: P < 0.01). However, the attention mediated by NMDA receptors (controlled by ${\sigma }_{\mathit{NMDA}}$) did not make significant modulation of Fano factors between layer 2 and layer 3 (Mann–Whitney U-test, decreased percentage with NMDA receptors: P = 0.2585). The attention mediated by AMPA receptors (controlled by ${\sigma }_{\mathit{AMPA}}$) made stronger effect on Fano factors in layer 3 than in layer 2 (Mann–Whitney U-test, decreased percentage with AMPA receptors: P < 0.01). The network model showed that attentional modulation on both firing rates and response variability became stronger in in higher layers compared to that in lower layers, which was consistent with the experimental reports.

Interactive effect of attention and the receptor activity (AMPA and NMDA) on firing rates and response variability

A recent report further demonstrated that block of NMDA or AMPA receptors by APV (NMDA receptor antagonist) or CNQX (AMPA receptor antagonist) impaired the attentional modulation of response variability, indicating that the activity of these two receptors was related to attention (Herrero et al. 2013). To investigate the relationship between receptors (AMPA and NMDA) and attentional modulation of neuronal activity, we considered influences of the AMPA and NMDA receptors’ activity on firing rates and Fano factors under the attention attended and unattended conditions, respectively. During the process of action potential transmission, we controlled the max fraction of bound AMPA or NMDA receptors by the parameter ${\text{Inf}}_{\text{AMPA}}$ or ${\text{Inf}}_{\text{NMDA}}$ (as indicated by $r_{\infty }$ in Eq. (9)). Therefore, when the value of ${\text{Inf}}_{\text{AMPA}}$ or ${\text{Inf}}_{\text{NMDA}}$ was higher, the activity of the AMPA or NMDA receptors would be stronger. In contrast, the activity of two receptors would be weaker. Block of NMDA or AMPA receptors by the antagonist indicated a smaller value of ${\text{Inf}}_{\text{AMPA}}$ or ${\text{Inf}}_{\text{NMDA}}$.

Since the attentional modulation on firing rates and Fano factors differed between layers, we modeled the interaction between the activity of AMPA or NMDA receptors and attention separately in layer 2 and layer 3. To simulate the effect of the activity of AMPA receptors and attention on neuronal responses in layer 2, the activity of NMDA receptors was maintained at a normal level and the activity of AMPA receptors of layer 2 neurons was changed. The value of the activity of AMPA receptors varied from 0 to 0.3 with a step of increment of 0.03 (we intercepted a section between 0.06 and 0.3, because the firing rate almost was zero when the AMPA activity was at a low level). Consistently, when we modeled the effect of the activity of NMDA receptors and attention on firing rates of neurons in layer 2, we also kept the activity of AMPA receptors at a normal level and let NMDA receptors activity change from 0 to 0.3 with a step of 0.03. Similarly, when modeling the interaction of the activity of the two receptors and attention in layer 3, we only changed the activity of the two receptors in layer 3, while kept their activity at a normal level in layer 2. Moreover, the parameters to control the attention attended and unattended conditions were as the same as used in previous sections.

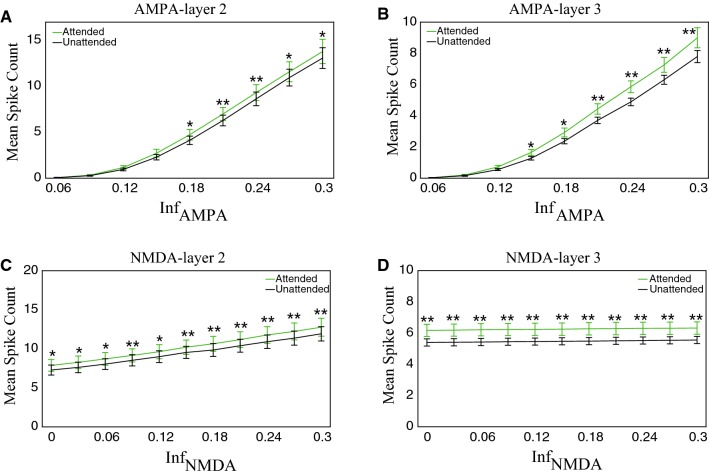
We first analyzed the effect of the activity of the two receptors on firing rates under the attention attended and unattended conditions. Figure 8a, b show the results of AMPA receptors in layer 2 and layer 3, respectively. It could be noted that firing rates in both the attended and unattended conditions increased when the activity of AMPA receptors became more active (indicating by the increasing value of ${\text{Inf}}_{\text{AMPA}}$). The firing rate in the attention attended condition was significantly higher than that in the unattended condition when the activity of AMPA receptors was larger than certain values (layer 2: ${\text{Inf}}_{\text{AMPA}}>0.18$; layer 3: ${\text{Inf}}_{\text{AMPA}}>0.12$). The relationship between the activity of NMDA receptors and firing rates in layer 2 or layer 3 is illustrated in Fig. 8c, d. The firing rate also increased with the increment of the activity of NMDA receptors, and it was significantly stronger in the attention attended condition. Compared with the results of AMPA receptors shown in Fig. 8a, b, the firing rate shown in Fig. 8c, d was maintained at a certain value that was much larger than zero and the attentional modulation still existed even when the activity of NMDA receptors was at a low level. However, the firing rate was almost zero and the attentional modulation disappeared when the activity of AMPA receptors was at a low level.

Fig. 8.

The mean spike counts of excitatory and inhibitory neurons were modulated by the activity of the two receptors and attention in layer 2 and layer 3. Here the mean spike count was the average cross excitatory and inhibitory neurons in the same layer. a, b The mean spike count was modulated by the activity of AMPA and attention in layer 2 (a) and layer 3 (b). c, d The mean firing rate was modulated by the activity of NMDA and attention in layer 2 (c) and layer 3 (d). The statistical significance between the attended and unattended conditions was examined by Mann–Whitney U test with Bonferroni correction (*p < 0.05; **p  < 0.01). The light green curves indicate the attention attended condition and the black curves indicate the attention unattended condition. Error bars indicate s.e.m

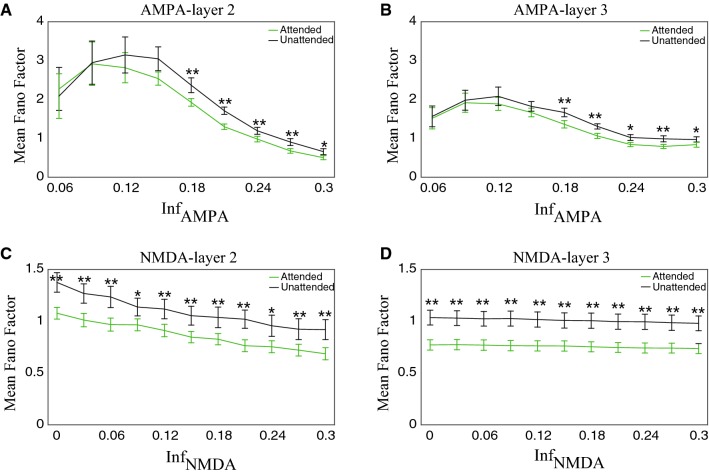
We next calculated the Fano factor of neurons in layer 2 and layer 3. Figure 9a, b separately show the relationship between the activity of AMPA receptors and Fano factors in layer 2 and layer 3. The Fano factor showed significant reduction in the attention attended condition compared to the attention unattended condition when the activity of AMPA receptors was at a high level (For example, in layer 2,${\text{Inf}}_{\text{AMPA}}$ = 0.3, mean attended = 0.50, unattended = 0.66, P < 0.01; in layer 3, ${\text{Inf}}_{\text{AMPA}}$ = 0.3, mean attended = 0.97, unattended = 0.84, P < 0.01, Mann–Whitney U-test). When the activity of AMPA receptors was at a low level, the Fano factor became large, while its attentional modulation became insignificant (For example, in layer 2, ${\text{Inf}}_{\text{AMPA}}$ = 0.09, mean attended = 2.917, unattended = 2.947, P = 0.6766; in layer 3, ${\text{Inf}}_{\text{AMPA}}$ = 0.09, mean attended = 1.98, unattended = 1.916, P = 0.7151, Mann–Whitney U-test). Thus, the reduction in the activity of AMPA receptors impaired the attentional modulation of Fano factors.

Fig. 9.

The mean Fano factors of excitatory and inhibitory neurons were modulated by the activity of the two receptors and attention in layer 2 and layer 3. Here the mean Fano factor was the average across excitatory and inhibitory neurons in the same layer. a, b The mean Fano factor was modulated by the activity of AMPA receptors and attention in layer 2 (a) and layer 3 (b). c, d The mean Fano factor was modulated by the activity of NMDA receptors and attention in layer 2 (c) and layer 3 (d). The statistical significance was examined by Mann–Whitney U test with Bonferroni correction (*p  < 0.05; **p  < 0.01). The light green curves indicate the attention attended condition and the black curves indicate the attention unattended condition. Error bars indicate s.e.m

The relationship between the activity of NMDA receptors and Fano factors in layer 2 and layer 3 is shown in Fig. 9c, d, respectively. With the activity of NMDA receptors decreased, the Fano factor increased, but it was significantly reduced by attention. Interestingly, even when NMDA receptors were completely blocked (the value of ${\text{Inf}}_{\text{NMDA}}$ was set as zero), we still observed significant attentional modulation of Fano factors, suggesting that AMPA and NMDA receptors may have different functional roles in attentional modulation of neuronal activity.

Discussion

We made the hypothesis in the network model that attention may reduce the variability and increase the reliability in the process in which neurotransmitters are released from synaptic vesicles, transmitted in the synaptic cleft and bound with AMPA or NMDA receptors in the postsynaptic membrane. The randomness in the binding process with AMPA and NMDA receptors was controlled by the two parameters ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ in our model, respectively. We set two different values for ${\sigma }_{\mathit{AMPA}}$ or ${\sigma }_{\mathit{NMDA}}$ to indicate the attention attended and unattended conditions. Based on this hypothesis, our network model simulated attention-induced modulation of neuronal activity, such as, enhancing firing rates of neurons (see Figs. 3, 5), reducing their response variability (see Figs. 4, 6). Visual attention had also stronger effect on inhibitory neurons than excitatory neurons, on neurons in higher layers than neurons in lower layers.

It has been reported in neurophysiological experiments that the binding process of neurotransmitters with receptors is a stochastic process (Gibb 1978; Yang and Xu-Friedman 2013). In a single-unit recording experiment, it has been found that attention can reduce the response variability of neurons and improve the reliability of information transmission between them (Briggs et al. 2013), indicating that attention may modulate neural spike activity at the synaptic level. In our model, the two parameters of ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ determined the fraction of bound AMPA and NMDA receptors located in membranes of postsynaptic neurons. When the values of ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ became smaller, the proportion of bound receptors would increase, so synaptic currents into the postsynaptic neuron became larger, which could increase the probability to evoke a postsynaptic action potential. At the same time, with reducing the values of ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ the randomness in the binding process of AMPA and NMDA receptors became smaller (see Fig. 2). It implied that the postsynaptic neuron received more stable synaptic currents to evoke action potentials in same repeated trials, and the response variability of the postsynaptic neuron became lower (see Figs. 4, 6). Therefore, visual attention may enhance efficient and reliable communication between neurons through the method of reducing the randomness in the neurotransmitter binding process.

Most of attention models explained attention-modulated phenomenon based on firing rates of neurons (at the neural level), not at the synaptic level (Ardid et al. 2007; Beuth and Hamker 2015; Reynolds and Heeger 2009; Bazhenov et al. 2004). We developed the three-layer network model of attention at the synaptic level, in which single excitatory and inhibitory neurons were modeled by the H–H model with different ion channels. The H–H model can describe the spike activity of neurons more precisely than other integrate-and-fire models. In particular, the H–H model could characterize spike waveforms of excitatory and inhibitory neurons. In the network model, excitatory neurons had broad spike waveforms and low firing rates and inhibitory neurons had narrow waveforms and high firing rates. These response properties were usually used to classify neurons as putative pyramidal cells or as putative interneurons in extracellular recording experiments (Thiele et al. 2016; Fan et al. 2017; Ardid et al. 2015). The excitatory and inhibitory neurons in our model were considered as putative pyramidal cells and interneurons, respectively based on their response properties. The attentional modulation on inhibitory neurons was stronger than on excitatory neurons (see Table 2, 3, 4 and 5), consistent with the experimental findings that interneurons had stronger attentional modulation than did pyramidal cells (Mitchell et al. 2007; Thiele et al. 2016; Ison et al. 2011; Anderson et al. 2013). In the current model, we set two higher values of ${\sigma }_{\mathit{AMPA}}$ and ${\sigma }_{\mathit{NMDA}}$ for the inhibitory than excitatory neurons in the attention unattended condition, indicating inhibitory neurons had a higher level of randomness in the neurotransmitters binding process and a higher value of Fano factors. Attention reduced the randomness in the binding process to a same level for both excitatory and inhibitory neurons, which enabled inhibitory neurons to have a larger reduction in Fano factors. Further experiments are needed to clarify how attention influences the neurotransmitter binding process in synapses of excitatory and inhibitory neurons.

In this model, we investigated interactive effect between the activity of AMPA and NMDA receptors (represented by the values of ${\text{Inf}}_{\mathit{AMPA}}$ and ${\text{Inf}}_{\mathit{NMDA}}$) and attention on firing rates of neurons (see Fig. 8), as well as Fano factors (see Fig. 9). From the aspect of the model, when the activity of AMPA receptors was at a high level, attention reduced the randomness of the binding process, which effectively increased the fraction of bound receptors, and thereby the Fano factor decreased in the attention attended condition (see Fig. 9a, b). In contrast, when the activity of AMPA receptors was at a low level, indicating the maximal fraction of effective receptors in the postsynaptic membrane was small. The attentional modulation on this small fraction of effective receptors was not obvious, which did not induce significant change in the Fano factor. The relation between the activity of NMDA receptors and firing rates or Fano factors showed a different pattern. Even when the activity of NMDA receptors was set as zero (in this case the activity of AMPA receptors was normal), firing rates and Fano factors were significantly modulated by attention (see Figs. 8c, d, 9c, d). One possible reason is due to different intrinsic properties of AMPA and NMDA receptors. AMPA receptors are faster activated, while NMDA receptors are more slowly activated and its channel is open after the postsynaptic neuron is active. Therefore, when the activity of AMPA receptors was at a low level, the postsynaptic neuron can’t be activated even the activity of NMDA receptors was at a normal level. In contrast, when the activity of NMDA receptors was at a low level, the postsynaptic neuron can be still activated through normal AMPA receptors. The different dynamical properties of AMPA and NMDA receptors suggest that the two receptors play different roles in attention-modulated neural activity.

It was reported in single-unit recording experiments that attention-induced modulation of firing rates was stronger in higher visual areas compared to in lower visual cortexes. Attention almost did not increase firing rates of neurons in the macaque primary visual cortex (V1) (Herrero et al. 2013), but increased firing rates over 20% in the area V4 (Mitchell et al. 2007), 40% in the area MT and 65% in the area MST (Treue and Maunsell 2005; Lee and Maunsell 2010). We found in the model that the attention-induced changes were indeed stronger for neurons in higher layers (see Fig. 7), consistent with the evidence observed in those neurophysiological experiments. The layer-dependent attentional modulation could be explained by signal transmission between layers from the viewpoint of the network model. In the current model, neurons were connected each other through chemical synapses that were modeled as a stochastic process. Due to the noise in this process, the possibility to generate an action potential would become less during transmission from the lower layer to the higher layer. It indicated that the spike train of each neuron evoked by the external current was more irregular in higher layers than that in lower layers. In the attention attended condition, the same values of ${\sigma }_{\mathit{AMPA}}$ or ${\sigma }_{\mathit{NMDA}}$ were set for each type of neurons in all three layers, thus attentional effects on firing rates and Fano factors were larger in the higher layer. We found an exception that Fano factors mediated by NMDA receptors did not significantly differ between layer 2 and layer 3 (see Fig. 7h). It might be caused by different dynamical properties between NMDA receptors (slowly activated channel) and AMPA receptors (fast activated channel).

According to our knowledge, there is no direct experimental evidence to show that attention reduces the variability in the stochastic binding process till now. Some studies have reported that attention could improve the reliability of communication between neurons and block of AMPA and NMDA receptors would impair attentional modulation on neuronal activity, suggesting that attention is involved in the signal processing in synapses (Herrero et al. 2013; Briggs et al. 2013). Many computational models of attention assume that attentional signal is an external input to an isolated network and neurons in the network use the attentional signal and their sophisticated connecting structure to generate attention-modulated activity (Beuth and Hamker 2015; Wagatsuma et al. 2013; Kanashiro et al. 2017). Actually the external signal is not only specific to attention, it could be explained as other types of signal (for example, reward signal) but generate attention-like activity. In our hypothesis, attention is considered as a process that reduces the randomness in the binding process to modulate neural activity. Our model does not require sophisticated connection patterns among neurons to evoke attention-modulated activity. We could observe the attentional activity even in the three-layered feedforward network. Our model provides a way to investigate synaptic mechanisms of attention. It has reported that the single-molecule imaging method is able to measure the spatial and temporal course of bound receptors in membranes of postsynaptic cells in vivo (Ueda and Shibata 2007; Varela et al. 2016). The new technology could be applied to measure bound AMPA or NMDA receptors when an animal performs an attention task and statistical properties of measured receptors could be compared directly in the attention attended and unattended conditions to verify our hypothesis.

There were several limitations in the neural network model of attention. First, there were only 25 neurons in each layer and 75 neurons in total in the network model. The number of neurons was very few. Because the H–H equation was used as the model for individual neuron, computing cost would increase very quickly with the increase of neurons in the network model. Second, there were only 3 layers in the network model, and three types of synaptic connections, two types of excitatory synapses (AMPA receptors and NMDA receptors) and one inhibitory synapse (GABA_A receptors). In this study, we only focused on attention mediated through AMPA and NMDA receptors. We have not simulated attention-induced effects through GABA receptors. Third, the model utilized two different values of ${\sigma }_i$ (i = AMPA, NMDA) to represent the attention attended and unattended conditions. But it has not provided an automatic way to switch between the two values according to the attention condition in the model. It is important to understand mechanisms how attention controls the randomness in the binding process with further experimental and theoretical studies. Fourth, many studies have demonstrated that acetylcholine (Ach) plays important roles in attention (Herrero et al. 2008; Klinkenberg et al. 2011; Gratton et al. 2017). The current model has not taken into account the function of Ach. In the central nerve system, Ach appears to act as a neuromodulator, rather than engaging in direct synaptic transmission between specific neurons (Picciotto et al. 2012). Ach influences the release of other neurotransmitters, such as glutamate, GABA, and so on, to alter the neuronal activity (Thiele and Bellgrove 2018). Theoretically, it is possible that Ach could control the randomness in the binding process to generate attention-like signals in the attention task. Fifth, the network model could explain some basic properties of attention-modulated activity. But this model has not taken into account for functions of each neuron, such as its selectivity to orientation, moving direction, specific features, or spatial locations. Further studies would integrate these functions of each neuron into the current network model to better understand synaptic mechanisms of spatial and feature-based attention.

Funding

This study was funded by National Natural Science Foundation of China (Nos. 11232005, 11472104, 11702096, 11872180) and sponsored by Shanghai Pujiang Program (No. 13PJ1402000).

Compliance with ethical standards

Conflict of interest

All authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.