Abstract
Empirical records of epidemics reveal that fluctuations are important factors for the spread and prevalence of infectious diseases. The exact manner in which fluctuations affect spreading dynamics remains poorly known. Recent analytical and numerical studies have demonstrated that improved differential equations for mean and variance of infected individuals reproduce certain regimes of the SIS epidemic model. Here, we show they form a dynamical system that follows Hamilton’s equations, which allow us to understand the role of fluctuations and their effects on epidemics. Our findings show the Hamiltonian is a constant of motion for large population sizes. For small populations, finite size effects break the temporal symmetry and induce a power-law decay of the Hamiltonian near the outbreak onset, with a parameter-free exponent. Away from the onset, the Hamiltonian decays exponentially according to a constant relaxation time, which we propose as a metric when fluctuations cannot be neglected.
Subject terms: Applied mathematics, Biological physics, Statistical physics
Introduction
Models of disease transmission, or epidemic models for short, have been an integral part of the epidemiological toolkit, dating back from pioneer models of Kermack and McKendrick1. The main goal of epidemic models can be summarized as the ability to accurately predict spreading patterns of a given communicable disease afflicting a specific population. These models allow decision makers to assess the various intervention strategies available to them and to plan accordingly. Several approaches have been developed to model disease outbreaks2, namely, compartmental equations, stochastic equations, agent-based simulations, etc. Each approach suits a particular aspect of the outbreak being studied, built upon hypotheses compatible with empirical records or based on a phenomenological context. They include, but are not restricted to, biological content of the disease, mechanisms behind pathogen transmission, social interactions among the target population and its spatial structure3. By the same token, different models for the same disease and population may produce inconsistent results, possibly due to conflicting underlying hypotheses. For instance, the random-mixing hypothesis–i.e. the population is assumed to be homogeneous and its elements mix at random–seems reasonable to model pathogen transmission for airborne disease like influenza, but it seems equivocated for sexually transmitted diseases4. Recent studies using household data shows that the random-mixing hypothesis can produce reliable predictions for households, even for heterogeneous contact networks5. In general, available empiric data and numerical simulations provide evidence that the disease spreading is largely affected by the heterogeneity of contact network of the population6–12.
Despite the significant advances obtained in the past few decades, several challenges remain open. One issue concerns the failure to account for effects unrelated to diseases themselves, such as vaccination skepticism, which ultimately reduces children immunization rate. Outbreaks of treatable communicable diseases, like measles, are on the rise13. Another issue deals with understanding the complex dynamics and processes behind infections in both small and large scales14–16. To put it simply, there are too many variables and their effects are not entirely known due to the non-linear nature of the problem. As a consequence, the full extent of variable changes or their fluctuations remains poorly understood, which may produce sub-optimal intervention strategies. As an example, detailed field data from the recent Ebola epidemic have shown that smaller outbreaks from different localities are asynchronous17. The lack of synchronization between different populations reduces the likelihood of pathogen eradication on a global scale, as long as migration is allowed in some form18,19. The effects of migration and spatial structures in epidemic models and pathogen variability have been under investigation for some time20,21, and they have been linked to chaotic dynamics in local population22. Experiments on the effects of migration between metapopulations, i.e. similar populations but spatially separated, subjected to temporal fluctuations have shown that pathogen prevalence is greatly influenced by the nature of the fluctuation23, highlighting the interplay between synchronization and pathogen prevalence in epidemics24.
Traditionally, the detailed examination of fluctuations–either temporal or spatial–and their effects on system dynamics have been largely described by correlation functions23,25. More recently, autocorrelation functions have been used to reveal the nature and general aspects of fluctuations in a simple agent-based epidemic model for a population of size N, in which temporal fluctuations are divided into two broad classes: gaussian and non-gaussian26. In the gaussian regime, the prevalence of the disease is well described by its instantaneous average, finite variance, and higher cumulants can be neglected. This is remarkable as it allows one to derive the exact contributions of fluctuations to disease outbreaks in the asymptotic limit N 1. Here, we show that the dynamical equations form a Hamiltonian dynamical system, and the way external noise can be incorporated to model disease outbreaks. This approach allows us to discuss quantitatively the relevant scales of the problem, and interpret the resulting Lagrangian and canonical transformations.
Model
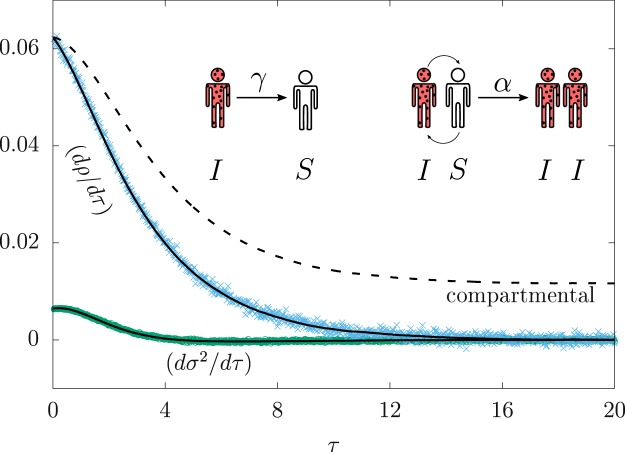
We begin our discussion using the susceptible-infectious-susceptible (SIS) epidemic model. The SIS model describes the dissemination of a single communicable disease in a susceptible population of size N. The transmission of the pathogen occurs when infectious hosts transmit the disease pathogen to healthy susceptible individuals. The infectious period extends throughout the whole course of the disease until the recovery of the patient, warranting a two-stage model: either infected or susceptible. The essence of the model is summarized by inset in Fig. 1.
Figure 1.
Numerical simulations of the SIS model. (inset) Infected hosts (I) recover to susceptible state (S) with rate γ (left). The adequate interaction between an infected host with a susceptible one may trigger a new infection, with rate α (right). Stochastic effects are far more relevant for small population sizes (N = 50, γ/α = 1/2), reducing the accuracy of compartmental equations. The forward-derivative dρ/dτ from data (cross) agrees with Eq. (5a) (solid line), while the compartmental equation Eq. (1) fails to reproduce the data (dashed line). The forward-derivative dσ2/dτ from data (circles) also agrees with the formula in Eq. (5b) (line). All the lines are drawn using the simulated data for 〈ρ(τ)〉, σ2(τ), and Δ3(τ).
The traditional formulation of the problem assumes the random-mixing hypothesis (see Introduction) holds for a large population size N1, compromised of statistically equivalent individuals. Under these circumstances, the only relevant variable is the instantaneous density of infected elements ρ(t), which means that fluctuations can be safely neglected. Furthermore, ρ(t) decreases with rate γρ, where γ is the recovery rate. New infections per unit of time (disease incidence) are proportional to αρ(1 − ρ), i.e., they depend on the chance that infected elements interact with susceptible ones, with intensity given by the transmission rate α. This picture provides an interpretation where ρ(t) is continuously exchanged between two compartments, leading a simple description called compartmental equation: dρ(t)/dt = αρ(1 − ρ) − γρ. For the sake of convenience, redefine the timescale as τ ≡ αt and ρ0 ≡ 1 − γ/α, so that
| 1 |
Clearly, the equilibrium density can either be ρeq = 0 or ρeq = ρ0. Also, ρ0 is related to the basic reproduction number R0 = N(α/γ) which provides an estimate on the number of new infections per generation27.
In light of its long age, compartmental equations have met considerable success in predicting the time evolution of disease outbreaks, providing valuable insights for intervention strategies and funding allocation28. However, outbreaks that fail to meet the underlying hypotheses (random mixing and large population of statistically equivalent elements) can contradict compartmental equations. These inconsistencies are largely attributed to stochastic effects and their inherent fluctuations2.
Improved Compartmental Equations
Stochastic variables are known to cause the emergence of critical phenomena in computer simulations of epidemic models, under certain parameter ranges29,30. One key ingredient common to critical phenomena is the scale invariance of fluctuations. This special symmetry remains the foundation of cooperative phenomena and critical phase transitions, whose contributions span over a broad set of research fields such as condensed-matter, quantum field theories, and neuroscience to name a few31–36. In these systems, fluctuations occur in all sizes and dictate the general behavior of the problem, which prompts for in-depth studies of their effects in epidemic models.
Stochastic epidemic models include non-deterministic events that intrinsically occurs during the course of the disease spreading process. Examples of these events include the transmission of the pathogen, and the elapsed time required for the complete recovery of patients. The inclusion of these effects brings the models closer to more realistic expectations, which in turn can deviate from predictions using compartmental equations37–39. One prime example is the effects of the absorbing state in the SIS model, which has been examined in detail by Nåsell and others40–42. New experiments on this subject provide evidence that temporal fluctuations can drastically alter the prevalence of pathogens23. Spatial heterogeneity also introduces an extra layer of complexity as it may trap or delay the pathogen transmission20. As a result, the requirements of statistical equivalence may not hold for all scales. To deal with this issue, stochastic formulations and numerical simulations have been the default tools to investigate fluctuations in disease outbreaks. In what follows, we outline the general ideas behind the agent-based approach to describe the SIS model. A more detailed account of the results listed here are explained in detail in refs26,43,44.
Our discussion assumes the disease spreading follows a Markov chain in discrete time δt. Moreover, δt is such that at most a single recovery or transmission event is likely to occur during the course of its duration. Under these requirements, the master equation of the SIS model in discrete time reads
| 2 |
Here, Pμ(t) refers to the instantaneous probability to observe the system in the μ-th configuration. Configuration labels follow the binary ruling , where nk = 1 if the k-th agent is infected, or nk = 0 otherwise, with k = 0, 1, …, N − 1. For instance, for N = 3, the configuration |μ = 3〉 = |110〉 states that only the agent with label k = 2 is susceptible. The matrix elements Hμν express the transition rates from configuration ν to configuration μ. By virtue of probability conservation, in each time step the transition rules satisfy . The matrix elements are computed from projections on the time step operator
| 3 |
where is the adjacency matrix, represents the k-th occupation operator (with eigenvalues nk = 1 if infected, 0 otherwise), and are the localized spin-1/2 ladder operators that produce the transition S → I. Clearly, produce the opposite transitions, I → S in relation the k-th agent. As notation, the hat symbol always accompanies operators to quickly distinguish them from numbers.
The master equation Eq. (2) provides the means to evaluate the time evolution of relevant statistical moments of ρ(t). Notice that the average density of infected agents in the system reads
| 4 |
Applying the time derivative, and using Eq. (2), one arrives at the equation of motion for 〈ρ(t)〉. Useful expressions are known only for a few types of adjacency matrix A. The simplest one is the complete graph , which recovers the random mixing hypothesis. In those particular instances, the complete time evolution of the system comprehends a set of hierarchical equations that involves the statistical moments of ρ(t), as shown in refs. 43,45. More explicitly45, the first two equations for instantaneous mean 〈ρ〉 and variance σ2 = 〈ρ2〉 − 〈ρ〉2 are
| 5a |
| 5b |
where Δ3(τ) = 〈ρ3(τ)〉 − 〈ρ(τ)〉3. These results find excellent agreement with simulated data using an ensemble with 106 replicas starting from the same initial condition (see Fig. 1).
Comparing Eqs (1) and (5), the case that considers temporal fluctuations decays faster than the compartmental equation by σ2(τ), even in the regime . Both equations are equivalent whenever σ(τ) becomes irrelevant compared to 〈ρ〉. Therefore, a generalization of compartmental equations for the SIS model is readily available by retaining both mean and variance, neglecting higher statistical moments. Thus, the dynamical system describes a gaussian variable evolving along time. The skewness coefficient vanishes as a direct consequence of this assumption, so that Δ3(τ) ≈ 3〈ρ(τ)〉σ2(τ). For , the resulting equations are
| 6a |
| 6b |
We emphasize that the variance in Eq. (6a) slows down the growth rate of 〈ρ(τ)〉, recalling the Allee effect28,46.
The dynamical system represented by Eq. (6) can also be obtained from a stochastic expansion following the guidelines in ref.47. In this case, assume the density ρ = 〈ρ〉 + η is well described by its instantaneous average plus some noise function η(τ). We assume 〈η〉 = 0 and 〈η2〉 = σ2(τ) for the sake of consistency. The additional requirement ensures stochastic effects act as perturbations. Expanding Eq. (1) as a Taylor series around ρ = 〈ρ〉, and then taking the ensemble average, produces
| 7 |
where g(ρ) = ρ(ρ0 − ρ). Since 〈η〉 vanishes, the expansion recovers Eq. (6a) up to o(η4). The task to obtain the equation of motion of σ2 is greatly simplified by noting that
| 8 |
Taking the ensemble average, one obtains (1/2)(d/dt)lnσ2 = [ρ0 − 2〈ρ〉] − 〈η3〉/σ2. Now, since η mimics a gaussian variable, 〈η3〉 = 0 and Eq. (6b) is recovered as well.
Equation (6) can be further combined into a single second-order differential equation26, with solution
| 9a |
| 9b |
The constants c1 and c2 depend solely on the initial conditions. The special case recovers the usual solution of Eq. (1). We assumed that fluctuations behave as gaussian fluctuations. While reasonable for various situations, the assumption does not hold for γ/α around unity or small population sizes, according to numerical simulations26, in which Eq. (5b) should be used instead of Eq. (6b). For the sake of completeness, there is another solution in which σ2(τ) = 〈ρ(τ)〉2, with.
Hamilton Equations
The fact that the dynamical system Eq. (6) can be combined into a single second-order differential equation suggests an interpretation of the epidemic model in terms of Hamilton equations48. Hamiltonian systems are ubiquitous in Physics, serving as basis to describe and explain countless physical phenomena. The hallmark of systems are the Hamilton equations:
| 10a |
| 10b |
where q(t) and p(t) are conjugated variables, and the Hamiltonian function encodes some information about the problem–usually associated with energy for conservative systems but not restricted to them. Besides classical mechanics and related areas, quantum field theories and statistical mechanics are deeply intertwined with Hamilton’s principle and Liouville theorem. Despite its usefulness in Physics, Hamilton formulation and surrounding principles are rarely used in population dynamics, ecological problems, or epidemic models, where first-order differential equations are dominant. The lack of second-order differential equations in these areas, although not prohibitive, raises questions about the description of the dynamics, as discussed extensively in ref. 49. In part, because it means some interactions and stochastic effects acting on the system remain unaccounted. Significant advances in the Hamiltonian formulation of stochastic epidemic models have been obtained using the eikonal approximation, with emphasis on the disease extinction and vaccination50,51. Generalizations for heterogeneous networks have also been investigated, providing improved control strategies52,53. Even more, the aforementioned Hamiltonian formulation explains other effects, such as the emergence of noise-induced metastable states54. The crucial ingredient of these studies concerns the eikonal approximation, in which either the generating function or the density of infected is written as the exponential of the classical action of the system55. For populations with fixed size, one variable describes 〈ρ(t)〉, while its conjugate variable encompasses fluctuations52. However, the description of epidemics using this conjugate pair remains a complex task because the conjugate variable is not directly related to familiar statistics such as the standard deviation or variance. In what follows, instead of using the eikonal approach, we argue that Hamilton dynamics for the stochastic SIS model can be constructed from 〈ρ(τ)〉 and σ(τ).
In view of the inherent stochasticity behind disease spreading, it seems necessary to determine whether Eq. (6) form a Hamiltonian system or not. A brief inspection shows the pair (〈ρ〉, σ2) does not satisfy the usual Hamilton equations. The solution to this issue is obtained by assuming, instead, that the correct conjugated pair is (〈ρ〉, h(σ2)), where h(x) is some analytical function. Inspiration from common pairs of conjugate variables can be used to refine the choice of h(x). For instance, the product 〈ρ〉 × h(σ2) should be dimensionless, in close analogy the scalar product between position and wave vectors. One possible candidate is h(x) = x−1/2, which entails 1/σ as the conjugated variable to 〈ρ〉.
Define the dynamical variables q(τ) = 〈ρ(τ)〉 and p(τ) = 1/σ(τ) to describe the SIS model. In addition, consider the following Hamiltonian
| 11 |
Plugging these expressions in Eq. (10), one obtains the equations of motion:
| 12a |
| 12b |
Thus, at first glance appears to be a valid candidate to describe the SIS model. Even more, replacing (q, p) by Eq. (9) in Eq. (11) shows that the Hamiltonian is a constant of motion . The upper index in is a reminder that calculations take place in the absence of finite size corrections.
However, taking finite size corrections into account changes drastically the notion of as a constant of motion. In fact, as Fig. 2 depicts, numerical simulations for finite populations reveal changes continuously along time until equilibrium sets in, akin to a non-conservative system. The precise meaning of in the epidemiological context is still murky, at best. A detailed analysis of correlations between changes in and the spreading pattern of real outbreaks is mandatory to understand the action-reaction analogy. In the meantime, it is instructive to study for τ ≪ 1 and τ ≫ 1 (see Fig. 2). For τ ≪ 1, where incidentally fluctuations vary the most (see Fig. 1), a remarkable feature appears via the relation with λ = 1/2. In particular, the exponent λ seems insensitive to changes in the epidemiological parameter γ. This parameter-free behavior is not observed for the remaining statistics, 〈ρ(τ)〉 and σ(τ). Power-laws are crucial to identify scaling relations and the emergence of universal features, and they are usually related to the symmetry of the problem rather than microscopic details. Here, evidence of universal behavior is captured by the data collapse (Fig. 2a inset). From these observations, we can infer fluctuations play a larger role in the early disease spreading, being largely independent of exact values of epidemiological parameters.
Figure 2.
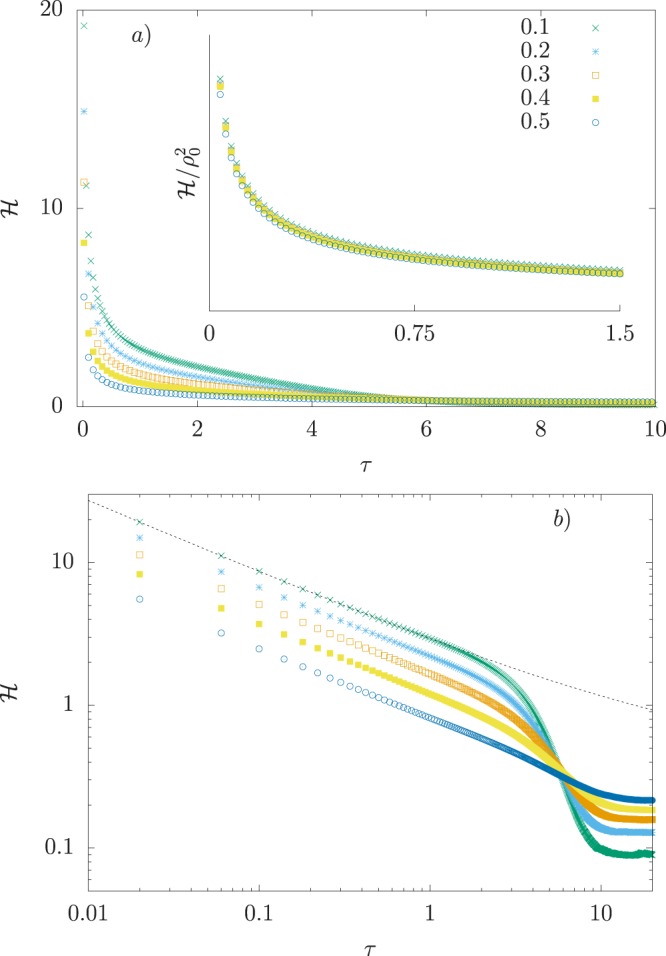
Finite size effects on the Hamiltonian. (a) Simulated data with N = 50 and 106 Monte Carlo runs for various ratios γ/α. (inset) Data collapse using the scaling factor ρ02, suggesting an universal behavior at the beginning of the outbreak. (b) Initial decay of compatible with power-law, . The exponent λ = 1/2 remains constant for different ratios γ/α, suggesting an universal behavior.
An effective decay describes the general behavior of away from the outbreak onset. The relaxation time τeff depends on N and the ratio γ/α, and it can be estimated from data by fitting to an exponential function plus a constant. Alternatively, it can be evaluated as
| 13 |
From a formal point of view, the evaluation of τeff requires the solutions of Eqs (5a) and (5b) in Eq. (11), followed by an integration. Surely, the procedure is arguably more demanding than estimating R0. However, as others have reasoned before, R0 provides a naive estimation on secondary infections because the growth rate of the outbreak changes continuously along time56. In contrast, τeff mimics a constant of motion.
Lagrangian and Canonical Transformations
Another insight from τeff links the temporal integral of with the mechanical action S. A formal connection with S is desirable because it brings a large machinery revolving around variational principles and conservation laws. However, the action is a functional of the Lagrangian . It turns out that can obtained from by inspection. From Eqs (15) and (7), takes the following form: . Recalling the formal expression , it becomes clear that
| 14 |
where we have used Eq. (6a) and considered only the positive root. Thus, is proportional to the standard deviation while the action entails the accumulated deviation over the course of the outbreak. To check our result for large populations , the minimal action recovers Eq. (1) as expected for a noise-free system. In general, the equation of motion reads
| 15 |
The fact that contains solely the standard deviation allows us to understand how to add uncorrelated fluctuations into the model. By virtue of Var[x + y] = Var[x] + Var[y] for uncorrelated random variables x and y, the perturbed Lagrangian can be obtained by adding a σext2(τ) to the variance of the system σ2(τ):
| 16 |
This picture is consistent with addition of a noise function σext2(τ) to Eq. (6a). The perturbed Lagrangian describes, ultimately, the time evolution of the disease prevalence in environments with noise. Note that this description differs from the usual derivation of Langevin equations, in which the noise function (force) r(τ) couples linearly with q, i.e., . By the same token, the addition of correlated signals η(τ) to the Lagrangian entails corrections from the covariance matrix: since Var[X + Y] = Var[X] + Var[Y] + 2Cov[X, Y], then . The covariance matrix can estimated or modeled directly from data, promoting further understanding on the spreading of co-existing diseases, where facilitation or competition processes are in place.
With both Hamiltonian and Lagrangian formalisms secured, canonical transformations become available. These transformations are particularly useful to highlight properties of the dynamical systems and to solve them. They change the old variables (q, p) into new variables (Q, P), while preserving Hamilton’s equations. There are a large number of transformations available: it would render impossible to cover all of them here. Instead, we show that at least one canonical transformation exists, and that it promotes the interpretation of the stochastic spreading process as effective mechanical systems. Consider: P1(t) = 2p1/2q and Q1(t) = −p1/2. The Poisson bracket {Q1, P1}q,p = (∂Q1/∂q)(∂P1/∂p) − (∂Q1/∂p)(∂P1/∂q) = 1 shows the transformation is canonical. Setting m = 2, the Hamiltonian in terms of the canonical variables (Q1, P1) becomes
| 17 |
One may interpret as the Hamiltonian of an effective mechanical problem in one-dimension, in which the particle has mechanical momentum P1(τ), with generalized coordinate Q1(τ), subjected to a velocity dependent potential.
Conclusion
The description of several real-world problems often includes stochastic fluctuations. The SIS epidemic model includes them due to uncertainties associated with pathogen transmission. For small fluctuation amplitudes, 〈ρ(τ)〉 and σ2(τ) are adequate descriptors. Our findings demonstrate 〈ρ(τ)〉 and 1/σ(τ) are conjugated variables, and they satisfy Hamilton’s equation. These results link the stochastic SIS epidemic model with a pure dynamical system, which can be solved and manipulated using standard analytical tools. We find the Hamiltonian is a constant of motion for N 1. However, finite size effects break the temporal symmetry of the system: follows a power-law around the outbreak onset. A clear explanation for this scaling is still lacking. The relaxation time τeff portrays the decay of until equilibrium sets in, meaning that it can also be used to characterize the SIS epidemic. Unlike popular estimates of epidemic growth rate, τeff remains constant along time and can be extracted from data values of . Finally, our results also suggest a way to incorporate interactions into the SIS model via the Lagrangian function. This finding has intriguing implications for our understanding of facilitation-competition mechanisms between co-occurring diseases since it does not replicate the canonical procedure to obtain Langevin equations.
Acknowledgements
The authors acknowledge funding from CNPq 309851/2018-1 and Capes 88882.317630/2019-01.
Author contributions
G.M.N. wrote the paper, performed research, and executed numerical simulations; A.S.M. edited the paper and designed the research. All authors reviewed the manuscript.
Data availability
Numerical codes, simulation data and data descriptors are available at 10.17605/OSF.IO/WFCEP.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc. Royal Soc. A. 1927;115:700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 2.Heesterbeek H., Anderson R. M., Andreasen V., Bansal S., De Angelis D., Dye C., Eames K. T. D., Edmunds W. J., Frost S. D. W., Funk S., Hollingsworth T. D., House T., Isham V., Klepac P., Lessler J., Lloyd-Smith J. O., Metcalf C. J. E., Mollison D., Pellis L., Pulliam J. R. C., Roberts M. G., Viboud C. Modeling infectious disease dynamics in the complex landscape of global health. Science. 2015;347(6227):aaa4339–aaa4339. doi: 10.1126/science.aaa4339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015;87:925–979. doi: 10.1103/RevModPhys.87.925. [DOI] [Google Scholar]
- 4.Keeling M, Eames K. Networks and epidemic models. J. Royal Soc. Interface. 2005;2:295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Goeyvaerts N, et al. Household members do not contact each other at random: implications for infectious disease modelling. Proc. Royal Soc. B. 2018;285:20182201. doi: 10.1098/rspb.2018.2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200–3203. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 7.Eames KTD, Keeling MJ. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl. Acad. Sci. USA. 2002;99:13330–13335. doi: 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Keeling M. The implications of network structure for epidemic dynamics. Theor. Popul. Biol. 2005;67:1–8. doi: 10.1016/j.tpb.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 9.Newman MEJ. The structure and function of complex networks. SIAM Rev. 2003;45:167–256. doi: 10.1137/S003614450342480. [DOI] [Google Scholar]
- 10.Bansal S, Grenfell BT, Meyers LA. When individual behaviour matters: homogeneous and network models in epidemiology. J. Royal Soc. Interface. 2007;4:879–891. doi: 10.1098/rsif.2007.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Durrett R. Some features of the spread of epidemics and information on a random graph. Proc. Natl. Acad. Sci. USA. 2010;107:4491–4498. doi: 10.1073/pnas.0914402107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang H, et al. Effect of the interconnected network structure on the epidemic threshold. Phys. Rev. E. 2013;88:022801. doi: 10.1103/PhysRevE.88.022801. [DOI] [PubMed] [Google Scholar]
- 13.Horne Z, Powell D, Hummel JE, Holyoak KJ. Countering antivaccination attitudes. Proc. Natl. Acad. Sci. USA. 2015;112:10321–10324. doi: 10.1073/pnas.1504019112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roberts Mick, Andreasen Viggo, Lloyd Alun, Pellis Lorenzo. Nine challenges for deterministic epidemic models. Epidemics. 2015;10:49–53. doi: 10.1016/j.epidem.2014.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Britton Tom, House Thomas, Lloyd Alun L., Mollison Denis, Riley Steven, Trapman Pieter. Five challenges for stochastic epidemic models involving global transmission. Epidemics. 2015;10:54–57. doi: 10.1016/j.epidem.2014.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pellis Lorenzo, Ball Frank, Bansal Shweta, Eames Ken, House Thomas, Isham Valerie, Trapman Pieter. Eight challenges for network epidemic models. Epidemics. 2015;10:58–62. doi: 10.1016/j.epidem.2014.07.003. [DOI] [PubMed] [Google Scholar]
- 17.Chowell G, Sattenspiel L, Bansal S, Viboud C. Mathematical models to characterize early epidemic growth: A review. Phys. Life Rev. 2016;18:66–97. doi: 10.1016/j.plrev.2016.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ruxton GD. Low levels of immigration between chaotic populations can reduce system extinctions by inducing asynchronous regular cycles. Proc. Royal Soc. B. 1994;256:189–193. doi: 10.1098/rspb.1994.0069. [DOI] [Google Scholar]
- 19.Earn DJD, Rohani P, Grenfell BT. Persistence, chaos and synchrony in ecology and epidemiology. Proc. Royal Soc. B. 1998;265:7–10. doi: 10.1098/rspb.1998.0256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Real LA, Biek R. Spatial dynamics and genetics of infectious diseases on heterogeneous landscapes. J. Royal Soc. Interface. 2007;4:935–948. doi: 10.1098/rsif.2007.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hastings A. Timescales, dynamics, and ecological understanding. Ecol. 2010;91:3471–3480. doi: 10.1890/10-0776.1. [DOI] [PubMed] [Google Scholar]
- 22.Allen JC, Schaffer WM, Rosko D. Chaos reduces species extinction by amplifying local population noise. Nat. 1993;364:229. doi: 10.1038/364229a0. [DOI] [PubMed] [Google Scholar]
- 23.Duncan AB, Gonzalez A, Kaltz O. Stochastic environmental fluctuations drive epidemicology in experimental host-parasite metapopulations. Proc. Royal Soc. B. 2013;280:20131747. doi: 10.1098/rspb.2013.1747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Marguta R, Parisi A. Periodicity, synchronization and persistence in pre-vaccination measles. J. Royal Soc. Interface. 2016;13:20160258. doi: 10.1098/rsif.2016.0258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Cardy, J. L. Phase Transition and Critical Phenomena, vol. 11 (Academic Press, New York, 1987).
- 26. Nakamura, G., Cardoso, G. & Martinez, A. Robust parameter determination in epidemic models with analytical descriptions of uncertainties. arXiv e-prints arXiv:1807.05301 Preprint at, https://arxiv.org/abs/1807.05301v1 (2018).
- 27.Alves D, Haas V, Caliri A. The predictive power of r0 in an epidemic probabilistic system. J. Biol. Phys. 2003;29:63–75. doi: 10.1023/A:1022567418081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Murray, J. D. Mathematical Biology: an Introduction, vol. 1, 3rd edition edn (Springer, New York, 2002).
- 29.Rhodes C, Anderson R. Epidemic thresholds and vaccination in a lattice model of disease spread. Theor. Popul. Biol. 1997;52:101–118. doi: 10.1006/tpbi.1997.1323. [DOI] [PubMed] [Google Scholar]
- 30.Rhodes CJ, Jensen HJ, Anderson RM. On the critical behaviour of simple epidemics. Proc. Royal Soc. B. 1997;264:1639–1646. doi: 10.1098/rspb.1997.0228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wilson Kenneth G. Confinement of quarks. Physical Review D. 1974;10(8):2445–2459. doi: 10.1103/PhysRevD.10.2445. [DOI] [Google Scholar]
- 32.Kogut JB. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys. 1979;51:659–713. doi: 10.1103/RevModPhys.51.659. [DOI] [Google Scholar]
- 33.Egu´ıluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys. Rev. Lett. 2005;94:018102. doi: 10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- 34.Schneidman E, Berry MJ, II, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nat. 2006;440:1007. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Alcaraz FC, Nakamura GM. Phase diagram and spectral properties of a new exactly integrable spin-1 quantum chain. J. Phys. A: Math. Gen. 2010;43:155002. doi: 10.1088/1751-8113/43/15/155002. [DOI] [Google Scholar]
- 36.Meloni F, Nakamura GM, Granzotti CR, Martinez AS. Vegetation cover reveals the phase diagram of patch patterns in drylands. Phys. A. 2019;534:122048. doi: 10.1016/j.physa.2019.122048. [DOI] [Google Scholar]
- 37.Keeling MJ. Metapopulation moments: coupling, stochasticity and persistence. J. Animal Ecol. 2000;69:725–736. doi: 10.1046/j.1365-2656.2000.00430.x. [DOI] [PubMed] [Google Scholar]
- 38.Van Mieghem P, Cator E. Epidemics in networks with nodal self-infection and the epidemic threshold. Phys. Rev. E. 2012;86:016116. doi: 10.1103/PhysRevE.86.016116. [DOI] [PubMed] [Google Scholar]
- 39.Cator E, Van Mieghem P. Second-order mean-field susceptible-infected-susceptible epidemic threshold. Phys. Rev. E. 2012;85:056111. doi: 10.1103/PhysRevE.85.056111. [DOI] [PubMed] [Google Scholar]
- 40.Nåsell I. The quasi-stationary distribution of the closed endemic sis model. Adv. Appl. Prob. 1996;28:895–932. doi: 10.2307/1428186. [DOI] [Google Scholar]
- 41.Nåsell I. On the time to extinction in recurrent epidemics. J. Royal Stat. Soc. B. 1999;61:309–330. doi: 10.1111/1467-9868.00178. [DOI] [Google Scholar]
- 42.Nåsell I. Extinction and quasi-stationarity in the verhulst logistic model. J. Theor. Biol. 2001;211:11–27. doi: 10.1006/jtbi.2001.2328. [DOI] [PubMed] [Google Scholar]
- 43.Nakamura GM, Monteiro ACP, Cardoso GC, Martinez AS. Efficient method for comprehensive computation of agent-level epidemic dissemination in networks. Sci. Rep. 2017;7:40885. doi: 10.1038/srep40885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nakamura Gilberto M., Monteiro Ana Carolina P., Cardoso George C., Martinez Alexandre S. Finite Symmetries in Agent-Based Epidemic Models. Mathematical and Computational Applications. 2019;24(2):44. doi: 10.3390/mca24020044. [DOI] [Google Scholar]
- 45.Kiss IZ, Simon PL. New moment closures based on a priori distributions with applications to epidemic dynamics. Bull. Math. Biol. 2012;74:1501–1515. doi: 10.1007/s11538-012-9723-3. [DOI] [PubMed] [Google Scholar]
- 46.dos Santos RV, Ribeiro FL, Martinez AS. Models for allee effect based on physical principles. J. Theor. Biol. 2015;385:143–152. doi: 10.1016/j.jtbi.2015.08.018. [DOI] [PubMed] [Google Scholar]
- 47.Vilar JMG, Rubi JM. Determinants of population responses to environmental fluctuations. Sci. Rep. 2018;8:887. doi: 10.1038/s41598-017-18976-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Goldstein, H. Classical mechanics (Addison-Wesley, 1950).
- 49.Chester Marvin. A law of nature? Open Journal of Ecology. 2011;01(03):77–84. doi: 10.4236/oje.2011.13011. [DOI] [Google Scholar]
- 50.Kamenev A, Meerson B. Extinction of an infectious disease: A large fluctuation in a nonequilibrium system. Phys. Rev. E. 2008;77:061107. doi: 10.1103/PhysRevE.77.061107. [DOI] [PubMed] [Google Scholar]
- 51.Dykman MI, Schwartz IB, Landsman AS. Disease extinction in the presence of random vaccination. Phys. Rev. Lett. 2008;101:078101. doi: 10.1103/PhysRevLett.101.078101. [DOI] [PubMed] [Google Scholar]
- 52.Hindes J, Schwartz IB. Epidemic extinction and control in heterogeneous networks. Phys. Rev. Lett. 2016;117:028302. doi: 10.1103/PhysRevLett.117.028302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hindes J, Schwartz IB. Epidemic extinction paths in complex networks. Phys. Rev. E. 2017;95:052317. doi: 10.1103/PhysRevE.95.052317. [DOI] [PubMed] [Google Scholar]
- 54.Parker M, Kamenev A, Meerson B. Noise-induced stabilization in population dynamics. Phys. Rev. Lett. 2011;107:180603. doi: 10.1103/PhysRevLett.107.180603. [DOI] [PubMed] [Google Scholar]
- 55.Schwartz IB, Billings L, Dykman M, Landsman A. Predicting extinction rates in stochastic epidemic models. J. Stat. Mech.: Theory Exp. 2009;2009:P01005. doi: 10.1088/1742-5468/2009/01/p01005. [DOI] [Google Scholar]
- 56.Heffernan J, Smith R, Wahl L. Perspectives on the basic reproductive ratio. J. Royal Soc. Interface. 2005;2:281–293. doi: 10.1098/rsif.2005.0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Numerical codes, simulation data and data descriptors are available at 10.17605/OSF.IO/WFCEP.