Fundamental helical geometry consolidates the plant photosynthetic membrane

Significance

The intricate structure of the membrane network that hosts the primary steps of photosynthesis in plant chloroplasts has intrigued scientists for decades. Here, we used electron tomography to determine this structure. We found that the network is consolidated by arrays of right- and left-handed helical structures. Similar arrangements of pitch-balanced helical elements of alternating handedness were proposed to be present in the endoplasmic reticulum and, remarkably, in ultradense nuclear matter. These arrays thus likely represent a universal means to connect between densely packed layers or sheets.

Abstract

Plant photosynthetic (thylakoid) membranes are organized into complex networks that are differentiated into 2 distinct morphological and functional domains called grana and stroma lamellae. How the 2 domains join to form a continuous lamellar system has been the subject of numerous studies since the mid-1950s. Using different electron tomography techniques, we found that the grana and stroma lamellae are connected by an array of pitch-balanced right- and left-handed helical membrane surfaces of different radii and pitch. Consistent with theoretical predictions, this arrangement is shown to minimize the surface and bending energies of the membranes. Related configurations were proposed to be present in the rough endoplasmic reticulum and in dense nuclear matter phases theorized to exist in neutron star crusts, where the right- and left-handed helical elements differ only in their handedness. Pitch-balanced helical elements of alternating handedness may thus constitute a fundamental geometry for the efficient packing of connected layers or sheets.

The shape of biological objects is essential for their function. One of the most complex structures found in cells is the extensive network of flattened vesicles, called thylakoids (1, 2), that accommodate the primary steps of oxygenic photosynthesis in the chloroplasts of vascular plants and some green algae (3, 4). In these species, the thylakoid network consists of 2 domains that possess distinct morphological, compositional, and functional characteristics: grana, cylindrical stacks comprising multiple thylakoid discs tightly packed on top of each other, and stroma lamellae, unstacked thylakoids that interconnect the grana (Fig. 1A and refs. 3–5). Together, these 2 domains form an elaborate, continuous 3-dimensional (3D) membrane system that occupies a large fraction of the chloroplast volume (6, 7). The unique, bipartite organization of the plant thylakoid membrane has been proposed to serve various mechanistic and regulatory functions which likely played an important role in the evolution of terrestrial plants (4, 8–11).

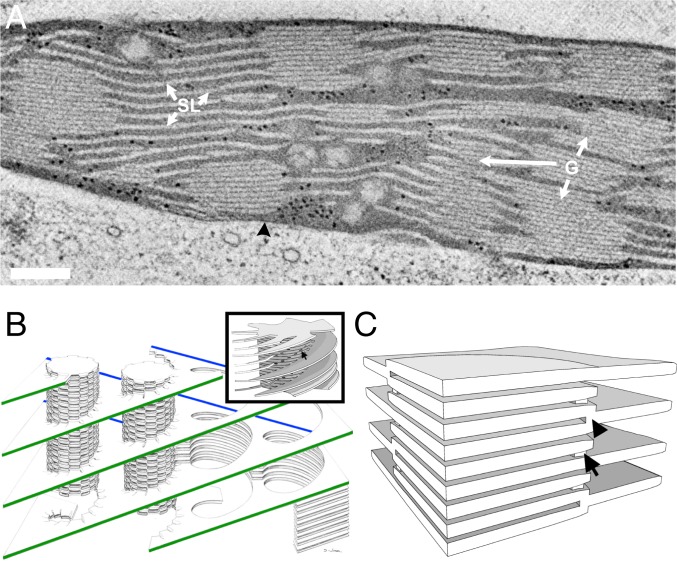
Fig. 1.

Models of the plant thylakoid membrane. (A) A 10-nm-thick STEM tomographic slice of lettuce chloroplast. The grana stacks (G) are interconnected by unstacked stroma thylakoids (SL). Both membrane domains are immersed in an aqueous matrix, called stroma, which in turn is bordered by the chloroplast envelope (black arrowhead). (Scale bar, 200 nm.) (B) The helical model. The stroma lamellae wrap around the grana as right-handed helices, connecting to the thylakoids within the stack through slit-like apertures located at the rim of the stacks. A single file of grana is shown, with its oppositely sloped long edges marked in green and blue. Reprinted with permission from ref. 21. (Inset) A model of a granum–stroma assembly, configured akin to the helical model, composed of a granum core surrounded by multiple helical frets. The arrow marks a slit at the edge of the granum. Adapted by permission from ref. 75, Springer Nature: Plant Molecular Biology, copyright 2011. (C) The bifurcation model. The grana stacks are formed by bifurcations of the stroma lamellae (black arrowhead). Neighboring discs in the stacks are additionally connected by internal membrane bridges located near the bifurcation sites at the grana periphery (arrow).

Studies of plant chloroplasts began in the 19th century with the aid of the optical microscope (12–14). These were followed by various electron microscopy (EM) investigations which commenced upon the introduction of the electron microscope in the late 1930s (15, 16). Based on the EM investigations, several models have been proposed for the 3D organization of the thylakoid membranes within the chloroplast (17–25; reviewed in refs. 3 and 4). The most prevalent of these is the so-called helical model (or helical fretwork model), which was formulated by Paolillo and coworkers during the second half of the 1960s (21, 22, 26) based on serial thin-section analyses and previous models proposed by Heslop-Harrison (18) and Wehrmeyer (24). The model holds that each granum is surrounded by multiple stroma lamellae that are wound around it in a right-handed helical fashion and are connected to the granum thylakoids through narrow slits located at the rim of the stack (Fig. 1B). Subsequent serial-section EM (27) and freeze-fracture (28) studies, graphic-based modeling (29), and, more recently, electron tomography analyses of isolated thylakoids (30–32) and chloroplasts (33) have supported the organization proposed by the helical model. However, as we show in this work, a 2D collection of such interconnected homochiral helical elements cannot maintain its planar orientation and will result in inevitable long-range twisting of the membranes (see Fig. 5 and SI Appendix, Fig. S8).

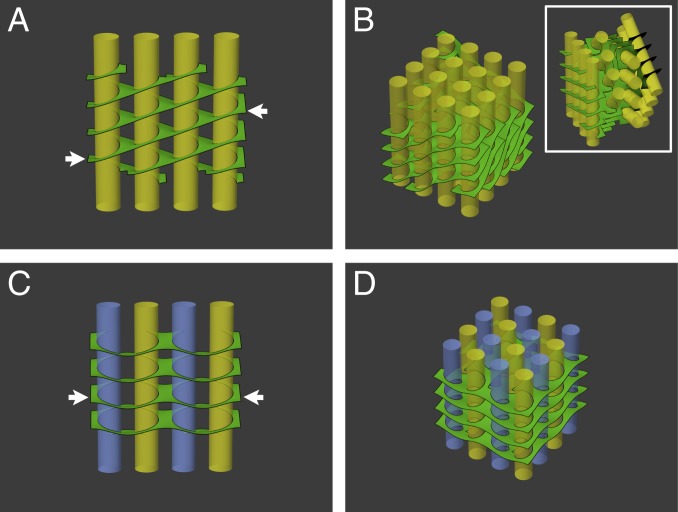
Fig. 5.

Surface energy minimization of networks assembled from various arrangements of helical elements. (A) Surface area minimization of a single file of grana (yellow) surrounded by right-handed helical structures, akin to the helical model (Fig. 1B), results in oppositely sloped long edges of the lamellar sheets (arrows). Extension of A to 2D arrays of grana columns requires either significant bending and twisting of the lamellae (B) or rigid, successive rotations of the grana files to match the orientation of their lamellar boundaries (B, Inset). (C) A single file of grana surrounded by alternating right- and left-handed helical membrane elements (indicated respectively by yellow and blue grana columns). The slope of the lamellar sheets at the boundary of the file is reduced to zero (compare arrows in A and C). (D) Extension of C to 2D arrays, with alternating handedness of the helical elements both between and within files, as observed experimentally, preserves the coorientation of the grana columns and allows the stroma lamellae to remain orthogonal to the grana cylinders.

Interestingly, the first electron tomography study of plant thylakoid membranes (34) led to a model that differed qualitatively from the helical model. According to this model, referred to as the “bifurcation model,” the stroma lamellae run largely perpendicular to the grana columns and bifurcate at the edges of the grana, seamlessly merging with the thylakoids in the stacks (Fig. 1C). Membrane bridges, located at the rim of the stacks, transversely join consecutive granum discs, stabilizing the stacks and increasing their connectivity. Bifurcation or “forking” of stroma lamellae at the grana margins has frequently been observed (17–19, 35, 36), including in recent electron tomography studies (30, 32, 33). Splits or branches have likewise been observed in developing thylakoid networks, both in monocots (27) and dicots (37), as well as in cyanobacterial thylakoid membranes (38, 39) and in the eukaryotic green alga Chlamydomonas reinhardtii (40). The bifurcation model, however, fails to incorporate the right-handed helical structures formed by the stroma lamellae around the grana, as reported by others.

What, then, is the structure of the plant thylakoid membrane?

Here, we employed transmission EM (TEM), scanning TEM (STEM), and focused ion beam scanning EM (FIB-SEM) tomography to reconstruct and model large chloroplastic volumes from high-pressure frozen, freeze-substituted leaf samples. The 3D models generated by segmentation, some of which comprise tens of grana and interconnecting stroma lamellae, reveal that the plant thylakoid membrane has a structure which is much more complex than that presented by either the helical- or the bifurcation model, and in fact combines elements from both. A notable feature of our model is the formation, by the bifurcations, of left-handed helical surfaces at the interface between the lamellar sheets and the right-handed helices that surround the grana. Theoretical modeling using surface area minimization reveals that these elements alleviate stresses that would otherwise be present and cause the network to deform from its planar conformation.

Results

Electron Tomography.

All tomograms were obtained from dark-adapted lettuce leaves subjected to high-pressure freezing followed by freeze-substitution and resin embedding (34, 37, 41, 42). We have shown previously that thylakoid membrane ultrastructure and organization in samples prepared by this method closely match those observed in vitreous leaf sections by cryo-TEM (43). The analysis comprised a total of 9 tomograms: 4 serial-section (∼250 nm thick each) tomograms obtained by dual-axis TEM tomography (34), 4 tomograms acquired by dual-axis STEM tomography on 500- to 700-nm-thick sections, and a tomogram acquired by serial-view SEM imaging of FIB-milled surfaces amounting to a total thickness of ∼3 µm. The reconstructed volumes that were segmented and modeled were between ∼1.5 and 4 µm³, for each of the TEM/STEM tomograms, and over 30 µm³ for the FIB-SEM tomogram. STEM-based tomography allows analyzing thicker sections as compared to TEM-based tomography (44). FIB-SEM provides a means to reconstruct significantly larger volumes, albeit at a lower resolution than the S/TEM. Nonetheless, the lower resolution of the FIB-SEM data did not compromise discerning and segmenting the main features of interest within the thylakoid membrane network, and at the same time provided a continuous overall view of a large volume of the chloroplast, complementing the S/TEM data.

Overall Network Architecture.

Fig. 2A presents a 3D tomographic model of the thylakoid membrane, along with representative slices through the reconstructed volumes (Fig. 2 C and D; see also Movie S1 of the model being sliced). Two additional large-scale 3D models are shown in SI Appendix, Fig. S1 A and B (an embedded 3D figure of the model from SI Appendix, Fig. S1A is provided in SI Appendix, Fig. S2). Overall, the networks have a regular structure composed of 2 interconnected components, grana and stroma lamellae, readily distinguishable from one another. The grana, which constitute the appressed thylakoid domains, are not evenly spaced within the chloroplast volume but rather are assembled into roughly parallel columns, each comprising several stacks (Fig. 2B and SI Appendix, Fig. S2 A and C–E). Individual grana measure ∼300 nm (278 ± 43 [mean ± SD], n = 68) in diameter and 160 nm (159 ± 94, n = 52) in height. The number of thylakoids in the grana varies between 3 and 19, averaging 9.0 ± 5.4 (n = 70). The narrower distribution of grana diameters, as compared to their height (which varies primarily with the number of thylakoids in the stacks), is in accordance with the observation that grana diameter is quite conserved, including between species (45). By contrast, the number of thylakoids in the stacks is known to be more variable, changing significantly between species as well as with light conditions (10, 46, 47). The centers of the stacked grana comprising the columns are not perfectly aligned along the vertical stacking axis, resulting in a slightly staggered arrangement that increases the absorption cross-section of the columns. The assembly into stacks and columns requires that the individual grana possess a high degree of orientational order relative to each other, which they in fact have, with deviations from exact parallel alignment being typically less than 20° (SI Appendix, Fig. S3B). The column structure observed here in dark-adapted networks is reminiscent of the extensive grana stacks seen in shade plants and in plants grown under low light where they serve to maximize light absorption (48, 49). A parallel organization of the grana cylinders is expected to give rise to a regular membrane morphology (21), as is indeed observed.

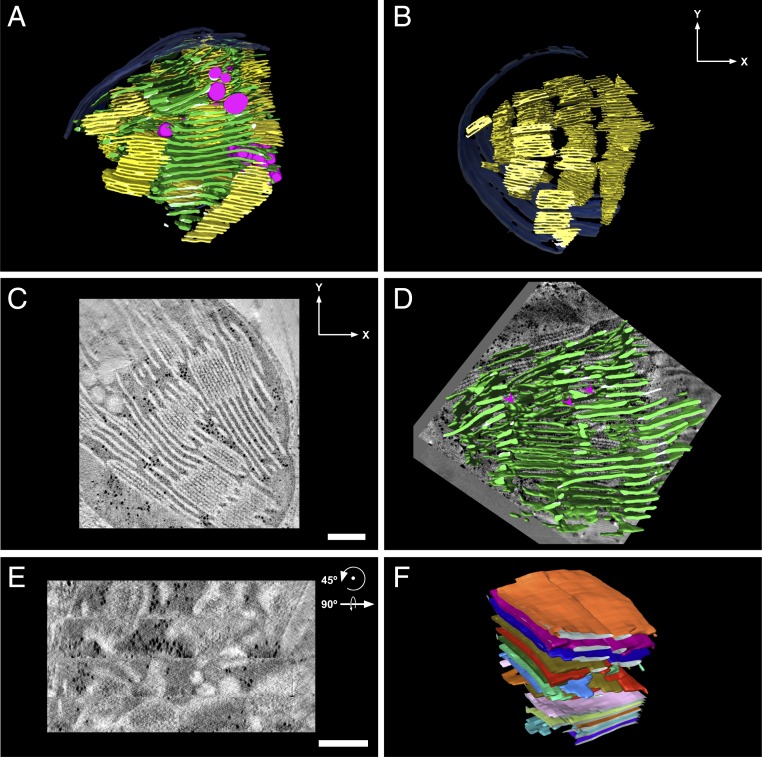
Fig. 2.

Overall network architecture and domain organization. (A) A 3D model of a dark-adapted lettuce thylakoid network generated by segmentation of a tomographic reconstruction by TEM. The grana and stroma thylakoids are colored yellow and green, respectively; the chloroplast envelope is shown in blue and the magenta-colored inclusions associated with the thylakoids are plastoglobules. (C and D) Tomographic slices ∼10 nm thick presented approximately perpendicular (C) and parallel (D) to the plane of the grana thylakoids. The 4 horizontal segments apparent in D correspond to the 4 serial sections that constitute the tomogram. Models showing (B) only grana stacks, to enable visualization of grana piling into columns, (E) only stroma lamellae (superimposed on a ∼10-nm-thick tomographic slice), to enable visualization of the sheets, cross-overs, and bifurcations, and (F) a group of stroma lamellar sheets with each individual sheet displayed in a different color, depicting the parallel organization of the sheets. (Scale bars, 250 nm.)

The second component of the network, the stroma lamellae, are organized in wide sheets that generally run perpendicular to the grana cylinders (or parallel to the plane of the thylakoids within the stacks; Fig. 2 and SI Appendix, Figs. S1 and S4) and parallel to each other. Exceptions are apparent mainly at the transition zones between the stroma lamellae and grana, where the former bend into right-handed helices that wind around the latter (discussed in the next section). The sheets have the same average thickness as the granum layers and are generally flat, exhibiting only small undulations for the most part. Bending of the stroma lamellar sheets along the contours of the chloroplast envelope, as well as occasional cross-overs and fusions between layers, are sometimes observed (Fig. 2D). The latter, which might be the consequence of localized defects introduced during the formation or growth of the lamellar system, act to increase the connectivity of the network and, as a result, its mechanical stability. Intersection of thylakoid layers is also observed in thylakoid membranes of cyanobacteria (4, 38, 39, 50) and eukaryotic algae, including Chlamydomonas (40) and Phaeodactylum (51), where they likely serve a similar function (3, 4).

Right-Handed Stroma Lamellar Helices around the Grana.

We now zoom into the basic unit of the network—the granum-stroma assembly. According to the helical model, these 2 domains connect through wrapping of the stroma lamellae around the granum bodies (21, 22, 26, 27, 29–33). (The lamellar structures that spiral around the grana actually form helical surfaces that intersect the grana columns along linear helical trajectories [helices]. However, for the sake of consistency with the literature, we will adhere to the term “helices” also when referring to these structures.) Fig. 3 and SI Appendix, Fig. S5 present an assortment of such structures in different assemblies, containing 1, 2, or several grana stacks, each surrounded by multiple, sequential, right-handed helices (see Fig. 3D where individual helices are shown in different colors). The helices wind around the grana cylinders more or less uniformly, running roughly parallel to, and evenly spaced from, each other, with adjacent frets separated on average by 45.8 ± 5.8 nm (n = 69; Fig. 3D). The tilt angle of the helices is conserved, averaging 15.9 ± 2.5° (n = 60), and is smaller than the values reported previously (typically, 20° to 25°; refs. 21, 22, 27, 31, and 33). This may reflect differences in sample preparation, species, and/or illumination conditions during growth or sampling. Tilting of the stroma lamellae relative to the grana stacks begins some 40 to 60 nm (averaging 51.9 ± 11.5 nm [n = 87]) away from the grana edges (Fig. 3B), beyond which they rapidly become perpendicular to the grana cylinders. Measured at a distance of ∼65 nm away from the grana edges, the stroma lamellae are only tilted by an average of 3.7 ± 3.6° (n = 25). The number of stroma lamellar helices wound around the grana exhibits small variations, with most grana surrounded by 4 to 6 helices (averaging 4.5 ± 0.6 [n = 28]). The number of helices is positively correlated with grana diameter (Fig. 3C) and is independent of the number of layers in the stack, such that, regardless of grana diameter, the spacing between helices around all grana in the network is held relatively constant. As detailed below, this is required for optimally connecting the helices to the flanking lamellae.

Fig. 3.

Grana are surrounded by multiple right-handed helices. (A, B, and D) A 3D model generated from segmentation of TEM (A) and STEM (B and D) tomographic data consisting of single and multiple grana (yellow) each surrounded by multiple stroma lamellar helices (light blue). In B, the tilt angle of the helices relative to the grana is depicted by an angle symbol on the top right and the width of the helices is depicted by a curly bracket on the left. (C) A plot of the number of helices per granum vs. grana diameter (n = 28). The plot resembles a staircase ceiling function whose bound depends on the tilt angle of the helices, their spacing along the granum cylinder, and the circumference of the grana. As discussed in the text, the first 2 parameters are fairly conserved among grana in the network. In D, the model is shown superimposed on a ∼10-nm-thick tomographic slice with curly brackets showing the uniformity of separation of the helices (left) as well as their pitch (right). (D, Inset) The model is shown from another angle without the superimposed tomographic slice). (E–G) Tomographic slices ∼10 nm thick presented approximately perpendicular (E) and parallel (F and G) to the plane of the grana thylakoids from D. Several grana are shown from the top view (F); the specific granum from D is outlined (white dotted line) and a close-up is provided (G). (D, E, and G) The 4 right-handed helices that surround the granum are separately colored (orange, white, purple, and light blue) to facilitate visualization of their winding along the granum cylinder. (G) The slits connecting between the grana discs and the stroma lamellar helices, referenced in the text, are depicted by pink lines, and one is also shown by a pink arrow in E. The specific granum layer shown in G is also colored yellow in E. (Scale bars, 250 nm.)

The stroma lamellar helices and the appressed thylakoids in the stacks are connected by slit-like apertures located at the grana margins (21, 27, 29, 32, 33). These connections ensure continuity of the lipid and aqueous (luminal) phases throughout the granum–stroma assembly. Previous studies yielded variable estimates of slit length. While Mustárdy et al. (32) reported values ranging from 13 to 70 nm, those reported by Austin and Staehelin (33) had a substantially broader distribution, between 30 and over 400 nm. Examining the contact area between the grana discs and the stroma lamellar helices in our tomographic models (Fig. 3 E and G), we observe that the average maximal slit length is 80 ± 19 nm (n = 87), close to the upper limit reported by Mustárdy et al. (32).

Left-Handed Helical Membrane Surfaces Interface between the Stroma Lamellar Helices and Sheets.

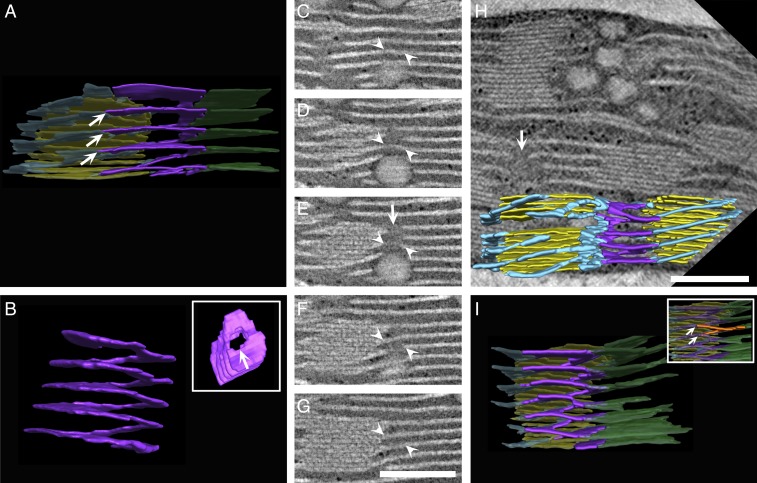
Analyzing a large number of granum–stroma assemblies, available to us from the extensive volumes we reconstructed and modeled, we found that only parts of the lamellar sheets convert into right-handed helices that surround the grana. Other parts bifurcate near the granum–stroma interface and fuse to the winding lamellae, with each sheet connecting to a pair of adjacent helical strips, above and below the lamellar surface (see the purple surfaces in Figs. 4 and 7 and SI Appendix, Fig. S6). This differs from our original model in which the lamellar sheets connect directly (through the bifurcations) to the grana thylakoids (34). Connections of the bifurcations with successive helices are made at approximately the same radial point along the granum circumference (arrows in Fig. 4 A and I, Inset; an embedded 3D figure of the model from Fig. 4I is provided in SI Appendix, Fig. S7), such that the 2 contact sites of the bifurcations with the helices are vertically displaced from one another by ∼50 nm (the spacing between adjacent helical strips around the grana). This allows the stromal sheets to remain parallel to the thylakoids in the stacks and the stacks to remain aligned to each other. The result is an ordered organization that maximizes the packing density of the membranes.

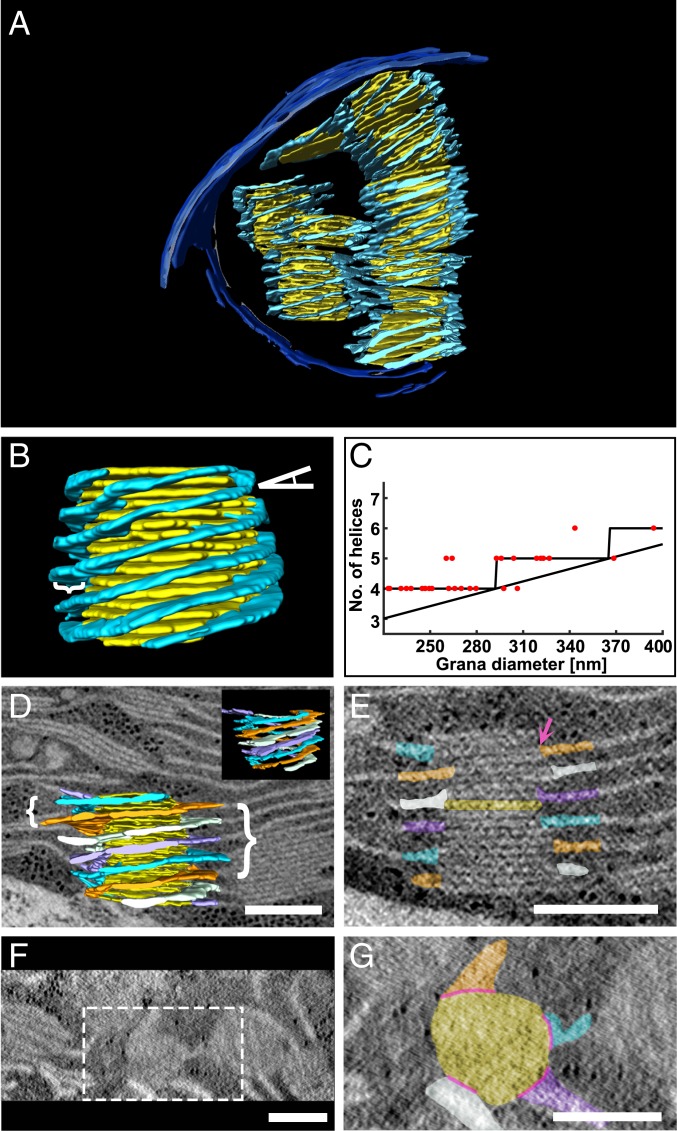
Fig. 4.

Left-handed helical junctions bridge between the right-handed helices and stromal sheets or adjacent right-handed helices. (A, H, and I) Three-dimensional models generated from segmentation of tomographic reconstructions by STEM, showing left-handed helical junctions (purple) connecting between the stroma lamellar sheets (green) and the right-handed helices (light blue) that surround the grana (yellow) (A and I), or between right-handed helices that belong to adjacent grana (H). The left-handed helical structure shown in A is isolated and shown from side and top views (B, Inset). (C–G) Tomographic sequential slices ∼10 nm thick, which were segmented and rendered to obtain the model in A, allow tracking the left-handed helical junction from front to back (a portion is marked with white arrowheads). White arrows in B, E, and H mark the elongated channel formed by the left-handed helical junction. (A and I, Inset) Contact sites of the bifurcations with the helices (marked with multiple white arrows) are vertically displaced from one another by ∼50 nm. One such bifurcation is segmented orange in I, Inset. All elements in A and I, aside from the left-handed helical junctions, are shown in transparency. Additional modeled assemblies from TEM and FIB-SEM are provided in SI Appendix, Fig. S5. (Scale bars, 250 nm.)

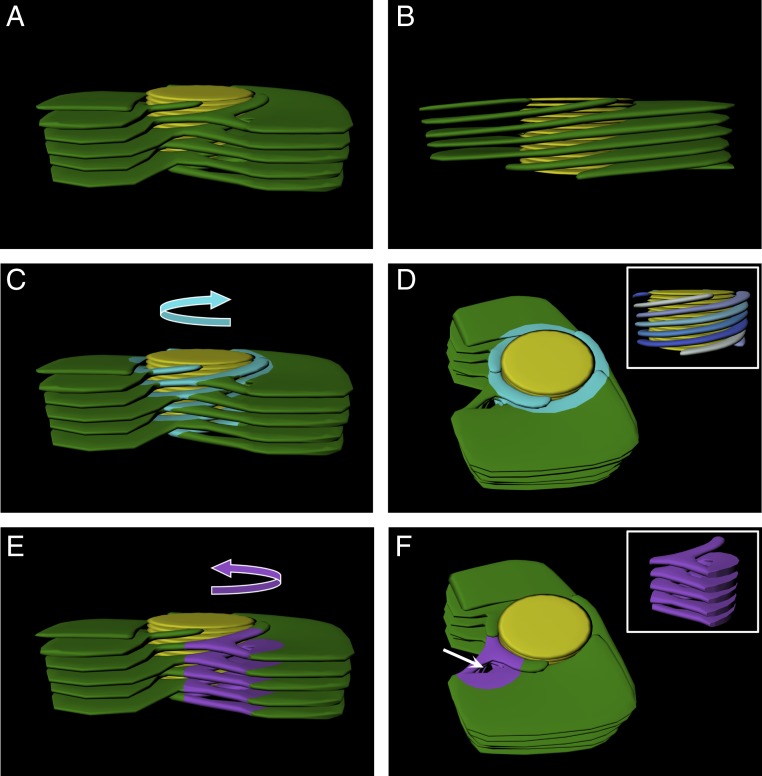
Fig. 7.

Idealized 3D model of the granum–stroma assembly. An idealized model was constructed with one left-handed helical connector per granum for visualization of all features of the granum–stroma assembly. The average number of helical connectors per granum found in the networks that were analyzed was about 4, further relieving elastic deformations at different points around the grana. In all panels, granum thylakoids are shown in yellow and the stroma lamellar sheets are shown in green. Right-handed helices (C and D) and the left-handed helical connector (E and F) are highlighted in light blue and purple, respectively, and their handedness is demonstrated with curved arrows in C and E. (D, Inset) Side view of the right-handed helices with blue hue colors highlighting the distinct helices around the granum. (A, B, C, and E) Side view of the assembly, with A, C, and E presenting a front view showing the connections between the helices, helical junction, and the sheets and B presenting a back view, allowing for better visualization of the winding of the stroma lamellae around the granum body connecting directly to sheets. (D and F) Top-angle view showing the channel formed by the left-handed helical connector (white arrow in F). (F, Inset) Side view of the isolated left-handed helical connector. The slit-like apertures that connect between the right-handed stroma lamellar helices and the grana thylakoids are not shown.

Notably, analysis of the aforementioned split junction connections reveals that they are arranged into left-handed helical surfaces (see Figs. 4 and 8 I–P and SI Appendix, Fig. S6). These surfaces bridge between the bifurcations, which assume a left-handed helical organization, and the right-handed helices. They thus provide a mechanism for balancing the long-range twist imposed by the homochiral arrangement of the lamellae around the grana. The structure of the junctions resembles a spiral staircase, similar to that of the helical ramps shown by Terasaki et al. (52) to connect between the stacked sheets of the rough endoplasmic reticulum (ER) (see also ref. 53). The tilt angle of the helical surfaces is 16.6 ± 4.6° (n = 37), very similar to that of the right-handed helices surrounding the grana. By contrast, their pitch (44.4 ± 11.9 nm [n = 37]) is quite different, about one-fourth to one-fifth that of the right-handed helices (averaging ∼200 nm). It closely matches, however, the spacing between consecutive helices around the grana, as well as the spacing between neighboring lamellar sheets, enabling smooth connection between the 2 stroma lamellar components (white arrows in Fig. 4 A and I).

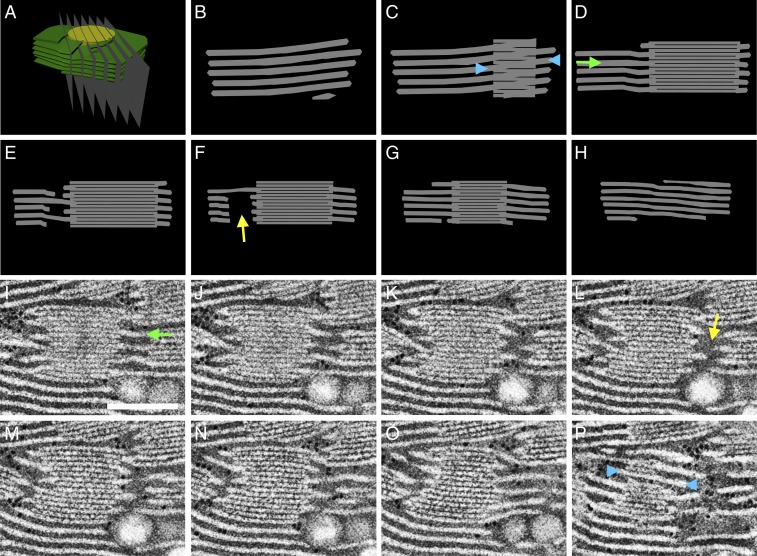
Fig. 8.

Cross-sections through the idealized model of the granum–stroma assembly accurately reproduce the tomographic data. (A) The idealized 3D model of a granum–stroma assembly, with a single left-handed helical junction (Fig. 7), is sliced by serial planes (B–H). The resulting cross-sections are consistent with serial slices from the tomograms. One such example, from the TEM data, encompassing a left-handed helical junction is presented in I–P. (Scale bar, 250 nm.) In both modeled and tomographic sections, discontinuities of the lamellar extensions (yellow arrows) are visible in slices traversing the central void of the helical connectors. Likewise, in both cases the stroma lamellae generally extend orthogonally (green arrows) to the grana stacks, aside from at the grana–stroma interface where they wrap the grana obliquely (blue arrowheads) to form right-handed helices. Note that in C and P the granum is viewed from the front and the back, respectively.

In addition to connecting between the lamellar sheets and right-handed helices, the left-handed helical junctions also connect between helices that belong to neighboring grana when the grana lie in close proximity to each other (Fig. 4H and SI Appendix, Fig. S6 E and F). Here, the junctions seamlessly join the 2 sets of helices, relieving bending strain caused by (even small) differences in phase and tilt angle of the helices, as well as in the orientation of the grana around which they are wound. Thus, many of the connections of the right-handed helices that surround the grana, whether to the lamellar sheets or to the helices of neighboring grana, are made via the left-handed helical junctions.

On average, about 4 (3.7 ± 0.2) left-handed helical junctions are present per granum, situated at the outer boundary of the surrounding right-handed helices. Those junctions are found along the entire length of grana stacks, and even for grana with only a few layers. To determine the above ratio, we probed 3 sections (from different chloroplasts) from the top view, ranging in area from 0.6 to 0.9 μm² (see one of these in Fig. 6F), with a total analyzed area of 2.1 μm². Because the grana are relatively large, some of them appear only partially in the reconstructed sections. We therefore counted the grana according to their fractional contributions; for example, a granum at the edge contributes one-half to the sum (see Fig. 6E). Counted this way, each section contained between 3.1 and 3.3 grana and 11 and 13 left-handed helical connectors. This arrangement results in an irregular, pitch-balanced array consisting of comparatively wide assemblies of intertwined right-handed helices interspaced by narrower left-handed helical structures (see Fig. 6).

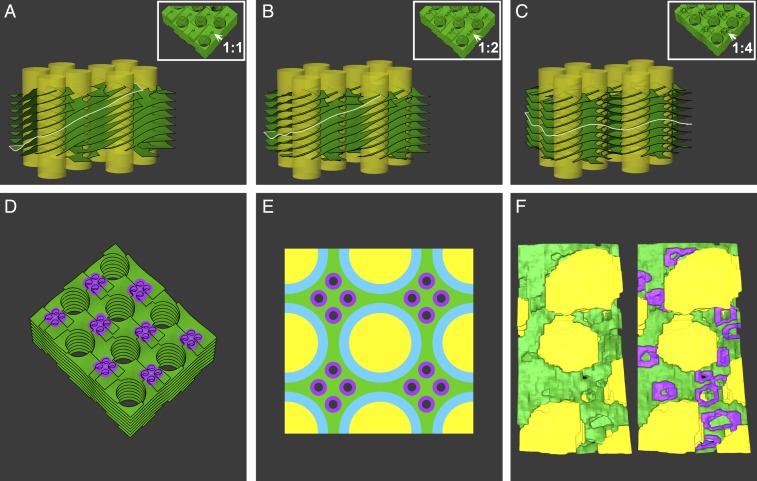
Fig. 6.

The effect of the density of the left-handed helical junctions on network energy. (A–D) Surface energy minimization of idealized thylakoid network architectures, with each grana column surrounded by 4 distinct, intertwined right-handed helices. The grana are interconnected by interspacing left-handed helical junctions, whose pitch and diameter are about one-quarter of those of the right-handed helices. The system was modeled with varying densities of left-handed helical junctions: 1 (A), 2 (B), and 4 (C) per granum. (D) A top view of the model in C is shown with junctions highlighted in purple. The densities are labeled in A–C, Insets, which show a portion of each model from the top view with arrows pointing to left-handed helical junctions. (A–C) The edge of one layer is highlighted in white to show its tilt in relation to the grana columns; with a ratio of 4:1 (C), the layers are on average orthogonal to the grana columns. The ratio of helical junctions to grana was calculated for the bulk of the assembly, with grana located at the edges of the model making fractional contributions (1/2 for grana at the edges and 1/4 for those at the corners). (E) Top view schematic of the arrangement corresponding to the minimum surface energy of the network (modeled in C and D), with 4 helical junctions associated on average with each granum (depicted here as 16 helical connectors per 4 grana). Grana and stroma lamellae are colored in yellow and green, the right-handed helices in light blue, and the left-handed helical junctions are highlighted in purple (with a hole representing the elongated channel—see Fig. 4B). (F) A section of a 3D reconstructed model providing a similar view of the corresponding elements (shown with and without left-handed helical junctions segmented in purple). The average number of helical junctions per granum is ∼4, as was generally the case for the networks analyzed in this work.

The Left-Handed Helical Junctions Minimize Network Surface and Bending Energies.

Membrane mechanics is commonly described by the following Hamiltonian:

$$H_0=\frac{1}{2}\gamma {\displaystyle \int dA}+\frac{1}{2}B{\displaystyle \int dA{\left(C_1+C_2\right)}^2}+\overline{B}{\displaystyle \int dA{C}_1{C}_2},$$ [1]

where the first term accounts for surface tension and the remaining terms, which are known as the Canham–Helfrich Hamiltonian, account for membrane bending (54, 55). $C_1$ and $C_2$ are the surface’s principal curvatures, $\gamma$ is the surface tension, $B$ and $\overline{B}$ are the effective bending moduli, and ${\displaystyle \int dA}$ represents integration over surface area. A class of solutions that minimize H₀ is given by minimal surfaces—surfaces that locally minimize their own area, characterized by a vanishing mean curvature $\left(C1+C2\right)/2$ and (with one exception) possess a negative Gaussian curvature (C₁C₂). Indeed, a minimal surface geometry has been shown to be adopted by prolamellar bodies, which are precursors of thylakoid membranes in dark-grown leaves (56). Considering a closely related system of tightly packed lamellar sheets in the ER, Terasaki et al. (52) showed that the elastic energy is minimized when the helicoidal ramps connecting the sheets display alternating handedness and are organized in arrays with checkerboard-like patterns. A similar conclusion was reached by subsequent analyses conducted by Guven et al. (57) and Berry et al. (58).

To obtain minimal surfaces with prescribed boundary conditions, which naturally minimize the Hamiltonian H_0, we employed a numerical method for surface area minimization (59). The paired membranes constituting the sheets and helical elements are considered to have a roughly uniform thickness, stabilized by membrane and luminal proteins, and therefore are treated as a single deformable surface (as performed in refs. 52 and 57). We prescribed the topology of the network by connecting the otherwise parallel-packed sheets by helical membrane motifs varying their spatial arrangement and handedness. We then optimized the resulting surface’s configuration numerically to obtain a minimal surface and compared the obtained elastic energies.

We first consider the helical model as proposed by Paolillo and coworkers, where the left-handed helical junctions are not present in the membrane network. For a single file of grana (Figs. 1B and 5A), this architecture results in oppositely sloped long edges, much like the geometry of a sloped parking lot [in which the floors themselves are sloped and no room is wasted (see refs. 60–62); note this geometry is different from the “parking ramps” (in refs. 52 and 57) which refer to localized helical motifs]. However, extending the structure to a 2D array of grana columns requires either significant bending and twisting of the connecting lamellae (Fig. 5B and SI Appendix, Fig. S8 A and C) or successive rotation of the files, to match the orientation of their boundaries (Fig. 5 B, Inset). The latter inevitably changes the orientation of the grana columns in different files (Fig. 5 B, Inset). Furthermore, a uniform density of grana, each surrounded by right-handed helical connections to the stroma lamellae, will result in a finite pitch angle between the lamellar sheets and grana layers (Fig. 5B and SI Appendix, Fig. S8C). This is contrary to the observation that they are oriented roughly parallel to each other.

Next, we modeled the network with alternating right- and left-handed helical junctions. For a single file of grana columns, we found that, even in this simple case, the slope of the sheets at the boundary of the file is reduced to zero (see arrows in Fig. 5 A and C); however, it does not significantly lower the energy of the network. For the 2D arrays, we alternated the handedness of the junctions both between and within files (Fig. 5D and SI Appendix, Fig. S8 B and D), as observed experimentally. Here, the geometrical (and, hence, energetic) relief offered by the alternating helical arrangement becomes dramatically more evident. This organization preserves the coorientation of the grana and also allows the stroma lamellae to remain parallel and aligned to the grana layers (compare yellow lines in SI Appendix, Fig. S8 C and D). Such an arrangement was previously shown by Terasaki et al. (52) to have minimal bending energy of sheet edges and surfaces of stacked ER cisternae.

We computed the relative energies of the above configurations as well as of several other 1- and 2D arrangements of grana stacks interconnected by lamellar sheets. As a baseline, we used a single column surrounded by a single, helically wound lamella. Arranging 4 grana columns surrounded by right-handed helices in a row (Figs. 1B and 5A) increased the energy only slightly. This is because connecting the stacks within a single file does not require significant distortion of the membranes (and, therefore, an increase in their area), although it does result in lamellae with oppositely sloped long edges. The energetic cost of extending this organization to 2D strongly depends on whether the grana retain their orientation or not. In the case where the grana files are allowed to rotate relative to each other, which is not observed experimentally, the cost is roughly the same as that computed for a single file. This is because rotations of the files allow alignment of the edges with minimal distortion. However, imposing the native organization, in which the grana maintain their orientation, results in an energy increase that scales with the number of stacks. For the 4 × 4 array shown in Fig. 5B and SI Appendix, Fig. S8C it is about 20%. This excess energetic cost would manifest physically as a torque acting to rotate the grana columns to the aforementioned, nonnative conformation of successively rotated files and reduce the associated surface area. Notably, relieving the geometrical constraint by an arrangement in which adjacent helical junctions have opposite handedness (Fig. 5D and SI Appendix, Fig. S8D) brings the energy of the array down to that computed for the reference structure.

Finally, we examined the energy of the network as affected by the density of the left-handed helical connectors in the membranes (Fig. 6). Toward this, we used a more realistic description of the network in which each granum is surrounded by 4 distinct but intertwined right-handed helices interconnected by interspacing left-handed helical motifs. The pitch and diameter of the latter are about one-quarter of those of the right-handed helices, close to the values derived from the tomographic data. This arrangement thus consists of right-handed helices with pitch 4 h, interspaced by 4 left-handed helical junctions with pitch h. The system was modeled with a variable number of left-handed helical junctions per grana (Fig. 6 A–C). We found that a ratio of 4 left-handed helical connections per granum (Fig. 6E), which brings the system to a local pitch balance, completely negates the overall twist of the stroma lamellae induced by the right-handed helices. This ratio matches the experimentally observed stoichiometry (see Left-Handed Helical Membrane Surfaces Interface between the Stroma Lamellar Helices and Sheets and Fig. 6F). In cases where a larger number of intertwined right-handed helical lamellae surround a single grana column (5 or 6 helices as, e.g., described in Fig. 3C), each of these helical motifs is associated with a larger pitch (5 h or 6 h respectively, where h is the spacing between adjacent lamellae). The stoichiometry of left-handed connectors in such cases is also expected to change to balance this pitch for the bulk of the network. We note that for a collection of pitch-balanced helical motifs, the addition or subtraction of layers to individual stacks does not change this property.

Quite remarkably, much of the essential morphology of the thylakoid membrane system can be explained solely by minimization of surface and elastic bending energies. We note, however, that surface area consideration predicts that the diameter of the left-handed helical junctions would match the thickness of the thylakoids they connect (∼20 nm), to yield a minimal surface. The observed diameter of the junctions is, however, ca. 50 nm. Sustaining this mismatch in curvatures likely requires membrane proteins that stabilize the internal edges of the junctions.

The Left-Handed Helical Junctions Form Aqueous Conduits across the Membrane Network.

Each left-handed helical junction, whether bridging between right-handed helices on neighboring grana or between right-handed helices and stromal sheets, demarcates an elongated channel that runs parallel to the granum cylinder (see white arrows in Figs. 4 B, E, and H and 7F). As mentioned above, these channels or pores have an internal diameter of about 50 nm (50.5 ± 18.3 nm [n = 37]), sufficiently large to accommodate massive macromolecular complexes and even small inclusions. Traversing the lamellar sheets connected to the grana with which they are associated, the collection of these channels crosses the entire lamellar network, providing a means for trafficking throughout the chloroplast volume.

Discussion

An idealized model of the granum–stroma assembly, constructed based on the tomographic data, is presented in Fig. 7 and SI Appendix, Fig. S9. Serial sections generated from the model closely match sections observed experimentally in the tomograms (Fig. 8). The model thus accurately reproduces the 3D structure of the basic unit of the plant thylakoid network.

A central feature of the model is that the interaction between the stroma lamellar-derived components of the membrane network—the lamellar sheets and the right-handed helices that surround the grana—requires specific connectors in order to minimize surface and elastic energy. The connectors consist of bifurcations that join adjacent sheets or helices and are configured such that the orientations of the interacting components are preserved in the melded structure. Notably, repetition of the bifurcations along the interaction interface results in the formation of left-handed helical junctions that run along the edges of the gaps between the stromal sheets and the right-handed helices or between right-handed helices present on adjacent grana (Fig. 4I). These junctions are thus composite structures, constructed from elements of both the lamellar sheets and helices.

Several attributes make the left-handed helical junctions ideally suited to bridge between the stroma lamellar sheets and helices. Proxying minimal surfaces, they are natural minimizers of surface energy and elastic terms associated with bending (52, 57, 58). Second, their handedness is opposite to that of the stroma lamellar helices that surround the grana, counterbalancing their topological charges that would otherwise reflect in a long-range twist of the connecting sheets. This allows alignment between the mirror symmetric edges of the interacting surfaces with minimum bending and twisting. Were this not the case, the connections would actually lead to significant deformation of the interacting membrane domains, as evident from the simulations. The importance of this “charge” neutralization is further supported by the observation that a minimum energy is achieved only when the number of helical junctions associated with each granum equals the number of right-handed helices that are wrapped around it. Third, their pitch closely matches the spacing between adjacent lamellar sheets and between helices present on consecutive grana. Together, these properties enable the helical junctions to smoothly mitigate the geometrical mismatches between the right-handed helices and the sheets, minimizing local bending and twisting and preventing propagation of the deformations into neighboring regions.

As mentioned above, helical membrane elements were previously identified in the ER where they serve to connect between adjacent sheets (52). In acinar secretory cells of the parotid salivary gland, these helical connectors have an internal diameter of ∼70 nm and a pitch of about 80 nm, comparable to those (∼50 nm) of the left-handed helical junctions in the thylakoid membranes. This similarity is likely governed by a similar intersheet distance in the 2 lamellar systems (about 80 and 50 nm in the ER and thylakoid membranes, respectively). As observed in the plant thylakoid membrane, both left- and right-handed helical structures are present in the ER. While the overall design of these structures is similar, some differences nonetheless exist between the 2 systems. In the ER, the left- and right-handed helical structures differ only in their handedness. By contrast, the corresponding elements in the thylakoid membranes have different pitch and internal and external diameters, with the left-handed helical junctions being narrower and shorter. This difference underlies the different stoichiometries of the left- and right-handed forms of the helical structures in the 2 membrane systems, which are 1:1 and 4:1, in the ER and in the thylakoid membrane, respectively. In both systems, however, the net effect is that the pitch of the helical elements per unit area averages to zero. This pitch balancing is a fundamental geometric characteristic that likely underlies the arrangement of helical membrane motifs of alternating handedness independently of system characteristics. While this arrangement could be directly observed in the thylakoid membrane it could only be inferred by modeling for the ER due to a low density of the connectors in the ER sheets. The latter appears to be determined by a balance between long-range attractions, driven by tension, and short-range repulsions associated with bending (57). Given the fundamental nature of pitch balancing, the basic topology of the network is also expected to be maintained in light-adapted plants. While exposure to light was shown to be associated with several alterations in network structure and organization, its overall architecture is mostly preserved under all physiologically relevant light conditions (3, 4, 63–65).

The high membrane curvature at the internal edges of the right- and left-handed helical structures is likely stabilized by specialized proteins, such as reticulon and DP1 proteins that serve this role in the ER (52, 66). Presently, the identity of these proteins is unknown. In chloroplasts, curvature thylakoid1 (CURT1) proteins were shown to induce membrane curvature at the highly curved regions of the grana margins, probably in a process involving self-oligomerization (67, 68). A cyanobacterial homolog (and likely ancestor) of CURT1, called curT, has likewise been demonstrated to induce membrane bending and is required to maintain native network architecture (67, 69). Both CURT1 and CurT contain 2 transmembrane domains and an N-terminal amphipathic α-helix that is believed to account for their membrane-deforming activity (67, 69, 70). CURT1 proteins are therefore potential candidates for the stabilization of the curvature at the edges of the helical membrane connectors. For the right-handed helices that surround the grana, stabilization of the internal edges may also be achieved by their connection with the thylakoids in the stacks.

Besides their role in connecting between the lamellar sheets and helices, the left-handed helical junctions may have additional functions. One such function is increasing the connectivity of the stroma lamellar domains. Without the helical connectors, the stroma lamellae, which make up about half of the network, would be connected to each other only indirectly, through their associations with the thylakoids in the grana. The presence of multiple connections between the lamellar sheets and the helices surrounding the grana, through the helical junctions, endows the stroma lamellae with a high degree of connectedness, facilitating molecular and macromolecular trafficking both within the membranes and the enclosed luminal space.

Another possible function relates to the trafficking of molecules and macromolecules in the chloroplast stroma. In mature mesophyll cells, thylakoid membranes may occupy up to 60% of the chloroplast volume. Given that the membranes have a multilayered organization that extends along the entire length of the chloroplast, a means allowing for unperturbed traffic through the lamellar network is essential for organellar function. In cyanobacteria, where the thylakoid membranes are often similarly arranged in multiple (concentric) layers, such traffic is enabled by the presence of multiple perforations, ranging from 20 to 150 nm in diameter, within the membranes (38, 71). Such perforations or gaps are also observed in plant thylakoid membranes, but only rarely, and appear to be fortuitous. The elongated tubes demarcated by the left-handed helical junctions provide an alternative route for trafficking within the chloroplast volume. With an internal diameter of about 50 nm, they can readily accommodate large macromolecular complexes, such as ribosomes and ribonucleoprotein complexes, and even small inclusions, along with small solutes. Running in parallel to the grana cylinders, across the interconnecting lamellar sheets, they provide multiple passageways that traverse the entire membrane network.

Remarkably, arrayed spiral ramps of alternating handedness connecting between sheets of nucleons were observed in molecular dynamics simulations of dense nuclear matter phases, termed “nuclear pasta,” predicted to exist in the inner crust of neutron stars and in core-collapse supernovae, which are some 14 orders of magnitude denser than the cellular environment (58, 72, 73). Twisted bridges similar to helical ramps were likewise observed in simulations of densely grafted polymer brushes of amphiphilic homopolymers (74). This geometry, based on a pitch-balanced arrangement of heterochiral helical elements, thus appears to be a universal means to connect between densely packed flat layers, irrespective of their composition, properties, or size scale (58).

Materials and Methods

Plants.

Dark-adapted Lactuca sativa L. (lettuce) plants used in this study were obtained from an organic field and grown in a controlled environment as specified in SI Appendix, SI Materials and Methods.

Electron Tomography.

Small leaf pieces (∼2 mm in diameter) were high-pressure-frozen, freeze-substituted, resin-embedded, and poststained as described in refs. 34, 37, and 43. The serial dual-axis TEM tomograms analyzed in the current study were those used in Shimoni et al. (34). Electron tomography by dual-axis STEM and FIB-SEM is described in SI Appendix, SI Materials and Methods.

Image Processing and Analysis.

Image alignment, 3D reconstruction, segmentation, processing, and statistical analysis are detailed in SI Appendix, SI Materials and Methods.

Modeling.

Idealized models and animations were constructed using the Autodesk Maya 3D animation software (https://www.autodesk.com/products/maya/overview). Surface energy minimization was performed with Surface Evolver (59) as described in SI Appendix, SI Materials and Methods.