Carrier localization in perovskite nickelates from oxygen vacancies

Significance

Oxygen vacancies and their associated electrons, ubiquitous in oxide materials, can lead to emergent phenomena. Control of these vacancies allows the manipulation and exploitation of such properties. Using an ultralow oxygen partial pressure environment, we are able to systematically control the oxygen vacancy concentration in thin films of rare-earth nickelates. We find that oxygen vacancies lead to strong carrier localization arising from Ni valence reduction to 2+, resulting in an increase of room-temperature electrical resistivity by several orders of magnitude while maintaining the perovskite structure throughout. The oxygen vacancies can be redistributed by electric fields, leading to analog resistance behavior.

Abstract

Point defects, such as oxygen vacancies, control the physical properties of complex oxides, relevant in active areas of research from superconductivity to resistive memory to catalysis. In most oxide semiconductors, electrons that are associated with oxygen vacancies occupy the conduction band, leading to an increase in the electrical conductivity. Here we demonstrate, in contrast, that in the correlated-electron perovskite rare-earth nickelates, RNiO₃ (R is a rare-earth element such as Sm or Nd), electrons associated with oxygen vacancies strongly localize, leading to a dramatic decrease in the electrical conductivity by several orders of magnitude. This unusual behavior is found to stem from the combination of crystal field splitting and filling-controlled Mott–Hubbard electron–electron correlations in the Ni 3d orbitals. Furthermore, we show the distribution of oxygen vacancies in NdNiO₃ can be controlled via an electric field, leading to analog resistance switching behavior. This study demonstrates the potential of nickelates as testbeds to better understand emergent physics in oxide heterostructures as well as candidate systems in the emerging fields of artificial intelligence.

Complex oxides, relevant across physics, chemistry and engineering, host a number of interesting and useful properties. From multiferroics (1) and superconductors (2) to catalysts (3, 4) and ionic conductors (5, 6), a material’s composition and structure determine its functionality. Modification of the composition and structure of these oxides, for example by introducing oxygen vacancies, can be both the source and limiting factor of interesting physics. The ability to manipulate oxygen vacancies and understand how they modify properties therefore yields significant insight and control.

Oxygen vacancies in ABO_3-δ perovskites play a myriad of roles, such as influencing thermal transport (7), acting as shallow donors in SrTiO₃ (STO) (8–10) and deep donors in LaAlO₃ (LAO) (11, 12), participating in luminescence, and likely contributing to the conducting electron gas found at the SrTiO₃/LaAlO₃ interface (13, 14). A single vacancy donates 2 electrons; how these electrons behave determines the effect such vacancies have on the material. For instance, the electrons could remain trapped by the vacancy, localize in the vicinity, or become itinerant. In severely oxygen-deficient perovskites the vacancies lead to a reduction of the B-site oxygen coordination and can order to produce a variety of crystal structures. For example, many ferrites and cobaltates undergo a topotactic phase transition from perovskite to brownmillerite as oxygen is removed (15–18). The structural changes are accompanied by a reduction in the B-site valence and can be reversed upon annealing in an oxygen-rich environment.

The properties of perovskite rare-earth nickelates, RNiO₃ (R = La-Lu), are particularly interesting with a rich temperature-composition phase diagram including a metal-to-insulator phase transition coinciding with a nickel charge ordering (19, 20). The unoccupied states at the bottom of the conduction band have substantial oxygen character, corresponding to an oxygen ligand hole consistent with a negative charge transfer character for the system (21, 22). In a nondisproportionated structure, the nickel sites have nominal valence 3+ and the oxygen ligand holes are distributed equally among all of the NiO₆ octahedra, resulting in a d⁸L configuration, where L denotes an oxygen ligand hole. Oxygen vacancies in rare-earth nickelates modify the structure and act as electron donors. Electron doping of RNiO₃ at high concentrations, through the use of intercalated H⁺ and Li⁺ ions in NdNiO₃ (NNO) and SmNiO₃ (SNO) (23, 24), fluorine substitution of oxygen in NNO (25), and interfacial charge transfer at interfaces with LaNiO₃ (LNO) (26–28), has been shown to lead to a highly insulating state. This insulating state arises from electron localization on the NiO₆ octahedra, resulting in a Mott state. The added electron can be regarded as converting nickel from its nominal 3+ valence state to 2+, or as converting the nickel site in the NiO₆ octahedron from d⁸L to d⁸. In oxygen-deficient NNO and SNO, an accompanying increase in resistivity has been observed (29–32). Furthermore, in LNO oxygen vacancies not only lead to an increase in the resistivity, but large deficiencies lead to ordered structural phases consisting of chains of nickel–oxygen octahedra and square planar configurations in both powders (33, 34) and thin films (35–37). These results raise the fundamental question of how the electrons donated by the oxygen vacancies modify the properties of rare-earth nickelates.

To address this, here we systematically control the oxygen content in thin films of both SNO and NNO (SNO_3-δ and NNO_3-δ) with a Mg trap reaching a deficiency of almost δ = 0.5, which can be reversed via exposure to oxygen. While maintaining the overall perovskite structure, oxygen vacancies are created modifying the nickel–oxygen coordination and the crystal field splitting (Fig. 1A). The electrons introduced by each oxygen vacancy localize on nearby nickel sites, reducing the valence state to 2+. This results in a large on-site gap stemming from electron–electron correlations and the crystal field splitting (Fig. 1B). As a result, the oxygen vacancies lead to a global localization of carriers and drive the films to a highly insulating state with nearly 7 orders of magnitude increase in the resistivity. The changes to the nickel–oxygen coordination make the electronic structure of oxygen-deficient SNO distinct from SNO that is electron-doped via intercalated ions (38, 39). Furthermore, the resistance state can be controlled via voltage pulse by altering the vacancy distribution. These findings elucidate the effect of oxygen vacancies on rare-earth nickelates and how they can be used to control their electronic and optical properties.

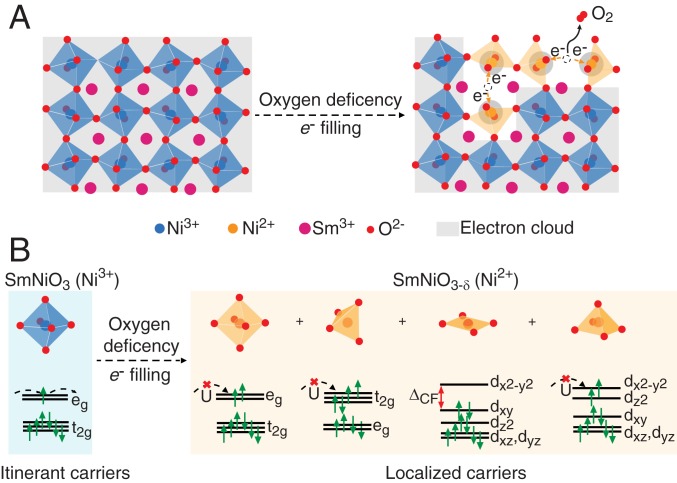
Fig. 1.

Schematic of charge localization mechanism in oxygen-deficient SmNiO_3-δ (SNO_3-δ). (A) Oxygen vacancy formation in SNO changes the local symmetry from octahedral to tetragonal, square planar, and square pyramid, as well as introduces charge (i.e., electrons) into the material. (B) The electrons accompanying the oxygen vacancies localize on nearby Ni and reduce its valence state to Ni²⁺_, where the strong on-site Coulomb interaction of electrons as well as crystal field splitting of the Ni 3d orbitals synergistically leads to carrier localization and opening of bandgap.

Results and Discussions

We start with a discussion of oxygen-deficient SNO film preparation and quantification of the level of oxygen deficiency using synchrotron X-ray photoemission measurements (XPS). We then present the effect of oxygen vacancies on carrier localization in SNO_3-δ by having characterized the electrical, structural, and optical properties, as well as the second harmonic near field response. Having established the carrier localization signatures of SNO_3-δ, the reversibility and stability window of the films is demonstrated. To further elucidate the charge localization, we present our first-principles calculations focusing on the microscopic changes to electronic structure upon vacancy formation. We further show the universality of carrier localization behavior in oxygen-deficient NNO, employ X-ray absorption spectroscopy (XAS) to quantify the valence change of the nickel sites with increasing deficiency, and, finally, design and demonstrate a proof-of-concept solid-state memristor using oxygen-deficient NNO.

We utilized an oxygen-starved environment created by an Mg trap to create oxygen vacancies in SNO and NNO thin films (SI Appendix, Fig. S1A). We used this setup to generate a low oxygen partial pressure (LPO2) environment reaching as low as p(O₂) ∼ 10⁻²⁶ atm (SI Appendix, Fig. S1B) and then annealed the perovskite nickelate thin films to promote reduction. This technique enables us to fabricate nickelates with varying levels of oxygen deficiency by controlling the temperature and time of the annealing process without the need for forming gas mixing. Annealing pristine SNO for 60 min at various temperatures (SI Appendix, Fig. S1C), a substantial increase in the electrical resistivity of the film was exhibited above ∼300 °C, indicating the temperature threshold necessary for oxygen vacancy formation in SNO. By annealing SNO at a constant temperature (400 °C) for various durations (from 22 to 105 min), we fabricated nickelates with varying levels of oxygen deficiency (SI Appendix, Fig. S1D).

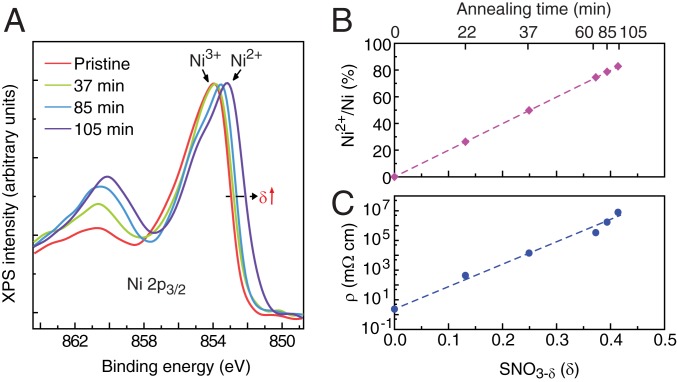
To study the evolution of the valence state of Ni and quantify the oxygen deficiency concentration of SNO_3-δ samples upon LPO2 annealing, we carried out XPS. As shown in Fig. 2A, the spectral weight of the Ni 2p_3/2 core-level peak shifts gradually from ∼853.9 eV, predominantly from Ni³⁺ in pristine SNO, to a lower binding energy of ∼853.2 eV, indicating a reduction in the valence state of nickel ions toward Ni²⁺ upon oxygen vacancy doping (40). The oxygen deficiency level of SNO_3-δ under various LPO2 annealing conditions is estimated by the ratio of the effective peak area of Sm 3d_5/2 and O 1s after a Shirley background was subtracted (SI Appendix, Fig. S2). The oxygen deficiency level of SNO_3-δ after LPO2 annealing at 400 °C for 105 min is δ ∼ 0.41 (SI Appendix, Fig. S2). As a result, nearly 83% of the nickel is estimated to be reduced to the Ni²⁺ state in the heavily oxygen-deficient sample (Fig. 2B). Simultaneously, we observed a ∼7 order of magnitude increase in electrical resistivity of SmNiO_3-δ thin films (Fig. 2C) that depends on oxygen deficiency in a nonlinear manner. Utilizing an experimentally motivated Monte Carlo simulation, considering electron–nucleus and electron–electron interactions, we found a corresponding nonlinear dependence of the resistivity with an increasing number of charged dopants which act to localize electrons (SI Appendix, Supplementary Text 3 and Fig. S3).

Fig. 2.

Carrier localization in LPO2-annealed SmNiO₃ (SNO). (A) Ni 2p_3/2 XPS of SmNiO₃ thin films annealed in an LPO2 environment at 400 °C for various durations. The Ni 2p_3/2 photoemission peak shifts to lower binding energy with increasing annealing time, indicating the reduction of Ni due to oxygen vacancy formation. (B) The population of Ni²⁺ in SmNiO_3-δ estimated from XPS analysis, where almost 83% of Ni is reduced to 2+ valance state after 105 min of annealing. (C) Electrical resistivity at room temperature as a function of oxygen-deficient level in SNO_3-δ. More than 6 orders of magnitude of increase appears, indicating the localization of carriers.

We measured the electronic transport properties of representative SNO_3-δ films down to 60 K for δ ∼ 0 and 0.37. Fitting the resistivity versus temperature to a variable range-hopping model, we estimate the localization length scale of carriers (SI Appendix, Supplementary Text 2 and Fig. S4 A–C). The resistivity versus temperature curve of pristine SNO is well parameterized by the Mott variable range-hopping model with a coherence length of ∼6.49 nm. The oxygen-deficient SNO is well fit by the Efros–Shklovskii variable range-hopping mechanism, suggesting the appearance of a Coulomb gap due to the electron–electron interactions. The localization length scale drops to 0.07 nm in SNO_3-δ (δ ∼ 0.37), indicating that carriers are localized within one pseudocubic unit-cell (∼0.38 nm), consistent with the massive increase in electrical resistivity.

To investigate the structural evolution and stability of SNO_3-δ thin films as oxygen vacancies are incorporated, X-ray diffraction analysis (XRD) was performed. Fig. 3A shows the XRD profile of SNO_3-δ samples as the oxygen deficiency increases. The diffraction peak from (200) plane of SNO (pseudocubic notation) shifts to a lower 2θ angle by ∼0.8°, resulting in an expansion of the out-of-plane lattice constant of ∼1.6% due to oxygen deficiency (Fig. 3 C, Upper). Moreover, there are no extra diffraction peaks appearing in the XRD results of SNO over wide-angle scans (SI Appendix, Fig. S5).

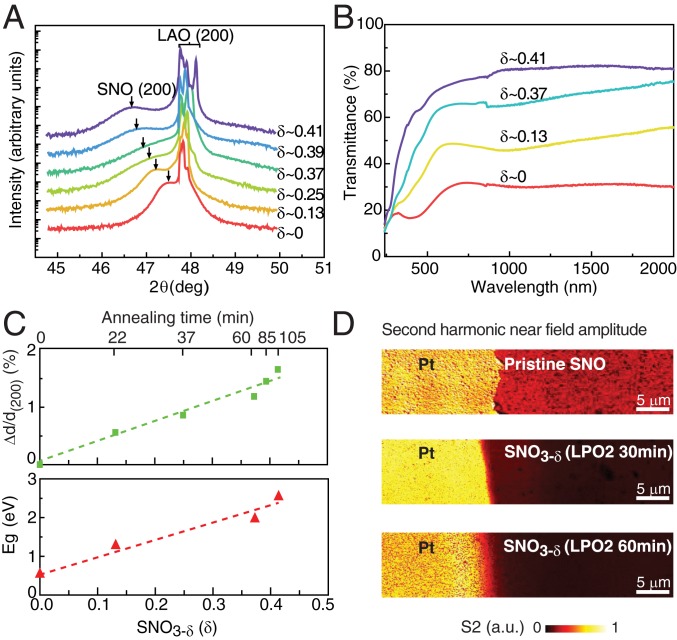
Fig. 3.

Characterization of oxygen-deficient SNO_3-δ films. (A) XRD curves of SNO_3-δ thin films after LPO2 annealing, where the diffraction peak of SNO (200) plane (pseudocubic notation) shifts to a lower 2θ angle, demonstrating film expansion. (B) Corresponding optical transmission spectrum of SNO_3-δ thin films, where the transmittance of SNO exhibits an increase of 300% spanning visible and infrared range. (C) Lattice expansion and optical bandgap as a function of oxygen-deficient level in SNO_3-δ thin films, the values of which are extracted from A and SI Appendix, Fig. S6A. (D) Second harmonic near-field amplitude s₂ images of pristine and SNO_3-δ. The lowering of the normalized amplitude in pristine, 30-min LPO2-annealed and 60-min LPO2-annealed SNO with respect to Pt indicates a reduction of the local optical conductivity at the microscopic scale.

Accompanying the change in the electrical properties, the optical properties of SNO also show a profound modulation. Upon the creation of oxygen vacancies, the optical transmittance of SNO_3-δ thin films (Fig. 3B) shows 300% increase in the visible and infrared ranges. The optical band gap of SNO_3-δ, estimated from the absorption coefficient (SI Appendix, Fig. S6A), increases from ∼0.5 eV to ∼2.5 eV as δ increases from 0 to 0.41 (Fig. 3 C, Lower). The scaling factor between electrical resistivity and band gap (SI Appendix, Fig. S6B) is found to be smaller than that for a typical semiconductor, suggesting the local coexistence of insulating and conducting regions in oxygen-deficient SNO samples annealed under various conditions.

To investigate optical conductivity changes at the nanoscale, we implemented high-resolution nanoimaging in the midinfrared frequency range using scattering-type scanning near-field optical microscope (s-SNOM). Fig. 3D shows the midinfrared (λ = 10.5 µm) nanoimages of pristine and oxygen-deficient SNO samples. The corresponding topography images of SNO films are shown in SI Appendix, Fig. S7A. The second harmonic near-field amplitude values, s₂ (SI Appendix, Fig. S7B), normalized to a Pt reference deposited on top of the samples, are highest for pristine SNO and decreases with annealing time in the LPO2 environment. The relative scattering amplitude contrast can be explained by the Drude response of free carriers to the electric field of the scattered beam between the tip and sample, in which a higher carrier concentration results in more scattering by the tip, giving rise to a larger normalized amplitude approaching unity (41, 42). The reduction of the normalized amplitude s₂ from ∼0.35 to ∼0.1 upon LPO2 annealing then confirms the change in charge carrier concentration at the microscopic scale.

Having characterized the signature of carrier localization due to oxygen vacancies, we explored the reversibility of oxygen vacancy creation in SNO. The resistivity modulation under the annealing (400 °C, 30 min in LPO2) and recovery (400 °C, 10 min in air) process (SI Appendix, Fig. S8A) is reversible and can be maintained over multiple annealing steps. After repeating the annealing and recovery process 4 times, the XRD profile of the SNO thin film remained almost the same as that of the pristine state (SI Appendix, Fig. S8B). By LPO2 annealing at a higher temperature for extended periods of time, the stability window of SNO can be identified. As SI Appendix, Fig. S9 shows, SNO remained in the perovskite structure upon LPO2 annealing at 450 °C for 1 h (SI Appendix, Fig. S9B) and exhibited a large increase in electrical resistivity and optical transparency (SI Appendix, Fig. S9A), consistent with the results presented in Figs. 2 and 3. Increasing annealing time to 2 h, however, the sample turned black and the electrical resistivity dropped (SI Appendix, Fig. S9A). Moreover, a new diffraction peak corresponding to the (400) diffraction plane of Sm₂O₃ appeared (SI Appendix, Fig. S9B), demonstrating the phase decomposition and limit of the stability window of SNO upon oxygen starvation for extended timescales.

To elucidate the microscopic effect of oxygen vacancies on the electronic structure and the coupling with crystal structure, we performed first-principles density functional theory (DFT) + U calculations of SNO_3-δ drawing on previous studies of electron doping of SNO that show added electrons localize on NiO₆ octahedra (24, 38, 39). This localization results in high-spin (S = 1) Ni²⁺ and expanded NiO₆ octahedra. The localized electrons occupy states at the bottom of the conduction band shifting them to the top of the valence band, while leaving the rest of the electronic structure relatively unchanged. As a result, an on-site Mott gap of ∼3 eV for each Ni²⁺ site opens, and when an electron doped at a concentration of 1e⁻/Ni, SNO becomes insulating with a gap of ∼3 eV. In the case of an isolated oxygen vacancy, there are 2 neighboring NiO₅ square pyramids and 2 available electrons. In a supercell of 8 formula units with one vacancy (δ = 0.125), we find that the 2 electrons localize on Ni–O polyhedra, converting the valence state of the nickel from Ni³⁺ to high-spin Ni²⁺. As the nickel site is reduced the hybridization of the unoccupied Ni 3d states with O 2p states shows a marked decrease. Surprisingly, we find that the electrons prefer to localize on more distant NiO₆ octahedra rather than the adjacent NiO₅ square pyramids (SI Appendix, Table S1). As seen in previous work, the reduction of the nickel valence state involves states shifting from the bottom of the conduction band to the top of the valence band (Fig. 4 B and C and SI Appendix, Figs. S10 A–C and S11). The remaining unoccupied states associated with the Ni²⁺ are pushed up in energy, resulting in a gap between spin-up and spin-down e_g states due to the on-site electron correlations. Compared to the NiO₆ octahedra, the change in coordination of the NiO₅ square pyramids leads to a different local electronic structure due to the different crystal field splitting, resulting in a smaller Ni²⁺ on-site gap. All other nickel sites, whether NiO₆ octahedra or NiO₅ square pyramids, remain Ni³⁺ and their associated density of states remains relatively unchanged.

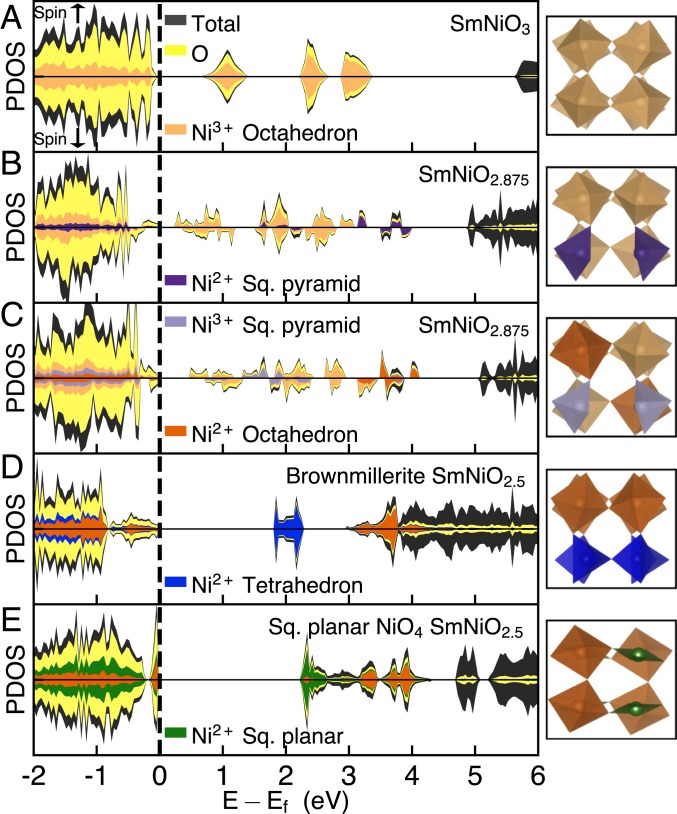
Fig. 4.

Electronic structure of SNO with oxygen vacancies. (A) Density of states (DOS) of pristine SNO with G-type (checkerboard) magnetic ordering. Projected DOS (PDOS) of nickel in light orange, oxygen in yellow, and the sum total (including samarium) in dark gray. (B) DOS of SNO_2.875 with electrons localized on NiO₅ square pyramids neighboring the vacancy resulting in Ni²⁺. PDOS of Ni²⁺ (in square pyramids) in dark purple. (C) DOS of SNO_2.875 with electrons localized on NiO₆ octahedra. PDOS of Ni³⁺ in square pyramids in light purple and Ni²⁺ in octahedra in dark orange. DOS of SNO_2.5, with only Ni²⁺, in a (D) brownmillerite structure, with alternating layers of octahedra and tetrahedra and (E) with chains of square-planar NiO₄. PDOS of Ni²⁺ in NiO₄ tetrahedra in blue and in the square-planar coordination in green. All Ni²⁺ are in a high-spin (S = 1) configuration except for the square planar coordination, in which the crystal field splitting results in a low-spin (S = 0) configuration. Corresponding structure of supercell shown in the left column, showing only the nickel–oxygen polyhedra (nickel centered with oxygens at the vertices) and omitting the samarium atoms for clarity. Polyhedra color corresponds to the colored PDOS.

For an oxygen vacancy concentration of δ = 0.5, all nickels are in a 2+ valence state. This high concentration of oxygen vacancies greatly reduces the number of NiO₆ octahedra and leads to new coordination types such as NiO₅ square pyramids, NiO₄ tetrahedra, and/or NiO₄ square-planar configurations. Here we present the density of states for 2 structures, the brownmillerite structure observed in cobaltates and ferrites with alternating layers of octahedra and tetrahedra (Fig. 4D) and the square-planar structure adopted from LNO_2.5 with chains of NiO₆ octahedra and NiO₄ square-planar configurations (Fig. 4E). The band structure is given in SI Appendix, Fig. S11.

The brownmillerite structure has all high-spin Ni²⁺. The nickel octahedral sites have an on-site gap of ∼3 eV between spin-up and spin-down e_g states. On the other hand, the nickel tetrahedral sites have an on-site gap of ∼1.8 eV between spin-up and spin-down t_2g states as the tetrahedral crystal field splitting has inverted e_g and t_2g states (Fig. 1B). Thus, we find that the effect of the on-site Coulomb repulsion is dependent on the orbital symmetry. For the SNO_2.5 square-planar structure, the nickel octahedral sites are again high-spin Ni²⁺ with an on-site gap of ∼3 eV, whereas the square planar sites are low-spin Ni²⁺. This low-spin configuration results purely from the crystal field splitting between the e_g states (Fig. 1B), leading to an on-site gap of ∼2.1 eV. We note that the structure comprised entirely of NiO₅ square pyramids has a ∼1.8 eV gap consistent with the on-site gap for Ni²⁺ in NiO₅ square pyramids in the single vacancy case (SI Appendix, Fig. S10D). From the XRD and resistivity characterization, we posit that such ordered structures are not present in the highly deficient case, but more likely that the system is a mixture of these structures or disordered structure with various Ni–O polyhedra. The nature of the gap originates both from the crystal field splitting of the different Ni–O polyhedra present and the on-site Coulomb repulsion present for high-spin Ni²⁺. This significantly differs from electron doping with interstitial hydrogen in which the NiO₆ octahedra remain intact and the crystal field splitting is not modified. In this case the larger ∼3 eV gap arises purely from the on-site Coulomb repulsion for an NiO₆ octahedral site (39).

To experimentally establish the differences of electron doping via interstitial hydrogen versus via oxygen vacancies, we compared the gaps of hydrogen-doped and oxygen-deficient samples. We prepared hydrogenated and oxygen-deficient SNO films possessing a similar amount of Ni²⁺(SI Appendix, Fig. S12A), determined by similar line shape and shifts of the Ni 2p XPS spectra in comparison with the pristine state. The transmission spectrum and absorption coefficient of both samples are shown in SI Appendix, Fig. S12 B and C. It is observed that the hydrogenated SNO (HSNO) is more transparent than the oxygen-deficient one in the whole wavelength range. The difference becomes more obvious in the visible wavelength range. The extracted optical bandgap from transmission spectra for HSNO and SNO_3-δ is 2.8 and 2.5 eV, respectively, consistent with the trend seen in the DFT calculations.

NNO thin films show charge localization behavior similar to that of SNO upon oxygen vacancy formation (SI Appendix, Fig. S13A), indicating the generality of charge transfer in this family. The X-ray absorption near edge structure prepeak at the O K-edge (∼530 eV) is gradually suppressed upon electron doping via oxygen vacancies (SI Appendix, Fig. S13C), corresponding to the filling of oxygen ligand hole states. At the Ni L₃-edge (SI Appendix, Fig. S13B), the spectral weight of the higher-energy component (centered around 856 eV), which is contributed to mainly by Ni 2p to 3d⁸Lⁿ excitation (43, 44), decreases upon doping. Simultaneously, the Ni L₂-edge splits into 2 peaks and the spectra of NNO_3-δ resemble that of NiO (45).

A quantitative description of the electronic structure evolution is shown in SI Appendix, Fig. S13D, where the Ni L₃ XAS spectra were fitted by a 2 Gaussian model with a linear background. The individual Gaussian components for the most oxygen-deficient sample are highlighted at the bottom. The area of the high-energy component (blue, ∼856 eV) is suppressed by the oxygen deficiency, while the low-energy component (orange, ∼854.5 eV) only experiences a small shift toward lower energy. The doping-induced changes are better depicted by the area ratio of the 2 Gaussian components (blue/orange). The area ratio exhibits a monotonic decrease down to the level of NiO (dashed line in SI Appendix, Fig. S13E) upon oxygen vacancy formation. The XAS analysis, therefore, demonstrates the charge transfer from oxygen vacancies to the unoccupied states (i.e., ligand holes) in Ni 3d – O 2p hybridized orbitals and dominance of Ni²⁺ with 3d⁸ configuration in oxygen-deficient nickelates.

Oxygen-deficient NNO_3-δ thin-film devices were investigated for electric field-driven resistance modulation (SI Appendix, Supplementary Text 4 and Fig. S14A). By applying a bias voltage (SI Appendix, Fig. S14B) at room temperature, the oxygen vacancies are driven toward the top Pd electrode and accumulate there. The oxygen vacancies cause charge localization near the interface and an opening of a wide band gap, resulting in a larger Schottky barrier and a higher resistance state. By reversing the polarity of the field (SI Appendix, Fig. S14C), the oxygen vacancies are redistributed and pushed away from the top electrode, which results in a gradual metallization of NdNiO_3-δ near the interface and a narrower band gap, allowing for a smooth tuning of the resistance by voltage control.

The resistance modulation of representative vertical NNO_3-δ devices with and without oxygen deficiency is shown in SI Appendix, Fig. S14D. Before introducing oxygen vacancies, the device is in a low-resistance state (since pristine NNO is a correlated metal at room temperature) and the resistance is almost independent of the pulse voltages applied. However, by applying successive negative voltage pulses (−3 V for 1 s), the resistance of the oxygen-deficient NNO_3-δ device increases gradually by 80% and becomes almost saturated after pulse number i >50. It is consistent with the working principle proposed in SI Appendix, Fig. S14B and indicates the accumulation of oxygen vacancies near the Pd/NNO_3-δ interface. Upon reversing the bias voltage, a gradual recovery of the resistance state appears, indicating the depletion of oxygen vacancies near the interface. A linear scaling between resistance modulation and electrical energy (V²t) is achieved (SI Appendix, Fig. S14E). As a result, multiple resistance states of NNO_3-δ devices can be reached by adjusting the magnitude and duration envelope of electric bias. Preliminary endurance testing further shows the stability of NNO_3-δ devices over 10⁴ switching cycles (SI Appendix, Fig. S14F) in ambient conditions. This analog behavior of NNO_3-δ 2-terminal devices, based on the charge localization induced by oxygen vacancies, suggests potential for future design of neural synaptic electronics. In addition, the oxygen-vacancy-induced charge localization and resulting changes to the electronic and optical properties could potentially manifest in a range of materials beyond the RNiO₃ series. Following the antidoping mechanism proposed recently by Liu et al. (46), such an effect could also be observed in other transition-metal-based negative charge transfer compounds under oxygen deficiency. More generally, the essential ingredients are substantial ligand character of the low-lying unoccupied states, which helps to localize added charge on the coordinated transition metal site, with a large on-site Coulomb repulsion to produce a large gap in the fully doped insulating state.

Summary

We demonstrate that oxygen vacancies lead to electron localization in rare-earth nickelates by reducing the nickel site valence from 3+ to 2+. Unlike other cases of electron doping in rare-earth nickelates, the vacancies lead to a change in stoichiometry that changes the local electronic structure and has a macroscopic effect on the electrical and optical properties as seen in the DFT + U calculations and experiments. Utilizing an oxygen-starved environment created with an Mg trap, we introduced oxygen vacancies into SNO and NNO thin films, leading to strong charge localization with a substantial increase of the electrical resistance and an opening of the bandgap. This behavior is reversible over multiple cycles and can be further explored in solid-state devices for their analog resistance switching behavior. Such a localization behavior upon charge filling, being opposite to most oxide materials, positions perovskite nickelates as a functional charge-blocking platform of interest to a diverse set of fields spanning interface science to neuromorphic hardware.

Methods

Synthesis of SmNiO₃ and NdNiO₃ Thin Films.

Perovskite nickelate thin films (SNO and NNO) were synthesized on LaAlO₃ (001) substrates (LAO) by magnetron cosputtering of elemental targets at room temperature followed by high-pressure annealing in pure oxygen gas. Prior to the film growth, the LAO substrates were cleaned with acetone and isopropanol and blow-dried with Ar gas. During deposition, the pressure of the growth chamber was maintained at 5 mTorr with flow of 40 standard cubic centimeters per minute (sccm) Ar and 10 sccm O₂ gases. To obtain the optimal stochiometric ratio, the sputtering powers were set as 170 W (radio frequency, RF) Sm and 85 W (direct current, DC) Ni for SNO and 160 W (RF) Nd and 85 W (DC) Ni for NNO, which were calibrated using energy-dispersive X-ray spectroscopy. The thin films were then annealed at 500 °C for 24 h in a high-pressure vessel filled with 1,500 pounds per square inch of oxygen gas to obtain the perovskite phase. Films with thickness of ∼60 nm were utilized in this work.

Creation of LPO2 Environment and Annealing of SNO and NNO.

The experimental setup to generate an LPO2 environment is shown in SI Appendix, Fig. S1A. Ultrahigh purity (UHP) Ar with flow rate of 30 mL/min was filtered with a home-built Mg trap. The trace amount of oxygen molecules in UHP Ar is reacted with magnesium powder and, therefore, an oxygen-starved environment is created. To enhance the oxidization reaction between Mg and O₂, the oxygen trap was maintained at ∼500 °C using a heating tape. The Ar gas with LPO2 was then introduced into the annealing chamber, the temperature of which was controlled by a tube furnace. To prevent the oxygen contamination from outside, a water trap was utilized at the end port. During annealing, the oxygen partial pressure of the system was monitored by a zirconia-based oxygen sensor. As shown in SI Appendix, Fig. S1B, the oxygen partial pressure p(O₂) of the annealing chamber can reach ∼10⁻²⁶ atm, which, therefore, provides a clean way to study the role of oxygen vacancies in complex oxide materials. Thermodynamic analyses of the Mg trap environment and working principles of oxygen sensor can be found elsewhere (47).

Characterization Techniques.

For details of the electrical property characterization, optical spectrum measurements, midinfrared nanoimaging, XRD measurements, X-ray photoelectron spectroscopy, and XAS see SI Appendix, Supplementary Text 1.

DFT Calculation of SmNiO_3-δ.

First-principles DFT calculations were carried out using VASP (48) using the Perdew–Burke–Ernzerhof exchange-correlation potential (49) along with projector augmented wave potentials (50, 51). A Hubbard U [within the rotationally invariant method of Liechtenstein et al. (52)] was included using U = 4.6 eV and J = 0.6 eV, and a plane wave cutoff of 520 eV. The density of states calculations used the tetrahedral method with Blöchl corrections (53). Calculations of SmNiO_2.875 were carried out using a 2 × 2 × 2 supercell, relative to the 5-atom perovskite primitive cell, with one oxygen vacancy. The internal coordinates were relaxed such that the forces were less than 0.005 eV/Å while keeping the lattice parameters fixed to a = 5.278 Å, b = 5.818 Å, c = 7.421 Å, and β = 90.005°. The relaxed structure of SNO had G-type magnetic ordering (38). To aid in localizing electrons on a particular octahedron or square pyramid the orbital occupation of each nickel was controlled (54). A selection of stoichiometries commonly present in oxygen-deficient perovskites were explored (55) for SmNiO_2.5. These calculations were carried out in a supercell commensurate with the chosen stoichiometry while the lattice parameters were fixed to that of pristine SNO. The same parameters (as stated above) were used and the internal coordinates were allowed to relax.

Oxygen Vacancy-Mediated Solid-State Device Fabrication and Characterizations.

With photolithography techniques, vertical NdNiO_3-δ-based devices were fabricated. The pristine NdNiO₃ thin films of ∼50 nm thickness were synthesized by magnetron sputtering from NdNiO_x ceramic target at 250 W (RF) in 40 sccm Ar and 10 sccm O₂ gas mixture with pressure of 5 mTorr on fluorine-doped tin oxide substrates. The as-deposited thin films were subsequently annealed in air at 500 °C for 24 h to form the perovskite phase. To introduce oxygen vacancies, the NdNiO₃ thin films were then LPO2-annealed at 400 °C for 40 min.

To fabricate the device, the sample was spin-coated by AZ5214E photo resist at 4,000 rpm for 1 min before exposure to ultraviolet light. The first step exposure time was extended to avoid under-edge cut. After exposure and development, the sample was wet etched in a dilute HCl solution (HCl:H₂O = 1:3 in volume percentage). It was then rinsed in distilled water. Then the AZ5214E on sample was removed by Remover-PG with ultrasonic for 15 min, followed by a 5-min soak in acetone. Then the sample was cleaned by isopropanol and blow-dried by a N₂ gun. The bilayer photo resists used for the second photo lithography were LOR-3A and S1813. After the photo lithography, the Pd electrodes with a thickness of ∼100 nm were deposited by sputtering. Then Remover-PG heated up to 80 °C was used for lift-off process, followed by a 5-min soak in acetone. Finally, the sample was cleaned by isopropanol and blow-dried by a N₂ gun. An image of a representative device is shown in SI Appendix, Fig. S14A. The diameters of NdNiO_3-δ functional layer and Pd electrode disks are designed as 300 μm and 200 μm, respectively, in this work. The voltage pulse training and resistance measurement of devices were performed with a Keithley 2635A source meter at ambient conditions.