Time-trend impact on treatment estimation in two-arm clinical trials with a binary outcome and Bayesian response adaptive randomization

Abstract

Clinical trial design and analysis often assume study population homogeneity, although patient baseline profile and standard of care may evolve over time, especially in trials with long recruitment periods. The time-trend phenomenon can affect the treatment estimation and the operating characteristics of trials with Bayesian response adaptive randomization (BRAR). The mechanism of time-trend impact on BRAR has received little attention. The goal of this research is to quantify the bias in treatment effect estimation due to the use of BRAR in the presence of time-trend. In addition, simulations are conducted to compare the performance of three commonly used BRAR algorithms under different time-trend patterns with and without early stopping rules. The results demonstrate that using these BRAR methods in a two-arm trial with time-trend may cause type I error inflation and treatment effect estimation bias. The magnitude and direction of the bias are affected by the parameters of the BRAR algorithm and the time-trend pattern.

1. Introduction

Clinical trial design and analysis often assume study population homogeneity.¹ In trials with long recruitment periods due to the large sample sizes or rare disease conditions, patient baseline profile and standard of care can evolve over time.² Response adaptive randomization (RAR) changes treatment allocation ratio based on obtained patient response information in the ongoing trial, motivated by consideration of patient ethical benefit and trial efficiency.^3,4 The combination of RAR and time-trend affects the treatment effect estimation and the trial operating characteristics, and has received researchers’ attention for many years.⁵ Studies suggest that RAR may lead to type I error inflation when time-trend exists.^6,7,8 Recent work by Villar et al. indicated that both time-trend and RAR algorithm affect the trial performance, including a myopic BRAR type of rule as the ones studied in this paper.⁹

Table 1 presents a conceptual scenario illustrating the mechanism of how bias in treatment effect estimation is occurred as a result of the combination of the use of RAR and the presence of time-trend. Consider a two-arm trial with a fixed equal allocation stage of 200 patients, a RAR stage of 200 subjects, and one allocation update based on the result of an interim analysis at the end of the first stages. Suppose the response rate in stage 1 is 35% and 25% for the treatment arm and the control arm respectively. Assume a time-trend of 10% increase in the response rate from stage 1 to stage 2 occurs in both arms, so that the response rate in stage 2 is 45% and 35% respectively for the two arms. Let 7:3 be the updated allocation ratio between the treatment and the control given by the chosen RAR algorithm based on the observed response rates in stage 1. The combination of the time-trend and the RAR algorithm assigns 140 patients with a response rate of 45% to the treatment arm, and 60 patients with a response rate of 35% to the control arm.

Table 1.

Treatment effect estimation bias due to RAR in the presence of a time-trend.

	Stage 1		Stage 2*		Total
Size	200		200		400
Allocation Ratio	1:1		7:3		3:2
Arm	Treatment	Control	Treatment	Control	Treatment	Control
Subjects	100	100	140	60	240	160
Success	35	25	63	21	98	46
Response Rate	35%	25%	45%	35%	40.8%	28.8%
Treatment Effect Estimation	10%		10%		12%

^*:with 10% time-trend response rate increase in both arms.

The overall observed treatment effect estimation will be (40.8% – 28.8%) = 12%, a 2% inflation from the actual treatment effect size of 10%.

As an essential component of Bayesian adaptive clinical trial, Bayesian response adaptive randomization (BRAR) has gained increasing application in recent years, not only in small early phase trials, but also in some large confirmatory trials, which are vulnerable to time-trend. The combined impact of time-trend and BRAR on the statistical performance of the trial is critical for the design and analysis of Bayesian adaptive clinical trials. Thall et al. reported a simulation study with a linear time-trend and BRAR update of every one subject, without burn-in period, and found that the treatment effect estimation may be biased with a magnitude affected by the stopping rules, and the type I error and power could be inflated to an undesirable level.7 Previous researches also indicated that early stopping results in biased treatment estimates,^10,11 and the size of the fixed allocation burn-in period impacts the type I error and power.¹² However, the mechanism of the impacts of the time-tend, the BRAR, the stopping rule, and the burn-in period size on the treatment effect estimation and the error rates remains unclear, and requires more studies at different scenarios of trial settings, time-trend patterns, and BRAR algorithms and their implementation parameters.

In this paper, three commonly used BRAR algorithms with various implementation parameters are examined in two-arm binary outcome trial scenarios with different time-trend patterns. The goal of this research is to quantify the impact of time-trend and BRAR algorithm on the treatment effect estimation bias, the error rates, and the final treatment allocation, so that investigators could be better informed when designing a Bayesian adaptive trial and choosing an BRAR algorithm. The contents of this study is focused on the two-arm trials in order to gain a better understanding of the impact under a simplified situation before addressing the more complex multi-arm setting.

Section 2 describes a generalized formula for three commonly used BRAR algorithms and time-trend patterns, provides the analytical results of the bias under different time-trend patterns, and defines the study scenarios. Section 3 presents the analytical and simulation results. Section 4 presents potential solutions to minimize the time-trend impact, followed by discussions of the limitations of this research as well as future research directions in Section 5.

2. Method

To quantitatively assess the impact of time-trend on the performance of Bayesian adaptive trials, factors from three areas are included in this study: the Bayesian response adaptive randomization (BRAR) algorithm; the pattern and magnitude of the time-trend; and trial implementation parameters such as the burn-in period size, the interim analysis plan and associated stopping boundaries.

2.1. A generalized formula for BRAR algorithms

With a BRAR for a two-arm trial with a binary outcome, the target treatment allocation r₁ : r₂ for the next stage of the trial is updated based on the posterior probabilities obtained according to the so far observed response data and the BRAR algorithm. Commonly used BRAR algorithms can be expressed with a generalized formula:

$$r_j\propto \frac{P_j^{\alpha }Var{\left(p_j\right)}^{\beta }}{n_j^{\gamma }}(j=1,2).$$ (1)

Here n_j, p_j., and Var(p_j) are respectively the number of patients enrolled, the posterior probability of success, and its variance for arm j. Assuming the probability of success for arm j has a uniform non-informative prior distribution P_j ~ Beta(1,1), i.e. one success and one failure in the two subjects prior to the start of the trial. P_j = Pr[P_j = max(p₁, p₂)] is the posterior probability that arm j is the better arm than the other. Tuning parameters for P_j, Var(p_j), and n_j. are α, β, and γ, respectively.

Three commonly used BRAR algorithms are: the probability-weighted allocation with α = 1/2, β = 0, and γ = 0, referred to as BRAR(1/2);¹³ the information-weighted allocation with α = 1/2, β = 1/2, and γ = 1/2, referred to as BRAR(1/2,σ²);^14,15 and, the lead-in allocation with α = n/2N, β = 0, and γ = 0, referred to as BRAR(n / 2N). Here n and N are the enrolled sample size and the maximum sample size, respectively.¹³ The evaluation of the posterior probability Pr[p_j = max(p₁, p₂)] involves the integration of incomplete beta function, which has no direct solution. A closed-form solution based on normal approximation is given by Cook et al.¹⁶

$$\text{Pr}\left(p_1>p_2\right)\approx \Phi \left(\frac{{\mu }_1-{\mu }_2}{\sqrt{{\sigma }_1^2+{\sigma }_2^2}}\right)\approx \Phi \left(\frac{\mathrm{\Delta }}{\sqrt{{\sigma }_1^2+{\sigma }_2^2}}\right).$$ (2)

Here μ₁, μ₂ are the means, and ${\sigma }_1^2$, ${\sigma }_2^2$ are the variances for the independent random variables for the success rates in arm 1 and arm 2 respectively. As sample size increases, μ₁−μ₂ is approximately equal to the observed difference in the success rates between the two arms (Δ). In the presence of time-trend and BRAR, Δ is expected to increase along with the value of $\Phi \left(\mathrm{\Delta }/\sqrt{{\sigma }_1^2+{\sigma }_2^2}\right)$ (i.e. Pr(p₁ > p₂)), because the BRAR will push the allocation ratio further away from the balanced point based on the inflated treatment effect estimation.

2.2. Time-trend patterns and impacts on bias

Constancy in patients’ risk background over time is a critical assumption for obtaining valid inferences in trials with long-term enrollment. In practice, patients’ responses to study treatments may change over time. Such time-trend may occur in both arms or in one arm but not the other. The actual pattern of the time-trend is usually unpredictable. A linear time-trend is often used by researchers to explore its impact on treatment effect estimation bias and trial operating characteristics.^6,7

Consider applying a BRAR to a two-arm trial with m interim stages and a linear time-trend in the response rate for each treatment arm:

$$p_{j,k}={\tilde{p}}_j+k{\tau }_j(j=1,2;k=1,2,\dots ,m)$$ (3)

Let ${\tilde{p}}_j$ be the true response rate for arm j without time-trend; k be the stage on which the treatment allocation is updated based on the BRAR algorithm; τ_j be the time-trend effect in the response rate for arm j, and p_j,k be the expected response rate for arm j within stage k. Let $\mu ={\tilde{p}}_1-{\tilde{p}}_2$ be the treatment effect of the trial without time-trend. Let δ_j = mτ_j be the overall time-trend effect throughout the entire study period.

Without time-trend (τ_j = 0), the expected response rate does not change over time for either arm. The expected cumulative response rate difference between the two treatment arms from stage 1 to stage k is a constant.

$${\mathrm{\Delta }}_k=\frac{{\sum }_{s=1}^k{p}_{1,s}\times n_{1,s}}{{\sum }_{s=1}^k{n}_{1,s}}-\frac{{\sum }_{s=1}^k{p}_{2,s}\times n_{2,s}}{{\sum }_{s=1}^k{n}_{2,s}}=\frac{p_{1,s}{\sum }_{s=1}^k{n}_{1,s}}{{\sum }_{s=1}^k{n}_{1,s}}-\frac{p_{2,s}{\sum }_{s=1}^k{n}_{2,s}}{{\sum }_{s=1}^k{n}_{2,s}}=p_{1,s}-p_{1,s}={\tilde{p}}_1-{\tilde{p}}_2=\mu$$ (4)

With an equal time-trend for both arms, i.e. τ₁ = τ₂ = τ, the expected cumulative response rate difference between two treatment arms up to stage k is

$${\mathrm{\Delta }}_k=\frac{{\sum }_{S=1}^k\left({\tilde{p}}_1+s\tau \right)\times n_{1,S}}{{\sum }_{S=1}^k{n}_{1,S}}-\frac{{\sum }_{S=1}^k\left({\tilde{p}}_2+s\tau \right)\times n_{2,S}}{{\sum }_{S=1}^k{n}_{2,S}}=\left({\tilde{p}}_1-{\tilde{p}}_2\right)+\tau \left(\frac{{\sum }_{S=1}^{k}s{n}_{1,S}}{{\sum }_{S=1}^k{n}_{1,S}}-\frac{{\sum }_{S=1}^{k}s{n}_{2,S}}{{\sum }_{S=1}^k{n}_{2,S}}\right).$$ (5)

The bias increases from (k-1)^th to k^th interim stage can be defined as follows:

$${\mathrm{\Delta }}_k-{\mathrm{\Delta }}_{k-1}=\tau \left[\left(\frac{\sum _{s=1}^{k}s{n}_{1,s}}{\sum _{s=1}^k{n}_{1,s}}-\frac{\sum _{s=1}^{k}s{n}_{2,s}}{\sum _{s=1}^k{n}_{2,s}}\right)-\left(\frac{\sum _{s=1}^{k-1}s{n}_{1,s}}{\sum _{s=1}^{k-1}{n}_{1,s}}-\frac{\sum _{s=1}^{k-1}s{n}_{2,s}}{\sum _{s=1}^{k-1}{n}_{2,s}}\right)\right]$$ (6)

Let the allocation ratio between arm 1 and arm 2 at stage k be r_k = n_1,k / n_2,k, equation (6) can be reformatted as (see appendix 1 for details):

$${\mathrm{\Delta }}_k-{\mathrm{\Delta }}_{k-1}=\tau \left(\frac{n_{1,k}\sum _{s=1}^{k-1}s{n}_{1,s}}{\left(\sum _{s=1}^k{n}_{1,s}\right)\left(\sum _{s=1}^{k-1}{n}_{1,s}\right)}-\frac{n_{2,k}\sum _{s=1}^{k-1}s{n}_{2,s}}{\left(\sum _{s=1}^k{n}_{2,s}\right)\left(\sum _{k=1}^{k-1}{n}_{2,s}\right)}\right)=\frac{\tau n_{2,k}\sum _{a=1}^{k-1}\sum _{b=1}^{k-1}\sum _{c=1}^{k-1}k{n}_{2,a}{n}_{2,b}{n}_{2,c}\left(r_a{r}_k-r_b{r}_c\right)}{\left(\sum _{s=1}^k{n}_{1,s}\right)\left(\sum _{s=1}^{k-1}{n}_{1,s}\right)\left(\sum _{s=1}^k{n}_{2,s}\right)\left(\sum _{s=1}^{k-1}{n}_{2,s}\right)}$$ (7)

With BRAR, the adaptive allocation ratio increases over stages, r_k−1 < r_k (1 < k < m) (see appendix 2 for details). Therefore, the result from equation (7) is always positive, indicating that the bias increases with the drift increase in the adaptive allocation ratio over interim stages.

With different time-trend effects for the two arms, the expected cumulative response rate difference between two treatment arms up to stage k is

$$\begin{gathered} {\mathrm{\Delta }}_k-{\mathrm{\Delta }}_{k-1}=\frac{{\tau }_1{n}_{1,k}\sum _{s=1}^{k-1}k{n}_{1,s}}{\left(\sum _{s=1}^k{n}_{1,s}\right)\left(\sum _{s=1}^{k-1}{n}_{1,s}\right)}-\frac{{\tau }_2{n}_{2,k}\sum _{s=1}^{k-1}k{n}_{2,s}}{\left(\sum _{s=1}^k{n}_{2,s}\right)\left(\sum _{k=1}^{k-1}{n}_{2,s}\right)} \\ =\frac{n_{2,k}\sum _{a=1}^{k-1}\sum _{b=1}^{k-1}\sum _{c=1}^{k-1}a{n}_{2,a}{n}_{2,b}{n}_{2,b}\left({\tau }_1{r}_k{r}_a-{\tau }_2{r}_b{r}_c\right)+r_k{n}_{2,k}{n}_{2,k}\sum _{a=1}^{k-1}\sum _{b=1}^{k-1}a{n}_{2,a}{n}_{2,b}\left({\tau }_1{r}_a-{\tau }_2{r}_b\right)}{\left(\sum _{s=1}^k{n}_{1,s}\right)\left(\sum _{s=1}^{k-1}{n}_{1,s}\right)\left(\sum _{s=1}^k{n}_{2,s}\right)\left(\sum _{s=1}^{k-1}{n}_{2,s}\right)} \end{gathered}$$ (8)

The magnitude of bias increases (or decreases) depending on the time-trend magnitude (τ₁, τ₂) and the adaptive allocation ratio (r_k).

2.3. Trial setting and simulation study scenarios

Consider a two-arm trial with a maximum sample size of 302 to detect the response rate difference between treatment and control, p₁ = 0.4, p₂ = 0.3. The maximal sample size is selected based on the number of interim stages and the size of each stage. Three time-trend patterns are examined: no time-trend (δ₁ = δ₂ =0); equal time-trend (δ₁ = δ₂ =0.1); and unequal time-trend (δ₁ = 0, δ₂ =0.1). The expected performance of BRAR is evaluated based on bias in treatment effect estimation and drift in adaptive allocation ratio. For all three time-trend scenarios, $\mu ={\tilde{p}}_1-{\tilde{p}}_2$ represents the actual treatment effect without time-trend. To examine the behavior of BRAR under the impact of time-trend, different levels are set for the three turning parameters: 11 values for α (from 0 to 1 with an increment of 0.1); 5 values for β (0, 0.2, 0.5, 0.8, and 1); and 3 levels for γ (0, 0.5 and 1).

Simulation studies are conducted to assess the distribution of trial operating characteristics based on the three commonly used BRAR algorithms. The simulation study starts with an equal allocation burn-in period of 50 patients, followed by maximal 9 BRAR stages of 28 patients each, with or without early stopping for efficacy after interim analyses. Information on trial settings are assembled based on the trial design and implementation parameters listed in Table 2.

Table 2.

Trial scenarios and parameters max sample size=302, # arms=2, balanced burn-in period=50,p₂=0.3, and allocation update frequency=28.

Study Description	Expected Performance Based on BRAR algorithm	Simulation Studies without stopping rules	Simulation Studies with stopping rules
Treatment efficacy profile	p1=0.4	p1=0.4;	Scenario 1: p1=0.3; Scenario 2: p1=0.4; Scenario 3: p1=0.5.
Time-trend (linear)	No trend: δ1=0, δ2=0; Equal trend: δ1=0.1, δ2=0.1; Unequal trend: δ1=0, δ2=0.1.	No trend: δ1=0, δ2=0 Equal trend: δ1=0.1,δ2=0.1 Equal trend: δ1=0.2, δ2=0.2. Unequal trend: δ1=0, δ2=0.1.	No trend: δ1=0, δ2=0; Equal trend: δ1=0.1, δ2=0.1; Equal trend: δ1=0.2, δ2=0.2. Unequal trend: δ1=0, δ2=0.1.
RAR algorithm parameters	$r_j\propto \frac{P_j^{\alpha }Var{(p_j)}^{\beta }}{n_j^{\gamma }}$ α=0 to 1 by 0.1; β=0,0.2,0.5,0.8,1; γ=0, 0.5,1;	BRAR (1/2) BRAR (1/2, σ2) BRAR (n/2N)	BRAR (1/2) BRAR (1/2, σ2) BRAR (n/2N)
Efficacy stopping rule	None	None	$P_j>0.99$
Estimation of type I error	___________	_______________	Proportion of simulation runs with: $P_j>0.99$ under efficacy scenario 1.
Estimator of power	___________	_______________	Proportion of simulation runs with: $P_j>0.99$ under efficacy scenarios 2 and 3.
Simulation iteration	___________	10,000 per scenario	10,000 per scenario.

Note: p_j are the posterior probability of success that arm j is better than the other arms, j=1,2.

3. Results

3.1. Expected performance of BRAR without early stopping under three time-trend patterns

The expected performance of BRAR without early stopping under three time-trend patterns is shown in Figure 1. Without interim analyses and time-trend (δ₁ = δ₂ =0), there is no bias across all tuning parameter scenarios (Figure 1a). The treatment allocation ratio changes from 1:1 to 1:1.52, driven by the treatment effect size ${\widehat{p}}_1-{\widehat{p}}_2=0.1$ and BRAR (Figure 1b). The magnitude of the allocation ratio drift increases as α increases. The variation of the allocation ratio decreases as β increases.

Figure 1.

Expected performance of BRAR without early stopping

With equal time-trend(δ₁ = δ₂ = 0.1), the bias in the treatment effect estimation is small. It increases slightly from 0 to a range of 0.016–0.022 as α increases from 0 to 1 (Figure 1c). However, the allocation ratio shift and its variation increase rapidly as α increases (Figure 1d). A greater β value helps to reduce the deviations in allocation ratio and bias in treatment effect estimation. A greater value of γ also helps to reduce the allocation ratio shift.

When time-trend occurs only in the control arm, the treatment effect estimation is biased downward, with its magnitude increases as α increases (Figure 1e). Meanwhile, the allocation ratio drift also increases as α increases, but at a reduced pace due to the negative bias in the observed treatment effect estimation (Figure 1f).

3.2. Impact of time-trend on BRAR design without early stopping

Figure 2 displays the distributions of the bias under three commonly used BRAR algorithms and four time-trend patterns, without early stopping for efficacy. There is no bias in the treatment estimation for any time-trend pattern under fixed equal allocation. When using BRAR without time-trend, the bias is negligible (Figure 2a). With equal time-trend for both arms, all three BRAR algorithms have bias in treatment effect estimation, with the magnitude increases as study stage increases (Figures 2b and 2c). The probability-weighted allocation BRAR(1/2) has the greatest variability and magnitude of bias, followed by BRAR(1/2, σ²) and BRAR(n/2N). When time-trend occurs only in the control arm, the treatment effect estimation is biased downwards for all the three BRAR algorithms (Figure 2d).

Figure 2.

Bias in treatment effect estimation (mean ± sd) by interim stage

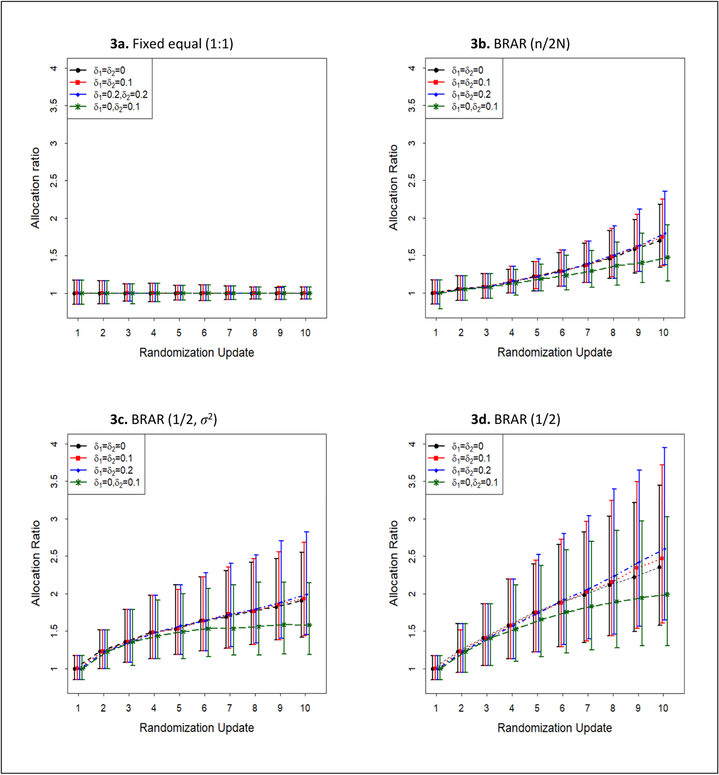
Figure 3 shows the cumulative treatment assignments over allocation ratio update stages under different time-trend patterns and BRAR algorithms without early stopping for efficacy. Fixed equal allocation has well-controlled and gradually decreased variation over stages, without being affected by the time-trend (Figure 3a). With equal time-trend, a larger trend can lead to unexpected allocation drift for all the three BRAR algorithms. Among them, the probability-weighted allocation BRAR(1/2) has the greatest variability and magnitude of allocation shift over allocation ratio update stages (Figure 3d), followed by information-weighted allocation BRAR(1/2, σ²) (Figure 3c) and lead-in allocation BRAR(n/2N) (Figure 3b).

Figure 3.

Allocation ratio n₁/n₂ (median, 25^th and 97.5^th percentile) by interim stage

3.3. Impact of time-trend on BRAR design with early stopping

Table 3 reports the type I error, power and bias for fixed and BRAR algorithms in the presence of a time-trend and early stopping for efficacy. The magnitude of bias is not affected by the presence of equal time-trend under fixed equal allocation. However, unequal time-trend will affect all BRAR designs and is dependent on the direction of the time-trend. Under the trial settings in this study, BRAR may have a higher power in the presence of equal time-trend at the cost of type I error rate inflation, when compared to fixed equal allocation.

Table 3.

Impact of time-trend on operating characteristics of BRAR with early stopping rule maximum sample size=302, burn-in size=50, allocation update frequency=28, Efficacy stop=0.99

Randomization algorithm	Efficacy profile	Trend pattern	Sample size	Efficacy stopping in favor of Arm 1 Arm 2	% better arm (SD)	Bias(SD)
Fixed equal (1:1)	P1=P2=0.3	δ1=0, δ2=0	289 (51)	0.04	0.036	0.50 (0.031)	0.0007(0.084)
		δ1=0.1, δ2=0.1	289 (50)	0.038	0.037	0.50 (0.031)	0.0009(0.083)
		δ1=0.2, δ2=0.2	289 (49)	0.039	0.036	0.50 (0.031)	0.0008(0.084)
		δ1=0, δ2=0.1	286 (52)	0.023	0.087	0.50 (0.032)	−0.047 (0.083)
	P1=0.4, P2=0.3	δ1=0, δ2=0	246 (84)	0.382	0.001	0.50 (0.036)	0.029 (0.096)
		δ1=0.1, δ2=0.1	246 (85)	0.371	0.002	0.50 (0.037)	0.029 (0.099)
		δ1=0.2, δ2=0.2	246 (85)	0.374	0.002	0.50 (0.036)	0.029 (0.097)
		δ1=0, δ2=0.1	260 (82)	0.237	0.002	0.50 (0.035)	−0.014(0.108)
	P1=0.5, P2=0.3	δ1=0, δ2=0	148 (81)	0.899	0	0.50 (0.048)	0.044 (0.094)
		δ1=0.1, δ2=0.1	147 (82)	0.895	0	0.50 (0.048)	0.049 (0.097)
		δ1=0.2, δ2=0.2	149 (83)	0.887	0	0.50 (0.049)	0.047 (0.097)
		δ1=0, δ2=0.1	164 (95)	0.767	0	0.50 (0.047)	0.028 (0.112)
BRAR(n/2N)	P1=P2=0.3	δ1=0, δ2=0	289 (50)	0.034	0.038	0.50 (0.077)	−0.0014 (0.083)
		δ1=0.1, δ2=0.1	288 (50)	0.04	0.046	0.50 (0.079)	−0.0008 (0.089)
		δ1=0.2, δ2=0.2	286 (52)	0.058	0.055	0.50 (0.082)	−0.0002 (0.098)
		δ1=0, δ2=0.1	286 (51)	0.025	0.09	0.47 (0.075)	−0.048 (0.085)
	P1=0.4, P2=0.3	δ1=0, δ2=0	248 (84)	0.355	0.001	0.58 (0.064)	0.028 (0.094)
		δ1=0.1, δ2=0.1	244 (84)	0.411	0.002	0.58 (0.065)	0.037 (0.096)
		δ1=0.2, δ2=0.2	238 (85)	0.469	0.003	0.57 (0.065)	0.046 (0.097)
		δ1=0, δ2=0.1	260 (81)	0.241	0.002	0.56 (0.069)	−0.010 (0.108)
	P1=0.5, P2=0.3	δ1=0, δ2=0	150 (84)	0.874	0	0.56 (0.067)	0.046 (0.097)
		δ1=0.1, δ2=0.1	145 (80)	0.909	0	0.56 (0.067)	0.052 (0.092)
		δ1=0.2, δ2=0.2	143 (77)	0.928	0	0.56 (0.065)	0.054 (0.091)
		δ1=0, δ2=0.1	163 (95)	0.772	0	0.57 (0.070)	0.032 (0.109)
BRAR(1/2,σ2)	P1=P2=0.3	δ1=0, δ2=0	290 (47)	0.036	0.034	0.50 (0.095)	0.0008 (0.082)
		δ1=0.1, δ2=0.1	288 (51)	0.047	0.044	0.50 (0.096)	0.0013 (0.091)
		δ1=0.2, δ2=0.2	284 (55)	0.061	0.061	0.50 (0.099)	0.0002 (0.101)
		δ1=0, δ2=0.1	287 (51)	0.024	0.09	0.46 (0.093)	−0.048 (0.086)
	P1=0.4, P2=0.3	δ1=0, δ2=0	251 (82)	0.344	0.003	0.61(0.076)	0.029 (0.097)
		δ1=0.1, δ2=0.1	245 (84)	0.396	0.002	0.61 (0.076)	0.037 (0.097)
		δ1=0.2, δ2=0.2	239 (85)	0.453	0.003	0.61 (0.076)	0.045 (0.100)
		δ1=0, δ2=0.1	260 (80)	0.24	0.004	0.59 (0.083)	−0.009 (0.110)
	P1=0.5, P2=0.3	δ1=0, δ2=0	157 (86)	0.858	0	0.63 (0.078)	0.046 (0.097)
		δ1=0.1, δ2=0.1	150 (83)	0.89	0	0.62 (0.080)	0.054 (0.096)
		δ1=0.2, δ2=0.2	144 (78)	0.919	0	0.62 (0.077)	0.059 (0.091)
		δ1=0, δ2=0.1	170 (96)	0.747	0	0.62 (0.079)	0.030 (0.110)
BRAR(1/2)	P1=P2=0.3	δ1=0, δ2=0	290 (49)	0.032	0.038	0.50 (0.129)	−0.0022 (0.086)
		δ1=0.1, δ2=0.1	287 (52)	0.049	0.05	0.50 (0.135)	0.0001 (0.096)
		δ1=0.2, δ2=0.2	283 (55)	0.069	0.07	0.50 (0.138)	−0.0016 (0.107)
		δ1=0, δ2=0.1	287 (50)	0.023	0.085	0.46 (0.128)	−0.049 (0.088)
	P1=0.4, P2=0.3	δ1=0, δ2=0	255 (81)	0.316	0.002	0.64 (0.102)	0.028 (0.096)
		δ1=0.1, δ2=0.1	246 (83)	0.394	0.003	0.64 (0.100)	0.041 (0.096)
		δ1=0.2, δ2=0.2	237 (84)	0.481	0.003	0.64 (0.102)	0.053 (0.098)
		δ1=0, δ2=0.1	262 (79)	0.232	0.004	0.62 (0.111)	−0.007 (0.110)
	P1=0.5, P2=0.3	δ1=0, δ2=0	162 (90)	0.82	0	0.65 (0.099)	0.046 (0.096)
		δ1=0.1, δ2=0.1	153 (84)	0.882	0	0.65 (0.098)	0.054 (0.091)
		δ1=0.2, δ2=0.2	146 (79)	0.917	0	0.64 (0.096)	0.060 (0.088)
		δ1=0, δ2=0.1	176 (98)	0.712	0	0.65 (0.101)	0.029 (0.110)

Under BRAR, in comparison to no time-trend, equal time-trend (δ₁ = δ₂ = 0.1 or δ₁ = δ₂ = 0.2) yields a greater probability of stopping early at the cost of increased bias in the treatment effect estimation. When time-trend occurs only in the control arm, i.e. δ₁ =0, δ₂ =0.1, the average sample size slightly increases while the power for identifying better treatment drops considerably as the control arm catches up with the treatment. The average final allocations are similar regardless of time-trend patterns, although the variability of allocation across randomization update stages may be large (as in Figure 1). The presence of time-trend is more likely to cause bias in treatment effect estimation in addition to the early stopping. And the bias of BRAR is largely due to the presence of time-trend in addition to the early stopping. Among all BRAR algorithms, BRAR(1/2) is most vulnerable to time-trend, yielding a greater type I error, followed by BRAR(1/2, σ²) and BRAR(n/2N).

It is known that observed treatment effect sizes are inflated when trials stop early for overwhelming efficacy.^9,11 Figure 4 displays the distributions of treatment estimation bias at final stage of the trial by BRAR algorithms under four time-trend patterns, comparing trials with and without interim early stopping. Simulation results shown that early stopping can lead to significantly large variation in treatment effect estimation. Without time-trend and early stopping, there is no bias in the treatment effect estimation when fixed equal randomization is used (Figures 4a, 4c, 4e, and 4g). The bias caused by BRAR alone is quite minimal. However, bias increases for all the three BRAR algorithms and time-trend scenarios when early stopping rule is incorporated (Figures 4b, 4d, 4f, and 4dh).

Figure 4.

Distribution of bias in treatment estimation at end of the trial

4. Methods to control type I error inflation due to time-trend

The impact of time-trend can be controlled either in the analyses or during randomization.¹⁷ Efforts have been made to identify appropriate statistical methods for data analysis with potential time-trend such as stratified analysis and randomization test.^6,8 The block-stratified analysis may reduce the impact of time-trend, but may also impair the trial efficiency by increasing sample size and the chance of patients being assigned to the inferior treatment.¹⁸ Incorporating time-trend information into the regression analysis can be considered as a promising technique to control the confounding effect. However, including unnecessary covariates in the model can result in an ambiguous interpretation of the trial result.¹⁹ In practice, the cause of time-trend may not be measured,²⁰ and therefore is hard to be included in the analysis model.

Alternatively, the time-trend effect can be consider as a function of time or interim stage and modify the BRAR allocation ratio based on time-trend adjusted treatment effect.²¹ Let y_i,k be the binary outcome variable, x_i be the binary treatment indicator, and U be the set of potential confounding factors. The binary response outcome for i^th patient enrolled in interim stage k is assumed to follow a Bernoulli distribution y_i,k ~ Bern(p_i,k), y_i,k = 0,1. The time dependence will be modeled through a logistic regression with a fixed treatment effect and an underlying time-trend process.

$$\text{log\hspace{0.17em}}it\left(p_{i,k}\right)={\beta }_0+{\beta }_{trt}{x}_i+U_k,i=1,2,\dots ,n_k,k=1,\dots ,m.$$ (9)

Here k denotes the stage of BRAR allocation update and the timing for interim analysis, i is the subject indicator, and U_k is the linear time-trend component. Assume that response outcome follows a deterministic time linear trend with effect of β_k :

$$U_k={\beta }_{k}k$$ (10)

Here β_k defines an expected increase in the linear time-trend from stage k−1 to stage k. The prior distributions are carefully chosen for the treatment effect and intercept. The priors are normally distributed with center 0 and precision ψ for beta coefficients. In logistic regression, normal prior distributions with large variance are no longer non-informative in the probability scale.²² Therefore, the precision parameter is assigned with a hyper prior of gamma distribution, in order to yield a standard deviation of 1.4 (or precision of 0.5), and to achieve evenly distributed outcome in the probability scale.

$$\begin{gathered} {\beta }_0~N\left(0,{\psi }_{{\beta }_0}^{-1}\right),{\psi }_{{\beta }_0}~\text{Gamma}(0.2,0.4). \\ {\beta }_{trt}~N\left(0,{\psi }_{{\beta }_{trt}}^{-1}\right),{\psi }_{{\beta }_{trt}}~\text{Gamma}(0.2,0.4). \\ {\beta }_t~N\left(0,{\psi }_{{\beta }_t}^{-1}\right),{\psi }_{{\beta }_t}=1/{\sigma }_{{\beta }_t}^2,{\sigma }_{{\beta }_t}~U(0,10). \end{gathered}$$ (11)

The three BRAR algorithms are defined based the posterior probability that one treatment is better than the other i.e. π₁₂ = Pr(p₁ > p₂), where p₁ and p₂ is the posterior probability of success for arm 1 and arm 2 respectively. An alternative way of contrasting two rates is the odds ratio $O{R}_{12}=\frac{p_1/\left(1-p_1\right)}{p_2/\left(1-p_2\right)}$ which can be directly obtained from the logistic regression posterior estimation $O{R}_{12}=e^{{\beta }_{trt}}$, where β_trt is the model adjusted coefficient parameter for treatment effect comparing two arms from the logistic regression model. To replace π₁₂ by estimation λ₁₂ = P(OR₁₂ > 1), the step function in Winbugs²³ is used to identify the proportion of simulations runs with OR greater than 1. This model based approach uses the allocation ratio adjusted by the amount of information (sample size) for patient randomization.²¹

$$r_j=\frac{\sqrt{{\lambda }_j/n_j}}{{\sum }_{j=1}^m\sqrt{{\lambda }_j/n_j}}(j=1,2)$$ (12)

Using similar trial settings specified in Section 2, a simulation study was conducted to explore the performance of this new approach, with the BRAR algorithm being replaced by the model based randomization. The results show that the type I error inflation is controlled after this adjustment (Table 4) as compared to the three BRAR algorithms under the impact of a time-trend of 0.1 for both arms, with a cost of power lose. The model adjusting for the time-trend confounding effect is shown to prevent the over-estimation of treatment effect, and it also tends to reduce the power when the actual treatment effect exists. In addition, compared to the stratified analysis by block of 6 patients, the model-based adjustment approach has an advantage of accommodating both the interim analysis and treatment allocation ratio during the trial.

Table 4.

Impact of time-trend on operating characteristics of BRAR with early stopping rule maximum sample size=302, burn-in size=50, allocation update frequency=28, Efficacy stop=0.99, # simulation =1000.

Algorithms	Time-trend effect	Efficacy profile	BRAR(1/2,σ2), time trend
			Sample size	% better arm (SD)	Type I error/Power	Bias (SD)
BRAR(1/2,σ2)	δ1=δ2=0	P1=P2=0.3	290(47)	0.50(0.10)	0.07	0(0.082)
		P1=0.5, P2=0.3	157(86)	0.63(0.08)	0.858	0.046(0.097)
	δ1=δ2=0.1	P1=P2=0.3	288(51)	0.50(0.10)	0.091	0(0.091)
		P1=0.5, P2=0.3	150(83)	0.62(0.08)	0.89	0.054(0.096)
	δ1=δ2=0.2	P1=P2=0.3	284(55)	0.50(0.10)	0.122	0(0.101)
		P1=0.5, P2=0.3	144(78)	0.62(0.08)	0.919	0.059(0.091)
Time-trend Adjusted Randomization (TTAR)	δ1=δ2=0.1	P1=P2=0.3	292(41)	0.50 (0.11)	0.06	0 (0.087)
		P1=0.5, P2=0.3	184(84)	0.64(0.07)	0.815	0.049(0.092)
	δ1=δ2=0.2	P1=P2=0.3	291(46)	0.49 (0.09)	0.067	0(0.092)
		P1=0.5, P2=0.3	185(86)	0.64(0.07)	0.783	0.054(0.093)

5. Discussion

Potential ethical benefit is one of the motivations of conducting BRAR in clinical trials. BRAR increases proportion of patients assigned to the observed better performing arm. Due to the random variable nature of observed data in clinical trials, the distinction between better and worse is meaningful only within the scope of so-far collected data, and may be changed or even flipped by newly collected data in the next stage of the trial. The presence of time-trend amplifies the uncertainty of BRAR’s ethical benefit in terms of estimation and in some cases decision making. It is well known that fixed equal allocation maximizes the power of two-arm trials with binary outcomes. Some may point out that this is at the cost of ignoring an ethical benefit of allocating patients to the better performing treatment arm. The use of BRAR includes both aspects which creates a scenario where investigators need to determine the balance between ethical benefit and trial power. This research focuses on methods and procedures for exploring the mechanism of time-trend impact on the performance of BRAR in terms of treatment estimation and allocation ratios. Two-arm binary outcome trial setting is selected as a simple case. The numerical analyses simulation study results from this research are not necessarily applicable to complex trial settings with multiple arms, and/or continuous outcomes. However, the research strategies described in this manuscript for the assessment of time-trend impacts could be applied to more complex trial setting scenarios. This research isolates the bias due to early stopping in order to understand the true impact of the time-trend on BRAR operating characteristics. Most importantly, it is observed that, compared to fixed equal allocation, increase in treatment effect estimation bias caused by the BRAR under the influence of time-trend is mainly driven by the allocation ratio changing. Values of tuning parameters affect the bias. As expected, simulation results also suggest that under BRAR with early stopping for efficacy, the type I error rate is inflated for all time-trend patterns, including unequal time-trends. The magnitude and direction of bias and the quantity of type I error inflation vary by the BRAR algorithms and time-trend patterns. The combination of BRAR and time-trend results in treatment effect estimation bias, although the treatment effect size within each interim stage remains the same. The biased treatment effect estimation will further push the allocation ratio away from the equal allocation, leading to a more biased treatment effect estimation, and causing type I error inflation. A model-based approach is proposed to adjust for the time-trend and to control the type I error inflation, at a cost in the power of detecting the treatment effect, because the covariate-adjustment in logistic regression may increase the standard error for treatment effect estimates.²⁴ Further research is needed to justify the choice of priors and model specification. Compared to the block stratified analysis, the model-based adjustment has the advantage of the accommodating both the interim analysis and interim treatment allocation ratio update. Also, the stratified analysis by interim block may reduce the trial efficiency by increasing the sample size and inferior treatment assignment.¹⁸ For BRAR trials with unknown time-trend, randomization test could be used to preserve the type I error rate.8 However, it does not provide the point estimate for the treatment effect. To accommodate the unknown time-trend, the model-based approach may be also useful to adjust for the time-trend by stage-wise indication. More complex simulation scenarios should be examined to validate this method.

The unequal time-trend pattern, with the response rate increasing in the control arm only and keep unchanged in the treatment arm, used in this research was motivated by real trials with long-term patient recruitment. The improvement in standard of care may over time increase the response rate in the control group, but not in the treatment group due to the ceiling effect. Trials with unequal time-trends must be interpreted with caution and the reason for the unequal time-trend should be investigated.

This simulation study uses complete randomization for sequential treatment assignment, which leads to a great variability in the observed allocation distribution. The mass weighted urn design²⁵ has been used to increase the treatment allocation accuracy. However, simulation results show a negligible impact. In addition, this work also provides a brief discussion on the potential methods for addressing the time-trend issue in BRAR designed studies. Further detailed investigations are needed to evaluate the performance of model-based randomization approach. This manuscript focuses on the linear pattern of the time-trend, while in reality, the time-trend pattern could be non-linear and hard to detect. The model-based approach should also further take this into consideration and accommodate the practical situation.

The conclusions of this research only apply to the particular BRAR methods being discussed in this manuscript, the other type of RAR methods (e.g. RAR under frequentist setting) may not have the similar type I error (potential) inflation and estimation issues. In addition, the authors chose to focus on the specific aspects of treatment estimation and allocation with BRAR whereas others may expand simulation studies to include other important points such as the impact on moving the correct treatment forward and the impact on patient benefit. Simulation studies should be conducted to evaluate the potential time-trend effect under specific trial settings. Finally, an equally important aspect is trial setting including safety concerns, severity of the disease and interaction with the data and safety monitoring board (DSMB). These aspects are difficult to be included in a simulation study and require detailed discussions prior to the onset of the study.

The goal of this research is to promote an in-depth understanding on the mechanism of time-trend impact on the response adaptive randomization within the Bayesian paradigm for a two-arm trial with binary outcomes, and to provide recommendations on how to choose an appropriate algorithm to conduct BRAR and to reduce the negative impact of the time-trend. It is worth noting that other trial elements could inevitably exert influence on the BRAR performance including the number of arms, sample size, and allocation updating frequencies. Simulations tailored to specific trial design should be conducted.