Abstract
Photonic force optical coherence elastography (PF-OCE) is a new approach for volumetric characterization of microscopic mechanical properties of three-dimensional viscoelastic medium. It is based on measurements of the complex mechanical response of embedded micro-beads to harmonically modulated radiation-pressure force from a weakly-focused beam. Here, we utilize the Generalized Stokes-Einstein relation to reconstruct local complex shear modulus in polyacrylamide gels by combining PF-OCE measurements of bead mechanical responses and experimentally measured depth-resolved radiation-pressure force profile of our forcing beam. Data exclusion criteria for quantitative PF-OCE based on three noise-related parameters were identified from the analysis of measurement noise at key processing steps. Shear storage modulus measured by quantitative PF-OCE was found to be in good agreement with standard shear rheometry, whereas shear loss modulus was in agreement with previously published atomic force microscopy results. The analysis and results presented here may serve to inform practical, application-specific implementations of PF-OCE, and establish the technique as a viable tool for quantitative mechanical microscopy.
1. Introduction
Optical micromanipulation was first demonstrated by Ashkin in 1970, when he showed that radiation pressure from a low numerical aperture (NA) beam was able to accelerate neutral microparticles in aqueous suspension [1]. This work paved the way for his invention (more than a decade later) of the now ubiquitous “optical tweezers” (OTs) [2]. OTs have since become the cornerstone for numerous discoveries in single-molecule biophysics and nanoscale sciences [3–5]. In addition, OTs are also widely adopted in both passive and active microrheology [6,7] for quantification of microscopic viscoelasticity of soft materials, including biological hydrogels and living cells [8–11]. Meanwhile, optical micromanipulation by low-NA radiation pressure has led to relatively fewer applications in the life sciences [12–14].
Using optical coherence tomography (OCT) to monitor the dynamics of accelerated beads in real-time, we recently performed the ‘OCT-version’ of Ashkin’s seminal experiment and measured depth-resolved radiation-pressure force profile from a low-NA Gaussian beam on polystyrene micro-beads in various viscous fluids [15]. We found that radiation-pressure force on the order of 0.1 pN/mW could be achieved depending on the characteristics of the forcing beam as well as the properties of the beads and the medium. Notably, the motions of the beads induced by the radiation-pressure force extended over hundreds of micrometers about the focal plane of the forcing beam. The combination of radiation pressure from a low-NA beam and OCT detection of particle displacements has the potential to open up new modes of quantitative optical micromanipulation and sensing with large depth coverage.
We proposed one such application, photonic force optical coherence elastography (PF-OCE), for three-dimensional (3D) mechanical microscopy of soft materials such as biological hydrogels [16]. PF-OCE is a class of optical coherence elastography (OCE) [17–19] techniques that utilizes spatially localized mechanical excitation provided by a focused optical beam, and makes use of embedded microparticles similar to prior active microrheological approaches [8–10]. Other OCE techniques that utilize focused optical excitation include nanobomb OCE [20] and laser-induced surface acoustic wave OCE [21], however, they are fundamentally based on different principles of mechanical excitation and subsequent reconstruction of mechanical properties. These techniques use absorption (as opposed to radiation pressure arising from the transfer of photon momentum) of a short-pulse focused laser to generate localized heating, which generates propagating mechanical waves resulting from rapid thermo-elastic expansion. Furthermore, absorption-mediated photothermal effects, including the thermo-optic effect and thermal expansion, are the physical basis for photothermal OCT (PT-OCT) [22–24], a functional variant of OCT imaging that detects optical path length changes associated with the presence of absorbers in the sample. Meanwhile, magnetomotive OCE also performs microrheological measurements on embedded particles, but is based on displacements of embedded magnetic nanoparticles in response to a modulated external magnetic field [25]. Beyond elastographic measurements, particle tracking by OCT has also been adopted for passive microrheological characterization of fluid viscosity [26] and pore sizes of polymer networks [27].
Our PF-OCE technique utilizes harmonically modulated radiation-pressure force to apply localized mechanical excitation on beads randomly distributed over an extended depth range in viscoelastic medium, and leverages phase-sensitive OCT to detect the resulting bead oscillations (on the order of picometers to a few nanometers) [16]. After compensating for the accompanying photothermal response (the same effects utilized in PT-OCT) of the medium [16], we can isolate the complex mechanical response of each bead from the measured changes in optical path length. With the potential to reconstruct viscoelastic properties from bead mechanical response, our preliminary experiments demonstrated PF-OCE as a new approach for performing high-throughput volumetric microrheological measurements of 3D engineered biological systems [16]. Nevertheless, the quantification of viscoelastic properties from bead mechanical response and the challenges associated with that process have not been explicitly addressed in our previous study.
In this paper, we combined our PF-OCE approach [16] with depth-resolved radiation-pressure force measurement [15] to quantitatively reconstruct microscopic complex shear modulus around each probed bead in polyacrylamide (PAM) gels, and compare our quantitative PF-OCE results to shear rheometry. In order to obtain reliable measurements of bead mechanical response for quantitative PF-OCE, we analyzed measurement noise at key processing steps and identified data exclusion criteria based on three noise-related parameters. We also discuss modifications that have been made to the previously presented technique [16] in order to improve the performance of PF-OCE for quantitative reconstruction of viscoelastic properties. The analysis and results presented here can serve as a guide to inform future implementations of PF-OCE for specific applications, such as the study of cell-induced microscopic spatiotemporal variation in extracellular matrix (ECM) mechanical properties [9,28] in the rapidly growing field of mechanobiology [29–32].
2. Methods
2.1 Experimental setup
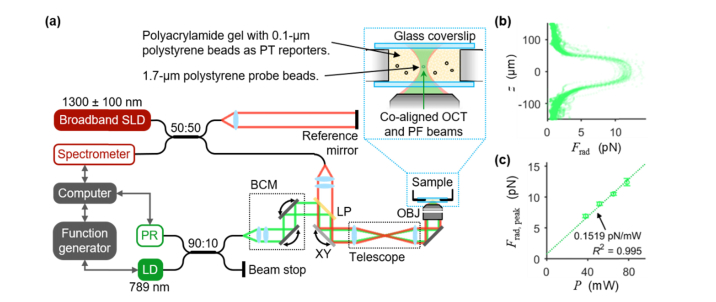
The optical setup for PF-OCE (Fig. 1(a)) was based on a spectral domain (SD)-OCT system with an additional forcing beam (PF beam) for providing radiation-pressure force, Frad(z), excitation, combined in free-space with the OCT sample arm beam, as previously described [15,16]. The SD-OCT system used a broadband superluminescent diode source (Thorlabs, LS2000B) with a center wavelength of 1300 nm and a full-width-half-maximum (FWHM) bandwidth of 200 nm. Spectral data was acquired with a spectrometer (Cobra 1300, Wasatch Photonics) with a bandwidth of 245 nm and a line scan camera (GL2048, Sensors Unlimited) with 2048 pixels. The axial resolution of the OCT system was 3.7 µm in air. The PF beam was provided by a laser diode at the wavelength of 789 nm (Frankfurt Laser Company, FLU0786M250, HI780 fiber output). Both the OCT and the PF beams were focused by an air objective lens (Olympus, LCPLN20XIR). The OCT beam had an effective NA of 0.28 with a transverse resolution of 2.3 µm. The PF beam had an effective NA of 0.18 and a FWHM focal spot size of 2.2 µm.
Fig. 1.
Experimental setup and sample configuration. (a) The optical setup consisted of an SD-OCT system and a PF beam combined in free space with the OCT sample arm beam such that the foci of both beams were co-aligned in 3D space. Current-control input from a function generator modulated the power of the PF beam. SLD: superluminencent diode, LD: laser diode, PR: photoreceiver, LP: long-pass dichroic filter, BCM: beam control module, XY: two-axis galvanometer, OBJ: objective lens. (b) Profile of Frad(z) as a function of depth, z, w.r.t. the focal plane of the PF beam at 78-mW PF beam power. (c) Peak Frad as a function of PF beam power, P, at the sample. Linear best-fit line is shown. In (b) and (c), Frad(z) was measured on 1.7-µm polystyrene beads in 10% glycerol-water mixture (refractive index 1.3469).
2.2 Sample preparation
The preparation and the naming convention of chemically-crosslinked PAM gels was based on Tse et al [33]. First, acrylamide monomer (40% Acrylamide Solution, Bio-Rad), bis-acrylamide crosslinker (2% Bis Solution, Bio-Rad), and deionized water were mixed at desired concentration (Table 1). Then, aqueous suspensions of 1.7-µm diameter (Spherotech, PP-15) and 0.1-µm diameter (Sigma-Aldrich, LB1) polystyrene beads were added to the mixture at concentrations of 28 µL/mL (mean particle separation of 15 µm) and 1.2 µL/mL (mean particle separation of 2 µm) mixture volume, respectively. The 1.7-µm bead size was selected for optimal bead oscillation amplitude when forced by the harmonically-modulated 2.2-µm PF beam. The 0.1-µm beads provided background scattering signals in the medium and served as photothermal reporters [16]. After careful stirring, the monomer-crosslinker-bead solution was desiccated for 15 minutes. Then, a portion of the solution was set aside for bulk mechanical testing by shear rheometry.
Table 1. List of polymer concentrations and bulk mechanical properties of PAM gels. Polymer concentrations are given in volume percent (% v/v); remaining percentage corresponds to deionized water. Uncertainties reported for shear moduli represent standard deviations from 5 measurements (see Section 2.6 for details).
| Name | Polymer concentrations |
Shear rheometry at 20 Hz |
||||||
|---|---|---|---|---|---|---|---|---|
| Acrylamide (%) | Bis-acrylamide (%) | Storage modulus, G′ (Pa) | Loss modulus, G″ (Pa) | |||||
| 3T1C | 3 | 0.03 | 63 ± 24 | 19 ± 7 | ||||
| 3T2C | 3 | 0.06 | 257 ± 22 | 22 ± 4 | ||||
| 4T1C | 4 | 0.04 | 376 ± 48 | 40 ± 8 | ||||
| 4T2C | 4 | 0.08 | 901 ± 59 | 32 ± 5 | ||||
| 5T1C | 5 | 0.05 | 960 ± 130 | 60 ± 13 | ||||
| 5T2C | 5 | 0.10 | 1970 ± 140 | 22 ± 12 | ||||
| 6T1C | 6 | 0.06 | 2115 ± 77 | 47 ± 20 | ||||
To the remaining solution, redox initiator, 10% ammonium persulfate (APS, Bio-Rad), and catalyst, tetramethylethylenediamine (TEMED, Bio-Rad), were added at the concentrations of 10 µL/mL and 1 µL/mL, respectively. After mixing, 100 µL of the activated solution was pipetted into the well in a glass-bottomed imaging petri dish. Another glass coverslip was placed on top of the well, concealing the PAM gel, and the edges were sealed with mineral oil to prevent evaporation. The gel was allowed to polymerize for 60 minutes prior to the PF-OCE measurements. One sample was prepared per PAM gel concentration.
2.3 System alignment procedure and data acquisition
Prior to each experiment, co-alignment between the foci of the OCT beam and the PF beam in 3D space was verified by comparing the detected OCT signal against the confocal response of the PF beam acquired with a photoreceiver (Newport, 2051-FS), as previously described [16]. Beam alignment was adjusted by the beam control module (Fig. 1(a)) as needed. A total of 13 M-mode OCT data sets were acquired in each sample. The first 9 data sets were acquired with a 1.7-µm bead located at the focal planes of the PF and OCT beams, and aligned to the optical axis of these beams—these provided PF-OCE measurements on 9 different beads per PAM gel concentration. The remaining 4 data sets were acquired without a 1.7-µm bead directly in the beam path—these served as additional data for depth-dependent photothermal response measurements.
Each M-mode data set consisted of 10 frames and 32000 A-scans per frame, acquired at a line-scan rate of 10 kHz and an exposure time of 16 µs. The function generator (Tektronix, AFG3051C) harmonically modulated the output power of the PF beam at the modulation frequency of 20 Hz and peak power of 78 mW at the sample (Fig. 1(a)), corresponding to a peak force of 12 pN at the focal plane (Fig. 1(c)). The modulation was synchronized to the acquisition of A-scans such that the PF beam power remained at 0 mW until the modulation began at the 321st A-scan in each frame. The sample was first positioned axially such that the focal plane of the OCT beam (co-aligned with the PF beam focal plane) was located roughly at the center of the PAM gel (i.e., mid-way between the petri dish bottom and the coverslip placed on top of the well). Then, the sample was only translated laterally to change the imaging location between data sets. For the 9 data sets containing a 1.7-µm bead at the focal plane, the bead was positioned in the OCT beam path (co-aligned with the PF beam path) by laterally translating the sample to maximize the M-mode OCT intensity of the bead at the focal plane. This procedure was repeated for each of the 9 beads measured per sample.
2.4 Data processing
M-mode OCT images, S̃(z,t), were reconstructed according to a standard SD-OCT reconstruction procedure (background subtraction, spectrum resampling, dispersion correction, and inverse Fourier transformation). The complex M-mode OCT images are given by:
| (1) |
where t denotes the time at each A-scan and z denotes the depth w.r.t. the focal plane of the PF and OCT beams at each pixel depth. The following processing steps were performed independently at each pixel depth to obtain the oscillatory response induced by the harmonically modulated PF beam.
First, average OCT signal-to-noise ratio (SNR) was calculated for each pixel depth, as previously described [16]. Then, pixel depths with OCT SNR < 10 dB were removed and excluded from further processing. The rationale supporting this exclusion criteria will be discussed in Section 3.2. The raw optical path length changes, ΔOPL(z,t), induced by the harmonic modulation was extracted from the raw phase of the complex OCT signal. This phase must be registered to the reference phase obtained from the petri dish bottom surface in order to eliminate any systematic phase drifts in the system [16]. The registered phase angle was extracted from the product of the complex OCT signal at each pixel depth and the complex conjugate of the OCT signal at depth zref, corresponding to the pixel depth with maximum average OCT intensity on the petri dish bottom surface:
| (2) |
where λ0 and n denote the center wavelength of the OCT beam and the refractive index of the medium, respectively. The resulting phase-registered ΔOPL response was averaged across all 10 frames to suppress random noise in the phase of the complex OCT signal. From the phase-registered ΔOPL(z,t), the noise amplitude, δA(z), of the ΔOPL response was calculated from the root-mean-square of the frequency spectrum adjacent to the response peak at the 20-Hz modulation frequency [16]. Then, the ΔOPL response at the modulation frequency was isolated via multiplication with a brick-wall filter (20-Hz center frequency and ± 0.4-Hz passband) in the frequency domain. The complex filtered ΔOPL response can be expressed as the product of a depth-dependent phasor and the PF drive waveform:
| (3) |
where is the PF drive waveform expressed as a complex exponential of unit amplitude with a phase shift φdrive. A(z) and φ(z) denote the amplitude and phase shift w.r.t. h̃(t) of the ΔOPL response at each pixel depth, respectively. Note that with this notation, φ < 0 corresponds to a phase delay w.r.t. h̃(t). For brevity, any mention of phase shift from this point on shall imply a shift w.r.t. h̃(t), according to Eq. (3). Given that the sample is assumed to behave linearly, and the modulation was provided at a single frequency, the oscillation amplitude and phase shift are expected to be constant in time. Thus, A(z) and φ(z) were obtained by taking the median of the amplitude and the phase shift of ΔOPL(z,t) over the duration that the modulation was applied in each frame (approximately 3 s):
| (4) |
| (5) |
where med{…}t denotes median operation along t.
After obtaining ΔOPL(z,t), δA(z), A(z), and φ(z), the data was further excluded based on oscillation amplitude-to-noise ratio, A/δA, where pixel depths with A/δA ≤ 6 were removed and excluded from further processing. Then, the remaining data was segmented into a photothermal response data region (corresponding to the 0.1-µm beads and the coverslip surface) and a total response data region (corresponding to the 1.7-µm beads) based on OCT SNR thresholds, as previously described [16]. However, the specific threshold values were adjusted to account for differences in the noise performance of the system, acquisition schemes, and bead sizes; values used in the presented experiments were 10 dB ≤ OCT SNR < 20 dB for the 0.1-µm beads and OCT SNR ≥ 22 dB for the 1.7-µm beads.
After the segmentation, the photothermal response data region from all 13 data sets acquired per sample was combined to obtain a single depth-dependent photothermal response amplitude, APT(z), and phase shift, φPT(z), for each PAM gel concentration. APT(z) and φPT(z) were obtained via nonlinear least-square curve-fitting of the theoretically simulated depth-dependent photothermal response amplitude and phase shift curves [16] to the measured A(z) and φ(z) data (in the photothermal response data region), respectively. The obtained best-fit curves represented APT(z) and φPT(z) for each PAM gel concentration.
Mechanical response (oscillation) of the 1.7-µm beads induced by the harmonically modulated Frad was isolated from the filtered ΔOPL(z,t) in the total response data region after compensating for the photothermal response by:
| (6) |
where ΔOPLmech(z,t), ΔOPLtot(z,t), and ΔOPLPT(z,t) denote the complex mechanical, total, and photothermal responses at each pixel depth, respectively. ΔOPLmech(z,t) can also be expressed as the product of a depth-dependent phasor and the PF drive waveform:
| (7) |
where the mechanical response amplitude, Amech(z), and phase shift, φmech(z), were obtained from Eqs. (4) and (5), respectively. In order to assess the reliability of the measured Amech(z) and φmech(z), the standard deviation of the mechanical response amplitude and phase shift, denoted by σA(z) and σφ(z), were computed over the duration that the modulation was applied in each frame. This matter will be discussed fully in Section 3.2.
After obtaining Amech(z), φmech(z), σA(z), and σφ(z), the results were further excluded based on the stability in the time domain of the ΔOPLmech(z,t) response, where pixel depths with σA/Amech ≥ 0.1 or σφ ≥ π/16 were removed and excluded from further analysis. The remaining pixel-wise Amech(z) and φmech(z) results from the pixel depths comprising each 1.7-µm bead were grouped together and the median values were taken to represent the mechanical response amplitude and phase of each bead [16]. These bead-wise Amech and φmech results were used to reconstruct the local complex shear modulus, , of the PAM medium around each bead via the Generalized Stokes-Einstein Relation (GSER) [34,35] by:
| (8) |
where zb denotes the depth at the center of the beads w.r.t. the focal plane of the PF beam and a denotes the radius of the beads. Refer to Section 2.5 for the experimental measurement of depth-resolved Frad(z). We reiterate that φmech is the phase shift of ΔOPLmech w.r.t. h̃(t), where a negative value of φmech implies that bead oscillation lags behind the mechanical excitation provided by the modulated Frad. In other words, the mechanical ‘phase delay’ (as referred to in rheometry) is given by ‒φmech.
2.5 Radiation-pressure force measurement
Depth-resolved measurement of the axial profile of Frad(z) with OCT followed a previously reported method [15]. Briefly, 1.7-µm beads were dispersed in a solution of 10% glycerol in distilled water (approximating the refractive index of the PAM gels). Then, the beads were accelerated by the PF beam operating at a constant power, during which the axial trajectories of the beads were tracked in real-time via M-mode OCT imaging. Instantaneous velocity and acceleration of each bead were computed from its trajectory. Then, the axial equation of motion for a spherical bead in viscous fluid was solved to obtain the instantaneous magnitude of Frad at each depth. The axial profile of Frad(z) at the PF beam power of 78 mW at the sample is shown in Fig. 1(b). At the focal plane, the peak force per unit PF beam power was 0.15 pN/mW (Fig. 1(c)).
2.6 Shear rheometry
Bulk complex shear modulus of each PAM sample was measured with a parallel-plate shear rheometer (TA Instruments, DHR-3) using a 20-mm diameter plate. APS solution and TEMED were added to the monomer-crosslinker solution immediately before each measurement. After mixing well, 200 µL of the activated polymer solution was pipetted onto the bottom plate of the rheometer before the top plate was lowered down to achieve a gap of 500 µm. Excess polymer solution was wiped away, then, the sample was sealed around the gap with mineral oil to prevent evaporation. Polymerization progress was monitored in a time-sweep oscillatory test at oscillation frequency of 1 rad/s and shear strain of 0.5%, measuring the complex shear modulus as a function of polymerization time. All samples were left to polymerize for 60 minutes; stabilization of shear moduli within this time frame confirmed complete polymerization of the PAM gels. After polymerization, frequency-sweep oscillatory test was performed at the oscillation frequency ranging from 1 to 50 Hz and applied torque of 10 µN⋅m. Two different samples were tested per PAM concentration. The test was repeated 2 times on one sample and 3 times on the other, totaling 5 measurements per PAM gel concentration.
2.7 Statistical analysis
For the comparison of complex shear modulus measured by quantitative PF-OCE to shear rheometry measurements, Pearson’s linear correlation test was performed on the median value of G′ and G″ measured on all beads in each PAM gel concentration by PF-OCE against the mean value of G′ and G″ from 5 measurements in each PAM gel concentration by shear rheometry.
3. Results
3.1 Bead response to harmonically-modulated radiation pressure
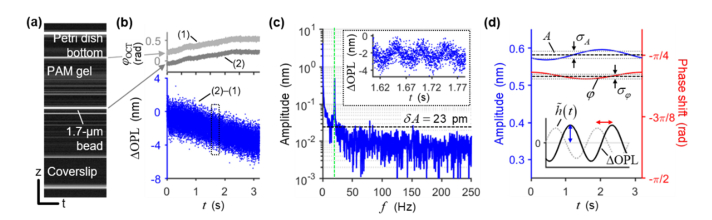
An example of the reconstructed space-domain M-mode OCT image shows a 1.7-µm bead located at the focal plane of the OCT beam, which was co-aligned to the focal plane of the PF beam (Fig. 2(a)). Elsewhere inside the PAM gel, lower intensity background signals from the 0.1-µm beads and the intrinsic scattering of the PAM gel can be observed. The petri dish bottom, which was used for phase registration, appears at the top of the image due to the inverted imaging configuration (Fig. 1(a)). Similarly, the glass coverslip, which was placed on top of the petri dish well, appears at the bottom of the image. The signal from the surface of the coverslip in contact with the PAM gel encoded the total cumulative photothermal response.
Fig. 2.
Response of 1.7-µm bead induced by 20-Hz harmonic modulation of Frad. (a) M-mode OCT image. Scale bar: 200 µm (vertical) and 1 s (horizontal). (b) Raw φOCT at pixel depths corresponding to the surface of the petri dish bottom and the 1.7-µm bead (top), and the resulting ΔOPL response at the bead depth after the phase registration (bottom), as a function of t. (c) Frequency-domain representation of the amplitude of ΔOPL. Green dashed line indicates the 20-Hz modulation frequency. Black dashed line indicates the noise amplitude, δA, at 20 Hz. Inset shows zoom-in view of the time-domain ΔOPL response in (b). (d) Amplitude (blue) and phase shift (red) w.r.t. the PF drive waveform, h̃(t), of filtered ΔOPL as a function of t. Black dashed lines and gray dotted lines indicate the median values and standard deviations over the time, respectively. Inset graphically illustrates amplitude (blue arrow) and phase shift (red arrow), where a delay in the bead response corresponds to a negative-valued phase shift.
The raw phase of the complex OCT signals, φOCT, contained a systematic drift over time that was presented at all pixel depths. The oscillatory response of the 1.7-µm bead, ΔOPL, was obtained after registering its phase to that of the petri dish bottom surface (Fig. 2(b)). Note that this ΔOPL represents the total response, which still contains the contribution of the photothermal response of the PAM medium. The 20-Hz response, induced by the harmonically modulated PF beam, is evident in the frequency-domain representation of ΔOPL (Fig. 2(c)). In this data set, the phase noise amplitude, δA, adjacent to the 20-Hz response was 23 pm. After isolating the 20-Hz response via a brick-wall filter, the oscillation amplitude and phase shift were extracted according to Eqs. (4) and (5), respectively. Both the amplitude and the phase shift exhibited variations over time, with the median values of A and φ, and the standard deviations of σA and σφ, respectively (Fig. 2(d)). As shown in the inset of Fig. 2(d), a phase lag in the ΔOPL response w.r.t. to h̃(t) corresponds to a negative-valued phase shift.
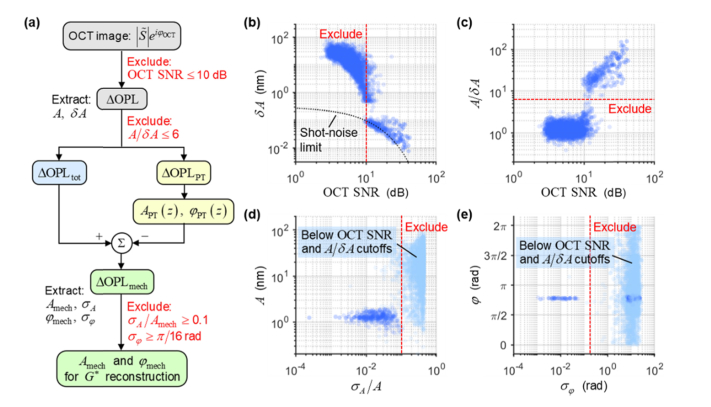
3.2 Analysis of noise and criteria for quantitative PF-OCE
In order to obtain reliable bead mechanical responses for the quantitative reconstruction of complex shear modulus, PF-OCE data was excluded based on noise-related parameters at several processing steps, as described in Section 2.4. A flowchart summarizes key processing steps and associated exclusion criteria (Fig. 3(a)). These exclusion criteria were based on three factors that contribute to the errors in the PF-OCE measurements of Amech and φmech: 1) SNR of the OCT signal, 2) oscillation amplitude-to-noise ratio of the ΔOPL response, and 3) instability of the ΔOPL response in the time domain. In the results that follow, measurements from all pixel depths (regardless of the OCT SNR thresholds) in a PAM gel sample are included for analysis purpose.
Fig. 3.
Noise analysis and exclusion criteria for quantitative PF-OCE. (a) Data processing flowchart with exclusion criteria at each step. (b) Noise amplitude, δA, in measured ΔOPL at all pixel depths in a PAM gel sample as a function of OCT SNR (in dB, plotted on a logarithmic scale). Black dotted curve indicates theoretical shot-noise limited noise floor [36]. (c) Oscillation amplitude-to-noise ratio, A/δA, as a function of OCT SNR. (d) Measured A as a function of metric for amplitude instability in time domain, σA/A. (e) Measured φ as a function of metric for phase instability in time domain, σφ. In (d) and (e), data points in light blue correspond to those that were excluded based on the criteria in (b) and (c). In (b)–(e), red dashed lines indicate the exclusion cutoffs.
First, the SNR of the OCT signal has a direct effect on the level of noise that is presented in φOCT [36,37]. Phase noise amplitude at 20 Hz, δA, in the raw ΔOPL response was plotted as a function of the average OCT SNR at each pixel depth (Fig. 3(b)). Remarkably, for pixel depths with OCT SNR above 10 dB, δA followed the theoretical shot-noise limited prediction [36]. However, at pixel depths with OCT SNR below 10 dB, the measured ΔOPL contained over an order of magnitude larger δA than the theoretical shot-noise limits, suggesting that the measured signals at these SNR levels were dominated by other sources of phase noise. Based on the trends observed in Fig. 3(b), it was determined that the 20-Hz oscillatory response induced by the modulated Frad could only be reliably obtained at the pixel depths with OCT SNR ≥ 10 dB, where the phase noise obeyed the theoretical shot-noise limited noise floor [36].
Second, as a direct consequence of SNR-dependent δA, the oscillation amplitude-to-noise ratio, A/δA, of the measured ΔOPL response is also influenced by the OCT SNR. In order to accurately measure the amplitude and phase shift of the oscillatory response to the modulated Frad, the oscillation amplitude must be sufficiently larger than the noise amplitude at the modulation frequency. Two data regimes, with higher and lower A/δA, can be clearly observed in the plot of A/δA as a function of average OCT SNR (Fig. 3(c)), where the boundary between these two regimes also predominantly coincide with the OCT SNR cutoff at 10 dB. Based on the two regimes observed in Fig. 3(c), it was determined that only the ΔOPL response with A/δA > 6, corresponding to a relative power of approximately 15 dB, would facilitate reliable calculations of A and φ.
Third, any variation in time of the mechanical response amplitude and phase shift, despite the constant modulation frequency, is an indication of uncertainties in the isolated mechanical response. Potential sources of this instability over time include the measurement phase noise, power fluctuation of the PF beam, or any drifting of the 1.7-µm beads relative to the PF beam while each frame is being acquired. As a result, an unstable ΔOPLmech response in time may imply that the corresponding Amech and φmech results cannot be accurately extracted by Eqs. (4) and (5), respectively. To analyze the instability of the ΔOPL response over time, standard deviations of its amplitude and phase shift, σA and σφ, were calculated over the duration of the applied modulation (see Section 2.4) and plotted as a function of the corresponding median values, A and φ (Figs. 3(d) and 3(e)). Larger values of σA/A and σφ, indicating a higher degree of instability in the ΔOPL response over time, correspond to erroneous calculated values of A and φ that are spread out over a wide range. Notably, most of these data points also coincide with those that exhibit OCT SNR < 10 dB and A/δA ≤ 6 (light blue markers). This observation may suggest that the instability in the time domain is largely a result of the SNR-dependent phase noise in the measured ΔOPL response. In addition, this observation also supports the effectiveness of the two previous exclusion criteria in selecting the pixel depths with stable response that allowed for reliable calculation of A and φ. Based on the analysis in Figs. 3(d) and 3(e), only Amech and φmech results from the isolated mechanical response with σA/Amech < 0.1 or σφ < π/16 were considered reliable for the quantitative PF-OCE reconstruction of complex shear modulus.
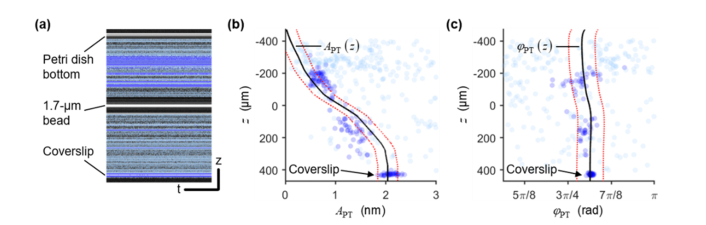
3.3 Depth-dependent photothermal responses
In order to isolate the mechanical response of the 1.7-µm beads from the measured total response, the depth-dependent photothermal response of the PAM medium was obtained for each PAM gel concentration. Pixel depths in the photothermal response data region were excluded based on the OCT SNR and the A/δA criteria prior to fitting to the theoretical curves to obtain APT(z) and φPT(z) (Fig. 4). Although all pixel depths in the photothermal data region are displayed, only data points from the pixel depths that have passed the first two exclusion criteria (dark blue markers) contributed to the curve fit in Figs. 4(b) and 4(c). For the 4T1C gel shown in Fig. 4, the photothermal response amplitude and phase shift at the focal plane (z 0) were 1.1 ± 0.2 nm and 2.55 ± 0.12 rad, respectively. Note that the positive-valued phase shifts in Fig. 4(c) does not imply that the photothermal response is in advance of the PF drive waveform; they reflect the decrease in optical path length as the temperature increases [16,38] as a result of the dominating effect of the negative-valued thermo-optic coefficient of water [39], which produces an almost out-of-phase response w.r.t. h̃(t).
Fig. 4.
Depth-dependent photothermal response of 4T1C gel. (a) M-mode OCT image with photothermal response data region highlighted in blue. (b) and (c) APT and φPT as a function of z, respectively, where z is defined w.r.t. to the focal plane of the OCT beam. Blue markers are data points from the photothermal response data region. Black solid lines are the best-fit curves obtained from fitting the data to the theoretical curves. Red dotted lines indicate ± 1 median absolute difference between the best-fit curves and the data. In (a)–(c), light blue indicates pixel depths that were excluded from analysis based on the first two exclusion criteria. Dark blue indicates pixel depths that were used for the curve fit to produce APT(z) and φPT(z).
3.4 Reconstruction of complex shear modulus and comparison to shear rheometry
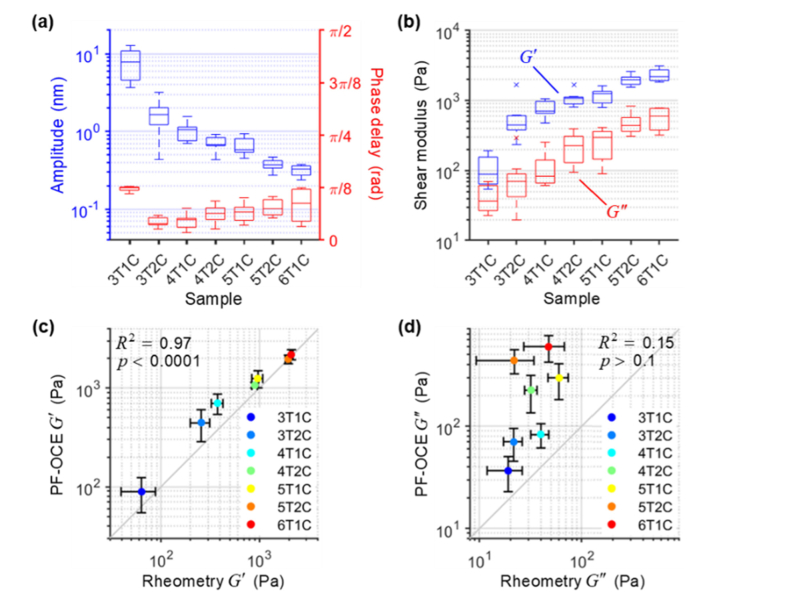
Bead mechanical response amplitude, Amech, and phase shift, φmech, were obtained for each measured 1.7-µm bead in the PAM gels after compensating for the photothermal response according to Eq. (6), using the respective APT(z) and φPT(z) curves (Figs. 4(b) and 4(c)) for each PAM concentration, and enforcing the time-domain instability exclusion criteria described in Section 3.2 (Fig. 5(a)). A decreasing trend from 3T1C–6T1C was apparent for Amech, consistent with the expected increasing trend in stiffness of the PAM gels as the polymer concentrations increased. For consistency with rheometry convention, the mechanical phase delay, ‒φmech, is plotted instead of the calculated phase shift. Under this definition, a completely elastic solid is characterized by the phase delay of 0 rad while a viscous fluid is characterized by the phase delay of π/2 rad. The phase delay was close to 0 rad for all PAM gel concentrations, with the 3T1C gel exhibiting a relatively more viscous behavior than the rest at a median phase delay of π/8 rad.
Fig. 5.
Quantitative PF-OCE in PAM gels and comparison to shear rheometry. (a) Box plots of bead mechanical response amplitude, Amech, and phase delay, ‒φmech, measured by PF-OCE in different PAM gel concentrations (N = 7, 9, and 4 beads for 3T1C, 3T2C–5T2C, and 6T1C, respectively). (b) Box plots of shear storage, G′, and loss, G″, moduli obtained from PF-OCE measurements of Amech and φmech via GSER [34,35]. In (a) and (b), boxes indicate interquartile range, with median indicated by horizontal line inside. Whiskers represent approximately ± 3 standard deviations (if data were normally distributed); data points outside of this range are considered outliers. (c) and (d) Comparison of G′ and G″ obtained from quantitative PF-OCE versus parallel-plate shear rheometry at 20 Hz. Data points represent median of PF-OCE measurements against mean (N = 5 trials per PAM gel concentration) of shear rheometry measurements. Vertical and horizontal error bars represent median absolute difference of PF-OCE measurements and standard deviation of shear rheometry measurements, respectively. R2 and p denote correlation coefficient and p-value of Pearson’s linear correlation test, respectively.
Complex shear modulus was reconstructed from Amech and φmech of each 1.7-µm bead via GSER [34,35] using to Eq. (8) (Fig. 5(b)). This represents the microscopic local viscoelastic properties of the medium around each bead. In this study, the PAM gels were assumed to be microscopically homogeneous at the length scale of the 1.7-µm bead size. This assumption is supported by [35,40]. An increasing trend from 3T1C–6T1C could be observed for both G′ and G″. Quantitative PF-OCE results showed statistically significant correlation to bulk shear rheometry measurements at 20-Hz oscillation frequency for G′ (R2 = 0.97, p < 0.0001) (Fig. 5(c)) but not for G″ (R2 = 0.15, p > 0.1) (Fig. 5(d)). Whereas PF-OCE measured G″ in the range 40-400 Pa, with a monotonic increasing trend from 3T1C–6T1C, bulk rheometry measured G″ in the range 10-60 Pa with no apparent trend w.r.t. the polymer concentrations.
4. Discussion
4.1 Modifications from previous work in order to enable quantitative PF-OCE
We previously demonstrated volumetric PF-OCE measurements of bead mechanical responses in agarose hydrogels, which revealed microscopic heterogeneity in the mechanical properties of the porous medium [16]. In order to be able to utilize PF-OCE as a new tool for microscopic mechanical characterization of soft materials, the technique had to be fine-tuned to improve the accuracy of bead mechanical response measurements and enable quantitative reconstruction of mechanical properties. The first modification was to minimize the magnitude of the photothermal contribution to the measured ΔOPL response. This was achieved by changing the wavelength of the PF beam from 976 nm in our previous study [16] to 789 nm, since the latter has approximately an order of magnitude lower absorption coefficient in water than the former [41]. As a result, APT measured in this paper with the 789-nm PF beam was on the order of 1 nm, a six-fold decrease from the 6 nm with the 976-nm beam in our previous study [16].
The second modification was the redesign of the optical setup to achieve larger bead oscillation amplitude and lower the phase noise floor, in order to maximize A and minimize δA. In a given sample, achievable Amech per unit Frad can be increased by using a smaller bead size, since Amech is inversely proportional to the radius of the bead [16,34,42]. In order to maintain an optimal Frad with the use of smaller beads, the focal spot size of the PF beam must also scale down accordingly [16]. The improved system presented in this paper, with a 2.2-µm PF beam optimized for the 1.7-µm diameter beads, is theoretically expected to demonstrate a 44% increase in Amech per unit PF beam power relative to the system used in our previous study (3.8-µm PF beam and 3-µm diameter beads) [16]. In addition to increasing Amech, the use of smaller beads is also desirable for biological applications with live-cell imaging, where the total volume fraction of exogenous beads in the sample must be kept under the levels that can be tolerated by cells [28,43]. In order to lower the noise floor of the system, mechanical vibration in the optical setup was minimized by lowering the height of entire optical setup on the optical table and designing the collimator arms for both OCT and PF beams to be as compact as possible. Although we did not quantitatively analyze the effects of these factors on the SNR-dependent δA, the improved system demonstrates δA that reaches the theoretical shot-noise limit (Fig. 3(b)) whereas the previous system was not able to [16].
The third modification was to ensure the accuracy of the calculated Amech and φmech for quantitative PF-OCE by implementing exclusion criteria based on quantifiable noise-related parameters at key processing steps. We found that an OCT SNR ≥ 10 dB was needed to achieve optimal shot-noise limited δA (Fig. 3(b)). This is particularly important for the photothermal response, which is primarily measured from the low-SNR photothermal reporters (0.1-µm beads). In our previous system using the 976-nm PF beam, an OCT SNR of only 3 dB was used to measure the photothermal response [16]. However, as a direct consequence of the lower photothermal response due to the lower absorption of 789 nm in water, a lower δA is now required to make these measurements. We also found that a stable oscillation amplitude and phase shift could only be calculated from the ΔOPL responses with A/δA > 6 (Figs. 3(c)–3(e)). This corresponds to a relative signal power of approximately 15 dB, which is higher than our previous estimate of 3 dB [16]. Lastly, we also found that the instability of the ΔOPL response over time degraded the accuracy of Amech and φmech that were calculated from the median values of its amplitude and phase shift, respectively (Figs. 3(d) and 3(e)). This provided the last criteria for obtaining reliable Amech and φmech values for quantitative PF-OCE.
4.2 Reconstruction of complex shear modulus and comparison to shear rheometry
By combining PF-OCE measurements of Amech and φmech with OCT depth-resolved measurement of Frad(z) [15], the local complex shear modulus of the PAM gel around each measured 1.7-µm bead was reconstructed via GSER (Eq. (8)). We note that under our experimental conditions (e.g., bead size, modulation frequency, sample properties etc [44].), GSER is consistent with the forward prediction of bead dynamics by other more rigorous mathematical models, such as the Oestriecher’s model [42] or the solution to the generalized 3D equations of motion for forced harmonic oscillation of a sphere in viscoelastic medium [45,46] (data not shown). Our quantitative PF-OCE results were compared to shear rheometry measurements, under the premise that the PAM gels are microscopically homogeneous at the length scale of the 1.7-µm beads, owing to the mesh size of the polymer networks being on the order of 10-100 nm for chemically cross-linked PAM gels [35,40].
Quantitative PF-OCE was consistent with shear rheometry for the measurements of G′, demonstrating a correlation coefficient of 0.97 between the results from the two approaches (Fig. 5(c)). However, results in each PAM gel concentration showed slight discrepancy, with quantitative PF-OCE measuring a larger G′ (i.e., higher stiffness) in general, suggesting that PF-OCE tends to measure smaller Amech than expected. This can be attributed to any deviation from a perfect lateral alignment between the optical axis of the PF beam and the center of the 1.7-µm beads, either from the initial positioning of the sample or any subsequent displacement of the beads (e.g., via diffusion) during the measurements. Nevertheless, our results show that quantitative PF-OCE is in good agreement with standard shear rheometry for the characterization of the stiffness of the PAM gels.
In contrast, quantitative PF-OCE measurements of G″ did not show statistically significant correlation to shear rheometry (Fig. 5(d)). In general, quantitative PF-OCE measured larger G″ (greater relative viscosity) than shear rheometry, and demonstrated an increasing trend as a function of increasing polymer concentration. We note that other microscopic characterizations of PAM gel viscoelasticity using atomic force microscopy (AFM) have yielded G″ similar to our quantitative PF-OCE results [47,48]. This suggests that the discrepancy between quantitative PF-OCE and shear rheometry may be attributed to different viscoelastic behaviors of the PAM gels at the microscopic versus macroscopic scale. Viscosity in hydrogels arises from the viscous drag due to the flow of fluid and any other frictional interactions in the polymer networks. Based on this physical interpretation, the relative viscosity of the PAM gels is likely to be more affected by the length scale at which the measurements are carried out than the stiffness. Our results suggest that a direct micro- to macroscale connection between different mechanical characterizations of the porous PAM gels may only be valid for elasticity (storage modulus) but not viscosity (loss modulus). For other types of porous hydrogels, particularly those with larger pore sizes such as the agarose hydrogels used in our previous work [16] or those with highly fibrous microstructure such as collagen gels [28], this connection across length scales may not be valid for either elasticity or viscosity if the medium cannot be considered homogeneous at the length scale of the microscopic measurements.
4.3 Implications for future applications
By working above the OCT SNR cutoff where the experimental δA obeys the theoretical shot-noise limit, the maximum sample stiffness that can be measured by quantitative PF-OCE (limited by the minimum measurable Amech) can be estimated based on the A/δA > 6 criterion. For the M-mode acquisition scheme implemented in this paper, the maximum stiffness that can be accurately measured with OCT SNR of 22 dB (minimum threshold for segmenting the 1.7-µm beads) is shear modulus of 5.2 kPa. We note that this is merely an estimate because the actual measured ΔOPL response is the total response, which has the contribution of the photothermal response of the medium. This estimate also applies to 3D mechanical microscopy applications with the previously demonstrated beam-scanning BM-mode acquisition scheme [16].
For the same peak power of the modulated PF beam, several trade-offs exist between maximum measurable stiffness, volumetric throughput, and depth coverage. For a given PF-OCE system, there is a trade-off between volumetric throughput and the maximum measurable stiffness, where the minimum acquisition time per volume is determined by the minimum number of BM-mode frames required per slow-axis position to achieve the desired δA [16]. In order to measure smaller bead oscillation amplitude in a stiffer sample, a longer measurement time is required to achieve lower δA [16,36] and maintain adequate A/δA ratio. For instance, a volumetric measurement at 500-Hz frame rate with lateral pixel size of 1 µm2 and lateral FOV of 200 µm × 200 µm would require up to 30 minutes of acquisition time in a sample with maximum expected shear modulus of 2 kPa; the same measurement could be made in only 8 minutes if the maximum expected shear modulus were only 1 kPa. For a given desired acquisition time, another trade-off exists between the volumetric depth coverage and the maximum measurable stiffness. On the one hand, the optical system could be designed to have a higher NA (i.e., smaller PF beam focal spot size) so that measurements could be made with smaller beads to increase the achievable Amech in a given sample. This would increase the maximum measurable stiffness, but at the cost of narrowing the depth range in which Frad can be exerted. On the other hand, larger depth coverage could be achieved by lowering the NA of the optical system, but at the cost of decreasing the achievable Amech for a given sample stiffness.
The optical design of the PF-OCE system and the acquisition scheme utilized in each experiment can be adapted to optimize the desired information in an application-specific manner, using the system noise performance and data requirements for quantitative PF-OCE investigated in this paper as a guide. For instance, a study of the spatiotemporal variation ECM mechanical properties induced by the contractile dynamics of a single cell over minute-to-hour timescale may benefit from a relatively high-NA system with limited depth-coverage but large maximum detectable stiffness within 1-10 minutes of acquisition time [49,50]. On the other hand, dynamics over a longer timescale such as the phenotypic change of cells or the migration of cancer cells from cellular spheroids may benefit from a long time-lapsed imaging study with extended depth coverage (on the order of 102 µm), but with temporal resolution of 20-40 minutes per volume [51–53].
5. Conclusion
We have demonstrated microrheological quantification of viscoelastic properties of PAM gels with quantitative PF-OCE, combining depth-resolved measurement of radiation-pressure force with OCT [15] and previously introduced PF-OCE technique [16], and compared our results to shear rheometry. Our analysis of measurement noise culminated in data exclusion criteria, based on OCT SNR, oscillation amplitude-to-noise ratio, and instability of the measured response over time, to enable quantitative PF-OCE. These outcomes serve to extend the viability of PF-OCE as a new technique for quantitative mechanical microscopy of viscoelastic media, such as the 3D substrates used in engineered biological systems. The comparison to shear rheometry validates quantitative PF-OCE reconstruction of sample stiffness. However, the comparison between relative viscosities obtained from microscopic measurements by quantitative PF-OCE to bulk measurements by shear rheometry may not be valid. These findings are consistent with previous microscopic measurements with AFM [47,48]. The results presented here can be used to inform the optical system design and data acquisition scheme for specific applications of PF-OCE, such as live-cell imaging studies of the cellular-scale spatiotemporal variation in ECM mechanical properties that are induced by dynamic, biophysical cell-ECM interactions.
Acknowledgments
This work made use of the Cornell Center for Materials Research Shared Facilities which are supported through the NSF MRSEC program (DMR-1719875). The authors thank Colin D. Mackey for assisting with shear rheometry measurements.
Funding
National Institutes of Health (NIBIB-5R21EB024747, NIBIB-5R21EB022927).
References
- 1.Ashkin A., “Acceleration and trapping of particles by radiation pressure,” Phys. Rev. Lett. 24(4), 156–159 (1970). 10.1103/PhysRevLett.24.156 [DOI] [Google Scholar]
- 2.Ashkin A., Dziedzic J. M., Bjorkholm J. E., Chu S., “Observation of a single-beam gradient force optical trap for dielectric particles,” Opt. Lett. 11(5), 288–290 (1986). 10.1364/OL.11.000288 [DOI] [PubMed] [Google Scholar]
- 3.Grier D. G., “A revolution in optical manipulation,” Nature 424(6950), 810–816 (2003). 10.1038/nature01935 [DOI] [PubMed] [Google Scholar]
- 4.Stevenson D. J., Gunn-Moore F., Dholakia K., “Light forces the pace: optical manipulation for biophotonics,” J. Biomed. Opt. 15(4), 041503 (2010). 10.1117/1.3475958 [DOI] [PubMed] [Google Scholar]
- 5.Bowman R. W., Padgett M. J., “Optical trapping and binding,” Rep. Prog. Phys. 76(2), 026401 (2013). 10.1088/0034-4885/76/2/026401 [DOI] [PubMed] [Google Scholar]
- 6.Brau R. R., Ferrer J. M., Lee H., Castro C. E., Tam B. K., Tarsa P. B., Matsudaira P., Boyce M. C., Kamm R. D., Lang M. J., “Passive and active microrheology with optical tweezers,” J. Opt. A, Pure Appl. Opt. 9(8), S103–S112 (2007). 10.1088/1464-4258/9/8/S01 [DOI] [Google Scholar]
- 7.Mizuno D., Head D. A., MacKintosh F. C., Schmidt C. F., “Active and Passive Microrheology in Equilibrium and Nonequilibrium Systems,” Macromolecules 41(19), 7194–7202 (2008). 10.1021/ma801218z [DOI] [Google Scholar]
- 8.Kotlarchyk M. A., Shreim S. G., Alvarez-Elizondo M. B., Estrada L. C., Singh R., Valdevit L., Kniazeva E., Gratton E., Putnam A. J., Botvinick E. L., “Concentration independent modulation of local micromechanics in a fibrin gel,” PLoS One 6(5), e20201 (2011). 10.1371/journal.pone.0020201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Keating M., Kurup A., Alvarez-Elizondo M., Levine A. J., Botvinick E., “Spatial distributions of pericellular stiffness in natural extracellular matrices are dependent on cell-mediated proteolysis and contractility,” Acta Biomater. 57, 304–312 (2017). 10.1016/j.actbio.2017.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wei M. T., Zaorski A., Yalcin H. C., Wang J., Ghadiali S. N., Chiou A., Ou-Yang H. D., “A comparative study of living cell micromechanical properties by oscillatory optical tweezers,” Opt. Express 16(12), 8594–8603 (2008). 10.1364/OE.16.008594 [DOI] [PubMed] [Google Scholar]
- 11.Mas J., Richardson A. C., Reihani S. N. S., Oddershede L. B., Berg-Sørensen K., “Quantitative determination of optical trapping strength and viscoelastic moduli inside living cells,” Phys. Biol. 10(4), 046006 (2013). 10.1088/1478-3975/10/4/046006 [DOI] [PubMed] [Google Scholar]
- 12.Guck J., Ananthakrishnan R., Mahmood H., Moon T. J., Cunningham C. C., Käs J., “The optical stretcher: a novel laser tool to micromanipulate cells,” Biophys. J. 81(2), 767–784 (2001). 10.1016/S0006-3495(01)75740-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dholakia K., MacDonald M. P., Zemánek P., Cizmár T., “Cellular and colloidal separation using optical forces,” Methods Cell Biol. 82, 467–495 (2007). 10.1016/S0091-679X(06)82017-0 [DOI] [PubMed] [Google Scholar]
- 14.Jonás A., Zemánek P., “Light at work: the use of optical forces for particle manipulation, sorting, and analysis,” Electrophoresis 29(24), 4813–4851 (2008). 10.1002/elps.200800484 [DOI] [PubMed] [Google Scholar]
- 15.Leartprapun N., Iyer R. R., Adie S. G., “Depth-resolved measurement of optical radiation-pressure forces with optical coherence tomography,” Opt. Express 26(3), 2410–2426 (2018). 10.1364/OE.26.002410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leartprapun N., Iyer R. R., Untracht G. R., Mulligan J. A., Adie S. G., “Photonic force optical coherence elastography for three-dimensional mechanical microscopy,” Nat. Commun. 9(1), 2079 (2018). 10.1038/s41467-018-04357-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mulligan J. A., Untracht G. R., Chandrasekaran S., Brown C. N., Adie S. G., “Emerging Approaches for High-Resolution Imaging of Tissue Biomechanics With Optical Coherence Elastography,” IEEE J. Sel. Top. Quantum Electron. 22(3), 246–265 (2016). 10.1109/JSTQE.2015.2481705 [DOI] [Google Scholar]
- 18.Larin K. V., Sampson D. D., “Optical coherence elastography - OCT at work in tissue biomechanics [Invited],” Biomed. Opt. Express 8(2), 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kennedy B. F., Wijesinghe P., Sampson D. D., “The emergence of optical elastography in biomedicine,” Nat. Photonics 11(4), 215–221 (2017). 10.1038/nphoton.2017.6 [DOI] [Google Scholar]
- 20.Liu C. H., Nevozhay D., Schill A., Singh M., Das S., Nair A., Han Z., Aglyamov S., Larin K. V., Sokolov K. V., “Nanobomb optical coherence elastography,” Opt. Lett. 43(9), 2006–2009 (2018). 10.1364/OL.43.002006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li C., Guan G., Zhang F., Nabi G., Wang R. K., Huang Z., “Laser induced surface acoustic wave combined with phase sensitive optical coherence tomography for superficial tissue characterization: a solution for practical application,” Biomed. Opt. Express 5(5), 1403–1419 (2014). 10.1364/BOE.5.001403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adler D. C., Huang S. W., Huber R., Fujimoto J. G., “Photothermal detection of gold nanoparticles using phase-sensitive optical coherence tomography,” Opt. Express 16(7), 4376–4393 (2008). 10.1364/OE.16.004376 [DOI] [PubMed] [Google Scholar]
- 23.Skala M. C., Crow M. J., Wax A., Izatt J. A., “Photothermal optical coherence tomography of epidermal growth factor receptor in live cells using immunotargeted gold nanospheres,” Nano Lett. 8(10), 3461–3467 (2008). 10.1021/nl802351p [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lapierre-Landry M., Gordon A. Y., Penn J. S., Skala M. C., “In vivo photothermal optical coherence tomography of endogenous and exogenous contrast agents in the eye,” Sci. Rep. 7(1), 9228 (2017). 10.1038/s41598-017-10050-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crecea V., Oldenburg A. L., Liang X., Ralston T. S., Boppart S. A., “Magnetomotive nanoparticle transducers for optical rheology of viscoelastic materials,” Opt. Express 17(25), 23114–23122 (2009). 10.1364/OE.17.023114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chhetri R. K., Kozek K. A., Johnston-Peck A. C., Tracy J. B., Oldenburg A. L., “Imaging three-dimensional rotational diffusion of plasmon resonant gold nanorods using polarization-sensitive optical coherence tomography,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83(4 Pt 1), 040903 (2011). 10.1103/PhysRevE.83.040903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Blackmon R. L., Sandhu R., Chapman B. S., Casbas-Hernandez P., Tracy J. B., Troester M. A., Oldenburg A. L., “Imaging Extracellular Matrix Remodeling In Vitro by Diffusion-Sensitive Optical Coherence Tomography,” Biophys. J. 110(8), 1858–1868 (2016). 10.1016/j.bpj.2016.03.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hall M. S., Alisafaei F., Ban E., Feng X., Hui C. Y., Shenoy V. B., Wu M., “Fibrous nonlinear elasticity enables positive mechanical feedback between cells and ECMs,” Proc. Natl. Acad. Sci. U.S.A. 113(49), 14043–14048 (2016). 10.1073/pnas.1613058113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Discher D. E., Janmey P., Wang Y. L., “Tissue cells feel and respond to the stiffness of their substrate,” Science 310(5751), 1139–1143 (2005). 10.1126/science.1116995 [DOI] [PubMed] [Google Scholar]
- 30.Eyckmans J., Boudou T., Yu X., Chen C. S., “A hitchhiker’s guide to mechanobiology,” Dev. Cell 21(1), 35–47 (2011). 10.1016/j.devcel.2011.06.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Guilak F., Cohen D. M., Estes B. T., Gimble J. M., Liedtke W., Chen C. S., “Control of stem cell fate by physical interactions with the extracellular matrix,” Cell Stem Cell 5(1), 17–26 (2009). 10.1016/j.stem.2009.06.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wirtz D., Konstantopoulos K., Searson P. C., “The physics of cancer: the role of physical interactions and mechanical forces in metastasis,” Nat. Rev. Cancer 11(7), 512–522 (2011). 10.1038/nrc3080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tse J. R., Engler A. J., “Preparation of hydrogel substrates with tunable mechanical properties,” Curr. Protoc. Cell Biol. 10, 16 (2010). [DOI] [PubMed] [Google Scholar]
- 34.Mason T. G., Weitz D. A., “Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids,” Phys. Rev. Lett. 74(7), 1250–1253 (1995). 10.1103/PhysRevLett.74.1250 [DOI] [PubMed] [Google Scholar]
- 35.Gittes F., Schnurr B., Olmsted P. D., MacKintosh F. C., Schmidt C. F., “Microscopic Viscoelasticity: Shear Moduli of Soft Materials Determined from Thermal Fluctuations,” Phys. Rev. Lett. 79(17), 3286–3289 (1997). 10.1103/PhysRevLett.79.3286 [DOI] [Google Scholar]
- 36.Chang E. W., Kobler J. B., Yun S. H., “Subnanometer optical coherence tomographic vibrography,” Opt. Lett. 37(17), 3678–3680 (2012). 10.1364/OL.37.003678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Park B., Pierce M. C., Cense B., Yun S. H., Mujat M., Tearney G., Bouma B., de Boer J., “Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 microm,” Opt. Express 13(11), 3931–3944 (2005). 10.1364/OPEX.13.003931 [DOI] [PubMed] [Google Scholar]
- 38.Lapierre-Landry M., Tucker-Schwartz J. M., Skala M. C., “Depth-resolved analytical model and correction algorithm for photothermal optical coherence tomography,” Biomed. Opt. Express 7(7), 2607–2622 (2016). 10.1364/BOE.7.002607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hawkes J. B., Astheimer R. W., “The temperature coefficient of the refractive index of water,” J. Opt. Soc. Am. 38(9), 804–806 (1948). 10.1364/JOSA.38.000804 [DOI] [PubMed] [Google Scholar]
- 40.Stellwagen N. C., “Apparent pore size of polyacrylamide gels: comparison of gels cast and run in Tris-acetate-EDTA and Tris-borate-EDTA buffers,” Electrophoresis 19(10), 1542–1547 (1998). 10.1002/elps.1150191004 [DOI] [PubMed] [Google Scholar]
- 41.Hale G. M., Querry M. R., “Optical Constants of Water in the 200-nm to 200-microm Wavelength Region,” Appl. Opt. 12(3), 555–563 (1973). 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
- 42.Oestreicher H. L., “Field and Impedance of an Oscillating Sphere in a Viscoelastic Medium with an Application to Biophysics,” J. Acoust. Soc. Am. 23(6), 707–714 (1951). 10.1121/1.1906828 [DOI] [Google Scholar]
- 43.Legant W. R., Miller J. S., Blakely B. L., Cohen D. M., Genin G. M., Chen C. S., “Measurement of mechanical tractions exerted by cells in three-dimensional matrices,” Nat. Methods 7(12), 969–971 (2010). 10.1038/nmeth.1531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schnurr B., Gittes F., MacKintosh F. C., Schmidt C. F., “Determining Microscopic Viscoelasticity in Flexible and Semiflexible Polymer Netowrks from Thermal Fluctuations,” Macromolecules 30(25), 7781–7792 (1997). 10.1021/ma970555n [DOI] [Google Scholar]
- 45.Ilinskii Y. A., Meegan G. D., Zabolotskaya E. A., Emelianov S. Y., “Gas bubble and solid sphere motion in elastic media in response to acoustic radiation force,” J. Acoust. Soc. Am. 117(4 Pt 1), 2338–2346 (2005). 10.1121/1.1863672 [DOI] [PubMed] [Google Scholar]
- 46.Urban M. W., Nenadic I. Z., Mitchell S. A., Chen S., Greenleaf J. F., “Generalized response of a sphere embedded in a viscoelastic medium excited by an ultrasonic radiation force,” J. Acoust. Soc. Am. 130(3), 1133–1141 (2011). 10.1121/1.3613939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Abidine Y., Laurent V., Michel R., Duperray A., Palade L. I., Verdier C., “Physical properties of polyacrylamide gels probed by AFM and rheology,” EPL 109(3), 38003 (2015). 10.1209/0295-5075/109/38003 [DOI] [Google Scholar]
- 48.Goudoulas T. B., Germann N., “Viscoelastic properties of polyacrylamide solutions from creep ringing data,” J. Rheol. (N.Y.N.Y.) 60(3), 491–502 (2016). 10.1122/1.4945819 [DOI] [Google Scholar]
- 49.Carey S. P., Goldblatt Z. E., Martin K. E., Romero B., Williams R. M., Reinhart-King C. A., “Local extracellular matrix alignment directs cellular protrusion dynamics and migration through Rac1 and FAK,” Integr. Biol. 8(8), 821–835 (2016). 10.1039/C6IB00030D [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mulligan J. A., Feng X., Adie S. G., “Quantitative reconstruction of time-varying 3D cell forces with traction force optical coherence microscopy,” Sci. Rep. 9(1), 4086 (2019). 10.1038/s41598-019-40608-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ban E., Franklin J. M., Nam S., Smith L. R., Wang H., Wells R. G., Chaudhuri O., Liphardt J. T., Shenoy V. B., “Mechanisms of Plastic Deformation in Collagen Networks Induced by Cellular Forces,” Biophys. J. 114(2), 450–461 (2018). 10.1016/j.bpj.2017.11.3739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Carey S. P., Martin K. E., Reinhart-King C. A., “Three-dimensional collagen matrix induces a mechanosensitive invasive epithelial phenotype,” Sci. Rep. 7(1), 42088 (2017). 10.1038/srep42088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Labernadie A., Kato T., Brugués A., Serra-Picamal X., Derzsi S., Arwert E., Weston A., González-Tarragó V., Elosegui-Artola A., Albertazzi L., Alcaraz J., Roca-Cusachs P., Sahai E., Trepat X., “A mechanically active heterotypic E-cadherin/N-cadherin adhesion enables fibroblasts to drive cancer cell invasion,” Nat. Cell Biol. 19(3), 224–237 (2017). 10.1038/ncb3478 [DOI] [PMC free article] [PubMed] [Google Scholar]