3 degree-of-freedom resonant scanner with full-circumferential range and large out-of-plane displacement

Abstract

Microsystems-based scanning technologies can achieve deflection angles of several tens of degrees and translational displacements of a couple hundred microns. Emerging applications need performance with multi-fold greater torsional and translational motion. A compliant lever-based mechanism is introduced into the comb-drive actuators of a MEMS resonant scanner to achieve full-circumferential range and large out-of-plane displacement at ambient pressures. A 1.5 mm diameter mirror is demonstrated that generates 494° total deflection angle and 561 μm translational displacement at either 853 or 956 Hz and either 100 or 90V, respectively. At 40V, an optical scan angle of ~200° and translational displacement of ~310 μm are achieved.

1. Introduction

Resonant devices fabricated using micro-electro-mechanical systems (MEMS) technology can perform fast scanning with large angular deflections, low power consumption, and high mechanical reliability. The design and fabrication of high-speed MEMS scanners with wide deflection angles and large translational displacement in a compact footprint is very challenging. Emerging optical technologies require larger mirror dimensions to capture more light, and need greater forces and torques to achieve higher scan amplitudes at faster speeds. Larger mirror dimensions are hampered by an increased effect of air damping. Early devices demonstrated only tens of degrees of optical scan angle or a couple hundred microns of translational displacement.

Current microsystems-based applications include projection display, light detection and ranging (LiDAR), 3-dimensional (3D) depth sensing, endomicroscopy, and Fourier transform infrared (FTIR) spectroscopy [1–9]. Scanners designed using conventional actuators have achieved optical scan angles up to 90° [10]. This level of performance is adequate for many applications. However, emerging technologies, such as panoramic imaging and surround-view monitoring, need larger deflection angles. Wide-angle optics have been attempted, but this approach is limited by high complexity and increased size requirements [11–15]. Actuation techniques that use large force or torque, motion conversion mechanisms [16], high-fracture-toughness materials as flexible pivots [17], and vacuum packaging for reduced damping [18,19] are also being are being developed, but limited success has been achieved.

Electrostatic, electromagnetic, electrothermal, and thin-film piezoelectric mechanisms have achieved translational displacements of a couple hundred microns [20–25]. These MEMS-based methodologies have potential for mass manufacture with low-cost batch fabrication. Current resonant scanners are designed to achieve either large translational or torsional motion. However, few technologies can achieve large amplitudes in both modes [6,16,26,27]. Deformable thin-film structures in piezoelectric and electrothermal MEMS scanners are usually designed with sufficient length to provide large motions at the expense of reduced scan speeds. Electrostatic actuation offers fast response time, low power consumption, and ease of integration, despite limited operational range from the pull-in effect and high actuation voltage requirements. Here, we present a 3 degree-of-freedom (DOF) parametrical resonance scanner design that can achieve full-circumferential range >360° with large out-of-plane translation >500 μm in ambient pressure.

2. Scanner design

2.1. Schematic

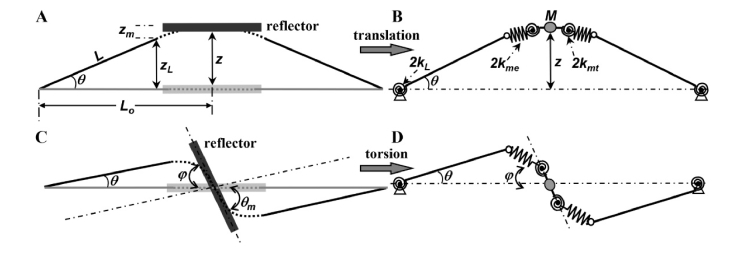
A schematic (top view) of the 3-DOF resonance scanner is shown, Fig. 1(a). A 1.5 mm diameter reflector is supported on opposite sides by lever-arm suspensions. Two rows of comb-drive actuators provide torque. Displacement of the lever-arms create either torsional or translational motion, Figs. 1(b) and 1(c). An H-shaped (torsional) spring anchored to each corner of the structure is used as a pivot to create large angular rotations while providing high resistance to lateral bending, Fig. 1(d). A set of 4 multi-turn central-clamped folded-beam springs are used to attach the central axis of the reflector to each suspension, and allows for large deflections in the bending direction, Fig. 1(e). A straight bar connects this spring to the reflector.

Fig. 1.

Schematic. (A) A 1.5 mm diameter reflector is supported by two symmetric lever-based suspensions that are actuated by two rows of in-plane comb-drive actuators at resonance (top view). The suspensions form a compliant mechanism to convert motion between the (B) translational and (C) rotational modes (side view). (D) H-shaped torsional springs attached to the corners of the chip allow for large angular rotations while providing high resistance to lateral bending. (E) Multi-turn central-clamped folded-beam springs attach the reflector to the levers, and provide large deflection angles in the folding direction while resisting lateral bending. This spring is connected to the central axis of the reflector via a straight bar to achieve a high ratio for either torsion or translation of the reflector to torsion of the lever.

The dimensions of the torsional spring, multi-turn central-clamped folded-beam spring, and lever used for device fabrication are shown, Table 1. L_H, L_M, and L_A define the length, and W_H and W_M designate the width of the structures, respectively. The torsional and multi-turn central-clamped folded-beam springs have a thickness of 50 μm, and a total of 1 and 17 turns, respectively.

Table 1. Geometric parameters for the 3-DOF parametrical resonance scanner.

	length	width	thickness	# of turns
torsional spring	LH = 200 μm	WH = 10 μm	50 μm	1
folded-beam spring	LM = 400 μm	WM = 7 μm	50 μm	17
lever-arm	LA = 1475 μm	─	50 μm	─

2.2. Scanner model

A rigid body model is developed to characterize the dynamic motion of the reflector and levers. The total vertical displacement z and rotation angle φ are determined by rotation of the lever and deformation of the folded-beam spring, respectively, Figs. 2(a)–2(d).

Fig. 2.

Rigid-body model for scanner. (A) Schematic of reflector in translational mode is shown (side view). z_L defines the vertical displacement of the free end of the lever, and z_m represents the distance generated by the folded-beam spring. L is the length of the lever arm, and θ is the rotation angle. L_o is the distance from the lever pivot to the central axis of the reflector. (B) M is the reflector mass, and k_L and k_me are spring constants for the torsional and folded-beam spring, respectively. k_mt is the equivalent torsional spring constant. (C),(D) In torsional mode, φ is defined as the rotation angle of the reflector.

The folded-beam spring is modeled as tension and torsion springs connected in series. The equation of motion is expressed as follows:

$$z=z_L+z_m=L\times \sin \theta +{\displaystyle \sum _i{z}_i}$$ (1)

$$\varphi ={\theta }_m-\theta ={\displaystyle \sum _i{\theta }_i}-\theta ,$$ (2)

where z_i and θ_i are the vertical displacement and torsional angle, respectively, of the individual beams of the folded-beam spring.

Large vertical displacements and scan angles are achieved by using long levers with soft springs at low resonant frequencies. The geometric parameters of multiple components can be modified in this lever-based compliant mechanism to provide design flexibility and meet the desired requirements for scanner amplitude and speed. Per Eqs. (1) and (2), large vertical displacements and scan angles can be achieved with a small rotation of the lever. The comb-drive actuators between the lever and frame are designed to generate large electrostatic torque throughout a large part of the oscillation period. Because individual z_i and θ_i contribute to only a fraction of the vertical displacement and torsion angle, respectively, the risk for fracture caused by large deformations and stress is dramatically reduced.

The equations of motion are derived using the Euler-Lagrange method, and torsional motion is described as follows:

$$J_M{\varphi }^{\text{'}\text{'}}+b_{Mr}{\varphi }^{\text{'}}+4k_{mt}(\varphi +\theta )=0$$ (3)

where J_M and b_Mr are the inertia of the reflector and the damping coefficient in torsional mode, respectively, and k_mt is the equivalent torsional spring constant.

$$J_L{\theta }^{\text{'}\text{'}}+b_L{\theta }^{\text{'}}+2k_L\theta =T_{es}+2k_{me}\times L_{O}L\sin \theta \times \frac{\sqrt{{\left(L\sin \theta \right)}^2+{\left(L_O-L\right)}^2-\left(L_O-L\right)}}{{\left(L_O-L\cos \theta \right)}^2+{\left(L\sin \theta \right)}^2}$$ (4)

where J_L and b_L are the inertia and damping coefficient of the lever, k_L is the spring constant of the torsional spring, T_es is the electrostatic torque, k_me is the equivalent extension spring constant of a single folded-beam spring, and L_o is the distance from the pivot of the lever to the central axis of the mirror.

The equation for out-of-plane translational motion is described where M is the mass of the reflector, b_Mt is the damping coefficient of the reflector in translational mode, and k_me is the equivalent extension spring constant of the folded-beam spring.

$$M{z}^{\text{'}\text{'}}+b_{Mt}{z}^{\prime }+4k_{me}\times \frac{{(z-L\sin \theta )}^2}{\sqrt{{(z-L\sin \theta )}^2+{(L_O-L\cos \theta )}^2}}=0$$ (5)

2.3. Modal analysis

The structure of the 3-DOF parametrical resonance scanner is optimized using a finite element model (FEM) to achieve stable motion in the torsional and translational modes and to minimize crosstalk from mechanical and electrical coupling. The results of the FEM modal analysis are shown, Figs. 3(a) and 3(b). The first and second modes are torsional and translational, respectively. In a parametric resonance system, large amplitude motion is achieved using a drive frequency that is twice that of the eigenfrequency [28]. This model is used to tune the resonance frequencies of the structure and prevent crosstalk.

Fig. 3.

FEM modal analysis. (A) The first mode of the scanner designed with the compliant lever-based mechanism is torsional, and occurs at a resonant frequency of 792 Hz. (B) The second mode is translational, and occurs at a resonant frequency of 1000 Hz.

2.4. Scanner fabrication

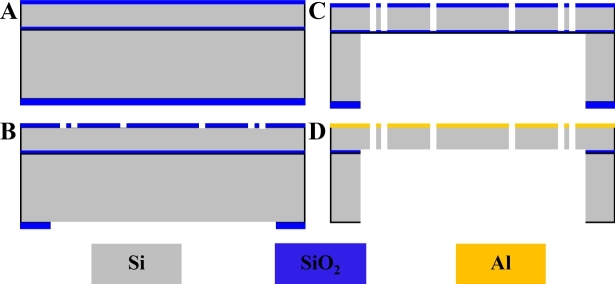
The 3-DOF parametrical resonance scanner is fabricated using a two masks process. Plasma enhanced chemical vapor deposition (PECVD) is used to deposit silicon dioxide (SiO2) on a silicon-on-insulator (SOI) wafer, Fig. 4(a). Hard masks are used to pattern the device structures and protect the substrate from scratches and contamination. The top and bottom surfaces are patterned with lithography using top structure and backside masks, respectively, Fig. 4(b).

Fig. 4.

Process flow for scanner fabrication. (A) A SOI wafer with a 50 μm silicon device layer, 0.5 μm SiO₂ buried layer, and a 415 μm silicon handle layer is used. (B) A 0.6 and 2.5 μm SiO₂ layer is deposited on the front and back side of the substrate, respectively. (C) DRIE is performed to etch the exposed silicon and handle layers. (D) A BHF etch process is performed to remove the SiO₂ layers, and IPA is used to release the movable structures. Electron beam evaporation is performed to coat the reflector with a ~60 nm layer of Al.

Plasma etching is used to remove the PECVD deposited SiO2 layers, and deep-reactive-ion-etching (DRIE) is performed to etch the exposed silicon and handle layers, Fig. 4(c). A buffered hydrofluoric acid (BHF) etch process is used to remove the SiO2 layers, and an isopropyl alcohol (IPA) rinse, and a dry process is performed to release the movable structures, Fig. 4(d). An electron beam evaporation process is used to deposit a ~60 nm layer of aluminum (Al) on the bare surface of the silicon device layer to form the reflector surface. This thickness is adequate to achieve a reflectivity >85%. A scanning electron microscope (SEM) image of a microfabricated device is shown, Fig. 5(a). The chip size is 3.7 × 2.8 × 0.466 mm³ (L × W × H). Structural details of the torsional and folded-beam springs are shown, Figs. 5(b) and 5(c).

Fig. 5.

SEM image of scanner. (A) The locations of the reflector, comb-drive actuators, and lever in the fabricated device are shown (top view). Expanded views of the (B) torsional (red box) and (C) folded-beam springs (blue box) are shown.

3. Scanner performance

3.1. Scanner setup

An optical profiler (New View 5000, Zygo) is used to characterize the quality of the reflector surface. A 635 nm laser beam with ~0.7 mW of power and 0.5 mm spot size is deflected to measure the optical scan angle 2φ, Fig. 6(a). The distance between the reflector and the projection plane is 15 cm. A radius of curvature of 3 m with a root mean square (rms) roughness of 2 nm is measured. The dynamic performance of the scanner is determined by sweeping the drive frequency to electrostatically activate resonant modes. This parameter is defined as the interior angle of the arc scan α projected in a plane perpendicular to the torsional axis of the reflector.

Fig. 6.

Optical scan angle measurement. (A) Schematic of experimental set-up is shown. Photos show (B) reflector mounted on substrate along one edge, (C) vertical displacement >466 μm (chip thickness) in translation mode, (D) mechanical scan angle ~90° in torsion mode, and (E) scanner reflecting laser beam in 360° pattern.

Only one edge of the substrate is mounted to prevent the deflected beam from being obstructed when scanning in the torsional mode. Squeeze damping in the translational mode is also reduced, Fig. 6(b). A displacement sensor is used to measure the out-of-plane travel. Reflector motion at resonance is shown with translational displacement >466 μm and ± 90° mechanical scan angle, Figs. 6(c) and 6(d), respectively. The pattern generated by the reflected laser beam demonstrates a full circumferential rotational scan angle, Fig. 6(e). The diameter of the projected circle is 9 mm, and is determined by the distance between the reflector and the projection plane and the incident angle of the beam.

3.2. Torsional mode

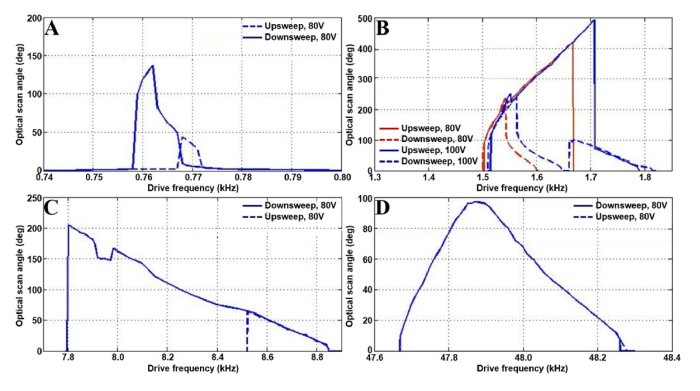
The 3-DOF scanner exhibits profound non-linear behaviors when activated in torsional mode. Previously reported MEMS-based parametric oscillators show super-harmonic and sub-harmonic resonances with drive frequencies near 2ω_r/n, where ω_r is the resonant frequency of the structure and n is a positive integer [28]. Our device exhibits not only a fundamental resonance near the natural resonance frequency in the torsional mode (ω_rt) and the sub-harmonic resonance of order 1/2, but also at other sub-harmonic resonances. The optical scan angle at the fundamental resonance is shown, Fig. 7(a). The frequency response at sub-harmonic resonance of order 1/2 shows a stiffness-hardening-softening-mixed behavior resulting in an optical scan angle of 494° with a sine-wave drive signal of 1.707 kHz and 100V, Fig. 7(b).

Fig. 7.

Frequency response in torsional mode. (A) Fundamental resonance. (B) Sub-harmonic resonance of order ½, a maximum optical scan angle of 494° is obtained by using a sine-wave drive signal of 1.707 kHz and 100V with an upsweep in frequency. (C) Sub-harmonic resonance near 10ω_rt. (D) Sub-harmonic resonance near 62ω_rt.

This maximum value is achieved at a jump frequency with an upsweep where the drive signal is near twice the resonance frequency. At this drive frequency, the amplitude of the response changes abruptly. With a sine-wave drive signal near the sub-harmonic resonance near 10ω_rt at 80V, a typical stiffness-softening phenomenon is exhibited, and a large scan angle up to 205° is achieved, Fig. 7(c). With a sine-wave drive signal approaching the sub-harmonic resonance near 62ω_rt at 80V, the upsweep and downsweep frequency response curves coincide, and the unstable region disappears, Fig. 7(d). Other sub and super-harmonic resonances are not observed at ambient pressures.

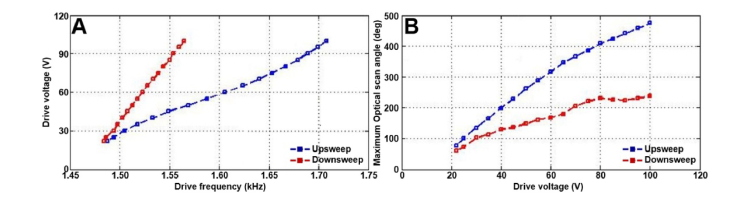
The relationship among the jump frequency, voltage, and maximum optical scan angle is shown using a square wave drive signal with 50% duty cycle near twice the natural frequency in the torsional mode, Figs. 8(a) and 8(b). A large scan angle of ~200° can be achieved at a low voltage of 40V.

Fig. 8.

Torsional mode at sub-harmonic resonance of order 1/2. The relationships are shown between the (A) drive voltage and jump frequency and (B) the maximum optical scan angle and drive voltage for the 3-DOF scanner.

3.3. Translational mode

The 3-DOF scanner also exhibits profound non-linear behavior when activated in translational mode. Similar to the torsional mode, the fundamental, sub-harmonic resonance of order ½, and other sub-harmonic resonances are observed. The frequency response curves are shown, Figs. 9(a)–9(d). The ultra-large motion is attributed a stiffness-softening behavior when the device is driven near resonance.

Fig. 9.

Frequency response in translational mode. (A) Subharmonic resonance of order ½, a maximum vertical displacement of 561 μm is obtained with a downsweep in frequency using a square-wave with 50% duty-cycle near 1912 Hz at 80V. (B) Fundamental resonance. (C) Subharmonic resonance at near at near 5ω_ro. (D). Subharmonic resonance at near at near 51ω_to.

The largest out-of-plane motion is obtained at the sub-harmonic resonance of order 1/2. The relationship among the jump frequency, voltage, and maximum displacement with a square-wave signal and 50% duty-cycle sweeping frequencies near 2ω_ro, the natural frequency of the out-of-plane translational mode, is shown, Figs. 10(a) and 10(b). A maximum vertical displacement of 561 μm is obtained with a downsweep in frequency using a square-wave with 50% duty-cycle near 1912 Hz at 80V. A displacement of ~310 μm is obtained with a low drive voltage of 40V.

Fig. 10.

Translational mode at sub-harmonic resonance of order 1/2. The relationship between the (A) maximum vertical displacement and drive voltage and (B) the drive voltage and jump frequency are shown.

4. Other 3-DOF scanners

Devices are designed and fabricated using different reflector dimensions and frequency response to demonstrate the flexibility of this approach. A 0.7 mm diameter reflector achieves out-of-plane translational displacement of ~320 μm at 4.405 kHz and torsional scan with ~90° mechanical scan angles at 8.425 kHz is shown, Figs. 11(a) and 11(b), respectively. A 3 mm diameter reflector performs out-of-plane displacement of ~780 μm at 652 Hz and torsional scans with ~90° deflection at 188 Hz is shown, Figs. 11(c) and 11(d). A 3D device that performs switchable horizontal/vertical 2D scanning is shown, Fig. 11(e). A ring-shaped Lissajous pattern is generated using a horizontal 2D scan, Fig. 11(f). The densely filled illumination demonstrates promise for future use in OCT, wide-field fluorescence, and photoacoustice endoscopes.

Fig. 11.

3-DOF scanners. Scanners with different dimensions using the compliant lever-based mechanism to achieve large amplitude motions are shown. Translational and torsional motions, respectively, are shown for reflectors with a diameters of (A),(B) 0.7 and (C),(D) 3 mm. (E) A scanner that performs switchable horizontal/vertical 2D scanning produces a (F) large Lissajous scan pattern.

5. Discussion

Here, we report a flexible design for a compliant lever-based mechanism that significantly increases the torsional and translational range for a comb-drive resonant MEMS scanner. This design results in an ultra-large scan range in ambient pressure with little risk for mechanical fracture. The comb-drive devices demonstrated show high performance, including extraordinarily large scan amplitudes and fast speeds with low power consumption, compact size, and ease of fabrication. Although relatively high voltages are required to obtain large scan range, vacuum packaging was not required. This level of performance is very promising for integration into miniature systems in optical applications, such as panoramic imaging and surround-view monitoring.

The actuator is located between the chip frame and the lever-arm, and generates only a fraction of the motion of the mirror. This lever-based compliant mechanism can be integrated into resonant MEMS scanners that use other actuation techniques, such as thin-film piezoelectric and electromagnetic actuation, to achieve ultra-large scan range at low drive voltages. The devices demonstrated have a broad frequency response, and specific drive frequencies can be selected to achieve a high-frame-rate Lissajous scanning pattern for imaging applications.

The devices were designed with a large open area to allow air to pass through easily for reduced damping. This effect limited the performance of our previous devices that were designed with a high fill-in factor for a more compact geometry. A previous parametric resonance scanner designed with a unique geometry to match the dual-axes confocal architecture had limited scan angle [6]. Another scanner was designed for multi-photon microscopy that emphasized large-amplitude translational motion only [7].

The reflector roughness of 2 nm rms is much less than the wavelength of visible, near-infrared, and infrared light [29]. The large radius of curvature measured of 3 m is adequate for most imaging applications and for projection displays. While the voltages required for this scanning mechanism are high by comparison with other designs, a relatively large scan range was achieved using relatively low voltages. The drive voltage can be further reduced by modifying the position of the H-shaped torsional spring or the position of the comb-drives.

A ~60 nm thick layer of aluminum was deposited on the reflector surface to provide high reflectivity for visible light. Also, coating the bond pads with aluminum provides robust electrical contact for wire bonding. A thin layer is used to minimize roughness of the reflector surface that may occur using PECVD fabrication methods. Deep and narrow trenches are used to isolate the electrical pads, and work as a shadow mask for coating the pad metal layer. Our experimental results showed no electrical isolation problems using a 200 nm layer of either aluminum or gold.

Scanners designed using the principle of parametric resonance have several limitations. This mechanism of action can be susceptible to the ‘pull-in’ phenomenon that can affect device reliability. Also, these devices work in the resonance mode only, and cannot be used for applications that require a quasi-static mode, such as tracking or positioning.

6. Summary

A compliant lever-based mechanism is introduced into the comb-drive actuators of a parametric resonance scanner. H-shaped (torsional) and multi-turn folded-beam springs are used to achieve ultra-large angular deflections and translational displacements. The ultra-large motions are attributed to a stiffness-softening-hardening-mixed behavior in the torsional mode and a stiffness-softening behavior in the translational mode, respectively. A reflector that generates 494° total deflection angle and 561 μm translational displacement is demonstrated.

Funding

National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health (R01 EB020644).