A Bayesian Sensitivity Analysis to Partition Body Mass Index Into Components of Body Composition: An Application to Head and Neck Cancer Survival

Abstract

Previous studies have suggested a “J-shaped” relationship between body mass index (BMI, calculated as weight (kg)/height (m)²) and survival among head and neck cancer (HNC) patients. However, BMI is a vague measure of body composition. To provide greater resolution, we used Bayesian sensitivity analysis, informed by external data, to model the relationship between predicted fat mass index (FMI, adipose tissue (kg)/height (m)²), lean mass index (LMI, lean tissue (kg)/height (m)²), and survival. We estimated posterior median hazard ratios and 95% credible intervals for the BMI-mortality relationship in a Bayesian framework using data from 1,180 adults in North Carolina with HNC diagnosed between 2002 and 2006. Risk factors were assessed by interview shortly after diagnosis and vital status through 2013 via the National Death Index. The relationship between BMI and all-cause mortality was convex, with a nadir at 28.6, with greater risk observed throughout the normal weight range. The sensitivity analysis indicated that this was consistent with opposing increases in risk with FMI (per unit increase, hazard ratio = 1.04 (1.00, 1.08)) and decreases with LMI (per unit increase, hazard ratio = 0.90 (0.85, 0.95)). Patterns were similar for HNC-specific mortality but associations were stronger. Measures of body composition, rather than BMI, should be considered in relation to mortality risk.

Several studies of the association between body mass index (BMI, weight (kg)/height (m)²) and mortality related to head and neck cancer (HNC; oral cavity, pharynx, and larynx) have indicated that HNC cancer survivors with ideal weight are at greater risk of death than those with overweight or obesity (1–6). One explanation for these observations is that BMI is a less than ideal measure of adiposity, especially as it relates to mortality among cancer survivors, because it does not distinguish between lean and adipose tissue (7, 8). Adipose tissue is a source of hormones and inflammatory cytokines related to cancer progression (9), while lean mass is associated with greater insulin sensitivity (10) and lower inflammation (11, 12), which might be related to longer survival. However, lower BMI, including values within the range of ideal weight, might reflect a state of low lean mass more than an ideal level of adiposity, even when assessed before cancer treatment (13–15). Low lean mass has previously been observed to be associated with greater mortality among HNC patients (2), but how this could skew the observed relationship regarding mortality and BMI has not been explored. Distinguishing the associations between mortality and individual aspects of body composition would provide valuable insight and help resolve potentially confusing messages regarding obesity and cancer survival (16).

Previously, Allison et al. (17) illustrated a hypothetical scenario where a U- or J-shaped relationship between mortality and BMI could be explained by a simultaneous increase in risk of death with greater adipose tissue and decrease in risk of death with greater lean mass. Body composition is not routinely assessed in observational epidemiologic studies, but in the absence of such information the approach taken by Allison et al. can be formally applied using Bayesian methods. Considering body composition as a latent variable, its relationship with observed factors can be informed from external data, and the relationship between fat mass, lean mass, and mortality can be explored. A number of strategies for similar analyses have been proposed across a range of other applications, but a Bayesian approach offers several advantages, including systematic incorporation of the uncertainty in the relationship between the observed and latent variables (18–20).

In the present study, we estimated the relationship between mortality and BMI among a cohort of newly diagnosed HNC cases from a population-based study in North Carolina. We outlined a Bayesian approach for estimating the independent relationship between mortality and unmeasured indices of body composition. We applied this method, with priors informed by external data, to explore the potential role of adiposity and lean mass on the observed relationship between BMI and mortality in this cohort.

METHODS

Study population

Our analysis used data from the mortality follow-up of HNC cases from the Carolina Head and Neck Cancer Epidemiology (CHANCE) study, a population-based case-control study of head and neck squamous cell carcinoma in Central and Eastern North Carolina. Details of the case-control study have been previously reported (21, 22). The study was approved by the University of North Carolina Institutional Review Board.

Participants for this study were residents in a 46-county region in Central and Eastern North Carolina between the ages of 20 and 80 years, who were diagnosed with a new first primary squamous cell carcinoma of the oral cavity or pharynx (International Classification of Diseases for Oncology, Third Revision, topography codes C0.00–C14.8) or larynx (C32.0–C32.9) between January 1, 2002, and February 28, 2006. Eligible cases were identified through a rapid case-ascertainment system by the North Carolina Central Cancer Registry, including monthly contact with the cancer registrars of 54 hospitals within the study area. After physician consent, contact was made with 98% of eligible cases. Of these, 82% provided written consent to participate, after which in-home interviews were conducted.

Outcome assessment

Date and cause of death through December 31, 2013, were established through linkage with the National Death Index (23), a standard source of mortality data for epidemiologic research (24). Details of the specific procedure for identifying matches between our data and the National Death Index database have been previously reported (25). For the head and neck squamous cell carcinoma cases, we constructed variables indicating death from any cause and death due to HNC using International Classification of Diseases codes C01–C06, C09, C10, C12–C14, or C32. Follow-up time was calculated from the date of diagnosis to the date of death or, for cases without a death record match in the National Death Index database, December 31, 2013.

Covariate assessment

Interviewers administered a structured questionnaire to collect information on demographic, lifestyle, and dietary characteristics. Data for this analysis included anthropometric measures (self-reported height and weight 1 year prior to the date of the interview), cigarette smoking (number of years smoked), alcohol use (number of servings per week of beer, wine, and liquor), reported comorbidities (cardiovascular disease, pulmonary disease, renal disease, diabetes, and other cancers) and education. Usual diet before diagnosis was assessed with a validated food frequency questionnaire (26). BMI was calculated by dividing total body weight in kilograms by height in meters squared. Data on stage at diagnosis (summary stages I–IV) were gathered through medical record abstraction. To avoid small counts for analyses stratified by stage, we collapsed that variable into categories representing summary stages I–II and III–IV. Out of the 1,389 head and neck squamous cell carcinoma cases, we initially excluded 143 participants below the 1st and above the 99th percentiles of total energy consumption to reduce the likelihood of including implausible dietary intakes; of these, 53 were missing prediagnosis BMI. Subsequently, subjects were excluded if they were missing data on any other covariate: 65 were missing lifetime alcohol intake, and 2 were missing smoking duration. The final analytical sample consisted of 1,180 cases of head and neck squamous cell carcinoma (82% of the original sample of cases), with 655 deaths overall and 224 attributed to HNC.

Statistical methods

Analysis of BMI and mortality

Analyses were conducted in a Bayesian framework. The standard model specified the hazard of mortality as a function of BMI and other covariates using a piecewise exponential proportional hazards model assuming a baseline hazard that was allowed to vary between three 4-year intervals over the approximately 12 years of follow-up. The piecewise exponential model is common in Bayesian survival analyses given its ability to flexibly model the baseline hazard with few terms (27). Denoting the outcome (time of death) by t, the measure of adiposity by x, and the vector of other covariates by w, the hazard function is specified as:

$$\log \left[h(t|\mathbf{x},\mathbf{w})\right]=\log ({\mathrm{\lambda }}_j)+\mathbf{x}\mathrm{\beta }+\mathbf{w}\mathrm{\gamma }\mathrm{for}j\in 1,\dots ,3,$$ (1)

where λ_j is the baseline hazard for interval j and β and γ the vectors of log-hazard ratios on the exposure and confounder variables, respectively. For the BMI-mortality analysis, the vector x corresponds to the terms for a restricted quadratic spline for BMI, with knots at quartiles among those who died (22.2, 25.1, 29.2), while in the outcome model for body composition-mortality (described below), it corresponds to simple linear terms for fat mass index and lean mass index. The variables included in w were confounders identified a priori and included age at diagnosis (continuous linear), race (black/white/other), sex (male/female), years smoked (<9, 10–19, 20–39, 40–49, ≥50), lifetime consumption of ethanol in milliliters (nondrinker; 0–133,294; 133,295–747,550; ≥747,551), education (up to high school, some college, completed college or above), total servings of fruit per day and total servings of vegetables per day (each continuous linear), number of comorbidities reported at diagnosis, and disease stage (I/II vs. III/IV). We note that treatment might lie on the causal pathway between body size and mortality (28), and thus adjustment for it would be inappropriate (29). In the BMI analysis, independent normal priors were specified for all regression parameters $(\log (\mathrm{\lambda }),\mathrm{\beta },\mathrm{\gamma })$ with, for each parameter, a prior mean of 0 and precision (reciprocal of variance) of τ = 10⁻⁴.

Bayesian analysis of latent body composition

It is widely acknowledged that inconsistent relationships between mortality and BMI result from the conflation of fat and lean mass (8, 30, 31), with the latter inversely associated with mortality, including among those with cancer (15). This can be addressed through the decomposition of BMI into distinct components of the fat mass index (FMI, adipose tissue (kg)/height (m)²) and lean mass index (LMI, lean tissue (kg)/height (m)²) (17) as follows:

$$\begin{array}{c}\mathrm{BMI}=\mathrm{BMI}\times p_{\mathrm{BF}}+\mathrm{BMI}\times (1-p_{\mathrm{BF}})\hfill \\ =\frac{\mathrm{adipose}\mathrm{tissue}\mathrm{in}\mathrm{kg}}{{\mathrm{height}\mathrm{in}\mathrm{m}}^2}+\frac{\mathrm{lean}\mathrm{tissue}\mathrm{in}\mathrm{kg}}{{\mathrm{height}\mathrm{in}\mathrm{m}}^2}\hfill \\ =\mathrm{FMI}+\mathrm{LMI}\hfill \end{array},$$ (2)

where $p_{\mathrm{BF}}$ represents an individual’s proportion of body fat. We would ideally include terms for both FMI and LMI in the outcome model (equation 1), but these data are difficult to collect in large epidemiologic studies. However, this could be done in the context of a sensitivity analysis, treating $p_{\mathrm{BF}}$ as a latent (unmeasured) covariate and specifying its relationship to other covariates informed by external data. This approach requires simultaneous specification of a model for the outcome given the covariates of interest, and for the distribution of the latent covariates. Here we outline a Bayesian method to this approach.

Following the example by Allison et al. (17), we include simple linear terms for FMI and LMI in the outcome model, which allows for linear relationships in the log-hazard of the outcome with these variables, which is reasonable for a sensitivity analysis. Thus, the log-hazard function in the outcome model is:

$$\begin{array}{c}\log \left[h(t|x_{\mathrm{FMI}},x_{\mathrm{LMI}},\mathbf{w})\right]\hfill \\ =\log ({\mathrm{\lambda }}_j)+x_{\mathrm{FMI}}{\mathrm{\beta }}_{\mathrm{FMI}}+x_{\mathrm{LMI}}{\mathrm{\beta }}_{\mathrm{LMI}}+\mathbf{w}\mathrm{\gamma }\hfill \\ \mathrm{for}j=1,\dots ,3,\hfill \end{array}$$ (3)

where the covariates for FMI and LMI are calculated by the interactions: $x_{\mathrm{FMI}}=x_{\mathrm{BMI}}\times p_{\mathrm{BF}}$ and $x_{\mathrm{LMI}}=x_{\mathrm{BMI}}\times (1-p_{\mathrm{BF}})$, respectively, with $x_{\mathrm{BMI}}$ the covariate for BMI.

Next, we specify the distribution of the proportion of body fat, $p_{\mathrm{BF}}$, using its logit transformation with a linear model for its mean as a function of other covariates:

$$\begin{array}{c}\mathrm{logit}\left(p_{\mathrm{BF}}\right)\sim \mathrm{N}\left({\mathrm{\mu }}_{p_{\mathrm{BF}}},{\mathrm{\sigma }}_{p_{\mathrm{BF}}}^2\right)\\ {\mathrm{\mu }}_{p_{\mathrm{BF}}}={\mathrm{\alpha }}_0+x_{\mathrm{BMI}}{\mathrm{\alpha }}_1+\mathbf{z}\prime {\mathrm{\alpha }}_2\end{array}$$ (4)

where $x_{\mathrm{BMI}}$ is the observed value of BMI, and z is a vector of other covariates that predict body composition. The logit transformation is used here to ensure that predicted values of $p_{\mathrm{BF}}$ lie between 0 and 1.

For the proportional hazards model (equation 3), we again specified vague normal priors as above for $\log (\mathrm{\lambda })$ and γ. For the parameters of interest, ${\mathrm{\beta }}_{\mathrm{FMI}}$ and ${\mathrm{\beta }}_{\mathrm{LMI}}$, we specified normal priors centered at 0, with a precision parameter of 10, corresponding to a 95% prior credible interval of (0.54, 1.86) per 1-unit change for FMI and LMI. Specification of informative prior distributions for the parameters $\mathrm{\alpha }=({\mathrm{\alpha }}_0,{\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2)$ and ${\mathrm{\sigma }}_{p_{\mathrm{BF}}}^2$ from the distribution given by equation 4 are required to imply relationships between body composition and the observed covariates, importantly BMI. To inform these priors we fit a regression of the logit of the proportion of body fat on age, sex, race, and cigarette smoking (ever/never) using dual-energy X-ray absorptiometry (DEXA)-based body composition data on US adults (age ≥18) from the 2005–2006 National Health and Nutrition Examination Survey (NHANES) (32), weighted to the age distribution of the analytical sample of HNC cases in the CHANCE study. These covariates were selected from those expected to predict body composition and for which we had similar measures in the CHANCE data. We specified a multivariate normal prior for α, with mean and covariance matrix from the parameter estimates from this model (model 1) and based ${\mathrm{\sigma }}_{p_{\mathrm{BF}}}^2$ on the residual variance from the regression from the NHANES-based model. We acknowledge that it would be preferable to base these priors on data on the proportion of body fat among cancer survivors, but such data are not available. This is likely a minor limitation because the reference time for BMI was before treatment, a period during which these patients would be less likely to experience wasting.

We additionally performed a series of sensitivity analyses to explore the robustness of our models to the prior specification by modifying the parameter values in the prior for the proportion of body fat. In model 2, we attenuated the mean of the BMI coefficient $({\mathrm{\alpha }}_1)$ in equation 4 by 10% to imply that BMI is less strongly related to body fat proportion, and in model 3 we separately increased the residual error $({\mathrm{\sigma }}_{\mathrm{BF}}^2)$ by 10% to imply less certainty in the prior for body fat. We also report FMI and LMI associations by disease stage using estimates from models with a multiplicative term for interaction between dichotomous disease stage (I/II vs. III/IV) and the linear body composition terms for both all-cause and HNC-specific mortality.

For the BMI models, and models 1–3 described above, we obtained 3 chains of 300,000 samples each from the posterior distribution of the parameters of the outcome model given the data through Markov chain Monte Carlo (MCMC) sampling (33) after discarding the initial 50% as burn-in samples (34, p. 282), thinning to every 5th iteration for the BMI model, and thinning to the 25th iteration for the latent body composition models. For the models with interaction by stage, we increased the total number of MCMC iterations to 500,000 and thinned every 50th iteration. Additional iterations and thinning are often required due to slow mixing in complex models such as these. Sampling was conducted using the Nimble package (35) in R (R Foundation for Statistical Computing, Vienna, Austria) (36). Sample R and NIMBLE code for our analysis is presented in Web Appendix 1 (available at https://academic.oup.com/aje). For all models, we report the posterior median of the hazard ratios and corresponding 95% percentile-based credible intervals. Convergence was assessed by visual inspection of trace and density plots as well as the Geweke and Gelman-Rubin tests in the CODA package (37). Convergence diagnostics for a representative model are presented in Web Appendix 2, Web Table 1. In preliminary analyses, we found no evidence of interaction by race, sex, smoking status (ever/never), and cancer site (oral/pharyngeal vs. laryngeal), so we omit those results in the interest of space.

RESULTS

Descriptive statistics for the 1,180 HNC cases, by quartiles of BMI according to the distribution of those who died, and overall, are presented in Table 1. Age was similar across BMI categories, while those with lower BMI were more likely to be female or black and less likely to have education beyond high school than those in the higher BMI categories. Smoking and alcohol use were more frequent among those with lower BMI. Alcohol intake and years of smoking were lower in this population as BMI increased. Laryngeal cancers were somewhat less common, and oral cancers somewhat more common, among those in the lower BMI categories compared with those in the upper categories. Advanced stage was more common among underweight individuals than in the other BMI categories, but there was little variation in stage across the upper BMI categories.

Table 1.

Characteristics of Head and Neck Cancer Cases According to Quartiles of Body Mass Index Among Those Who Died, Carolina Head and Neck Cancer Epidemiology Study, North Carolina, 2002–2013

Variable	Body Mass Indexa
	15.6–22.2		22.3–25.1		25.2–29.2		29.2–69.1		Total Cohort
	(n = 240)		(n = 275)		(n = 319)		(n = 346)		(n = 1,180)
	No.	%	No.	%	No.	%	No.	%	No.	%
Person-years	1,293.77		1,794.20		2,219.35		2,393.11		7,700.43
Deaths	168		160		163		164		655
Ageb	57.5 (10.7)		58.5 (10.4)		60.2 (10.5)		57.8 (9.9)		58.6 (10.4)
Sex
Male	168	70.0	215	78.2	267	83.7	251	72.5	901	76.4
Female	72	30.0	60	21.8	52	16.3	95	27.5	279	23.6
Education
High school	177	73.8	164	59.6	186	58.3	193	55.8	720	61.0
Some college	44	18.3	63	22.9	84	26.3	101	29.2	292	24.7
College or above	19	7.9	48	17.5	49	15.4	52	15.0	168	14.2
Race
White	140	58.3	208	75.6	252	79.0	278	80.3	878	74.4
Black	97	40.4	64	23.3	57	17.9	59	17.1	277	23.5
Other	3	1.2	3	1.1	10	3.1	9	2.6	25	2.1
Alcohol intake, mL
Nondrinker	13	5.4	21	7.6	29	9.1	55	15.9	118	10.0
133,294	33	13.8	39	14.2	66	20.7	81	23.4	219	18.6
133,295–747,550	58	24.2	87	31.6	88	27.6	95	27.5	328	27.8
747,551	136	56.7	128	46.5	136	42.6	115	33.2	515	43.6
Years smoked
≤9	15	6.3	22	8.0	48	15.0	79	22.8	164	13.9
10–19	14	5.8	21	7.6	38	11.9	39	11.3	112	9.5
20–39	108	45.0	104	37.8	111	34.8	124	35.8	447	37.9
40–49	66	27.5	87	31.6	79	24.8	71	20.5	303	25.7
≥50	37	15.4	41	14.9	43	13.5	33	9.5	154	13.1
No. of comorbiditiesb	0.5 (0.8)		0.5 (0.7)		0.7 (0.8)		0.7 (0.9)		0.6 (0.8)
Site
Laryngeal	70	29.2	98	35.6	116	36.4	133	38.4	417	35.3
Oral	134	55.8	149	54.2	176	55.2	186	53.8	645	54.7
Pharyngeal	36	15.0	28	10.2	27	8.5	27	7.8	118	10.0
Stage
I	50	20.8	61	22.2	88	27.6	77	22.3	434	36.8
II	41	17.1	53	19.3	61	19.1	68	19.7	40	3.4
III	41	17.1	44	16.0	46	14.4	64	18.5	397	33.6
IV	108	45.0	117	42.5	124	38.9	137	39.6	309	26.2

^a Weight (kg)/height (m)².

^b Values are expressed as mean (standard deviation).

Analysis of BMI and mortality

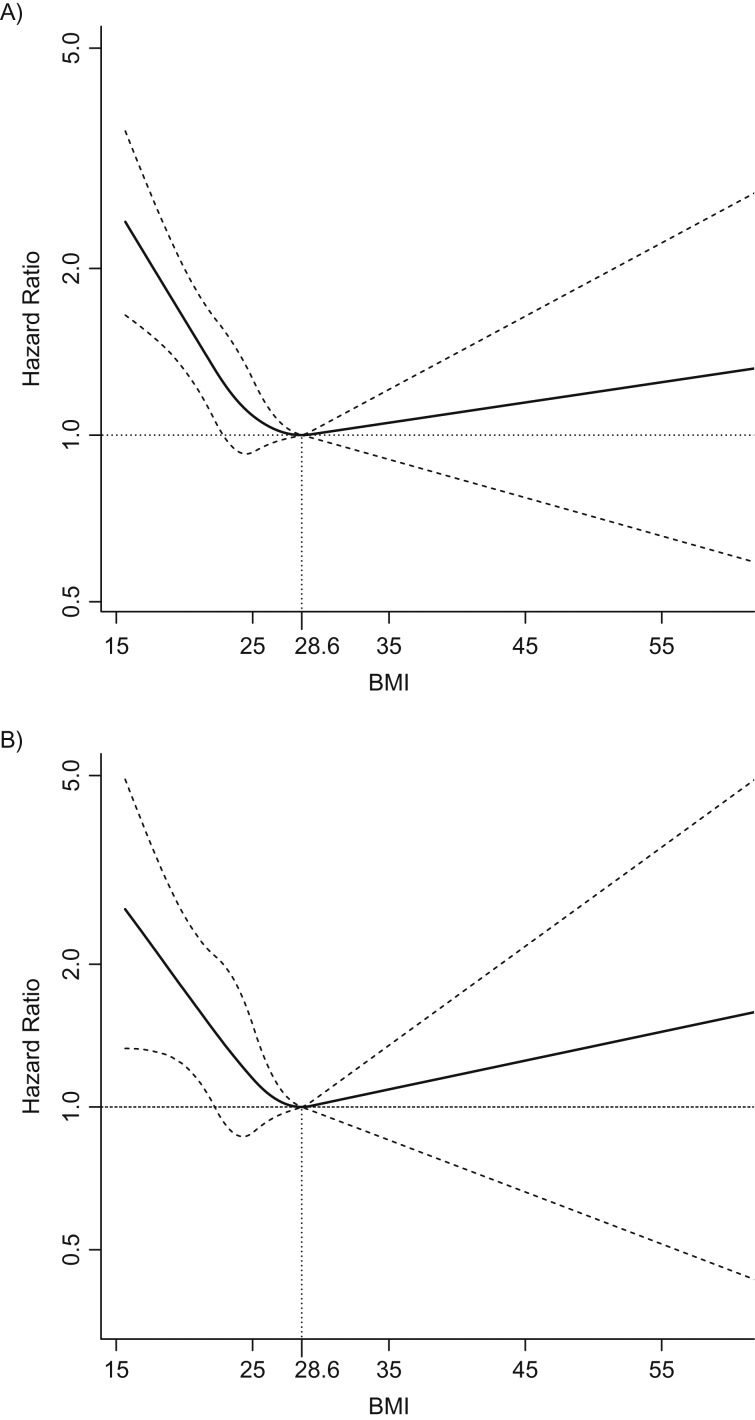
Posterior median hazard ratios and pointwise credible intervals for the relationship between BMI and all-cause and HNC-specific mortality are presented in Figure 1. The nadir was 28.6 for both all-cause mortality and HNC-specific mortality; therefore, hazard ratios were calculated relative to these values. We note that the nadirs lie at the upper end of the overweight range (25 ≤ BMI < 30) (38). We observed a “reverse J-shaped” relationship for both outcomes with greater risk of death among those at the extremes of the BMI distribution. Increases in risk relative to the nadir were more pronounced among those with lower BMI than those with higher BMI, even among those with ideal weight (18.5 ≤ BMI < 25), and this pattern was somewhat more pronounced among HNC-specific deaths. As representative comparisons, for all-cause mortality, the hazard ratio comparing BMI of 21.75 with the nadir of 28.6 was 1.38 (95% credible interval (CrI): 1.12, 1.69), and for 33.25 relative to the nadir was 1.04 (0.93, 1.15) (the midpoint of the normal weight range, and a similar distance above the lower cutpoint for the obese category, respectively). These comparisons for HNC-specific mortality were 1.53 (95% CrI: 1.06, 2.15) for 21.75 vs. 28.4 and 1.06 (95% CrI: 0.89, 1.24) for 33.25 versus 28.4.

Figure 1.

Adjusted posterior median hazard ratios and pointwise 95% credible intervals for the relationship between BMI (body mass index, weight (kg)/height (m)²) and all-cause (A) and HNC-specific (B) mortality, Carolina Head and Neck Cancer Epidemiology study, North Carolina, 2002–2013. Reference level at nadir (BMI of 28.6) for all-cause mortality. BMI modeled as restricted quadratic spline with knots at 22.2, 25.1, and 29.2. Hazard ratios were adjusted for age (continuous), sex, race, years smoked (≤9, 10–19, 20–39, 40–49, ≥50), lifetime alcohol intake (nondrinkers and, in mL: ≤133,294; 133,295–747,550; ≥747,551), total intake of fruits (continuous), total intake of vegetables (continuous), number of comorbidities reported (cardiovascular disease, pulmonary disease, renal disease, diabetes, and other cancers), and stage (I/II vs. III/IV).

Bayesian sensitivity analysis of latent body composition

The results of the regression of the logit of the proportion of body fat on BMI, age, sex, race, and smoking using data from NHANES is presented in Table 2. Fat mass was positively related to BMI and age and inversely related to male sex and smoking status.

Table 2.

Prior Mean and Precision Parameters for the Association Between the Logit of the Proportion of Body Fat and Covariates, Estimated From Linear Regression Using Data From the National Health and Nutrition Examination Survey, United States, 2005–2006

Covariate	Mean	Precision × 103
		Intercept	BMIa ÷ 10	Age ÷ 10	Male	Black Race	Other Race	Ever Smoked
Intercept	−1.65	93.38
BMIa÷ 10	0.37	267.44	797.22
Age ÷ 10	0.04	416.51	1,204.05	2,049.84
Male sex	−0.53	48.51	136.85	215.17	48.13
Black race/ethnicity	−0.09	22.26	66.10	101.53	11.29	22.29
Other race/ethnicity	0.03	27.82	79.12	118.23	14.65	0.01	27.66
Ever smoked cigarettes	−0.01	45.20	127.21	209.57	27.21	9.54	11.35	44.71
Residual error	0.03

Abbreviation: BMI, body mass index.

^a Weight (kg)//height (m)².

In the sensitivity analysis presented in Table 3, given the model and priors described above, the aforementioned “reverse J-shaped” relationship between all-cause mortality and BMI is consistent with a simultaneous positive association between mortality and adiposity (FMI) and an inverse relationship with lean mass (LMI) (model 1, per unit increase in FMI, hazard ratio (HR) = 1.04 (95% CrI: 1.00, 1.08); per unit increase in LMI, HR = 0.90 (95% CrI: 0.85, 0.95)). These results were robust to reducing the strength of the prior parameters for the $\mathrm{BMI}-\mathrm{logit}(p_{BF})$ relationship (model 2) and increasing the residual variance of the $\mathrm{logit}(p_{BF})$ model (model 3) for both outcomes. In the analysis stratified by stage (Table 4), the positive relationship between adiposity and all-cause mortality appeared to be more pronounced among those with lower stage at diagnosis (per unit increase in FMI, for stage I/II, HR = 1.06 (95% CrI: 1.01, 1.11); stage III/IV, HR = 1.03, 95% CrI: (95% CrI: 0.98, 1.07), but the inverse association between lean mass and mortality appeared stronger among those with more advanced stage (per unit increase in LMI, for stage I/II, HR = 0.93 (95% CrI: 0.86, 1.00); stage III/IV, HR = 0.88 (95% CrI: 0.82, 0.94). These patterns were similar for HNC-specific deaths.

Table 3.

Posterior Median Hazard Ratios From Bayesian Sensitivity Analysis of the Association Between Body Composition and Head and Neck Cancer–Related Mortality, Carolina Head and Neck Cancer Epidemiology Study, North Carolina, 2002–2013

Variable	Overall Mortality						Head and Neck Cancer Mortality
	Model 1a,b		Model 2a,c		Model 3a,d		Model 1a,b		Model 2a,c		Model 3a,d
	HRe	95% CrI	HRe	95% CrI	HRe	95% CrI	HRe	95% CrI	HRe	95% CrI	HRe	95% CrI
FMI	1.04	1.00, 1.08	1.05	1.00, 1.10	1.04	1.00, 1.08	1.04	0.98, 1.10	1.05	0.98, 1.13	1.04	0.98, 1.10
LMI	0.90	0.85, 0.95	0.90	0.84, 0.95	0.89	0.84, 0.94	0.89	0.81, 0.98	0.89	0.81, 0.98	0.88	0.80, 0.98

Abbreviations: BMI, body mass index, CrI, credible interval; FMI, fat mass index; HR, hazard ratio; LMI, lean mass index.

^a For each model, the logit of proportion of body fat was specified as a function of age, race, sex, and smoking status, which was then used to calculate the LMI (lean tissue (kg)/height (m)²) and FMI (adipose tissue (kg)/height (m)²).

^b Priors for proportion of body fat model used parameters in Table 2.

^c Priors for proportion of body fat model as in model 1 with mean for BMI coefficient multiplied by 0.90.

^d Priors for proportion of body fat model as in model 1 with residual error multiplied by 1.10.

^e Hazard ratios per unit increase, adjusted for age (continuous), sex, race, years smoked (0, 1–9, 10–19, 20–39, 40–49, ≥50), lifetime alcohol intake (nondrinkers and, in mL: ≤133,294, 133,295–747,550, ≥747,551), total intake of fruits (continuous), total intake of vegetables (continuous), number of comorbidities reported (cardiovascular disease, pulmonary disease, renal disease, diabetes, and other cancers), and stage (I/II vs. III/IV).

Table 4.

Posterior Median Hazard Ratios for the Association Between Body Composition and All-Cause and Head and Neck Cancer–Specific Mortality According to Stage at Diagnosis, Carolina Head and Neck Cancer Epidemiology Study, North Carolina, 2002–2013

Variable	Overall Mortalitya				Head and Neck Cancer Mortalitya
	Stage I/II		Stage III/IV		Stage I/II		Stage III/IV
	HRb	95% CrI	HRb	95% CrI	HRb	95% CrI	HRb	95% CrI
FMI	1.06	1.01, 1.11	1.03	0.98, 1.07	1.08	1.00, 1.15	1.02	0.94, 1.08
LMI	0.93	0.86, 1.00	0.88	0.82, 0.94	0.94	0.82, 1.06	0.88	0.79, 0.98

Abbreviations: CrI, credible interval; FMI, fat mass index; HR, hazard ratio; LMI, lean mass index.

^a For each model, the logit of fat mass proportion was specified as a function of age, race, sex, and smoking status, which was then used to calculate the LMI and FMI. Priors for proportion body fat model used parameters in Table 2.

^b Hazard ratios per unit increase, adjusted for age (continuous), sex, race, years smoked (0, 1–9, 10–19, 20–39, 40–49, ≥50), lifetime alcohol intake (nondrinkers and, in mL: ≤133,294, 133,295–747,550, ≥747,551), total intake of fruits (continuous), total intake of vegetables (continuous), and number of comorbidities reported (cardiovascular disease, pulmonary disease, renal disease, diabetes, and other cancers).

DISCUSSION

Our observation regarding an increased risk of HNC-related mortality for individuals with BMI in the range of normal weight relative to overweight or obesity is consistent with previous reports (1–6). However, the ambiguity of BMI with regard to body composition makes the clinical and public health implications of such findings unclear and potentially confusing to patients, clinicians, and the public at large (39, 40). Results from our Bayesian sensitivity analysis suggest that, given our model specifications and priors informed by NHANES data, the BMI-mortality relationship observed in HNC patients is consistent with a positive relationship between adiposity and mortality and an inverse association between lean mass and mortality.

Our analysis was motivated by the fact that, as a measure of adiposity, BMI is limited by its relationship with lean mass, and decomposing BMI into individual aspects of body composition could clarify the association between mortality and adiposity. Researchers have noted that BMI has significant potential to misclassify those at elevated risk of obesity-related health outcomes—it has been reported that approximately 50% of individuals with high adiposity (measured objectively) are classified as having ideal body weight (41). This has motivated researchers to consider more specific measures of body composition in relation to health outcomes (31), such as the FMI and LMI measures considered here. The influence of lean mass has been proposed as an explanation for paradoxical BMI-mortality relationships observed among cancer survivors (8, 13, 15, 42), but the mechanisms remain speculative (15). Low muscle mass among cancer survivors has been associated with greater mortality in several recent studies (2, 13, 14, 42), but the measures of body composition considered have varied. In the one study limited to patients with HNC, low muscle (using a dichotomized index of cross-sectional skeletal muscle area, different from the measure we considered) was associated with nearly twice the rate of death of those with adequate muscle (2), but the authors did not consider body fat. Our findings are in agreement with that study but further indicate that greater adiposity might still be an important factor in HNC-related survival.

It is plausible that body composition is a consequence of more aggressive disease. The nature of the NHANES data used to inform the priors for the FMI distribution precluded inclusion of disease characteristics into that prior. However, Grossberg et al. (2) report that although approximately 58% of those classified as having low skeletal muscle presented with more advanced tumors, nearly half of those with a normal amount of skeletal muscle also presented with advanced disease, and thus muscle mass is not necessarily indicative of stage. Nevertheless, it is difficult to ascertain the directionality and consequence of the body composition-disease stage relationship. Our bias analysis stratified by stage emphasizes that relationships between body composition and mortality should be considered in the context of markers of disease progression.

To our knowledge, ours is the first analysis to explore the potential independent associations between adipose tissue and muscle mass on mortality among HNC survivors using a Bayesian approach to sensitivity analysis similar to those applied to other scenarios of unmeasured confounding (43). Recently, Banack et al. (44) applied stratified probabilistic bias analysis to consider misclassification of obesity status using BMI, considering dual-energy x-ray absorptiometry (DEXA)-based body fat assessments as the gold-standard measure in a subgroup of the Women’s Health Initiative (WHI) study. They reported that bias-corrected estimates of the risk difference indicated stronger effects of obesity on mortality than the traditional, BMI-based definition. Together, our studies suggest the potential for methods from quantitative bias analysis to illuminate the relationship between adiposity and mortality. Additionally, an important use of bias analysis is to identify opportunities for new data collection (45), and ours in particular points to the need for assessment of measures of body composition in studies of obesity and cancer-related mortality rather than relying on BMI alone.

Care must be taken to specify reasonable and informative prior distributions in both Bayesian and probabilistic bias analyses, which can be perceived as a hindrance to their adoption. Without a subsample of study participants with body composition data, we used external data from NHANES, which facilitated our ability to specify meaningful priors for the exposure of interest that was crucial to our sensitivity analysis. Additionally, the approach we followed is flexible with regard to the specification of the distribution of the mismeasured covariate (body composition), which allowed us to consider it continuously with regard to disease risk, incorporate important variables that are related to body composition (including lifestyle factors such as smoking status), and consider interaction between the latent covariates and disease stage. Historically, computational issues have been a significant limitation in employing Bayesian methods over deterministic or probabilistic methods for bias analysis, but the advent of easy-to-use software for Markov chain Monte Carlo sampling—including OpenBUGS (46), JAGS (47), Stan (48), and Nimble (35), as well as proc MCMC in SAS (SAS Institute, Inc., Cary, North Carolina) (49)—has greatly increased accessibility of these techniques and efficient computation. We provide sample code in the supplemental material to encourage application of these methods.

Strengths of our analysis include our use of data from a large population-based study of HNC survivors. We also used a principled analytical framework to investigate the potential relationship of distinct elements of body composition with mortality. We note that there is some controversy regarding the causal interpretation of the association between anthropometric measures and mortality (50), but there are compelling arguments to support such an interpretation (51, 52). One limitation of our study is the use of self-reported height and weight, but relationships between BMI and health risks have been shown to be similar when using self-reported or measured anthropometry (53). Sensitivity analyses are always limited by the accuracy of the prior assumptions and can be sensitive to their distributions. Our analysis relied on applying relationships observed in the NHANES data to our sample of individuals with HNC, in which these relationships might have differed somewhat. Reassuringly, the relationships we observed regarding lean mass are qualitatively similar to a previous analysis of muscle area and BMI in HNC patients (2). Additionally, our use of Bayesian methods allowed us to formally incorporate uncertainty in these parameters through their priors, with this uncertainty reflected in the posterior distribution of the hazard ratios. Nevertheless, it would be preferable to have data on measures of body composition within the study population, or on a similar group of individuals with HNC.

Specific measures of body composition might provide more accurate inferences with regard to risk of death than BMI, especially among cohorts of cancer survivors. Future research in this area should emphasize these measures instead of relying only on BMI. Analysts should consider the use of methods for bias analysis, such as the Bayesian approach employed here, to investigate the potential influence of more precise metrics of exposure in explaining seemingly paradoxical results.

Abbreviations

BMI

body mass index

CHANCE

Carolina Head and Neck Cancer Epidemiology

CrI

credible interval

FMI

fat mass index

HNC

head and neck cancer

HR

hazard ratio

LMI

lean mass index

NHANES

National Health and Nutrition Examination Survey