Development of optimal genetic evaluations for teat and udder structure in Canadian Angus cattle

Abstract

Despite their heritability and influence on female productivity, there are currently no genetic evaluations for teat and udder structure in Canadian Angus cattle. The objective of this study was to develop optimal genetic evaluations for these traits in the Canadian Angus population. Guidelines recommended by Beef Improvement Federation (BIF) were used to score teat and udder structure in 1,735 Canadian Angus cows from 10 representative herds. Cows scored ranged in parity from 1 to 13; however, >70% of cows were parity ≤4. Scores ranged from 1 (large, bottle shaped) to 9 (very small) for teats and from 1 (very pendulous) to 9 (very tight) for udders. Consistent with parity distribution, >70% of teat and udder scores were ≥6. Teat and udder scores (TS₉ and US₉, respectively) were modeled using a multiple trait animal model with random effects of contemporary group (herd-year-season) and additive genetic effect, and fixed effects of breed, parity group, and days between calving and scoring. To test good versus poor structure, a binary classification of 1 or 2 (TS₂, US₂) [comprised of scores 1 to 5 = 1 (poor structure) and scores 6 to 9 = 2 (good structure)] was created. Further, to assess the impact of grouping less frequently observed poor scores, a 1 to 7 scale (TS₇, US₇) was created by combining teat and udder scores 1 to 3. Analyses for teat and udder scores on scales TS₉, US₉, TS₇, US₇, and TS₂, US₂ were compared. In addition, both threshold and linear animal models were used to estimate variance components for the traits. Data treatment and models were evaluated based on correlation of resulting estimated breeding value (EBV) with corrected phenotypes, Spearman’s rank correlation coefficient, average EBV accuracies (r), and deviance information criteria (DIC). TS₉, US₉ scales for teat and udder scores and linear models performed best. Estimates of heritability (SE) for teat and udder score were 0.32 (0.06) and 0.15 (0.04), respectively, indicating these traits were moderately heritable and that genetic improvement for teat and udder scores was possible. Estimates of phenotypic and genotypic correlations for teat and udder score were 0.46 (0.02) and 0.71 (0.09), respectively. Estimates of genotypic correlations with birth weight (BW), weaning weight (WW), and yearling weight (YW), ranged from −0.04 (0.10) to −0.20 (0.12), verifying the importance of selecting for improved teat and udder score as individual traits, alongside performance traits.

Introduction

Poor teat and udder structure have been associated with production inefficiencies (Arnold et al., 2017) through increased mastitis (Persson Waller et al., 2014) and early culling of cows (Arthur et al., 1992; Riley et al., 2001). In addition, poor teat and udder structure can impact calf survival and growth (Haggard et al., 1983; Wittum and Perino, 1995; McGee and Earley, 2018) through delayed teat finding and suckling (Kruse, 2010; Bunter et al., 2013) and mastitis-associated decreased milk yield and quality (Paape et al., 2000; Contreras et al., 2015).

Genetic evaluations are evolving to include traits that impact production efficiencies and animal health and welfare (Miller, 2018). In addition, the Beef Improvement Federation (BIF) (2016) recommended scoring for teat and udder structure, and selecting for tight udder suspension and small, symmetrical teats. As teat and udder structure deteriorate with age (Smith et al., 2017), early identification of cows that maintain effective structure would be beneficial. Previous estimates of heritability for teat and udder score in Holstein, Hereford, and Brahman composites ranged from 0.14 to 0.49 (Boettcher et al., 1998; Bunter and Johnston, 2014; Bradford et al., 2015) indicating opportunity to select for improved mammary structure.

Although teat and udder score are usually considered as linear traits, Ramirez-Valverde et al. (2001) suggested threshold treatment of type traits may more accurately predict genetic merit. In addition, Sapp et al. (2003) suggested that score scales may be collapsed. We assessed these suggestions with the aim to optimize genetic evaluations. Toward the development of a genetic evaluation for teat and udders in Canadian Angus, our objectives were to: 1) identify the most effective data treatment (scoring scales) and models; 2) estimate (co)variance components for teat and udder scores; and 3) estimate genetic and phenotypic correlations of teat and udder scores with performance traits.

Materials and Methods

Collection of teat and udder scores was done in accordance with the Canadian Code of Practice for the care and handling of farm animals. All procedures involving cattle were reviewed and approved by the University of Calgary Animal Care Committee (Protocol AC16-0218).

Herd Selection

Ten Canadian Angus cow herds were recruited to participate, based on previously expressed interest in research and sampling convenience factors (e.g., location and herd size). Both Black Angus and Red Angus cattle were included, as the Canadian Angus herdbook includes both. To be eligible to participate, herds were required to have: 1) a handling facility through which they could process all their cows to enable phenotyping; and 2) have complete pedigree and performance records at the Canadian Angus Association (CAA).

Teat and Udder Scores

Using BIF scoring guidelines, 2,912 Canadian Angus cows, across 10 herds, were scored (only once) during calving seasons from 2014 to 2017, by 1 of 3 trained scorers. From parallel scoring during training, inter-scorer agreement was 80% (kappa coefficient = 0.78). The BIF scoring system ranged from 1 to 9, where the smallest teats and tightest udders were both assigned a score of 9, and large bottle-shaped teats and pendulous udders that had lost support from suspensory ligaments were both assigned a score of 1 (Beef Improvement Federation, 2016). As suggested by the guidelines, all bred females in each herd were scored, recording teat and udder on the weakest quarter of each cow. A deviation from guidelines, that recommend scoring within 24 h post-calving, occurred as teat and udder scores were observed at producer convenience. Hence, scoring time relative to calving date ranged from −121 days to +128 days. Of the 2,912 Canadian Angus cows, 617 were omitted for being scored prior to calving and a further, 560 cows were removed due to a lack of age, parity, or calf information.

After quality control of phenotypic data set, 1,735 teat and udder scores remained with means (SD) of 6.68 (1.49) and 6.56 (1.61), respectively. Consistent with Beard et al. (2018), we created a threshold (binary) scale (TS₂, US₂) of 1 to 2 in which scores from 1 to 5 were designated as class 1 and scores from 6 to 9 were designated as class 2. To assess condensing less frequently observed teat and udder scores, scores 1 to 3 were designated into 1 group creating a 1 to 7 scale (TS₇, US₇). Thus, optimal data treatment analyses for teat and udder scores were carried out on all 3 scales (TS₉, US₉, TS₇, US₇, and TS₂, US₂).

Pedigree and Performance Data:

A 4-generation pedigree file for 1,735 cows and their calves was extracted from the CAA database. Thus, the pedigree file consisted of 52,024 animals, including 8,199 dams and 3,227 sires. Additional performance data on cows and their calves, including date of birth, parity, sex, birth weight (BW), weaning weight (WW), and yearling weight (YW) were also available. It was noteworthy that BW, WW, and YW information extracted from the CAA database were already adjusted for age of dam (BW and WW), and age at measure (WW and YW) as per BIF (2016). All WW under 136 kg and YW over 635 kg were removed. Contemporary groups (CG) (defined as herd of origin, year, and season of birth; with 4 seasons January to March, April to June, July to September, and lastly October to December) with less than 3 animals and those with no variation were excluded. The 275 CG for BW contained an average of 36 animals (min = 3; max = 676), the 259 CG for WW contained an average of 31 animals (min = 3; max = 480), and the 187 YW CG averaged 26 animals (min = 3; max = 248). Ultimately, 9,916 BW, 8,110 WW, and 4,828 YW measures were available for further analyses.

Data Analyses

An animal model was used to estimate (co)variance components among traits using Bayesian inference with the BLUPF90 family of programs (Misztal et al., 2014). Specifically, threshold and linear models were performed using THRGIBBS1F90 and GIBBS2F90 programs, respectively. In preliminary analyses, factors that significantly affected each of the scores were determined using general linear models in SAS 9.4 software (SAS Institute, 2015). Factors tested for significance (P-value ≤ 0.05) and subsequently included in the model were breed (Black Angus = 1, Red Angus = 2, Black–Red Angus Cross = 3), CG, number of days between calving and the date of teat and udder assessment with linear effect (DAYS) [with β (SE) = 0.001 (0.003) and 0.009 (0.003) for teat and udder, respectively] and quadratic effect of DAYS (DAYS2) [with β (SE) −0.0003 (0.0001) for udder scores only], and parity group (defined as parity 1 = parity group A, parity 2 = parity group B, parity 3 to 4 = parity group C, parity 5 to 7 = parity group D, and parity ≥ 8 = parity group E) (Table 1). Contemporary group (defined by herd, year of measurement, and calving season; with 2 calving seasons from January to June and from July to December) was fitted as a random effect, whereas breed, DAYS (DAYS2 for udder), and parity group were fitted as fixed effects. As suggested by Van Tassell et al. (1998) and Varona et al. (1999), threshold models were adopted for univariate analysis of teat and udder scores (TS₉, US₉, TS₇, US₇, and TS₂, US₂). For comparison, linear models were also used to analyze TS₉, US₉ and TS₇, US₇ scoring systems. The most appropriate teat and udder score scale (TS₉, US₉, TS₇, US₇, TS₂, US₂) and model (threshold vs. linear) were defined based on correlation between estimated breeding values (EBVs) and corrected phenotypes, Spearman’s rank correlation coefficients, average EBV accuracies (r), and deviance information criteria (DIC) of univariate analysis, and subsequently used for bivariate analysis of teat and udder score with BW, WW, and YW.

Table 1.

Effects included in models to evaluate birth weight (BW), weaning weight (WW), yearling weight (YW), teat score (TS₉, TS₇, TS₂), and udder score (US₉, US₇, US₂)¹

Trait	CG2	Breed	Sex	MAT3	MPE4	Pgrp5	Days6	Days7
BW	x	x	x	x	x
WW	x	x	x	x	x
YW	x	x	x	x
Teat score (TS9, TS7, TS2)	x	x				x	x
Udder score (US9, US7, US2)	x	x				x	x	x

¹TS₉ = teat score on a 1 to 9 scale; US₉ = udder score on a 1 to 9 scale; TS₇ = teat score on a 1 to 7 scale; US₇ = udder score on a 1 to 7 scale; TS₂ = teat score on a 1 to 2 binary scale; US₂ = udder score on a 1 to 2 binary scale; x = significant (P < 0.05) and included in the model for the trait.

²CG = contemporary group as random effect.

³MAT = maternal additive genetic effect as random effect.

⁴MPE = maternal permanent environmental effect as random effect.

⁵Pgrp = parity group as fixed effect.

⁶Days = days as covariate with linear effect.

⁷Days = days as covariate with quadratic effect.

Linear animal models were used for univariate analyses of BW, WW, and YW. For analyses of BW, WW, and YW, CG was fitted as a random effect, whereas breed and sex were fitted as fixed effects (Table 1). Maternal additive genetic (for BW, WW, and YW) and maternal permanent environmental (for BW and WW) effects were included.

The general animal model used can be represented by the following matrix notation:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{\beta }+{\mathit{Z}}_1\mathit{a}+{\mathit{Z}}_2\mathit{m}+{\mathit{Z}}_3\mathit{c}+{\mathit{Z}}_4\mathit{d}+\mathit{e}}\end{array}}$$

where y is the vector of observations; β is the vector of fixed effects; a is the vector of additive genetic effects; m is the vector of maternal additive genetic effects; c is the vector of maternal permanent environment effects; d is the vector of CG; e is the vector of residual effects; and X, Z₁, Z₂, Z₃, and Z₄ are incidence matrices relating β,a,m,c, and d to y. It was assumed that E[y] = Xβ; Var(a) = A⊕G; Var(m) = A⊕G_m; Var(c) = I⊕MPE, and Var(e) = I⊕R, where A is the relationship matrix among all animals in the pedigree data set, ⊕ is the direct Kronecker product, G is the (co)variance matrix of direct additive genetic effects, G_m is the (co)variance matrix of maternal additive genetic effects, MPE is the (co)variance matrix of maternal permanent environmental effects, I is the identity matrix, and R is the (co)variance matrix of residual effects. Vectors β, a, m,c, and d are location parameters from the conditional distribution. A uniform distribution of β was assumed a priori, reflecting no prior knowledge about this vector. For the (co)variance matrices of random effects, inverted Wishart distributions were defined as prior distributions. Thus, the distribution of y given the parameters of location and scale was assumed according to Van Tassell et al. (1998):

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}|\beta ,\mathit{a},\mathit{m},\mathit{c},\mathit{d},\mathit{R}\sim MVN[\mathit{X}\beta \times Z_1\mathit{a}\times {\mathit{Z}}_2\mathit{m}\times {\mathit{Z}}_3\mathit{c},{\mathit{I}}_N\mathit{R}].}\end{array}}$$

For each analysis, 700,000 iterations were generated, retaining every 50th sample. The first 200,000 iterations were discarded as fixed burn-in. Thus, 10,000 samples were used for (co)variance and genetic parameter estimations. Data convergence was checked through graphical analysis of sampled values.

Model selection criteria were based on correlation of resulting EBV with corrected phenotypes, Spearman’s rank correlation coefficient, average r, and DIC. Estimations of r were calculated using prediction error variance (PEV), as suggested by Misztal and Wiggans (1988):

$${\displaystyle \begin{array}{l}{\displaystyle r=\sqrt{1+\frac{PEV}{{\sigma }_a^2}}}\end{array}}$$

Average r was calculated using EBVs for phenotyped animals only. Statistical significance of the difference between average r for individual analyses was determined using Student’s t-tests.

Results and Discussion

Population

Consistent with the CAA herdbook, 70% of cows were Black Angus, 22% were Red Angus, and 8% were Black and Red Angus crosses. Herd sizes ranged from 35 to 213 cows. And, cows scored ranged in parity from 1st to 13th.

Teat and Udder Scores

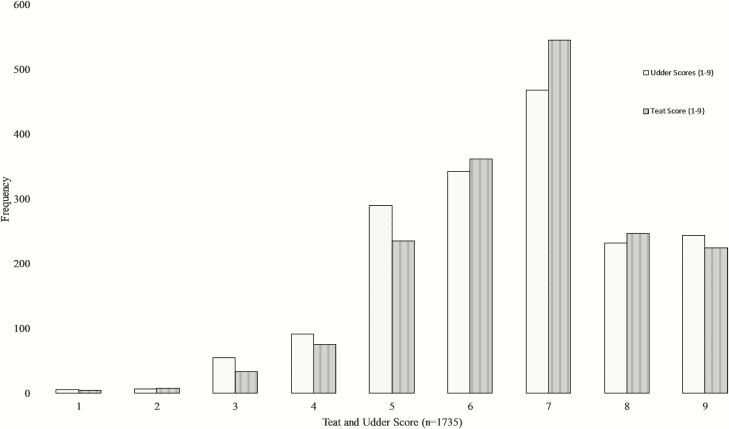
Observed teat and udder scores ranged from 1 to 9, indicating trait variation in the Canadian Angus population, and are presented in Table 2. Consistent with previous observations that producers include teat and udder structure as culling criteria (Arthur et al., 1992), significantly few low (poor) teat and udder scores were observed (Fig. 1). Boldt et al. (2018) showed favorable genetic correlations between cow longevity and high teat and udder scores (0.30 ± 0.11, and 0.23 ± 0.11, respectively) also reflecting the frequency of lower teat and udder scores in the current study. Thus, the advantages of collapsing teat and udder scores into different scales (TS₇ US₇ and TS₂ and US₂) were tested.

Table 2.

Descriptive statistics for teat scores and udder scores (TS₉, US₉, TS₇, US₇, TS₂, US₂) for n = 1,735 Canadian Angus cows¹

Teat and udder scoring scale	Mode	Min	Max
Teat score, TS9	7	1	9
Udder score, US9	7	1	9
Teat score, TS7	5	1	7
Udder score, US7	5	1	7
Teat score, TS2	2	1	2
Udder score, US2	2	1	2

¹TS₉ = teat score on a 1 to 9 scale; US₉ = udder score on a 1 to 9 scale; TS₇ = teat score on a 1 to 7 scale; US₇ = udder score on a 1 to 7 scale; TS₂ = teat score on a 1 to 2 binary scale; US₂ = udder score on a 1 to 2 binary scale.

Figure 1.

Distribution of teat and udder scores observed for 1,735 Canadian Angus cows using the BIF (2016) scoring guideline where the smallest teats and tightest udders were both assigned a score of 9, and large bottle-shaped teats and pendulous udders that had lost support from suspensory ligaments were both assigned a score of 1.

To estimate (co)variance components and genetic parameters 700,000 cycles with fixed burn-in periods of 200,000 cycles for both univariate and bivariate analyses were adequate to obtain convergence, achieve low SD and a relatively narrow 95% highest posterior density interval (HPD). Posterior means of CG variance, additive genetic variance, residual variance, and heritability obtained for teat and udder scores (TS₉, US₉, TS₇, US₇, TS₂, US₂) are shown (Table 3). Posterior means of heritability for teat and udder score ranged from 0.11 ± 0.05 to 0.33 ± 0.09 and were consistent with previous estimates for these traits in populations of beef (Sapp et al., 2003; MacNeil et al., 2006; Bradford et al., 2015) and dairy (Dube et al., 2009; Eriksson et al., 2017) cows.

Table 3.

Estimates of variance components and heritability (h²) of birth weight (BW), weaning weight (WW), yearling weight (YW) using linear models, and teat and udder scores (TS₉, US₉, TS₇, US₇, TS₂, US₂) using linear models and threshold models

Trait	σ 2cg ± PSD1	σ 2a ± PSD2	σ 2e ± PSD2	h 2 ± PSD2
Performance traits	Linear models
BW	6.49 ± 1.20	40.06 ± 3.12	39.97 ± 1.83	0.43 ± 0.03
WW	177.99 ± 72.98	1,469.30 ± 113.43	2,072.60 ± 78.89	0.20 ± 0.19
YW	11,590.0 ± 1,321.3	2,533.90 ± 350.72	6,132.90 ± 278.92	0.18 ± 0.03
Teat and udder scores4	Linear models
Teat score, TS9	0.16 ± 0.11	0.53 ± 0.09	0.93 ± 0.08	0.32 ± 0.06
Udder score, US9	0.42 ± 0.27	0.22 ± 0.06	0.89 ± 0.06	0.15 ± 0.04
Teat score, TS7	0.15 ± 0.11	0.52 ± 0.09	0.88 ± 0.07	0.34 ± 0.05
Udder score, US7	0.41 ± 0.26	0.20 ± 0.05	0.85 ± 0.05	0.14 ± 0.04
Teat and udder scores	Threshold models
Teat score, TS9	0.18 ± 0.14	0.30 ± 0.14	2.19 ± 0.25	0.11 ± 0.05
Udder score, US9	0.38 ± 0.28	0.45 ± 0.14	2.10 ± 0.28	0.15 ± 0.05
Teat score, TS7	1.39 ± 1.10	4.14 ± 0.92	7.55 ± 2.35	0.33 ± 0.09
Udder score, US7	3.21 ± 2.19	2.45 ± 0.61	8.71 ± 1.48	0.17 ± 0.05
Teat score, TS2	0.19 ± 0.22	0.33 ± 0.33	1.00 ± 0.05	0.18 ± 0.14
Udder score, US2	0.33 ± 0.29	0.52 ± 0.37	1.00 ± 0.05	0.26 ± 0.12

¹σ ²_cg = contemporary group variance ± posterior standard deviation, PDS.²σ ²_a = additive genetic variance ± posterior standard deviation, PDS.³σ ²_e = residual variance ± posterior standard deviation, PDS.⁴TS₉ = teat score on a 1 to 9 scale; US₉ = udder score on a 1 to 9 scale; TS₇ = teat score on a 1 to 7 scale; US₇ = udder score on a 1 to 7 scale; TS₂ = teat score on a 1 to 2 binary scale; US₂ = udder score on a 1 to 2 binary scale.

Linear and Threshold Models

Pearson correlations between corrected phenotypes and EBVs, Spearman’s rank correlation coefficients between corrected phenotypes and EBVs, average r, and estimates of DIC from analyses based on linear and threshold models are presented in Table 4. Linear models outperformed threshold models (TS₉, US₉ and TS₇, US₇) with significantly (P < 0.05) higher corrected phenotype and EBV correlations, higher Spearman’s rank correlations, and lower estimates of DIC. Differences in average r were significant for TS₉, US₉ and there was no significant difference for TS₇, US₇.

Table 4.

Pearson correlation of corrected phenotypes with EBVs using linear and threshold models, and TS₉, US₉, TS₇, US₇ and TS₂, US₂ scales for teat and udder score

	Linear models1				Threshold models1
Traits2	Cor (EBV, y*)	Rho	Average r	DIC	Cor (EBV, y*)	Rho	Average r	DIC
Teat score, TS9	0.88	0.85	0.64 (0.03)	5,353.77	0.64	0.65	0.45 (0.05)	6,617.77
Udder score, US9	0.72	0.71	0.52 (0.04)	5,033.45	0.54	0.57	0.49 (0.04)	5,685.75
Teat score, TS7	0.88	0.86	0.65 (0.03)	5,261.34	0.78	0.77	0.62 (0.04)	8,084.93
Udder score, US7	0.72	0.71	0.50 (0.04)	4,985.51	0.64	0.63	0.51 (0.05)	8,475.42
Teat score, TS2					0.78	0.44	0.21 (0.09)	4,383.76
Udder score, US2					0.59	0.43	0.38 (0.09)	1,442.99

¹Rho = Spearman’s rank correlation coefficient, r = EBV accuracy; Cor = Pearson correlation; DIC = deviance information criteria.²TS₉ = teat score on a 1 to 9 scale; US₉ = udder score on a 1 to 9 scale; TS₇ = teat score on a 1 to 7 scale; US₇ = udder score on a 1 to 7 scale; TS₂ = teat score on a 1 to 2 binary scale; US₂ = udder score on a 1 to 2 binary scale.

Despite suggestions (Weller et al., 1988; Van Tassell et al., 1998), that threshold models are most appropriate for traits of ordinal nature, we inferred a linear model was more appropriate for analysis of structural traits in Canadian Angus cows. Linear models are frequently used for the evaluation of ordinal type traits in livestock species (Bradford et al., 2015; Pérez-Cabal and Charfeddine, 2015; McLaren et al., 2016; de Lacerda et al., 2019) and should be explored when evaluating ordinal type traits, if appropriate. In cases where the most advantageous phenotype is not at one end of the scale, such as feet and leg structure (Jeyaruban et al., 2012), threshold models may be most effective.

Teat and Udder Score Scales

Pearson correlations between corrected phenotypes and EBVs, Spearman’s rank correlation coefficients, average r, and estimates of DIC from analyses based on TS₉, US₉, TS₇, US₇, TS₂, US₂ are presented in Table 4. Using linear models, there was no significant (P < 0.05) advantage of either scoring scale (TS₉, US₉ or TS₇, US₇). Using threshold models, TS₇, US₇ resulted in higher corrected phenotype and EBV correlations than TS₉, US₉, and higher Spearman’s rank correlation and average r than TS₉, US₉ and TS₂, US₂. However, estimates of DIC using TS₇, US₇ were also higher.

Based on the suggestion that there may be a threshold where teat and udder structure impact cow health and longevity as well as calf performance from birth to weaning, and that a good verses bad structure scoring system may be easier for producers (Persson Waller et al., 2014; Beard et al., 2018), a binary analysis of teat and udder score (TS₂, US₂) was attempted. Using threshold models and DIC values for model evaluation, DIC values were lowest for TS₂, US₂, and highest for TS₇, US₇. In addition, correlations between corrected phenotypes and EBVs for TS₂, US₂ were higher than the TS₉, US₉ but not different from TS₇, US₇. Conversely, when compared to TS2, US2, average r was better for TS₇, US₇ and TS9, US9. In addition, Spearman’s rank correlation coefficients were lower for TS₂ and US₂ and highest for TS₇ and US₇. When compared, using correlations, rank correlations, and average r estimates from linear models (TS₉, US₉ and TS₇, US₇) treating teat and udder score as a binary trait may result in slower genetic gain. Furthermore, as producers make genetic gain for these traits observations of scores below 6 should decrease. Thus, necessitating a reconstruction of the binary classes, or necessitating increasing the number of classes.

Teat and Udder Correlations

Estimates of genotypic and phenotypic correlations between teat and udder score were 0.71 (0.09) and 0.46 (0.02), respectively (Table 5). These results are in agreement with previous correlations reported for Hereford and Brahman composites (Bunter and Johnston, 2014; Bradford et al., 2015). Bradford et al. (2015) observed that correlations between teat and udder scores were lower when taken by trained scorers than producer-collected data. It is possible that producers are not able to separate intrinsic factors of each trait and thus they group teat and udder as one mammary unit. Therefore, to achieve highest rates of genetic gain, evaluation and selection of these two traits should be done independently.

Table 5.

Estimates (SD) of genetic correlations (above diagonal) and phenotypic correlations (below diagonal) for teat and udder scores (TS₉, US₉) with birth weight (BW), weaning weight (WW), and yearling weight (YW)

	BW	WW	YW	Teat1, TS9	Udder2, US9
BW	1	0.35 (0.06)	0.38 (0.07)	−0.14 (0.08)	−0.04 (0.10)
WW	0.28 (0.02)	1	0.79 (0.17)	−0.09 (0.17)	−0.06 (0.18)
YW	0.22 (0.02)	0.60 (0.03)	1	−0.14 (0.10)	−0.20 (0.12)
Teat1, TS9	−0.08 (0.03)	−0.08 (0.04)	−0.14 (0.06)	1	0.71 (0.09)
Udder2, US9	−0.04 (0.03)	0.01 (0.04)	−0.01 (0.06)	0.46 (0.02)	1

¹TS₉ = teat score on a 1 to 9 scale;²US₉ = udder score on a 1 to 9 scale.

Performance Traits

Descriptive statistics for performance traits are shown in Table 6. Posterior means of heritability for BW, WW, and YW were 0.54 ± 0.02, 0.20 ± 0.19, and 0.14 ± 0.02, respectively (as shown in Table 3). These values were consistent with estimates used by CAA and the American Angus Association (American Angus Association, 2017) as well as previously estimated for Angus populations (Bennett and Gregory, 1996; Espasandin et al., 2013). Linear models were used for bivariate analysis of teat and udder scores (TS₉, US₉) with BW, WW, and YW. Genetic and phenotypic correlations of teat and udder score with performance traits (BW, WW, and YW) were of low magnitude, and not different from zero, ranging from −0.04 (0.01) to −0.20 (0.12). Had genetic and phenotypic correlations of teat and udder score with performance traits (BW, WW, and YW) been of larger magnitude and consistent with previously reported negative correlations (Sapp et al., 2004; Smith et al., 2017) then selection to improve calf performance from birth to yearling could, in long term, impact teat and udder structure in the Angus cow herd negatively. No significant genetic correlations with production traits, primary selection goals within beef herds, emphasize the importance of scoring teat and udder structure aiming to promote progress for both performance and structure simultaneously.

Table 6.

Descriptive statistics for performance traits including birth weight (BW), weaning weight (WW), yearling weight (YW) on progeny of 1,735 Canadian Angus cows measured for teat and udder structure

Performance traits	N 1	CG,2N	Mean, kg	SD3	Min, kg	Max, kg
BW	9,916	275	37.82	10.01	17.24	58.06
WW	8,110	259	271.79	108.70	136.53	439.08
YW	4,828	187	431.09	212.82	210.92	635.03

¹ N = total number.

²CG = contemporary group.

³SD = standard deviation.

Inference

Bovine mammary structure is complex (Franz et al., 2009) and critical to the economic value of the cattle industry (Rowson et al., 2012). In dairy, the significance and impact of teat and udder structure on milk production is well documented (Ventorp and Michanek, 1992; Dube et al., 2009). Teat and udder structure evaluations for dairy cattle are designed for milk production and automated milking efficiencies; there are numerous relevant traits, including udder attachment, udder height, udder width, udder depth, udder balance, teat placement, teat angle, teat length, teat thickness, somatic cell count, and milking speed (Boettcher et al., 1998; Samoré et al., 2010; Carlström et al., 2016). In beef cattle, impacts of teat and udder structure are multifaceted, influencing both cow health and longevity, as well as calf performance. As cows with large, funnel-shaped teats and pendulous udders were at increased risk of mastitis (Persson Waller et al., 2014), this can directly impact cow health and increase antibiotic use. Mastitis has also been reported to impact calf performance due to mammary tenderness that causes cows to kick when a calf attempts to suckle or through reductions in milk volume and quality (Nickerson et al., 2000; Lents et al., 2002). Consequently, mastitis can result in an average 9.6 to 19 kg reduction in WW (Haggard et al., 1983; Watts et al., 1986; Newman et al., 1991). Teat and udder structure also impact calves’ ability to suckle, as pendulous udders and large bottle-shaped teats are more difficult to find and suckle (Bunter and Johnston, 2014), whereas well-attached udders and moderate teats were associated with better calf performance (Paputungan and Makarechian, 2000; Goonewardene et al., 2003). In another study (Smith et al., 2017), calf performance was greatest from dams with moderate teat and udder scores. In the present study, the youngest cows generally had the smallest teats and udders, consistent with numerically lower teat and udder scores associated with older cows observed by Smith et al. (2017). It is likely that cows that maintain moderate teat and udder scores throughout their productive life are optimal. Thus, BIF identified 2 traits, udder suspension and teat size, as priorities for the beef industry.

Bradford et al. (2015) reported that teat and udder are only moderately repeatable with values (SE) ranging from 0.44 (0.01) to 0.47 (0.01), suggesting that producers may not be able to accurately identify, early in life, heifers that are likely to maintain efficient teat and udder structures. Early identification of optimal genetics can impact profitability of beef production and significantly increase health and welfare of the cow herd (Van Eenennaam et al., 2011; Samarajeewa et al., 2012; Ramsey et al., 2015; White et al., 2015). Estimates of heritability (SD) for teat and udder scores [0.32 (0.06) and 0.15 (0.04), respectively] for this population indicated that genetic selection can be successful. Optimal genetic improvement for teat and udder structure within Canadian Angus cattle depends on the development of optimal genetic evaluations for the traits. Investigation of possible data treatment and model selection toward an optimal genetic evaluation for teat and udder structure indicated that, for this population, teat and udder traits using TS₉, US₉ and linear models were most appropriate, and that there was no advantage to collapsing score categories or applying threshold models.