Bayesian vector autoregressive model for multi‐subject effective connectivity inference using multi‐modal neuroimaging data

Abstract

In this article a multi‐subject vector autoregressive (VAR) modeling approach was proposed for inference on effective connectivity based on resting‐state functional MRI data. Their framework uses a Bayesian variable selection approach to allow for simultaneous inference on effective connectivity at both the subject‐ and group‐level. Furthermore, it accounts for multi‐modal data by integrating structural imaging information into the prior model, encouraging effective connectivity between structurally connected regions. They demonstrated through simulation studies that their approach resulted in improved inference on effective connectivity at both the subject‐ and group‐level, compared with currently used methods. It was concluded by illustrating the method on temporal lobe epilepsy data, where resting‐state functional MRI and structural MRI were used. Hum Brain Mapp 38:1311–1332, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Within the past few decades, advances in imaging acquisition have given rise to a large number of in vivo techniques for brain mapping. Such imaging techniques include both functional imaging modalities, such as functional MRI, electroencephalography, magnetoencephalography and positron emission tomography, as well as structural imaging modalities, such as structural MRI and diffusion tensor imaging. These techniques are often employed to study connectivity, that is, how brain regions interact with each other within networks in order to handle cognitive processes [Friston, 2011]. Here, we are concerned in particular with the estimation of effective connectivity based on resting‐state functional MRI (fMRI) data. The fMRI measures hemodynamic flow due to spontaneous neural activity. Effective connectivity refers to the directed influence of one neural system over another and often employs biologically plausible generative models of a typically small network of connected brain regions. Connectivity studies, in particular, can elucidate pathophysiology by helping the understanding of the role that connectivity patterns, and their disruption, play in mental health disorders and brain diseases [Belmonte et al., 2004; Garrity et al., 2007; Chiang and Haneef, 2014; Waites et al., 2006]. For example, epilepsy is a prototypical disease characterized by abnormal connectivity, whose study may benefit from statistical advances in methods for estimating connectivity [Engel et al., 2013].

Statistical approaches for inferring effective connectivity include directed causal modeling (DCM) [Friston et al., 1993], structural equation modeling (SEM) [Mclntosh and Gonzalez‐Lima, 1994], Bayesian networks (BNs), and Granger causal modeling (GC) [Goebel et al., 2003; Granger, 1969]. DCM approaches model interactions among brain regions directly at the unobserved neuronal level using fMRI time series, through the coupling of a dynamic bilinear model with an underlying model of how the observed BOLD signal is generated from the unobserved neuronal activity. SEM approaches infer causality by comparing the predicted variance–covariance matrix between regional responses based on a pre‐specified model to the variance–covariance matrix observed from the data. DCM and SEM are both useful confirmatory techniques for testing pre‐formulated hypotheses about the underlying brain architecture [Friston, 2011]. However, these models require prespecification of the existence and direction of influence between regions and, in the case of DCM models, rely on complex biological assumptions, such as how the neuronal states enter a region‐specific hemodynamic model to produce the BOLD responses [Valdes‐Sosa et al., 2011]. Bayesian networks, on the other hand, estimate effective connectivity by modeling brain networks as directed acyclic graphs, in which brain regions are depicted as nodes and where edges represent direct causal dependencies between the regions. Dynamic Bayesian networks (DBNs), a subset of BNs that model temporal processes, have been applied to infer effective connectivity from fMRI data in both single‐subject and multi‐subject approaches [Kim et al., 2008; Li et al., 2008, 2011; Rajapakse and Zhou, 2007]. One disadvantage of Bayesian networks, however, is the assumption of acyclic graphical structure, as the high prevalence of reciprocal connections commonly renders brain connectivity cyclic [Friston, 2011].

Granger causal identification using vector autoregressive (VAR) modeling provides an approach to effective connectivity inference which is based on the central notion that causes both precede and help predict effects [Goebel et al., 2003; Granger, 1969]. In GC analysis, effective connectivity inference is performed via the VAR coefficients of the fitted model. In contrast to DCM and SEM, GC infers effective connectivity without relying on prior specification of connectivity linkages in the brain network. Furthermore, unlike Bayesian networks, VAR modeling does not require an assumption of acylicity. It should be pointed out that, when applied to fMRI signals, GC inference via VAR models can only estimate interactions at the hemodynamic level and not at the underlying neural response level, which occurs at a much higher temporal resolution than the fMRI sampling [Goebel et al., 2003; Gorrostieta et al., 2013; Roebroeck et al., 2005]. Nevertheless, GC modeling has been very useful in a large number of neurological diseases, including epilepsy [Ji et al., 2013; Morgan et al., 2011], Alzheimer's disease [Miao et al., 2011], schizophrenia [Demirci et al., 2009], and autism [Pollonini et al., 2010].

In multi‐subject studies, methods for group‐level inference in GC via VAR models are not yet established. In particular, two‐stage approaches have generally been adopted, in which a VAR model is fit on each subject in the first stage, and between‐subject variations in the VAR coefficient estimates are obtained in the second stage [Deshpande et al., 2009; Morgan et al., 2011]. Despite their common usage, there are several known shortcomings of two‐stage estimation approaches. Firstly, two‐step approaches are suboptimal for group inference due to the loss of information which results from summarizing the time‐series data from each subject into a summary statistic (the VAR coefficient) on which group inference is subsequently performed. Secondly, random variability is introduced but not accounted for in the second stage, through replacement of the unobserved subject‐level VAR coefficients with point estimates derived in the first stage [Verbeke and Molenberghs, 2009]. To overcome these issues, Gorrostieta et al. [2012] proposed a mixed‐effects generalization of the usual VAR model which decomposes connectivity into group‐specific and subject‐specific components. In a Bayesian extension, sparsity was additionally induced at the group level through a Bayesian elastic net prior on the group‐specific components [Gorrostieta et al., 2013]. However, those methods maintain the common assumption of independence between the elements of the connectivity matrices.

Another shortcoming of current VAR approaches for effective connectivity inference is that such methods do not easily allow for the integration of multi‐modal imaging data, a feature which is especially desirable in models for multi‐subject inference. For example, it is generally accepted that structural connectivity constrains effective connectivity, as structural connectivity provides estimates of axonal connections between neurons or neuronal populations, while effective connectivity provides estimates of the causal influences mediated by these axonal connections [Aertsen and Preissl, 1991; Friston et al., 1994]. In particular, evidence from multiple studies has shown that the strength of resting‐state functional connectivity is positively correlated with structural connectivity strength; however, functional connectivity may also be present between regions for which little or no structural connectivity is present [Andrews‐Hanna et al., 2007; Greicius et al., 2009; Hagmann et al., 2008; Honey et al., 2009; Koch et al., 2002; Lowe et al., 2008; Skudlarski et al., 2010]. Furthermore, although increased structural connectivity predicts increased functional connectivity, increased functional connectivity does not predict increased structural connectivity [Honey et al., 2009; Koch et al., 2002]. Objective inclusion of structural information may therefore be incorporated into modeling of functional and effective connectivity, by allowing stronger structural connectivity to lead to a greater probability of non‐zero functional or effective connectivity. The use of structural imaging data to constrain connectivity estimation has demonstrated improvements in DCM [Stephan et al., 2009] and may confer benefits to inference in VAR models as well.

In this work, we develop a multi‐subject vector autoregressive (VAR) modeling approach that allows for simultaneous inference on effective connectivity at both the subject‐ and group‐level. With respect to previous approaches, our framework allows for the presence of highly connected and persistent hubs in the brain networks [Van den Heuvel and Sporns, 2011] by relaxing the assumption of independence between connectivities through an intrinsic conditional autoregressive prior. Furthermore, we achieve multi‐modal imaging data integration by incorporating structural information into our prior construction, effectively encouraging connectivity between structurally connected regions. We demonstrate through simulation studies that the approach results in improved inference on effective connectivity at both the subject‐ and group‐level, compared with currently used methods. We also illustrate the method on data from a temporal lobe epilepsy study, where we use resting‐state functional MRI and structural MRI data. The group‐level effective connectivities we infer include both known relationships between resting‐state networks, as well as relationships of potential interest for future investigation.

The rest of the article is organized as follows. In section “Materials and Methods,” we describe the proposed model, the prior construction and our strategy for posterior inference. We assess the performance of our methodology on simulated data and perform comparisons with existing multi‐step methods as well as single‐step generalizations of vector autoregressive models for effective connectivity inference. We then apply our proposed methodology to data on a case study of effective connectivity in temporal lobe epilepsy. Section “Results” presents the performance of our methodology as well as the experimental results. Section “Discussion and Conclusions” discusses limitations and possible future directions, and concludes the article.

MATERIALS AND METHODS

Bayesian Vector Autoregressive Model

Let $x_{t,j}^{(s)}$ be the fMRI BOLD response of subject s at time t in region j, for $t=1,\dots ,T,\hspace{0.17em}j=1,\dots ,R,\hspace{0.17em}s=1,\dots ,n$. Here, we view regions as micro‐areas of the brain that comprise several voxels. For example, in the application we discuss in section “Resting State Experiment: Data Description and Preprocessing” we use Independent Component Analysis (ICA) components as groups of voxels that covary in time. ICA is an increasingly utilized approach in fMRI data analyses which allows to identify components that are maximally independent in space and has been found to effectively identify functional networks in both task‐based and resting‐state data [Calhoun et al., 2001; Garrity et al., 2007; Sorg et al., 2007; Van Den Heuvel and Pol, 2010; Yu et al., 2013]. It is important to note, however, that our modeling approach does not depend on how the regions were derived (e.g., ICA‐based, anatomical) and how the time series within each ROI was computed. It is generally applicable to any choice of regions for which effective connectivity is of interest.

We envision that the n subjects belong to G separate groups (e.g., epilepsy and healthy controls, or different subtypes of epilepsy). Let η_s be the observed group label for subject s, with ${\eta }_s=g$ if the sth subject belongs to group g. We deal with the supervised setting, in which the group labels η_s are known. We model temporal correlation in the time series through a multivariate linear vector autoregressive (VAR) process of order L

$$({\mathit{x}}_t^{(s)} |{\eta }_s=g,{\varphi }_{l,g}^{(s)},\Xi )={\displaystyle \sum _{l=1}^L{\varphi }_{l,g}^{(s)}}{\mathit{x}}_{t-l}^{(s)}+e_t^{(s)},\hspace{1em}{e}_t^{(s)}={\mathit{e}}_t\sim \mathrm{N}(0,\Xi ), s=1,\dots ,n,$$ (1)

where $\Xi =\text{diag}({\zeta }_1,\dots ,{\zeta }_R)$, is the VAR covariance matrix; ${\mathit{x}}_t^{(s)}=[x_{t,1}^{(s)},\dots ,x_{t,R}^{(s)}]\prime$, the $R\times 1$ vector of fMRI BOLD responses at time t for subject s; and ${\varphi }_{l,g}^{(s)}$ the R × R lag‐specific effective connectivities between the R regions for subject s. We assume that the data have been centered after the pre‐processing steps. We also place hyperpriors on the ζ_j's as ${\zeta }_j\sim \text{IG}(h_1,h_2), j=1,\dots ,R$.

Model (1) can be written in the standard multivariate linear regression form as

$$\underset{1-by-R}{\underbrace{{\mathit{x}}_t^{\prime (s)}}}=\underset{1-by-RL}{\underbrace{{\mathit{u}}_t^{\prime (s)}}}\underset{RL-by-R}{\underbrace{B_g^{(s)}}}+\underset{1-by-R}{\underbrace{{\mathit{e}}_t^{\prime (s)}}},$$

for $t=1,\dots ,T$, where ${\mathit{u}}_t^{\prime (s)}=[{\mathit{x}}_{t-1}^{\prime (s)},{\mathit{x}}_{t-2}^{\prime (s)},\dots ,{\mathit{x}}_{t-L}^{\prime (s)}]$, is the $1\times RL$ vector of concatenated lagged BOLD data; and $B_g^{(s)}=[{\varphi }_{1,g}^{(s)},{\varphi }_{2,g}^{(s)},\dots ,{\varphi }_{L,g}^{(s)}]\prime$, the RL × R matrix of concatenated subject‐specific effective connectivities. For T time points, this is

$$\underset{(T-L)-by-R}{\underbrace{X^{(s)}}}=\underset{(T-L)-by-(RL)}{\underbrace{U^{(s)}}}\underset{(RL)-by-R}{\underbrace{B_g^{(s)}}}+\underset{(T-L)-by-R}{\underbrace{E^{(s)}}}.$$

As typical with VAR models we use the vec notation

$$\begin{array}{c}{\underset{¯}{x}}^{(s)}=vec(X^{(s)})\\ {\underset{¯}{\beta }}_g^{(s)}=vec(B_g^{(s)})\\ {\underset{¯}{e}}^{(s)}=vec(E^{(s)})\end{array}$$

where $vec(X^{(s)})$ denotes the columns of $X^{(s)}$ stacked on top of each other. Thus, we write

$$\underset{(T-L)R-by-1}{\underbrace{{\underset{¯}{x}}^{(s)}}}=\underset{(T-L)R-by-(RL)R}{\underbrace{(\underset{R-by-R}{\underbrace{I}}\otimes \underset{(T-L)-by-(RL)}{\underbrace{U^{(s)}}})}}\underset{(RL)R-by-1}{\underbrace{{\underset{¯}{\beta }}_g^{(s)}}}+\underset{(T-L)R-by-1}{\underbrace{{\underset{¯}{e}}^{(s)}}},$$

where ${\underset{¯}{e}}^{(s)}\sim \mathrm{N}(0,\underset{R-by-R}{\underbrace{\Xi }}\otimes \underset{(T-L)-by-(T-L)}{\underbrace{I}})$.

Following the finite mixture model formulation, we can then write model (1) for subject s in group g as

$$({\underset{¯}{x}}^{(s)}|{\eta }_s=g,{\underset{¯}{\beta }}_g^{(s)},\Xi )\sim \mathrm{N}\left((I\otimes U^{(s)}){\underset{¯}{\beta }}_g^{(s)},\Xi \otimes I\right),$$ (2)

with parameters ${\underset{¯}{\beta }}_g^{(s)}$ that capture subject‐level effective connectivities. Figure 1 provides a graphical representation of the model, the components of which are described in sections “Prior on Lag‐Specific Subject‐Level Effective Connectivity” and “Prior on Lag‐Specific Group‐Level Effective Connectivity” below.

Figure 1.

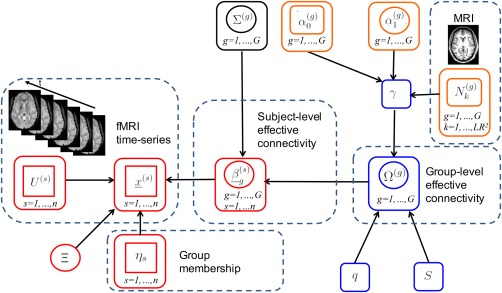
Graphical formulation of the proposed probabilistic model. Nodes in circles denote parameters, nodes in squares denote observables. A link between two nodes denotes direct probabilistic dependence between the nodes. The vector autoregressive (VAR) model is depicted in red; the intrinsic conditional autoregressive (ICAR) prior in blue; the probit prior in orange. For visual clarity, not all hyperparameters are shown. [Color figure can be viewed at http://wileyonlinelibrary.com]

Prior on Lag‐Specific Subject‐Level Effective Connectivity

We model the subject‐level parameters in Eq. (2) as random deviations from a baseline process, which represents the vectorized group‐specific effective connectivity for group g. Specifically, we put

$$p({\underset{¯}{\beta }}_g^{(s)}|{\Omega }^{(g)},{\Sigma }^{(g)})=\mathrm{N}\left({\Omega }^{(g)},{\Sigma }^{(g)}\right),$$ (3)

for all s such that ${\eta }_s=g$, with $g=1,\dots ,G$. Here, ${\Omega }^{(g)}$ is a baseline process for the vectorized VAR coefficients, or effective connectivities, for group g, and ${\Sigma }^{(g)}$ is the $L{R}^2-by-L{R}^2$ variance‐covariance matrix for group g. We assume diagonal variance‐covariance matrices ${\Sigma }^{(g)}=\text{diag}({\sigma }_1^{(g)},\dots ,{\sigma }_{L{R}^2}^{(g)})$. Our proposed model is still able to capture dependencies at the group level both across lags, and between effective connectivities within a given lag, via the specification of the prior model for group effective connectivity that we describe below.

Prior on Lag‐Specific Group‐Level Effective Connectivity

We identify group‐level effective connectivities by imposing spike‐and‐slab priors on the corresponding parameters, also capturing smoothness at the group level, either temporally across lags or spatially between effective connectivities within a given lag, through an intrinsic conditional autoregressive slab prior. Additionally, we integrate structural imaging information into the prior model, allowing connections with stronger structural connectivity to increase the prior probability that the effective connectivity is non‐zero.

Let ${\Omega }^{(g)}$ be the $L{R}^2-by-1$ vector with elements ${\omega }_k^{(g)},k=1,\dots ,L{R}^2$. In order to infer effective connectivities, we introduce binary indicators ${\gamma }_k^{(g)}$ such that ${\gamma }_k^{(g)}=1$ indicates that effective connectivity ${\omega }_k^{(g)}$ is non‐zero, and 0 otherwise. Next, we enforce sparsity of effective connectivities at the group level by imposing “spike‐and‐slab” mixture priors [George and McCulloch, 1993, 1997] on the elements of ${\Omega }^{(g)}$. Furthermore, to take into account spatial smoothness from the presence of highly connected hubs in brain networks, as well as the smoothness across time from the hemodynamic response function, we specify the slab portion of the mixture prior as an intrinsic conditional autoregressive (ICAR) distribution [Banerjee et al., 2014],

$${\omega }_k^{(g)}\sim {\gamma }_k^{(g)}\mathrm{N}\left(\frac{{\displaystyle {\sum }_{k\prime =1}^{L{R}^2}{S}_{kk\prime }}{\omega }_{k\prime }^{(g)}}{{\displaystyle {\sum }_{k\prime =1}^{L{R}^2}{S}_{kk\prime }}},\frac{q}{{\displaystyle {\sum }_{k\prime =1}^{R^2}{S}_{kk\prime }}}\right)+(1-{\gamma }_k^{(g)}){\delta }_0({\omega }_k^{(g)}),$$ (4)

where ${\delta }_0({\omega }_k^{(g)})$ is a spike at zero, and S is a $L{R}^2\times L{R}^2$ symmetric matrix of binary elements. The ICAR prior allows for smoothness by encouraging effective connectivities to vary smoothly across temporal lags or groupings of VAR coefficients (see the case study application in section “Resting State Experiment: Data Description and Preprocessing” for more details). The specification S = I corresponds to the case of no prior knowledge about spatial and temporal smoothness. We also impose priors on the diagonal elements of ${\Sigma }^{(g)}$ in Eq. (3) and allow separate variances for zero and non‐zero group‐level connectivities. In particular, for all effective connectivities k such that ${\gamma }_k^{(g)}=1$, we put ${\sigma }_k^{(g)}=c_1^{(g)}\sim \text{IG}(a_1^{(g)},b_1^{(g)})$, while for all k such that ${\gamma }_k^{(g)}=0$ we put ${\sigma }_k^{(g)}=c_0^{(g)}\sim \text{IG}(a_0^{(g)},b_0^{(g)})$ for all groups $g=1,\dots ,G$ and connectivities $k=1,\dots ,L{R}^2$.

Structural connectivity is generally considered the substrate of effective connectivity [Greicius et al., 2009]. In particular, presence of a direct structural connection entails connectivity, although connectivity may also exist in the absence of direct structural connections [Deco et al., 2011]. Accordingly, we inform the prior probability of the selection indicator via prior information on the strength of the corresponding structural connection. We achieve this by imposing a probit regression prior on the variable selection indicator ${\gamma }_k^{(g)}$ as

$$p({\gamma }_k^{(g)}=1)=F\left({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)}\right), k=1,\dots ,L{R}^2,$$ (5)

where $N_k^{(g)}$ is a measure of structural connectivity between the two regions corresponding to the kth element of ${\Omega }^{(g)}$ and F is the CDF of a standard normal distribution. In the application of section “Resting State Experiment: Data Description and Preprocessing” we obtain the $N_k^{(g)}$'s from structural MRI data. Probit regression priors of type Eq. (5) have been proposed in the variable selection literature as a convenient way of incorporating prior information [Cassese et al., 2015; Quintana and Conti, 2013]. The parameter ${\alpha }_0^{(g)}$ regulates the prior probability of non‐zero effective connectivity in group g, either in the absence of structural connectivity or if there is no relationship between structural and effective connectivity. In particular, if ${\alpha }_1^{(g)}$ or $N_k^{(g)}$ are zero, then the prior probability that ${\gamma }_k^{(g)}$ is non‐zero reduces to $p({\gamma }_k^{(g)}=1)=F({\alpha }_0^{(g)})$. The parameter ${\alpha }_1^{(g)}$ captures the effect of an increase in the strength of structural connectivity on the probability that the corresponding effective connectivity is non‐zero. To complete the model, we impose a Normal prior ${\alpha }_1^{(g)}\sim \mathrm{N}(w^{(g)},{\tau }^{2^{(g)}})$, for $g=1,\dots ,G$.

Posterior Inference

We used Metropolis‐within‐Gibbs MCMC sampling methods in order to sample from the joint posterior of the parameter vector $\{{\underset{¯}{\beta }}_g^{(s)},{\gamma }^{(g)},{\Omega }^{(g)},{\xi }_1^{(g)},{\xi }_0^{(g)},z_k^{(g)},{\alpha }_1^{(g)},{\zeta }_j\}$, with $g=1,\dots ,G$; $s=1,\dots ,n$ and $j=1,\dots ,R$. We give details of the full conditional distributions in Appendix A at the end of the article. In brief, a generic iteration of the MCMC algorithm comprises the following steps:

1. Update ${\underset{¯}{\beta }}_g^{(s)}$: This is a Gibbs step from a normal distribution, ${\underset{¯}{\beta }}_g^{(s)}\sim \mathrm{N}({\mu }_{\beta }^{(s)},{\nu }_{\beta }^{(s)})$ for all s such that ${\eta }_s=g$ and $g=1,\dots ,G$, with ${\mu }_{\beta }^{(s)}$ and ${\nu }_{\beta }^{(s)}$ as defined in Appendix A.

2. Joint update for $({\mathit{\gamma }}^{(g)},{\Omega }^{(g)})$: We perform a between‐model step by updating these two parameters jointly, using a Metropolis‐Hastings step. For each $g=1,\dots ,G$, in order to propose a new candidate ${\mathit{\gamma }}^{{(g)}^{\star }}$, we randomly choose between two transition moves:

   1. Add/delete: Randomly choose one of the LR ² indices in ${\mathit{\gamma }}^{(g)}$, and change its value.

   2. Swap: Choose independently and at random a 0 and 1 in ${\mathit{\gamma }}^{(g)}$, and switch their values.

      If ${\gamma }_k^{(g)\star }=0$, set ${\omega }_k^{(g)\star }=0$. Else, if ${\gamma }_k^{(g)\star }=1$, sample ${\omega }_k^{(g)\star }\sim \mathrm{N}({\rho }_k^{(g)},{\kappa }_k^{(g)}),\hspace{0.17em}k=1,\dots ,L{R}^2,\hspace{0.17em}g=1,\dots ,G$, with ${\rho }_k^{(g)}$ and ${\kappa }_k^{(g)}$ as defined in Appendix A.

3. Update ${\Omega }^{(g)},\hspace{0.17em}g=1,\dots ,G$: We perform a within‐model step using a Gibbs step to improve mixing. For all ${\omega }_k^{(g)}$ such that ${\gamma }_k^{(g)}=1$, sample ${\omega }_k^{(g)}\sim \mathrm{N}({\rho }_k^{(g)},{\kappa }_k^{(g)}),\hspace{0.17em}k=1,\dots ,L{R}^2,\hspace{0.17em}g=1,\dots ,G$. This step is performed to improve the mixing of the chain.

4. Update ${\xi }_1^{(g)},\hspace{0.17em}g=1,\dots ,G$: This is a Gibbs step, draw ${\xi }_1^{(g)}\sim \text{IG}({\chi }_1^{(g)},{\psi }_1^{(g)})$ for $g=1,\dots ,G$, with ${\chi }_1^{(g)}$ and ${\psi }_1^{(g)}$ as given in Appendix A.

5. Update ${\xi }_0^{(g)},\hspace{0.17em}g=1,\dots ,G$: This is a Gibbs step, draw ${\xi }_0^{(g)}\sim \text{IG}({\chi }_0^{(g)},{\psi }_0^{(g)})$ for $g=1,\dots ,G$, with ${\chi }_0^{(g)}$ and ${\psi }_0^{(g)}$ given in Appendix A.

6. Update latent variable $z_k^{(g)},\hspace{0.17em}k=1,\dots ,L{R}^2,g=1,\dots ,G$: This is a Gibbs step from a truncated normal.

7. Update ${\alpha }_1^{(g)}$: This is a Gibbs step, draw ${\alpha }_1^{(g)}\sim \mathrm{N}({\mu }_{\alpha }^{(g)},{\nu }_{\alpha }^{(g)})$ for $g=1,\dots ,G$, with ${\mu }_{\alpha }^{(g)}$ and ${\nu }_{\alpha }^{(g)}$ as given in Appendix A.

8. Update ζ_j, $j=1,\dots ,R$: This is a Gibbs step, draw ${\zeta }_j\sim \text{IG}(d_1,d_2)$ for $j=1,\dots ,R$, with d ₁ and d ₂ as given in Appendix A.

For posterior inference, our primary interest is in the selection of the non‐zero effective connectivities at the group level, via the estimation of the marginal posterior probabilities (MPPs) of the ${\gamma }_j^{(g)}$'s, and in the estimation of the magnitude and directionality of the non‐zero group‐level and subject‐level effective connectivities, via inference on the parameters ${\Omega }^{(g)}$ and ${\beta }_g^{(s)}$, respectively, for $g=1,\dots ,G$ and $s=1,\dots ,n$. Marginal posterior probabilities $p({\gamma }_j^{(g)}=1\backslash \text{left}|\text{data})$ can be estimated as the proportions of MCMC samples for which ${\gamma }_j^{(g)}=1$, across all iterations and after burn‐in. Non‐zero effective connectivities at the group level can then be selected as those with MPP exceeding a threshold value ${\kappa }^{(g)}$, with the threshold chosen to ensure a pre‐specified Bayesian false discovery rate FDR; Newton et al. [2004],

$$\text{FDR}({\kappa }^{(g)})=\frac{{\displaystyle {\sum }_{j=1}^R(1-MP{P}_j^{(g)})}{I}_{(MP{P}_j^{(g)}>{\kappa }^{(g)})}}{{\displaystyle {\sum }_{j=1}^R{I}_{(MP{P}_j^{(g)}>{\kappa }^{(g)})}}},$$

with $MP{P}_j^{(g)}$ the MPP for region j in group g, and $I_{(MP{P}_j^{(g)}>{\kappa }^{(g)})}$ the indicator function such that $I_{(MP{P}_j^{(g)}>{\kappa }^{(g)})}=1$ if ${\text{MPP}}_j^{(g)}>{\kappa }^{(g)}$, and 0 otherwise. In all analyses of this article, we set the FDR to 0.05 and choose ${\kappa }^{(g)}$ accordingly. Furthermore, we obtain estimates of the non‐zero VAR coefficients ${\Omega }^{(g)}$ and the subject‐level effective connectivities ${\beta }_g^{(s)}$ by averaging over the corresponding MCMC sampled values.

Simulation Experiment: Data Generation

We considered a set of simulated data to illustrate our model's ability to accurately infer effective connectivity at the group‐ and subject‐level. We generated synthetic time‐series data for a network of R = 5 regions, with n = 20 subjects belonging to G = 2 groups. The first 10 subjects belonged to group 1 and the second 10 to group 2. The simulated time‐series for each subject were generated from model (2) using a VAR process of order L = 1 and T = 300 time points, with a starting value of ${\mathit{x}}_0^{(s)}=\mathit{0}$, and an error covariance matrix $\Xi ={\mathbb{I}}_R$. Group‐specific effective connectivities were generated as

$${\omega }_k^{(g)}\sim {\gamma }_k^{(g)}\text{Unif}(0,0.5)+(1-{\gamma }_k^{(g)}){\delta }_0({\omega }_k^{(g)}),$$

for g = 1, 2 and $k=1,\dots ,L{R}^2$. Notice that the generating mechanism uses a distribution which is different from the assumed prior model (4). We generated ${\mathit{\gamma }}^{(g)},\hspace{0.17em}g=1,2,$ according to Eq. (5), with ${\alpha }_0=[{\alpha }_0^{(1)},{\alpha }_0^{(2)}]=[-1.5,-1.5]$ and ${\alpha }_1=[{\alpha }_1^{(1)},{\alpha }_1^{(2)}]=[5,5]$, corresponding to a prior probability of non‐zero effective connectivity, in the absence of structural connectivity, of $[F({\alpha }_0^{(1)}),F({\alpha }_0^{(2)})]=[0.07,0.07]$, respectively, for group 1 and 2. Structural connectivity matrices were set to

$${\mathit{N}}^{(1)}=vec\left(\left[\begin{array}{ccccc}0.6& 0.9& 0.1& 0.1& 0.1\\ 0.9& 0.95& 0.1& 0.7& 0.6\\ 0.1& 0.1& 0.8& 0.1& 0.1\\ 0.1& 0.7& 0.1& 0.1& 0.1\\ 0.1& 0.6& 0.1& 0.1& 0.1\end{array}\right]\right)$$

for group 1 and to

$${\mathit{N}}^{(2)}=vec\left(\left[\begin{array}{ccccc}0.1& 0.9& 0.8& 0.1& 0.5\\ 0.9& 0.1& 0.1& 0.1& 0.1\\ 0.8& 0.1& 0.1& 0.1& 0.9\\ 0.1& 0.1& 0.1& 0.1& 0.1\\ 0.5& 0.1& 0.9& 0.1& 0.1\end{array}\right]\right),$$

for group 2. This allowed us to simulate a scenario in which higher structural connectivity generally leads to increased probability of the presence of an effective connectivity, but effective connectivity may also exist in the absence of high structural connectivity. The resulting ${\mathit{\gamma }}^{(1)}$ and ${\mathit{\gamma }}^{(2)}$ were

$${\mathit{\gamma }}^{(1)}=vec\left(\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 1& 1& 0& 1& 1\\ 0& 1& 1& 0& 1\\ 0& 1& 0& 0& 0\\ 0& 1& 1& 0& 0\end{array}\right]\right)$$

and

$${\mathit{\gamma }}^{(2)}=vec\left(\left[\begin{array}{ccccc}0& 1& 1& 0& 1\\ 1& 1& 0& 0& 1\\ 1& 0& 0& 0& 1\\ 0& 0& 1& 0& 0\\ 1& 0& 1& 0& 0\end{array}\right]\right).$$

To generate subject‐specific effective connectivities, first we generated random matrices $A^{(s)}=Q{\prime }^{(s)}\Lambda Q^{(s)}$, with $\Lambda =Diag(-0.4,-0.25,-0.1,0.05,0.2)$ and $Q^{(s)}$ a randomly generated orthogonal matrix from the QR decomposition of a matrix of standard normal random deviates. We then sampled the subject‐level connectivities as

$${\beta }_g^{(s)}\sim \left({\Omega }^{(1)}+vec(A^{(s)})\right){\mathbf{1}}_{[1\le s\le 10]}+\left({\Omega }^{(2)}+vec(A^{(s)})\right){\mathbf{1}}_{[11\le s\le 20]}.$$

Again, notice that the generating mechanism of the subject‐level deviations from the group connectivity is different than the prior model. Figure 2 shows the simulated group‐level structural connectivity, the non‐zero group‐level effective connectivity and the group‐level VAR coefficients for the two groups.

Figure 2.

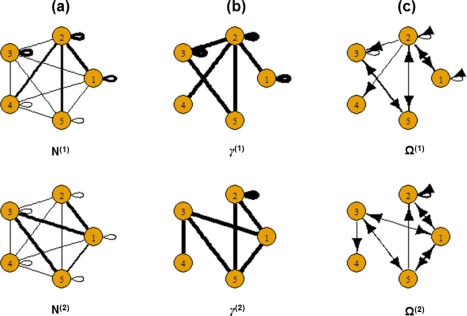
Simulated data: (a) Simulated group‐level structural connectivity, (b) Simulated non‐zero group‐level effective connectivity, (c) Simulated values of group‐level effective connectivity. The thickness of the edges is proportional to magnitude. [Color figure can be viewed at http://wileyonlinelibrary.com]

Simulation Experiment: Comparative Study

To evaluate the performance of our model, we performed a comparison study with respect to (1) detection of effective connectivity at the group‐level, and (2) VAR coefficient inference on the subject‐ and group‐level. We compared our method to two multi‐step methods for effective connectivity inference based on Granger causality (GC) and with two approaches based on VAR models, briefly described below. In order to better assess performance, we compared estimation results averaged over 30 replicated datasets.

Detection of effective connectivity at the group level was assessed with respect to the false positive rate (FPR), false negative rate (FNR), accuracy, and the F ₁‐score, all averaged over 30 replicated datasets. The FPR is defined as $FPR=\frac{FP}{FP+TN}$ where FP is the number of false positives and TN is the number of true negatives. The FNR is defined as $FNR=\frac{FN}{FN+TP}$ where FN is the number of false negatives and TP is the number of true positives. Accuracy is defined as $Accuracy=\frac{TP+TN}{TP+TN+FP+FN}.$ Lastly, the F ₁‐score is defined as $F_1=2·\frac{\left(TP/(TP+FP)\right)\left(TP/(TP+FN)\right)}{\left(TP/(TP+FP)\right)+\left(TP/(TP+FN)\right)}.$

For the first GC approach we used in our comparison study, subject‐level estimates of VAR coefficients were obtained using standard Granger causal inference through ordinary least squares. Next, group‐level inference on effective connectivity was performed through one‐sample t‐tests on the VAR coefficients. Non‐zero effective connectivities were identified by thresholding P‐values with false discovery rate control at the 0.05 level. Lastly, inference on the group‐level VAR coefficients were obtained by computing the mean of the subject‐level VAR coefficient estimates for non‐zero effective connectivities. The second approach we considered is similar to what done by Deshpande et al. [2009]. Subject‐level estimates of VAR coefficients were obtained from standard Granger causal inference through ordinary least squares. Subject‐level P‐value maps were then obtained from the empirical null distribution following the procedure proposed by Theiler et al. [1992]. In particular, the original time‐series data for each subject was transformed by fast Fourier transform to the frequency domain, and the phase randomized to be uniformly distributed over $(-\pi ,\pi )$. The randomized signal was then transformed back to the time domain to generate surrogate data. This procedure generated datasets in the same spectrum as the original data, but with no causal phase relations between the signals. The empirical null distribution of each of the LR ² connectivities was generated by repeating this procedure 1,000 times. Subject‐level P‐values were then obtained by comparing the estimated subject‐level VAR coefficient to its corresponding null distribution. Group‐level inference was then performed by combining the P‐values from individual subjects using Fisher's method to generate group‐level P‐values. Non‐zero effective connectivities were identified by thresholding group‐level P‐values with false discovery rate control at the 0.05 level. Lastly, inference on the group‐level VAR coefficient estimates was obtained by computing the mean of the subject‐level VAR coefficient estimates for non‐zero effective connectivities.

Additionally, we compared our method to two single‐step generalizations of VAR models: (a) the mixed‐effects VAR generalization (ME‐VAR), as proposed by Gorrostieta et al. [2012], which decomposes connectivity into group‐level and subject‐level components, and (b) a Bayesian extension of the same model, which imposes shrinkage on group coefficients through an elastic net prior (BME‐VAR) proposed by Gorrostieta et al. [2013]. Parameters in the ME‐VAR and BME‐VAR models were estimated using Matlab code provided by the authors. Hypothesis testing in the ME‐VAR model was carried out after correcting for multiple comparisons with a false discovery rate control at the 0.05 level. The BME‐VAR model was run for 30,000 iterations with 20,000 sweeps as burn‐in. Non‐zero group effective connectivities using the BME‐VAR model were identified based on 95% credible intervals, as suggested by Gorrostieta et al. [2013].

Resting State Experiment: Data Description and Preprocessing

We applied the proposed methodology to resting‐state fMRI and structural MRI data from a study on temporal lobe epilepsy. Temporal lobe epilepsy (TLE) is the most common focal epilepsy [Spencer and Spencer, 1985]. Although TLE is traditionally associated with mesial temporal sclerosis involving the hippocampus, evidence increasingly suggests that other resting‐state networks (RSNs), far from the hippocampus, are also affected in TLE. These networks control higher‐order brain functions, such as attention, executive control, and language [McIntosh, 2000]. For example, connectivity between the default mode network (DMN), a set of brain regions involved in spontaneous thought, and “task‐positive networks,” such as the executive function, language, or attention networks, is thought to represent competitive relationships which allow the brain to toggle between introspection and extrospectively oriented attentional networks [Heine et al., 2012]. Evidence of alterations between RSNs in TLE has implications for understanding psychiatric and cognitive complications, including the impairment of higher‐order brain functions often observed in TLE patients [Cataldi et al., 2013]. A better understanding of how connectivity between RSNs is affected in TLE may additionally facilitate the development of clinical markers of disease severity and cognitive progression.

We have available data from a resting‐state fMRI study conducted at the University of California, Los Angeles Seizure Disorder Center, to investigate effective connectivity between RSNs in temporal lobe epilepsy patients and healthy controls. The study group consisted of 48 adult subjects, including 23 healthy controls and 25 patients with temporal lobe epilepsy. Healthy control subjects had normal structural MRIs, no history of neurologic illness, and were not taking neurologic medications. TLE patients were recruited from the University of California, Los Angeles (UCLA) Seizure Disorder Center. Diagnostic evaluation for all patients included video‐EEG monitoring, high‐resolution MRI, FDG‐PET scanning, and neuropsychological testing. A two‐sample t‐test with unequal variances and Fisher exact test showed no significant difference in age, gender, or handedness, respectively, at the α = 0.05 level of significance. Baseline characteristics of subject groups are shown in Table 1. The study was in compliance with the Code of Ethics of the World Medical Association (Declaration of Helsinki). Written informed consent was obtained prior to scanning for all subjects in accordance with guidelines from the UCLA Institutional Review Board.

Table 1.

Temporal lobe epilepsy dataset: Baseline characteristics of subject groups

	Healthy controls	TLE patients
	(n = 23)	(n = 25)	P‐value
Age, mean (SD)	31.1 (6.5)	33.6 (7.8)	0.24a
Female	8	12	0.39b
Right‐handed	23	21	0.11b

^aTwo‐sided t‐test with unequal variances.

^bFisher exact test.

Imaging was performed with a 3T MRI system (Siemens Trio, Erlangen, Germany). Functional imaging was performed with the following parameters: TR = 2,000 ms, TE = 30 ms, FOV = 210 mm, matrix = 64 × 64, slice thickness 4 mm, 34 slices. Subjects were instructed to relax with eyes closed during imaging. No auditory stimulus was present except for the acoustic noise from imaging. High‐resolution structural images were obtained during the same imaging study with the parameters: TR = 20 ms, TE = 3 ms, FOV = 256 mm, matrix = 256 × 256, slice thickness 1 mm, 160 slices. The images were acquired in the axial plane using a spoiled gradient recalled (SPGR) sequence for the anatomical images and an echo planar imaging (EPI) sequence for the functional images. To limit the influences of motion, images were checked to ensure that no subjects had a maximum translation of greater than 1.5 mm. Resting‐state fMRI was performed for TLE patients after the comprehensive epilepsy surgery evaluation and prior to epilepsy surgery. Patients remained on their regular medications during the fMRI. None of the patients had a seizure in the 24 hours preceding the imaging. None of the patients had seizures during the study as confirmed by the simultaneous EEG obtained during fMRI.

Preprocessing of fMRI data was performed using FSL (fMRIB Software Library) version 5.0.7 (Oxford, United Kingdom, http://www.fmrib.ox.ac.uk/fsl) and included slice‐timing correction, motion correction, spatial smoothing, and intensity normalization. Group ICA was used to decompose images into independent components using the fMRI Toolbox (GIFT) of Calhoun et al. [2001], producing a single set of group components that is interpretable across subjects. Components corresponding to resting‐state networks, as described in Allen et al. [2011], were extracted and ICA maps from individual subjects were then back‐reconstructed from the aggregated mixing matrix. Of the extracted independent components, six components of interest were identified as corresponding to the (1) anterior DMN (ADMN), (2) posterior DMN (PDMN), (3) alerting network (ALT), (4) salience network (SAL), (5) premotor cortex (MOT), and (6) primary somatosensory cortex (SEN). Figure 3 shows the six components of interest, overlaid in standard Montreal Neurological Institute (MNI) space. Mean time‐series for each component were computed for each subject. The stacked time‐series formed our data ${\underset{¯}{x}}^{(s)}$, as described in Eq. (2).

Figure 3.

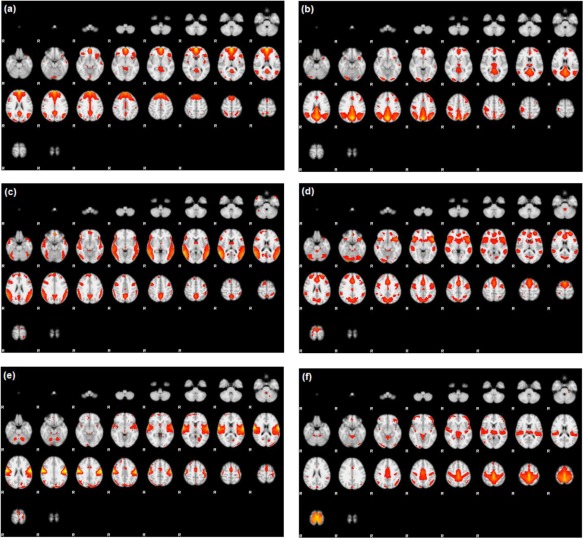
Temporal lobe epilepsy dataset: Z‐score maps of components of interest, overlaid in Montreal Neurological Institute (MNI) space: (a) Anterior DMN, (b) Posterior DMN, (c) Alerting network, (d) Salience network, (e) Premotor cortex, and (f) Primary somatosensory cortex. Orientation is radiological. [Color figure can be viewed at http://wileyonlinelibrary.com]

Resting State Experiment: Incorporating Structural Information

In our analyses we also made use of the subjects' structural MRI data. As structural connectivity is generally considered the substrate for effective connectivity, integrating structural MRI and fMRI data is expected to allow for improved inference on connectivity [Bowman et al., 2012; Damoiseaux and Greicius, 2009; Greicius et al., 2009; Iyer et al., 2013]. Preprocessing of the structural MRI data was performed using FSL version 5.0.7 and included inhomogeneity correction, skull stripping, probabilistic tissue classification of grey matter, white matter and cerebrospinal fluid, and nonlinear registration to a standard image in T₁ space. The grey matter volume within each independent component mask, normalized for subject head size, was estimated with SIENAX [Smith et al., 2001, 2002]. SIENAX starts by extracting brain and skull images from the single whole‐head input data [Smith, 2002]. The brain image is then affine‐registered to MNI152 space [Jenkinson and Smith, 2001; Jenkinson et al., 2002] using the skull image to determine the registration scaling. This is primarily in order to obtain the volumetric scaling factor, to be used as a normalization for head size. Next, tissue‐type segmentation with partial volume estimation is carried out [Zhang et al., 2001] in order to calculate total volume of brain tissue, including separate estimates of volumes of grey matter, white matter, peripheral grey matter and ventricular CSF.

We calculated partial Pearson correlations between the grey matter volume of each pair of components, separately in each subject group. Negative correlations were set to zero. This resulted in two 6 × 6 partial correlation matrices, with each within‐group matrix giving the association between the grey matter volume of each of the 15 possible pairs of components. Covariance analysis of MRI‐based measures of grey matter volume or cortical thickness has been used to obtain structural networks [Bassett et al., 2008; Bernhardt et al., 2013 ; Lerch et al., 2006; Mechelli et al., 2005]. In general, high positive correlation in grey matter volume or cortical thickness between two regions is interpreted as a strong structural connection, due to common trophic and maturational influences behind axonally connected regions [Wright et al., 1999; Zhang and Sejnowski, 2000]. In our approach we used the partial correlation matrices as prior information on the strength of structural connectivity, in order to inform the prior probability of non‐zero effective connectivity in Eq. (5).

RESULTS

Simulation Experiment: Model Fitting

The MCMC chain was run for 20,000 iterations with 10,000 sweeps as burn‐in. Hyperparameters were set to be weakly informative as follows. We set noninformative IG priors on the variance parameters ζ_j of the error term, by specifying $h_1=2$ and $h_2=1$, and on the variance parameters of the prior Eq. (3) on the subject‐level connectivities, by specifying $a_0^{(g)}=a_1^{(g)}=2,\hspace{0.17em}{b}_0^{(g)}=b_1^{(g)}=1$ for g = 1, 2. We fixed q = 5 in the ICAR prior and set S to the identity, representing no prior knowledge about spatio‐temporal smoothness. We also fixed the prior mean and variance of the probit regression hyperparameter ${\alpha }_1^{(g)}$ to $w^{(g)}=0$ and ${\tau }^{2^{(g)}}=100$, for g = 1, 2. Below we first show results we obtained by setting $F({\alpha }_0^{(g)})=0.01$, for g = 1, 2, and then comment on sensitivity.

When running the MCMC, we initialized the chain with 13 non‐zero randomly selected effective connectivities for group 1 and 12 for group 2. The non‐zero effective connectivities for group 1 were initialized to 0.5 and those for group 2 were initialized to −0.5. Subject‐level effective connectivities were initialized to zero. We set the initial values of the other parameters as ${\alpha }_1=[0.1\hspace{0.17em}0.1],{\Sigma }^{(g)}={\mathbb{I}}_{L{R}^2}, g=1,2,\hspace{0.17em}{\zeta }_j=5, j=1,\dots ,R$. With our R implementation, 1,000 iterations of the MCMC algorithm took 10 min on an Intel Core i7 station (2.50 GHz) with 16 GB RAM.

We tested our model on the set of simulated data described in section “Simulation Experiment: Data Generation” to validate the model's ability to perform effective connectivity inference on the subject‐ and group‐levels. Figure 4 shows the MPP plots for the two groups. A threshold of 0.05 on the Bayesian false discovery rate, corresponding to thresholds on the MPPs of $(0.50,0.47)$ for group 1 and group 2, respectively, achieved 0 false positives and 2 false negatives for group 1 and 2 false positives and 1 false negatives for group 2. As for the estimation of the group‐level connectivities, Figures 5 and 6 show heat maps of the posterior estimates of ${\Omega }^{(g)}$ for the two groups, where the non‐zero elements are estimated by averaging over the MCMC samples. Our method is able to recover these estimates well, with a mean square error (MSE) of 0.0041 for group 1 and MSE of 0.0047 for group 2. Furthermore, Figure 7 show s posterior mean estimates versus true values for all subject‐level effective connectivities ${\underset{¯}{\beta }}_g^{(s)}$'s, for $s=1,\dots ,n$ and g = 1, 2. Our method recovers subject‐level effective connectivity with high accuracy, attaining an averaged MSE of 0.0044 across all subjects.

Figure 4.

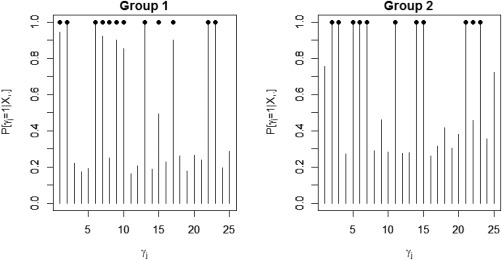
Simulated data: Marginal posterior probabilities (MPPs) of group‐level effective connectivity for (a) group 1 and (b) group 2. Black dots indicate true non‐zero connectivities.

Figure 5.

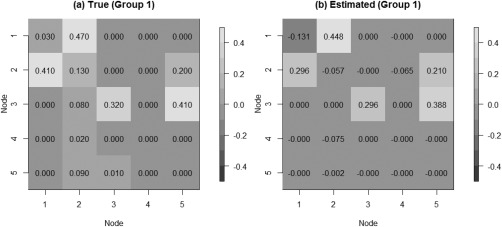
Simulated data: Group‐level estimation of effective connectivity for group 1. (a) Heatmap of true VAR coefficients and (b) Heatmap of posterior mean estimates.

Figure 6.

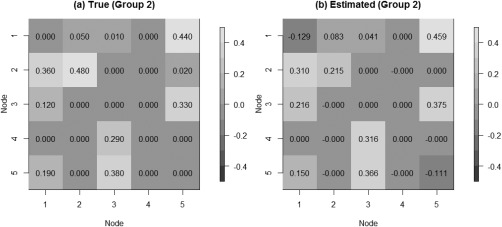
Simulated data: Group‐level estimation of effective connectivity for group 2. (a) Heatmap of true VAR coefficients and (b) Heatmap of posterior mean estimates.

Figure 7.

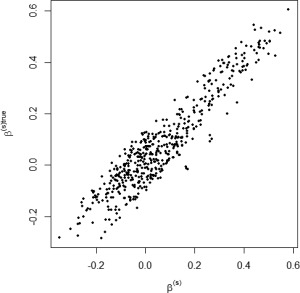
Simulated data: Subject‐level estimation of effective connectivity. Scatterplot of posterior mean estimates versus true values, for all n subjects.

When examining the sensitivity of our model's performance to changes in the values of the model hyperparameters, we found that modest changes in the values of the hyperparameters did not affect the accuracy of the estimation and, as expected, we observed some sensitivity to the parameter ${\alpha }_0^{(g)}$, which regulates the prior probability of non‐zero group‐level effective connectivity. In general, we found relatively robust performance for the identification of non‐zero effective connectivity, with greater sensitivity to ${\alpha }_0^{(g)}$ for non‐zero effective connectivities with small magnitude but strong corresponding structural connectivity (Fig. 8). In particular, for these types of connectivities, more sparse prior settings (smaller ${\alpha }_0^{(g)}$) allowed for more relative influence in the probit regression prior of structural connectivity, thus increasing the correct detection of effective connectivities with weak magnitude. For effective connectivities with small or moderate magnitude and weak corresponding structural connectivity, the opposite effect was observed, with more sparse prior settings (smaller ${\alpha }_0^{(g)}$) leading to decreased MPPs.

Figure 8.

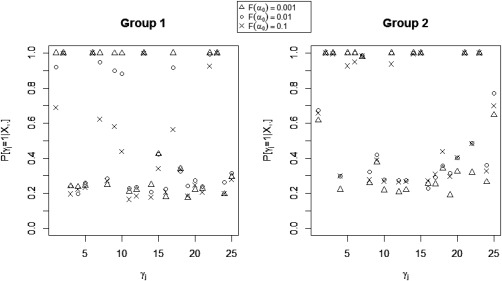
Simulated data: Marginal posterior probabilities (MPPs) of group‐level effective connectivities for various values of the probit prior parameter ${\alpha }_0^{(g)}$.

Simulation Experiment: Comparative Study

Table 2 compares the performance of our method, the two multi‐step procedures, and the two single‐step VAR generalizations. Results in Table 2 show superior performance of our unified method for detecting effective connectivity at the group level compared with standard approaches using Granger causal inference as well as the ME‐VAR and BME‐VAR models. In general, the t‐test approach outperformed the Fisher method, with both higher accuracy as well as F ₁‐score for accurately identifying effective connectivities. The ME‐VAR and BME‐VAR models attained lower FNR than the t‐test method, but at the expense of a higher FPR. Our unified method, on the other hand, attained both higher accuracy and F ₁‐score than the other approaches.

Table 2.

Simulated data: Performance comparison between the proposed method and existing approaches for effective connectivity

			Multi‐step methods		Single‐step methods
		Proposed	t‐test method	Fisher method	ME‐VAR	BME‐VAR
Group 1	FPR	0.0103	0.2744	0.7026	0.4077	0.3821
	FNR	0.1806	0.3111	0.1639	0.1722	0.1944
	Accuracy	0.9080	0.7080	0.5560	0.7053	0.7080
	F 1‐score	0.8920	0.6909	0.6413	0.7295	0.7254
Group 2	FPR	0.1357	0.3952	0.6762	0.5333	0.6381
	FNR	0.0909	0.1152	0.2393	0.0787	0.0606
	Accuracy	0.8840	0.7280	0.5160	0.6667	0.6160
	F 1‐score	0.8735	0.7417	0.5805	0.7098	0.6836

Results are reported as averages over 30 replicated datasets. FPR, false positive rate; FNR, false negative rate.

Furthermore, with respect to inference on VAR coefficient estimates, we observed that our method attained lower MSE for estimating effective connectivity at both the group‐ and subject‐level than the other procedures (Fig. 9). Our method obtained an average MSE of 0.0039 for group 1 and 0.0032 for group 2, and an average MSE of 0.0041 for subject‐level effective connectivity inference. In comparison, the t‐test approach obtained an average MSE of 0.0056 for group 1 and 0.0055 for group 2, and an average MSE of 0.0044 for subject‐level effective connectivity inference, whereas the Fisher approach obtained an average MSE of 0.0065 for group 1 and 0.0062 for group 2, and an average MSE of 0.0042 for subject‐level effective connectivity inference. The ME‐VAR and BME‐VAR models performed similarly to the Fisher method, with an average MSE of 0.0065 for group 1, an average MSE of 0.0062 for group 2, and an average MSE of 0.0050 for subject‐level inference using the ME ‐VAR model; and an average MSE of 0.0061 for group 1, an average MSE of 0.0063 for group 2, and an average MSE of 0.0062 for subject‐level inference using the BME‐VAR model.

Figure 9.

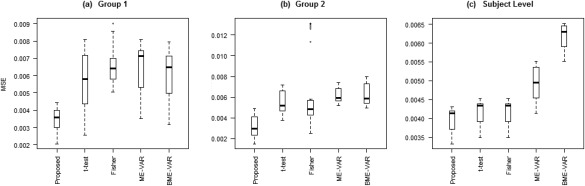
Simulated data: Boxplots of MSE for proposed method and standard Granger causal methods: (a) group 1 VAR coefficients, (b) group 2 VAR coefficients, (c) mean MSE across subjects of subject‐level VAR coefficients.

Although the single‐step ME‐VAR and BME‐VAR models allow for simultaneous estimation of group‐ and subject‐level parameters, thereby allowing for the propagation of probabilistic uncertainty in their estimation procedures, the increase in the number of parameters for single‐step procedures may contribute to a higher FPR, offsetting a lower FNR compared with multi‐step procedures, as well as overall larger MSE for inference on VAR coefficient estimates. In contrast, our proposed approach integrates prior information on structural connectivity into inference on effective connectivity, while accommodating single‐step inference on subject and group‐level parameters, thus allowing for a more efficient exploration of the high‐dimensional parameter space. This, in turn, results in the attainment of a lower FPR and a lower FNR for the detection of non‐zero effective connectivity, as well as lower MSE for VAR coefficient estimation.

Resting State Experiment: Model Fitting

To evaluate the utility of the proposed model on experimentally acquired functional MRI data, we applied the above model to the data described in section “Resting State Experiment: Data Description and Preprocessing.” We report results obtained by setting the lag order of the VAR model to L = 2. Typically, with fMRI data, VAR models of order one or two are recommended, given the low temporal resolution of the data. Diagnostics are often based on auto‐correlation of the residuals. Also, criterion functions such as the Schwarz's Bayesian information criterion (BIC) [Schwarz et al., 1978] have gained popularity. Here, we found that a model with lag order L = 2 minimized the BIC, that is, $BIC=(12.76,12.31,12.65)$ for $L=(1,2,3)$, respectively.

For hyperparameters setting, similarly to the simulation study, we set $h_1=2,\hspace{0.17em}{h}_2=1,\hspace{0.17em}{a}_0^{(g)}=a_1^{(g)}=2,\hspace{0.17em}{b}_0^{(g)}=b_1^{(g)}=1,\hspace{0.17em}{w}^{(g)}=0$, and ${\tau }^{2^{(g)}}=100$ for $g=1,\dots ,G$. We also set the prior slab variance to q = 1. We investigated two choices of the probit regression sparsity prior parameter, ${\alpha }_0=[-2.326,-2.326]$, corresponding to a prior sparsity of 0.01 for each of the two groups, in the absence of structural connectivity, and ${\alpha }_0=[-1.282,-1.282]$, corresponding to a prior sparsity of 0.10. The matrix S was set to $S=({\mathbb{I}}_{LR}\otimes {\mathbf{1}}_R)+A+A^T$, where A is an $L{R}^2-by-L{R}^2$ matrix with the $((j-1)LR+lR+j\prime ,(j-1)LR+j\prime )$ th element equal to 1 and 0 otherwise, for all $j=1,\dots ,R,\hspace{0.17em}j\prime =1,\dots ,R,\hspace{0.17em}l=1,\dots ,L-1$. In particular, $S_{kk\prime }=1$ indicates either connectivities at a given lag that initiate from the same node (e.g., MOT → ADMN at lag 1, MOT → SAL at lag 1) or connectivities between the same nodes at different lags (e.g., MOT → ADMN at lag 1, MOT → ADMN at lag 2). Figure 10 shows the matrix S.

Figure 10.

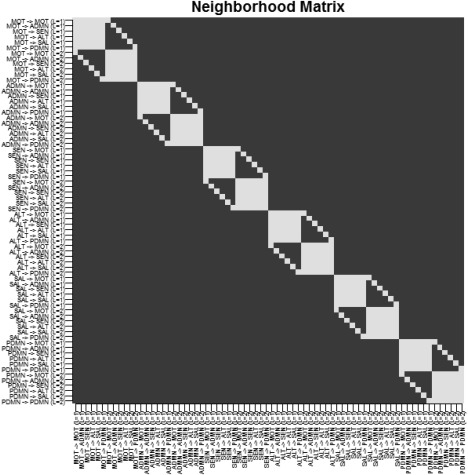
Temporal lobe epilepsy dataset: Matrix S, with white squares denoting $S_{kk\prime }=1$.

Results we report here are based on the combined posterior output from three MCMC chains. Each chain was run for 50,000 iterations, with the first 20,000 sweeps discarded as burn‐in, and initialized with a different number of randomly chosen non‐zero effective connectivities. Specifically, the first chain was initialized with 26 non‐zero connectivities in the healthy control group and 24 in the TLE group; the second chain was initialized with 35 and 33 non‐zero connectivities, respectively, in healthy controls and the TLE group; and the third chain was initialized with 15 and 13 non‐zero connectivities. Non‐zero effective connectivities for the healthy controls were initialized to 0.5 and for the TLE group to −0.5. All subject‐level effective connectivities were initialized to zero. Other initial values were set as in the simulation study. Convergence of each chain was assessed using the Raftery–Lewis diagnostic [Raftery et al., 1992]. In addition, convergence of the multiple chains was assessed using the Gelman–Rubin potential scale reduction factor, based on the implementation in the R package “coda” [Raftery and Lewis, 1992].

Trace plots for γ, ${\Omega }^{(g)}$, and ${\varphi }^{(s)}$ showed good mixing for all chains (figures not shown). Convergence diagnostics from the Raftery–Lewis dependence factor and Gelman–Rubin potential scale reduction factor indicated convergence to the stationary distribution and are shown in Table 3. Agreement between MCMC chains was assessed through the Pearson correlation between the marginal posterior probabilities for each pair of chains. Good agreement was present between the chains, with pairwise correlation coefficients ranging between 0.989 and 0.990 for healthy controls and 0.992 and 0.994 for the TLE group for the setting ${\alpha }_0=[-2.326,-2.326]$, and between 0.987 and 0.989 for healthy controls and 0.982 and 0.985 for the TLE group for the setting ${\alpha }_0=[-1.282,-1.282]$.

Table 3.

Temporal lobe epilepsy dataset: Markov chain convergence tests

${\alpha }_0^{(g)}$		Raftery–Lewis	Gelman–Rubin PSRF
−2.326	Chain 1	0.97–2.21
	Chain 2	0.97–2.10	0.999–1.007
	Chain 3	0.97–2.00
−1.282	Chain 1	0.97–2.24
	Chain 2	0.97–2.29	0.999–1.005
	Chain 3	0.97–2.24

PSRF, potential scale reduction factor.

Marginal posterior probabilities (MPPs) for group‐level effective connectivities are shown in Figure 11 for healthy controls and in Figure 12 for TLE patients, with different graphical symbols for the settings of ${\alpha }_0=[-2.326,-2.326]$ (o) and ${\alpha }_0=[-1.282,-1.282]$ (x). Under the prior setting ${\alpha }_0=[-2.326,-2.326]$, a threshold of 0.05 on the Bayesian false discovery rate, corresponding to thresholds on the MPPs of $(0.685,0.705)$ for the healthy control group and the TLE group, respectively, identified 16 non‐zero effective connectivities at lag 1 and 13 at lag 2, in the healthy control group, and 15 and 11 non‐zero effective connectivities at lags 1 and 2, respectively, in the TLE group. Selected effective connectivities, MPP values and estimated VAR coefficients are listed in Tables 4 and 5 and the corresponding estimated connectivity networks are depicted in Figure 13. This set of effective connectivities largely overlapped with the set identified at the less sparse prior setting of ${\alpha }_0=[-1.282,-1.282]$, where two additional effective connectivities at lag 1 (ALT → ADMN, SAL → MOT) and one additional at lag 2 (PDMN → SAL) were identified in the healthy control group, one additional effective connectivity at lag 1 (SEN → ADMN) and two additional at lag 2 (SEN → MOT, SEN → PDMN) were identified in the TLE patient group, and the effective connectivity from SAL → ADMN at lag 1 and lag 2 no longer selected in the TLE group. As noted in section “Simulation Experiment: Model Fitting,” increased MPPs in less sparse prior settings are observed in the presence of effective connectivities with small to moderate magnitude and weak corresponding structural connectivity. For example, this explains the increase in MPP for ALT → ADMN at lag 1 in the healthy control group and for SEN → ADMN at lag 1 and SEN → PDMN at lag 2 in TLE patients, as weak structural connectivity was estimated between these networks through the structural MRI data, allowing for a greater relative influence of the prior sparsity level.

Figure 11.

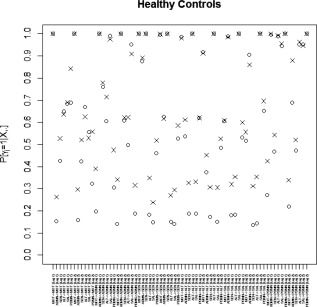
Temporal lobe epilepsy dataset: Marginal posterior probabilities (MPPs) for group‐level effective connectivities among healthy controls at lags 1 and 2. Different graphical symbols are used for prior sparsity levels of 0.01 (o) and 0.1 (x).

Figure 12.

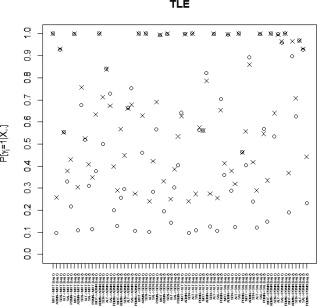
Temporal lobe epilepsy dataset: Marginal posterior probabilities (MPPs) for group‐level effective connectivities among TLE patients at lags 1 and 2. Different graphical symbols are used for prior sparsity levels of 0.01 (o) and 0.1 (x).

Table 4.

Temporal lobe epilepsy dataset: Effective connectivities among healthy controls selected with a Bayesian FDR control of 5%, with corresponding marginal posterior probabilities (MPPs) and estimates of VAR coefficients ${\Omega }_{j,j\prime }$, for a prior sparsity of 0.01

	Healthy controls
	Effective connectivity	MPP	${\Omega }_{j,j\prime }$
Lag 1	MOT → MOT	1.000	1.136
	PDMN → MOT	0.690	−0.083
	ADMN → ADMN	1.000	0.960
	SEN → ADMN	0.759	0.063
	SAL → ADMN	0.991	−0.140
	MOT → SEN	1.000	0.339
	ADMN → SEN	0.875	0.089
	SEN → SEN	1.000	0.915
	MOT → ALT	0.987	0.138
	ALT → ALT	1.000	1.084
	ADMN → SAL	0.990	−0.135
	SAL → SAL	1.000	0.999
	ADMN → PDMN	0.995	0.192
	ALT → PDMN	0.988	0.157
	SAL → PDMN	0.944	−0.124
	PDMN → PDMN	1.000	0.905
Lag 2	MOT → MOT	1.000	−0.409
	ADMN → ADMN	1.000	−0.297
	SAL → ADMN	0.952	0.110
	MOT → SEN	0.997	−0.209
	SEN → SEN	1.000	−0.233
	MOT → ALT	0.917	−0.098
	ALT → ALT	1.000	−0.327
	ADMN → SAL	0.905	0.080
	SAL → SAL	1.000	−0.291
	ADMN → PDMN	0.688	−0.084
	ALT → PDMN	0.951	−0.127
	SAL → PDMN	0.951	0.123
	PDMN → PDMN	1.000	−0.234

Table 5.

Temporal lobe epilepsy dataset: Effective connectivites among temporal lobe epilepsy patients selected with a Bayesian FDR control of 5%, with corresponding marginal posterior probabilities (MPPs) and estimates of VAR coefficients ${\Omega }_{j,j\prime }$, for a prior sparsity of 0.01

	Temporal lobe epilepsy patients
	Effective connectivity	MPP	${\Omega }_{j,j\prime }$
Lag 1	MOT → MOT	1.000	0.979
	SEN → MOT	0.927	0.125
	ADMN → ADMN	1.000	0.620
	ALT → ADMN	0.843	0.081
	SAL → ADMN	0.728	−0.001
	MOT → SEN	1.000	0.432
	SEN → SEN	1.000	0.884
	ADMN → ALT	0.998	0.202
	ALT → ALT	1.000	0.990
	ADMN → SAL	0.997	−0.197
	SAL → SAL	1.000	0.937
	ADMN → PDMN	1.000	0.264
	ALT → PDMN	0.999	0.192
	SAL → PDMN	0.959	−0.155
	PDMN → PDMN	1.000	0.667
Lag 2	MOT → MOT	0.999	−0.299
	SAL → ADMN	0.752	0.013
	MOT → SEN	0.994	−0.218
	SEN → SEN	0.998	−0.232
	ADMN → ALT	0.821	−0.066
	ALT → ALT	0.999	−0.274
	ADMN → SAL	0.893	0.085
	SAL → SAL	0.998	−0.231
	ADMN → PDMN	0.897	−0.153
	ALT → PDMN	0.969	−0.143
	SAL → PDMN	0.928	0.127

Figure 13.

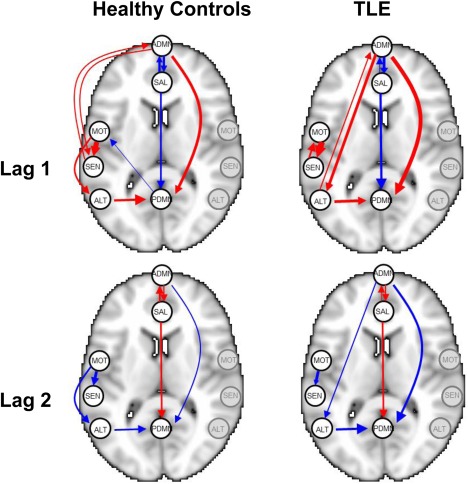
Temporal lobe epilepsy dataset: Estimated group‐level effective connectivity between resting‐state networks, using a Bayesian FDR control of 5%, for a prior sparsity of 0.01. Edge widths are proportional to the magnitude of the estimated VAR coefficients, with red edges denoting positive values and blue edges denoting negative values. Nodes in the graph are overlaid for representative purposes as point landmarks on half of a standard Montreal Neurological Institute (MNI) template brain and not indicative of the entire network. For simplicity, self‐connections are not shown. [Color figure can be viewed at http://wileyonlinelibrary.com]

DISCUSSION AND CONCLUSIONS

In this work we have developed a novel multi‐subject vector autoregressive (VAR) modeling approach for inference on effective connectivity based on resting‐state functional MRI data. Our framework uses a Bayesian variable selection approach to allow for simultaneous inference on effective connectivity at both the subject‐ and group‐level. Furthermore, it accounts for multi‐modal data by integrating structural imaging information into the prior model, encouraging effective connectivity between structurally connected regions. Through simulations, we have shown that our model attains superior performance at both the subject‐ and group‐level, compared with multi‐step approaches as well as single‐step approaches which do not incorporate structural imaging information into the inference.

A key distinction of our approach with respect to current methods for Granger causal inference is the simultaneous estimation of both subject‐ and group‐level effective connectivity, which allows for probabilistic propagation and improvements in group‐level inference. With respect to other Bayesian approaches, our modeling setting relaxes the assumption of independence between effective connectivity parameters through the use of an intrinsic autoregressive prior. Furthermore, the use of probit regression priors allows to incorporate multi‐modal imaging data to constrain effective connectivity inference. Integration of prior information into the modeling framework aids estimation in settings with increased number of parameters.

Additionally, we have illustrated the utility of our model in an analysis of resting‐state fMRI and structural MRI data on healthy controls and temporal lobe epilepsy patients, where we corroborated several known brain connectivity relationships and identified potentially novel ones. The application of our model to the temporal lobe epilepsy dataset demonstrated that patients with temporal lobe epilepsy exhibit a number of differences as well as similarities in effective connectivity between resting‐state networks in comparison with healthy controls. Hemodynamic influence, for example, was found in both healthy controls and TLE patients from the anterior to posterior DMN at lag 1 and lag 2, but not in the opposite direction. Although the DMN has traditionally been thought to represent a single network, recent studies have challenged this idea, showing instead that the DMN is divided into different functional subsystems [Haneef et al., 2012; Uddin et al., 2009]. Our work suggests that, during the resting‐state, the self‐referential processing involved by the anterior DMN likely dominates the familiarity and/or autobiographical memory functions involved by the posterior DMN. Previous research has also found evidence of unidirectional influence from the anterior to posterior DMN in healthy controls using two‐step GC inference [Uddin et al., 2009], supporting our finding.

Our model also identified evidence of hemodynamic influence at lag 1 and lag 2 from the premotor cortex to primary somatosensory cortex in healthy controls. In contrast, in TLE patients, bidirectional hemodynamic influence was identified at lag 1 followed by unidirectional influence at lag 2 between the premotor cortex and primary somatosensory cortex. The interactions between the premotor cortex and primary somatosensory cortex play a large part of the ability to perform complex voluntary movements through the internal forward model of motor planning and control referred to as efference copy (EC) [Miall and Wolpert, 1996], and several attempts using non‐human primate models have been made to understand the relative timing of activation of these areas [Felleman and Van Essen, 1991; Fetz et al., 1980; Johnson et al., 1996; Soso and Fetz, 1980; Wise et al., 1997]. Recently, Sun et al. [2015] found using electrocorticography (ECoG) in humans that, during motor tasks, activation of the premotor cortex precedes activation of the primary somatosensory cortex, which precedes activation of the primary motor cortex. Our detection of hemodynamic influence from the premotor to primary somatosensory cortex during the resting‐state is consistent with this finding. The ability of our model to detect this relationship using fMRI signal rather than ECoG suggests that the precedence of premotor activation before primary somatosensory activation is also detectable at lower temporal resolutions, which may provide a means of studying this relationship through non‐invasive techniques. Additionally, detection of this relationship during the resting‐state suggests a method for studying this relationship in subject populations that exhibit difficulty performing motor tasks. In TLE, however, a bidirectional relationship was observed between the premotor and primary somatosensory cortex at lag 1. Evidence from functional connectivity studies using fMRI [Zhang et al., 2009] have also demonstrated abnormalities in the functional organization of the sensorimotor cortex in TLE. It has been shown that seizure activity from the hippocampus produces long‐distance effects on the sensorimotor cortex [Van Rooyen et al., 2006], which may mediate the changes observed in our study. Our finding of differences in effective connectivity may suggest an alteration of normal efference copy mechanisms in temporal lobe epilepsy, and requires further research with electrophysiological techniques to better understand the underlying pathophysiology.

The salience network, which includes the anterior cingulate gyrus and bilateral insulae, is thought to be central to responding to behaviorally salient events and in signaling the need to change behavior [Menon and Uddin, 2010; Seeley et al., 2007]. Functional connectivity studies have indicated that activity in the salience network is negatively correlated with activity in the default mode network. Further evidence from task‐based fMRI studies has shown that the salience network exhibits a regulatory role on DMN function [Bonnelle et al., 2012; Rilling et al., 2008; Sridharan et al., 2008], although whether the anterior or posterior DMN is influenced is not clear. Our study identified effective connectivity from the salience network to the DMN in healthy controls as well as TLE, suggesting that the influence of the salience network on the DMN is detectable during the resting state as well. In particular, we found that the salience network exhibited influence on both the anterior and posterior DMN in healthy controls. In TLE, a high marginal posterior probability of influence on both the anterior and posterior DMN was also identified. However, the magnitude of influence on the anterior DMN was much lower in TLE patients (−0.001 vs. −0.140). A reciprocal influence of the anterior DMN on the salience network was also identified in both healthy controls and TLE patients. This suggests that regulation of the salience network by the DMN proceeds primarily through the anterior rather than posterior DMN during the resting‐state.

In contrast to the salience network, the alerting network is postulated to be responsible for achieving and maintaining a state of readiness for incoming stimuli [Posner, 2008]. Previous research using functional connectivity to study the alerting network has found that, although TLE patients exhibit a smaller overall area as well as intensity of activation of the alerting network during alertness tasks, several additional regions are recruited in TLE which are not recruited in controls, including the thalamus, limbic lobe, and cingulate gyrus [Zheng et al., 2012]. Consistent with these findings, we also found that effective connectivities into and out of the alerting network encompass a different spatial pattern in TLE compared with healthy controls. In particular, while we observed effective connectivity from the alerting network to posterior DMN in both TLE and healthy controls, TLE patients experienced bidirectional effective connectivity also between the alerting network and the anterior DMN. Furthermore, TLE patients exhibited a greater magnitude of effective connectivity from the alerting network to posterior DMN, consistent with the previous study's finding of increased activation of the posterior cingulate gyrus in TLE [Zheng et al., 2012].

Recent literature in neuroimaging is putting forward evidence that connectivity may be non‐stationary [Balqis‐Samdin et al., 2016; Chiang et al., 2016; Havlicek et al., 2010; Hutchison et al., 2013], therefore suggesting the use of dynamic models, where coefficients are indexed by time. Our approach can in principle be extended to such framework, although it would lead to models with a very large number of parameters to be estimated. Another possible extension of our model may include connectivity‐specific parameters ${\alpha }_{1,k}^{(g)}$ in the probit regression (5), for $k=1,\dots ,L{R}^2$. This would permit greater flexibility in estimation, by relaxing the assumption that the relationship between structural and functional coupling is constant across all connections. Indeed, the coupling of structural and functional/effective connectivity networks has found to be disrupted in different disease states, such as schizophrenia [Skudlarski et al., 2010] and epilepsy [Zhang et al., 2011; Chiang et al., 2015], with evidence that this disruption may be modulated by surrounding white matter injury [Reijmer et al., 2015].

Our proposed approach uses MCMC to sample from the posterior distribution. MCMC algorithms allow a full exploration of the posterior, although they come with a high computational cost. The current computation time of our method was found reasonable for exploratory investigations, such as the one conducted in this article. For applications that require a greater computational speed, for example brain mapping applications for neurosurgery, approximation techniques, such as the variational Bayes (VB) method, may be used. In such cases, it is advisable to perform comparisons of the VB results against posterior estimates generated by the MCMC algorithm proposed here, to evaluate the accuracy of the VB estimates.

APPENDIX A.

MCMC Algorithm

In order to sample from the joint posterior, we used Metropolis‐within‐Gibbs MCMC sampling methods. Furthermore, we employed a data augmentation step to simplify the sampling of the parameters of the probit prior (5). Following Albert and Chib [1993], we introduced latent variables $z_k^{(g)}$, where the $z_k^{(g)}$ are independent $\mathrm{N}({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)},1)$ and such that ${\gamma }_k^{(g)}=1$ if $z_k^{(g)}>0$ and ${\gamma }_k^{(g)}=0$ otherwise. Then it can be shown that the ${\gamma }_k^{(g)}$'s are independent Bernoulli random variables with $p({\gamma }_k^{(g)}=1)=F({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)})$ and Eq. (5) can be written as follows:

$$\begin{array}{c}p({\gamma }_k^{(g)}|z_k^{(g)})=\mathbf{1}(z_k^{(g)}>0)\\ p(z_k^{(g)}|{\alpha }_1)=\mathrm{N}({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)},1)\\ {\alpha }_1^{(g)}\sim \mathrm{N}(w^{(g)},{\tau }^{2^{(g)}}).\end{array}$$

A generic iteration of the MCMC algorithm comprises the following steps:

1. Update ${\underset{¯}{\beta }}_g^{(s)}$: This is a Gibbs step from a normal, ${\underset{¯}{\beta }}_g^{(s)}\sim \mathrm{N}({\mu }_{\beta }^{(s)},{\nu }_{\beta }^{(s)})$, with ${\mu }_{\beta }^{(s)}={[{\Xi }^{-1}\otimes (U{\prime }^{(s)}{U}^{(s)})+{\Sigma }^{-1(g)}]}^{-1}[({\Xi }^{-1}\otimes U{\prime }^{(s)}){\underset{¯}{x}}^{(s)}+{\Sigma }^{-1(g)}{\Omega }^{(g)}]$ and ${\nu }_{\beta }^{(s)}={[{\Xi }^{-1}\otimes (U{\prime }^{(s)}{U}^{(s)})+{\Sigma }^{-1(g)}]}^{-1}$, for all s such that ${\eta }_s=g,\hspace{0.17em}g=1,\dots ,G$.

2. Joint update for $({\mathit{\gamma }}^{(g)},{\Omega }^{(g)})$, $g=1,\dots ,G$: We perform a between‐model step by updating these two parameters jointly, using a joint Metropolis–Hastings step. For each $g=1,\dots ,G$: To propose a new candidate ${\mathit{\gamma }}^{{(g)}^{\star }}$, randomly choose between two transition moves:

   • a. Add/delete: Randomly choose one of the LR ² indices in ${\mathit{\gamma }}^{(g)}$, and change its value either from 0 to 1, or 1 to 0.

   • b. Swap: Choose independently and at random a 0 and 1 in ${\mathit{\gamma }}^{(g)}$, and switch their values.

     If ${\gamma }_k^{(g)\star }=0$, set ${\omega }_k^{(g)\star }=0$. Else, if ${\gamma }_k^{(g)\star }=1$, sample ${\omega }_k^{(g)\star }\sim \mathrm{N}({\rho }_k^{(g)},{\kappa }_k^{(g)}),\hspace{0.17em}k=1,\dots ,L{R}^2,\hspace{0.17em}g=1,\dots ,G$, with

     $$\begin{array}{c}{\rho }_k^{(g)}=\frac{{\mathbb{Z}}_k^{(g)}-\frac{1}{2}{\displaystyle {\sum }_{\{m:m\ne k\}}{\omega }_m^{(g)}}{\Theta }_{km}^{(g)}-\frac{1}{2}{\displaystyle {\sum }_{\{m:m\ne k\}}{\omega }_m^{(g)}}{\Theta }_{mk}^{(g)}+\frac{1}{q}{\displaystyle {\sum }_{k\prime =1}^{L{R}^2}{S}_{kk\prime }}{\omega }_{k\prime }^{(g)}}{{\Theta }_{kk}^{(g)}+\frac{1}{q}{\displaystyle {\sum }_{k\prime =1}^{L{R}^2}{S}_{kk\prime }}}\\ {\kappa }_k^{(g)}=\frac{1}{{\Theta }_{kk}^{(g)}+\frac{1}{q}{\displaystyle {\sum }_{k\prime =1}^{L{R}^2}{S}_{kk\prime }}}\end{array}$$

     where $\mathbb{Z}={\Sigma }^{{(g)}^{-1}}{\displaystyle {\sum }_{\{s:{\eta }_s=g\}}{\underset{¯}{\beta }}_g^{(s)}},\hspace{0.17em}{\Theta }^{(g)}=n_g{\Sigma }^{{(g)}^{-1}}$, and n_g is the number of subjects in Group g. Jointly accept the proposed candidate $({\mathit{\gamma }}^{{(g)}^{\star }},{\Omega }^{{(g)}^{\star }})$ with probability

     $$\begin{array}{c}\text{min}\left\{1,\frac{p({\mathit{\gamma }}^{{(g)}^{\star }},{\Omega }^{{(g)}^{\star }}|{\left\{{\underset{¯}{\beta }}_g^{(s)}\right\}}_{s:{\eta }_s=g},\Sigma )}{p({\mathit{\gamma }}^{(g)},{\Omega }^{(g)}|{\left\{{\underset{¯}{\beta }}_g^{(s)}\right\}}_{s:{\eta }_s=g},\Sigma )}\right\}\\ =\text{min}\left\{1,\frac{{\displaystyle {\prod }_{\{s:{\eta }_s=g\}}p}({\underset{¯}{\beta }}_g^{(s)}|{\Omega }^{{(g)}^{\star }},{\Sigma }^{(g)})\left[{\displaystyle {\prod }_{k=1}^{L{R}^2}p}({\omega }_k^{{(g)}^{\star }}|{\mathit{\gamma }}^{{(g)}^{\star }})\right]\left[{\displaystyle {\prod }_{k=1}^{L{R}^2}p}({\gamma }_k^{{(g)}^{\star }})\right]}{{\displaystyle {\prod }_{\{s:{\eta }_s=g\}}p}({\underset{¯}{\beta }}_g^{(s)}|{\Omega }^{(g)},{\Sigma }^{(g)})\left[{\displaystyle {\prod }_{k=1}^{L{R}^2}p}({\omega }_k^{(g)}|{\mathit{\gamma }}^{(g)})\right]\left[{\displaystyle {\prod }_{k=1}^{L{R}^2}p}({\gamma }_k^{(g)})\right]}\right\}\end{array}$$

3. Update ${\Omega }^{(g)},\hspace{0.17em}g=1,\dots ,G$: We perform a within‐model step using a Gibbs step to improve mixing. For all ${\omega }_k^{(g)}$ such that ${\gamma }_k^{(g)}=1$, sample ${\omega }_k^{(g)}\sim \mathrm{N}({\rho }_k^{(g)},{\kappa }_k^{(g)}),\hspace{0.17em}k=1,\dots ,L{R}^2,\hspace{0.17em}g=1,\dots ,G$, with ${\rho }_k^{(g)}$ and ${\kappa }_k^{(g)}$ as defined above.

4. Update ${\xi }_1^{(g)},\hspace{0.17em}g=1,\dots ,G$: This is a Gibbs step, draw ${\xi }_1^{(g)}\sim \text{IG}({\chi }_1^{(g)},{\psi }_1^{(g)})$, for $g=1,\dots ,G$, where

   $$\begin{array}{c}{\chi }_1^{(g)}=\frac{1}{2}{n}_g{p}_{({\gamma }^{(g)})}+a_1^{(g)}\\ {\psi }_1^{(g)}=\frac{1}{2}{\displaystyle \sum _{\{s:{\eta }_s=g\}}{\left({\underset{¯}{\beta }}_{g({\gamma }^{(g)})}^{(s)}-{\Omega }_{({\gamma }^{(g)})}^{(g)}\right)}^T}\left({\underset{¯}{\beta }}_{g({\gamma }^{(g)})}^{(s)}-{\Omega }_{({\gamma }^{(g)})}^{(g)}\right)+b_1^{(g)}.\end{array}$$

   Here, n_g is the number of subjects in Group g; $p_{({\gamma }^{(g)})}$ denotes the number of non‐zero values of ${\mathit{\gamma }}^{(g)}$; and ${\underset{¯}{\beta }}_{g({\gamma }^{(g)})}^{(s)}$ and ${\Omega }_{({\gamma }^{(g)})}^{(g)}$ denote the values of ${\underset{¯}{\beta }}_g^{(s)}$ and ${\Omega }^{(g)}$, respectively, corresponding to non‐zero values of ${\mathit{\gamma }}^{(g)}$.

5. Update ${\xi }_0^{(g)},\hspace{0.17em}g=1,\dots ,G$: This is a Gibbs step, draw ${\xi }_0^{(g)}\sim \text{IG}({\chi }_0^{(g)},{\psi }_0^{(g)})$ for $g=1,\dots ,G$, where

   $$\begin{array}{c}{\chi }_0^{(g)}=\frac{1}{2}{n}_g{p}_{({\gamma }^{C^{(g)}})}+a_0^{(g)}\\ {\psi }_0^{(g)}=\frac{1}{2}{\displaystyle \sum _{\{s:{\eta }_s=g\}}{\left({\underset{¯}{\beta }}_{g({\gamma }^{C^{(g)}})}^{(s)}-{\Omega }_{({\gamma }^{C^{(g)}})}^{(g)}\right)}^T}\left({\underset{¯}{\beta }}_{g({\gamma }^{C^{(g)}})}^{(s)}-{\Omega }_{({\gamma }^{C^{(g)}})}^{(g)}\right)+b_{(0)}^{(g)}\end{array}$$

   Here, $p_{({\gamma }^{C^{(g)}})}$ denotes the number of zero values of ${\mathit{\gamma }}^{(g)}$; and ${\underset{¯}{\beta }}_{g({\gamma }^{C^{(g)}})}^{(s)}$ and ${\Omega }_{({\gamma }^{C^{(g)}})}^{(g)}$ denote the values of ${\underset{¯}{\beta }}_g^{(s)}$ and ${\Omega }^{(g)}$, respectively, corresponding to zero values of ${\mathit{\gamma }}^{(g)}$.

6. Update latent variable $z_k^{(g)},\hspace{0.17em}k=1,\dots ,L{R}^2,\hspace{0.17em}g=1,\dots ,G$: This is a Gibbs step from a truncated normal. Draw

   $$\begin{array}{c}p(z_k^{(g)}|{\gamma }_k^{(g)}=1,{\alpha }_1)\propto p({\gamma }_k^{(g)}=1|z_k^{(g)},{\alpha }_1)p(z_k^{(g)}|{\alpha }_1)\\ =\mathbf{1}(z_k^{(g)}>0)\mathrm{N}({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)},1)\\ p(z_k^{(g)}|{\gamma }_k^{(g)}=0,{\alpha }_1)\propto p({\gamma }_k^{(g)}=0|z_k^{(g)},{\alpha }_1)p(z_k^{(g)}|{\alpha }_1)\\ =\mathbf{1}(z_k^{(g)}<0)\mathrm{N}({\alpha }_0^{(g)}+{\alpha }_1^{(g)}{N}_k^{(g)},1)\end{array}$$

7. Update ${\alpha }_1^{(g)}$: This is a Gibbs step, draw ${\alpha }_1^{(g)}\sim \mathrm{N}({\mu }_{\alpha }^{(g)},{\nu }_{\alpha }^{(g)})$ for $g=1,\dots ,G$, with ${\mu }_{\alpha }^{(g)}=\frac{{\sum }_{k=1}^{L{R}^2}[(z_k^{(g)}-{\alpha }_0^{(g)})N_k^{(g)}]+w^{(g)}/{\tau }^{2^{(g)}}}{{\sum }_{k=1}^{L{R}^2}{N}_k^{{(g)}^2}+1/{\tau }^{2^{(g)}}}$ and ${\nu }_{\alpha }^{(g)}=\frac{1}{{\sum }_{k=1}^{L{R}^2}{N}_k^{{(g)}^2}+1/{\tau }^{2^{(g)}}}$.

8. Update ζ_j, $j=1,\dots ,R$: This is a Gibbs step, draw ${\zeta }_j\sim \text{IG}(d_1,d_2)$ for $j=1,\dots ,R$, with

   $$\begin{array}{c}{d}_1=h_1+\frac{n(T-L)}{2}\\ d_2=h_2+{\displaystyle \sum _{s=1}^n[\frac{1}{2}{\displaystyle \sum _{t=1+L}^T{X}_{tj}^{{(s)}^2}}-{\displaystyle \sum _{k=1}^{LR}{B}_{gkj}^{(s)}}\left({\displaystyle \sum _{t=1+L}^T{X}_{tj}^{(s)}}{U}_{tk}^{(s)}\right)+\frac{1}{2}{\displaystyle \sum _{k=1}^{LR}{\displaystyle \sum _{k\prime =1}^{LR}{B}_{gkj}^{(s)}}}{B}_{gk\prime j}^{(s)}{\mathit{V}}_{kk\prime }]}\end{array}$$

   where $\mathit{V}=U{\prime }^{(s)}{U}^{(s)}$.