Quantifying risk stratification provided by diagnostic tests and risk predictions: Comparison to AUC and Decision Curves

Abstract

[Summary]A property of diagnostic tests and risk models deserving more attention is risk stratification, defined as the ability of a test or model to separate those at high absolute risk of disease from those at low absolute risk. Risk stratification fills a gap between measures of classification (i.e. AUC) that do not require absolute risks and decision-analysis that requires not only absolute risks but also subjective specification of costs and utilities. We introduce Mean Risk Stratification (MRS) as the average change in risk of disease (posttest-pretest) revealed by a diagnostic test or risk model dichotomized at a risk threshold. MRS is particularly valuable for rare conditions, where AUC can be high but MRS can be low, identifying situations that temper overenthusiasm for screening with the new test/model. We apply MRS to the controversy over who should get testing for mutations in BRCA1/2 that cause high risks of breast and ovarian cancers. To reveal different properties of risk-thresholds to refer women for BRCA1/2 testing, we propose an eclectic approach considering MRS and other metrics. The value of MRS is to interpret AUC in the context of BRCA1/2 mutation prevalence, provide a range of risk thresholds at which a risk model is ”optimally informative”, and to provide insight into why Net Benefit arrives to its conclusion.

1. Introduction

When a new biomarker is considered for development into a predictive test or for inclusion into risk prediction models, several properties of the marker are elucidated in order. First, the marker has to be associated with the outcome, typically quantified by odds-ratios. Second, classification accuracy is quantified, typically by Youden’s Index(1) or Area Under the Curve (AUC)(2).

The next step is quantifying predictiveness. In contrast to classification of currently observed outcomes (i.e. diagnostic testing), predicting future outcomes (i.e. risk prediction) is inherently stochastic and perfect prediction is generally not possible. Prediction requires calculating predictive values or developing an absolute risk model. A key property of predictive markers and models is absolute risk stratification. Risk stratification is a broadly used term, but we define it as the ability of a test or model to separate those at high risk of disease from those at low risk(3). Risk stratification is a ubiquitous term in medicine (33,107 papers in PubMed; 26Apr2018), but is much less common in the statistical literature (18 papers in Scopus; 26Apr2018). Absolute risks and risk differences are best for clinicians and patients to understand risks, benefits and harms (4; 5)

Important advances in risk stratification include the predictiveness curve(6; 7) and its summary metric Total Gain(1). However, most recent research has focused on metrics for risk-reclassification(9; 10) or decision-making(11; 12; 2). While both concepts are important, neither focuses on risk stratification. Importantly, risk stratification fills a gap between measures of classification (i.e. AUC) that do not require absolute risks and decision-analysis that requires not only absolute risks but also subjective specification of costs and utilities. Quantifying risk stratification helps to better understand the relatively objective concept of absolute risk predictiveness before embarking on decision-analysis, which additionally requires subjective quantities.

To quantify risk stratification, we introduced Mean Risk Stratification (MRS) as the average change in risk of disease (posttest-pretest) revealed by a diagnostic test(14). In this paper, we provide the first formal statistical treatment of MRS, and equally importantly, extend it to continuous risk models and consider risk thresholds. Herein also we introduce a linked metric, the Net Benefit of Information (NBI): the increase in expected utility from using the marker/model to select people for intervention versus randomly selecting people for intervention. NBI quantifies the ”informativeness” of a marker/model. The key results are:

1. MRS provides an interpretation of Youden’s index and AUC for risk stratification. Namely, when expressed as functions of MRS, Youden’s index and AUC are seen to be relative measures of risk stratification.

2. MRS and NBI provide Youden’s index and AUC with risk-stratification and decision-theoretic rationales, lack of which are used to criticize Youden’s index and AUC(15; 4).

3. NBI is a function of only MRS and the risk-threshold for action, which provides a decision-theoretic rationale for MRS. MRS and NBI provide insight into why Net Benefit (from Decision Curve Analysis(12)) arrives to its conclusion.

4. MRS and NBI provide a range of risk thresholds for which the marker/model is ”optimally informative”, in the sense that the risk-thresholds maximize both risk-stratification and the expected gain in utility over random selection.

Because different metrics reveal different aspects of a marker or risk model, we propose an eclectic strategy. First, calculate Youden’s index and AUC as measures of classification. Then use MRS to understand the absolute risk stratification implications of Youden’s index and AUC. Finally, use Net Benefit (12) and NBI to understand the implications of risk stratification in light of decision-making. We show that the ranges of useful risk-thresholds, as produced by Youden’s index, AUC, MRS, NBI, and Net Benefit, always overlap at risk threshold equaling disease prevalence, but contrasting the different endpoints is insightful.

We apply our eclectic strategy to the controversy over who should get tested for mutations in the BRCA1/2 genes, which cause high risks of breast and ovarian cancer(17). The mutations are rare in the general population (≈ 0.25%), but are 10 times more common among Ashkenazi-Jews(18). Current US and UK guidelines refer women for mutation testing only if they have a strong family history of breast or ovarian cancer(19), as quantified by a risk model calculating that their risk of carrying a BRCA1/2 mutation exceeds 10%(20). However, as mutation-testing costs plummet, prominent voices have called for testing all women(21; 22). Others counter that testing millions of women is impractical, would strain clinical resources, and will cost billions of dollars(23).

In light of plummeting costs, thresholds below the current US/UK 10% guideline should be considered. We recently showed that a threshold of 0.78% identified 80% of Ashkenazi-Jewish mutation-carriers by testing only 44% of Ashkenazi-Jewish women(24). In this paper, we consider AUC, MRS, NBI, and Net Benefit to better understand the properties of different risk thresholds. The value of MRS and NBI is (1) interpret AUC in the context of prevalence, (2) provide a range of risk thresholds for which the risk model is optimally informative, and (3) provide insight into why Net Benefit arrives to its conclusion. Our MRS webtool is available (http://analysistools.nci.nih.gov/biomarkerTools).

2. Mean Risk Stratification (MRS)

Because continuous markers or risk models require dichotomization to determine action, we refer to a marker or model M, dichotomized at a cutpoint m₀, as a test: $M+=\{M\ge m_0\}$ is positive and $M-=\{M<m_0\}$ is negative. In the absence of test results or other pretest information, each individual can only be assigned as a best guess the same population-average risk P(D+). Upon taking the test, 2 outcomes are possible:

1. With probability P(M+), the test is positive. The person’s risk increases from P(D+) to Positive Predictive Value $(PPV=P(D+|M+))$, an increase of PPV − P(D+).

2. With probability P(M−), the test is negative. The person’s risk decreases from P(D+) to complement of Negative Predictive Value: $cNPV=P(D+|M-)$. The person’s risk decreases by P(D+) − cNPV.

Mean Risk Stratification (MRS) is a weighted average of the increase in risk in those who test positive and the decrease in risk in those who test negative:

$$MRS(m_0)=\{PPV-P(D+)\}P(M+)+\{P(D+)-cNPV\}P(M-)$$ (1)

MRS is the average difference between predicted post-test individual risk (either PPV or cNPV ) and pretest population-average risk P(D+). Simply, MRS is the average change in risk that a test reveals. For example, a 6% MRS means that a person, using this test, will learn that their disease risk will increase or decrease by an average of 6 disease cases per 100 people.

Note that MRS is a function of the cutpoint m₀ that defines risk thresholds, via the definition of M+ and M−. The m₀ that maximizes MRS is where the risk threshold equals disease prevalence (see Appendix); here MRS equals Total Gain (see Webappendix). We will plot MRS for each m₀ to produce the range of risk thresholds where MRS is near its peak, and this range will always contain disease prevalence.

MRS measures association by equaling twice the covariance of disease and marker, and is related other association measures (see Appendix). MRS also equals twice the cross-product difference of the joint probabilities inside a 2×2 table, easily remembered by analogy with odds ratios (see Appendix).

Negative MRS means that M+ is inversely associated with disease. When test positive/negative are interchanged, MRS changes sign. MRS is not Net Reclassification Index (NRI)(10), because under dichotomization, NRI equals Youden’s index.

The MRS is an average of the 2 possible post-test changes in risk (i.e. PPV − P(D+) and P(D+) − cNPV ), which may themselves be very different. MRS is useful as the average change risk before taking the test. After the test is taken, MRS has no further use.

The Webappendix shows the variance of MRS, performance of MRS confidence intervals, and p-values for comparing MRSs.

3. Net Benefit of Information and Mean Risk Stratification

Decision-theoretic metrics of test performance are based on the expected utility from using the test (see(2) for a comprehensive review). Calculating expected utility requires specification of the utility for the 4 possible outcomes: the utility of true positive prediction U_TP, the utility of true negative prediction U_TN, the utility of false positive prediction U_FP, and the utility of false negative prediction U_FN. Furthermore, the cost of marker M is U_Test. These 5 utilities require considering the benefits, harms, and costs of the test and all subsequent interventions, which may be personal and difficult to quantify.

However, a risk-threshold can encapsulate the utilities(25). The marker/model is dichotomized at risk threshold $R:P(D+ |M=m_0)=R$. The R that maximizes expected utility is determined by the ratio of benefit (B = U_TP − U_FN) to costs (C = U_TN − U_FP), which is R = 1/(1 + B/C)(25). The risk-threshold weighs the utility of true-positives versus false-positives, e.g. a 10% threshold means that a rational person will accept 9 false-positives for every true-positive. Decision-theoretic metrics of test performance are calcualted for each risk threshold R (as defined by cutpoints m₀) to gain insight on the value of each risk threshold.

To derive Net Benefit of Information, we first calculate the expected utility of the test, which averages utilities, weighted by the joint probabilities for the outcomes, plus test cost:

$$U=U_{TP}P(D+,M+)+U_{FN}P(D+,M-)+U_{TN}P(D-,M-)+U_{FP}P(D-,M+)+U_{Test}.$$

In particular, note that randomly selecting people for intervention, with the same positivity p = P(M+) and cost U_Test as the test of interest, has utility(26, Ch.9)

$$U_{RS}=U_{TP}\pi p+U_{FN}\pi (1-p)+U_{TN}(1-p)(1-\pi )+U_{FP}(1-\pi )p+U_{Test},$$

where π = P(D+). Random selection is the minimum utility possible for a reasonable test (which need not be zero) and provides a baseline utility that must be substantially exceeded. A test is more informative the higher its utility is than randomly selecting people for intervention.

Next, plugging in the following identities (see Webappendix)

$$P(D+,M+)=MRS/2+p\pi$$

$$P(D-,M-)=MRS/2+(1-p)(1-\pi )$$

$$P(D+,M-)=(1-p)\pi -MRS/2$$

$$P(D-,M+)=(1-\pi )p-MRS/2$$

into the expected-utility equation yields

$$U=\frac{MRS}{2}(U_{TP}-U_{FN}-U_{FP}+U_{TN})+U_{RS}=\frac{MRS}{2}(B+C)+U_{RS}.$$

Finally, we scale utility in units of benefit to define Net Benefit of Information (NBI) as the increase in (scaled) utility from using the test to select people for intervention versus randomly selecting people for intervention:

$$NBI(m_0)=\frac{U-U_{RS}}{B}=\frac{MRS(m_0)}{2}\frac{B+C}{B}=\frac{MRS(m_0)/2}{1-R}.$$ (2)

NBI is a function of test characteristics only via the MRS, and for small risk thresholds, NBI is close to half the MRS. This provides NBI a concrete risk-stratification interpretation, and vice versa, provides a decision-theoretic interpretation for MRS.

Because MRS is a function of the cutpoint m₀ that defines the risk threshold R (equation 1), so is NBI. We will plot NBI(m₀) over the range of risk thresholds R defined by cutpoints m₀. The risk thresholds where NBI(m₀) is near its peak is where the most utility is gained over random selection. This range of risk-thresholds is where the marker/risk-model is ”optimally informative”. For small R, where NBI ≈ MRS/2, this range of risk-thresholds also has highest MRS(m₀). Parenthetically, in this paper we presume that each m₀ indeed corresponds to an optimal risk threshold R, so that varying m₀ is also varies the implicit utilities underlying R.

4. Relationship of MRS/NBI to Youden’s Index, AUC, and risk differences

4.1. Relationship of MRS and NBI to Youden’s Index and AUC

MRS and NBI can be calculated by combining prevalence with Youden’s index or AUC for a dichotomized marker. Equation 5 in the Appendix shows that MRS can be written as

$$MRS=2\{P(D+,M+)-P(D+)P(M+)\}=2(Sens-p)\pi ,$$

where sensitivity Sens = P(M + |D+), π = P(D+), and p = P(M+). Denote specificity Spec = P(M− |D−). Because $p=Sens\times \pi +\left(1 -Spec\right)\left(1 -\pi \right)$,

$$\begin{gathered} MRS(m_0)=2(Sens-Sens\times \pi -(1-Spec)(1-\pi ))\pi \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\pi (1-\pi )J(m_0). \end{gathered}$$ (3)

MRS is Youden’s index (J (m₀) = Sens(m₀) + Spec(m₀) − 1) rescaled by disease prevalence. Note that Youden’s index is function of cutpoint m₀. MRS can be calculated by combining an estimate of Youden’s index J with an external estimate of disease prevalence π, which we will do in section 5.2.

While AUC is usually calculated for continuous markers, for a dichotomized marker, AUC(m₀) = (J (m₀) + 1)/2(27). Thus

$$MRS(m_0)=4(AUC(m_0)-0.5)\pi (1-\pi ).$$ (4)

Similarly, NBI(m₀) is a function of J (m₀) or AUC(m₀) via the above MRS expressions. MRS, NBI, Youden’s index, and AUC are maximized when cutpoint m₀ implies that risk threshold equals prevalence (see Appendix).

The key point is that MRS/NBI interpret Youden’s index and AUC in light of prevalence. In particular, for rare diseases

$$MRS\approx 2J\pi \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}NBI\approx J\pi /(1-R).$$

For rare diseases, MRS and NBI naturally temper overenthusiasm for markers with high AUC. In particular, a high Youden’s index or AUC might not imply much risk stratification or informativeness. Furthermore, prevalence bounds MRS/NBI:

$$MR{S}_{perfect}=2\pi (1-\pi )$$

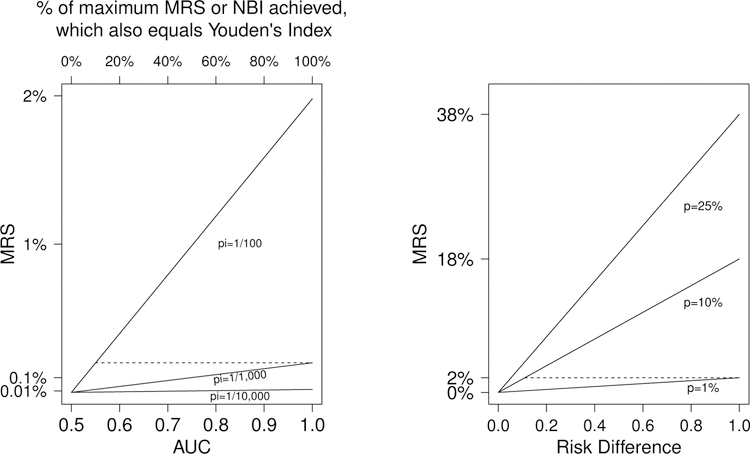
(AUC = 1 in equation 4), and $NBI=\pi ,\forall R$. Thus if disease is rare, there may be little risk stratification or NBI even for perfect tests. Figure 1 (left panel) plots the relationship of MRS to AUC for 3 uncommon disease prevalences. The importance of disease prevalence is illustrated by noting that, the maximum MRS (achieved if AUC=1) is also obtained if AUC=0.55 for diseases 10 times more prevalent; AUC=0.6 suffices if disease is 5 times more prevalent. Thus a perfect marker for a rare disease provides the same risk-stratification as a weakly-associated marker for a disease that is 5–10 times as prevalent.

Figure 1:

Left: Mean Risk Stratification (MRS) vs. AUC for 3 disease prevalences (1/100, 1/1,000, and 1/10,000). The top axis is the fraction of maximum MRS or NBI achieved by the corresponding AUC on the bottom axis. Right: MRS vs. Risk Difference for 3 test positivities (1%, 10%, and 25%).

4.2. Simple and useful decision-theoretic interpretation of Youden’s index and AUC

A perfect test has maximal NBI and MRS for a disease. The fraction of this maximum NBI and MRS achieved by the test is Youden’s index:

$$\frac{NBI}{NB{I}_{perfect}}=\frac{MRS}{MR{S}_{perfect}}=\frac{2\pi (1-\pi )J(m_0)}{2\pi (1-\pi )}=J(m_0).$$

Thus Youden’s index is both the fraction of the maximum possible risk-stratification and the fraction of the maximum possible utility gain over random selection, that is attained by the test. Thus MRS/NBI indeed provide Youden’s index (and thus AUC) with simple and useful decision-theoretic and risk-stratification interpretations.

However, since Youden’s index and AUC reflect on multiplicative gains in MRS and NBI, for rare diseases, a high Youden’s index or AUC can mask small absolute MRS and NBI (Fig. 1, left plot). For example, perfect AUC = 1 achieves 100% of the possible MRS; for disease prevalence π = 1/1000 this yields MRS = 0.20%. However, this very same MRS is achieved, for a disease of 1% prevalence, for a test with AUC = 0.55, which only achieves 10% of the MRS for perfect test.

Since J = 2 ×AUC − 1, a 1% increase in AUC implies a 2% increase in the fraction of maximal MRS or NBI that is achieved. Thus MRS and NBI double from AUC=0.6 to 0.7. An AUC=0.6 is widely considered to be ”modest”, and indeed, only 20% of maximal MRS and NBI is achieved. An AUC=0.7 is widely considered ”good”, but only 40% of maximal MRS and NBI is achieved. An AUC=0.95 is required to achieve 90% of maximal MRS and NBI. AUC is a valuable measure of relative increases in risk, while MRS shows the absolute risk meaning of AUC.

4.3. MRS and NBI for a rarely-positive test: Relationship to the risk difference

The risk difference is $RD=PPV -cNPV\left(\text{recall}\hspace{0.17em}cNPV=P\left(D+|M-\right)\right)$. Risk stratification is sometimes (mis)measured by the risk difference: a large spread in risks is considered evidence of good risk stratification. Starting from equation (5):

$$MRS=2\{P(D+,M+)-P(D+)P(M+)\}=2(PPV-\pi )p.$$

Substituting $\pi =PPV\times p+cNPV(1 -p)$,

$$\begin{gathered} MRS=2(PPV(1-p)-cNPV(1-p))p \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2p(1-p)\times RD. \end{gathered}$$

A large risk difference does not imply much risk stratification, and hence NBI, if the test is rarely positive. Figure 1 (right panel) plots the relationship of MRS to the risk-difference for 3 test positivity rates. When risk-difference is 1, the maximum MRS for a perfect test is achieved. The importance of test positivity is illustrated by noting that, the MRS achieved for risk-difference of 1 is also obtained for a risk-difference of approximately only 0.1 when the test is 10 times as positive (dashed line). Thus a perfect marker for a rarely positive test provides the same risk-stratification, and hence NBI, as a weakly associated marker 10-times as positive.

5. Informativeness of risk models to select people for BRCA1/2 testing

As detailed in the Introduction, mutations in the BRCA1/2 genes cause high risk of breast and ovarian cancers. The mutations are rare in the general population (≈ 0.26%), but much more common among Ashkenazi-Jews (≈ 2.3%). Currently, women are asked to provide their family history of cancer (e.g. see Webappendix), and she is offered mutation-testing in the UK and US if a risk model calculates that her risk of carrying a mutation exceeds 10%(20). Popular risk models are BRCAPRO(28) or BOADICEA(29). We focus on BRCAPRO.

However, as mutation-testing costs plummet, prominent voices have called for testing all women, which would strain clinical resources by testing millions of women, 99.75% of whom will test negative. Instead, a lower risk threshold, below 10%, might identify most all mutation-carriers, yet avoid unnecessary testing for most women. We recently showed that a low 0.78% risk-threshold would identify 80% of Ashkenazi-Jewish mutation-carriers yet test only 44% of Ashkenazi-Jewish women(24). We use AUC, MRS, NBI, and Net Benefit to throw light on properties of BRCAPRO to select women for BRCA1/2 testing at risk thresholds between 0%−10%.

We use data on 4,589 volunteers (102 BRCA1/2 mutation carriers) from the Washington Ashkenazi Study (WAS)(18). We calculated each volunteer’s risk of carrying a mutation, based on their self-reported family-history of breast/ovarian cancers, using BRCAPRO. Here M is the BRCAPRO risk score, and because BRCAPRO is a well-calibrated risk model(24), m₀ = R, i.e. the cutpoint m₀ equals the risk threshold R. Disease D indicates the presence of a BRCA1/2 mutation. We calculate confidence intervals and p-values (see Webappendix).

We do not have comparable data for BRCA1/2 mutations in the general-population. As suggested by equation 3, we approximate MRS and NBI for the general-population by combining the general-population mutation-prevalence (0.26%) with sensitivity/specificity from the WAS. We can do this because BRCA1/2 mutations induce the same cancer risk for Ashkenazi-Jews and the general-population(17); only mutation prevalence differs between populations. Thus the Bayes Factor used by BRCAPRO is the same regardless of population(30). We use BRCAPRO to calculate risks of carrying mutations with WAS data, but substitute the mutation prevalence in the general-population (0.26%) as the prior. Because these approximations are meant only to make a methodologic point about the effect of prevalence given fixed AUC, we do not calculate their variances.

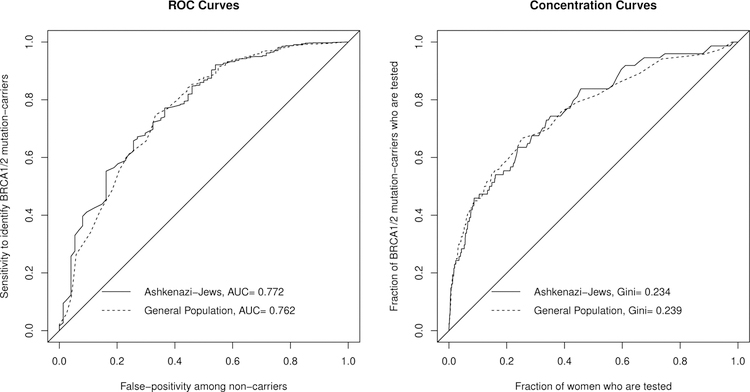
Figure 2 shows that Ashkenazi-Jews and the general population indeed have similar ROC curves and Lorenz curves, despite having very different prevalences. This reinforces that ROC, AUC, and Lorenz curves do not distinguish between populations when only prevalence differs between them.

Figure 2:

ROC curves (left plot) and Concentration (Lorenz) curves (right plot) for the BRCAPRO risk model to predict if a woman carries a BRCA1/2 mutation, for Ashkenazi-Jews and the general population. Note the curves are similar between populations, even though mutation prevalence is 10-times higher among Ashkenazi-Jews.

5.1. AUC and MRS for BRCAPRO at different risk-thresholds

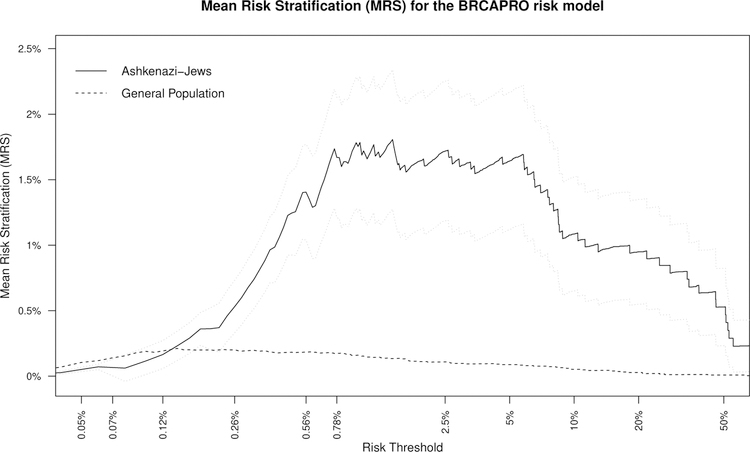
Recall that MRS(m₀) is a function of the cutpoint used to decide M+ (equation 1). Figure 3 plots MRS(m₀) for BRCAPRO over a range of risk thresholds R (= m₀) to refer women for BRCA1/2 mutation testing.

Figure 3:

Mean Risk Stratification (MRS) vs. risk threshold for the BRCAPRO risk model for Ashkenazi-Jews and the general population. The gray lines are 95% pointwise confidence bands for MRS (see Webappendix) for Ashkenazi-Jews.

For risk thresholds above 0.12%, the MRS for Ashkenazi-Jews is much larger than for the general population (Figure 3), even though Ashkenazi-Jews and the general population have similar AUC (Figure 2). This illustrates that MRS accounts for the much larger mutation prevalence for Ashkenazi-Jews (2.3% vs 0.26%), and thus BRCAPRO generally provides much more risk stratification. However, for risk thresholds below 0.12%, BRCAPRO actually provides more risk stratification in the general population. This occurs because below 0.12% there are hardly any Ashkenazi-Jewish mutation-carriers, but by the Lorenz curve (Figure 2), 33% of mutation-carriers remain in the general population. MRS demonstrates that the population with higher prevalence does not always have greater risk stratification, but that risk stratification depends on the risk thresholds being considered.

For Ashkenazi-Jews, BRCAPRO has best MRS ≈ 1.7% (95%CI: 1.2% to 2.2%) for risk thresholds in a ”sweetspot” of 0.78% to 5%. An MRS=1.7% means that a woman who uses BRCAPRO, dichotomized at any threshold between 0.78% to 5% to refer her for mutation-testing, will learn that her risk of carrying a mutation will increase or decrease by 1.7% on average. In contrast, for the general population, BRCAPRO has best MRS of only ≈ 0.20% for risk thresholds in a ”sweetspot” of 0.12%−0.56%.

Both populations have similar AUC ≈ 0.69 at their risk threshold sweetspots, indicating that only 38% of the maximum MRS (for a perfect test) is achievable by BRCAPRO. This shows that AUC is valuable to reveal relative changes in risk. However, the perfect test for Ashenazi-Jews has MRS of 4.5% (= 2π(1 ≈ π); see section 4.1) while in the general population the perfect test has MRS of only 0.52%. MRS reveals the very different absolute risk stratification implications of AUC=0.69 in each population.

In contrast, the current 10% threshold yields a substantially lower MRS for Ashkenazi-Jews of 1.1% (95%CI: 0.7% to 1.5%; p=0.039 versus MRS=1.7% at the 0.78% threshold). The risk-threshold sweetspot of 0.78%−5% identifies 45%−80% of BRCA1/2 mutation-carriers (Figure 2). The 10% threshold identifies only 28% of BRCA1/2 mutation-carriers. For the general population, the 10% threshold yields an MRS of only 0.05%, identifying only 11% of mutation-carriers. BRCAPRO is substantially less informative at the current 10% threshold than at lower thresholds.

Note that for Ashkenazi-Jews, the 10% threshold yields a much higher risk-difference than the 0.78% threshold: 12.58% vs. 3.39% respectively. Thus MRS was lower at the 10% threshold, in spite of a higher risk-difference, because the 10% threshold has only 4.5% test-positivity (vs. 44% at the 0.78% threshold). Rarely positive tests have low risk-stratification (see section 4.3).

5.2. Complementary perspectives of Net Benefit and NBI

Net Benefit is an important modern approach to identify risk-thresholds where a marker/model is useful for clinical actions(12). We briefly review Net Benefit, then compare insights from it and NBI.

5.2.1. Brief review of Net Beneftt

Recall that NBI subtracts the expected utility of random selection U_RS from the utility of the test U, standardized by benefit B (see section 3). In contrast, Net Benefit (NB) subtracts the utility of calling everyone negative $(U_N=U_{FN}\pi +U_{TN}(1 -\pi ))$ from the utility of the test, standardized by benefit:

$$NB(R)=\frac{U-U_N-U_{Test}}{B}=\pi Sens-\frac{R}{1-R}(1-Spec)(1-\pi ),$$

under the assumption, commonly used in practice, of a costless test (U_Test = 0). In particular, the Net Benefit of calling everyone positive (NB_P) is the difference in the utilities of calling everyone positive $(U_P=U_{FP}(1 -\pi ) +U_{TP}\pi )$ vs. negative:

$$N{B}_P(R)=\frac{U_P-U_N}{B}=\pi -\frac{R}{1-R}(1-\pi ).$$

The goal of Net Benefit is to identify the range of risk thresholds where the marker/model provides more utility than all-or-nothing actions. These thresholds will be those where the Net Benefit is positive (where the test provides more utility than calling everyone negative) and greater than NB_P (where the test provides more utility than calling everyone positive). To summarize this logic, we focus on the Net Benefit Gain (NB_Gain)

$$N{B}_{Gain}(R)=NB(R)-max(0,N{B}_P(R)).$$

The thresholds where NB_Gain(R) > 0 are thresholds where the risk model is better than all-or-nothing actions. For risk-thresholds that are smaller, intervening on everyone has the greatest utility, and for risk-thresholds that are larger, intervening on no one has the greatest utility. Interestingly, NB and NBI are special cases of a more general framework for the net benefits for tests that rule-out or rule-in for interventions(3). Note that NB requires that risk threshold R be the optimal risk threshold R = B/(B + C)(2).

Importantly, NBI and Net Benefit coincide at risk threshold equals prevalence (see Webappendix), where they and MRS achieve their maximum (see Appendix). Thus the ranges of useful risk-thresholds, according to Youden’s index, AUC, MRS, NBI and Net Benefit, will all overlap at prevalence.

5.2.2. Comparing insights from Net Beneftt and NBI

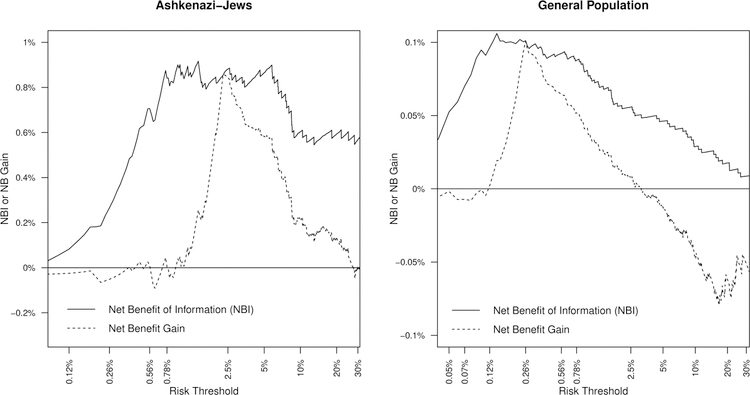
Figure 4 (left panel) compares NBI to Net Benefit Gain for the BRCAPRO model for Ashkenazi-Jews. Net Benefit Gain is positive for risk thresholds between 1.7% and 30%: below 1.7%, all Ashkenazi-Jews should be referred for mutation testing, and above 30%, none should be referred. Although 1.7% is within the 0.78%−5% MRS ”sweetspot”, 30% is far outside it. The 30% threshold has MRS=0.79% (95%CI: 0.4% to 1.2%; p=0.0005 vs. 1.7%) and AUC=0.59, compared to much higher MRS ≈ 1.7% and AUC ≈ 0.69 within the sweetspot (n.b., the AUC depends on risk-threshold because it is the dichotomized AUC based on Youden’s index (see Section 4.1)). Net Benefit suggests usefulness of high risk-thresholds, while MRS and NBI emphasize that BRCAPRO is much less uninformative at high risk-thresholds.

Figure 4:

Net Benefit of Information vs. Net Benefit Gain for the BRCAPRO risk model at different risk thresholds for Ashkenazi-Jews (left) and general population (right).

Vice versa, at 0.78%, NBI peaks and the BRCAPRO risk-model is optimally informative, but Net Benefit implies that all Ashkenazi-Jews should undergo BRCA1/2 testing (left panel, Figure 4). MRS and NBI emphasize that the model is optimally informative at 0.78%, identifying 80% of BRCA1/2 mutation-carriers while testing only 44% of Ashkenazi-Jews. In contrast, Net Benefit emphasizes that a 0.78% threshold implies that a truly rational person trades-off 127 false-positives for 1 true-positive. Rationally, false-positives are relatively unimportant, and one should not use the model (even though it is optimally informative) but rather refer all Ashkenazi-Jews for BRCA1/2 testing. Thus MRS and NBI emphasize that BRCAPRO remains informative at low risk thresholds, but Net Benefit emphasizes that low risk thresholds are inherently less useful.

NBI and MRS/2 are almost identical for risk thresholds below 10% for both populations (compare y-axes of Figure 3 vs. Figure 4). Thus MRS and NBI identify the same ”sweetspot” of risk thresholds for which BRCAPRO is optimally informative. The value of NBI is as a natural comparison to Net Benefit, and as a decision-theoretic interpretation of MRS.

For the general population (right plot, Figure 4), MRS and NBI are highest at risk thresholds of 0.12% to 0.56%, while Net Benefit is positive between 0.12% to 2.5%. Again, MRS and NBI emphasize the uninformativeness of high risk thresholds such as 2.5% (MRS=0.11%, AUC=0.61) while Net Benefit emphasizes that low risk thresholds < 0.12% are inherently less useful.

MRS/NBI help to understand why Net Benefit arrives to a conclusion. For example, surprisingly, at the current 10% risk-threshold in the general-population, Net Benefit finds that no one should undergo BRCA1/2 testing (i.e NB_Gain(10%) < 0 on the right side of the graph; Figure 4 right panel). The very low MRS/NBI at 10% (MRS=0.05%, NBI=0.055%) demonstrate that it is the first reason why Net Benefit says to not use BRCAPRO at a 10% threshold: BRCAPRO is simply uninformative at 10%.

6. Discussion

Absolute risk stratification fills a gap between classification metrics (i.e. AUC) that do not require absolute risks and decision-analysis that requires not only absolute risks but also subjective specification of costs and utilities. To quantify absolute risk stratification, we introduced two new broadly applicable, linked metrics: Mean Risk Stratification (MRS) and Net Benefit of Information (NBI). MRS and NBI reveal the absolute risk stratification implications of AUC. MRS immediately clarifies that, for rare diseases, high AUC does not imply high risk-stratification. However, Youden’s index and AUC remain valuable by measuring multiplicative relative gains in risk-stratification (MRS) and test informativeness (NBI). Thus MRS and NBI provide Youden’s index and AUC with decision-theoretic and risk-stratification interpretations, the lacks of which have long been a criticism of Youden’s index and AUC. MRS has a decision-theory rationale via its intimate connection to NBI. MRS and NBI provide a range of risk thresholds for which the risk model is ”optimally informative”: risk-thresholds that maximize both risk-stratification and the utility gain over random selection. The ranges of risk-thresholds that maximize each of Youden’s index, AUC, MRS, NBI, and Net Benefit, always overlap at risk threshold equaling disease prevalence, but contrasting their different endpoints yields insights. Finally MRS and NBI can help explain why Net Benefit arrives to a conclusion.

MRS and NBI reinforce that disease prevalence and test-positivity are crucial for evaluating risk-stratification and interpreting AUC. An AUC=0.6 achieves only 20% of maximum risk-stratification and AUC=0.95 is required to achieve 90%. There is little risk-stratification or NBI possible for rare diseases or for rarely positive tests. Although experts are aware of the importance of disease prevalence(2, Sec. 10), or can modify the ROC curve to account for prevalence(4) (see Webappendix), our website allows anyone to routinely calculate MRS to better interpret the AUC (http://analysistools.nci.nih.gov/biomarkerTools).

Because no single metric reveals all properties of the performance of markers and risk-models, we examined multiple metrics. First, calculate Youden’s index and AUC as relative measures of risk stratification. Then use MRS and NBI to understand the implications of Youden’s index and AUC for absolute risk stratification and test informativeness. Last, use Net Benefit to compare the utility of the risk stratification provided by the test versus the utilities of never intervening or always intervening.

Each metric revealed different and useful properties of risk-thresholds for the BRCAPRO risk model to refer women for BRCA1/2 mutation-testing. The AUC=0.69 for both Ashkenazi-Jews and the general population reveals that 38% of maximum risk stratification can be achieved by BRCAPRO. The MRS corresponding to this AUC is 1.7% for Ashkenazi-Jews, meaning that a woman who uses BRCAPRO will learn that her risk of carrying a mutation will increase or decrease by 1.7% on average. At AUC=0.69, MRS is only 0.20% for the general population, where mutations are much rarer. BRCAPRO provides much more absolute risk stratification for Ashkenazi-Jews, but not at extremely low risk thresholds (< 0.12%) where nearly all Ashkenazi-Jews would be tested anyway. This caveat clarifies that risk stratification is not always greater when prevalence is greater, but also depends on the risk thresholds being considered.

In the BRCA1/2 example, NBI emphasized the uninformativeness of high risk thresholds, while Net Benefit emphasized that low risk thresholds are inherently less useful. Net Benefit emphasized that risk thresholds below 1.7% are so low that false-positives are unimportant and thus all Ashkenazi-Jews should be tested; instead, risk-thresholds up to 30% could be considered for using the BRCAPRO model. NBI emphasized that for risk thresholds in 0.78% to 5%, the BRCAPRO model is optimally informative, referring only a minority of Ashkenazi-Jews for BRCA1/2 testing yet identifying the big majority of mutation-carriers. NBI noted a substantial loss of BRCAPRO informativeness at risk thresholds above 5%, and especially at 30%.

MRS and NBI can help explain why Net Benefit from Decision Curve Analysis(12) arrives to a conclusion. Under the current 10% risk-threshold, Net Benefit found that BRCA1/2 testing should never have been done in the general-population. This could be due to BRCAPRO being uninformative, the cost of genetic testing is high, or that prophylactic treatments are expensive or marginally life-extending. The low MRS and NBI show that it is because BRCAPRO is uninformative at a 10% threshold.

Although it is tempting to jump to decision-analysis or Net Benefit as the ”final answer”, the 10% threshold example suggests caution for 3 reasons. First, the range of risk thresholds from Net Benefit that favor using the biomarker might, unbeknownst to the analysis, be totally unacceptable thresholds in practice. Ideally, one needs to calculate the dollars per ”benefit” that is associated with a threshold to know if it is acceptable in practice. Simply put, no metric can determine the risk threshold without prespecifying utilities. If a threshold is not optimally informative, that fact should be noted but does not disqualify the threshold. Second, most applications of Net Benefit assume a costless marker. But this is not true even for use of risk models, which engender real costs via doctor time for shared decision-making. Third, accounting for biomarker cost in Net Benefit requires specifying not only test cost U_Test but also benefit B (see Sections 3 and 5.2.1). This is a practical difficulty because a key reason for Net Benefit’s popularity is to not require B, which is an abstract ”benefit” utility that is hard to directly specify.

More research is needed on the statistical aspects of MRS. Methodology is needed for calculating MRS and NBI from risk models, such as logistic regression or Cox models. Work is needed on the effect of model miscalibration, small sample sizes, or correcting for over-optimism in both the range and location of the sweetspot of risk-thresholds with maximal MRS and NBI.

Much work, and empirical experience, is needed to make MRS and NBI usable in practice. Because MRS is on the scale of the outcome, no single MRS could be considered as usefully informative across outcomes. For example, the MRS=1.7% for BRCAPRO represents a 1.7% average change in risk of carrying a cancer-causing mutation. However, carrying a mutation is not as severe as a 1.7% average change in yearly risk of developing cancer itself, much less a 1.7% average change in yearly risk of death. Understanding how to define a clinically significant MRS is a key issue for future research. In addition, more work needs to be done to understand how to use MRS to decide on how to use tests to rule-in or rule-out people for intervention (3; 32).

Appendix

A. MRS is maximized when dichotomizing at disease prevalence

Equation 3 notes that $MRS(m_0)=2J(m_0)\pi (1-\pi )$, where J (m₀) is Youden’s index calculated at cutpoint m₀. MRS is maximized as a function of cutpoint m₀ when Youden’s index J (m₀) is maximized, which occurs when dichotomizing at disease prevalence: $P(D+|M=m_0)=P(D+)=\pi$. To prove this we differentiate Youden’s index as a function of m₀

$$J(m_0)={\int }_{m_0}^{\infty }P(M=m|D+)-P(M=m|D-)dm$$

with respect to the cutpoint m₀ using the Leibnitz Integral Rule:

$$\frac{dJ(m_0)}{d{m}_0}=P(M=m_0|D-)-P(M=m_0|D+).$$

Setting the derivative equal to zero, and using Bayes’ rule:

$$\begin{gathered} \frac{P(D+|M=m_0)P(M=m_0)}{\pi }=\frac{P(D-|M=m_0)P(M=m_0)}{1-\pi } \\ \hspace{0.17em}\hspace{0.17em}P(D+|M=m_0)=\pi \end{gathered}$$

Thus choosing the m₀ that dichotomizes marker/model M at disease prevalence π maximizes Youden’s index and thus MRS. Thus the ”sweetspot” of risk-thresholds that maximize MRS will always include disease prevalence. At this cutpoint m₀, MRS equals Total Gain(1) (see Webappendix).

B. MRS measures association: MRS is twice the covariance of disease and marker

Recall that $PPV=P\left(D+|M+\right)$ and $cNPV=P\left(D+ |M-\right)$. Rewriting MRS equation (1):

$$\begin{gathered} MRS=\{PPV-P(D+)\}P(M+)+\{P(D+)-cNPV\}P(M-) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\{PPV-P(D+)\}P(M+)+P(D+)\{1-P(M+)\}-\{P(D+)-P(D+,M+)\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\{P(D+,M+)-P(D+)P(M+)\}. \end{gathered}$$ (A.1)

MRS is simply twice the covariance of D and M. MRS is zero if and only if disease and marker are independent. Other association measures, such as Pearson’s correlation, Cohen’s Kappa, Matthews correlation coefficient, the Phi coefficient, and Yule’s Q use MRS as a numerator but standardize it with different denominators. MRS is the numerator of the Mantel-Haenszel and Cochran’s tests(33).

The Webappendix demonstrates that MRS also equals the departure of any of the 4 joint probabilities of D and M from the product of their margins:

$$\begin{gathered} MRS=2\{P(D+,M+)-P(D+)P(M+)\}=2\{P(D+)P(M-)-P(D+,M-)\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\{P(D-,M-)-P(D-)P(M-)\}=2\{P(D-)P(M+)-P(D-,M+)\} \end{gathered}$$

C. MRS is twice the cross-product difference of joint probabilities inside 2×2 tables

Denote a = P(D+,M+), b = P(D+,M−), c = P(D−,M+), d = P(D−,M−). Plugging into MRS equation (5) yields

$$\begin{gathered} MRS=2\{P(D+,M+)-P(D+)P(M+)\}=2\{a-(a+b)(a+c)\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\{a(1-a)-ab-ac-bc\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\{a(b+c+d)-ab-ac-bc\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\{ad-bc\} \end{gathered}$$

MRS is simply twice the cross-product difference of the joint probabilities in the interior of the 2×2 table. The cross-product difference is also the determinant of the 2×2 table as a matrix. In contrast, the odds ratio (OR) is the cross-product ratio. Being a ratio, the OR is dimensionless, while the MRS is on the scale of risk differences. MRS as a cross-product difference is easy for scientists to remember.