Abstract
Regional morphological analysis represents a crucial step in most neuroimaging studies. Results from brain segmentation techniques are intrinsically prone to certain degrees of variability, mainly as results of suboptimal segmentation. To reduce this inherent variability, the errors are often identified through visual inspection and then corrected (semi)manually. Identification and correction of incorrect segmentation could be very expensive for large-scale studies. While identification of the incorrect results can be done relatively fast even with manual inspection, the correction step is extremely time-consuming, as it requires training staff to perform laborious manual corrections. Here we frame the correction phase of this problem as a missing data problem. Instead of manually adjusting the segmentation outputs, our computational approach aims to derive accurate morphological measures by machine learning imputation. Data imputation techniques may be used to replace missing or incorrect region average values with carefully chosen imputed values, all of which are computed based on other available multivariate information. We examined our approach of correcting segmentation outputs on a cohort of 970 subjects, which were undergone an extensive, time-consuming, manual post-segmentation correction. A random forest imputation technique recovered the gold standard results with a significant accuracy (r=0.93, p<0.0001; when 30% of the segmentations were considered incorrect in a non-random fashion). The random forest technique proved to be most effective for big data studies (N>250).
Keywords: Brain Segmentation, FreeSurfer, post-segmentation correction, imputation, random forest, big data
Introduction
MRI-based neuroanatomical studies are commonly performed using morphological analysis and feature extraction of brain structural images. Such analysis opens a more specific window into morphological cortical characteristics in development, aging and gender differences in health and disease (Eckert, 2004; Long et al., 2012; Luders et al., 2006; Perez et al., 2018; Sepehrband et al., 2018; Vijayakumar et al., 2016). FreeSurfer is one such example as an open-source software used to automatically extract and quantify cortical features from neuroimaging and has been widely used to study morphological characteristics of neuroanatomical structures, such as the cortical thickness and volume of the brain (Fischl, 2012). Several studies have assessed the reliability and accuracy of the brain segmentation techniques and concluded that they are intrinsically prone to certain degree of variability, mainly arising from suboptimal segmentation or miss-classification (Eggert et al., 2012; Gronenschild et al., 2012; Makowski et al., 2017; Perlaki et al., 2017; Tustison et al., 2014). Suboptimal segmentation are mainly related to incorrect inclusion of non-brain tissue. Many factors could result to such incorrect segmentation, including low T1 contrast-to-noise ratio, image artifacts (e.g. due to subject motion), field inhomogeneity, error in pre-processing steps (e.g. skull stripping errors) and segmentation imperfection (Gedamu et al., 2008; Klapwijk et al., 2019; Mortamet et al., 2009; Waters et al., 2018). These findings emphasize the need for quality control of the neuroanatomical measures obtained with automated segmentation pipelines such as FreeSurfer.
Post-processing of the automated brain segmentation results consists of identification and correction of the suboptimal segmentations. Identification of suboptimal segmentations can be accomplished through manual inspection or outlier detection analysis in a relatively time efficient fashion. The step that makes the brain segmentation techniques extremely costly is the correction step where conventional approaches adopt manual correction of the parcel boundaries. However, such quality control requires training staff to perform manual corrections, the process of which can be extremely time-consuming, costly, and inefficient for big data studies. Another possible remedy is to simply discard incorrect segmentation outputs. One can perform a complete-case analysis, which assumes the complete cases are a random sample of the original. Alternatively subjects with incorrect segmentation can be excluded. However, these manipulations can reduce the sample size to a small portion of the original sample, decreasing overall statistical power and limiting statistical learning implementation (Dinov, 2018; Hastie et al., 2009). Furthermore, deleting cases with missing data, is costly and ineffective in neuroimaging studies, given the cost and effort that is invested to acquire the MR images in first place.
Here we frame the correction step of the brain segmentation as a missing data problem and employ statistical and analytical data imputation techniques to make this step automated and efficient. Missing data can be defined as: data missing completely at random (MCAR), when the probability of a missing value does not depend on the data themselves; or data missing not at random (MNAR), when the probability of a missing value depends on the observed, known data in the dataset (Dinov, 2018; Rubin, 2004). One way to deal with the missing data is to simply fill the missing data values with the mean of the population. This solution is not optimum, as it could introduce systematic bias to the dataset (Lee et al., 2015) and does not take advantage of the multivariate information found in the dataset (Dinov, 2018). Using multivariate data imputation techniques, neuroanatomical similarities of large sample cohorts can be exploited to extract the missing information.
The current study aims to answer the following questions: (1) Can missing morphometric values be recovered through data imputation techniques? (2) What statistical or analytical technique provides an optimal solution to this problem? and (3) What is the effect of sample size on the reliability of the data imputation techniques? In the present study, we compare four methodologically diverse imputation methods, namely averaging, k-nearest neighbors, random forest, and low-rank matrix approximation on the Philadelphia Neurodevelopment Cohort (PNC) study (Satterthwaite et al., 2016, 2014), with a large sample size of N=970.
Methods
Dataset
The Big Data for Discovery Science (BBDS: http://bd2k.ini.usc.edu) (Toga et al., 2015) toolset was utilized to pre-process datasets of cross-sectional structural T1-weight MRI images from the single-site Philadelphia Neurodevelopment Cohort (PNC) study (Satterthwaite et al., 2016, 2014). Neuroimaging data from 997 participants, ages 8 – 22 years (mean age ± SD = 14.6 ± 3.4), comprised of 512 females, were acquired through the database of Genotypes and Phenotypes (dbGaP). MRI scans consisted of three-dimensional (3D) T1-weighted structural MRI scans and were acquired using T1-weighted MPRAGE sequence with the following parameters: TR = 1810 ms, TE = 3.5 ms, FOV = 180 × 240 mm2, matrix = 256 × 192, 160 slices, TI = 1100 ms, flip angle = 9, effective voxel resolution = 0.9 × 0.9 × 1 mm3. A 3T Siemens Tim Trio whole-body MRI with 32-channel head coil was utilized to collect the data. 27 participants were excluded from the present analysis due to poor image quality, or failure in pre-processing, leaving 970 participants with complete data.
Data preparation
Data preparation comprised of feature extraction using the FreeSurfer (v5.3.0) software package, which is documented and freely available for download online (http://surfer.nmr.mgh.harvard.edu/) (Fischl, 2012) and data processing using the Laboratory of Neuro Imaging (LONI) pipeline system (http://pipeline.loni.usc.edu) (Dinov et al., 2010, 2009; Moon et al., 2015; Torri et al., 2012). Cortical volume (mm3), surface area (mm2), and average cortical thickness (mm) were derived for cortical regions drawn from the Desikan-Killiany atlas (Desikan et al., 2006a). The morphological measurements were performed using recon-all module of the FreeSurfer, which uses an atlas-based parcellation approach. Prior to registration, recon-all applies following pre-processing steps: motion correction, non-uniform intensity normalization, Talairach transform computation, intensity normalization and skull stripping (Dale et al., 1999; Desikan et al., 2006b; Fischl et al., 2004b, 2004a, 2002, 1999; Fischl and Dale, 2000; Reuter et al., 2012, 2010; Reuter and Fischl, 2011; Segonne et al., 2007, 2004; Sled et al., 1998; Waters et al., 2018). The final dataset matrix had 970 × 70 dimensions for each cortical morphometry (i.e., 970 subjects and 70 cortical thicknesses). All 70 cortical thickness measures were used as the input for the multi-variate imputation techniques. In comparing data imputation techniques, the present study focuses mainly on the cortical thickness variables, as cortical thickness is more prone to error compare to cortical volume and area measures, and, therefore, more challenging to recover.
A team of specialist at LONI USC manually quality corrected the dataset and inspected the segmented cortex for each subject. Suboptimal segmentations were manually corrected following FreeSurfer guidelines. The Deriva Scientific Data Asset management system was utilized for data management (http://bd2k.ini.usc.edu/tools/deriva/), with the BDbag tool used for the retrieval of neuroimaging data and demographic information (http://bd2k.ini.usc.edu/tools/bdbag/). The data preparation process resulted in a complete, quality-controlled dataset.
Generating missingness
The complete, quality-controlled dataset featuring the cortical thickness of participants (N = 970) were obtained from the GitHub repository of (Sepehrband et al., 2018), which served as the gold standard for the present study (https://github.com/sepehrband/Mining_NeuroAnat). This study simulated different types of missing data in the neuroimaging datasets using the missing completely at random (MCAR) approach and the missing not at random (MNAR) approach (Dinov, 2018). This process is summarized in Figure 1. The MCAR approach removed percentages of data (from 10% to 60%) completely at random to create artificial datasets with missing values. The MNAR approach removed similar percentages (10% to 60%) from only a given, randomly-selected, part of the brain. The latter scenario aligns more with real-world cases of brain segmentation compared to the former. MNAR occurs when the segmentation error occurs more frequently in certain regions of the brain for all subjects. For example, if segmentation errors are mostly observed in the medial temporal lobe, then the output of the data form in to a MNAR. To ensure that the regional selection does not affect the imputation performance, the MNAR region-of-interest was reordered five times, which corroborated the initial observation.
Figure 1.
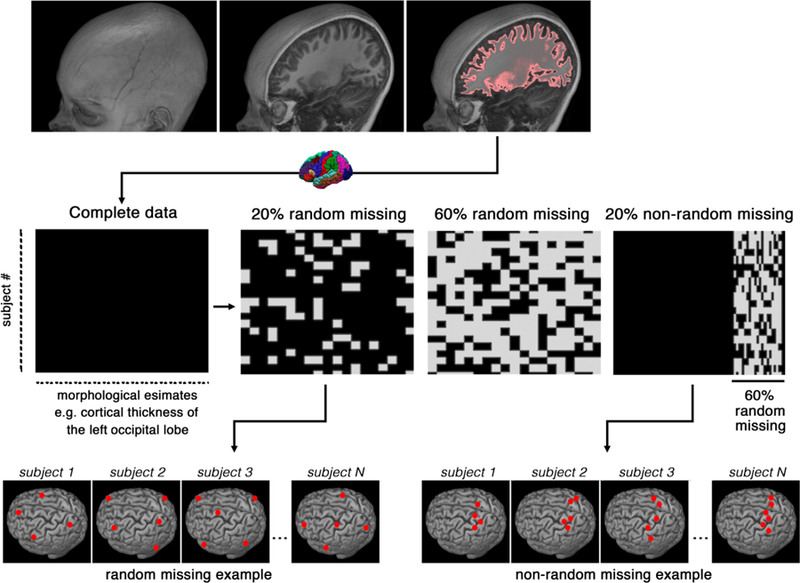
Schematic representation of the data preparation and types of missingness. The x-axis represents morphological features from FreeSurfer segmentation (e.g., cortical thickness, volume or surface area), the y-axis represents study subjects. Examples of random and non-random missingness are presented at the bottom row.
Data imputation techniques
Four data imputation techniques were selected to represent different statistical approaches, namely the “mean” method, k-nearest neighbors (KNN), the low-rank matrix approximation and random forest (RF).
“Mean” technique
The mean technique recovers missing value with the mean value of all available subjects. Mean imputation is among the simplest of imputation techniques and can defined as the replacement of a missing observation with the mean of the non-missing observations for that variable. Though the method has advantages (maintained sample size, ease of use) the variability in the data is reduced. With systematic bias introduced to the data, the standard deviations and variance estimates tend to be underestimated (Gómez-Carracedo et al., 2014).
K-Nearest Neighbor (KNN)
A type of supervised machine learning algorithm, K-nearest neighbors is a non-parametric method used for classification and regression predictive problems. As a non-parametric method, KNN does not make any assumptions about the data, and instead, models based on the observed dataset (Hastie et al., 2016). The method is used with databases in which data points are separated into several classes, which are then utilized in predicting the classification of a new data point. The process first begins with the calculation of the distance of a new data point to all other available data points and selects the K-nearest data points. The algorithm them assigns the new data point to the class to which the majority of K-data points belong, ultimately replacing the missing data with data created from K-nearest neighboring data. More specifically, for regression problems, KNN generates a new data point for the object based on the average of the values of its nearest K-neighbors. This method is used for its ease of interpretation, versatility, and quick results, while still achieving relatively competitive prediction results.
Here KNN uses nearest neighbor averaging principle for imputing the missing values through unsupervised regression. We found the K nearest neighbors using a Euclidean metric, confined to the columns for which that neuroanatomical feature is not missing. These nearest neighbors were then averaged to impute the missing data. The R package impute was used for KNN implementation. After testing a range of K values between 2 to 50, we observed that at K=20 the imputation performance reaches the peak plateau and therefore K of 20 was used for KNN implementation.
Low-rank matrix approximation
Low-rank approximation is a popular technique in image processing, machine learning, and data mining that compresses more compact representations of the data with limiting loss of information (Markovsky and Usevich, 2012). This is achieved by creating a matrix with a lesser rank compared to the original matrix. The rank of a matrix is the number of linearly independent columns, or vectors, with a low rank being the lowest number of linearly independent vectors. Low-rank matrix approximation is useful for dimension reduction, compression, classification, and regression tasks. Several algorithms achieve the low-rank approximation of matrices, include singular value decomposition, which provides the true rank and gives the best low-rank approximation of a matrix. Disadvantages of the technique involve computational demands involving large datasets.
The low-rank matrix approximation method was implemented using the softImpute R package (Mazumder et al., 2010). This technique fits a low-rank matrix approximation to a matrix with missing values via nuclear-norm regularization. The algorithm works similar to the traditional Expectation-Maximization technique, filling in the missing values with the current guess, and then solving the optimization problem on the complete matrix using a soft-thresholded singular value decomposition. Default parameter was used to implement this technique.
Non-parametric Missing Value Imputation using Random Forest
The RF-based imputation was implemented using missForest R package (Stekhoven and Bühlmann, 2011), which captures the complex interactions and nonlinear relations between variables and observations using a nonparametric, machine learning-based approach. RF is a non-parametric method used in performing both regression and classification tasks. This algorithm addresses missing values and outlier values by using dimensional reduction methods. missForest builds a RF model for each variable in the dataset and utilizes these individual models to build a powerful model consisting of multiple trees. This model is then used to predict missing values in the variable based on the observed values. Applicable to various data types, the algorithm can be used to impute continuous and/or categorical data (i.e., averages in the case of regression tasks) and yield an out-of-bag imputation error estimate without need of a test set. Advantages of this method is its ability to handle large datasets with high dimensionality and relatively high accuracy with large proportions of missing data. Disadvantages comprise of its regression range. Specifically, RF does not predict beyond the range in the training data and may be prone to over-fitting noisier datasets. For missForest implementation, parameters were set to the recommended values (Stekhoven and Bühlmann, 2011): number of trees = 100, number of iterations = 10, number of variables randomly sampled at each split = 8, which is the square root of the number of features (70 cortical measurements).
Evaluation criteria
Imputation methods were compared based on their imputation accuracy, with comparisons made between the original values of the gold standard and the imputed values of the artificial datasets. Specifically, the evaluation criteria of the data imputation techniques for both MCAR and MNAR assumptions comprised of the following: (1) Prediction error, which was measured by mean error, normalized root mean square error and the mean absolute error, and (2) Correlations with the gold standard. Correlation statistics was based on Pearson’s product moment correlation coefficient and follows a t-distribution with N-2 degrees of freedom if the samples follow independent normal distributions. Additionally, the relationship between sample size and accuracy of imputation for different percentages of missing data was examined. All the analysis was performed using R version 3.3.1.
Results
Figures 2 and 3 shows the comparisons of prediction error measures and correlational analyses when applying the data imputation techniques to the PNC dataset. As expected, imputation performance was weaker when a larger percentage of the data was missing. Normalized root mean square error (NRMSE) and mean absolute error (MAE) of all data imputation methods increased with higher percentages of missing values. In datasets generated under MCAR and MNAR assumptions, random forest (RF) outperformed all other methods under RMSE, MAE and correlation criteria. The effectiveness of RF compared to other techniques can be better appreciate when a high percentage of the data is missing. The amount of error found imputing with RF on datasets with 60% missing data was almost as low as the amount of error found imputing with low-rank Matrix Approximation (MA) on datasets with 20% missing data. Furthermore, RF demonstrates zero mean error measured in millimeters, which indicates that no systematic bias is observed in applying the technique.
Figure 2.
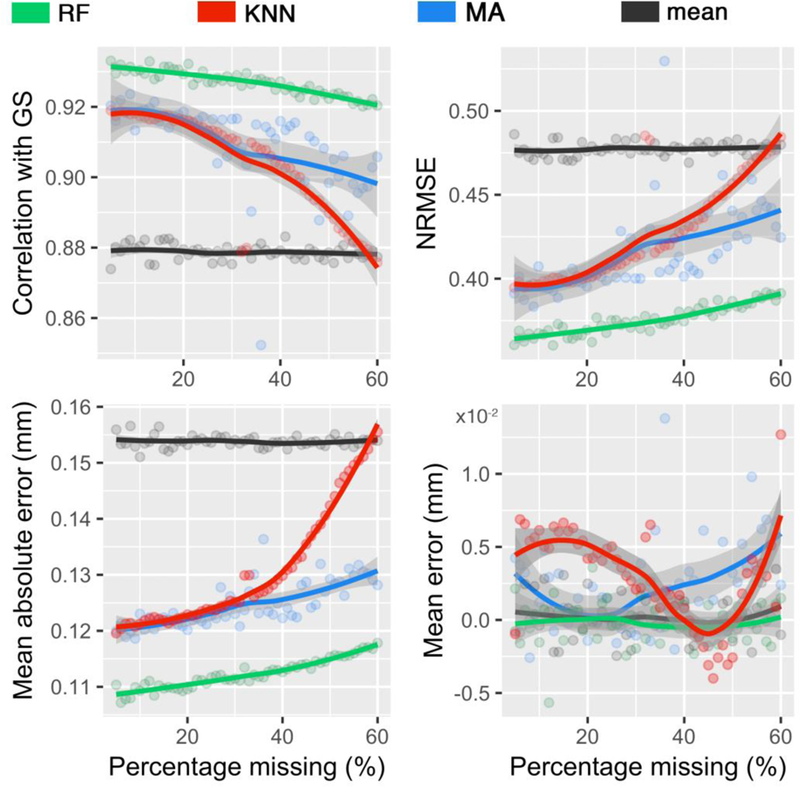
Performances of different imputation techniques, for a varying percentage of missing values based upon the missing completely at random (MCAR) assumption. Imputed values were compared against the gold standard (GS) values. Techniques include random forest (RF), k-nearest neighbors (KNN), low-rank matrix approximation (MA), and mean. The gray zone around each line displays 0.95 confident interval around at each percentage.
Figure 3.
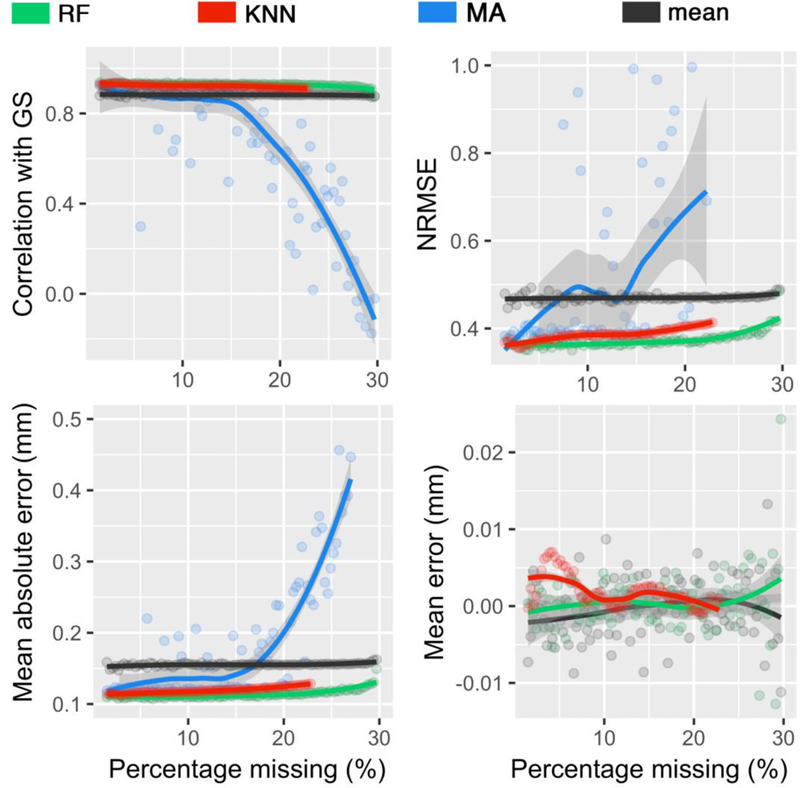
Performances of different imputation techniques, for a varying percentage of missing values based upon the missing not at random (MNAR) assumption. Imputed values were compared against the gold standard (GS) values. Techniques include random forest (RF), k-nearest neighbors (KNN), low-rank matrix approximation (MA), and mean. The gray zone around each line displays 0.95 confident interval around at each percentage.
The mean technique was found to be the least accurate method when applied to the MCAR and MNAR-generated PNC datasets, with the highest rates of error and weakest correlational strength. The exception to this was observed in the MA results of MNAR dataset when more than 15% of the data is missing (see blues line in Figure 3). Similarly, k-Nearest Neighbors (KNN) demonstrates similar, low performance to mean with increasing percentage of missing values in datasets generated under the MCAR assumption. However, KNN’s performance in MNAR datasets improved substantially, with RMSE, MAE, and ME rates similar to RF. It should be noted KNN did not converge when more than 80% of the data of a column is missing.
Figure 4 and 5 plots the correlation between the gold standard and the predicted values by the data imputation methods under the MCAR assumption and the MNAR assumptions, respectively. There were significant correlations between gold standard and predicted values for all techniques at 20% and 60% missingness under the MCAR assumption (p < 0.0001; detailed statistics are included in Tables 1). As expected, stronger correlations were found at 20% missing data across all techniques. Under both MCAR and MNAR, RF demonstrated the strongest correlations and was the least affected by sample size, further reinforcing its effectiveness above other data imputation techniques. Notably, quantization artifacts were introduced to the mean technique, given the univariate nature of this technique. A similar artifact was noted in KNN techniques at 60% missing under the MCAR assumption, as the search domain for the nearest neighbors becomes narrower with increased missingness in the data. Furthermore, RF and KNN data imputation techniques performed almost equally well on datasets under the MNAR function. In contrast, there were weak correlations between the gold standard and predicted values for MA and mean techniques. In particular, MA error variance dramatically increased when a high percentage of the data was missing or under MNAR assumption.
Figure 4.
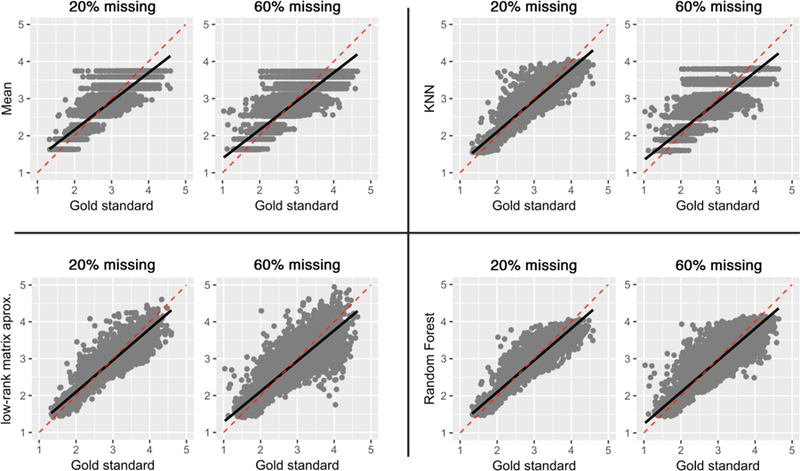
Correlations of predicted values with the gold standard under the missing completely at random (MCAR) assumption, at 20% and 60% missing data.
Figure 5.
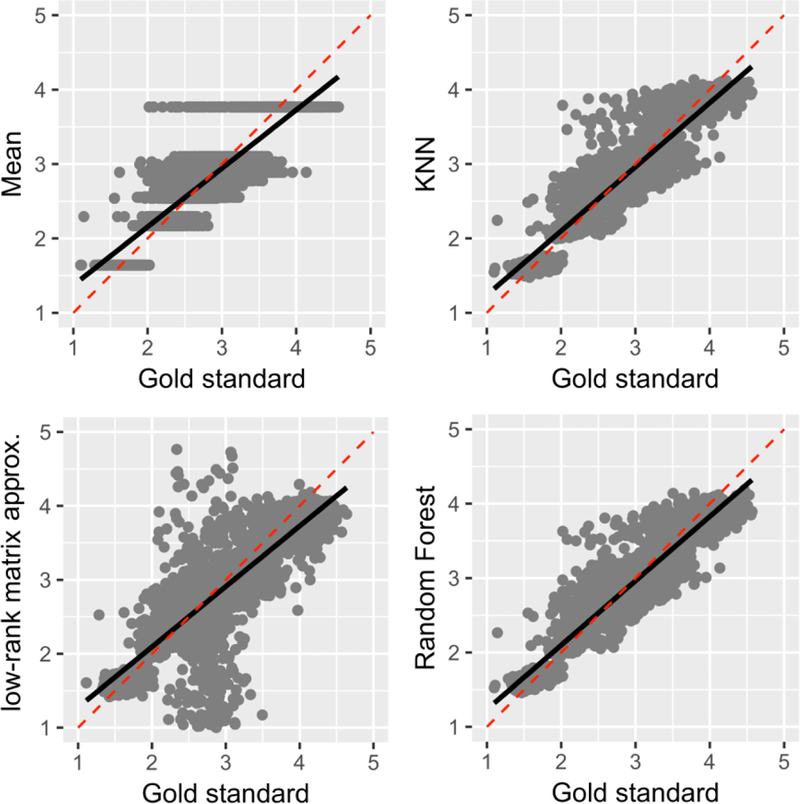
Correlations of predicted values with the gold standard under the missing not at random (MNAR) assumption at 20% missing in total (i.e., 60% of missing data was simulated under the MNAR assumption in 30% of the original data, making for 20% missing in total).
Table 1.
Pearson’s correlation of different techniques at 20% missing data with the gold standard under MCAR and MNAR assumptions. Degrees of freedom = 12220.
| missingness | Correlation (r) | t-statistics | confident interval | p-value | |
|---|---|---|---|---|---|
| Soft Impute | Random | 0.92 | 254.2 | 0.914 – 0.919 | < 0.0001 |
| Not random | 0.66 | 98.4 | 0.650 – 0.670 | < 0.0001 | |
| Mean | Random | 0.87 | 199.1 | 0.870 – 0.878 | < 0.0001 |
| Not random | 0.88 | 205.3 | 0.876 – 0.884 | < 0.0001 | |
| K-NN | Random | 0.92 | 255.1 | 0.914 – 0.920 | < 0.0001 |
| Not random | 0.92 | 256.4 | 0.915 – 0.920 | < 0.0001 | |
| RF | Random | 0.93 | 275.1 | 0.925 – 0.930 | < 0.0001 |
| Not random | 0.93 | 275.4 | 0.925 – 0.930 | < 0.0001 |
Tables 1 and 2 shows comparisons of the correlational analyses between the gold standard and the predicted values imputed by the methods under MCAR and MNAR assumptions. In corroboration with previous results, RF outperforms other methods and proves to be a substantial data imputation technique under both MCAR (r(12220) = .93, p < .0001) and MNAR (r(40738) = .92, p < .0001) assumptions. Notably, the strength of the correlation for RF is almost equally good in 20% missing data and 60% missing data.
Table 2.
Pearson’s correlation of different techniques at 60% missing data with the gold standard under MCAR assumptions. Degrees of freedom = 40738.
| Correlation (r) | t-statistics | confident interval | p-value | |
|---|---|---|---|---|
| MA | 0.73 | 213.3 | 0.720 – 0.730 | <0.0001 |
| Mean | 0.88 | 373.8 | 0.877 – 0.882 | <0.0001 |
| K-NN | 0.88 | 366.7 | 0.873 – 0.878 | <0.0001 |
| RF | 0.92 | 470.5 | 0.917 – 0.920 | <0.0001 |
Figure 6 plots the relationship between sample size and accuracy of the RF imputation technique measured by RMSE. Sample size positively and exponentially affects the performance of RF, with error decreasing exponentially as sample size increases. RF performance approaches the plateau around the sample sizes of 500 and becomes less reliable with small sample sizes (e.g., less than 250).
Figure 6.
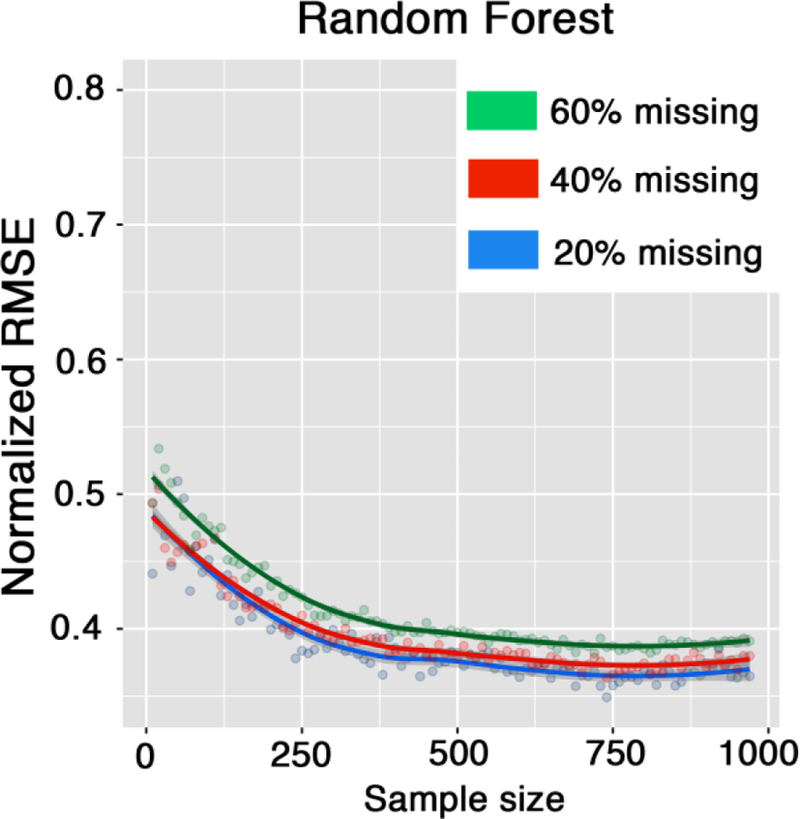
Sample size and imputation performance; plots show the influence of sample size on random forest performance for different percentages of missingness in the data.
Figure 7 demonstrates correlational analyses conducted with cortical area (left) and cortical volume (right) datasets. In alignment with the conclusions derived from the cortical thickness data, imputed values by the RF technique demonstrates the strongest correlations with the gold standard, outperforming other data imputation techniques.
Figure 7.
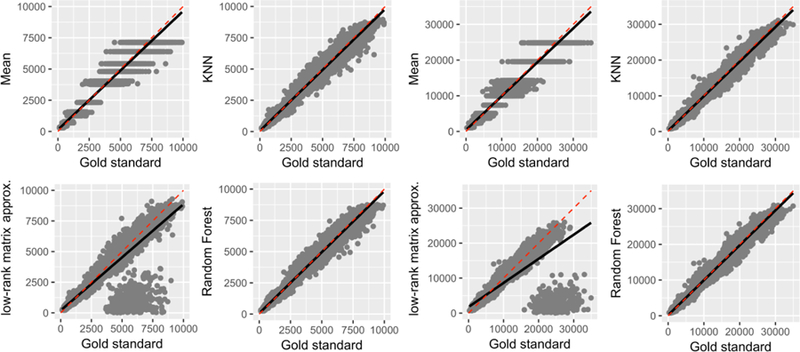
Correlations of predicted cortical area (left) and volume (right) values with the gold standard under the missing not at random (MNAR) assumption at 20% missing in total (i.e., 60% of missing data was simulated under the MNAR assumption in 30% of the original data, making for 20% missing in total). Note that low-rank matrix approximation technique failed to converge in number of instances.
Discussion
The current study provides insight into the effectiveness and reliability of data imputation technique as an alternative to the painstaking manual correction of the brain segmentation results of large neuroimaging datasets. Our proposed approach aims to substitute the correction step, assuming that the suboptimal segmentation results are identified and therefore, can be treated as missing values. Findings reveal data imputation to be effective in recovering missing values of morphological measures, specifically cortical thickness measures, via parameter estimation. Of the multivariate and univariate techniques, RF outperforms all other techniques with low prediction error measures (e.g., MAE of 0.11 mm) and strong significant correlations between the gold standard and imputed values (r=0.93, p<0.0001). Notably, RF worked best with higher percentages of missing data under both MNAR and MCAR assumptions, and its reliability is shown to be least affected by percentage of missing. This is in alignment with previous studies demonstrating RF as a substantial data imputation method (Hudak et al., 2008; Shah et al., 2014; Waljee et al., 2013).
The use of data imputation techniques can prove to be a useful cost-effective analysis in the biomedical field. Manual corrections of brain segmentation outputs can be time-consuming and costly. Consider a study cohort of 1000 subjects (e.g., the PNC dataset); if each manual correction took 30 minutes to an hour, trained staff could potentially take up to 60,000 minutes, to complete the correction once for all subjects. To decrease and quantify the inter-rater variability, the manual correction process is typically repeated, which can bring the total processing time up to 12,000 minutes (2000 hours) of trained staff time. Using the proposed technique, the correction step can be done under 4 minutes on a commercial personal computer. The current study focuses on cortical thickness data, as it is more prone to error compare to cortical volume and area measures, and, therefore, assumed to be more challenging to recover. Yet, results from similar analysis of other cortical measures were in complete corroboration with cortical thickness results (Figure 7).
Limitations of the study include its primary focus on a healthy cohort. The utility of multivariate techniques draws from the assumption that humans are neuroanatomically similar, which lends itself well to analyzing healthy, relatively similar cohorts. However, these analytical and statistical computational techniques may perform differently on populations with neurological disorders and abnormalities. The efficacy of the proposed approach in the presence of a neurological disorder is yet to be determined. In addition, this study employed the FreeSurfer program for brain segmentation. While results from other software could be slightly different (Eggert et al., 2012; Makowski et al., 2017; Morey et al., 2009; Perlaki et al., 2017; Tustison et al., 2014), it is independent of the overall goal of the study, which is to understand whether a data imputation technique can cover missing data in the brain segmentation results.
Indeed, we were not able compare all the existing imputation techniques. We selected four different techniques with distinct computation approach to imputation. The motivation for choosing these specific techniques were to cover a range of distinct statistical approaches including univariate (mean), analytical (low-rank matrix completion), inferential/computational (k-nearest neighbor), and statistical learning (RF). A number of other imputation techniques are available which are not included in this study (Gondara and Wang, n.d.; Graham, 2009; Schafer, 1999). For example, multiple imputation by chained equations (MICE) (Azur et al., 2011; Buuren and Groothuis-Oudshoorn, 2010) is a highly cited library that was not included given the similarity to the tested univariate approach.
It is challenging to identify the extent to which the quality of the individual data influences the imputation performance. Here low-quality data (27 MRIs) were excluded and a homogenous input data was assumed for the included subjects, meaning that the missingness is uniformly distributed across subjects. Therefore MRI-derived cortical measures were weighted equally when imputation techniques were applied. Inter-subject quality variance, derived from automated quality control techniques (Gedamu et al., 2008; Mortamet et al., 2009), could be additionally used as inclusion criteria or as weighting parameters for between group analysis. Image quality assurance and improvement are active research focuses (Waters et al., 2018), which may affect the imputation performance. For example, it has been shown that the filtering techniques, such as non-local mean filtering (Coupe et al., 2008; Manjón et al., 2010; Wiest-Daesslé et al., 2008), improves the reliability of brain tissue segmentation (Eskildsen et al., 2011). Such pre-processing could result into a smaller percentage of incorrect segmentation, subsequently lower percentage of missingness, resulting to a superior imputation performance.
Future work in data imputation may consider introducing other information and more modalities into the datasets, including demographic information, diffusion MRI, and functional MRI. Future studies may identify the most important units of information via regression analyses to result in the most effective data imputation. Recently, automated techniques for detecting FreeSurfer failures are proposed, namely FreeSurfer QA tool (https://surfer.nmr.mgh.harvard.edu/fswiki/QATools) and Qoala-T (Klapwijk et al., 2019). If combined with the proposed approach the entire quality assurance and correction may be automated. Finally, it is not known whether the proposed approach can be applied to the studies of neurological disorders. In the presence of a pathology non-uniform morphological alterations are expected, which could negatively affect multi-variate imputation reliability. We also anticipate imputation reliability may be different across neurological disorders given that they selectively affect brain regions. Therefore, unless validated, we do not recommend utilization of the proposed approach in neurological disorder studies.
Acknowledgement
This work was supported by the National Institute of Biomedical Imaging and Bioengineering (P41EB015922 and U54EB020406), the Eunice Kennedy Shriver National Institute of Child Health and Human Development (R00HD065832), the National Institute of Mental Health (R01MH094343; K01MH1087610), National Institute of Diabetes and Digestive and Kidney Diseases (P30DK089503), National Institute of Neurological Disorders and Stroke (P30DK089503), National Institute of Nursing Research (P20 NR015331). This work was partially supported by NSF grants 1734853, 1636840, 1416953, 0716055 and 1023115. Many colleagues, who are part of the Big Data Discovery Science (BDDS) community, contributed indirectly to this research. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIBIB, NICHD, NIMH, NIDDK, NINDS, NINR or NIH.
This study was conducted as part of the “Big Data Discovery and Diversity through Research Education Advancement and Partnerships (BD3-REAP)” Project funded by National Institutes of Health (NIH)-R25; Grant number is IR25MD010397–01. Data collection and sharing for this project was funded by the Philadelphia Neurodevelopmental Cohort (PNC) and the Pediatric Imaging, Neurocognition and Genetics Study (PING) (National Institutes of Health Grant RC2DA029475).
Footnotes
Information Sharing Statement
The raw data used in this article were obtained from the Philadelphia Neurodevelopmental Cohort (PNC) dataset, which can be downloaded at the website: https://www.nitrc.org/projects/pnc/. The processed, quality controlled data, which was used to evaluate imputation approach is described in this GitHub repository: https://github.com/sepehrband/Mining_NeuroAnat, and is available upon individual inquiry to the corresponding author, Farshid Sepehrband (farshid.sepehrband@loni.usc.edu). LONI pipeline can be accessed and downloaded at the website: http://pipeline.loni.usc.edu. The imputation techniques were implemented using available R libraries (including: impute: https://bioconductor.org/packages/release/bioc/html/impute.html, softImpute: https://cran.r-project.org/web/packages/softImpute/index.html, missForest: https://cran.r-project.org/web/packages/missForest/index.html).
Reference
- Azur MJ, Stuart EA, Frangakis C, Leaf PJ, 2011. Multiple imputation by chained equations: what is it and how does it work? Int. J. Methods Psychiatr. Res 20, 40–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buuren S. van, Groothuis-Oudshoorn K, 2010. mice: Multivariate imputation by chained equations in R. J. Stat. Softw 1–68. [Google Scholar]
- Coupe P, Yger P, Prima S, Hellier P, Kervrann C, Barillot C, 2008. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Trans. Med. Imaging 27, 425–441. doi: 10.1109/TMI.2007.906087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale A, Fischl B, Sereno MI, 1999. Cortical Surface-Based Analysis: I. Segmentation and Surface Reconstruction. Neuroimage 9, 179–194. doi: 10.1006/nimg.1998.0395 [DOI] [PubMed] [Google Scholar]
- Desikan RS, S?gonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ, 2006a. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980. doi: 10.1016/j.neuroimage.2006.01.021 [DOI] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ, 2006b. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980. doi: 10.1016/j.neuroimage.2006.01.021 [DOI] [PubMed] [Google Scholar]
- Dinov I, Lozev K, Petrosyan P, Liu Z, Eggert P, 2010. Neuroimaging Study Designs, Computational Analyses and Data Provenance Using the LONI Pipeline. PLoS One 5, e13070. doi: 10.1371/journal.pone.0013070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinov ID, 2018. Data Science and Predictive Analytics: Biomedical and Health Applications Using R Springer. [Google Scholar]
- Dinov ID, Van Horn JD, Lozev KM, Magsipoc R, Petrosyan P, Liu Z, MacKenzie-Graham A, Eggert P, Parker DS, Toga AW, 2009. Efficient, distributed and interactive neuroimaging data analysis using the LONI pipeline. Front. Neuroinform 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert M, 2004. Neuroanatomical markers for dyslexia: a review of dyslexia structural imaging studies. Neuroscientist 10, 362–371. doi: 10.1177/1073858404263596 [DOI] [PubMed] [Google Scholar]
- Eggert LD, Sommer J, Jansen A, Kircher T, Konrad C, 2012. Accuracy and reliability of automated gray matter segmentation pathways on real and simulated structural magnetic resonance images of the human brain. PLoS One 7, e45081. doi: 10.1371/journal.pone.0045081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eskildsen S, Coupé P, Fonov V, Ostergaard LR, Collins L, 2011. Effect of non-local means denoising on cortical segmentation accuracy with FACE, in: Organization for Human Brain Mapping 2011 Annual Meeting. [Google Scholar]
- Fischl B, 2012. FreeSurfer. Neuroimage 62, 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM, 2000. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci 97, 11050LP–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, Van Der Kouwe A, Killiany R, Kennedy D, Klaveness S, 2002. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron 33, 341–355. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJW, Makris N, Ségonne F, Quinn BT, Dale AM, 2004a. Sequence-independent segmentation of magnetic resonance images. Neuroimage 23, S69–S84. doi:DOI: 10.1016/j.neuroimage.2004.07.016 [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale A, 1999. Cortical Surface-Based Analysis: II: Inflation, Flattening, and a Surface-Based Coordinate System. Neuroimage 9, 195–207. doi: 10.1006/nimg.1998.0396 [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Ségonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM, 2004b. Automatically Parcellating the Human Cerebral Cortex. Cereb. Cortex 14, 11–22. doi: 10.1093/cercor/bhg087 [DOI] [PubMed] [Google Scholar]
- Gedamu EL, Collins DL, Arnold DL, 2008. Automated quality control of brain MR images. J. Magn. Reson. Imaging 28, 308–319. doi: 10.1002/jmri.21434 [DOI] [PubMed] [Google Scholar]
- Gómez-Carracedo MP, Andrade JM, López-Mahía P, Muniategui S, Prada D, 2014. A practical comparison of single and multiple imputation methods to handle complex missing data in air quality datasets. Chemom. Intell. Lab. Syst 134, 23–33. [Google Scholar]
- Gondara L, Wang K, n.d. Multiple Imputation Using Deep Denoising [Google Scholar]
- Graham JW, 2009. Missing data analysis: making it work in the real world. Annu. Rev. Psychol 60, 549–576. doi: 10.1146/annurev.psych.58.110405.085530 [DOI] [PubMed] [Google Scholar]
- Gronenschild EHBM, Habets P, Jacobs HIL, Mengelers R, Rozendaal N, van Os J, Marcelis M, 2012. The effects of FreeSurfer version, workstation type, and Macintosh operating system version on anatomical volume and cortical thickness measurements. PLoS One 7, e38234. doi: 10.1371/journal.pone.0038234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Balasubramanian N, Chu G, 2016. impute: Imputation for microarray data. R package version 1.48 0. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J, 2009. The Elements of Statistical Learning, Springer Series in Statistics doi: 10.1007/b94608 [DOI] [Google Scholar]
- Hudak AT, Crookston NL, Evans JS, Hall DE, Falkowski MJ, 2008. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ 112, 2232–2245. [Google Scholar]
- Klapwijk ET, Van De Kamp F, Van Der Meulen M, Peters S, Wierenga LM, 2019. Qoala-T: A supervised-learning tool for quality control of FreeSurfer segmented MRI data. Neuroimage [DOI] [PubMed] [Google Scholar]
- Lee MR, Bartholow BD, McCarthy DM, Pedersen SL, Sher KJ, 2015. Two alternative approaches to conventional person-mean imputation scoring of the Self-Rating of the Effects of Alcohol Scale (SRE). Psychol. Addict. Behav 29, 231–236. doi: 10.1037/adb0000015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long X, Liao W, Jiang C, Liang D, Qiu B, Zhang L, 2012. Healthy aging: an automatic analysis of global and regional morphological alterations of human brain. Acad. Radiol 19, 785–793. doi: 10.1016/j.acra.2012.03.006 [DOI] [PubMed] [Google Scholar]
- Luders E, Narr KL, Thompson PM, Rex DE, Woods RP, DeLuca H, Jancke L, Toga AW, 2006. Gender effects on cortical thickness and the influence of scaling. Hum. Brain Mapp 27, 314–324. doi: 10.1002/hbm.20187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makowski C, Beland S, Kostopoulos P, Bhagwat N, Devenyi GA, Malla AK, Joober R, Lepage M, Chakravarty MM, 2017. Evaluating accuracy of striatal, pallidal, and thalamic segmentation methods: Comparing automated approaches to manual delineation. Neuroimage doi: 10.1016/j.neuroimage.2017.02.069 [DOI] [PubMed] [Google Scholar]
- Manjón JV, Coupé P, Martí‐Bonmatí L, Collins DL, Robles M, 2010. Adaptive non‐local means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imaging 31, 192–203. [DOI] [PubMed] [Google Scholar]
- Markovsky I, Usevich K, 2012. Low rank approximation Springer. [Google Scholar]
- Mazumder R, Hastie T, Tibshirani R, 2010. Spectral regularization algorithms for learning large incomplete matrices. J. Mach. Learn. Res 11, 2287–2322. [PMC free article] [PubMed] [Google Scholar]
- Moon SW, Dinov ID, Kim J, Zamanyan A, Hobel S, Thompson PM, Toga AW, 2015. Structural neuroimaging genetics interactions in Alzheimer’s disease. J. Alzheimer’s Dis 48, 1051–1063. doi: 10.3233/JAD-150335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morey RA, Petty CM, Xu Y, Hayes JP, Wagner HR 2nd, Lewis DV, LaBar KS, Styner M, McCarthy G, 2009. A comparison of automated segmentation and manual tracing for quantifying hippocampal and amygdala volumes. Neuroimage 45, 855–866. doi: 10.1016/j.neuroimage.2008.12.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mortamet B, Bernstein MA, Jack CRJ, Gunter JL, Ward C, Britson PJ, Meuli R, Thiran J-P, Krueger G, 2009. Automatic quality assessment in structural brain magnetic resonance imaging. Magn. Reson. Med 62, 365–372. doi: 10.1002/mrm.21992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez DL, Matin N, Williams B, Tanev K, Makris N, LaFrance WCJ, Dickerson BC, 2018. Cortical thickness alterations linked to somatoform and psychological dissociation in functional neurological disorders. Hum. Brain Mapp 39, 428–439. doi: 10.1002/hbm.23853 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlaki G, Horvath R, Nagy SA, Bogner P, Doczi T, Janszky J, Orsi G, 2017. Comparison of accuracy between FSL’s FIRST and Freesurfer for caudate nucleus and putamen segmentation. Sci. Rep 7, 2418. doi: 10.1038/s41598-017-02584-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter M, Fischl B, 2011. Avoiding Asymmetry-Induced Bias in Longitudinal Image Processing. Neuroimage 57, 19–21. doi: 10.1016/j.neuroimage.2011.02.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter M, Rosas HD, Fischl B, 2010. Highly Accurate Inverse Consistent Registration: A Robust Approach. Neuroimage 53, 1181–1196. doi: 10.1016/j.neuroimage.2010.07.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter M, Schmansky NJ, Rosas HD, Fischl B, 2012. Within-Subject Template Estimation for Unbiased Longitudinal Image Analysis. Neuroimage 61, 1402–1418. doi: 10.1016/j.neuroimage.2012.02.084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB, 2004. Multiple imputation for nonresponse in surveys John Wiley & Sons. [Google Scholar]
- Satterthwaite TD, Connolly JJ, Ruparel K, Calkins ME, Jackson C, Elliott MA, Roalf DR, Hopsona R, Prabhakaran K, Behr M, Qiu H, Mentch FD, Chiavacci R, Sleiman PMA, Gur RC, Hakonarson H, Gur RE, 2016. The Philadelphia Neurodevelopmental Cohort: A publicly available resource for the study of normal and abnormal brain development in youth. Neuroimage 124, 1115–1119. doi: 10.1016/j.neuroimage.2015.03.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, Gur RE, 2014. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. Neuroimage 86, 544–553. doi: 10.1016/j.neuroimage.2013.07.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer JL, 1999. Multiple imputation: a primer. Stat. Methods Med. Res 8, 3–15. doi: 10.1177/096228029900800102 [DOI] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B, 2004. A hybrid approach to the skull stripping problem in MRI. Neuroimage 22, 1060–1075. doi:DOI: 10.1016/j.neuroimage.2004.03.032 [DOI] [PubMed] [Google Scholar]
- Segonne F, Pacheco J, Fischl B, 2007. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE Trans Med Imaging 26, 518–529. [DOI] [PubMed] [Google Scholar]
- Sepehrband F, Lynch KM, Cabeen RP, Gonzalez-Zacarias C, Zhao L, D’Arcy M, Kesselman C, Herting MM, Dinov ID, Toga AW, 2018. Neuroanatomical morphometric characterization of sex differences in youth using statistical learning. Neuroimage 172, 217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah AD, Bartlett JW, Carpenter J, Nicholas O, Hemingway H, 2014. Comparison of random forest and parametric imputation models for imputing missing data using MICE: a CALIBER study. Am. J. Epidemiol 179, 764–774. doi: 10.1093/aje/kwt312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC, 1998. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imaging 17, 87–97. doi: 10.1109/42.668698 [DOI] [PubMed] [Google Scholar]
- Stekhoven DJ, Bühlmann P, 2011. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics 28, 112–118. [DOI] [PubMed] [Google Scholar]
- Toga AW, Foster I, Kesselman C, Madduri R, Chard K, Deutsch EW, Price ND, Glusman G, Heavner BD, Dinov ID, Ames J, Van Horn J, Kramer R, Hood L, 2015. Big biomedical data as the key resource for discovery science. J. Am. Med. Informatics Assoc 22, 1126–1131. doi: 10.1093/jamia/ocv077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torri F, Dinov ID, Zamanyan A, Hobel S, Genco A, Petrosyan P, Clark AP, Liu Z, Eggert P, Pierce J, Knowles JA, Ames J, Kesselman C, Toga AW, Potkin SG, Vawter MP, Macciardi F, 2012. Next generation sequence analysis and computational genomics using graphical pipeline workflows. Genes (Basel) 3, 545–575. doi: 10.3390/genes3030545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison NJ, Cook PA, Klein A, Song G, Das SR, Duda JT, Kandel BM, van Strien N, Stone JR, Gee JC, Avants BB, 2014. Large-scale evaluation of ANTs and FreeSurfer cortical thickness measurements. Neuroimage 99, 166–179. doi: 10.1016/j.neuroimage.2014.05.044 [DOI] [PubMed] [Google Scholar]
- Vijayakumar N, Allen NB, Youssef G, Dennison M, Yucel M, Simmons JG, Whittle S, 2016. Brain development during adolescence: A mixed-longitudinal investigation of cortical thickness, surface area, and volume. Hum. Brain Mapp 37, 2027–2038. doi: 10.1002/hbm.23154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waljee AK, Mukherjee A, Singal AG, Zhang Y, Warren J, Balis U, Marrero J, Zhu J, Higgins PD, 2013. Comparison of imputation methods for missing laboratory data in medicine. BMJ Open 3 doi: 10.1136/bmjopen-2013-002847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters AB, Mace RA, Sawyer KS, 2018. Identifying errors in Freesurfer automated skull stripping and the incremental utility of manual intervention [DOI] [PubMed] [Google Scholar]
- Wiest-Daesslé N, Prima S, Coupé P, Morrissey SP, Barillot C, 2008. Rician noise removal by non-local means filtering for low signal-to-noise ratio MRI: Applications to DT-MRI, in: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) doi: 10.1007/978-3-540-85990-1-21 [DOI] [PMC free article] [PubMed] [Google Scholar]


