A method (DeepRes) is presented to estimate a new local quality measure for 3D cryoEM maps that adopts the form of a ‘local resolution’ type of information. DeepRes is fully automatic and parameter-free and avoids the issues of most current methods, such as their insensitivity to enhancements owing to B-factor sharpening, among others.
Keywords: DeepRes, electron microscopy, single-particle analysis, local resolution, 3D reconstruction and image processing, single-particle cryoEM, structure determination, cryo-electron microscopy
Abstract
In this article, a method is presented to estimate a new local quality measure for 3D cryoEM maps that adopts the form of a ‘local resolution’ type of information. The algorithm (DeepRes) is based on deep-learning 3D feature detection. DeepRes is fully automatic and parameter-free, and avoids the issues of most current methods, such as their insensitivity to enhancements owing to B-factor sharpening (unless the 3D mask is changed), among others, which is an issue that has been virtually neglected in the cryoEM field until now. In this way, DeepRes can be applied to any map, detecting subtle changes in local quality after applying enhancement processes such as isotropic filters or substantially more complex procedures, such as model-based local sharpening, non-model-based methods or denoising, that may be very difficult to follow using current methods. It performs as a human observer expects. The comparison with traditional local resolution indicators is also addressed.
1. Introduction
Single-particle cryo-electron microscopy (cryoEM) has become a powerful technique for the three-dimensional (3D) structure determination of biological molecules. Recently, advances in instrumentation and software have dramatically improved the potential of single-particle cryoEM, generating density maps with a high level of detail. The quality of the map thus obtained is usually evaluated in terms of resolution. Different measures have been proposed to determine map resolution in cryoEM (Sorzano et al., 2017 ▸). Currently, the most-used definition is based on the Fourier shell correlation (FSC) curve (Saxton & Baumeister, 1982 ▸; Saxton, 1978 ▸; Harauz & van Heel, 1986 ▸). However, resolution is not a concept that can be uniquely defined. From the point of view of the microscope, we may define the resolution based on optics considerations (for instance, the Rayleigh criterion determines the minimum spatial separation between two points so that the two points can still be separated). From the point of view of signal processing, we may define the resolution in terms of some form of signal and noise comparison [for instance, the frequency at which there is more signal than noise; this is used in both the ResMap (Kucukelbir et al., 2014 ▸) and MonoRes (Vilas et al., 2018 ▸) approaches]. From the algorithmic reproducibility point of view, we may define the resolution as the maximum frequency at which the correlation between two bandpass-filtered versions of two reconstructions performed with the same algorithm but applied to two independent data sets is above a given threshold (this is the definition of the Fourier shell correlation). Or, from the point of view of the nature of the objects being visualized, for instance, we may define the resolution as the maximum frequency at which the features in the reconstructed object are consistent with the features observed in biological macromolecules filtered at that frequency. All of these definitions make sense and they all assess the quality of the reconstruction by attending to different aspects of the problem. In addition to this ambiguity, all of the methods described above require the choice of a threshold for the measured quantity (cross-correlation, signal-to-noise ratio etc.), which has also caused long debates on the issue. Additionally, it is already well known that the quality of a reconstruction depends on the region of the macromolecule (some regions are better resolved than others; Cardone et al., 2013 ▸; Kucukelbir et al., 2014 ▸; Vilas et al., 2018 ▸) and even on the direction (some directions are better resolved than others owing to an uneven angular distribution; Sorzano et al., 2001 ▸; Unser et al., 2005 ▸), although we will not consider directional effects in this work.
One of the first methods for considering the local characteristics of the map for calculation of the resolution was BlocRes (Cardone et al., 2013 ▸). This method calculates the resolution based on the FSC but using a moving window on the maps. In addition to having the limitations that are inherent to use of the FSC (focused on reproducibility only, lack of sensitivity to isotropic, nonvanishing filters etc.), BlocRes incorporates the variable of the window size.
The most-used method to date for local resolution estimation is ResMap (Kucukelbir et al., 2014 ▸), which is based on the detection of a sinusoidal wave above the noise level for each point on the map. Based on a similar principle, of detecting energy at different frequencies above noise, but on a totally different signal-processing approach, MonoRes (Vilas et al., 2018 ▸) was proposed. MonoRes is based on the use of monogenic signals, extracting the monogenic amplitude at different frequencies and comparing it with the monogenic amplitude of the noise at the corresponding frequency; a directional local resolution extension of MonoRes has also been proposed (manuscript under review). The main limitation of these two latter methods is that they require an estimate of the noise variance.
On the other hand, it is very common to introduce some form of map enhancement, from global B-factor correction to more complex post-processing operations such as model-based or non-model-based sharpening [as in LocScale (Jakobi et al., 2017 ▸) and LocalDeblur (Ramírez-Aportela et al., 2019 ▸), respectively] or the introduction of nonlinear noise-suppression operations, as in Xmipp Highres (Sorzano et al., 2018 ▸). In all of these cases, our current resolution indicators lose effectivity: in the former case (B-factor correction) because they are insensitive to this operation (see the supporting information and Supplementary Fig. S1) and in the latter case because the estimation of the level of noise in the map is also affected by these operations, impacting on the very basic mathematical framework on which they are based (operationally; if still used in this way this weakness translates into an overestimation of resolution).
However, it is certainly non-intuitive that our current resolution estimations are insensitive to operations that are aimed to increase the quality of our maps, even if sometimes these enhancements are mostly targeted to help the modeling task. Indeed, visibly different maps can present the same resolution as estimated by methods based either on the FSC or on some form of signal-to-noise ratio (SNR; see the supporting information and Supplementary Fig. S1). Therefore, we wanted to derive another ‘local quality measure’, formally of the type of a local resolution, that could be used in these cases and that indeed could ‘follow’ the results of these enhancing operations (i.e. it produces a better value when the map is supposed to be better by the application of some post-processing). Therefore, our primary motivation in developing DeepRes was to reconcile ‘what you see’ when working with a map with ‘what you get’ in terms of the calculated value of local resolution. Note that currently two maps, one sharpened and the other unsharpened, may have the same local resolution estimation but are certainly not judged as being the same by a human observer. An additional, more technical, motivation for our work on DeepRes was to have a way to calculate local resolution in those situations in which we did not have a proper noise estimation (as could be the case, for instance, when the reconstruction algorithm incorporates some noise-suppression prior, as in Xmipp Highres; Sorzano et al., 2018 ▸).
Naturally, a logical question for the cryoEM practioner is ‘and which is the true, final, local resolution?’. We will present our work in this area, which clearly indicates that some general consensus can indeed be achieved, even when working with very different ‘definitions’ of what resolution is.
In brief, in this work we introduce a new algorithm (DeepRes) for measuring the local resolution of biological macromolecules reconstructed by cryoEM. It is based on the comparison of the features of biological macromolecules observed at a particular resolution with the features observed in the map under evaluation. Our proposal makes use of deep learning. Deep learning is a new area of artificial intelligence that has recently emerged (Bengio, 2009 ▸) and that has already been successfully applied in cryoEM with excellent results (Wagner et al., 2018 ▸; Su et al., 2018 ▸). Avramov and coworkers have demonstrated that deep-learning models can learn resolution patterns from cryoEM density maps (Avramov et al., 2019 ▸). Our newly proposed method, DeepRes, overcomes some of the limitations of current local resolution methods such as their counter-intuitive insensitivity to isotropic, nonvanishing filters (B-factor correction) and many sharpening algorithms (for example LocalDeblur), and their inability to estimate the resolution when there is no region to estimate the noise distribution (a single masked reconstruction) or when the reconstruction method strongly suppresses noise in the reconstruction (for example Xmipp Highres; Sorzano et al., 2018 ▸).
2. Methods
The DeepRes algorithm is based on a convolutional neural network (CNN). The idea of our method is ‘to teach’ a neural network the characteristics of density maps filtered at different frequencies, creating a general network that can be used to estimate the local resolution of cryoEM maps.
2.1. Training data set
A set of 15 000 3D nonredundant macromolecule structures (including proteins and nucleic acids; Levy et al., 2006 ▸) was selected for the training of our 3D convolutional neural networks (CNNs). Each atomic model was simulated as a 3D density map, calling the function xmipp_volume_from_pdb from the Xmipp package (de la Rosa-Trevín et al., 2013 ▸; Sorzano et al., 2015 ▸), which uses electron atomic scattering factors. Two data sets were prepared with the aim of studying different resolution ranges: (i) 3D density maps simulated with a sampling rate of 1.0 Å per voxel (data set 1) and (ii) simulated maps with a sampling rate of 0.5 Å per voxel (data set 2). A description in more concrete terms is given below.
Data set 1. For each 3D map, a filter bank was created so that it was low-pass filtered to frequencies of between 2.5 and 13.0 Å (every 0.1 Å) with a raised cosine of 0.02 (in normalized units) using the xmipp_transform_filter function.
Data set 2. As data set 1, but in this case maps were low-pass filtered to frequencies of between 1.5 and 6.0 Å (every 0.1 Å) with a raised cosine of 0.02 (normalized units). The reason for creating this second data set was to analyze maps at very high resolution.
In order to locally study these maps, each filtered map was divided into boxes of 13 × 13 × 13 voxels, which correspond to edge lengths of 13 and 6.5 Å for data set 1 and data set 2, respectively. The density values of each box were normalized to have a unit norm and guarantee uniform intensity ranges of all filtered maps. Millions of simulated map boxes and their corresponding resolution labels were then used to train the neural network.
2.2. Training of the DeepRes network
DeepRes trains a convolutional neural network (CNN) for the automatic estimation of local quality. The CNN was implemented using the Keras 2.0.2 (http://keras.io) Python deep-learning library with the TensorFlow (Abadi et al., 2016 ▸) backend. Our CNN contained a convolutional layer that applied 32 13 × 13 × 13 filters (many other architectures were tested with similar results, but this was the simplest one tested, which was why we selected it), followed by a dense layer with 512 neurons and the output dense layer with just one neuron reporting the local quality label (note that we are addressing DeepRes as a regression analysis, rather than as a classification). We used the rectified linear unit (RELU) as an activation function. The padding ‘same’ was used following each layer to preserve the map dimensions. Dropout with a probability of 0.25 was applied to the convolutional layer output to regularize the network and avoid overfitting. To optimize the network parameters, we used the Adam optimizer (Kingma & Ba, 2014 ▸), which is an improved version of stochastic gradient descent. The optimizer determines how the gradient of the loss function is used to update the network parameters. In DeepRes, the loss function that is minimized is ‘mean_squared_error’.
2.3. DeepRes input and output
The algorithm requires as input a 3D cryoEM density map and a mask enclosing the macromolecule. These input maps are rescaled to a pixel size of 1.0 or 0.5, depending on the CNN that is going to be used. The map is then sampled in a sliding window of 13 × 13 × 13 voxels. Finally, the resolution estimate is assigned to the voxel located at the center of the cube.
2.4. Code availability
DeepRes is publicly available from Xmipp (de la Rosa-Trevín et al., 2013 ▸; http://xmipp.cnb.csic.es) in the development branches https://github.com/I2PC/xmipp/ and https://github.com/I2PC/scipion-em-xmipp/ (these branches will eventually become the next release of Xmipp), and is integrated into the image-processing framework Scipion (de la Rosa-Trevín et al., 2016 ▸; http://scipion.cnb.csic.es). A tutorial on how to use DeepRes can be found at https://github.com/I2PC/scipion-em-xmipp/wiki/DeepRes-local-resolution.
3. Results
Different visualization options have been implemented into Scipion (de la Rosa-Trevín et al., 2013 ▸) to analyze the results [for example, the local resolution map, a resolution histogram, colored slices of the resolution map and the display of the original map in UCSF Chimera (Pettersen et al., 2004 ▸) colored according to the obtained resolution values]. The validation of DeepRes was initially carried out through simulated maps for different scenarios. This exercise allows us to evaluate the method using maps for which the local resolution values are known a priori. The method was subsequently applied to different experimental maps and the results were compared using current methods of estimating local resolution (ResMap, MonoRes and BlocRes). For all methods, the same mask and default parameters were used. In ResMap, manual pre-whitening was performed to the best of our knowledge.
3.1. Tests with simulated data
In a first step to test the performance of DeepRes, the method was applied to two simulated maps that were not employed for training and for which local resolutions were known. For the first case we used the atomic model of the 39 kDa human cartilage glycoprotein tetramer (HCGP39; PDB entry 1hjv; Houston et al., 2003 ▸). For this structure, we generated a map with a sampling rate of 1.0 Å per pixel using xmipp_volume_from_pdb (Sorzano et al., 2015 ▸). Each monomer in the structure was selected and low-pass filtered at different frequencies of 3, 5, 7 and 9 Å with a raised cosine of 0.02 (in normalized units). After this, Gaussian noise with zero mean and a standard deviation (SD) of 0.08 was added.
The results of the DeepRes application in this test are shown in Fig. 1 ▸(a). Our method is capable of capturing the different characteristics within the map and provides a resolution map with values that match the cutoff frequencies. In particular, the median values obtained with DeepRes were 3.2, 5.0, 7.1 and 8.9 Å, with SDs of 0.2, 0.3, 0.5 and 0.5 Å, respectively.
Figure 1.
DeepRes results for simulated maps. (a) DeepRes resolution map from the simulated map of the 39 kDa human cartilage glycoprotein tetramer filtered at 3, 5, 7 and 9 Å (PDB entry 1hjv). (b) DeepRes resolutions maps from two simulated maps of φ29 pRNA (PDB entry 3r4f) filtered at 2 and 4 Å.
The second simulated test considered the crystal structure of the φ29 pRNA prohead-binding domain (PDB entry 3r4f; Ding et al., 2011 ▸). This case also allows us to check whether the method works well for nucleotides. As before, the atomic model was converted into a density volume with a sampling rate of 0.5 Å per pixel. Two low-pass-filtered maps were then generated at frequencies of 2 and 4 Å with a raised cosine of 0.02. Noise was added as in the previous case.
Fig. 1 ▸(b) shows that DeepRes produces quality measures close to the expected resolution values. For the map filtered at 2 Å the median resolution value estimated was 2.3 Å with a standard deviation (SD) of 0.3 Å [Fig. 1 ▸(b), blue], while for the map filtered at 4 Å the median resolution was 4.0 Å with an SD of 0.3 Å [Fig. 1 ▸(b), yellow].
The results obtained for the simulated data confirm that DeepRes estimates local resolutions that are very close to the expected theoretical values and validate the applicability of our method for macromolecules that contain both amino acids and nucleotides.
Additionally, the second simulated map (φ29 pRNA) was also used to investigate the basis of our method. Both MonoRes and ResMap are based on a comparison between the energy of the signal and the energy of the noise. To study whether DeepRes was only taking into account the frequential energy of the map, without any further connection to the underlying macromolecular structure, a test based on Fourier phase randomization was carried out. Thus, in the map filtered at 2 Å, the phases were randomized beyond 4 Å. The results of DeepRes for the original map and the phase-randomized map are shown in Supplementary Fig. S2. Clearly, when randomization is applied, DeepRes shifts the resolution values to 4 Å. These results show that DeepRes not only takes into account the energy but also detects the difference in texture in the analyzed maps.
3.2. Results on experimental maps
Once the effectiveness of our method for estimating local resolution with simulated maps had been proven, we applied DeepRes to five cryoEM maps and the results were compared using MonoRes, ResMap and BlocRes (Fig. 2 ▸ and Supplementary Fig. S3). The five analyzed maps (enterovirus D68, the PolIIIα–clamp–exonuclease–θ DNA complex, capsaicin receptor TRPV1, HSP104DWB and CMG helicase) were obtained from the EMDB (EMDB entries EMD-9631, EMD-4141, EMD-5778, EMD-0376 and EMD-3320, respectively) and correspond to maps that had been subjected to global B-factor (Rosenthal & Henderson, 2003 ▸) post-processing in RELION (Scheres, 2012 ▸).
Figure 2.
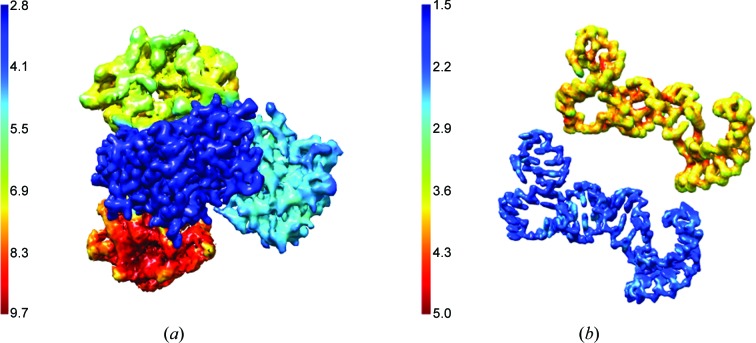
Local resolution results for experimental maps. The resolution histograms obtained by the different methods (MonoRes, ResMap, BlocRes and DeepRes) and the resolution map determined with DeepRes are shown for (a) enterovirus D68 (EMDB entry EMD-9631), (b) the PolIIIα–clamp–exonuclease–θ DNA complex (EMDB entry EMD-4141) and (c) capsaicin receptor TRPV1 (EMDB entry EMD-5778).
3.2.1. Enterovirus D68
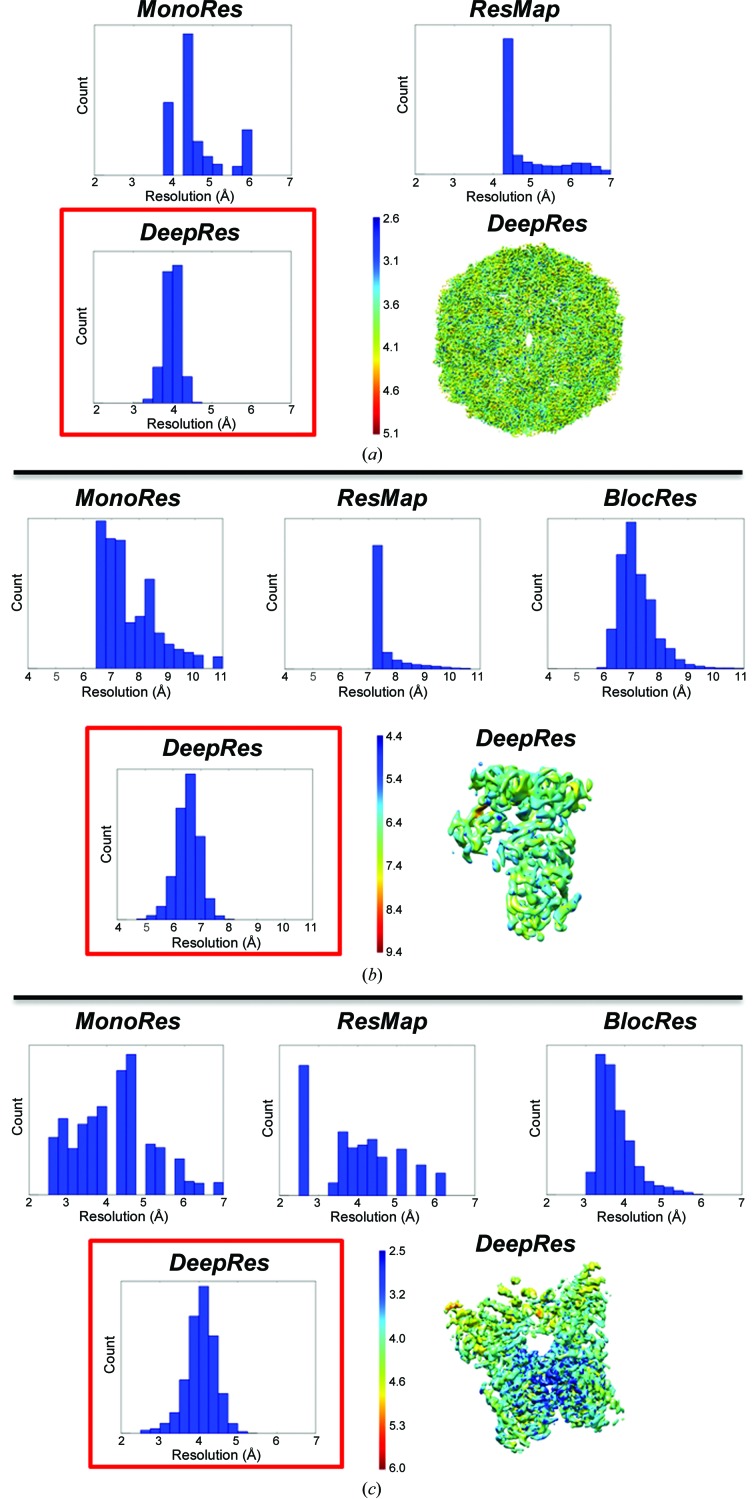
The first experimental case analyzed the map of enterovirus D68 (EMDB entry EMD-9631; Zheng et al., 2019 ▸) with a resolution of 4.0 Å as reported by the gold-standard FSC of 0.143. The resolution histograms obtained using DeepRes, MonoRes and ResMap are shown in Fig. 2 ▸(a). BlocRes was not applied in this test because the half maps were not deposited in the EMDB. DeepRes [red square in Fig. 2 ▸(a)] estimated the resolution values in a narrow range from 3.4 to 4.6 Å, with the median at 4.0 Å and an SD of 0.2 Å. This median resolution is in total agreement with the reported resolution of 4.0 Å (Table 1 ▸). The resolution map obtained with DeepRes is represented using UCSF Chimera in Fig. 2 ▸(a). The distribution with MonoRes ranges from 4.0 to 6.0 Å, with the median at 4.5 Å and an SD of 0.6 Å. Using ResMap a peak of resolution was obtained at 4.4 Å and values extended up to 7.0 Å, presenting a median resolution of 4.4 Å and an SD of 0.8 Å.
Table 1. Summary of median resolution for the experimental cases.
| EMDB code | FSC (Å) | MonoRes median (Å) | ResMap median (Å) | BlocRes median (Å) | DeepRes sharpened median (Å) | DeepRes unsharpened median (Å) |
|---|---|---|---|---|---|---|
| EMD-9631 | 4.0 | 4.5 ± 0.6 | 4.4 ± 0.8 | — | 4.0 ± 0.2 | — |
| EMD-4141 | 6.7 | 7.5 ± 1.1 | 7.4 ± 0.6 | 7.0 ± 0.7 | 6.5 ± 0.4 | — |
| EMD-5778 | 3.4 | 4.3 ± 1.1 | 4.0 ± 1.0 | 3.7 ± 0.5 | 4.1 ± 0.14 | — |
| EMD-0376 | 9.3 | 11.7 ± 2.3 | 10.2 ± 0.8 | — | 9.3 ± 1.2 | — |
| EMD-3320 | 10.2 | — | — | — | 10.1 ± 1.7 | — |
| EMD-3407 | 3.3 | 4.0 ± 1.1 | 3.8 ± 1.5 | — | 3.5 ± 0.4 | 5.0 ± 0.8 |
| EMD-9235 | 3.8 | 4.5 ± 1.8 | 4.9 ± 1.8 | 4.0 ± 1.0 | 4.4 ± 0.4 | 7.4 ± 1.0 |
| EMD-2660 | 3.2 | 4.0 ± 2.7 | 4.6 ± 1.7 | 3.6 ± 1.1 | 3.8 ± 0.9 | 6.3 ± 1.3 |
| EMD-0258 | 4.0 | — | — | — | 4.0 ± 0.3 | 5.5 ± 0.5 |
| EMD-7550 | 2.4 | — | — | — | 2.6 ± 0.4 | 3.2 ± 0.3 |
3.2.2. PolIIIα–clamp–exonuclease–θ DNA
The second case corresponds to the PolIIIα–clamp–exonuclease–θ DNA complex (EMDB entry EMD-4141; Fernandez-Leiro et al., 2017 ▸). The reported resolution for this map was 6.7 Å (gold-standard FSC of 0.143). The results obtained using the different methods are shown in Fig. 2 ▸(b). With MonoRes, the resolution range obtained ranges from 6.6 to 11 Å, with a median of 7.5 Å and an SD of 1.1 Å, although the highest peak in the distribution is between 6.6 and 7.4 Å. ResMap estimated a resolution peak at 7.4 Å with an SD of 0.6 Å, while the histogram of resolutions calculated with BlocRes is centered at 7.0 Å with an SD of 0.7 Å. The histogram representing the resolution values obtained using DeepRes is centered at 6.7 Å, with a median of 6.5 Å and an SD of 0.4 Å. As in the previous case, the median resolution of DeepRes is close to the reported FSC resolution (Table 1 ▸).
3.2.3. Capsaicin receptor TRPV1
The third experimental map used corresponds to the well known membrane protein TRPV1 (EMDB entry EMD-5778; Liao et al., 2013 ▸). The reported resolution for this density map was 3.4 Å at the gold-standard FSC of 0.143. This is an interesting case of a membrane protein with a wide range of local resolutions. We took special care to mask out the membrane and work only with the macromolecular complex, which is certainly a general procedure, but in our case it was especially important since DeepRes was only trained with proteins. The results and the comparison with current methods are shown in Fig. 2 ▸(c). DeepRes reported a median resolution of 4.1 Å with an SD of 0.4 Å, while these values were 4.3 ± 1.1, 4.0 ± 1.0 and 3.7 ± 0.5 Å for MonoRes, ResMap and BlocRes, respectively. As expected, DeepRes detected a high-resolution area corresponding to the center of the transmembrane region (<3.8 Å) and a lower resolution area on the ankyrin motif (>4.7 Å).
3.2.4. Low-resolution maps: HSP104DWB and CMG helicase
Two cases were used to validate the use of DeepRes with low-resolution maps. The first corresponds to the HSP104DWB map (EMDB entry EMD-0376; Lee et al., 2019 ▸) with a reported resolution of 9.3 Å at the gold-standard FSC of 0.143 [Supplementary Fig. S3(a)]. The histogram obtained with MonoRes shows resolutions above 8 Å, with a maximum at 9.6 Å and a median of 11.7 Å (Table 1 ▸), while the resolutions obtained with ResMap are above 10 Å with a median of 10.2 Å. The highest number of values obtained with DeepRes are between 8 and 11 Å resolution, with a median resolution of 9.3 Å and an SD of 1.2 Å (Table 1 ▸), which matches the FSC resolution reported for the map.
The second case corresponds to the CMG helicase map (EMDB entry EMD-3320; Abid Ali et al., 2016 ▸) with a reported resolution of 10.2 Å at the gold-standard FSC of 0.143 [Supplementary Fig. S3(b)]. In this case, the current methods could not be applied because the deposited map was masked and free of noise. The median resolution obtained by DeepRes is 10.1 Å with an SD of 1.7 Å (Table 1 ▸), which is in agreement with the resolution reported by the authors.
3.3. Local resolutions from unsharpened and sharpened maps
One of the main limitations of the current methods is that they are not able to cope with situations such as differentiating between unsharpened and sharpened maps. Indeed, both the FSC as well as the local resolution determined by the monogenic signal (Vilas et al., 2018 ▸) and the local sinusoids versus noise (Kucukelbir et al., 2014 ▸) are insensitive to isotropic, nonvanishing filters (Unser et al., 2005 ▸; Sorzano et al., 2017 ▸; see Supplementary Fig. S1). In particular, when a global B-factor-based sharpening is applied, all spectral components at a given radial frequency are modified proportionally (Unser et al., 2005 ▸) and therefore the statistically detected frequency above the noise level will remain invariant.
However, resolution changes after applying B-factor sharpening can be detected using DeepRes. Other maps that will benefit from DeepRes are those obtained with methods that modify the signal or minimize the noise level [for example, LocalDeblur (Ramírez-Aportela et al., 2019 ▸) or Xmipp Highres (Sorzano et al., 2018 ▸)]. Resolution changes determined with DeepRes before and after map sharpening are exemplified in Fig. 3 ▸ and Supplementary Fig. S4 with three different experimental cases, Escherichia coli GroEL, rabbit 80S ribosome and Plasmodium 80S ribosome maps, and in Fig. 4 ▸ with both the KdpFABC complex and rabbit muscle aldolase.
Figure 3.
Changes in local resolution between unsharpened maps and sharpened maps detected with DeepRes. Histograms determined with MonoRes, ResMap and BlocRes for unsharpened maps (left), the histograms determined for unsharpened and sharpened maps (center) with DeepRes and the resolution maps for unsharpened and sharpened maps (right) of (a) E. coli GroEL (EMDB entry EMD-3407) and (b) the rabbit 80S ribosome (EMDB entry EMD-9235). The sharpened maps were obtained with LocalDeblur and RELION post-processing for GroEL and ribosome, respectively. Note that the color scales of the resolution maps of the different specimens have been modified for better visualization.
Figure 4.
DeepRes results from unsharpened and sharpened maps. Histograms (left) and resolution maps (right) for sharpened and unsharpened maps of (a) the KdpFABC complex (EMDB entry EMD-0258) and (b) rabbit muscle aldolase (EMDB entry EMD-7550). The sharpened maps were obtained with RELION post-processing and Autosharpen for KdpFABC and muscle aldolase, respectively.
3.3.1. E. coli GroEL
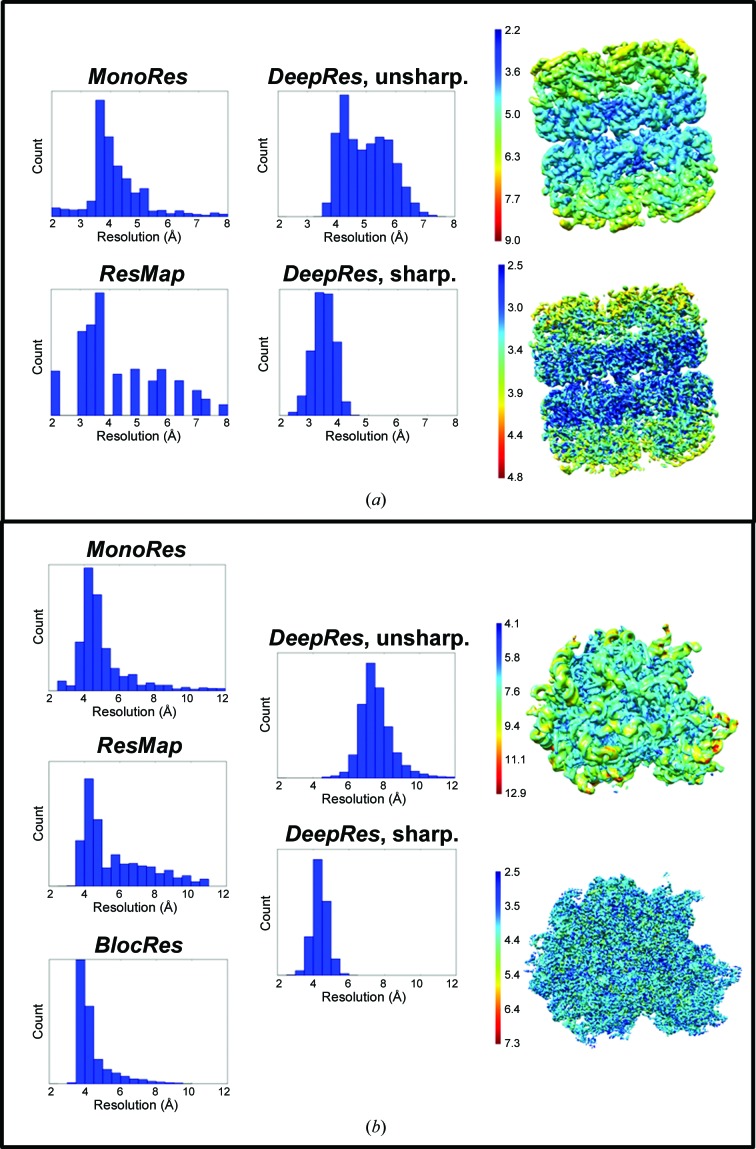
The first case is based on the E. coli GroEL map in the apo form (EMDB entry EMD-3407; Joseph et al., 2016 ▸) reconstructed at 3.3 Å resolution (gold-standard FSC of 0.143); in this case the unsharpened map was deposited and will be the map used in our first set of analyses. For the unsharpened map, MonoRes and ResMap estimated resolution ranges from 2.25 to 8.0 and 2.3 to 8.0 Å, with medians of 4.0 and 3.8 Å, respectively [Fig. 3 ▸(a) and Table 1 ▸]. However, the results with our method are markedly different. DeepRes detected resolutions ranging from 3.3 to 7.0 Å, with a median resolution of 5.0 Å. That is, when applied to the unsharpened map DeepRes reported resolutions that were lower than with any other methods.
We then proceed to sharpen the map using LocalDeblur (Ramírez-Aportela et al., 2019 ▸) and to determine the local resolution of GroEL using DeepRes [Fig. 3 ▸(a)]. Note that, as previously indicated, the use of algorithms such as MonoRes or ResMap on these modified maps is not mathematically justified (see the supporting information). Interestingly, DeepRes shows a clear increase in resolution with respect to the unsharpened map, estimating the resolution to be in the range 2.5–4.5 Å, with a median resolution of 3.5 Å. In general, DeepRes reports an average resolution gain for each domain of greater than 1.0 Å with respect to the unsharpened map. Note that the results obtained for the sharpened map using DeepRes are of the same order as the results obtained by the other methods for the unsharpened map (this observation will be further commented on in Section 4 and in the supporting information). Consequently, the results of DeepRes are very intuitive, which is not the case for the other approaches.
3.3.2. Rabbit 80S ribosome and Plasmodium 80S ribosome
The second case corresponds to the rabbit 80S ribosome map (EMDB entry EMD-9235; Brown et al., 2018 ▸), with a reported overall resolution of 3.8 Å (gold-standard FSC of 0.143). Note that in this case the original deposition contained the two half maps, so that BlocRes could also be applied. The results for this unsharpened density map also showed clear discrepancies between DeepRes and the current methods [Fig. 3 ▸(b)]. While MonoRes, ResMap and BlocRes estimated median resolutions of 4.5, 4.9 and 4.0 Å, respectively, DeepRes estimated a median resolution of 7.4 Å (Table 1 ▸).
When we determined the local resolution with DeepRes for the deposited map (Brown et al., 2018 ▸) post-processed with RELION, an increase in the resolution with respect to the unsharpened map was detected [Fig. 3 ▸(b)]. The histogram shows a resolution range from 3.1 to 6.0 Å, with a median of 4.4 Å and an SD of 0.4 Å. As for the GroEL maps, DeepRes detected a noticeable change in resolution after post-processing, so that the DeepRes-estimated local resolution values of the sharpened map are in the range of the resolutions estimated by the other methods.
A similar behavior is shown for the Plasmodium 80S ribosome map (EMDB entry EMD-2660; Wong et al., 2014; Supplementary Fig. S4). The unsharpened map presents a resolution range lower than those determined by the current methods, with a median resolution of 6.3 Å and an SD of 1.3 Å (Table 1 ▸). Moreover, the DeepRes histogram for the sharpened map with Autosharpen (Terwilliger et al., 2018 ▸) presents a resolution range similar to the other methods, with a median resolution of 3.8 Å and an SD of 0.9 Å. Both the sharpened and the unsharpened maps have a low resolution for the head region of the small 40S subunit owing to its inherent flexibility, as reported by the authors (Wong et al., 2014 ▸).
These changes are related to the capacity of DeepRes to detect increments in local resolution after sharpening, which the other approaches cannot detect. We will particularize the conceptually simple case of a global B-factor correction. Indeed, FSC, ResMap and MonoRes are intrinsically insensitive to quasi-flattening the spectrum of the map, since it affects the noise and signal equally. These methods are designed to extract correlations or SNRs irrespective of this enhancement; in a way, they already provide the best value that any simultaneous enhancement of signal and noise per frequency can obtain (see the detailed analysis presented in Supplementary Fig. S1 and its respective section). On the contrary, DeepRes is sensitive to these changes, so that when sharpening is applied the resolution improves and it then becomes very similar to the results of all other methods.
3.3.3. Other maps: the KdpFABC complex and rabbit muscle aldolase
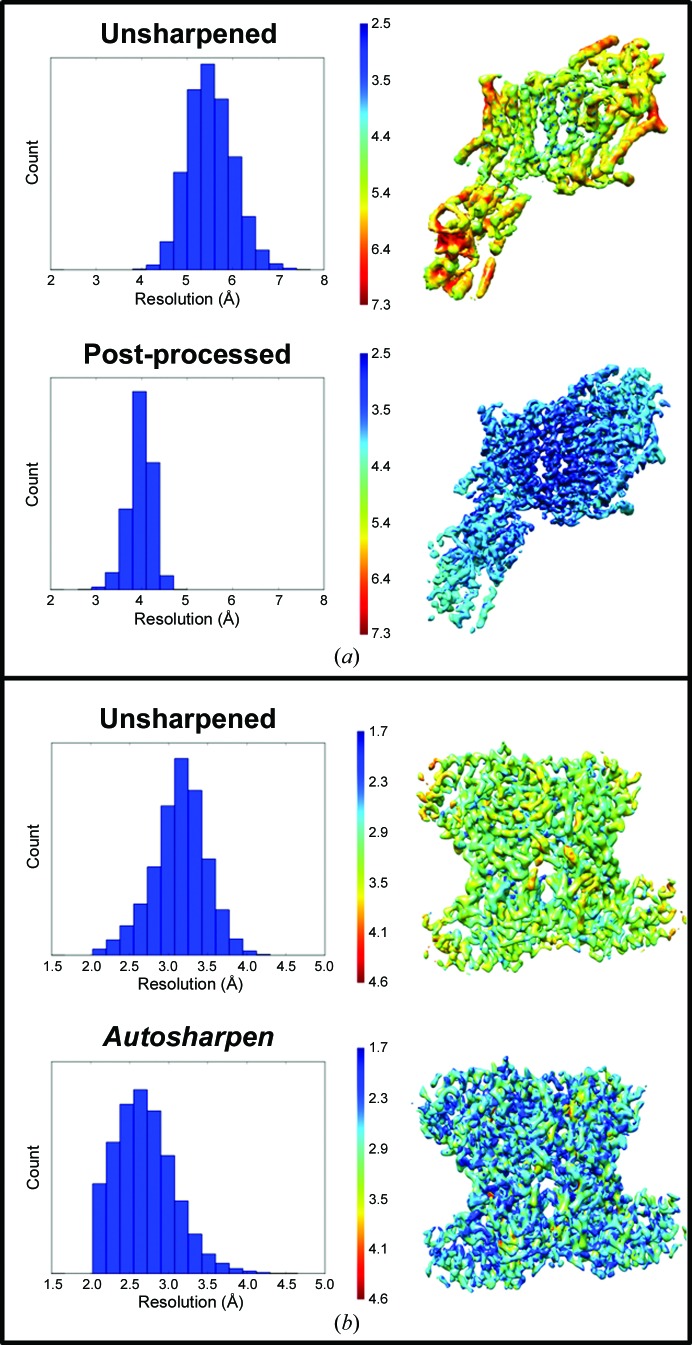
Two other cases were taken into account to evaluate the resolution when sharpening is applied (Fig. 4 ▸). One of the cases tested was the KdpFABC complex (EMDB entry EMD-0258; Stock et al., 2018 ▸). The original publication reported a resolution of 4.0 Å (gold-standard FSC of 0.143). Our DeepRes resolution estimates are between 4.0 and 7.0 Å for the unsharpened map and between 3.0 and 5.0 Å for the post-processed map [Fig. 4 ▸(a)]. The median resolution varied from 5.5 to 4.0 Å with post-processing, with the latter value being similar to that reported by the FSC (Table 1 ▸). In both maps, a better resolution zone (belonging to the KdpA domain) is observed with resolutions between 4.4 and 5.5 Å for the original map and between 3.0 and 4.0 Å for the sharpened map, and a lower resolution zone (belonging to KdpC and the N, P and A cytoplasmatic domains of KdpB) with resolutions between 6.2 and 7.0 Å for the original map and 4.3 and 5.0 Å for the sharpened map.
Finally, we analyzed a rabbit muscle aldolase reconstruction (EMDB entry EMD-7550; Kim et al., 2018 ▸). The original publication estimated a resolution of 2.4 Å (gold-standard FSC of 0.143). In this case, a comparison of our method was made with the unsharpened map and the map after having applied Autosharpen [Fig. 4 ▸(b)]. Both maps show resolutions that vary between 2.0 and 4.0 Å, but the median changed from 3.2 to 2.6 Å on the application of Autosharpen.
3.4. Oversharpening detection
The current methods (all of which are based on different ways of estimating the SNR) report the higher resolution of the map without detecting the degree of blurring, which results in a downweighting of the high-frequency components. Indeed, the choice of the applied B factor modifies the appearance of the map, but this change is not detected by the current methods because it is a radially symmetric operation. On the other hand, if a map is oversharpened then the resolution measures based on the SNR are not affected either. Unlike these methods, DeepRes is capable of detecting differences in resolution between the unsharpened and sharpened maps, which allow the sharpening quality to be evaluated. In the case of oversharpening, DeepRes would report an overestimation of the resolution. Consequently, a good strategy to detect and avoid oversharpening the maps is the combination of both kinds of methods, as exemplified in Fig. 5 ▸ and Supplementary Figs. S5 and S6. If the resolution reported by DeepRes is higher than the resolution reported by an SNR-based method then this is an indicator of oversharpening.
Figure 5.
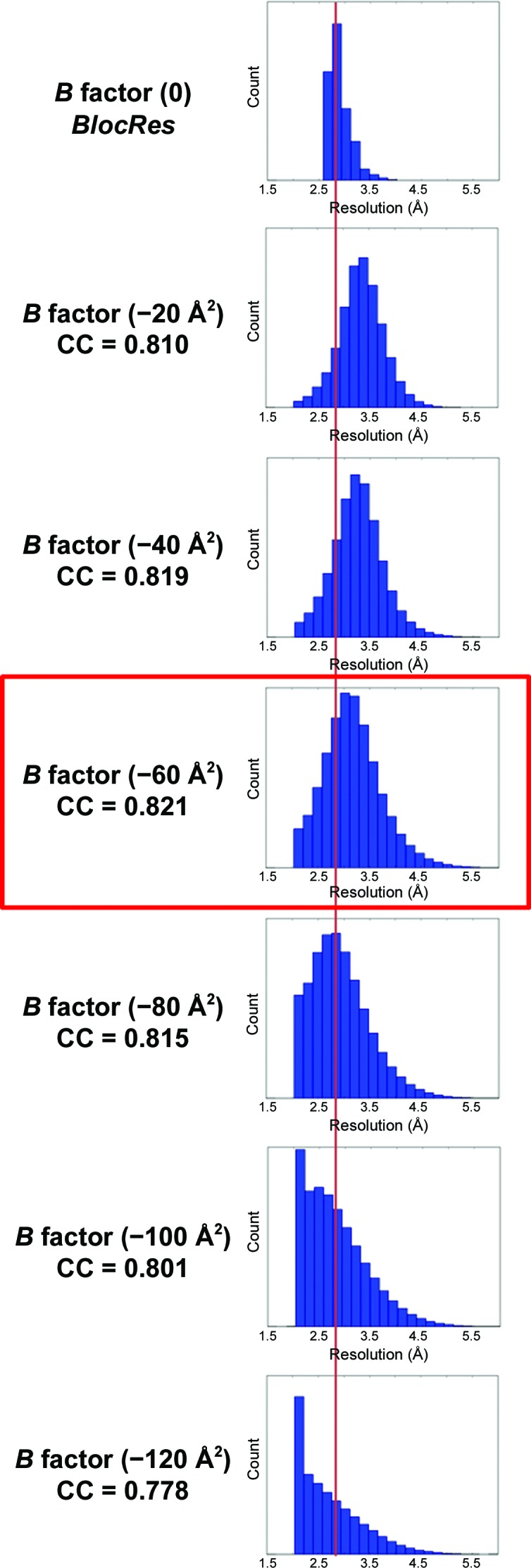
Oversharpening detection. Comparison of BlocRes applied to the unsharpened map (top of the figure) and DeepRes applied to each B-factor sharpened map. The correlation (CC) of each sharpened map and the generated map from the deposited atomic model (PDB entry 6bdf) was calculated using PHENIX. The red line corresponds to the 20% percentile of the local resolution distribution of BlocRes.
One of the monomers in the structure of the 39 kDa human cartilage glycoprotein tetramer (HCGP39; PDB entry 1hjv, chain A) was used to generate a map with a sampling rate of 1.0 Å per pixel. This map was low-pass filtered at a frequency of 3.5 Å with a raised cosine of 0.02. Gaussian noise with zero mean and an SD of 0.08 was added. The map was then sharpened using negative B factors of −60 and −100 Å2 and the resolution of the maps was determined using MonoRes and DeepRes (Supplementary Fig. S5). With MonoRes the resolution remained practically invariant, while with DeepRes the detected resolution increased and exceeded the limit determined by MonoRes (based on the SNR). This example demonstrates that the combination of methods is useful for detecting the oversharpening of density maps.
This strategy to detect oversharpening was applied to the 20S proteasome map (EMDB entry EMD-6287; Campbell et al., 2015 ▸; Fig. 5 ▸ and Supplementary Fig. S6). Several B factors were applied to the unsharpened map, and the correlations of each map and the generated map from the deposited atomic model (PDB entry 6bdf) were calculated using PHENIX (Afonine et al., 2018 ▸). Among the filtered maps, the maximum correlation was obtained for the sharpened map with a B factor of −60 Å2. The local resolution of the sharpened maps was then determined with DeepRes and compared with the local resolution obtained by BlocRes from the two halves of the unsharpened map. Without the atomic model, it would be impossible in a real experiment to know which is a global B factor that does not cause oversharpening. Using DeepRes, we have heuristically observed that a good B factor is one such that the 20% percentile of the local resolution distribution of BlocRes or MonoRes (unsharpened) and DeepRes (sharpened) coincide, as illustrated in Fig. 5 ▸ for BlocRes and in Supplementary Figs. S6 for MonoRes. In the example shown, the heuristic non-oversharpening B factor is −60 Å2 according to BlocRes and MonoRes.
4. Discussion
In this work, we have introduced a new approach aimed at estimating the local quality of a map using principles totally different from any other method previously used in the field, in which we have used deep learning. Our motivation to propose ‘still another’ local quality measure (another ‘local resolution’) is very simple and stems from the fact that most resolution-estimation methods currently used are intrinsically insensitive to isotropic, nonvanishing Fourier filters (by nonvanishing we mean that they do not set to zero-frequency components). Interestingly, this characteristic has been very little treated in the cryoEM literature [with exceptions, such as Unser et al. (2005 ▸) and Sorzano et al. (2017 ▸)], but effectively it means that transformations that change the spectrum of a macromolecule (for instance, by enhancing the amplitude of its Fourier components) are not detected by current methods or, in other words, the resolution values that they report will be the same before and after this enhancement. This result is totally counterintuitive, but it is rigorously demonstrated in depth in the supporting information, together with an illustrative example (Supplementary Fig. S1). Note that the comments above refer to the use of filters only, not to the combination of filters with other operations such as, for example, changing the mask (for example, making a mask tighter). We wanted to develop an approach that naturally renders lower quality values when maps have not been ‘enhanced’ and higher ones after ‘enhancement’, without any change of parameters or masks or any other operation.
We have used deep-learning technology to ‘teach’ a neural network the characteristics of filtered maps at different resolutions. Initially, our approach was tested with simulated maps in which the resolution values were known a priori. In these tests different scenarios were studied: maps with different resolutions and different types of macromolecules (amino acids and nucleotides). The results of DeepRes were excellent for the cases tested, assigning resolutions very similar to the expected values and validating the use of our method to estimate the local resolution in density maps.
However, the resolution values obtained with DeepRes for known experimental unsharpened maps were much more conservative than those estimated using the current methods. Still, when sharpening was applied to these maps, the DeepRes resolutions were in accordance with the current methods. The resolution medians obtained by DeepRes for the tested sharpened maps were also close to the resolutions reported by FSC.
As previously indicated, the current methods are insensitive to the application of a B factor, which means that different modifications of the map by the application of different B-factor values will not be reflected by a change in resolution. In this sense, our method offers a solution. With DeepRes, the changes that occur with an applied B factor are indeed detected. The results obtained indicate that the resolutions estimated by the current methods correspond to the resolutions that the map would have after restoration. However, our method reports the resolution as the similarity to biological macromolecules filtered at a given resolution, which is closer to the user observation that sharpening facilitates the atomic modeling of the macromolecule. We have also shown that comparison of the current methods (based on SNR) and DeepRes allows detection of the oversharpening of cryoEM maps.
Another advantage of DeepRes is that it does not depend on map noise estimations. Therefore, DeepRes can be used for maps with masks applied, with a low noise level owing to the processing technique or to locally enhanced signal using algorithms such as LocScale and LocalDeblur.
Supplementary Material
Insensitivity of resolution methods to isotropic filters, limitation of methods based on signal-to-noise ratio for maps affected by noise suppression and Supplementary Figures. DOI: 10.1107/S2052252519011692/fq5008sup1.pdf
Acknowledgments
We would like to thank Jose Luis Vilas and Ruben Sanchez-Garcia for their helpful commentary and critical reading of the manuscript. Author contributions are as follows. ER-A, JMC and COSS conceived the idea for this study. ER-A and COSS wrote the code. JM contributed to the development of the code. ER-A implemented the code in Scipion and designed the experiments. PC contributed to the implementation in Scipion. ER-A, JMC and COSS wrote the manuscript. All of the authors commented on and edited the manuscript. The authors declare no competing financial interests.
Funding Statement
This work was funded by Comunidad de Madrid grant CAM (S2017/BMD-3817). Ministerio de Economía, Industria y Competitividad, Gobierno de España grant BIO2016-76400-R. Horizon 2020 grant .
References
- Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M., Kudlur, M., Levenberg, J., Monga, R., Moore, S. G., Murray, D., Steiner, B., Tucker, P., Vasudevan, V., Warden, P. & Zhang, X. (2016). Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, pp. 265–283. Berkeley: The USENIX Assocation.
- Abid Ali, F., Renault, L., Gannon, J., Gahlon, H. L., Kotecha, A., Zhou, J. C., Rueda, D. & Costa, A. (2016). Nat. Commun. 7, 10708. [DOI] [PMC free article] [PubMed]
- Afonine, P. V., Klaholz, B. P., Moriarty, N. W., Poon, B. K., Sobolev, O. V., Terwilliger, T. C., Adams, P. D. & Urzhumtsev, A. (2018). Acta Cryst. D74, 814–840. [DOI] [PMC free article] [PubMed]
- Avramov, T. K., Vyenielo, D., Gomez-Blanco, J., Adinarayanan, S., Vargas, J. & Si, D. (2019). Molecules, 24, 1181. [DOI] [PMC free article] [PubMed]
- Bengio, Y. (2009). Mach. Learn. 2, 1–127.
- Brown, A., Baird, M. R., Yip, M. C., Murray, J. & Shao, S. (2018). Elife, 7, e40486. [DOI] [PMC free article] [PubMed]
- Campbell, M. G., Veesler, D., Cheng, A., Potter, C. S. & Carragher, B. (2015). Elife, 4, e06380. [DOI] [PMC free article] [PubMed]
- Cardone, G., Heymann, J. B. & Steven, A. C. (2013). J. Struct. Biol. 184, 226–236. [DOI] [PMC free article] [PubMed]
- Ding, F., Lu, C., Zhao, W., Rajashankar, K. R., Anderson, D. L., Jardine, P. J., Grimes, S. & Ke, A. (2011). Proc. Natl Acad. Sci. USA, 108, 7357–7362. [DOI] [PMC free article] [PubMed]
- Fernandez-Leiro, R., Conrad, J., Yang, J.-C., Freund, S. M. V., Scheres, S. H. W. & Lamers, M. H. (2017). Nat. Struct. Mol. Biol. 24, 140–143. [DOI] [PMC free article] [PubMed]
- Harauz, G. & van Heel, M. (1986). Optik, 73, 146–156.
- Houston, D. R., Recklies, A. D., Krupa, J. C. & van Aalten, D. M. F. (2003). J. Biol. Chem. 278, 30206–30212. [DOI] [PubMed]
- Jakobi, A. J., Wilmanns, M. & Sachse, C. (2017). Elife, 6, e27131. [DOI] [PMC free article] [PubMed]
- Joseph, A. P., Malhotra, S., Burnley, T., Wood, C., Clare, D. K., Winn, M. & Topf, M. (2016). Methods, 100, 42–49. [DOI] [PMC free article] [PubMed]
- Kim, L. Y., Rice, W. J., Eng, E. T., Kopylov, M., Cheng, A., Raczkowski, A. M., Jordan, K. D., Bobe, D., Potter, C. S. & Carragher, B. (2018). Front. Mol. Biosci. 5, 50. [DOI] [PMC free article] [PubMed]
- Kingma, D. P. & Ba, J. (2014). arXiv:1412.6980.
- Kucukelbir, A., Sigworth, F. J. & Tagare, H. D. (2014). Nat. Methods, 11, 63–65. [DOI] [PMC free article] [PubMed]
- Lee, S., Roh, S. H., Lee, J., Sung, N., Liu, J. & Tsai, F. T. F. (2019). Cell. Rep. 26, 29–36. [DOI] [PMC free article] [PubMed]
- Levy, E. D., Pereira-Leal, J. B., Chothia, C. & Teichmann, S. A. (2006). PLoS Comput. Biol. 2, e155. [DOI] [PMC free article] [PubMed]
- Liao, M., Cao, E., Julius, D. & Cheng, Y. (2013). Nature (London), 504, 107–112. [DOI] [PMC free article] [PubMed]
- Pettersen, E. F., Goddard, T. D., Huang, C. C., Couch, G. S., Greenblatt, D. M., Meng, E. C. & Ferrin, T. E. (2004). J. Comput. Chem. 25, 1605–1612. [DOI] [PubMed]
- Ramírez-Aportela, E., Vilas, J. L., Glukhova, A., Melero, R., Conesa, P., Martínez, M., Maluenda, D., Mota, J., Jiménez, A., Vargas, J., Marabini, R., Sexton, P. M., Carazo, J. M., Oscar, C. & Sorzano, S. (2019). Bioinformatics, https://doi.org/10.1093/bioinformatics/btz671.
- Rosa-Trevín, J. M. de la, Otón, J., Marabini, R., Zaldívar, A., Vargas, J., Carazo, J. M. & Sorzano, C. O. S. (2013). J. Struct. Biol. 184, 321–328. [DOI] [PubMed]
- Rosa-Trevín, J. M. de la, Quintana, A., del Cano, L., Zaldívar, A., Foche, I., Gutiérrez, J., Gómez-Blanco, J., Burguet-Castell, J., Cuenca-Alba, J., Abrishami, V., Vargas, J., Otón, J., Sharov, G., Vilas, J. L., Navas, J., Conesa, P., Kazemi, M., Marabini, R., Sorzano, C. O. S. & Carazo, J. M. (2016). J. Struct. Biol. 195, 93–99. [DOI] [PubMed]
- Rosenthal, P. B. & Henderson, R. (2003). J. Mol. Biol. 333, 721–745. [DOI] [PubMed]
- Saxton, W. O. (1978). Computer Techniques for Image Processing in Electron Microscopy. New York: Academic Press.
- Saxton, W. O. & Baumeister, W. (1982). J. Microsc. 127, 127–138. [DOI] [PubMed]
- Scheres, S. H. W. (2012). J. Struct. Biol. 180, 519–530. [DOI] [PMC free article] [PubMed]
- Sorzano, C. O. S., Marabini, R., Boisset, N., Rietzel, E., Schröder, R., Herman, G. T. & Carazo, J. M. (2001). J. Struct. Biol. 133, 108–118. [DOI] [PubMed]
- Sorzano, C. O. S., Vargas, J., Otón, J., Abrishami, V., de la Rosa-Trevin, J. M., del Riego, S., Fernández-Alderete, A., Martínez-Rey, C., Marabini, R. & Carazo, J. M. (2015). AIMS Biophys. 2, 8–20.
- Sorzano, C. O. S., Vargas, J., Otón, J., Abrishami, V., de la Rosa-Trevín, J. M., Gómez-Blanco, J., Vilas, J. L., Marabini, R. & Carazo, J. M. (2017). Prog. Biophys. Mol. Biol. 124, 1–30. [DOI] [PubMed]
- Sorzano, C. O. S., Vargas, J., de la Rosa-Trevín, J. M., Jiménez, A., Maluenda, D., Melero, R., Martínez, M., Ramírez-Aportela, E., Conesa, P., Vilas, J. L., Marabini, R. & Carazo, J. M. (2018). J. Struct. Biol. 204, 329–337. [DOI] [PubMed]
- Stock, C., Hielkema, L., Tascón, I., Wunnicke, D., Oostergetel, G. T., Azkargorta, M., Paulino, C. & Hänelt, I. (2018). Nat. Commun. 9, 4971. [DOI] [PMC free article] [PubMed]
- Su, M., Zhang, H., Schawinski, K., Zhang, C. & Cianfrocco, M. A. (2018). bioRxiv, 256792.
- Terwilliger, T. C., Sobolev, O. V., Afonine, P. V. & Adams, P. D. (2018). Acta Cryst. D74, 545–559. [DOI] [PMC free article] [PubMed]
- Unser, M., Sorzano, C. O. S., Thévenaz, P., Jonić, S., El-Bez, C., De Carlo, S., Conway, J. F. & Trus, B. L. (2005). J. Struct. Biol. 149, 243–255. [DOI] [PMC free article] [PubMed]
- Vilas, J. L., Gómez-Blanco, J., Conesa, P., Melero, R., de la Rosa-Trevín, J. M., Otón, J., Cuenca, J., Marabini, R., Carazo, J. M., Vargas, J. & Sorzano, C. O. S. (2018). Structure, 26, 337–344. [DOI] [PubMed]
- Wagner, T., Merino, F., Stabrin, M., Moriya, T., Gatsogiannis, C. & Raunser, S. (2018). Commun. Biol. 2, 218.
- Wong, W., Bai, X.-C., Brown, A., Fernandez, I. S., Hanssen, E., Condron, M., Tan, Y. H., Baum, J. & Scheres, S. H. W. (2014). Elife, 3, e03080. [DOI] [PMC free article] [PubMed]
- Zheng, Q., Zhu, R., Xu, L., He, M., Yan, X., Liu, D., Yin, Z., Wu, Y., Li, Y., Yang, L., Hou, W., Li, S., Li, Z., Chen, Z., Li, Z., Yu, H., Gu, Y., Zhang, J., Baker, T. S., Zhou, Z. H., Graham, B. S., Cheng, T., Li, S. & Xia, N. (2019). Nat. Microbiol. 4, 124–133. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Insensitivity of resolution methods to isotropic filters, limitation of methods based on signal-to-noise ratio for maps affected by noise suppression and Supplementary Figures. DOI: 10.1107/S2052252519011692/fq5008sup1.pdf