Divergence dating using mixed effects clock modelling: An application to HIV-1

Abstract

The need to estimate divergence times in evolutionary histories in the presence of various sources of substitution rate variation has stimulated a rich development of relaxed molecular clock models. Viral evolutionary studies frequently adopt an uncorrelated clock model as a generic relaxed molecular clock process, but this may impose considerable estimation bias if discrete rate variation exists among clades or lineages. For HIV-1 group M, rate variation among subtypes has been shown to result in inconsistencies in time to the most recent common ancestor estimation. Although this calls into question the adequacy of available molecular dating methods, no solution to this problem has been offered so far. Here, we investigate the use of mixed effects molecular clock models, which combine both fixed and random effects in the evolutionary rate, to estimate divergence times. Using simulation, we demonstrate that this model outperforms existing molecular clock models in a Bayesian framework for estimating time-measured phylogenies in the presence of mixed sources of rate variation, while also maintaining good performance in simpler scenarios. By analysing a comprehensive HIV-1 group M complete genome data set we confirm considerable rate variation among subtypes that is not adequately modelled by uncorrelated relaxed clock models. The mixed effects clock model can accommodate this rate variation and results in a time to the most recent common ancestor of HIV-1 group M of 1920 (1915–25), which is only slightly earlier than the uncorrelated relaxed clock estimate for the same data set. The use of complete genome data appears to have a more profound impact than the molecular clock model because it reduces the credible intervals by 50 per cent relative to similar estimates based on short envelope gene sequences.

1. Introduction

Molecular clocks enable the estimation of phylogenetic histories in units of time by sharing external time-calibration information across the phylogeny. From these time-scaled evolutionary histories, inferring divergence times is of broad interest in evolutionary biology with applications to a wide range of taxonomic groups and evolutionary time scales, from macroevolutionary processes of speciation to within-host evolution of viruses. Such histories are key in molecular epidemiology and phylodynamic inference of fast evolving viruses (Pybus and Rambaut 2009). They provide estimates of the time to the most recent common ancestor (tMRCA), offering insights into the origins of epidemics, as well as the times of all other branching events that often correspond to virus transmission from one case to the next. The latter insight has led to the development of formal phylodynamic approaches that adopt coalescent (e.g. Volz et al. 2009) or birth-death modelling (e.g. Stadler et al. 2012) to infer transmission dynamics from time-scaled phylogenies. To calibrate phylogenetic time scales for rapidly evolving viruses, phylodynamic inference generally relies on divergence accumulating over the sampling time interval to inform dated-tip molecular clock models (Rambaut 2000). All these models are implemented in Bayesian statistical inference frameworks that allow the joint estimation of time-scaled evolutionary histories, tree-generative processes, and also trait diffusion processes directly from sequences with their associated traits (Bouckaert et al. 2014; Suchard et al. 2018).

Early molecular clock models have assumed a constant rate of molecular evolution across the phylogeny, but models that explicitly incorporate rate variation now supersede these early clocks. Although numerous models relax the strict molecular clock assumption, they can be broadly categorized into models of uncorrelated and autocorrelated rates across phylogeny branches. For organisms evolving on macro-evolutionary scales, which are frequently characterized by correlations between substitution rate and life-history traits, a Brownian autocorrelated clock model provides a reasonable description of long-term changes in the substitution rate (Thorne, Kishino, and Painter 1998). Specifically, these autocorrelated clocks assume that the logarithm of the substitution rate evolves according to a Brownian motion (Thorne, Kishino, and Painter 1998), akin to how continuous traits are frequently modelled to evolve on trees (Felsenstein 1985). Viruses, however, are often characterized by short-term evolutionary time scales with little or no relevance in modelling rate variation according to the evolution of life history traits. This explains why an uncorrelated clock that assumes independent substitution rates across successive branches in the tree is the most commonly adopted relaxed clock for viruses. The most popular implementation draws branch-specific rates independently from an underlying (typically lognormal) distribution with an unknown, but estimable mean and variance (Drummond et al. 2006).

While commonly perceived to be a flexible relaxed clock model, the uncorrelated clock does not adequately accommodate all sources of rate variation in viruses. This has been illustrated in detail for the influenza A virus that is characterized by several host-specific lineages (Worobey, Han, and Rambaut 2014). Allowing these host lineages to have independent rates of evolution appears necessary to reliably estimate divergence times as well as tree topologies (Worobey, Han, and Rambaut 2014). This represents a specific case of local molecular clocks that induce strong rate autocorrelation and for which an uncorrelated clock is particularly ill-suited. Also for HIV-1 group M, considerable variation in rates has been demonstrated among different subtype clades (Wertheim, Fourment, and Kosakovsky Pond 2012). As this is not appropriately accommodated by the uncorrelated relaxed (UC) molecular clock, it may also affect divergence time estimates, as suggested by simulation analyses (Wertheim, Fourment, and Kosakovsky Pond 2012). Wertheim, Fourment, and Kosakovsky Pond (2012) refer to rate variation among lineages as heterotachy and conclude that the available relaxed clock implementations are unable to appropriately handle this.

While local molecular clocks, either specified a priori (Yoder and Yang 2000) or identified a posteriori (Drummond and Suchard 2010), offer a valuable alternative to the UC clock in different cases, local clocks alone may be overly rigid and lead to bias in divergence time estimation when considerable variation among branches exists in addition to clade or lineage-specific effects on the rate. In previous work on testing HIV-1 evolutionary rate differences within and between hosts, Vrancken et al. (2014) introduce a mixed effects (ME) molecular clock model that combines the merits of both uncorrelated and correlated, local clocks. Here, we aim to evaluate this model for divergence time estimation. Specifically, we use the ME clock model to revisit the problem of rate variation among HIV-1 group M subtypes and how this may affect tMRCA estimates (Wertheim, Fourment, and Kosakovsky Pond 2012). Because the origin of HIV-1 has in the past been subject to contentious theories, there stands longstanding interest in estimating the tMRCA of HIV-1 group M. Following simulations to assess the performance of the model, we characterize the rate variation among subtypes based on complete genome data. We subsequently accommodate major subtype differences in an ME model in order to estimate HIV-1 divergence times.

2. Materials and methods

2.1 Bayesian divergence time estimation using an ME clock model

To accommodate both clade-specific rates and uncorrelated rate variation among branches in the estimation of divergence times, we employ a molecular clock model that combines both fixed and random effects. We here present a more general formulation of the ME molecular clock model originally proposed by Vrancken et al. (2014), where the substitution rate parameter r_i on branch i follows:

$${\log r}_i={\beta }_0+\sum _{j=1}^p{X}_{\mathit{ij}}{\beta }_j+{ϵ}_i$$ (1)

where β₀ is an unknown grand mean representing the background rate, β_j is the estimated effect size of the jth covariate X_ij (out of p covariates), and ϵ_i are independent and normally distributed random variables with mean 0 and an estimable variance. For a clade-specific rate effect with estimable size β_j, we set X_ij =1 for all branches encompassed by the clade and X_ij =0 for all other branches. In the analyses of the simulated data, we specify a normal prior distribution for β₀ with mean −6 and a standard deviation of 3 and a normal prior distribution for β_j with mean 0 and a standard deviation of 1. For the larger empirical HIV data set, we specify normal prior distributions for both β₀ and β_j with mean 0 and a standard deviation of 100. Through simulation, we compare this ME model to other molecular clock models implemented in BEAST (Suchard et al. 2018), including a strict clock (SC), a fixed local (FL) clock (Yoder and Yang 2000; Worobey, Han, and Rambaut 2014), a random local (RL) clock (Drummond and Suchard 2010), and a UC clock model with a log normal distribution (Drummond et al. 2006). We approximate the joint posterior and its marginalizations using standard Markov chain Monte Carlo (MCMC) transition kernels (including random walk operators on the β parameters in the ME model). We use BEAGLE for efficient likelihood computation (Ayres et al. 2012) and simulate the MCMC chains sufficiently long to ensure stationarity and mixing as diagnosed using Tracer (Rambaut et al. 2018). We summarize posterior tree distributions in the form of maximum clade credibility (MCC) trees and visualize these trees using FigTree (http://tree.bio.ed.ac.uk/software/figtree/, last accessed on 20 October 2018).

2.2 Codon substitution rate estimation

We estimate absolute nonsynonymous (r_N) and synonymous substitution (r_S) rates using a codon substitution model approach (Baele et al. 2016) implemented in BEAST. This Bayesian evolutionary inference approach adopts the (Muse and Gaut 1994) substitution model (MG94) and, in order to scale the substitution process in units of time, applies a standardization that corresponds to $r_{\mathrm{N}}+r_{\mathrm{S}}$ expected rate changes per time unit (Baele et al. 2016). We model substitution rate variation among sites according to a discrete γ distribution with four categories. To reduce the computational burden associated with codon substitution likelihood computations in a Bayesian framework, we keep the tree topology fixed to the MCC tree obtained by a nucleotide substitution analysis (using a UC relaxed clock). As an approximation to the standard dN/dS selection measures, we summarize nonsynonymous over synonymous substitution rate ratios as $r_{\mathrm{N}}/3*r_{\mathrm{S}}$ as we expect about three times higher nonsynonymous substitution rate under neutrality. We compare these estimates to a maximum likelihood (ML) estimate of dN/dS under a MG94 codon substitution model obtained by HyPhy (Pond et al. 2005).

2.3 Simulations

We follow Wertheim et al. (2012) in simulating sequence data over a forty-taxon phylogeny comprised of four identical ten-taxon clades (Supplementary Fig. S1). The root of the tree is fixed at 80 years before present (ybp), and the four major clades (A, B, C, and D) have a fixed age of 40 ybp. The taxa within each clade are sampled at five different time points ($t=0,4,8,12,16$ ybp), two per time point. The simulations we aim to perform vary in the substitution rates that are assigned to the branches in the phylogeny, which are used to convert the tree in units of substitution. To emulate random effects on evolutionary rate variation, we draw branch-specific substitution rates from a lognormal distribution. For Clade D branches and branches ancestral to the four major clades, we draw rates from a lognormal distribution with a mean of ln(0.001) substitutions per site per year and a standard deviation of 0.25. The simulation scenarios vary in the lognormal parameterization for clades A, B, and/or C, with different means emulating different fixed effects on evolutionary rate variation. Standard deviations of lognormal distributions with different means are set to values that correspond to the same coefficient of variation ($=0.25/\text{ln}(0.001)$) as for the lognormal distribution on the branches ancestral to the clades. We use πBUSS (Bielejec et al. 2014) to simulate alignments of 1,000 nt under a general time-reversible (GTR) model of evolution parameterized using relative rates ($r_{\mathit{AC}}=0.234,r_{\mathit{AG}}=0.710,r_{\mathit{AT}}=0.113,r_{\mathit{CG}}=0.130,r_{\mathit{CT}}=1.000,r_{\mathit{GT}}=0.170$) and nucleotide frequencies (${\pi }_A=0.41,{\pi }_C=0.17,{\pi }_G=0.21,{\pi }_T=0.21$) as estimated from a complete genome HIV-1 group M data set (see below). Among-site rate heterogeneity was accommodated using a discrete γ distribution with four categories and a shape parameter of 0.40. For each rate configuration, we simulate 20 replicate data sets and analyse them using 5 different clock models implemented in BEAST: SC, FL, RL, UC (all four with default prior specification), and ME. As primary outcomes, we monitor relative error ($\left|x-\widehat{x}\right|\hspace{0.17em}/x$, where x is the true value and $\widehat{x}$ is the estimate) and coverage, the percentage by which the credible intervals include x, for tMRCA estimates for the four clades and the root node. Estimator coverage reflects the probability that the true value from which the data derive falls within the model estimated nominal credible interval and hence predicts the performance of the methods across a wide set of data sets. We note that in Bayesian inference a strict relationship between the coverage percentage and the percentage used to construct highest density posterior density (HPD) intervals does not necessarily hold. To represent a single measurement, we summarize mean relative errors and coverage expectations across the five nodes of interest, acknowledging that these do not provide independent estimates of the properties of interest. So, coverage, for example, is presented as the proportion of the 5 × 20 95 per cent HPD intervals that contain the true node age.

2.4 HIV-1 group M data set

We compiled a data set of 465 HIV-1 group M genomes, including 104A, 82B, 93C, 63D, 45F, 60G, 9H, 7J, and two K genomes. In Supplementary Data, we detail how the data set was compiled on a subtype by subtype basis. This generally involved selecting a subset of genomes available on GenBank, merging data sets from previously published studies or a combination of both, followed by a filtering step (removing multiple genomes per patient, duplicates, unusually divergent genomes, cultured viruses, and outliers in a root-to-tip divergence analysis) and recombination screening. The sequences were aligned using MAFFT (Katoh, Asimenos, and Toh 2009) and the resulting sequence alignment was manually edited, taking care to maintain the reading frames in coding genes. We investigated temporal signal in this data by plotting root-to-tip divergence as a function of sampling time using TempEst (Rambaut et al. 2016). As input for these analyses, we used an ML tree reconstructed by PhyML (Guindon et al. 2009) under a GTR substitution model with a discrete γ distribution to model rate variation among sites. For HIV-1 group M analyses, we generally exclude subtypes G, H, J, and K because of the possible confounding effect of recombination (subtype G) (Abecasis et al. 2007; Lemey et al. 2009), and the low number of representative genomes (subtype H, J, and K). For the codon substitution model analyses, we edited the alignment into a single coding reading frame by removing genome regions in which reading frames overlap.

BEAST analyses were performed under the same substitution model specifications as for the ML reconstruction. We first compare SC and UC estimates for the separate subtypes and then compare SC, UC as well as ME estimates on the complete group M data set. For the individual subtypes, we specify an exponential growth model as the coalescent tree prior except for subtype B, which follows a logistic growth model as previously established (Robbins et al. 2003; Worobey et al. 2016). To investigate the sensitivity of evolutionary rate estimates to the parametric coalescent prior specification, we also obtain UC rate estimates using a non-parametric coalescent model (Gill et al. 2013). For the complete group M data set, we follow Faria et al. (2014) in (i) specifying a ‘nested’ coalescent model with an overall exponential-logistic growth and a separate logistic model for the subtype B clade, and (ii) in including the sequence data from old samples as ‘internal controls’ in the node height estimation process. Specifically, we include the available sequence data for three old samples: the previously published short sequence stretches for ZR59 (Zhu et al. 1998) and 1960A (Worobey et al. 2008) and a newly obtained near complete genome from a DRC sample dating back to 1966 that clusters basal to subtype C (DRC66; Gryseels et al. 2019). The two independently obtained 1960A sequence stretches were combined into a single sequence (represented by a consensus sequence where they overlapped). Two stop codons in DRC66 were masked (replacing a C by a Y in both occasions). For these three taxa, we do not specify a sampling date but infer the height of the relevant tips together with the heights of the internal tree nodes (Shapiro et al. 2011). All alignment files, ML tree files, and the BEAST xml file for the ME model are available at https://github.com/phylogeography/HIVmixedEffectsClock (last accessed on 1 June 2019).

3. Results

3.1 Simulations

Because combining fixed and random effects in a molecular clock model may raise concerns about identifiability, we first use simulation to explore the performance of the model relative to other molecular clock models implemented in BEAST (Suchard et al. 2018). Specifically, we adopt the simulation setup and scenarios used by Wertheim, Fourment, and Kosakovsky Pond (2012) to illustrate the shortcomings of standard molecular clock models in the presence of different sources of rate variability among branches.

We first explore the impact of varying the mean rate in one of the four identical ten-taxon clades while also accommodating random variability in rates among branches (Fig. 1). When the rates in one clade are on average three to four times lower or higher than the rates on the other clades, the ME model consistently returns the smallest relative error for the divergence times of interest followed by the FL clock model. The latter is not surprising as the rate distributions are largely non-overlapping under these simulation settings. Interestingly, the UC clock yields the highest error in these cases, in agreement with the findings of Worobey, Han, and Rambaut (2014) for a scenario of highly correlated rates across branches. As mean rate differences decrease below twofold, relative errors shrink for all models and the models become virtually indistinguishable. Notably, for the same mean rate among all branches, which reduces to a scenario of exclusively random variation, the ME maintains good performance. So, while overparameterized for such rate variation, the model efficiently shrinks to an UC parameterization in practice.

Figure 1.

Simulation analyses for a different mean rate in one of four identical clades of a 40 taxa tree with dated tips. The scenario of rate variation is depicted on the left; the resulting mean relative errors and coverage proportions are shown in the middle and on the right, respectively, for the five different models (SC, strict clock; UC, uncorrelated relaxed; FL, fixed local; RL, random local; ME, mixed effects). The rate distributions are depicted on a log scale. In the simulations, rates are drawn from the grey rate distribution (with a mean rate of 0.001 substitutions per site per year) for all branches except for one of the clades (‘clade A’), for which rates are drawn from the pink distributions with means (μ_A) indicated on a natural scale in the plots. The relative rate bar plots summarize mean relative errors across 20 replicates, and for the age estimates for five nodes of interest in each replicate. The whiskers represent standard errors. Coverage bar plots summarize coverage proportions across 20 replicates and for the same age estimates. In the relative rate and coverage bar plots, we use a star to indicate the model with the lowest error and highest coverage, respectively (if there is a single best value).

For the divergence time 95 per cent HPDs used under all models, coverage remains under nominal expectations. The ME model, however, achieves coverages that are generally the closest to nominal, with little variation among the different simulation scenarios. Coverage for the SC and UC estimates on the other hand substantially decreases with larger mean rate differences.

In a second set of simulations, we explore twofold mean rate differences for two different clades as well as FL clock scenarios (Fig. 2). While twofold mean rate differences for two clades result in somewhat larger relative errors than for one clade, the ME model consistently yields the lowest errors. Also in these cases, the ME model coverage approximates nominal values better than any other model. Without random variation, the ME model also yields the lowest errors for twofold rate differences in one or two clades. Even without rate variation (i.e. an SC scenario), the ME model performs well. Although again overparameterized for such scenarios, the ME model efficiently shrinks to an FL clock or even an SC in practice. The fact that mean relative error for the ME can be lower than the FL clock in scenarios without random rate variation seems surprising, but could be attributed to the log-parameterization in the ME model and its associated prior specification (cf. Section 2). Indeed, when we re-analyse the last simulation scenario (${\mu }_{\mathrm{A}}={\mu }_{\mathrm{C}}=2.0$×10⁻³) using an FL clock model with the same log-parameterization and prior specification as for the ME model, we obtain a mean relative error of 0.08698 (stdev =0.06312), which was marginally lower than the mean relative error for the ME model (0.08736, stdev =0.06254). Coverage patterns are not as consistent among models in the FL (and SC) clock scenarios, but the ME clock maintains good performance.

Figure 2.

Simulation analyses for mean rate differences in two different clades and for fixed local clock scenarios. The scenario of rate variation is depicted on the left; the resulting mean relative errors and coverage proportions are shown in the middle and on the right, respectively, for the five different models (SC, strict clock; UC, uncorrelated relaxed; FL, fixed local; RL, random local; ME, mixed effects). The rate distributions are depicted on a log scale. In the first four simulations, rates are drawn from the grey rate distribution (with a mean rate of 0.001 substitutions per site per year) for all branches except for two of the clades (clades A and B or C), for which rates are drawn from the pink distributions with means (μ_A, μ_B, or μ_C) indicated on a natural scale in the plots. In the next four simulations, rates are fixed to the value indicated by the grey line (a rate of 0.001 substitutions per site per year) for all branches except for one or two of the clades for which rates are fixed to the value indicated by the pink line. The relative rate and coverage bar plots can be described as in Fig. 1.

3.2 HIV-1 group M

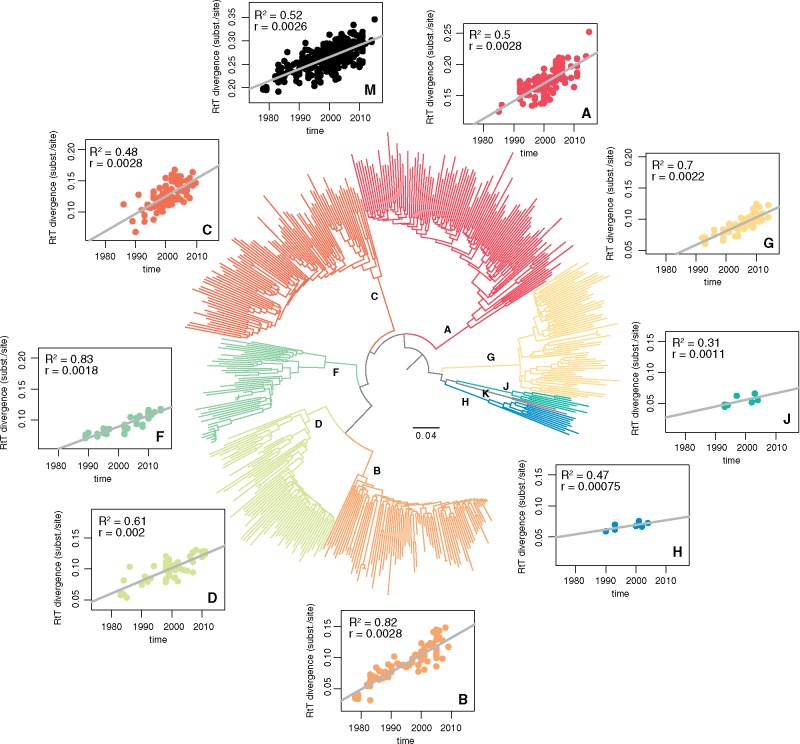
We investigate temporal signal in the HIV-1 group M complete genome data set and in the individual subtype clades by regressing root-to-tip divergence against sampling time (Fig. 3) (Rambaut et al. 2016). This analysis identifies a clear accumulation of genetic divergence over the sampling time range in each analysis albeit with differing proportions of variance explained by sampling time. Specifically, the sparsely sampled subtype H and J return the lowest coefficients of determination (Fig. 3). According to the slopes of the regressions, which are only rough indications of the evolutionary rate, subtypes A, B, and C evolve at similarly high rates of evolution, followed by subtype G, D, and F, and trailed by subtype J and H.

Figure 3.

Phylogenetic reconstruction and temporal signal for HIV-1 group M subtypes. All subtype clusters indicated in the ML tree reconstruction yielded maximum support according to the approximate likelihood ratio test. For the HIV group M (including subtypes A, B, C, D, and F) and for each separate subtype, except for subtype K (represented by only two genomes), we show root-to-tip divergence as a function of sampling year. Coefficients of determination (R²) and slope estimates are indicated in the upper left corner of the regression plots. Subtype clades and their respective data points are coloured according to a diverging colour scheme ordered by slope: fast (red) to slow (blue).

Next, we perform Bayesian inference of evolutionary rates and divergence dates using a UC clock model for the subtype-specific data sets and using a UC as well as an ME clock model for the HIV-1 group M data set (Fig. 4). In this comparison, we do not include the poorly represented subtypes H and J, which are associated with considerable uncertainty (Supplementary Fig. S2) and do not require relaxed molecular clock modelling (Supplementary Fig. S3). The separate evolutionary rate estimates for the different subtypes suggest lower rate of evolution for subtypes D and F compared with subtypes A, B, and C, and an elevated rate for subtype B among the latter three (Fig. 4A). A lower genomic substitution rate for HIV-1 subtype D has previously been demonstrated by Patiño-Galindo and González-Candelas (2017).

Figure 4.

Separate and joint estimates of HIV-1 subtype rates and tMRCAs. The separate estimates are obtained under an UC clock model while the joint estimates represent average branch-specific rates under an UC and ME clock model. The boxplot colouring by subtype follows the colours in Fig. 3. Similar UC clock model estimates are obtained using a non-parametric coalescent prior (Supplementary Fig. S4). Separate and joint estimates rate estimates under a strict clock model can be found in Supplementary Fig. S5.

To examine the extent to which varying selective pressure explains rate differences among the subtypes, we infer absolute synonymous and non-synonymous substitution rates using a recently developed Bayesian approach (Baele et al. 2016) (Fig. 5). Posterior estimates indicate that substitution rate differences between subtypes A and C and subtypes D and F are somewhat more reflected in synonymous substitution rates and hence they do not follow differences in dN/dS. The higher subtype B rate suggested by the relaxed clock analyses, however, can to a large extent be attributed to a higher nonsynonymous substitution rate as also indicated by a higher dN/dS.

Figure 5.

Bayesian estimates of synonymous and nonsynonymous substitution rates. The first and second panel summarize absolute rates of synonymous (r_S) and nonsynonymous (r_N) substitution, respectively. The third panel summarizes $r_{\mathrm{N}}/3*r_{\mathrm{S}}$; an ML estimate of dN/dS is also included as a grey cross (cf. Section 2). The boxplot colors follow the subtype colouring in Fig. 3.

The comparison of independent rate estimates to a summary of the branch-specific rates under an UC clock model in the group M analysis indicates a pronounced smoothing effect of the UC clock model on discrete rate differences across clades in the joint analysis (Fig. 4A). Except for the subtype D tMRCA estimate, which is associated with considerable uncertainty, the impact of the smoothing effect on tMRCA estimation is, however, not very pronounced (Fig. 4B). While joint posterior mean tMRCA estimates can be either more recent (subtypes A, D, and F) or older (subtypes B and C) compared to the independent estimates, such differences remain limited when taking into consideration the credible intervals of the estimates. So, although the joint estimates for the subtype tMRCAs may be somewhat more biased, they benefit from considerable shrinkage in uncertainty.

Based on the rate differences observed in the independent analyses, the ME molecular clock model for the group M data was set up with a fixed effect on the subtype B clade and a different shared fixed effect on the subtypes D and F clades. In line with expectations from the independent analyses, the ME model yields a positive effect estimate (on the log scale) for the subtype B rate (posterior mean: 0.221, 95% HPD [0.164, 0.272]) and a negative effect estimate on the subtypes D and F rate (−0.067 [−0.126, −0.027]). The model also demonstrates significant additional rate variation among branches as indicated by the posterior estimate for the standard deviation of the normal distribution over the random effects (0.184 [0.157, 0.211]). The ME rate estimates for the different subtypes generally fall in between the independent and joint UC rate estimates (Fig. 4A), and enjoy the smallest uncertainty. Only the subtype B ME rate is larger than both these estimates in agreement with the relatively large effect size estimated for this clade. The effect on subtype tMRCA estimates is relatively subtle (Fig. 4B), with intermediate age estimates for subtypes B and D, but slightly older age estimates for the other subtypes. In line with the limited differences for the subtype ages, the estimated HIV-1 group M tMRCA under the ME model is only marginally older (1918 [1910, 1926]) than the estimate under the UC model (1923 [1912, 1932]) indicating that, in this case, the major rate differences among subtypes do not have a strong impact on estimates of the origin of HIV-1 group M.

Our group M data set includes short sequence stretches from samples dating back to 1959 (ZR59; Zhu et al. 1998) and 1960 (1960A; Worobey et al. 2008), as well as a newly obtained near complete genome from a DRC sample dating back to 1966 (DRC66; Gryseels et al. 2019). We estimate the age of these tips in order to assess the broad accuracy of the inferred phylogenetic time scale. As expected, ZR59 is a sister lineage of subtype D (but with moderate posterior probability = 0.68), 1960A clusters within subtype A (basal to sub-subtype A4) and DRC66 falls basal to subtype C (Fig. 6). The credible intervals for the tip age estimates ([1949, 1964], [1952, 1980], and [1953, 1971] for ZR59, 1960A, and DRC66, respectively) all include the true age of the sample. In line with the subtle differences in tMRCA estimates between UC and ME, this is also the case for the tip date estimates under the UC model (data not shown).

Figure 6.

HIV-1 group M maximum clade credibility tree estimated using the mixed effects clock model. All subtype clades, except for subtype A, are represented as a single cartoon clade. The boxplot colouring by subtype follows the colors in Fig. 3. Because 1960A falls in subtype A as a sister clade to sub-subtype A4, we split up this subtype into a sub-subtype A1 clade (which also contains A3 and A6 strains) and sub-subtype A2 and A4. The marginal posterior age distribution for the 1959, 1960, and 1966 sequences are represented by a violin density (yellow, red, and orange, respectively) that is cut at the credible intervals. The sampling years of these sequences are represented by a dotted line within these violin densities. For the subtype clade tMRCAs and the nodes ancestral to these clades, blue node bars represent the node height credible intervals. The node circle sizes and colouring for these nodes are proportional to the respective posterior probability support values.

4. Discussion

In this study, we evaluate an ME molecular clock model to estimate divergence times in the presence of mixed sources of evolutionary rate variation. The model combines the concept of local molecular clocks, which allow specifying different rate parameters a priori to different collections of branches in a phylogeny (Yoder and Yang 2000; Worobey, Han, and Rambaut 2014), with the concept of UC molecular clocks, which draw branch-specific rates from an underlying distribution (Drummond et al. 2006). While the latter has grown into the default relaxed molecular clock choice in viral evolutionary studies, it is not flexible enough to accommodate discrete rate variation among a select number of clades or lineages. This has been demonstrated for different HIV-1 group M subtypes, calling into question the accuracy of tMRCA estimates (Wertheim, Fourment, and Kosakovsky Pond 2012). We note that our ME clock model is different from the mixed clock model recently developed by Lartillot, Phillips, and Ronquist (2016) because in the latter the correlated clock model component consist of a Brownian relaxed clock. As opposed to UC clocks, Brownian-like or autocorrelated clock models have not found much use in viral evolutionary studies. However, they may prove useful in specific cases and they could potentially be combined with the FL clock effects we use in our ME model.

Vrancken et al. (2014) introduced the ME model to quantify HIV-1 evolutionary rate differences within and between hosts in an extensively sampled known transmission history. In this case, the relative order and timing of divergence events could be constrained based on known time intervals for transmission in a custom coalescent model. Here, we propose a more general implementation of the ME model that allows an arbitrary number of fixed effects, and we assess its performance for divergence time estimation without particular node constraints. By examining relatively simple scenarios that were previously simulated to illustrate problems with UC molecular clock applications (Wertheim, Fourment, and Kosakovsky Pond 2012), we demonstrate good performance in terms of relative error and coverage even when sequences are simulated under more parsimonious molecular clock models. However, we caution against over-interpreting the lower ME mean relative errors under these simpler scenarios (e.g. relative to the FL clock) as we demonstrated such differences are impacted by different prior specification. Despite this and the limited exploration of our simulations, they reassure us that the true values of the model’s underlying parameters can be reasonably learned.

In our ME clock analyses, we do not assess the significance of the fixed effects for branch covariates. Confronted with similar problems in our evolutionary framework, we have shown that a Bayesian stochastic search variable selection procedure can successfully estimate Bayes factor support values for inclusion of covariates. In fact, such a procedure lies at the basis of identifying a number of unknown rate changes in the tree in the RL molecular clock approach (Drummond and Suchard 2010). It would be relatively straightforward to place spike-and-slab priors (Madigan and Raftery 1994) on the fixed effects within the ME clock model and simultaneously estimate their inclusion probabilities. Alternatively, Vrancken et al. (2014) demonstrated how to compute Bayes factor support for a fixed effect through the ratio of posterior odds over the prior odds that the rate on a collection of branches is different from the background rate. However, we do not pursue testing the significance of fixed effects here because the specification of these effects arose from prior analyses of the same data that we subsequently analyse using the ME model. Testing significance using the same data from which the hypotheses are derived would be a data dredging exercise. For the same reason and to avoid identifiability issues, we also remain relatively sparse in our fixed effects specification in the ME model.

In many cases, it may prove challenging to adequately partition the tree for fixed effects specification. Here, we rely on the HIV-1 group M subtype classification and separate rate estimates for the corresponding clades to specify our ME model. In this case, we cannot extend the fixed effects specification to deeper branches, but we hope that random effects accommodate rate differences on these branches. In addition, extensive sampling from Central Africa has revealed divergent lineages that obfuscate the subtype structure (Rambaut et al. 2001; Lihana et al. 2012). If complete genome sequences would be available for such lineages, their inclusion would complicate the specification of the fixed effects. For such challenging scenarios, it may be useful to examine whether an RL clock can assign rate changes to a select number branches with reasonable credibility, which could then serve as the basis for fixed effects specification in the ME model.

What underlies the evolutionary rate differences between the HIV-1 M subtypes remains an important question. Codon substitution model analyses indicate that the lower subtypes D and F rate is also reflected in synonymous substitution rates, which could point at different mutation rates or generation time differences. Although the latter could be the consequence of different replication rates, subtype D has been associated with faster disease progression (see, e.g. Kaleebu et al. 2001), so this stands at odds with the expected relationship between replication rate and disease progression (Lemey et al. 2007) and may point at an impact of the transmission dynamics on evolutionary rates (Maljkovic Berry et al. 2007; Vrancken et al. 2015). The high subtype B evolutionary rate could be attributed to differences in selective pressure. This can perhaps be explained by the fact that this subtype represents the founder effect of HIV-1 lineage from Africa into a predominantly Caucasian population with a distinct immunological profile (e.g. in terms of HLA variants and HLA haplotypes). Site-specific selection analyses may further clarify whether this founder effect is indeed associated with a stronger immune response and viral adaptation. To illustrate the plausibility of this scenario, Snoeck et al. (2011) mapped sites under positive selection in HIV-1 subtype B and found antibody epitopes to be significantly associated with positive selection across the genome, while CD4 and CD8 T-cell epitopes were significantly associated with positive selection in gp41 and in gag and gp120, respectively. If the evolutionary rate increase was indeed associated with the specific introduction of subtype B in North America, the fixed effect would be more appropriately specified on the North American subcluster that is nested within the Caribbean subtype B diversity (cf. Worobey et al. 2016). Finally, we acknowledge that alternative explanations may exist for evolutionary rate differences between subtypes, including differences in undetected levels of recombination, different risk group compositions (Vrancken et al. 2015), and differences in substitution patterns (Hilton and Bloom 2018).

Our HIV-1 complete genome analyses of separate subtypes reveals evolutionary rate differences that are not entirely consistent with those found by Wertheim, Fourment, and Kosakovsky Pond (2012). In contrast with our estimates, Wertheim, Fourment, and Kosakovsky Pond (2012) found a lower rate for subtype C and a relatively higher rate for subtype F. This could be due to differences in the data set used, in particular due to their focus on the conserved pol gene for which the temporal signal is likely to be weaker than for complete genome data. It is also possible that evolutionary rate differences vary across the genome, which can be modelled by partitioning and fitting partition-specific molecular clock models (Patiño-Galindo and González-Candelas 2017). Alternatively, genome evolution may be characterized by a more general process of heterotachy, in which specific sites switch substitution rate in particular lineages. If that is the case, it may be useful to examine the use of more complex models such as Markov-modulated substitution processes that allow sites to switch between different rates throughout the phylogeny (Gascuel and Guindon 2007).

A comparison of ME and UC clock model estimates indicates a limited impact of the major differences in rate between subtypes on the tMRCA estimation of HIV-1 group M. The somewhat older tMRCA estimate under the ME model compared with the UC clock model runs contrary to the expectations by Wertheim, Fourment, and Kosakovsky Pond (2012) of a younger tMRCA. However, these expectations are based on the relatively simple simulation scenarios and the impact may depend on the degree of rate variation and how it is distributed in the phylogeny. The complete genome data suggested the largest rate difference between subtypes B and D, which make up sister clades in group M. The smoothing effect of the UC clock model may therefore have the largest impact on the age estimates of both subtypes and the B&D MRCA, but it has less impact on deeper nodes in the tree including the root node. In this respect, it is worth noting that for both models the posterior age estimates for the sequences for three old samples approximate the true age very well, which provides reasonable reassurance of the accuracy to the estimated time scales.

Arguably more important than the clock model in our case is the use of complete genome data to estimate the tMRCA of HIV-1 group M. In Fig. 7, we compare our estimates to a series of previous estimates. In comparison to the previous most recent estimate by Faria et al. (2014) obtained using similar methodology for env C2V3 sequences, which was already relatively precise (1920 [1909, 1930]), the credible intervals of our estimates are further reduced by 50 per cent.

Figure 7.

tMRCA estimates for HIV-1 group M obtained by different studies. We summarize the estimates obtained by Korber et al. (2000), Salemi et al. (2001), Yusim et al. (2001), Worobey et al. (2008), Faria et al. (2014) and compare them to the uncorrelated (UC) and mixed effects (ME) model estimates for our complete genome data. For Yusim et al. (2001), we include the estimates based on the approach by Korber et al. (2000) (1) and those based on a relaxed clock model (2).

In conclusion, the ME clock provides a useful model to estimate divergence times when both discrete variation among lineages or clades and random noise affect the rate of evolution in phylogenetic histories. For HIV-1 group M, complete genome data suggest significant rate variation among subtypes that the ME model adequately captures, thereby addressing the problem put forward by Wertheim, Fourment, and Kosakovsky Pond (2012). The impact on divergence time estimates, in particular on the origin of HIV-1 group M, remains limited and the use of complete genome data to reduce estimation uncertainty appears to be more important than molecular clock model choice.