Abstract
The objective of this research was to examine the influence of nonideal sorption/desorption on the transport of PFAS in soil, with a specific focus on characterizing and quantifying potential extended, mass-transfer-limited elution behavior. PFOS was used as a representative PFAS, and miscible-displacement experiments were conducted with two soils comprising contrasting geochemical properties. The influence of nonlinear, rate-limited, hysteretic, and irreversible sorption/desorption on transport was investigated through experiments and model simulations. The breakthrough curves measured for PFOS transport in the two soils were asymmetrical and exhibited extensive elution tailing, indicating that sorption/desorption was significantly nonideal. The widely used two-domain sorption-kinetics (TDSK) model could not fully simulate the observed transport behavior, whereas a multi-rate model employing a continuous distribution of sorption domains (CDMR) was successful. The overall results indicated that sorption/desorption was significantly rate-limited, and that nonlinear, hysteretic, and irreversible sorption/desorption had minimal impact on PFOS transport. Comparison of PFOS transport data to data reported for two hydrophobic organic contaminants (HOCs) showed that the HOCs exhibited much more extensive elution tailing, likely reflecting differences in sorption/desorption mechanisms. The projected influence of rate-limited sorption/desorption on PFOS transport at the field scale was investigated through simulation. The results of the study suggest that rate-limited sorption/desorption may affect the field-scale transport of PFOS and other PFAS for systems influenced by transient or short-residence-time conditions, and in some cases could possibly increase the amount of flushing required to reduce PFOS concentrations to levels below those associated with human-health concerns.
Keywords: perfluoroalkyl substances, PFAS, sorption, nonlinear, rate-limited
1. Introduction
The transport and fate behavior of per and polyfluoroalkyl substances (PFAS) in the subsurface has become of great interest as concerns expand over the potential human-health impacts of PFAS contamination of soil and groundwater (1–4). Adsorption by soil is a primary process influencing the transport and fate of PFAS in the subsurface. Characterizing and quantifying the impact of adsorption on PFAS transport is necessary for accurate risk assessments and for developing and implementing effective remediation strategies. Research conducted over the past decade has demonstrated that PFAS adsorption is complex and is affected by both the physicochemical properties of the individual PFAS and the geochemical properties of the soil and solution, as discussed in a recent review (5).
Despite the great interest in PFAS transport behavior, very few miscible-displacement studies have been conducted to date to specifically examine the impact of adsorption on PFAS retention and transport in geomedia. McKenzie et al. (6) investigated the transport of perfluorooctanoic acid (PFOA), perfluorooctane sulfonic acid (PFOS), and other PFAS in a loamy sand. Lyu et al. (7) and Aly et al. (8) investigated the transport of PFOA and PFOS in quartz sands. Lv et al. (9) examined the transport of PFOA in quartz sand and in limestone. Brusseau et al. (10) investigated the transport of PFOS in a quartz sand and in a soil. The majority of the prior research has focused on PFAS transport in ideal, geochemically simple porous media. It is anticipated that the magnitude and complexity of PFAS adsorption will be greater for transport in soils.
One aspect critical to fully understanding and modeling solute transport is determining the potential influence of so-called nonideal sorption/desorption processes, including nonlinear, rate-limited, hysteretic, and irreversible behavior. Prior miscible-displacement studies of the transport of hydrophobic organic contaminants such as trichloroethene and atrazine in geomedia have demonstrated that nonlinear and rate-limited sorption/desorption can cause nonideal transport behavior characterized by asymmetrical breakthrough curves and extensive elution tailing (11–19). This phenomenon is rarely examined, and none of the prior PFAS transport studies specifically investigated extended elution behavior.
Another important component of characterizing solute transport is the appropriate selection and application of robust mathematical models. Transport data reported in the prior PFAS miscible-displacement studies were simulated with a variety of mathematical models. Models based on ideal (linear, instantaneous) sorption were used by McKenzie et al. (6) and Aly et al. (8). Models accounting for nonlinear and/or rate-limited sorption/desorption were used in the studies by Lv et al. (9) and Brusseau et al. (10). A detailed investigation of the applicability of these and other transport models for simulating PFAS transport has not yet been presented.
The objective of this research is to examine the influence of nonlinear, rate-limited, hysteretic, and irreversible sorption/desorption on the transport of PFAS in soil, with a specific focus on characterizing and quantifying potential mass-transfer-limited elution behavior. PFOS is used as a representative PFAS, and miscible-displacement experiments are conducted with two soils comprising contrasting geochemical properties. Two different solute-transport models incorporating nonideal sorption/desorption are used to simulate PFOS transport. The results obtained for PFOS are compared to transport data measured for a standard hydrocarbon surfactant and for select HOCs.
2. Materials and Methods
2.1. Materials
PFOS (CAS# 1763-23-1, Sigma-Aldrich- 98% purity) was the representative PFAS used for the experiments. Sodium dodecylbenzene sulfonate (SDBS) was used as a representative sulfonated hydrocarbon surfactant for comparison. Disodium 2-naphthol-3,6-disulfonate (DNDS) (CAS #135–51-3, Johnson Matthey Co.) was also used and represents a sulfonated non-surfactant compound comprising a naphthalene core with two sulfonate and one hydroxyl functional groups. Previously published data reported for two HOCs are used for additional comparison (14,18). Pentafluorobenzoic acid (99%, Strem Chemicals) was used as the nonreactive tracer (NRT). This compound is neither a PFAS nor a surfactant. It has been widely used as an NRT for transport studies employing a diverse range of porous media (e.g., refs 7,10,14–17). It is useful as an NRT for characterizing PFOS transport given their similar aqueous diffusion coefficients (SI).
Two soils were used in the experiments. The two media have similar median grain diameters, but quite different geochemical properties (Table 1). The Eustis soil (siliceous, thermic Psammentic Paleudults) is composed primarily of quartz, with small fractions of feldspar (0.5%) and clay minerals (1.7%, essentially all kaolinite). It has a total organic-carbon content of 0.38%, consisting of approximately 37% hard carbon (kerogen and black carbon) and 63% soft carbon (humic/fulvic acids, lipids). It has a relatively low metal-oxide content. The Vinton soil (sandy, mixed, thermic Typic Torrifluvent) consists of 54% silica, 36% feldspar, 3% amphibole, and 4.7% clay minerals. The clay minerals consist of similar proportions of kaolinite, vermiculite, and illite, with small fractions of montmorillonite and amorphous silica. It has a lower (0.1%) organic-carbon content and a higher metal-oxide content.
Table 1.
Properties of porous media. From Santamaria et al. (62).
| Porous Medium | Sand (%) | Silt (%) | Clay (%) | TOC†(%) | Median grain diameter d50 (mm) | Uniformity coefficient Uc (d60/d10) | Pore Diameter‡(μm) |
Particle density (g cm−3) | SiO2% | Fe§ μg/g | Al§μg/g | Mn§ μg/g | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| >100 | 100–10 | <10 | ||||||||||||
| Eustis | 95 | <1 | 4.4 | 0.38 | 0.27 | 2.3 | 8 | 81 | 11 | 2.64 | 97.7 | 310 | 690 | 19 |
| Vinton | 96 | 1.5 | 3.0 | 0. 1 | 0.26 | 2.0 | 21 | 61 | 18 | 2.69 | 54.4 | 1,700 | 1,400 | 130 |
TOC = total organic carbon
Percent of pores with designated size, determined from capillary pressure-saturation curves measured under primary drainage.
Elements dissolved from soils in 5 M HNO3 extractions
A synthetic groundwater solution was used as the background electrolyte for the experiments. The major cations in this synthetic groundwater (concentration, mg/L) are Na+1 (50), Ca+2 (36), Mg+2 (25), and major anions are NO3−1 (6), Cl−1 (60), CO3−2/HCO3−1 (133), and SO4−2 (99). The pH and ionic strength of the groundwater solution are 7.7 and 0.01M, respectively. Solutions were prepared using distilled, deionized water.
PFOS input concentrations (C0) of ~10 mg/L were used for the experiments. These concentrations are in the upper range of concentrations reported for groundwater (e.g., 20). They would also be representative of anticipated soil pore-water concentrations of PFAS in highly contaminated soils, such as those present at fire-training areas (21–22). The use of this higher concentration promotes characterization and quantification of potential asymptotic behavior associated with extended elution tailing. The effective analytical range for DNDS was extended by using a C0 of 100 mg/L.
2.2. Miscible-displacement Experiments
The columns used in this study were constructed of acrylic or stainless steel to minimize interaction with PFOS, and were 15–20 cm long with inner diameters of 2–2.5 cm. Porous plates were placed in contact with the porous media on the top and at the bottom of the column to support the media and to help promote uniform distribution of solution. Precision HPLC pumps were used to provide constant flow of solution.
The columns were packed with air-dried soil to obtain uniform bulk densities. The columns were oriented vertically for all experiments. Each column was first saturated with water by introducing water at a low flow rate (~0.05 mL/min) into the bottom of the column. Experiments were conducted with the nonreactive tracer to characterize the hydrodynamic properties of the packed columns. Experiments were then conducted with PFOS, SDBS, or DNDS to characterize the nature and impact of solid-phase sorption on transport. The experiments were conducted with a flow rate of 1 mL/min, equivalent to a mean pore-water velocity of ~30 cm/hr.
The PFOS experiments conducted for this work are presented in Table 2. Three sets of PFOS experiments were conducted for each soil. The first set replicates the standard method used for most miscible-displacement studies, and that was employed in the prior PFAS experiments, which is focused on characterizing the bulk portion of the breakthrough curve with minimal characterization of long-term elution behavior. A second experiment (Experiment 1b) was conducted for Vinton as a part of set 1, wherein the input pulse was extended to focus on potential arrival-wave tailing. The second set of experiments was conducted over an extended timeframe to specifically characterize potential long-term, asymptotic elution behavior. All experiment conditions were identical for sets 1 and 2, with the exception of the extended timeframe for set 2 and the longer step input for experiment 1b. Different column packs were used for sets 1 and 2.
Table 2.
Column experiments for PFOS.
| Experiment | Input Pulsea | Recoveryb (%) | R | Kd (cm3/g) |
|---|---|---|---|---|
| Eustis Set 1 | 7 | 96.5 | 3.6 | 0.56 |
| Eustis Set 2 | 15.5 | 100.2 | 4.2 | 0.76 |
| Vinton Set 1a | 5 | 94.0 | 2.8 | 0.48 |
| Vinton Set 1b (arrival wave only) | 15 | - | 3.0 | 0.53 |
| Vinton Set 2 | 17 | 98.3 | 3.3 | 0.54 |
Pore volumes
Recovery is based on integration of effluent concentrations
The third set of experiments comprised a contaminant-aging study to examine the impact of extended PFOS contact with the soil on retention and elution behavior. In this case, approximately 15 pore volumes of PFOS solution were injected into columns packed with the two soils. The injections were stopped and the columns were sealed with the PFOS solution residing within. The columns were stored for ~5 days, after which another 15 pore volumes of PFOS solution were injected. This two-step procedure was repeated over a period of approximately two weeks. A final injection of PFOS solution was implemented, followed immediately by injection of the SGW solution to initiate PFOS elution. With the exception of the extended contact of PFOS solution, all experiment conditions were identical to those employed for the prior miscible-displacement experiments.
2.3. Batch Sorption Experiment
A set of batch experiments was conducted to measure PFOS sorption for the two soils. A concentration range spanning three orders of magnitude representing the approximate range of the miscible-displacement experiments was used (initial concentrations of 0.01, 0.1, 1, and 10 mg/L). The PFOS solutions were prepared with the same SGW solution used for the miscible-displacement experiments. Approximately 15 mL of solution and 7.5 g of soil were placed into 20-mL glass vials. Triplicate vials were prepared for each concentration for both soils. Control sets containing solution but no soil were also created in triplicate for each concentration. Vials were capped and covered to avoid exposure to light. The experiment was conducted for 10 days, at a temperature of ~23 0C. The vials were agitated periodically rather than continuously to minimize potential for particle abrasion.
2.4. Analytical Methods
The pentafluorobenzoic acid and SDBS samples were analyzed by ultraviolet-visible (UV-Vis) spectrophotometry (Shimadzu, model 1601) at wavelengths of 262 and 226 nm, respectively. DNDS was analyzed using UV-Vis (273 nm) for higher concentrations and fluorescence spectrophotometry (Hitachi F-2000, excitation wavelength = 277 nm and emission wavelength = 462 nm) for lower concentrations. The quantitative detection limits (QDL) for UV-Vis and fluorescence are approximately 1 and 0.001 mg/L, respectively. The higher QDL for UV-Vis limits the ability to examine extended elution behavior for SDBS. Conversely, the QDL for fluorescence-spectrophotometric analysis of DNDS is similar to that for PFOS analysis reported below, thereby providing the opportunity for direct comparison of asymptotic elution.
PFOS samples were analyzed by two methods, with MBAS used for experiment set 1 and LCMS used for experiment sets 2 and 3 and for the batch experiment. A preliminary test demonstrated reasonable correspondence between the two methods (see Figure SI-1 in the Supplemental Information file). The first method employed the methylene blue active substances (MBAS) assay. This is a standard method used to quantify anionic surfactant concentrations (ASTM D2330–02), and has been used successfully for PFAS analysis under conditions wherein a single PFAS is present (10,23,24). Detailed description of the method is provided in the references cited. The quantifiable detection limit is ~0.4 mg/L for PFOS.
The second method for PFOS analysis employed High Performance Liquid Chromatography tandem mass spectrometry (LCMS). The analysis employed a Waters Alliance 2695 LC coupled to a Micromass Quattro Ultima Triple Quadrupole MS system, using negative electrospray ionization (ESI-). A Thermoscientific Betasil™ C18, 2.1 × 150mm, 5 μm particle size analytical column was used. Aqueous samples of 3 or 5 μL volume were injected directly. Elution was performed using two eluents, with a flow rate of 0.2 mL/min. Eluent A comprised water + 5 mM ammonium acetate while eluent B consisted of 90% acetonitrile + 10% water + 5 mM ammonium acetate. From 0 – 4.49 min, the solvent gradient was 80% A and 20% B. For 4.5 – 5 min, the solvent gradient was 4% A and 96% B. For 5 – 20 min, the solvent gradient was isocratic, comprising 100% B. The column was re-equilibrated for 15 min between samples at the initial conditions. The column temperature was maintained at 30 °C.
Standard QA/QC protocols were employed. Blanks, background samples, and check standards were analyzed periodically for each sample set. The results for the first two were lower than the quantifiable detection limit. The coefficients of determination (r2) for the calibration curves were larger than 0.99. The QDL is ~0.2 μg/L for PFOS. Background aqueous samples collected from the column effluent before injection of PFOS revealed no measurable concentrations or other interferences for all experiments.
2.5. Data Analysis
Two solute-transport models were used for the analysis, differing in the manner in which sorption-desorption kinetics are represented. The first model employs the standard two-domain approach, i.e., the two-domain sorption-kinetics (TDSK) model. The equations describing nonlinear, rate-limited adsorption-desorption of solute for the two-domain model are given as:
| (1) |
| (2) |
| (3) |
where C is the solution-phase solute concentration (M L−3), S1 is the sorbed-phase concentration (M M−1) for the “instantaneous” sorption domain, S2 is the sorbed-phase concentration (M M−1) for the rate-limited sorption domain, Kf is the Freundlich sorption coefficient (L3N M−N) related to the sorption capacity, N is the Freundlich exponent which characterizes the degree of nonlinearity, F is the fraction of sorbent for which sorption is instantaneous, and k2 is the first-order desorption rate coefficient (T−1). Note that the Freundlich isotherm is used because it is the mostly widely used nonlinear isotherm function for many contaminants of interest, including PFAS.
The following nondimensional equations describe one-dimensional solute transport governed by steady state water flow and nonlinear, rate-limited sorption (25,26):
| (4) |
| (5) |
with the following definitions for the nondimensional parameters:
| (6a) |
| (6b) |
| (6c) |
| (6d) |
| (6e) |
| (6f) |
| (6g) |
| (6h) |
where C0 is the solute input concentration (M L−3), v is the mean pore-water velocity (L T −1) (with v = q/θ), q is Darcy flux (L T−1), x is distance, L is column length, D is the dispersion coefficient (L2 T−1), ρb is soil bulk density (M L−3), and θw is volumetric soil-water content (porosity for water-saturated systems).
The parameter P is the Peclet number, R is the retardation factor, β is the fraction of retardation that is effectively instantaneous, and ω is the Damkohler number (nondimensional mass-transfer rate parameter). Values for these parameters must be determined to solve solute transport. The dispersivity and associated Peclet number are obtained from analysis of the nonreactive tracer breakthrough curve. The retardation factor, R, is calculated by moment analysis of the PFOS breakthrough curves. Hence, values for P and R for simulating PFOS transport were obtained independently and not from curve-fitting of the PFOS data. The parameters β and ω, representing rate-limited sorption/desorption effects on transport, are obtained by using a nonlinear least-squares optimization program.
While the two-domain approach is widely used, it has been shown to be inadequate for simulating the extensive, lower-concentration elution tailing often observed for long-term flushing of contaminated porous media. Such observations have led to the use of solute-transport models that incorporate a continuous distribution of domains and associated sorption/desorption rate coefficients, so-called multi-rate models (11, 27–33). This approach better represents the impact of pore/grain-scale heterogeneity on sorption/desorption.
The continuous-distribution, multirate (CDMR) model used for this study was presented in prior work (11,18,31). The parameter used to represent variable sorption/desorption kinetics is k2, which is treated as a random variable with a ln-normal distribution:
| (7) |
where μ is the mean of ln k2 and σk2 is the variance of ln k2. Variable sorption/desorption kinetics is incorporated into the advection-dispersion equation with a distribution of S and k2:
| (8) |
| (9) |
| (10) |
where m is the total number of retention domains. A value of 100 was used for m for this work based on the results of our prior studies that demonstrated this value was sufficient to capture the effective distribution (11,18,31). Three variables (F, μ, and σk2) were optimized through calibration of the model to the measured data. The model includes capability to address sorption–desorption hysteresis (18). This is accomplished by implementing two sets of sorption kinetics parameters (F, μ, and σk2), one set for the arrival wave and one set for the elution wave. A Freundlich N value of 0.85 was used as a representative value for the simulations incorporating nonlinear adsorption, based on the results of the batch experiment and prior reports in the literature for PFAS adsorption (e.g., 34,35).
3. Results
The transport of the nonreactive tracer was ideal for both soils, with sharp arrival and elution waves (minimal spreading), and retardation factors of 1 (see Figures 1 and 2). Simulations produced with the ideal advection-dispersion model, assuming a homogeneous porous medium and no retardation or mass-transfer limitations, provide excellent matches to the measured data. Dispersivities of 0.5 and 0.2 cm were determined for Eustis and Vinton, respectively. The results obtained for the nonreactive tracer tests indicate that the columns were well-packed and that water flow was uniform, with no significant preferential flow or presence of no-flow domains.
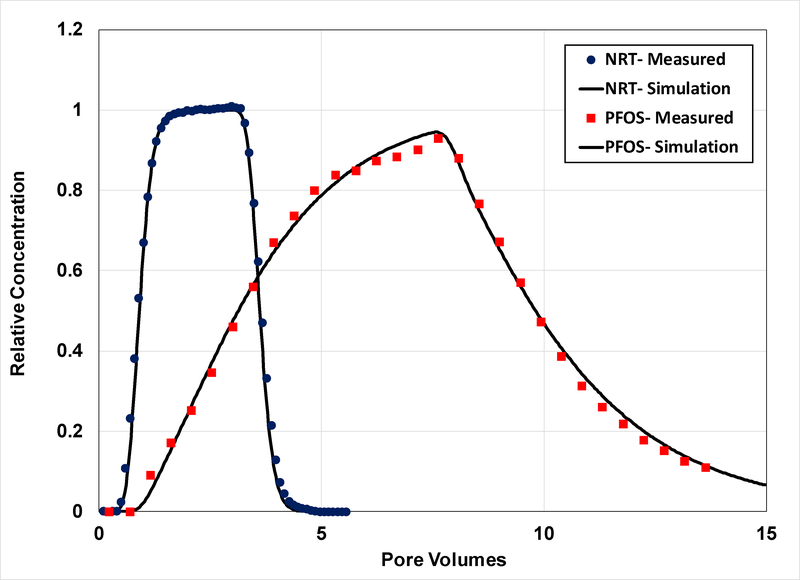
Figure 1.
Measured and simulated breakthrough curves for transport of the nonreactive tracer (NRT) and PFOS in Eustis soil (Experiment 1). The PFOS simulation is produced using a two-domain model that accounts for nonlinear, rate-limited sorption/desorption (β = 0.35, ω = 2.5).
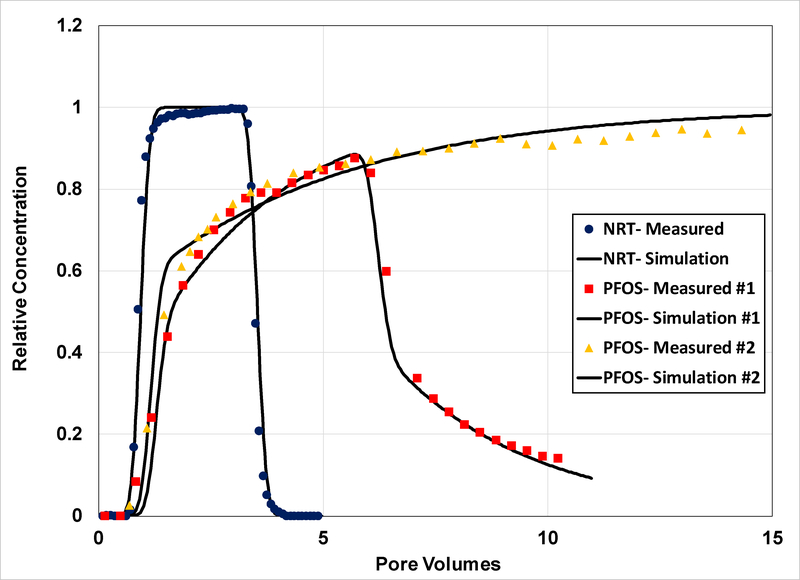
Figure 2.
Measured and simulated breakthrough curves for transport of the nonreactive tracer (NRT) and PFOS in Vinton soil (Experiments 1a and 1b). The PFOS simulation is produced using a two-domain model that accounts for nonlinear, rate-limited sorption/desorption (expt 1a: β = 0.39, ω = 0.5; expt 1b: β = 0.46, ω = 0.74).
The breakthrough curves for PFOS transport in the Eustis and Vinton soils are presented in Figures 1 and 2, respectively, for the first set of experiments. The breakthrough curves are noticeably asymmetrical, with prominent arrival-wave and elution-wave tailing. The extensive arrival-wave tailing is especially notable for Vinton experiment #1b (Figure 2), wherein an extended step input of tracer was employed. The observed behavior indicates the influence of nonideal sorption/desorption on transport. The measured retardation factors are 3.6 and 2.9 for transport in Eustis and Vinton, respectively (Table 2). These translate to Kd values of 0.56 and 0.5 cm3/g, respectively.
The breakthrough curves for SDBS transport in the Eustis and Vinton soils are presented in Figure SI-2. Similar to PFOS, the breakthrough curves are asymmetrical and exhibit tailing. The measured retardation factors are 6.6 and 3.7 for transport in Eustis and Vinton, respectively, which translate to Kd values of 1.3 and 0.6 cm3/g. Adsorption of SDBS is somewhat greater than that of PFOS, especially for Eustis. This is consistent with the larger size and greater associated hydrophobicity of SDBS versus PFOS. For example, the molar volumes for SDBS and PFOS are 349 and 272, respectively.
The breakthrough curves for PFOS transport in the Eustis and Vinton soils for the second set of experiments, with a specific focus on extended elution behavior, are presented in Figures 3 and 4, respectively. The breakthrough curve for DNDS transport in Eustis soil is presented in Figure 5. The data are plotted with concentration on log-scale to specifically examine the lower-concentration elution behavior. Extended tailing behavior is clearly observed for PFOS transport in both soils and for DNDS transport in Eustis. This indicates that nonlinear, hysteretic, and/or rate-limited sorption/desorption significantly influences PFOS and DNDS transport under the extant conditions.
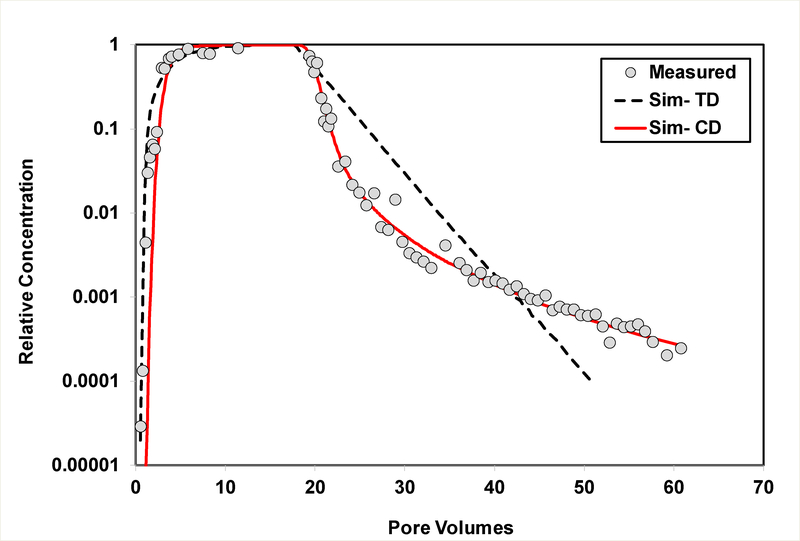
Figure 3.
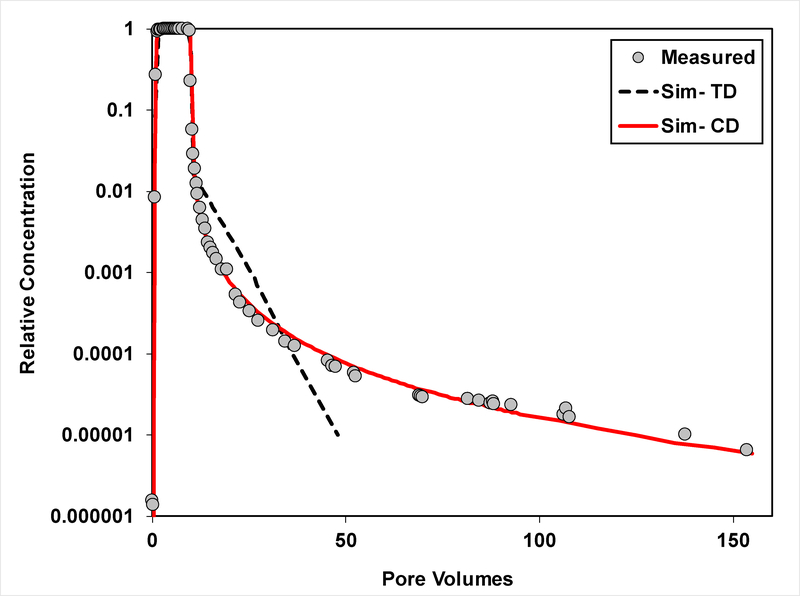
Measured and simulated breakthrough curves for transport of PFOS (Experiment 2) in Eustis soil. The simulations are produced using the two-domain sorption-kinetics model (TD) and the continuous-distribution multi-rate model (CD).
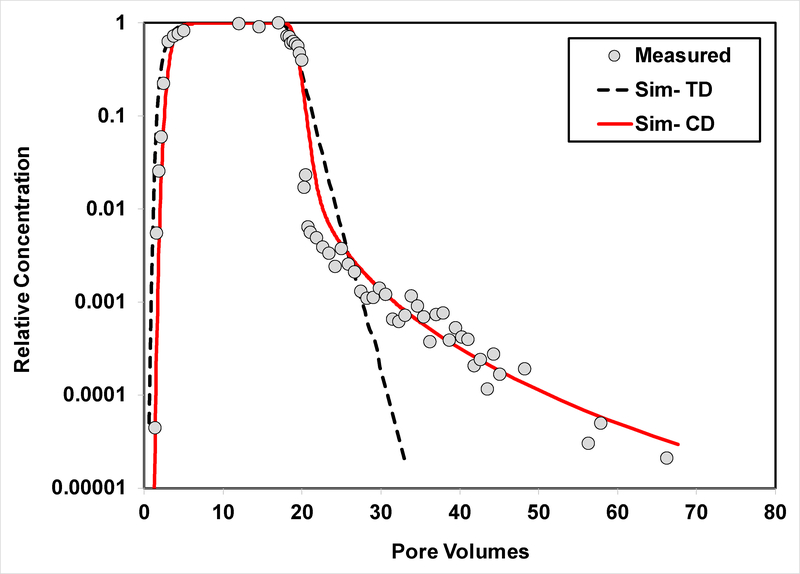
Figure 4.
Measured and simulated breakthrough curves for transport of PFOS in Vinton soil (Experiment 2). The PFOS simulations are produced using the two-domain sorption-kinetics model (TD) and the continuous-distribution multi-rate model (CD).
Figure 5.
Measured and simulated breakthrough curves for transport of DNDS in Eustis soil. The simulations are produced using the two-domain sorption-kinetics model (TD) and the continuous-distribution multi-rate model (CD).
The measured retardation factors obtained for experiment set 2 are 4.2 and 3.3 for transport in Eustis and Vinton, respectively. These correspond to Kd values of 0.76 and 0.48 cm3/g, respectively. The Kd values determined from the experiments employing extended input (Vinton #1b) or elution (Eustis #2, Vinton #2) characterization are larger compared to the values determined from the standard miscible-displacement experiments (Eustis #1, Vinton #1a).
The batch PFOS sorption results are presented in Figure SI-3. Sorption is observed to be somewhat nonlinear, and is well described by the Freundlich isotherm. However, the 95% confidence intervals for the Freundlich n variable span unity, indicating that the isotherms are not statistically different from linearity (see SI-3 figure caption). Equivalent Kd values calculated using the batch results for C0 = 10 mg/L, the influent concentration used for the miscible-displacement experiments, are 0.63 (0.2–2.4) for Eustis and 0.8 (0.4–1.8) cm3/g for Vinton (values in parentheses are 95% confidence intervals). The Kd values from the batch and miscible-displacement experiments are coincident for both soils.
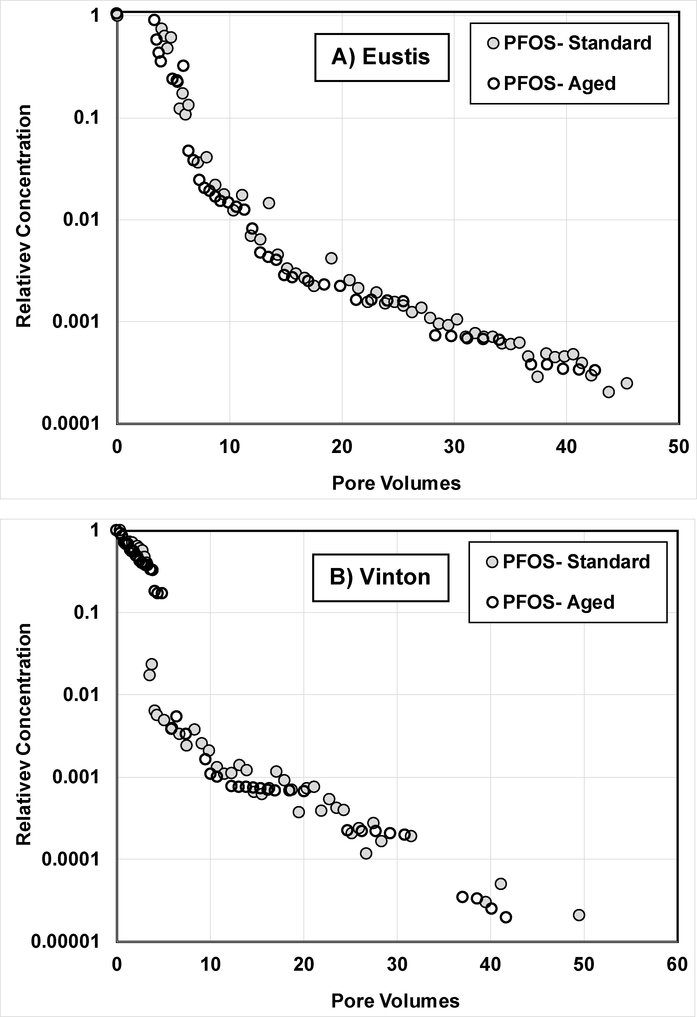
The results of the contaminant-aging experiments are presented in Figure 6. The elution curves measured for the aged media, wherein PFOS solution was in continuous contact with the soil for approximately two weeks prior to elution, are very similar to the elution curves measured for the standard miscible-displacement experiments. This similarity indicates that the significant mass-transfer constraint observed for PFOS transport under the short contact times associated with the standard miscible-displacement experiments is consistent with behavior produced under longer contact-time conditions. The observation that significant mass-transfer constraints are produced with short contact times is consistent with the results of a prior contaminant-aging study, wherein extensive elution tailing was observed for TCE transport in Eustis soil for an experiment conducted with a two pore-volume input pulse. In this case, a contact time of less than 1 h produced a sorbed phase that was relatively resistant to desorption (17). Similar results were reported for TCE transport in an aquifer material (12).
Figure 6.
Comparison of elution curves obtained for the contaminant-aging experiments (Aged) versus the experiment-2 miscible-displacement experiments (Standard).
The transport model incorporating the two-domain representation of sorption/desorption kinetics provides reasonably good simulations of the measured PFOS and SDBS data for experiment set 1 (Figures 1, 2, and SI-2). Conversely, the two-domain model cannot reproduce the extended elution tailing observed for the extended experiments (set 2), as seen in Figures 3–5. This is consistent with prior reports for HOC transport (11–15,17–19). In contrast, the continuous-distribution, multi-rate model reproduces the measured data quite well. The optimized parameter values and associated 95% confidence intervals obtained from the calibrations are reported in Table 3. The values for k2 (TDSK) and mean k2 (CDMR) are statistically similar among the different experiment sets for each of the two soils. These values are in the same range as first-order k values reported by Wei et al. (35) for PFOS sorption by several soils, which varied from 0.14 – 5.4 h−1 as determined from batch-kinetic experiments. The F values vary significantly between the two models for both soils, reflecting the difference in the conceptualization of the two models.
Table 3.
Modeling parameter values for PFOS.
| Experiment | Fa | k2 (hr−1)a,b | σk2 | Model |
|---|---|---|---|---|
| Eustis Set 1 | 0.10 (0.04–0.18) | 2.2 (1.6–2.8) | - | TDSK |
| Eustis Set 2 | 0.90 (0.85–0.95) | 3.2 (2.6–3.8) | 2.3 (1.1–3.5) | CDMR |
| Vinton Set 1a | 0.16 (0.1–0.2) | 0.9 (0.6–1.2) | - | TDSK |
| Vinton Set 1b (arrival wave only) | 0.08 (0.04–0.14) | 0.5 (0.4–0.6) | - | TDSK |
| Vinton Set 2 | 0.95 (0.92–0.98) | 1.7 (0.7–2.7) | 1.1 (0.1–2.1) | CDMR |
Values in parentheses represent the 95% confidence intervals
Represents mean k2 for CDMR model
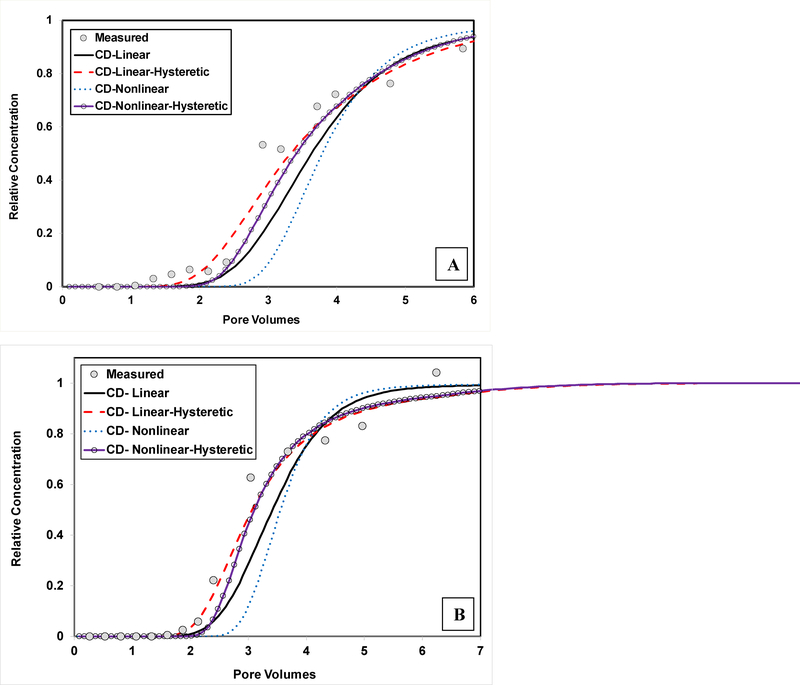
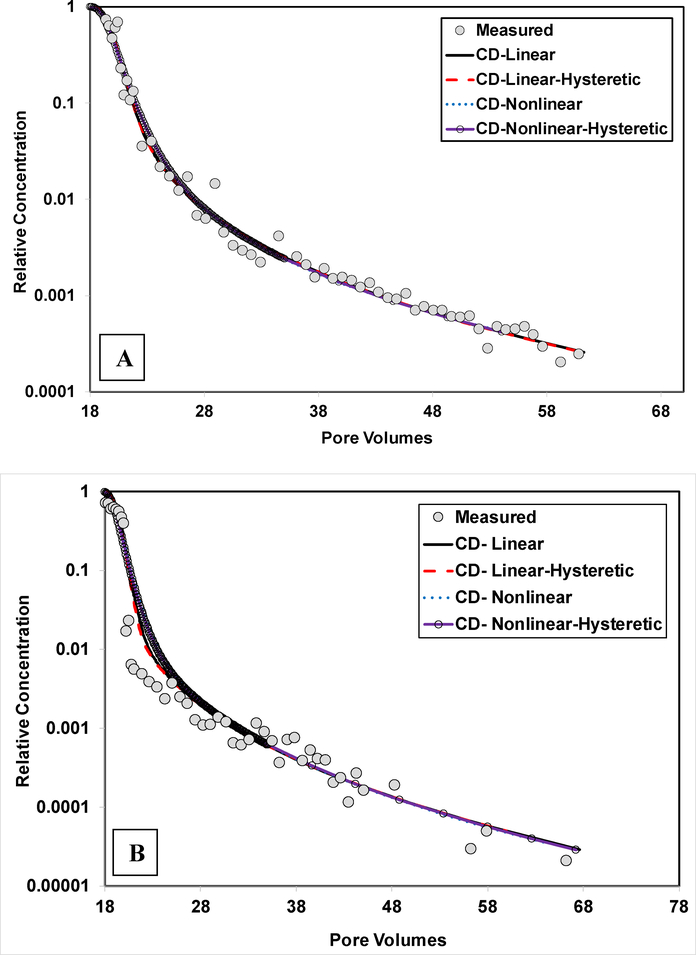
The PFOS recoveries are close to 100% for the extended experiments (Table 2). This indicates that sorption was reversible under the dynamic conditions of the miscible-displacement experiments. The influence of rate-limited, nonlinear, and hysteretic sorption/desorption on transport was examined by comparing simulations produced with and without these processes to the measured data. Simulations produced assuming instantaneous sorption/desorption cannot match the measured data (data not shown). The simulations produced with the CDMR model with linear, nonhysteretic sorption/desorption (Figures 3 and 4) are slightly improved for the arrival waves by employing hysteresis, as shown in Figure 7. Incorporating hysteresis provides additional fitting parameters, which is expected to improve curve fitting. Conversely, including hysteresis has minimal impact on the elution waves (Figure 8). Including nonlinear sorption decreases the goodness of fit for the arrival waves (Figure 7), and has minimal impact on the elution waves (Figure 8). These results indicate that the influence of irreversible, hysteretic, and nonlinear sorption on PFOS transport in these two soils is relatively insignificant and that the observed extensive elution tailing is caused by rate-limited sorption/desorption.
Figure 7.
Measured and simulated arrival waves for transport of PFOS in (A) Eustis soil (Experiment 2) and (B) Vinton soil (Experiment 2). The PFOS simulations are produced using the continuous-distribution multi-rate model with: linear, non-hysteretic sorption/desorption (CD-Linear), linear, hysteretic sorption/desorption (CD-Linear-Hysteretic), nonlinear, non-hysteretic sorption/desorption (CD-Nonlinear), and nonlinear, hysteretic sorption/desorption (CD-nonlinear-hysteretic).
Figure 8.
Measured and simulated elution waves for transport of PFOS in (A) Eustis soil (Experiment 2) and (B) Vinton soil (experiment 2). The PFOS simulations are produced using the continuous-distribution multi-rate model with: linear, non-hysteretic sorption/desorption (CD-Linear), linear, hysteretic sorption/desorption (CD-Linear-Hysteretic), nonlinear, non-hysteretic sorption/desorption (CD-Nonlinear), and nonlinear, hysteretic sorption/desorption (CD-nonlinear-hysteretic).
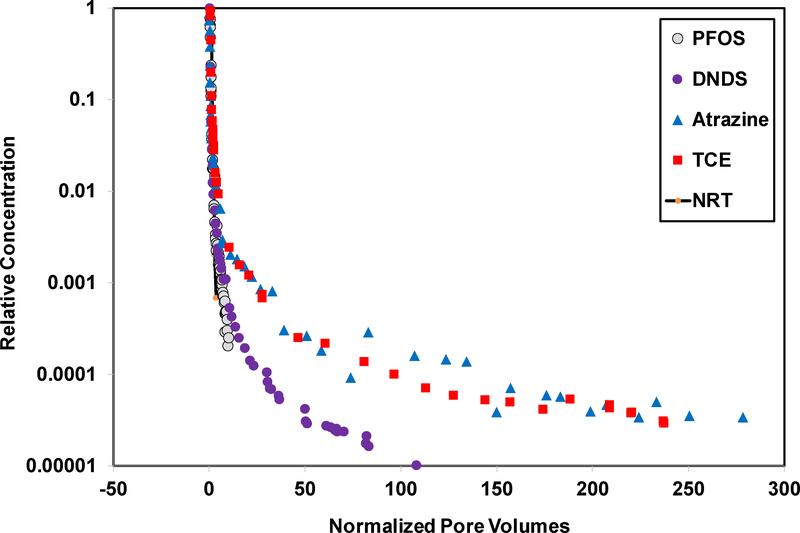
Prior miscible-displacement studies conducted by Brusseau and colleagues examined the transport of several HOCs in the Eustis soil (14,15,17,18,36–38). Representative elution-wave data sets for trichloroethene (TCE) and atrazine are presented in Figure 9 along with the PFOS, DNDS, and NRT data. The pore volume (x-axis) is normalized by the respective retardation factors of the compounds to eliminate the effect of differences in the magnitudes of retardation on the extents of tailing. The HOCs have much greater tailing compared to PFOS. It is noteworthy that the retardation factors for TCE and atrazine transport in the Eustis soil are 3 and 3.5, which are slightly smaller than that of PFOS. Hence, for similar magnitudes of sorption and retardation, TCE and atrazine exhibit much greater elution tailing compared to PFOS. Interestingly, DNDS exhibits much less tailing compared to the HOCs, whereas it has a similar extent of tailing as PFOS over the measured range of PFOS. The same data sets are presented in a dual-log plot in the SI file (Figure SI-4), which further demonstrates the differences in the extents of elution tailing between the NRT, PFOS and DNDS, and the HOCs. It is noted that the normalized elution curve for a solute undergoing linear, instantaneous sorption/desorption would be identical to that of the NRT curve.
Figure 9.
Measured elution curves for transport of PFOS, DNDS, two HOCs, and a non-reactive tracer (NRT) in Eustis soil. The pore volumes are normalized by dividing by the respective retardation factors (NRT = 1, PFOS = 4.2, DNDS = 1.2, atrazine = 3.5, and TCE = 3). The atrazine data were reported in Kempf and Brusseau (14) and the TCE data were reported in Schnaar and Brusseau (18).
4. Discussion
It is well established that the temporal first moment of solute breakthrough curves is independent of rate-limited mass-transfer constraints (see review in 39). As a result, retardation factors and associated Kd values determined from moment analysis of breakthrough curves are considered to be representative of true equilibrium sorption behavior, assuming no significant experimental limitations. The observation that R and Kd values determined from the experiments employing extended input or elution characterization are somewhat larger than the values determined from the standard miscible-displacement experiments is consistent with prior research showing their sensitivity to data truncation, especially when transport is affected by rate-limited mass transfer (e.g., 40,41). PFOS recoveries are greater for the extended experiments (see Table 2), which supports the possible influence of data truncation on the set-1 experiments.
As noted above, the Kd values determined from batch and miscible-displacement experiments were coincident for PFOS for both soils. Similar correspondence between batch and miscible-displacement Kds has been reported in prior research for other compounds (see for example discussions in 39 and 42). The correspondence between the two sets of values in this study indicates that the miscible-displacement experiments characterized true equilibrium sorption conditions. Also as noted above, the elution curves for the contaminant-aging experiments were consistent with the miscible-displacement elution curves. This supports that the miscible-displacement experiments characterized true equilibrium sorption.
Comparison of Kd values determined in this study to those reported in prior studies is difficult due to differences in geochemical properties of the different media employed. One way in which to resolve this limitation is to compare organic-carbon normalized distribution coefficients (log Koc). While the robustness of the Koc approach has potential significant uncertainty for PFAS, it is useful for discussion purposes. The log Koc values determined for Eustis and Vinton are 2.6 and 2.9, respectively (integrating column and batch data). Values in the range of 2.7–2.8 have been reported in the literature for PFOS based on batch experiments conducted with a wide range of media (34, 43–44). The values obtained in the present study are quite similar to the literature values. This supports the conclusion that the R and Kd values determined from the miscible-displacement experiments are robust and representative of equilibrium conditions. It was previously noted that sorption-rate coefficients determined in this study are similar to those reported in a prior batch-kinetic study. The results summarized in this and the preceding paragraph in total suggest that the miscible-displacement experiments conducted herein produced representative characterization of PFOS sorption behavior.
The results presented in Figure 9 indicate that the transport of the HOCs is influenced by rate-limited sorption/desorption to a much greater degree than is PFOS and DNDS. This significant difference in the magnitude of mass-transfer limitations likely reflects differences in the mechanisms mediating sorption/desorption of PFOS and DNDS versus the HOCs. Prior research has demonstrated that the sorption/desorption of HOCs in the Eustis soil is controlled by adsorption to and permeation within the soil organic carbon (15,17,36–38). Conversely, adsorption of PFOS and other PFAS can be influenced significantly by surface interactions with metal oxides and clay minerals as well as interaction with organic carbon (e.g., 34,35,43–50), similar to the adsorption behavior of hydrocarbon and bio-surfactants (e.g., 51–54). The representative characteristic times of adsorption for such surface interactions would typically be significantly shorter compared to those of permeation within organic materials.
The retardation factor and Kd measured for DNDS transport in the Eustis soil are 1.2 and 0.04 cm3/g, respectively. Recall that DNDS consists of a naphthalene core with two sulfonate groups (on opposite ends) and one hydroxyl group. One may speculate that given its molecular structure, it is unlikely that hydrophobic interactions contribute significantly to DNDS adsorption. In comparison, a Kd of 1 cm3/g was measured for sorption of naphthalene by the Eustis soil (36). The great disparity in Kd values supports the contention that hydrophobic interactions contributed minimally to DNDS adsorption. This suggests that its adsorption is governed primarily by electrostatic interactions between its functional groups and reactive constituents on the soil surface. The Kd for DNDS is more than 10-times smaller than for PFOS. The presence of the fluorocarbon tail greatly increases the contribution of hydrophobic interaction to PFOS adsorption compared to DNDS. If it can be assumed that DNDS adsorption approximates the contribution of electrostatic-based adsorption, then it can be estimated that this component contributed <10% of total PFOS adsorption for the Eustis soil. Thus, PFOS adsorption by the Eustis soil was likely governed primarily by interactions with soil organic carbon, similar to the results of prior research conducted with soils and sediments (e.g., 34,43,44,47,49).
The potential for additional sorption mechanisms beyond hydrophobic interaction can cause PFAS sorption to be considerably more complex compared to standard HOCs. This also results in PFAS sorption being more sensitive to solution and sorbent geochemical composition. The latter may provide an explanation for the difference in PFOS log Koc values reported for Eustis versus Vinton. Inspection of Table 1 reveals that Vinton soil has 3-times greater amounts of clay minerals, including expanding clays (vermiculite), and 3-times greater amounts of metal oxides compared to Eustis. The greater proportion of these soil constituents may enhance the potential for additional mechanisms to contribute to PFOS sorption for Vinton compared to Eustis. The greater contribution of multiprocess adsorption would result in a larger log Koc for Vinton considering that the contributions of all adsorption mechanisms are lumped into that parameter.
Implications
The results reported herein represent to our knowledge the first examination of the influence of nonideal sorption/desorption processes on PFAS transport in soil with a specific characterization of mass-transfer-limited elution tailing. The breakthrough curves measured for PFOS transport in two soils exhibited extensive elution tailing, indicating that sorption/desorption was significantly nonideal under the extant laboratory conditions. Based on the experiments and mathematical modeling, it was determined that the nonideal behavior was caused primarily by rate-limited sorption/desorption.
Standard miscible-displacement studies typically employ pore-water velocities and column lengths that are not representative of field conditions. A question of critical interest is the impact of rate-limited sorption/desorption on PFAS transport at the field scale. This issue was examined by conducting a set of simulations with the CDMR model wherein the mean pore-water velocity was decreased by a factor of 10 and the system length was increased by a factor of 10, resulting in an overall factor of 100 increase in mean hydraulic residence time. The simulations produced for parameter values representing PFOS and TCE transport in the Eustis soil are presented in Figure SI-5. The extent of elution tailing for PFOS is reduced but not eliminated, whereas TCE elution remains significantly rate limited. These results suggest that rate-limited sorption/desorption for PFOS may be relevant for conditions governed by relatively short residence times, such as for example, in near-well regions of induced-gradient well fields employed for remediation projects.
Concentrations of concern for potential human-health impacts of PFOS and other PFAS are much lower than for other organic contaminants. For example, the U.S. EPA recently established a lifetime health advisory level of 70 ng/L for PFOS and PFOA combined for exposure via drinking water. The number of pore volumes required to reach various effluent PFOS concentrations after the start of flushing with PFOS-free solution (i.e., elution pore volumes) can be determined from the PFOS-transport simulation presented in Figure SI-5. PFOS concentrations of 400, 70, 10, and 1 ng/L are attained after approximately 10, 13, 17, and 22 elution pore volumes, respectively. These are substantially larger than the approximately 5 elution pore volumes that would be required if sorption/desorption was instantaneous. Comparatively, the simulated effluent concentration for TCE is ~30 ug/L after 22 pore volumes of flushing (6-times above the MCL). It is important to keep in mind that the conditions for the simulations presented in Figure SI-5 represent a factor of 100 increase in hydraulic residence time, including a travel distance of 2 meters. Travel distances and associated residence times are substantially greater for many field sites, and the impact of rate-limited sorption/desorption is likely to become increasingly less significant for these greater residence times as the difference between the characteristic times of sorption/desorption and field-scale hydraulic-residence times increases. However, the results suggest that rate-limited sorption/desorption could under certain conditions increase the amount of flushing and the associated time required to reduce PFOS concentrations to levels below those associated with human-health concerns.
A full evaluation of the impact of nonideal sorption on PFAS transport in the subsurface requires consideration of the several other factors that can influence PFAS retention and transport. For transport in subsurface systems, one must consider the effects of physical and geochemical heterogeneity present at multiple scales. The impact of rate-limited sorption/desorption on PFAS transport is typically likely to be relatively minor in comparison to the impact of heterogeneity, similar to what has been observed in field-scale studies of contaminant transport in groundwater (55–57). Transport of PFAS at some contaminated sites may be complicated by the presence of co-contaminants and by the impact of remediation activities, which may affect sorption processes (6,43,58,59). Transport of PFAS in the vadose zone and in source zones containing trapped organic immiscible liquid (OIL) is complicated further by the additional retention processes of adsorption at air-water and OIL-water interfaces (2,7,10). This retention may be influenced by mass-transfer constraints, is sensitive to solution chemistry (10,60,61), and will be affected by transient conditions associated with infiltration/recharge events occurring in the vadose zone and remediation efforts that affect the disposition of the OIL. These topics require additional research and investigation to improve our understanding of the transport and fate of PFAS in subsurface systems.
Supplementary Material
Acknowledgements
This research was supported by the NIEHS Superfund Research Program (Grant #P42 ES 4940). We thank Asami Murao for her help with the DNDS experiment, and Hilary Janousek and Asma El Ouni for their help with the SDBS experiments. We thank the reviewers for their thoughtful and constructive comments.
References
- 1.NGWA (National Ground Water Association) 2017. Groundwater and PFAS: State Of Knowledge and Practice. NGWA Press, Westerville, OH. [Google Scholar]
- 2.Brusseau ML 2018. Assessing the potential contributions of additional retention processes to PFAS retardation in the subsurface. Science Total Environ. 613–614, 176–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hatton J, Holton C, DiGuiseppi B, 2018. Occurrence and behavior of per- and polyfluoroalkyl substances from aqueous film-forming foam in groundwater systems. Remediation 28, 89–99. [Google Scholar]
- 4.Anderson RH, Adamson DT, Stroo HF, 2019. Partitioning of poly-and perfluoroalkyl substances from soil to groundwater within aqueous film-forming foam source zones. J. Contam. Hydrol 220, 59–65. [DOI] [PubMed] [Google Scholar]
- 5.Du Z, Deng S, Bei Y, Huang Q, Wang B, Huang J, and Yu G 2014. Adsorption behavior and mechanism of perfluorinated compounds on various adsorbents—A review. J. Hazard. Mater 274, 443. [DOI] [PubMed] [Google Scholar]
- 6.McKenzie ER, Siegrist RL, McCray JE, Higgins CP, 2015. Effects of chemical oxidants on perfluoroalkyl acid transport in one-dimensional porous media columns. Environ. Sci. Technol 49 (3), 1681e1689. [DOI] [PubMed] [Google Scholar]
- 7.Lyu Y, Brusseau ML, Chen W, Yan N, Fu X, and Lin X 2018. Adsorption of PFOA at the air-water interface during transport in unsaturated porous media. Environ. Sci. Technol 52, 7745–7753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Aly YH, Liu C, McInnis DP, Lyon BA, Hatton J, McCarty M, Arnold WA, Pennell KD, Simcik MF, 2018. In situ remediation method for enhanced sorption of perfluoro-alkyl substances onto Ottowa sand. J. Environ. Eng 144, 04018086. [Google Scholar]
- 9.Lv X, Sun Y, Ji R, Gao B, Wu J, Lu Q, Jiang H, 2018. Physicochemical factors controlling the retention and transport of perfluorooctanoic acid (PFOA) in saturated sand and limestone porous media. Water Res. 141:251–258. [DOI] [PubMed] [Google Scholar]
- 10.Brusseau ML, Yan N, Van Glubt S, Wang Y, Chen W, Lyu Y, Dungan B, Carroll KC, Holguin FO, 2019. Comprehensive retention model for PFAS transport in subsurface systems. Water Res. 148, 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Johnson GR, Zhang Z, Brusseau ML, 2003. Characterizing and quantifying the impact of immiscible liquid dissolution and nonlinear, rate-limited sorption/desorption on low-concentration elution tailing. Water Resour. Res. 39, 61–68. [Google Scholar]
- 12.Johnson GR, Norris DK, Brusseau ML, 2009. Mass removal and low-concentration tailing of trichloroethene in freshly-amended, synthetically-aged, and field-contaminated aquifer material. Chemosphere 75, 542–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Deng J, Jiang X, Zhang X, Hua W, Crawford JW, 2008. Continuous time random walk model better describes the tailing of atrazine transport in soil. Chemosphere 70, 2150–2157. [DOI] [PubMed] [Google Scholar]
- 14.Kempf A, Brusseau ML, 2009. Impact of non-deal sorption on low-concentration tailing behavior for atrazine transport in two natural porous media. Chemosphere 77, 877–882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Russo A, Johnson GR, Schnaar G, Brusseau ML, 2010. Nonideal transport of contaminants in heterogeneous porous media: 8. Characterizing and modeling asymptotic contaminant-elution tailing for several soils and aquifer sediments. Chemosphere 81, 366–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Akyol NH, Yolcubal I, Yüksel DI, 2011. Sorption and transport of trichloroethylene in caliche soil. Chemosphere 82, 809–816. [DOI] [PubMed] [Google Scholar]
- 17.Brusseau ML, Russo AE, Schnar G, 2012. Non-ideal transport of contaminants in heterogeneous porous media: 9 - Impact of contact time on desorption and elution tailing. Chemosphere 89, 287–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schnaar G, Brusseau ML, 2014. Nonideal transport of contaminants in heterogeneous porous media: 11. Testing the experiment condition dependency of the continuous distribution rate model for sorption–desorption. Water Air Soil Pollut. 225, 2136–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Akyol NH, 2015. Characterizing and modeling of extensive atrazine elution tailing for stable manure-amended agricultural soil. Chemosphere 119, 1027–1032. [DOI] [PubMed] [Google Scholar]
- 20.Schultz MM, Barofsky DF, Field JA, 2004. Quantitative determination of fluorotelomer sulfonates in groundwater by LC MS/MS. Environ. Sci. Technol 38, 1828–1835. [DOI] [PubMed] [Google Scholar]
- 21.McGuire ME; Schaefer C; Richards T; Backe WJ; Field JA; Houtz E; Sedlak DL; Guelfo JL; Wunsch A; Higgins CP 2014, Evidence of remediation-induced alteration of subsurface poly- and perfluoroalkyl substance distribution at a former firefighter training area. Environ. Sci. Technol 48 (12), 6644–6652. [DOI] [PubMed] [Google Scholar]
- 22.Baduel C, Mueller JF, Rotander A, Corfield J, Gomez-Ramos M-J. 2017. Discovery of novel per- and polyfluoroalkyl substances (PFASs) at a fire fighting training ground and preliminary investigation of their fate and mobility. Chemo, 185, 1030–1038. [DOI] [PubMed] [Google Scholar]
- 23.Sharma R, Pyter R, Mukerjee P, 1989. Spectrophotometric determination of perfluorocarboxylic acids (heptanoic to decanoic) and sodium perfluorooctanoate and decyl sulfate in mixtures by dye-extraction. Anal. Lett. 22, 999–1007. [Google Scholar]
- 24.Moody CA, Field JA, 2000. Perfluorinated surfactants and the environmental implications of their use in fire-fighting foams. Environ. Sci. Technol 34, 3864–3870. [Google Scholar]
- 25.Brusseau ML, 1995. The effect of nonlinear sorption on transformation of contaminants during transport in porous media. J. Contam. Hydrol 17: 277–291. [Google Scholar]
- 26.Hu Q and Brusseau ML 1998. Coupled effects of nonlinear, rate-limited sorption and biodegradation on transport of 2,4-dichlorophenoxyacetic acid in soil. Environ. Toxicol. Chem 17, 1673–1680. [Google Scholar]
- 27.Chen W and Wagenet RJ, 1995. Solute transport in porous media with sorption-site heterogeneity. Environ. Sci. Tech, 29(11):2725–2734. [DOI] [PubMed] [Google Scholar]
- 28.Chen W, Wagenet RJ, 1997. Description of atrazine transport in soil with heterogeneous nonequilibrium sorption. Soil Sci. Soc. Am. J 61, 360–371. [Google Scholar]
- 29.Culver TB, Hallisey SP, Sahoo D, Deitsch JJ, Smith JA, 1997. Modeling the desorption of organic contaminants from long-term contaminated soil using distributed mass transfer rates. Environ. Sci. Technol 31, 1581–1588. [Google Scholar]
- 30.Ahn I, Lion LW, Shuler MW, 1999. Validation of a hybrid “two-site gamma” model for naphthalene desorption kinetics. Environ. Sci. Technol 33, 3241–3248. [Google Scholar]
- 31.Li Z, Brusseau ML, 2000. Nonideal transport of reactive solutes in heterogeneous porous media. 6. Microscopic and macroscopic approaches for incorporating heterogeneous rate-limited mass transfer. Water Resour. Res 36, 2853–2867. [Google Scholar]
- 32.Saiers JE, Tao G, 2000. Evaluation of continuous distribution models for rate-limited solute adsorption to geologic media. Water Resour. Res 36, 1627–1639. [Google Scholar]
- 33.Li N, Ren L, 2009. Application of continuous time random walk theory to nonequilibrium transport in soil. J. Contam. Hydrol 108 (3), 134–151. [DOI] [PubMed] [Google Scholar]
- 34.Higgins CP and Luthy RG 2006. Sorption of perfluorinated surfactants on sediments. Environ. Sci. Technol 40 (23), 7251–7256. [DOI] [PubMed] [Google Scholar]
- 35.Wei C; Song X; Wang Q; Hu Z Sorption kinetics, isotherms and mechanisms of PFOS on soils with different physicochemical properties. Ecotoxicol. Environ. Saf 2017, 142, 40–50. [DOI] [PubMed] [Google Scholar]
- 36.Brusseau ML, Jessup RE, and Rao PSC 1991. Nonequilibrium sorption of organic chemicals: elucidation of rate-limiting processes. Environ. Sci. Technol, 25, 134–142. [Google Scholar]
- 37.Nkedi-Kizza P, Brusseau ML, Rao PSC, Hornsby AG 1989. Nonequilibrium sorption during displacement of hydrophobic organic chemicals and 45Ca through soil columns with aqueous and mixed solvents. Environ. Sci. Technol, 23, 814–820. [Google Scholar]
- 38.Brusseau ML, Wood AL, and Rao PSC 1991. Influence of organic cosolvents on the sorption kinetics of hydrophobic organic chemicals. Environ. Sci. Technol, 25, 903–910. [Google Scholar]
- 39.Brusseau ML and Rao PSC 1989. Sorption nonideality during organic contaminant transport in porous media. CRC Crit. Rev. Environ. Control, 19, 33–99. [Google Scholar]
- 40.Young DF and Ball WP 2000. Column experimental design requirements for estimating model parameters from temporal moments under nonequilibrium conditions. Adv. Water Resour, 23, 449–460. [Google Scholar]
- 41.Schnaar G, and Brusseau ML (2013). Measuring equilibrium sorption coefficients with the miscible-displacement method. J. Environ. Sci. Health, Part A Environ. Sci, 48, 355–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Altfelder S, Streck T, Maraqa MA, and Voice TC 2001. Nonequilibrium sorption of organic compounds – compatibility of batch and column techniques. Soil Sci. Soc. Am. J, 65, 102–111. [Google Scholar]
- 43.Guelfo JL, Higgins CP, 2013. Subsurface transport potential of perfluoroalkyl acids at aqueous film-forming foam (AFFF)-impacted sites. Environ. Sci. Technol 47, 4164–4171. [DOI] [PubMed] [Google Scholar]
- 44.Milinovic J, Lacorte S, Vidal M, Rigol A 2015. Sorption behaviour of perfluoroalkyl substances in soils. Sci. Total Environ 511: 63–71. [DOI] [PubMed] [Google Scholar]
- 45.Zhao L, Bian J, Zhang Y, Zhu L, Liu Z, 2014. Comparison of the sorption behaviors and mechanisms of perfluorosulfonates and perfluorocarboxylic acids on three kinds of clay minerals. Chemosphere 114, 51–58. [DOI] [PubMed] [Google Scholar]
- 46.Tang CY, Fu QS, Gao D, Criddle CS, Leckie JO, 2010. Effect of solution chemistry on the adsorption of perfluorooctane sulfonate onto mineral surfaces. Water Res, 44, 2654–2662. [DOI] [PubMed] [Google Scholar]
- 47.Zhang R, Yan W, Jing C, 2015. Experimental and molecular dynamic simulation study of perfluorooctane sulfonate adsorption on soil and sediment components. J. Environ. Sci, 29, 131–138. [DOI] [PubMed] [Google Scholar]
- 48.Gao X, Chorover J, 2012. Adsorption of perfluorooctanoic acid and perfluorooctanesulfonic acid to iron oxide surfaces as studied by flow through ATR-FTIR spectroscopy. Environ. Chem 9, 148–157. [Google Scholar]
- 49.Pereira HC, Ullberg M, Kleja DB, Gustafsson JP, Ahrens L, 2018. Sorption of perfluoroalkyl substances (PFASs) to an organic soil horizon e effect of cation composition and pH. Chemosphere 207, 183–191. [DOI] [PubMed] [Google Scholar]
- 50.Li F, Fang X, Zhou Z, Liao X, Zou J, Yuan B and Sun W, 2019. Adsorption of perfluorinated acids onto soils: Kinetics, isotherms, and influences of soil properties. Sci. Total. Environ. 649, 504–514. [DOI] [PubMed] [Google Scholar]
- 51.Fink DH, Thomas GW, Meyer WJ 1970. Adsorption of anionic detergents by soils. J. Water Pollut. Control Fed, 42, 265–271. [Google Scholar]
- 52.Westall JC; Chen H; Zhang W; Brownawell BJ 1999. Sorption of linear alkybenzenesulfonates on sediment materials. Environ. Sci. Technol, 33, 3110–3118. [Google Scholar]
- 53.Noordman WH, Brusseau ML, Janssen DB, 2000. Adsorption of a multicomponent rhamnolipid surfactant to soil. Environ. Sci. Technol, 34, 832–838. [Google Scholar]
- 54.Ochoa-Loza FJ, Noordman WH, Janssen DB, Brusseau ML, and Maier RM 2007. Effect of clays, metal oxides, and organic matter on rhamnolipid biosurfactant sorption by soil. Chemo, 66, 1634–1642. [DOI] [PubMed] [Google Scholar]
- 55.Brusseau ML, Srivastava R, 1997. Nonideal transport of reactive solutes in heterogeneous porous media: 2. Quantitative analysis of the Borden natural-gradient field experiment. J. Contam. Hydrol 28, 115–155. [Google Scholar]
- 56.Brusseau ML, Srivastava R, 1999. Nonideal transport of reactive solutes in heterogeneous porous media: 4. analysis of the Cape Cod natural-gradient field experiment. Water Resour. Res. 35, 1113–1125. [Google Scholar]
- 57.Zhang Z and Brusseau ML, 1999. Nonideal transport of reactive solutes in heterogeneous porous media: 5. Simulating regional-scale behavior of a trichloroethene plume during pump-and-treat remediation. Water Resour. Res. 35 (10), 2921–2935. [Google Scholar]
- 58.McGuire ME, Schaefer C, Richards T, Backe WJ, Field JA, Houtz E, Sedlak DL, Guelfo JL, Wunsch A, Higgins CP, 2014. Evidence of remediation-induced alteration of subsurface poly- and perfluoroalkyl substance distribution at a former firefighter training area. Environ. Sci. Technol 48, 6644–6652. [DOI] [PubMed] [Google Scholar]
- 59.McKenzie ER, Siegrist RL, McCray JE, Higgins CP, 2016. The influence of a non-aqueous phase liquid (NAPL) and chemical oxidant application on perfluoroalkyl acid (PFAA) fate and transport. Water Res. 92, 199–207. [DOI] [PubMed] [Google Scholar]
- 60.Brusseau ML 2019. The influence of molecular structure on the adsorption of PFAS to fluid-fluid interfaces: Using QSPR to predict interfacial adsorption coefficients. Water Res, 152, 148–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Brusseau ML and Van Glubt S 2019. The influence of surfactant and solution composition on PFAS adsorption at fluid-fluid interfaces. Water Res, 161, 17–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Santamaría J, Brusseau ML, Araujo J, Orosz-Coghlan P, Blanford WJ, and Gerba CP 2012. Transport and Retention of Cryptosporidium Parvum Oocysts in Sandy Soils. J. Environ. Qual, 41, 1246–1252. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.