A Study in Nucleated Polymerization Models of Protein Aggregation

Abstract

The nucleated polymerization model is a mathematical framework that has been applied to aggregation and fragmentation processes in both the discrete and continuous setting. In particular, this model has been the canonical framework for analyzing the dynamics of protein aggregates arising in prion and amyloid diseases such as as Alzheimer’s and Parkinson’s disease.

We present an explicit steady-state solution to the aggregate size distribution governed by the discrete nucleated polymerization equations. Steady-state solutions have been previously obtained under the assumption of continuous aggregate sizes; however, the discrete solution allows for direct computation and parameter inference, as well as facilitates estimates on the accuracy of the continuous approximation.

1. Introduction

Prion proteins are the cause underlying a host of fatal, mammalian diseases – including bovine spongiform encephalopathy (mad cow disease), fatal familial insomnia, and Creutzfeldt-Jakob disease [1, 2, 17]. These diseases arise when a misfolded (prion) form of a protein appears and forms aggregates. Aggregates of the misfolded form act as templates to convert the normally folded protein to its misfolded state. Fragmentation of prion aggregates amplifies the number of templates facilitating the spread of the disease [8, 15]. Beyond prions, linear protein aggregates (amyloids) are associated with over 20 neurodegenerative diseases such as Alzheimer’s and Parkinson’s disease [9].

Since the formation of an initial stable nucleus of misfolded proteins is viewed as the time-limiting step in spontaneous or genetic prion diseases, most mathematical models have focused on the time-evolution of the aggregate size distribution [12, 13]. The nucleated polymerization model [11] has been extensively analyzed and results on the existence, uniqueness, and stability of solutions are known [5, 7, 16]; with a continuous relaxation on aggregate size, the asymptotic density is also known [5, 14]. While the continuous-size approximation is valid for large average aggregate sizes [4], this condition need not apply to all prion systems [3].

Aggregates of protein monomers are discrete in nature and much can still be said regarding the original, discrete formulation. We provide an explicit, closed-form solution for the steady-state distribution of discrete aggregate sizes. By doing so, we consider the asymptotic aggregate dynamics without resorting to continuous approximations. The closed form solution allows for explicit computation of statistics that may be useful for parameter inference. Finally, we compare our discrete steady-state solution to the continuous approximation.

2. Mathematical Analysis of Prion Aggregation and Fragmentation

2.1. Discrete Nucleated Polymerization Model

The dynamics of prion aggregates are typically modeled by the nucleated polymerization model first introduced by Masel et al. [11]. In this model, normal protein is converted to the prion form through contact with existing aggregates. Existing aggregates may also fragment into two smaller aggregates. The equations for the nucleated polymerization model may be written as follows:

$$\frac{ds}{dt}=\alpha -\mu s(t)-2\beta s(t)\sum _{i=n_0}^{\infty }{u}_i(t)+\gamma n_0\left(n_0-1\right)\sum _{i=n_0}^{\infty }{u}_i(t)$$ (1)

$$\frac{d{u}_i}{dt}=-2\beta s\left[u_i(t)-u_{i-1}(t)\right]-\mu u_i(t)-\gamma (i-1)u_i(t)+2\gamma \sum _{j=i+1}^{\infty }{u}_j(t).$$ (2)

Above, s(t) denotes the concentration of the healthy (non-prion) protein monomers, u_i(t) the concentration of prion aggregates of size i, n₀ the minimum stable aggregate size (we write ui(t) ≡ 0 for i < n₀), α the rate of translation of monomers, μ the dilution or degradation rate, and β the rate of conversion of monomers by prion aggregates. The parameter γ describes the rate of aggregate fragmentation. In our formulation, we follow the conventional assumption that prion aggregates are linear polymers and thus fragmentation may occur between any two prion monomers [5, 7, 11, 16]. That is, if γ is the rate of fragmentation between any two prion monomers, then the rate of fragmentation of an aggregate of size i ≥ n₀ is γ(i − 1). (Note that alternative models for aggregate conversion and fragmentation have also been considered [4, 6].)

The standard approach for analyzing the discrete nucleated polymerization model is to define auxiliary variables for the zeroth and first moments of the aggregate sizes [11, 17]. Let $\eta ={\sum }_{i=n_0}^{\infty }{u}_i$ and $z={\sum }_{i=n_0}^{\infty }i{u}_i$. Then, the system will close over the moments of the density:

$$\frac{ds}{dt}=\alpha -\mu s(t)-2\beta s(t)\eta (t)+\gamma n_0\left(n_0-1\right)\eta (t)$$ (3)

$$\frac{d\eta }{dt}=-\left[\mu +\gamma \left(2n_0-1\right)\right]\eta (t)+\gamma z(t)$$ (4)

$$\frac{dz}{dt}=2\beta s(t)\eta (t)-\mu z(t)-\gamma n_0\left(n_0-1\right)\eta (t).$$ (5)

This 3-dimensional system has two steady-state solutions, one corresponding to a disease-free state where all prion aggregates are eliminated and one corresponding to persistence of the prion disease [16], i.e. an endemic equilibrium. Furthermore, Prüss et al. [16] observed that the system can be transformed to a standard epidemiological model and found the basic reproductive number, ℛ₀, that determines the stability of the disease. However, these results say little about the density profile of aggregate sizes. Since this system has solutions that exist for all time, we treat s(t), η(t), and z(t) as known functions and rewrite (2) as follows:

$$\frac{d{u}_i}{dt}=-2\beta s(t)\left[u_i(t)-u_{i-1}(t)\right]-\mu u_i(t)-\gamma (i+1)u_i(t)+2\gamma \left[\eta (t)-\sum _{j=n_0}^{i-1}{u}_j(t)\right].$$ (6)

Henceforth we consider only the system at equilibrium, i.e. when $\frac{d{u}_i}{dt}=0$ for each i and $\frac{ds}{dt}=0$. We write s(t), η(t), z(t), u_i(t) → s, η, z, u_i as t → ∞, where s = α/μ, η = z = 0 in the case of the disease-free state or

$$\frac{2\beta s}{\gamma }=\left(n_0+\frac{\mu }{\gamma }\right)\left(n_0+\frac{\mu }{\gamma }-1\right),\frac{z}{\eta }=2n_0-1+\frac{\mu }{\gamma },s+z=\frac{\alpha }{\mu },$$ (7)

in the case of the endemic state.

2.2. Asymptotic Distribution of Aggregate Sizes

Let $\zeta =n_0+\frac{\mu }{\gamma }$ and define v_i = (u_n0−1+i)/η and v₀ = 0, w₀ = 1. Though we divided by η, we treat this formally – our result will still be valid in the disease-free case when η = 0. As observed by Masel et al. [11], the density will satisfy the following recurrence relation:

$$v_i=\frac{\left({\zeta }^2-\zeta \right)v_{i-1}+2w_{i-1}}{{\zeta }^2+i},$$ (8)

$$w_i=w_{i-1}-v_i.$$ (9)

We instead consider the equivalent 2nd order recurrence relation:

$$0=\left({\zeta }^2+i+2\right)v_{i+2}-\left(2{\zeta }^2-\zeta +i-1\right)v_{i+1}+\left({\zeta }^2-\zeta \right)v_i,$$ (10)

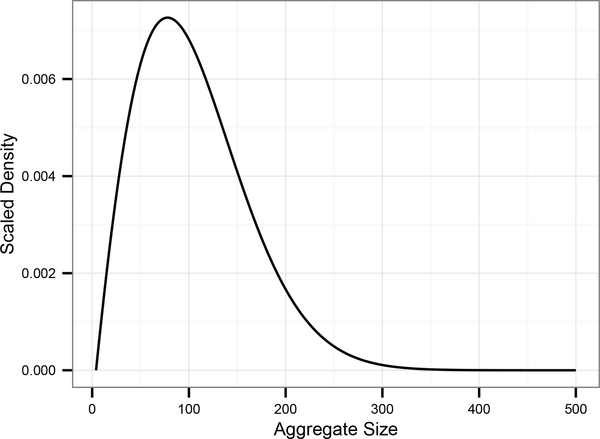
where v₀ = 0 and $v_1=\frac{2}{1+{\zeta }^2}$. The solution to (10) is plotted in Figure 1.

Figure 1:

Density solution of the discrete nucleated polymerization equations, with parameter values from Tanaka et al. [18]. (ζ = 101.25).

Our first contribution is an analysis of this 2nd order recurrence relation by finding its generating function. Other authors have considered related recurrence relations but resort to its approximation by an ODE in order to obtain an approximate solution [14]. We instead treat it exactly by defining $f(x)=\sum _{i=0}^{\infty }{v}_i{x}^i$; from (10), we obtain

$$f^{\prime }(x)+\left(\frac{{\zeta }^2}{x}+\frac{2}{1-x}-\zeta (\zeta -1)\right)f(x)=\frac{2}{1-x},$$ (11)

which has solution

$$f(x)=2\frac{{(1-x)}^2}{x^{{\zeta }^2}}{\text{e}}^{\zeta (\zeta -1)x}{\int }_0^x\frac{s^{{\zeta }^2}}{{(1-s)}^3}{\text{e}}^{-\zeta (\zeta -1)s}ds.$$ (12)

We refer the reader to the supplemental materials for the details, but after some manipulation, we find the power series for f(x) and determine

$$v_m=\{\begin{array}{ll}0\hfill & m=0\hfill \\ 2/\left(1+{\zeta }^2\right)\hfill & m=1\hfill \\ [2(\zeta -1)(2\zeta +1)]/\left[\left({\zeta }^2+1\right)\left({\zeta }^2+2\right)\right]\hfill & m=2\hfill \\ m(2\zeta +m-1)\frac{\mathrm{\Gamma }\left({\zeta }^2\right)}{\mathrm{\Gamma }\left({\zeta }^2+m+1\right)}{\zeta }^m{(\zeta -1)}^{m-1}\hfill & m\ge 3.\hfill \end{array}$$ (13)

This yields u_m, the steady-state concentration of aggregates of size m, since $u_m=\eta v_{m-n_0+1}$.

3. Comparison to the Continuous Approximation

As mentioned earlier, an alternative approach to studying aggregate size dynamics is to approximate aggregate sizes as continuous. This is a common approach to studying a broad class of “coagulation-fragmentation”-like equations, and generally speaking, the discrete system will converge to continuous system in the macroscopic limit; that is, as the average aggregate cluster size gets larger. This results remain true under very general assumptions on the coagulation and fragmentation terms of the model [10, 19]. This analysis was done specifically for the nucleated polymerization equations by Doumic et al. [4]. The scaling arguments in [4] yield weak convergence under more general modeling assumptions as well as over time; we will show a stronger convergence, but only at steady-state and under the assumptions used to derive our solutions.

Since ζ = n₀ + μ/γ is the average size in our scaled, translated system of {v_i}, we will study the limit _ζ → ∞ in relation to the continuous system solution, which we now describe. (We refer the reader to [5, 7, 16] for a full analysis of this continuous model.)

The evolution of the continuous aggregate size distribution is governed by the following system of ordinary and partial differential equations:

$$\frac{ds}{dt}=\alpha -\mu s(t)-2\beta s(t)\eta (t)+\gamma x_0^2\eta (t)$$ (14)

$$\frac{d\eta }{dt}=-\left[\mu +2\gamma x_0\right]\eta (t)+\gamma z(t)$$ (15)

$$\frac{dz}{dt}=2\beta s(t)\eta (t)-\mu z(t)-\gamma x_0^2\eta (t)$$ (16)

$$\frac{\partial u}{\partial t}=-2\beta s(t)\frac{\partial u}{\partial x}-\mu u(t,x)-\gamma xu(t,x)+2\gamma {\int }_x^{\infty }u(t,y)dy.$$ (17)

At steady-state, we have s = α/μ, η = z = 0 in the case of the disease-free state, or

$$\frac{2\beta s}{\gamma }={\left(x_0+\frac{\mu }{\gamma }\right)}^2,\frac{z}{\eta }=2x_0+\frac{\mu }{\gamma },s+z=\frac{\alpha }{\mu },$$ (18)

and

$$0=-2\beta s\frac{\partial u}{\partial x}-\mu u(x)-\gamma xu(x)+2\gamma {\int }_x^{\infty }u(y)dy.$$ (19)

in the case of the endemic equilibrium.

The analysis of and solution to Equation (19) is specifically studied in Engler et al. [5]; we list the solution below (writing v(x) = u(x + x₀)/η), alongside our discrete solution:

$$v_m=\frac{1}{{\zeta }^2(\zeta -1)}m(2\zeta +m-1)\frac{\mathrm{\Gamma }\left({\zeta }^2+1\right)}{\mathrm{\Gamma }\left({\zeta }^2+m+1\right)}{(\zeta (\zeta -1))}^m,$$

$$v(x)=\frac{1}{{\zeta }^3}x(2\zeta +x){\text{e}}^{-\frac{1}{2{\zeta }^2}x(2\zeta +x)}.$$ (21)

Note that in (21) we set x₀ = n₀ so that ζ is the same in both the continuous and discrete cases. Assume m ≪ ζ² and consider the following:

$$\begin{gathered} \log \frac{v_m}{v(m)}=-\log \left(1-\frac{1}{\zeta }\right)+\log \left(1-\frac{1}{2\zeta +m}\right)+\frac{m(2\zeta +m)}{2{\zeta }^2} \\ +m\log \left(1-\frac{1}{\zeta }\right)-\sum _{i=1}^m\log \left(1+\frac{i}{{\zeta }^2}\right) \\ =\frac{1}{\zeta }-\frac{1}{2\zeta +m}+\frac{m(2\zeta +m)}{2{\zeta }^2}-\frac{m}{\zeta }-\frac{1}{{\zeta }^2}\sum _{i=1}^{m}i+O\left(\frac{m}{{\zeta }^2}\right) \\ =\frac{1}{\zeta }-\frac{1}{2\zeta +m}+O\left(\frac{m}{{\zeta }^2}\right). \end{gathered}$$ (22)

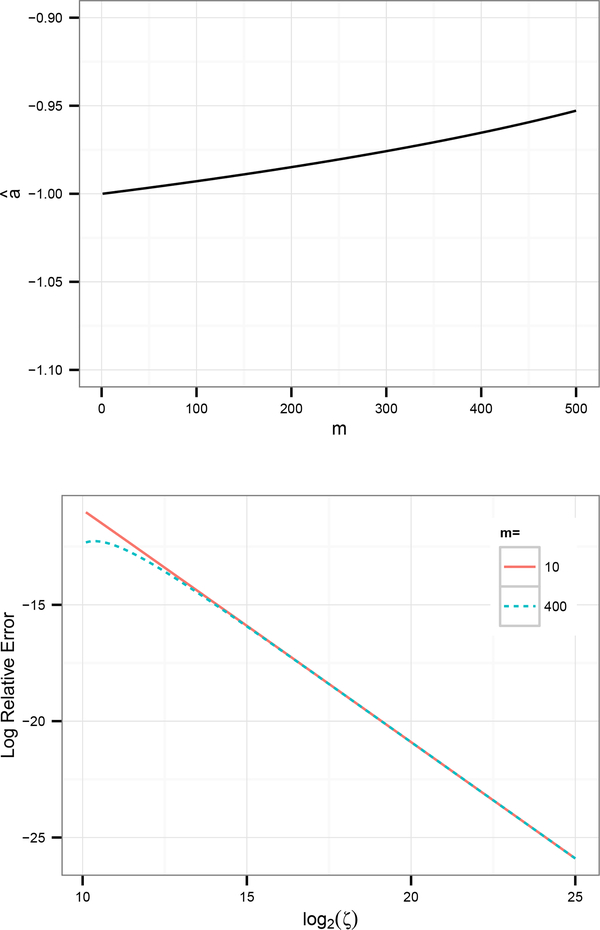
Clearly then, as ζ → ∞, v_m → v(m). Treating m as fixed, we have $\left|\frac{v_m-v(m)}{v(m)}\right|=O(1/\zeta )$, as demonstrated in Figure 2a. Finally, to compare the actual aggregate density we need the asymptotic relationship between the continuous and discrete values of η (denoted η_c and η_d, respectively). Let us also define $\kappa =\frac{2\alpha \beta }{\gamma \mu }$. Then,

$$\frac{{\eta }_d}{{\eta }_c}=\left(\frac{x_0+\zeta }{n_0-1+\zeta }\right)\left(\frac{\kappa -\zeta (\zeta -1)}{\kappa -{\zeta }^2}\right)=1+O(1/\zeta ).$$ (23)

Figure 2:

Numerical verification of asymptotic error estimates.

(a) m versus â, where â is the least-squares estimate from the linear model ${\log }_2\left|\frac{v_m-v(m)}{v(m)}\right|=a{\log }_2\zeta +b$; here, log₂ ζ is sampled uniformly in [10, 25). This is roughly in agreement with our asymptotic estimate – the slow increase in large m is due to violations of the assumption that m/ζ² ≪ 1.

(b) log₂ ζ versus ${\log }_2\left|\frac{v_m-v(m)}{v(m)}\right|$, for m = 10 and m = 400. Notice that for large m (dashed line), the scaling is not linear for small ζ. This effect is what decreases the least-squares estimate in Figure 2a and is remedied by considering only ζ where m/ζ² ≪ 1.

This yields

$$\left|\frac{u_m-u(m)}{u(m)}\right|=\left|\frac{\frac{{\eta }_d}{{\eta }_c}{v}_{m-n_0+1}-v\left(m-n_0+1\right)}{v\left(m-n_0+1\right)}\right|=O(1/\zeta ).$$ (24)

Therefore, the continuous aggregate size distribution converges to the discrete distribution at a relative rate proportional to O(ζ⁻¹). This is without requiring a continuity correction, e.g. $\overline{u}(m)={\int }_{m-1/2}^{m+1/2}u(x)dx$.

4. Discussion and Conclusions

Although continuous approximations of aggregate sizes are clearly useful, we anticipate that with increasing ability to resolve aggregate sizes from atomic force microscopy [20], the discrete nature of protein aggregates are likely to become an experimental reality. As such, the ability to consider discrete size distributions, will be important.

Using generating functions, we determined a closed form for the aggregate size distribution at steady-state under the nucleated polymerization model. With this solution, we were able to directly compare to the continuous relaxation and establish stronger convergence than was previously known for the limit of large, average aggregate sizes (ζ = n₀ + μ/γ → ∞). We provide additional calculations for novel statistics of the discrete density (mode and variance) in the supplemental materials that were also hitherto unknown; statistics that may facilitate parameter estimation.