Significance Statement
Risk calculators are widely used to predict kidney failure in people with CKD. These tools represent major advances compared with reporting eGFR alone because they provide objective risk assessment. These calculators are based on analysis methods that censor for death, which may result in overestimation of the risk of kidney failure. By analyzing data on a large population of patients with stage 4 CKD, the authors show that kidney failure risk estimates that censor for death consistently exceed the estimates from analyses that treat death as a competing risk, by 1%–27% at 5 years. Risk overestimation with methods that censor for death increases over time and is higher in people with more comorbidities. Not treating death as a competing risk in the risk calculator leads to overestimates of the risk of kidney failure in people with stage 4 CKD, which could have negative psychological effects on patients or contribute to overtreatment.
Keywords: Competing risks, chronic kidney disease, kidney failure
Visual Abstract
Abstract
Background
Most kidney failure risk calculators are based on methods that censor for death. Because mortality is high in people with severe, nondialysis-dependent CKD, censoring for death may overestimate their risk of kidney failure.
Methods
Using 2002–2014 population-based laboratory and administrative data for adults with stage 4 CKD in Alberta, Canada, we analyzed the time to the earliest of kidney failure, death, or censoring, using methods that censor for death and methods that treat death as a competing event factoring in age, sex, diabetes, cardiovascular disease, eGFR, and albuminuria. Stage 4 CKD was defined as a sustained eGFR of 15–30 ml/min per 1.73 m2.
Results
Of the 30,801 participants (106,447 patient-years at risk; mean age 77 years), 18% developed kidney failure and 53% died. The observed risk of the combined end point of death or kidney failure was 64% at 5 years and 87% at 10 years. By comparison, standard risk calculators that censored for death estimated these risks to be 76% at 5 years and >100% at 7.5 years. Censoring for death increasingly overestimated the risk of kidney failure over time from 7% at 5 years to 19% at 10 years, especially in people at higher risk of death. For example, the overestimation of 5-year absolute risk ranged from 1% in a woman without diabetes, cardiovascular disease, or albuminuria and with an eGFR of 25 ml/min per 1.73 m2 (9% versus 8%), to 27% in a man with diabetes, cardiovascular disease, albuminuria >300 mg/d, and an eGFR of 20 ml/min per 1.73 m2 (78% versus 51%).
Conclusions
Kidney failure risk calculators should account for death as a competing risk to increase their accuracy and utility for patients and providers.
People with severe, nondialysis-dependent CKD, defined as eGFR<30 ml/min per 1.73 m2 (stages 4 and 5 not on dialysis), have a high risk of kidney failure.1 Guidelines recommend that patients with stages 4–5 CKD engage in discussion with health care providers about management options for kidney failure, including renal replacement therapy (RRT) or conservative care.1 However, these patients also are at increased risk of death compared with otherwise similar people with normal kidney function.2,3 A common question for patients with severe CKD and their families is whether and when they will develop kidney failure, or whether they are more likely to die before kidney failure ensues.3–5
To inform patient counseling and advanced care planning, kidney failure risk calculators have been developed6,7 and introduced in clinical practice.8,9 These tools are largely based on standard methods for estimating time to kidney failure, in which observations are censored at death.7 Although this approach is appropriate to estimate the association between a risk factor and the hazard,10,11 it is problematic when studying disease incidence to predict individual risk.12 Censoring implies that the hazard of the event of interest is the same for individuals who are still under observation (event free) at a certain time and those who are censored for any reason (including a competing event) by that time.10,11 Because the hazard of kidney failure becomes zero after death, censoring for death when estimating the risk of kidney failure violates the independent censoring assumption.12 Failing to account for the competing risk of death may lead to overestimation of the risk of kidney failure.10–12
We studied the risk of kidney failure or death in a population-based cohort of adults with stage 4 CKD (eGFR of 15–30 ml/min per 1.73 m2). We hypothesized that censoring for death would lead to clinically important overestimates of the risk of kidney failure in this population. To test this hypothesis, we compared the results of standard analyses that censor for death to those from competing risk analyses with two events (kidney failure and death). We investigated how the absolute risks of kidney failure and death vary over time overall, and across subpopulations defined by baseline characteristics associated with these two clinical outcomes.
Methods
Study Design and Data Sources
We performed this population-based cohort study using linked administrative and laboratory provincial data from Alberta, Canada (Alberta Health database; Supplemental Material).13 We followed recommended reporting standards (Supplemental Table 1).14 This study was approved by the Conjoint Health Research Ethics Board of the University of Calgary, with a waiver of patient consent.
Population
All Alberta residents aged ≥18 years with stage 4 CKD (eGFR of 15–30 ml/min per 1.73 m2) were eligible for inclusion. We calculated eGFR using the CKD Epidemiology Collaboration equation, with serum creatinine values standardized to isotope dilution mass spectrometry traceable methods.15 Given the very low prevalence of people who self-identify as black in Alberta, we calculated eGFR assuming that all participants were white. To minimize the inclusion of people with AKI or unstable clinical conditions, we applied a moving average eGFR method to define stage 4 CKD, using outpatient laboratory measures made between July 30, 2002 and March 31, 2014.16 Starting on the date of the first eGFR<30 ml/min per 1.73 m2, we determined the average eGFR over a period of >90 days, provided that there were at least two measurements to calculate the mean, using the minimum value of eGFR when there were multiple measurements on the same day. When the average eGFR during this period was between 15 and <30 ml/min per 1.73 m2, the participant met the criterion for stage 4 CKD. We used the date of the last eGFR measurement included in the calculation of the average (index eGFR) to define cohort entry (index date). We excluded those who had received any RRT before study entry or had at least one outpatient eGFR<15 ml/min per 1.73 m2 before the episode qualifying study entry, using information available from May 1, 2002 for laboratory data and April 1, 1994 for RRT data.
Independent Variables
We considered demographics and other characteristics that are associated with death or kidney failure: lower index eGFR, more severe albuminuria, diabetes mellitus, and cardiovascular disease. The latter was defined as one or more of congestive heart failure, myocardial infarction, stroke or transient ischemic attack, or peripheral vascular disease (amputation or peripheral revascularization). We used validated coding algorithms applied to physician claims and hospitalization data to define comorbidities on the basis of the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) and International Statistical Classification of Diseases, Tenth Revision (ICD-10).17 We used the most recent albuminuria values (on or within the 2 years preceding the index date), with the following types of measurement in descending order of preference: albumin-to-creatinine ratio, protein-to-creatinine ratio, and urine dipstick. We categorized albuminuria as normal, moderate, severe, or unmeasured.18
Outcomes
The primary outcome was kidney failure, which we defined as the earliest of initiation of RRT (dialysis or kidney transplantation) or an eGFR<10 ml/min per 1.73 m2. We defined dialysis initiation on the basis of at least one inpatient or outpatient physician claim. The receipt of a kidney transplant was defined on the basis of at least one physician claim or hospitalization (Supplemental Table 2). For the eGFR criterion, we applied the moving average method to minimize the influence of a single or a few measurements above the threshold.16 Starting on the date of the first eGFR<10 ml/min per 1.73 m2, we determined the average of at least two inpatient or outpatient eGFR measurements made over a period of >90 days, using the minimum value of eGFR when there were multiple measurements on the same day. We used the date of the last eGFR measured during this period to define the event date. The threshold of <10 ml/min per 1.73 m2 is similar to the mean eGFR at dialysis start and allows for separation of the value defining cohort entry and the value defining the outcome. We considered other outcome definitions in sensitivity analyses.
Follow-Up Time
We followed participants until the earliest of kidney failure, death, or censoring. We censored observations at the date of emigration from the province, the study end date (March 31, 2017), or at 10 years after cohort entry. To minimize bias of outcome ascertainment, we censored observations at 1.5 years from an eGFR measurement, if there was no subsequent measurement within 1.5 years of this eGFR.
Statistical Analyses
General Approach
We used standard methods for qualitative and quantitative data to summarize baseline information and survival methods to estimate risks. We used Stata (www.STATA.com) and R (R-project.org) for analyses.
Cumulative Incidence Functions
To study the absolute risk of kidney failure accounting for the competing risk of death and the absolute risk of death without kidney failure, we estimated the crude (nonparametric)19 and model-based (adjusted) cumulative incidence functions (CIFs) of these two events and their 95% confidence intervals (95% CIs).20–23 We compared crude CIFs (Aalen–Johansen) with the corresponding crude (Kaplan–Meier) naïve incidence functions (NIFs). We also compared the model-based (adjusted) CIFs with the corresponding model-based NIFs (adjusted for the same covariates; Supplemental Material).21,22 In preliminary analyses, we created a new event type indicator to separate participants lost to follow-up before year 5 from those event-free and still under observation at 5 years. We compared the performance of the nonparametric CIF and NIF (tests) with the observed proportions of the three events at 5 years (reference). In all subsequent analyses, we treated all participants without events as censored observations and only considered the events kidney failure and death.
Hazard Models
We used flexible parametric regression to estimate the cause-specific hazard functions.24 As opposed to the Cox model that does not have distributional assumptions, flexible parametric models use restricted cubic spline functions to model the baseline cumulative hazard, baseline cumulative odds of survival, or some more general baseline distribution in survival analysis models (Supplemental Material). We summarized data graphically, for the whole cohort and in subgroups defined by higher versus lower risk combinations of clinical characteristics (sex, albuminuria, diabetes, and cardiovascular disease), holding age constant at a value close to the sample mean and considering two values of eGFR (20 and 25 ml/min per 1.73 m2).
Sensitivity Analyses
We tested consistency of findings in several sensitivity analyses. First, we defined kidney failure as initiation of RRT or occurrence of sustained eGFR <10 ml/min per 1.73 m2. We defined sustained eGFR <10 ml/min per 1.73 m2 by the occurrence of two or more consecutive eGFR values <10 ml/min per 1.73 m2 over a period of >90 days. We used the date of the last eGFR in the first episode of sustained eGFR measurements <10 ml/min per 1.73 m2 as event date. Second, we defined kidney failure as initiation of any RRT only. Third, we restricted the analyses to complete cases for albuminuria (excluding those with unmeasured values).
Results
Study Population
We identified 30,801 adults who met the criteria for stage 4 CKD during the accrual period (Supplemental Figure 1). Participants were on average 77 years old (±13.3), had an average eGFR of 26 ml/min per 1.73 m2 (±3.4), 44% were men, 45% had diabetes, and 59% had cardiovascular disease (Table 1). During follow-up (106,447 patient-years at risk), 5511 participants developed kidney failure (event rate 0.052 per patient-year; 95% CI, 0.05 to 0.05) and 16,285 died without kidney failure (event rate 0.154 per patient-year; 95% CI, 0.15 to 0.16). CIFs by event type, with participants at risk at the beginning of each year period, are summarized in Supplemental Figure 2.
Table 1.
Clinical characteristics at baseline
| Characteristics (n=30,801) | Descriptive Statistic |
|---|---|
| Age, yr, mean (SD) | 76.8 (13.3) |
| Men, n (%) | 13,507 (43.8) |
| eGFR, ml/min per 1.73 m2, mean (SD) | 26.2 (3.4) |
| Proteinuria/albuminuria missing, n (%) | 2978 (9.7) |
| A1, n (%) | 13,318 (43.2) |
| A2, n (%) | 7091 (23.1) |
| A3, n (%) | 7414 (24.1) |
| Diabetes | 13,906 (45.1) |
| Cardiovascular disease | 18,063 (58.6) |
| Myocardial infarction | 3692 (11.9) |
| Congestive heart failure | 13,073 (42.4) |
| Stroke or TIA | 7865 (25.5) |
| Peripheral vascular disease | 2285 (7.4) |
A1, A2, and A3 are categories of proteinuria. A1 defined as albuminuria <30 mg/24 h, proteinuria <150 mg/24 h, albumin-to-creatinine ratio [ACR] <3 mg/mmol (<30 mg/g), protein-to-creatinine ratio [PCR] <15 mg/mmol (<150 mg/g), or protein reagent strip negative to trace. A2 defined as albuminuria 30–300 mg/24 h, proteinuria 150–500 mg/24 h, ACR 3–30 mg/mmol (30–300 mg/g), PCR 15–50 mg/mmol (150–500 mg/g), or protein reagent strip 1+. A3 defined as albuminuria >300 mg/24 h, proteinuria >500 mg/24 h, ACR>30 mg/mmol (>300 mg/g), PCR>50 mg/mmol (>500 mg/g), or protein reagent strip ≥2+. TIA, transient ischemic attack.
Observed Risks
Risk estimates that used standard methods were higher than those accounting for competing events. Figure 1 shows the extent to which standard methods overestimated the proportions of participants who left the study early without event, developed kidney failure, or died by year 5. In contrast, risk calculations that used methods for competing risks agreed with the observed frequencies of each outcome at 5 years. Although the sum of the three event-specific CIFs totaled to 100%, the sum of the three event-specific NIFs exceeded 100%.
Figure 1.
Calculated versus observed risks at 5 years. NIF censors for competing events. CKD without kidney failure indicates individuals who are still in the initial state when study ends. Lost indicates observations with incomplete follow-up (separate event category used only in this analysis). The reference line indicates maximum possible risk.
Overall, clinically important risk overestimation was apparent by 2 years, increased over time, and was larger for the risk of kidney failure than for the risk of death. For example, the 5-year risks of kidney failure and death were 23% (95% CI, 22% to 23%; NIF) versus 16% (95% CI, 15% to 16%; CIF), and 53% (95% CI, 52% to 53%; NIF) versus 48% (95% CI, 47% to 48%; CIF), respectively. At 10 years, overestimation was even more striking: 41% (95% CI, 40% to 43%; NIF) versus 22% (95% CI, 21% to 23%; CIF), and 78% (95% CI, 77% to 78%; NIF) versus 65% (95% CI, 64% to 65%; CIF), respectively (Figure 2, top panels). Figure 2, bottom left panel, shows the sum of the two risk components obtained from competing risk analyses. The sum of the two CIFs was 64% at 5 years and 87% at 10 years from study entry (equaling the risk for the combined end-point of death or kidney failure obtained using the Kaplan–Meier method). The sum of the same two risks calculated separately using standard methods (NIF of kidney failure censoring at death and NIF of death censoring at kidney failure) were 76% at 5 years and >100% at 7.5 years (Figure 2, bottom right panel).
Figure 2.
Crude CIFs and NIFs overall. NIF censors for competing events. The reference line indicates maximum possible risk. In the stacked function plots the blue area represents the risk of death, the red area represents the risk of kidney failure, and the area above the top curve is probability of being alive without kidney failure.
Model-Based Risk Estimates
Male sex, diabetes, cardiovascular disease, lower eGFR, and more severe albuminuria were associated with increased risks of both kidney failure and death (Supplemental Tables 3 and 4). In adjusted analyses, we found that (1) risk overestimation with the standard approach was larger among higher risk versus lower risk participants; (2) risk overestimation from naïve methods tended to increase more over time in higher risk versus lower risk participants; and (3) within each risk subgroup, event-specific risk overestimation was similar (Figure 3). For example, for a 75-year-old person, the difference between the two estimates of the 5-year risk of kidney failure ranged from 1% (8% versus 9%) in a woman with an eGFR of 25 ml/min per 1.73 m2 without albuminuria, diabetes, or cardiovascular disease, to 27% in a man with an eGFR of 20 ml/min per 1.73 m2, albuminuria >300 mg/d, diabetes, and cardiovascular disease (51% versus 78%; Table 2). Results were similar for the risk of death.
Figure 3.
Overlaid model-based CIFs and NIFs by sex and baseline risk. CIFs (solid lines) and NIFs (dashed lines) estimated from the final cause-specific hazard model of kidney failure or death (Supplemental Table 3). Maroon lines: high-risk person (person with diabetes, cardiovascular disease, albuminuria >300 mg/d, and an eGFR of 20 ml/min per m2); navy lines: low-risk person (person without diabetes or cardiovascular disease, and with an eGFR of 25 ml/min per m2 and albuminuria <30 mg/d). In all cases age is 75 years.
Table 2.
5-year cumulative incidence and failure functions of kidney failure and death
| Event Type | Parametric | CIF | 95% CI | NIF | 95% CI |
|---|---|---|---|---|---|
| Kidney failure | Woman | ||||
| G25; A1; DM–; CV– | 0.08 | 0.07 to 0.09 | 0.09 | 0.08 to 0.10 | |
| G20; A3; DM+; CV+ | 0.44 | 0.41 to 0.47 | 0.66 | 0.62 to 0.69 | |
| Man | |||||
| G25; A1; DM–; CV– | 0.11 | 0.09 to 0.12 | 0.13 | 0.11 to 0.14 | |
| G20; A3; DM+; CV+ | 0.51 | 0.48 to 0.54 | 0.78 | 0.75 to 0.81 | |
| Death | Woman | ||||
| G25; A1; DM–; CV– | 0.24 | 0.23 to 0.25 | 0.25 | 0.24 to 0.27 | |
| G20; A3; DM+; CV+ | 0.42 | 0.4 to 0.45 | 0.62 | 0.58 to 0.66 | |
| Man | |||||
| G25; A1; DM–; CV– | 0.27 | 0.26 to 0.28 | 0.29 | 0.28 to 0.31 | |
| G20; A3; DM+; CV+ | 0.41 | 0.39 to 0.44 | 0.68 | 0.65 to 0.72 |
G25 and G20 refer to an eGFR of 20 and 25 ml/min per m2, respectively; A1 indicates albuminuria <30 mg/d; and A3 indicates albuminuria >300 mg/d. In all cases age is 75 years. DM–, diabetes absent; CV–, cardiovascular disease absent; DM+, diabetes present; CV+, cardiovascular disease present.
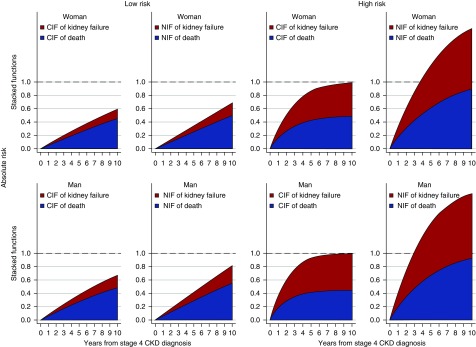
A graphical representation of the amount of bias induced by censoring for death is presented in Figure 4. Risk overestimation with standard NIF methods was relatively small among lower risk participants and over ≤2 years of follow-up. However, NIF methods clearly overestimated the risks for all participants once follow-up exceeded 2 years. In higher risk participants, the sum of the two risks using NIF methods exceeded 100% by year 3, when the corresponding estimate using CIF methods was <80%.
Figure 4.
Stacked model-based CIFs and NIFs. CIFs and NIFs estimated from the final cause-specific hazard model of kidney failure or death (Supplemental Table 3). The reference line indicates maximum possible risk. Top panels: female sex, bottom panels: male sex. Left panels: low-risk person (person without diabetes or cardiovascular disease, and with an eGFR of 25 ml/min per m2 and albuminuria <30 mg/d); right panels: high-risk person (person with diabetes and cardiovascular disease, an eGFR of 20 ml/min per m2, and albuminuria >300 mg/d). In all cases age is 75 years.
Sensitivity and Other Analyses
We obtained similar results in all sensitivity analyses (Supplemental Figures 3–8). Model assumptions were met in all models.
Discussion
In this population-based study, we found that standard analysis methods that censor for death consistently overestimate the risk of kidney failure in people with stage 4 CKD. The magnitude of this bias increases over time and is larger in people with multiple risk factors for adverse events. Although the risk estimates that result from standard methods are similar to the cumulative incidence of kidney failure when follow-up is relatively short, the bias from failing to account for the competing risk of death becomes larger when follow-up time exceeds 2 years, especially among people at higher risk. For example, among men at high-risk, standard methods overestimated the 5-year risk of kidney failure by >50%, leading to an absolute difference in estimated risk of 27% (78% versus 51%). Our findings indicate that kidney failure risk calculators in people with stage 4 CKD may provide misleading results because they do not account for the competing risk of death. Because practitioners, patients, and families rely on accurate prognostic information to make decisions about CKD management, this observation has clear implications for clinical practice.
Survival analysis methods are extensively used for estimating survival probabilities or risks. Time is measured for example from study entry until the event of interest occurs and observations that are lost during follow-up or are event-free at the study end date are censored. Censoring implies that (1) had follow-up been prolonged, the event of interest would eventually be observed in all participants; and (2) the censoring process is unrelated to individual prognosis. Although competing risks are often treated as censoring events,10,11 after a competing event the event of interest can no longer occur (e.g., “kidney failure” after death or “death without kidney failure” after kidney failure), regardless of how long the duration of follow-up is extended. Censoring for death when estimating the risk of kidney failure violates the requirement of independent (noninformative) censoring because the hazard of kidney failure becomes zero after death.12 Although substantial advances in competing risks methodology have been achieved over the past decades,10–12 many clinical studies do not capitalize on these new techniques.25
One large study in stages 3–5 CKD patients concluded that risk estimates from standard analyses censoring for competing events were similar to those that accounted for competing risks.7 Accordingly, subsequent tools6 to predict kidney failure were developed and validated on the basis of standard methods.7 Grams et al.26 developed a 2- and 4-year calculator to predict both probabilities and order of clinical events according to nine clinical characteristics in patients with stages 4–5 CKD. They found that risk estimates from competing risks analyses were similar to those on the basis of methods that censor for death.6,7 Smaller discrepancies between methods found in these studies, as compared with ours, may be the consequence of the younger and more selected populations they included. Considering that people referred for nephrology consultation have lower risk of death and higher risk of kidney failure,26 findings from our population-based study are consistent with existing studies.6,7,26 Conclusions from these studies are also based on a shorter follow-up time relative to our study (2–4 years versus 10 years) and on the reporting of average differences between standard and competing risk methods for an entire cohort. We compared standard methods to methods that account for competing risks for our full cohort and across patient subgroups defined by clinical characteristics. We found that overall risk functions do not capture the implications for individual patients and that discrepancies between the two methods are not uniform across patient subgroups or over time. Our data suggest that the risk estimates are similar (although not identical) only in the short term and among low-risk people with stage 4 CKD. Under real-world conditions, characterized by long-term follow-up of patients with a wide range of clinical characteristics, failing to account for the competing risk of death will lead to clinically relevant overestimation of the risk of kidney failure. This finding has been observed in studies of other diseases: standard methods censoring for death appear to substantially overestimate the 10-year risk of coronary heart disease, and classify 18% of people as high risk (>20% 10-year risk), compared with only 8% according to a model that accounted for the competing risk of death.27
Risk calculators of different complexity are increasingly being used for counseling patients and families about individual prognosis and to inform management decisions, including advanced care planning.26 These tools represent major advances compared with reporting eGFR alone, because they address the clinical need for objective risk assessment.6,26 In some settings, individual risk predictions obtained with these calculators are reported along with laboratory test results, with 5-year risk estimates used to advise ordering physicians about the need for nephrology referral.8,9 Some jurisdictions use prespecified risk thresholds, in addition to eGFR thresholds, to define eligibility for funded patient enrolment in multidisciplinary predialysis clinics.28 Our results suggest that the methods underpinning existing risk prediction tools6,7 may result in overly pessimistic predictions, particularly for higher-risk patients. This may have short- and long-term negative psychologic effects,29 might cause unnecessary interventions or overtreatment, and could reduce access to services and resources for those more in need.
In addition to the previously noted limitations of prior work, most previous similar studies in patients with CKD included people with stage 5 CKD and assessed the risk of kidney failure treated with dialysis or transplantation. Although renal replacement is clinically relevant, the decision to initiate dialysis or perform kidney transplantation is partially subjective, especially because some patients will prefer conservative management of kidney failure without renal replacement therapy. We used an objective outcome measure by considering a sustained decline of eGFR or renal replacement to define kidney failure. Other strengths include the use of population-based data from a geographically defined area served by a universal health care system, and a relatively large sample size and adequate follow-up. Also, we used validated algorithms for ascertaining the presence or absence of comorbidity and defined eligibility criteria to align sample characteristics to those of the target population with stage 4 CKD. Finally, we considered eGFR criteria to define kidney failure and assessed the robustness of our findings in sensitivity analyses. Our study also has limitations, including the use of routinely collected data from people who accessed medical services and the use of data from a single Canadian province with a very low prevalence of people who self-identify as black. Although our findings will require confirmation in other settings, we do not believe that these limitations pose a serious threat to the validity of our conclusions.
In conclusion, our study suggests that standard survival analysis methods that censor for death systematically overestimate the risk of kidney failure in people with stage 4 CKD. This bias increases over time, especially among people with more risk factors for kidney failure and death. These findings indicate that methods for estimating and predicting the risk of kidney failure in people with stage 4 CKD should account for the competing risk of death.
Data Sharing Statement
The Alberta Health Information Act prohibits us from making individual level data publicly available. Researchers who are interested in replicating our work can contact the data custodian, Alberta Health.
Disclosures
None.
Funding
Liu was supported by postdoctoral fellowships from the Canadian Institutes of Health Research, the Cumming School of Medicine of the University of Calgary, and the Libin Cardiovascular Institute of Alberta. Ravani, Quinn, Lam, Tonelli, Hemmelgarn, Manns, Oliver and James are supported by operating grants or Foundation awards from the Canadian Institutes of Health Research, by Alberta Innovates-Health Solutions, and by Canada Foundation for Innovation. Tonelli was supported by the David Freeze Chair in Health Services Research, Hemmelgarn was supported by the Baay Chair in Kidney Research and Manns was supported by the Svare Chair in Health Economics, all at the University of Calgary. The funding organizations had no role in the design and conduct of the study, in the collection, analysis, and interpretation of the data, or in the preparation, review, or approval of the manuscript.
Supplementary Material
Acknowledgments
Ravani had full access to all of the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analyses. Concept and design: Ravani and Tonelli. Acquisition, analysis, or interpretation of data: all authors. Drafting of the manuscript: Ravani and Tonelli. Critical revision of the manuscript for important intellectual content: all authors. Obtained funding: Ravani and Liu. Administrative, technical, or material support: Ravani and Tonelli. Supervision: Ravani and Tonelli. The lead authors (Ravani and Tonelli) affirm that this manuscript is an honest, accurate, and transparent account of the study being reported, that no important aspects of the study have been omitted, and that any discrepancies from the study as planned have been explained.
The authors are grateful to Dr. Mozumder SI (University of Leicester, UK) for providing assistance on the use of the STPM2CR package in STATA.
This study is based, in part, on data provided by Alberta Health and Alberta Health Services. The interpretation and conclusions contained herein are those of the researchers and do not represent the views of the Government of Alberta or Alberta Health Services. Neither the Government of Alberta, Alberta Health, nor Alberta Health Services express any opinion in relation to this study.
Footnotes
Published online ahead of print. Publication date available at www.jasn.org.
Supplemental Material
This article contains the following supplemental material online at http://jasn.asnjournals.org/lookup/suppl/doi:10.1681/ASN.2019060640/-/DCSupplemental.
Supplemental Table 1. The RECORD statement: checklist of items, extended from the STROBE statement, that should be reported in observational studies using routinely collected health data.
Supplemental Table 2. Codes for identifying dialysis or transplantation.
Supplemental Table 3. Cause-specific hazard parametric model of kidney failure and death.
Supplemental Table 4. Cause-specific hazard semiparametric model of kidney failure and death.
Supplemental Figure 1. Derivation of study cohort.
Supplemental Figure 2. Overlaid and stacked CIFs.
Supplemental Figure 3. Overlaid model-based CIFs and NIFs (sensitivity analysis 1).
Supplemental Figure 4. Overlaid model-based CIFs and NIFs (sensitivity analysis 2).
Supplemental Figure 5. Overlaid model-based CIFs and NIFs (sensitivity analysis 3).
Supplemental Figure 6. Stacked model-based CIFs and NIFs (sensitivity analysis 1).
Supplemental Figure 7. Stacked model-based CIFs and NIFs (sensitivity analysis 2).
Supplemental Figure 8. Stacked model-based CIFs and NIFs (sensitivity analysis 3).
References
- 1.Stevens PE, Levin A; Kidney Disease: Improving Global Outcomes Chronic Kidney Disease Guideline Development Work Group Members : Evaluation and management of chronic kidney disease: Synopsis of the kidney disease: Improving global outcomes 2012 clinical practice guideline. Ann Intern Med 158: 825–830, 2013 [DOI] [PubMed] [Google Scholar]
- 2.Matsushita K, van der Velde M, Astor BC, Woodward M, Levey AS, de Jong PE, et al.: Chronic Kidney Disease Prognosis Consortium : Association of estimated glomerular filtration rate and albuminuria with all-cause and cardiovascular mortality in general population cohorts: A collaborative meta-analysis. Lancet 375: 2073–2081, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tonelli M, Wiebe N, James MT, Klarenbach SW, Manns BJ, Ravani P, et al.: Alberta Kidney Disease Network : A population-based cohort study defines prognoses in severe chronic kidney disease. Kidney Int 93: 1217–1226, 2018 [DOI] [PubMed] [Google Scholar]
- 4.Demoulin N, Beguin C, Labriola L, Jadoul M: Preparing renal replacement therapy in stage 4 CKD patients referred to nephrologists: A difficult balance between futility and insufficiency. A cohort study of 386 patients followed in Brussels. Nephrol Dial Transplant 26: 220–226, 2011 [DOI] [PubMed] [Google Scholar]
- 5.O’Hare AM, Choi AI, Bertenthal D, Bacchetti P, Garg AX, Kaufman JS, et al.: Age affects outcomes in chronic kidney disease. J Am Soc Nephrol 18: 2758–2765, 2007 [DOI] [PubMed] [Google Scholar]
- 6.Tangri N, Grams ME, Levey AS, Coresh J, Appel LJ, Astor BC, et al.: CKD Prognosis Consortium : Multinational assessment of accuracy of equations for predicting risk of kidney failure: A meta-analysis. JAMA 315: 164–174, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tangri N, Stevens LA, Griffith J, Tighiouart H, Djurdjev O, Naimark D, et al.: A predictive model for progression of chronic kidney disease to kidney failure. JAMA 305: 1553–1559, 2011 [DOI] [PubMed] [Google Scholar]
- 8.Grill AK, Brimble S: Approach to the detection and management of chronic kidney disease: What primary care providers need to know. Can Fam Physician 64: 728–735, 2018 [PMC free article] [PubMed] [Google Scholar]
- 9.Hingwala J, Wojciechowski P, Hiebert B, Bueti J, Rigatto C, Komenda P, et al.: Risk-based triage for nephrology referrals using the kidney failure risk equation. Can J Kidney Health Dis 4: 2054358117722782, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Austin PC, Fine JP: Accounting for competing risks in randomized controlled trials: A review and recommendations for improvement. Stat Med 36: 1203–1209, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Austin PC, Lee DS, Fine JP: Introduction to the analysis of survival data in the presence of competing risks. Circulation 133: 601–609, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Putter H, Fiocco M, Geskus RB: Tutorial in biostatistics: Competing risks and multi-state models. Stat Med 26: 2389–2430, 2007 [DOI] [PubMed] [Google Scholar]
- 13.Hemmelgarn BR, Clement F, Manns BJ, Klarenbach S, James MT, Ravani P, et al.: Overview of the alberta kidney disease network. BMC Nephrol 10: 30, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Benchimol EI, Smeeth L, Guttmann A, Harron K, Moher D, Petersen I, et al.: RECORD Working Committee : The REporting of studies Conducted using Observational Routinely-collected health Data (RECORD) statement. PLoS Med 12: e1001885, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D: A more accurate method to estimate glomerular filtration rate from serum creatinine: A new prediction equation. Modification of diet in renal disease study group. Ann Intern Med 130: 461–470, 1999 [DOI] [PubMed] [Google Scholar]
- 16.Ishani A, Nelson D, Clothier B, Schult T, Nugent S, Greer N, et al.: The magnitude of acute serum creatinine increase after cardiac surgery and the risk of chronic kidney disease, progression of kidney disease, and death. Arch Intern Med 171: 226–233, 2011 [DOI] [PubMed] [Google Scholar]
- 17.Tonelli M, Wiebe N, Fortin M, Guthrie B, Hemmelgarn BR, James MT, et al.: Alberta Kidney Disease Network : Methods for identifying 30 chronic conditions: Application to administrative data. BMC Med Inform Decis Mak 15: 31, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leevin A, Stevens PE, Bilous RW, Coresh J, deFrancisco ALM, deJong PE, et al.: Kidney Disease: Improving Global Outcomes (KDIGO) CKD Work Group : KDIGO 2012 clinical practice guideline for the evaluation and management of chronic kidney disease. Kidney Int Suppl 3: 19–62, 2013 [Google Scholar]
- 19.Coviello V, Boggess M: Cumulative incidence estimation in the presence of competing risks. Stata J 4: 103–112, 2004 [Google Scholar]
- 20.Hinchliffe SR, Lambert PC: Extending the flexible parametric survival model for competing risks. Stata J 13: 344–355, 2013 [Google Scholar]
- 21.Lambert PC, Wilkes SR, Crowther MJ: Flexible parametric modelling of the cause-specific cumulative incidence function. Stat Med 36: 1429–1446, 2017 [DOI] [PubMed] [Google Scholar]
- 22.Lunn M, McNeil D: Applying Cox regression to competing risks. Biometrics 51: 524–532, 1995 [PubMed] [Google Scholar]
- 23.Mozumder SI, Rutherford MJ, Lambert PC: stpm2cr: A flexible parametric competing risks model using a direct likelihood approach for the cause-specific cumulative incidence function. Stata J 17: 462–489, 2017 [PMC free article] [PubMed] [Google Scholar]
- 24.Lambert PC, Royston P: Further development of flexible parametric models for survival analysis. Stata J 9: 265–290, 2009 [Google Scholar]
- 25.Koller MT, Raatz H, Steyerberg EW, Wolbers M: Competing risks and the clinical community: Irrelevance or ignorance? Stat Med 31: 1089–1097, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Grams ME, Sang Y, Ballew SH, Carrero JJ, Djurdjev O, Heerspink HJL, et al.: Predicting timing of clinical outcomes in patients with chronic kidney disease and severely decreased glomerular filtration rate. Kidney Int 93: 1442–1451, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wolbers M, Koller MT, Witteman JC, Steyerberg EW: Prognostic models with competing risks: Methods and application to coronary risk prediction. Epidemiology 20: 555–561, 2009 [DOI] [PubMed] [Google Scholar]
- 28.Ontario Renal Network: Multi-Care Kidney Clinic Best Practices, 2019. Available at: https://www.ontariorenalnetwork.ca/en. Accessed May 29, 2019
- 29.Brodersen J, Siersma VD: Long-term psychosocial consequences of false-positive screening mammography. Ann Fam Med 11: 106–115, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.