Spatial Coupling Tunes NMDA Receptor Responses via Ca²⁺ Diffusion

Abstract

In the CNS, NMDA receptors generate large and highly regulated Ca²⁺ signals, which are critical for synaptic development and plasticity. They are highly clustered at postsynaptic sites and along dendritic arbors, but whether this spatial arrangement affects their output is unknown. Synaptic NMDA receptor currents are subject to Ca²⁺-dependent inactivation (CDI), a type of activity-dependent inhibition that requires intracellular Ca²⁺ and calmodulin (CaM). We asked whether Ca²⁺ influx through a single NMDA receptor influences the activity of nearby NMDA receptors, as a possible coupling mechanism. Using cell-attached unitary current recordings from GluN1–2a/GluN2A receptors expressed in human HEK293 cells and from NMDA receptors native to hippocampal neurons from male and female rats, we recorded unitary currents from multichannel patches and used a coupled Markov model to determine the extent of signal coupling (κ). In the absence of extracellular Ca²⁺, we observed no cooperativity (κ < 0.1), whereas in 1.8 mm external Ca²⁺, both recombinant and native channels showed substantial negative cooperativity (κ = 0.27). Intracellular Ca²⁺ chelation or overexpression of a Ca²⁺-insensitive CaM mutant, reduced coupling, which is consistent with CDI representing the coupling mechanism. In contrast, cooperativity increased substantially (κ = 0.68) when overexpressing the postsynaptic scaffolding protein PSD-95, which increased receptor clustering. Together, these new results demonstrate that NMDA receptor currents are negatively coupled through CDI, and the degree of coupling can be tuned by the distance between receptors. Therefore, channel clustering can influence the activity-dependent reduction in NMDA receptor currents.

SIGNIFICANCE STATEMENT At central synapses, NMDA receptors are a major class of excitatory glutamate-gated channels and a source of activity-dependent Ca²⁺ influx. In turn, fluxed Ca²⁺ ions bind to calmodulin-primed receptors and reduce further entry, through an autoinhibitory mechanism known as Ca²⁺ -dependent inactivation (CDI). Here, we show that the diffusion of fluxed Ca²⁺ between active channels situated within submicroscopic distances amplified receptor inactivation. Thus, calmodulin-mediated gating modulation, an evolutionarily conserved regulatory mechanism, endows synapses with sensitivity to both the temporal sequence and spatial distribution of Ca²⁺ signals. Perturbations in this mechanism, which coordinates the activity of NMDA receptors within a cluster, may cause signaling alterations that contribute to neuropsychiatric conditions.

Introduction

In the mammalian CNS, ionotropic glutamate receptors mediate the majority of excitatory neurotransmission, with AMPA and NMDA receptors being the primary drivers of synaptic plasticity. Within the composite electrical signal generated by these two channel types, the slowly decaying NMDA receptor component sets the time interval for spike timing-dependent plasticity and mediates the majority of Ca²⁺ influx into the postsynaptic cell. However, excess elevations in intracellular Ca²⁺ through NMDA receptors is pathologic and contributes to many debilitating psychiatric and neurodegenerative conditions.

Glutamate receptors are organized along the postsynaptic membrane in compact microdomains (MacGillavry et al., 2013). These domains are critical for glutamate receptor regulation (Lur and Higley, 2015) and optimal alignment to presynaptic vesicle release sites (Tang et al., 2016). Scaffold proteins such as postsynaptic density-95 (PSD-95) mediate NMDA receptor clustering within synaptic and nonsynaptic regions (Jeyifous et al., 2016). Mutations that perturb PSD-95 association with its partners are strongly associated with neurological disorders such as autism, epilepsy, and schizophrenia (Fernández et al., 2017).

NMDA receptor-mediated Ca²⁺ flux is critical to initiating synaptic plasticity (Hardingham et al., 2001; Tigaret et al., 2016). Within the small dendritic spine volume (0.01–0.8 μm³), strong Ca²⁺ buffering capacity and restricted diffusion by narrow spine necks and electrostatic interactions with the membrane generally confine Ca²⁺ elevations to the spine compartment (Sabatini et al., 2002). In early development, the NMDA receptor-mediated Ca²⁺ signal is critical to spine development (Lee et al., 2016). However, excessive Ca²⁺ levels can be cytotoxic. NMDA receptors respond to intracellular elevations by a reduction in activity known as Ca²⁺-dependent inactivation (CDI; Legendre et al., 1993). NMDA receptor CDI is a rapid (τ_CDI, 0.5 s) form of activity-dependent inhibition mediated by calmodulin (CaM; Zhang et al., 1998; Merrill et al., 2007; Iacobucci and Popescu, 2017). CDI can also be elicited by Ca²⁺ spillover from AMPA receptors, voltage-gated Ca²⁺ channels (Kyrozis et al., 1995), or kainate receptors (Medina et al., 1994). Although NMDA receptors generate Ca²⁺ signals large enough to modulate remote SK channels (Ngo-Anh et al., 2005), it remains unknown whether individual NMDA receptor currents can induce CDI in neighboring NMDA receptors as a mechanism of fine-tuning the postsynaptic signal.

In this study, we tested whether NMDA receptor activity is sensitive to Ca²⁺ spillover from neighboring NMDA receptors. We probed the activity of NMDA receptors in multichannel cell-attached patches and obtained the first evidence that both recombinant and native NMDA receptors display negative cooperativity mediated by Ca²⁺ and calmodulin, enabling channels to coordinate their activity. Thus, CDI imparts NMDA receptors with an elegant spatiotemporal feedback mechanism. Our results provide insight to the roles of NMDA receptor CDI in physiologic and disease states.

Materials and Methods

Cell culture and transfection

HEK293 cells (CRL-1573, American Type Culture Collection; RRID:CVCL_0045), a gift from A. Auerbach (The State University of New York at Buffalo, Buffalo, NY), were grown in Invitrogen DMEM (Thermo Fisher Scientific) with 10% Gibco FBS (catalog #10437-028, Thermo Fisher Scientific), and 1% penicillin-streptomycin and were sustained in 5% CO₂ atmosphere at 37°C. Cultures at ∼50% confluence were transfected with rat GluN1–2a (U08262.1) or GluN1^ΔK838 (lacking the intracellular tail after K838); and either GluN2A (M91561.1) or GluN2A^ΔF1344 (lacking the intracellular tail after F1344) and yellow fluorescent protein (YFP)-CaM_WT, YFP-CaM₁₂, YFP-CaM₃₄, or YFP-CaM₁₂₃₄ in a 1:1:1 ratio; and PSD-95 as indicated in a 1:1:1:5 ratio. All YFP-CaM constructs were gifts from Dr. Takanari Inoue (Johns Hopkins University, Baltimore, MD) and Dr. Manu Ben-Johny (Columbia University, New York, NY). All constructs were verified by full insert sequencing. Commercial shRNA constructs against rat PSD-95 (catalog #TG710382, OriGene) have been previously validated for efficient knockdown of PSD-95 in mammalian neurons (Gross et al., 2013). The shRNA plasmid contained a GFP reporter for identification of neurons for electrophysiology experiments.

Hippocampal neurons were harvested from both male and female Sprague Dawley rat embryos at embryonic day 18. A pregnant rat was killed in a CO₂ chamber and decapitated, and the uterus was surgically removed. Embryos were decapitated, and the heads were placed on ice in 1× PBS. Hippocampi were removed and placed in cold Gibco HBSS (catalog #14185-052, Thermo Fisher Scientific) supplemented with 4 mm NaHCO₃, 1% penicillin/streptomycin, and 10 mm HEPES, pH 7.35. Hippocampi were minced and incubated for 20 min in warm 2.5% trypsin. Trypsin was removed by dilution with 1× Gibco Minimal Essential Medium (catalog #11090-081, Thermo Fisher Scientific) supplemented with 1 mm sodium pyruvate, 2 mm Gibco Glutamax (catalog #35050-061, Thermo Fisher Scientific), 0.6% glucose, 10% FBS, and 1% penicillin/streptomycin. Dissociation of cells was achieved by trituration in the presence of DNase I via a stereological pipette and passing cell suspension through a 40 μm strainer (BD Falcon). Dissociated cells were plated on poly-d-lysine-coated 35 mm dishes at a density of 5 × 10⁵ cells/ml. After 24 h at 37°C in 5% CO₂, the medium was replaced with Gibco Neurobasal A medium (catalog #10888-022, Thermo Fisher Scientific) containing 1× Gibco B27 supplement (catalog #17504-044, Thermo Fisher Scientific), 2 mm Glutamax, and 1% penicillin/streptomycin. Subsequently, half the medium was refreshed every 3 d. Cultures were used for electrophysiological measurements between days 15 and 30 after plating. Transfection of neurons was performed using Invitrogen Lipofectamine 3000 (catalog #L3000-001, Thermo Fisher Scientific) according to manufacturer instructions. All procedures were performed in accordance with National Institutes of Health guidelines and were approved by the Institutional Animal Care and Use Committee of the State University of New York at Buffalo.

Western blotting

We transfected HEK293 cells with the indicated constructs, and harvested and lysed them 24 h post-transfection, with 1% SDS lysis buffer. We removed debris and contaminating DNA/RNA by centrifugation 15 min at 13,000 rpm. Equal amounts of proteins in the supernatant were loaded onto a 15% SDS polyacrylamide gel to achieve separation among endogenous CaM (17 kDa), GFP (37 kDa), YFP-CaM (44 kDa), and GluN1-2a (100 kDa). Proteins were electrotransferred onto polyvinylidene difluoride membranes and probed with rabbit anti-CaM antibody [1:2500; catalog #ab45689, lot GR123440-4; Abcam; RRID:AB_725815 (http://www.abcam.com/)], mouse anti-GFP (1:5000; catalog #MAB1083, lot NG1720568, Millipore; RRID:AB_1587098), and rabbit anti-GluN1-pan (1:1000; catalog #MAB1589, lot 2739489, Millipore; RRID:AB_2279138). Hybridizations occurred overnight at 4°C for primary antibodies, and 1 h at room temperature for secondary antibodies (rabbit or mouse anti-HRP, 1:10,000 or 1:5000, respectively).

Calmodulin purification

For experiments requiring a defined CaM concentration (see Fig. 5), we purified CaM protein using an established protocol (Gopalakrishna and Anderson, 1982). Briefly, Rosetta bacterial strain transformed with vector encoding rat calmodulin (M19312.1; a gift from Geoffrey Pitt, Weill Cornell Medicine, New York, NY) was grown overnight at 37°C on LB/Amp/chloramphenicol plate. Single colonies were used to inoculate LB broth with 100 μg/ml Amp and 25 μg/ml chloramphenicol culture. Cells were grown at 37°C until A₆₀₀ = 0.6–0.8 and were chilled on ice for 30 min. Isopropyl β-d-1-thiogalactopyranoside (0.5 mm final) was added to induce protein expression, and cells were grown at 18°C for 18–24 h. Cells were centrifuged for 1 min at 16,000 × g and frozen as a pellet at −20°C. Expression was confirmed by a 12% SDS-PAGE gel and Coomassie stain. Pelleted cells were resuspended in ice-cold lysis buffer with protease inhibitors and 10 μm CaCl₂, and supplemented with lysozyme. Lysis was initiated with the addition of 10% Triton X-100 in lysis buffer with protease inhibitors and 10 μm CaCl₂, 100 mm MgCl₂, 10 mg/ml RNase A, 2 mg/ml DNase I (catalog #D5025, Sigma-Aldrich) and incubated on ice for 30 min with occasional inversion. Purification was performed using phenyl Sepharose (HiTrap Phenyl FF low sub). Protein was eluted with 50 mm Tris-HCl buffer, pH 7.5, containing 1 mm EGTA. CaM-containing fractions were dialyzed against distilled water and confirmed by gel electrophoresis.

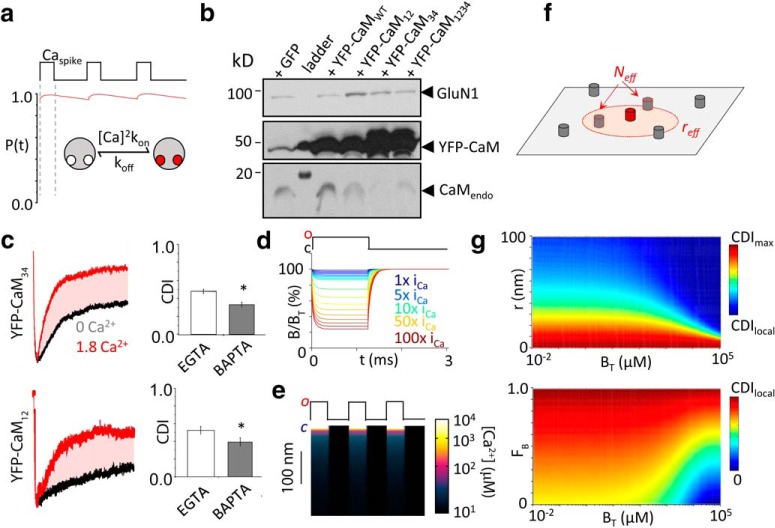
Figure 5.

Independence of CDI on Ca²⁺-binding kinetics of CaM lobe. a, Simulation of Ca²⁺/CaM C-lobe binding dynamics during a train of local Ca²⁺spikes at r_CaM (Ca_spike = 90 μm) demonstrate that C-lobe occupancy remains saturated during normal channel gating. b, Western blot confirms substantial overexpression of recombinant YFP-CaM constructs relative to CaM_endo and expressed channels (GluN1). c, Left, Whole-cell macroscopic currents from GluN1-2a/GluN2A receptors coexpressed with YFP-CaM₃₄ (top) or YFP-CaM₁₂ (bottom). Right, Each condition did not alter channel CDI or sensitivity to BAPTA. *p < 0.05 with Mann–Whitney U test. d, Simulation of free buffer concentration at r = 10 nm from channel pore during channel opening. Unitary i_Ca was progressively increased. e, Spatiotemporal simulation of Ca²⁺ diffusion in the presence of 10 mm BAPTA during channel gating. o, Open; c, closed. f, Schematic of a 2D membrane element with channels (cylinders) randomly distributed. For any given channel (red), an r_eff surrounding the channel sets the spatial limit that a neighboring channel must reside for Ca²⁺ influx to inactivate the primary channel (red dashed circle). g, Top, Evaluation of Equation 22 at fixed fractional channels preassociated with CaM (F_B = 0.4) predicts a broad CDI range across varying coupling distances, r, and B_T values. Bottom, Evaluation of Equation 22 at fixed coupling distance (r = 50 nm) at varying levels of channels preassociated with apoCaM.

Immunostaining and puncta size measurement

HEK293 cells [postnatal day 23 (P23) to P30] were plated on glass-bottom culture dishes coated with poly-l-ornithine and laminin. After 24 h of recovery in 37°C, transfected cells were live stained with wheat germ agglutinin (WGA) conjugated with Alexa Fluor 568 (1:500) in DMEM for 15 min at 37°C. Next, cells were washed, fixed with 4% paraformaldehyde in PBS, and blocked in BSA. Cells were then surface-stained for NMDA receptors with mouse anti-pan-GluN1 (1:1000; MAB1589, lot 2739489, Millipore; RRID:AB_2279138) overnight at 4°C. After permeablization with Triton X-100, they were washed and stained with rabbit anti-PSD-95 (1:500; ab18258, lot GR291396-1, Abcam; RRID:AB_444362) overnight at 4°C. Last, cells were incubated with secondary antibodies donkey anti-rabbit Alexa Fluor 647 (1:1000; catalog #ab150075, lot GR289683-1, Abcam; RRID:AB_2752244) and goat anti-mouse Alexa Fluor 488 (1:1000; catalog #ab150113, Abcam; RRID:AB_2576208). Imaging was performed with a CoolSnap HQ Camera (Roper Scientific) mounted on a Nikon TE-2000E Inverted Fluorescence Microscope with a 100× oil-emersion lens with 1.45 numerical aperture and MetaMorph imaging software. A 2 × 2 binning was applied, resulting in a 0.126 μm/pixel spatial resolution. For each field of view, images were taken with a 1 s exposure time. Images were subsequently analyzed using ImageJ (NIH) first by manually detecting particles using the Threshold tool and subsequently measuring punctae size using the Analyze Particle tool. Results were filtered to remove punctae with an area of 1 pixel² to minimize contribution of background noise to detection results.

Electrophysiology

Unitary currents were recorded in cell-attached patches with an applied potential of +80 mV. Borosilicate pipettes (15–25 MΩ) contained (extracellular) 150 mm NaCl, 2.5 mm KCl, 10 mm HEPBS [N-(2-hydroxyethyl)piperazine-N′-(4-butanesulfonic acid)], 0.1 mm EDTA, 0.1 mm glycine, 1 mm glutamate, pH 8 with NaOH, and with 1.8 mm buffered free CaCl₂ (MaxChelator software, Stanford University, Palo Alto, CA). Pipettes were not coated in dielectric as the intrinsic noise within our system is far below that of the unitary root mean squared variance in current (I_RMS = 0.2–0.3 pA²) and did not hamper event detection. The bath solution was PBS supplemented with 2 mm Ca²⁺ and Mg²⁺. All cells were pretreated with 6 μm FK-506 (CAS 109581-93-3, batch FK57-03, InvivoGen) to exclude the effects of endogenous calcineurin, which can modulate desensitization in a Ca²⁺-dependent manner. When indicated, cells were pretreated with either 20 μm EGTA-AM (CAS 99590-86-0; batch 97114, AnaSpec) or BAPTA-AM (CAS 126150-97-8, batch 5A/153906, Tocris Bioscience) supplemented with 20% Plurionic F-127 (CAS 9003-11-6, batch SLBL1780V, Sigma-Aldrich) in DMSO, for 30 min at 37°C. Treated cells were rinsed with PBS and allowed to rest for 10 min at room temperature before recording.

Unitary currents were amplified, low-pass filtered (10 kHz), and sampled at 40 kHz with Axopatch 200B (Molecular Devices; PCI-6229, National Instruments). The number of channels in each patch was determined by visual inspection of the record and counting of stacked openings during periods longer than 20 min. All data were acquired and processed with QuB software. Nonfiltered currents were idealized using the SKM algorithm with no applied dead time (Qin, 2004). Idealized records were exported as DWT files for coupling analysis in MATLAB 2017b (MathWorks). All unitary currents were displayed in figures with 1 kHz digital filtering. We monitored the liquid junction potential using the K⁺-salt bridge method. We found the liquid junction potential difference to be negligible (1.1 ± 0.1 mV in 0 Ca²⁺; and 0.8 ± 0.1 mV in 1.8 Ca²⁺; n = 5).

Ensemble currents were recorded with the whole-cell patch clamp held at −80 mV. Borosilicate pipettes (4–8 MΩ) were filled with intracellular solution containing 135 mm CsCl, 35 mm CsOH, 4 mm MgATP, 0.3 mm Na₂GTP, and either BAPTA or EGTA as indicated, and buffered to pH 7.4 (CsOH). Solutions for BAPTA titrations were made by diluting the intracellular solution containing 60 mm BAPTA with an isosmotic intracellular solution lacking BAPTA. Extracellular solutions contained 150 mm NaCl, 2.5 mm KCl, 10 mm HEPBS, 0.1 mm EDTA, and 0.1 mm glycine, and cells were bathed in PBS with Ca²⁺ and Mg²⁺. Free Ca²⁺ concentrations were obtained by adding CaCl₂, as calculated with MAXC software. For neuronal recordings, extracellular solutions also contained CNQX (40 μm) and ifenprodil (1 μm) to reduce responses from AMPA receptors and GluN2B-containing NMDA receptors. Solutions were applied using a focal perfusion pencil (Automate Scientific) attached to an eight-valve pressurized solution exchange system (BPS-8, ALA Scientific). After amplification and filtering at 2 kHz (4-pole Bessel; Axopatch 200B, Molecular Devices), currents were sampled at 5 kHz (Digidata 1440A, Molecular Devices) and acquired and analyzed with pCLAMP 10.5. For all recordings, seal quality was ascertained by monitoring series resistance.

We measured CDI with the method we reported recently that controls for changes in channel kinetics and unitary amplitude by modulators or mutations (Iacobucci and Popescu, 2017). Macroscopic currents were elicited by applying glutamate (1 mm) for 5 s in extracellular solutions without or with 1.8 mm Ca²⁺. To overcome the challenge of excluding external allosteric effects of Ca²⁺, we pre-equilibrated channels with external Ca²⁺ to saturate external Ca²⁺ binding sites before applying agonist. Thus, the effects of external Ca²⁺ will be present throughout the recording and does not change with time. Next, to exclude this time-independent effect from the analysis, macroscopic currents were normalized to their maximal peak amplitude in the absence of external Ca²⁺, such that we measure only the relative change in current that evolves with time upon channel opening. The peak (I_pk) current and current remaining after time t following glutamate application [I(t)] in the presence and absence of Ca²⁺ were measured to calculate the magnitude of CDI at time t as follows:

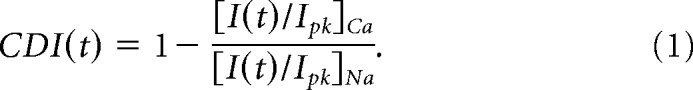We calculated CDI using I(t) measured at t = 5 s after glutamate application. Charge density (J) was measured as the ratio of whole-cell peak Na⁺ current (I_pk,Na) to the cell capacitance measured as the compensatory increase in the capacitive transient current upon entering whole-cell mode (C_m). Liquid junction potential between bath solution and Cs⁺ intracellular solutions was found to be 8.3 ± 0.1 mV (n = 5) in our system. Assuming a chord conductance of 53 pS and reversal potential of +2 mV in 1.8 mm Ca²⁺ (Maki and Popescu, 2014), this junction potential is expected to reduce the Ca²⁺ current by ∼8%, which is not expected to significantly impact elicited CDI based on prior measurements (Iacobucci and Popescu, 2017).

Analyses of channel cooperativity

In the measurements of cooperativity in cell-attached recordings, the allosteric effects of Ca²⁺ binding to individual channels is assumed to be independent of the activity of neighboring channels. Therefore, channels inhibited only by external Ca²⁺ would be expected to gate independently and would not affect our measurements of cooperativity by either the binomial or coupled Markov model method used in this study.

Binomial distribution analysis

A common test for channel gating cooperativity is to observe unitary current amplitude distributions in multichannel patches and compare it to the binomial distribution expected for channels that gate independently (Choi, 2014). Thus, we recorded unitary currents from multichannel patches containing N channels. The number of channels was determined by direct visual observation of unitary current summation due to simultaneous openings over a long recording time (>20 min). The occupancy of each conductance level, r, was measured by the definite integral of each N + 1 Gaussian component, F_r, fitted to the amplitude histogram generated from the unfiltered unitary current recordings, as follows:

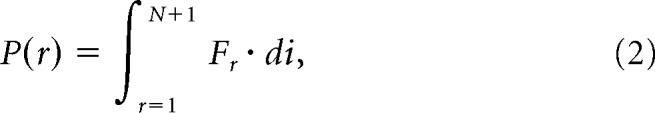where d_i is the histogram bin width. To generate model-free predictions of binomially distributed occupancies, we first computed the predicted single-channel P_o (stationary channel open probability) value from each multichannel recording assuming independent gating according to Yang and Sachs (1990), as follows:

where r = 1 referring to the measured probability of any channel being closed. The resulting P_o specific to each patch file was used to predict the binomial P(r) for each subsequent open conductance level (r = 2–5), as follows:

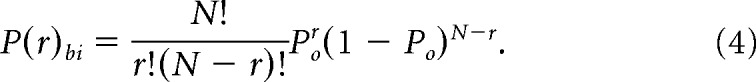The correlation between binomial predictions [P(r)_bi] and empirical measurements [P(r)] of open conductance class occupancies was determined using unconstrained linear regression. The resulting residual sum of square error was used to determine the degree of significance between 0 Ca²⁺ and 1.8 Ca²⁺ by an F test.

Coupled Markov chain analysis

The magnitude of channel cooperativity can be evaluated quantitatively by estimating a coupling factor κ, which can be calculated from transition probabilities (V) among conductance levels recorded from multichannel patches (Chung and Kennedy, 1996). Briefly, we modeled individual channels as two-state (open and closed) processes governed by a set of forward and reverse transition probabilities, α and β, respectively, as follows:

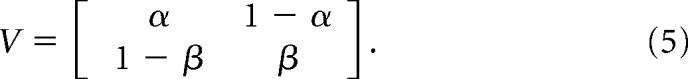For any N channels with independent gating, the transition probabilities are determined by the Kronecker product of V:

For N channels with perfect negatively coupled gating, the transition probability matrix converges to that of a single-channel transition matrix, as follows:

The two matrices are related by a single coupling coefficient, κ:

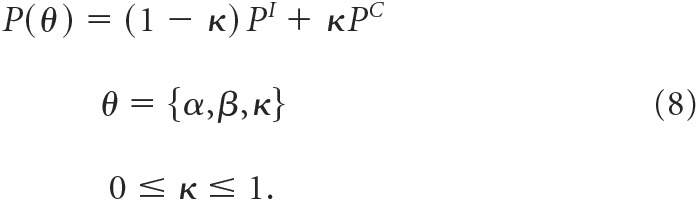We determined the parameters describing this model (α, β, and κ) from empirical transition probability matrices, Â, using the Baum–Welch algorithm in the MATLAB hmmestimate built-in function from multichannel patches using a gradient descent method, as follows:

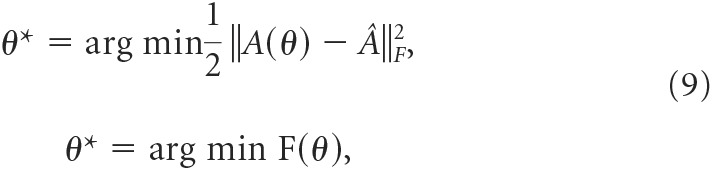minimizing the cost function, F(θ), where A(θ) is as follows:

R and L are state indexing functions to account for aggregate states indistinguishable by conductance amplitude (Chung and Kennedy, 1996). Within our datasets, the evaluation of the cost function across all values of the free parameters θ did not reveal local minima that would confound the analysis. All parameters were constrained between 0 and 1 and initialized at 0.5 at the start of fitting to minimize bias.

Diffusion simulations

We simulated Ca²⁺ diffusion in different buffers as described previously (Tadross et al., 2008, 2013; Iacobucci and Popescu, 2017). Briefly, channels were considered as point sources of Ca²⁺ in hemispherical space with the membrane as an infinite impermeable plane, thereby reducing the problem to a 1D set of differential equations. The free Ca²⁺ and buffer diffusion equations were discretized according to this geometry as a finite-element model of discrete shells.

Monte Carlo stochastic simulations of lateral diffusion of channels within the patch pipette were based upon algorithms used by MCell (Stiles and Bartol, 2001). We modeled the patch as a symmetric 2D circle of 500 nm diameter centered at x = 0 and y = 0 (Suchyna et al., 2009). The simulation is implemented with a discrete timestep, dt, during which channel movement is described by a displacement vector, v, with 2D Cartesian coordinates (Δx, Δy). The magnitude of v is given by Euclidean displacement r_Δ = $\sqrt{\Delta x^2+\Delta y^2}$ and is drawn from the following experimentally validated density functions:

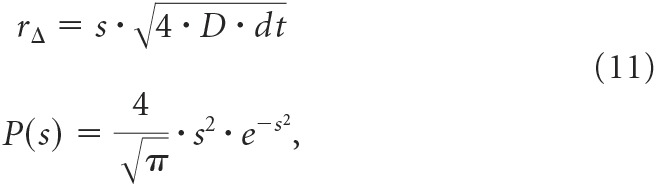where s is a unitless random variable and P(s) is the probability of s assuming a value between s and s + ds. During each timestep, r_Δ is calculated for each coordinate using the s value sampled randomly from P(s). The direction of each x and y component of the displacement is determined from multiplying r_Δ by a discrete random variable that adopts values of −1 or 1 with equal probability. The NMDA receptor diffusion coefficient was 0.01 μm²/s (Jézéquel et al., 2017). All diffusion simulations were performed using MATLAB R2017b (MathWorks).

Deriving analytical expression for channel coupling

Probing mechanism

We have previously shown that local Ca²⁺ transients during NMDA receptor activation drive CDI by activating a resident CaM molecule positioned close to the pore (Iacobucci and Popescu, 2017). Our observation of functional coupling due to submicroscopic Ca²⁺ diffusion between channels provides a conceptual challenge to unify these two forms of modulation (local autoinhibition and coordinated inhibitory coupling) into a single mechanism. CaM is composed of two lobes that bind two Ca²⁺ ions each independently of one another with different kinetics (Zhang et al., 2012). In L-type Ca²⁺ channels, these differential Ca²⁺-binding kinetics of CaM combined with the unique molecular interactions with the channel allow the N-lobe and C-lobe respond specifically to global and local Ca²⁺ signals, respectively (Tadross et al., 2008). Modeling Ca²⁺ binding to each lobe separately as a two-state kinetic scheme, the time-dependent occupancy of each state is calculated by solving the following:

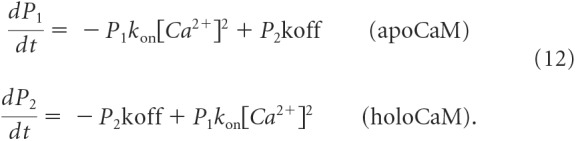From this system of equations, we see that, in response to a train of Ca²⁺ spikes, the local CaM molecule will undergo oscillations of activation. The fast binding and unbinding kinetics of the N-lobe will conform N-lobe activation to a pulsatile waveform. In contrast, the high-affinity C-lobe has slow unbinding kinetics. Thus, during a train of Ca²⁺ spikes the C-lobe remains relatively saturated throughout channel gating. Furthermore, the overexpression of CaM constructs engineered to restrict Ca²⁺ binding to either the C-lobe (CaM₁₂) or N-lobe (CaM₃₄) in HEK293 cells was sufficient to mediate NMDA receptor CDI. This is consistent with previous biochemical evidence demonstrating that either lobe of CaM is sufficient to displace α-actinin from C0, which is hypothesized to be a critical determinant of NMDA receptor CDI (Merrill et al., 2007). Thus, Ca²⁺ binding to the C-lobe of a local CaM molecule is sufficient to inactivate the channel. Given that this lobe remains saturated during channel gating, and assuming a CaM/channel stoichiometry of 1:1 (Wang et al., 2008), the additional Ca²⁺ from remote channels will unlikely facilitate further inactivation of the channel via this CaM molecule.

In our previous study, we probed CaM–channel interactions by overexpressing CaM effectively saturating channels to be preassociated or coupled with a CaM molecule. However, at synapses CaM is highly mobile and likely present at lower concentrations relative to the apoCaM K_D at the GluN1 C0 low-affinity binding site (Persechini and Stemmer, 2002; Ataman et al., 2007; Petersen and Gerges, 2015; Iacobucci and Popescu, 2017). Thus, only a fraction of NMDA receptors will likely be preassociated with apoCaM at any given time. We predict that for channels already bound with CaM, their local, high-amplitude Ca²⁺ influx will be the primary driver of CDI in this population. In contrast, for channels not bound with CaM, Ca²⁺ influx by remote channels will also activate a mobile pool of CaM that recruits to the fraction of unbound NMDA receptors to inactivate this secondary population. We sought to derive a testable analytic expression to describe this predicted behavior as a function of an experimentally controllable variable: Ca²⁺ buffer concentration.

Derivation of the general model

The single-channel case.

In various ion channels, CDI is conventionally studied by measuring the inhibition of macroscopic currents by Ca²⁺. Revealing CDI in individual ion channels has been more challenging due to the stochastic, quantized nature of CaM–channel interactions (Adams et al., 2014) and often relies on quantifying either coarse gating parameters (e.g., open probability) or the averaging of single-channel recordings to recapitulate a macroscopic current (Yue et al., 1990; Michikawa et al., 1999). Thus, the deterministic approximations of CDI used previously (Iacobucci and Popescu, 2017), which are, nevertheless, suitable for studying population-based channel behavior, may deviate from single-channel measurements. For a large population of N channels, the fraction of channels preassociated with apoCaM (F_B) can be represented at any time t by F_B(t) = N_B(t)/N, where NB(t) is the number of channels bound by apoCaM at time t at rest. For sufficiently large N, F_B(t) becomes approximately constant for the duration of the experiment. However, individual channels will cycle between bound (F_B = 1) and unbound (F_B = 0) states over time. For an ergodic process, the ensemble average over a large population of N molecules converges on the temporal moving average of a single molecule over a long trajectory relative to the duration of the process of interest. This allows the single molecule sufficient time to sample all conformational space. Thus, for sufficiently long recording times, the time-averaged fractional occupancy of the channel bound by CaM is equivalent to F_B for N channels. This is in contrast to the brief observation windows commonly used in Ca_V channels where the stochasticity of CaM–channel interactions becomes apparent.

In our previous work, we studied CDI under conditions of strong overexpression of CaM (Iacobucci and Popescu, 2017). This configuration results in an increased binding of CaM with channels at rest through mass action; thus, N_B = N and consequently F_B approaches 1 under these conditions. In the absence of Ca²⁺, ensemble currents relax to a steady-state value during which time individual channels gate with a normal basal P_o value. Dialysis of high Ca²⁺ (50 μm) into the cell saturates CDI to a limiting level (CDI = CDI_max = 0.8). This nonzero value of CDI is consistent with prior studies showing that inactive channels exhibit a low-P_o gating mode (Rycroft and Gibb, 2002). We model this behavior as a tiered model of gating whereby individual channels stochastically switch between active (A) and inactive (I) gating modes. Each mode exhibits unique channel-gating kinetics that will manifest as changes in the equilibrium P_o of individual channels. When in the active mode (A, not bound by Ca²⁺/CaM), the P_o value reflects the high-P_o of this mode. In contrast, channels in the inactive mode (I, bound with Ca²⁺/CaM) gate with the P_o value reflecting the low-P_o of this mode. In physiological conditions, because maximal CDI (CDI_max = 0.8) is not reached (CDI ≈ 0.4), not all channels will populate the I state at any given time. Equally, an individual channel will cycle between the A and I modes due to the stochastic nature of CaM–channel interactions.

Thus, the modulatory effect we observe in multichannel patches through the coupling factor κ likely reflects both the reduced channel P_o during CDI and the stochastic nature of CaM–channel interactions. Further, given the empirically demonstrated utility of macroscopically defined metrics of CDI in quantifying single-channel inactivation, we extend our theoretical model to multichannel recordings using these metrics.

Simplest case: two channels.

To develop a model of CDI that accounts for local and global mechanisms of inhibition, we first consider the behavior of the simplest case: two neighboring channels. For any arbitrary arrangement of these Ca²⁺-permeable channels along a 2D membrane element, each channel will be inactivated by both the train of high-amplitude Ca²⁺ spikes fluxed through its own pore (CDI_local) and the Ca²⁺ flux produced by the neighboring channel (CDI_global), as follows:

Based upon our hypothesis that the fraction of channels preassociated with apoCaM, F_B, were sensitive to local Ca²⁺ influx and unbound channels can respond to Ca²⁺ influx through remote channels, we scale each CDI term accordingly, as follows:

Intracellular Ca²⁺ dialysis experiments reveal that NMDA receptor sensitivity to intracellular Ca²⁺ can be described by the Hill equation (Iacobucci and Popescu, 2017), as follows:

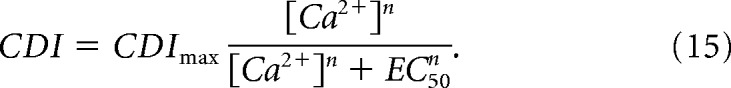where the Hill coefficient n = 1.8 and EC₅₀ = 4.7 μm were determined experimentally. Because both CDI_local and CDI_global components will be driven by the intracellular [Ca²⁺], this relation can be used to describe the Ca²⁺ sensitivity of both the local and global components of CDI, as follows:

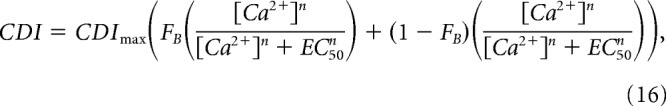We can deconstruct this relationship by its “local” and “global” components. The Ca²⁺ signal governing the CDI_local component is the high-amplitude Ca²⁺ transient generated by the channel (Ca_spike). The steady-state Ca_spike amplitude during a single channel-opening event is determined by the Ca²⁺ current, i_Ca, the distance of CaM from the pore, r_CaM, and the intracellular buffer concentration, B_T, as described by the Neher–Stern relation (Stern, 1992), as follows:

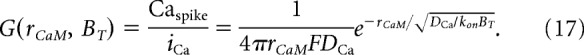We have previously determined the value of the single-channel gain, G, for GluN1–2a/GluN2A channels to be 235 μm/pA. Thus, the steady-state local Ca²⁺ signal can be described as follows: Ca_spike = i_CaG. During the stationary gating of the channel in a well mixed buffer, the time course of the Ca²⁺ transient reaches Ca_spike during channel opening and returns to 0 during channel closing within microseconds. Thus, the effective local Ca²⁺ amplitude can be approximated by the following time-averaged local Ca²⁺ signal:

where P_o is the stationary channel open probability. The global signal is potentially more complex. First, the close spatial proximity of channels may lead to local buffer saturating, thus boosting the local Ca²⁺ signals and skewing CDI predictions. We tested this possibility by spatiotemporal Ca²⁺ diffusion simulations from a point source in the presence of diffusible buffer. Using a physiologically relevant i_Ca value, a single channel could not lead to buffer saturating at r_CaM. Only by increasing i_Ca 100× could buffer saturating be observed (see Fig. 5d). Thus, in a cluster of only several channels, no substantial buffer saturating is expected. This allows for the linear summation of Ca²⁺ signals from multiple sources. The second concern is the temporal nature of the Ca²⁺ signal generated from distant channels. For local signals, the time-averaged approximation holds because the temporal Ca²⁺ waveform is a square-like step pulse that synchronizes with channel opening. To test whether this approximation holds for larger distances, we simulated a train of channel gating and extended the spatial boundaries to 300 nm. We found that even at these distances, rises in [Ca²⁺] closely synchronize with channel gating, allowing the time-averaged approximation to hold (see Fig. 5e).

For a given pair of channels, the Ca²⁺ signal generated by the neighboring channel can be described by the following:

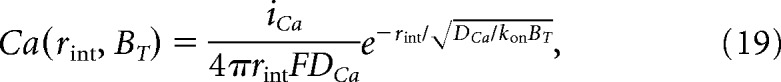where r_int is the interchannel distance.

Combining these relations into Equation 16, we arrive at the following:

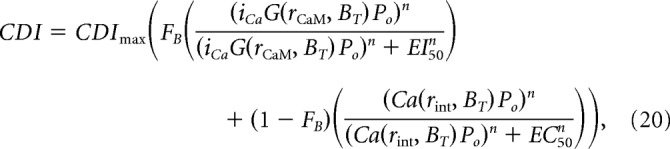where G(r_CaM, B_T) and Ca(r, B_T) are substituted by Equations 17 and 19, respectively.

A potential source of variation in the quantification of CDI between individual channels may be the lateral diffusion of channels within the membrane (see Fig. 6f). As channels diffuse independently of each other in a patch, for example, their interchannel distance can vary substantially. Consequently, at any given point in time, the probability of inactivation can follow an exponential distribution itself. Thus, for sufficiently long recording times, the observed degree of inactivation reflects the temporal average of this P(CDI) distribution.

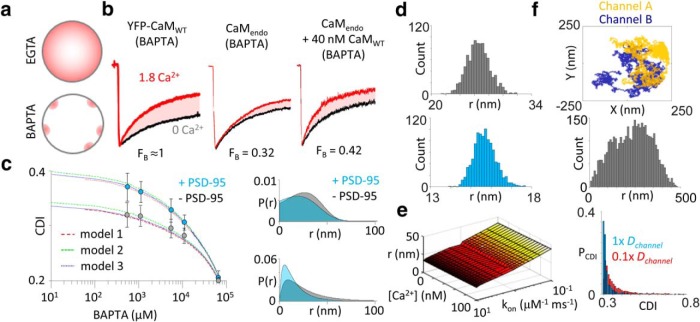
Figure 6.

PSD-95 decreases the effective coupling distance between NMDA receptors. a, Schematic of intracellular Ca²⁺ concentration gradients (pink) during whole-cell recordings in weak buffering (EGTA) and strong buffering (BAPTA) conditions. Restricting Ca²⁺ elevations within local nanodomains of the source reveals the fraction of channels preassociated with CaM. b, Representative whole-cell current from GluN1-2a/GluN2A and with YFP-CaM_WT (left), with CaM_endo or with 40 nm purified CaM_WT (right). c, Left, CDI measurements in cells either lacking (gray) or coexpressing (blue) PSD-95 and with increasing concentrations of intracellular BAPTA. Three variants of Equation 22 were fit to the data: model 1, r is constant; model 2, r is a skewed Gaussian distribution; and model 3, r is a weighted exponential distribution. Right, Hypothetical distributions of effective channel coupling distance predicted by models 2 (top) and 3 (bottom) using the parameter values determined from the fit. d, The statistical error of coupling distance parameter (r) estimation from the fits was determined by generating 1000 artificial datasets using a bootstrap procedure and analyzing these sets as the original by fit with generalized model. Histogram of coupling distances, r, of bootstrap analysis from cells not expressing (top) and expressing (bottom) PSD-95. e, Systematic error of the model was evaluated by systematically changing model parameter (BAPTA kinetics, k_on, and free basal Ca²⁺) values over two orders of magnitude. f, Monte Carlo simulation of lateral diffusion of channels within patch pipette. Top, Trajectories of two channels explored by lateral diffusion during a cell-attached patch-clamp experiment. Middle, Distribution of interchannel distances during patch-clamp recording. Bottom, Distribution of predicted CDI values calculated with Equation 22. The probability of CDI [P(CDI)] during single-channel recordings follows an exponential distribution as a result of lateral diffusion. Reduction of the diffusion coefficient (D_channel) shifts the distribution toward stronger CDI magnitudes.

Complex case: N channels.

For a population of N equivalent channels, the global Ca²⁺ signal is the linear sum of the time-averaged Ca²⁺ signal (Neher, 1998). However, because the Ca²⁺ signal generated by a channel decays exponentially by diffusion (Eq. 19), not all channels will be within sufficient range to contribute to the inactivation of a neighboring channel (see Fig. 5f). Thus, each channel has, on average, an effective number of neighboring channels, N_eff, which contribute to the global Ca²⁺ signal experienced by a given channel within group, as follows:

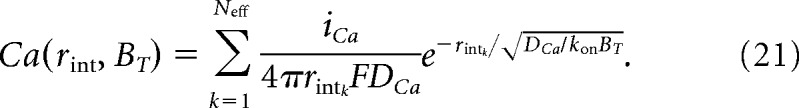In response to a train of Ca²⁺ spikes from channel gating, the high-affinity C-lobe of CaM will dominate the activation of CaM to elicit CDI in endogenous CaM. Thus, for channels already preassociated with apoCaM, the local Ca²⁺ influx via that channel will likely dominate the contribution to its inactivation. We have previously found that the magnitude of CDI increases upon overexpression of CaM_WT and given the low affinity for apoCaM (Iacobucci and Popescu, 2017), only a fraction of channels will be preassociated with apoCaM in resting conditions (F_B). Therefore, given the enrichment of CaM in dendritic spines (Petersen and Gerges, 2015), the remaining channel population (1 − F_B) will be the most susceptible to global Ca²⁺ inhibition.

Therefore, returning to Equation 20 and substituting Equation 21 as the driving Ca²⁺ signal for the CDI_global term, we arrive at the following:

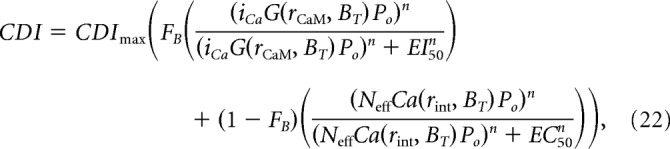where G(r_CaM, B_T) and Ca(r, B_T) are substituted by Equations 17 and 21, respectively. We experimentally gauge F_B values by measuring CDI with only endogenous CaM present (CDI_endo) and normalizing by CDI measured upon CaM_WT overexpression with the same construct (CDI_CaM,WT). This normalization approximates F_B values (Ben Johny et al., 2013), as follows:

The N_eff value was estimated by the following:

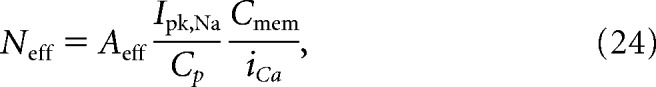where A_eff = πr_eff² is the effective circular area surrounding a channel where the time-averaged spatial Ca²⁺ gradient formed by a neighboring channel can generate CDI ≥ 0.001. I_pk,Na/C_p is the cell charge density. C_p,mem is the capacitance of the membrane equal to 1e6 pF/cm². In our cells, we found N_eff = 0.2 assuming a random distribution.

Model variants and fitting

For reconstructing hypothetical coupling distance distributions from the data, we substituted the r_int parameter in Equation 22 with the expected value of a skew normal distribution probability density function where the location, μ, and scale, σ, parameters were free and the shape, α, parameter was constrained to −1, as follows:

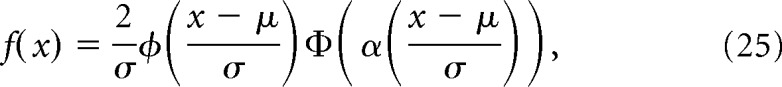over the range 0 < x < 200 nm where ϕ(x) is the normal probability density function and Φ(x) is the normal cumulative density function; or an exponential probability density function, as follows:

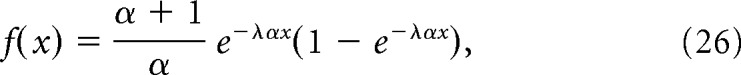where λ = 1/μ. For estimating the error on the coupling distance parameter for the model, we performed a bootstrapping procedure to generate 1000 artificial datasets from the original [BAPTA]-CDI data and analyzed as the original (Efron and Tibshirani, 1993; see Fig. 6d). This accounts for the variance within the data. Further, as values of certain parameters in the model are only approximately known in experimental conditions (e.g., BAPTA binding and resting Ca²⁺ in the cell), we systematically varied these parameter values in the model and refitted the data to assess how variance in these unknowns could influence the fitting results (see Fig. 6e).

Statistical analysis

We report CDI values as the rounded mean ± SE. Coupling distributions were shown as box-and-whisker plots indicating the minimum, maximum, 25th and 75th percentiles, and distribution median. All statistical analyses were performed in MATLAB and R. The nonparametric Mann–Whitney rank sum test was used to determine significance because CDI, coupling κ, and unitary conductance level occupancies tended to follow non-normal distributions as determined using the Anderson–Darling and Lillifore's tests in R. Fittings of models to data were performed using the built-in fittype command in MATLAB R2017b with the nonlinear least-squares error minimization method.

Results

NMDA receptor CDI varies with cellular charge density

Values reported in the literature for NMDA receptor CDI vary widely (∼20–60%; Legendre et al., 1993; Medina et al., 1995; Zhang et al., 1998; Vissel et al., 2002; Sibarov et al., 2015, 2016, 2018). Much of this variability persists even when controlling for other forms of NMDA receptor time-dependent changes in activity by normalizing the current drop (I_ss/I_pk) observed in the presence of external Ca²⁺ to that observed in the absence of Ca²⁺ (Iacobucci and Popescu, 2017; Fig. 1a; Eq. 1). The extent of NMDA receptor CDI depends on intracellular Ca²⁺ and CaM levels, but the observed variability could not be explained by differences in Ca²⁺ flux (Vissel et al., 2002) or by the variation in CaM expression levels (Iacobucci and Popescu, 2017). We showed recently that only receptors that are prebound with apoCaM are sensitive to local Ca²⁺ flux and that not all receptors are thus primed (Iacobucci and Popescu, 2017). Therefore, the possibility remains that Ca²⁺ elevations produced by vicinal Ca²⁺ sources (global Ca²⁺) may engage soluble apoCaM, and the resulting Ca²⁺/CaM binding to naive receptors would produce additional CDI. Various Ca²⁺-permeable channels are sensitive to the activity of their neighbors including voltage-gated Ca²⁺ channels (Imredy and Yue, 1992; Soong et al., 2002) and IP₃ receptors (Wiltgen et al., 2014). Specifically, the inactivation of Ca²⁺ channels correlates with charge density (Soong et al., 2002). We asked whether the variability of observed NMDA receptor CDI correlates with possible experimental variations in receptor crowding at the cell surface.

Figure 1.

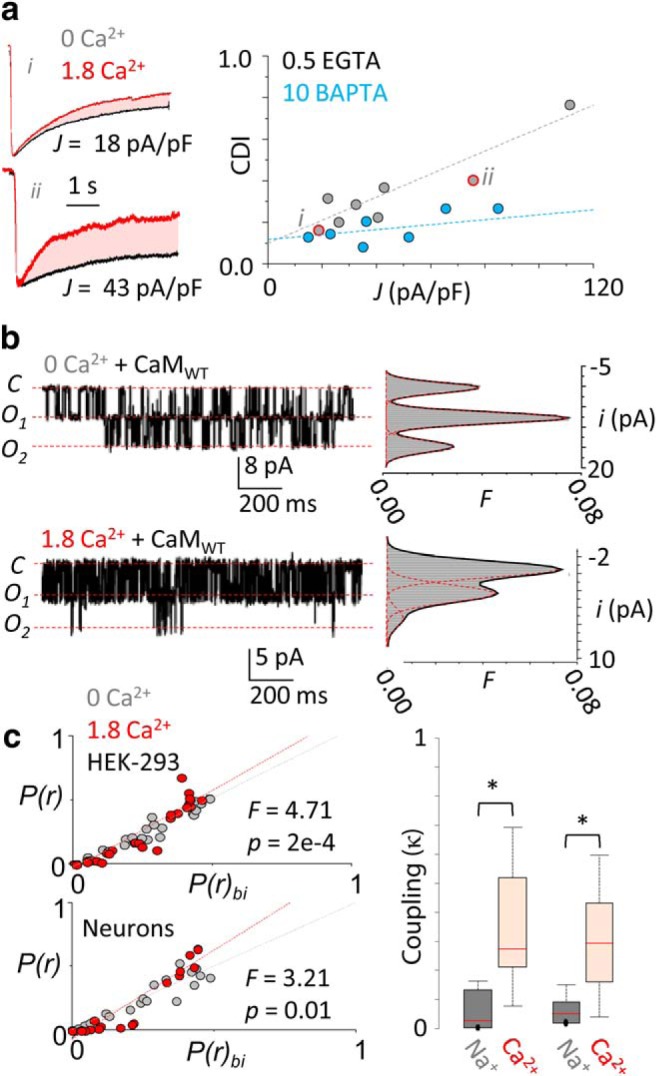
NMDA receptor currents display negative cooperativity. a, Left, Glutamate-elicited currents from two cells (i and ii, red data points in graph at right) expressing GluN1-2a/GluN2A receptors in the absence (black) and presence (red) of 1.8 mm extracellular Ca²⁺ (superimposed and normalized to peak). For each cell, the calculated CDI (shaded area) and the measured current densities (J) are indicated. Right, Linear regressions for CDI-J data. Intracellular Ca²⁺ buffering strongly influenced the correlation between CDI and charge density are as follows: EGTA, R² = 0.92; vs BAPTA, R² = 0.19. b, Left, Representative current traces (3 s) recorded from a cell-attached patch containing two active receptors pretreated with EGTA-AM (20 μm) in the absence (top) and presence (bottom) of external Ca²⁺. Right, Corresponding unitary amplitude (i) frequency (F) histograms with superimposed Gaussian fits (red dotted) and the overall probability density function (solid black). c, Left, Correlations between predicted conductance class occupancies from binomial distribution [P(r)_bi] and measured class occupancies [P(r)] for each record show deviations from independence in the presence of Ca²⁺ for both recombinant GluN1-2a/GluN2A receptors (top) and native receptors (bottom). c, Right, External Ca²⁺ increased κ values and variabilities in both recombinant (gray) and native receptors native (red). *p < 0.05, Mann–Whitney U test.

We measured the CDI of GluN1–2a/GluN2A receptors expressed in HEK293 cells and the corresponding cellular capacitance as a proxy for cellular surface area and found that, indeed, CDI magnitude was larger in cells with higher charge density. Importantly, this correlation disappeared when dialyzing cells with high concentrations (10 mm) of the fast Ca²⁺ chelator BAPTA, which restricts Ca²⁺ diffusion to only several nanometers from the channel pore (Fig. 1a). Together, these results show that NMDA receptor macroscopic currents inactivate more when channels are expressed more densely and that this correlation requires intracellular Ca²⁺ diffusion, consistent with a mechanism where NMDA receptors Ca²⁺ flux produces additional CDI by engaging naive nearby channels.

NMDA receptors display Ca²⁺ and CaM-dependent negative cooperativity

If indeed Ca²⁺ fluxed by vicinal channels can influence NMDA receptor activity, receptors should display gating cooperativity when Ca²⁺ is a permeant ion. To investigate this possibility, we recorded unitary channel openings in cell-attached patches containing at least two channels from HEK293 cells pretreated with EGTA-AM and expressing GluN1-2a/GluN2A receptors. We then evaluated how well the predicted conductance occupancies correlated with measured conductance occupancies for each recording. When Na⁺ was the only permeant ion, the occupancy of each conductance level conformed well to a binomial prediction indicating an absence of functional coupling (Fig. 1c, top left; R² = 0.97). In contrast, in 1.8 mm external Ca²⁺, channels dwelled more frequently in lower conductance levels (Fig. 1b) and shifted significantly the correlation with binomial predictions away from that measured in 0 external Ca²⁺ (Fig. 1c, top left; R² = 0.74, F = 4.71, p = 0.00019). We observed the same departure from independence in native receptors recorded from dissociated hippocampal neurons (Fig. 1c, bottom left; R² = 0.67, F = 3.21, p = 0.0095)

To measure the degree of the observed gating coupling, we used a previously described method to calculate a coupling factor κ, which varies from 0 to 1, to indicate complete independence, or tight coupling, respectively (Chung and Kennedy, 1996). Consistent with other studies, we used κ = 0.1 as a threshold for cooperativity (Dixon et al., 2015). With this approach, we found that in EGTA-AM-pretreated HEK293 cells expressing GluN1-2a/GluN2A receptors, the coupling factor κ was <0.1 for most patches in 0 Ca²⁺ (0.039 ± 0.016; n = 9), indicating the absence of cooperativity, whereas, with 1.8 mm Ca²⁺, κ values shifted significantly toward higher mean values (0.27 ± 0.05; n = 11; p = 0.001), indicating a moderate level of coupling. Similarly, in dissociated hippocampal neurons, 1.8 mm Ca²⁺ increased the coupling factor from 0.063 ± 0.022 (n = 7) to 0.30 ± 0.03 (n = 7; p = 0.002). This novel observation represents strong evidence for negative gating cooperativity in physiologic conditions among as few as two NMDA receptors, through a Ca²⁺-dependent mechanism (Fig. 1c, right, Table 1).

Table 1.

Coupled Markov model fit results

GluN1-2a/GluN2A		Hippocampal neuron		GluN1-2a/GluN2A + BAPTA-AM		GluN1-2a/GluN2A + YFP-CaM1234		GluN1-2a/GluN2A + PSD-95		GluN1-2a/GluN2AΔF1344 + PSD-95
Na+	Ca2+	Na+	Ca2+	Na+	Ca2+	Na+	Ca2+	Na+	Ca2+	Na+	Ca2+
n = 9	n = 11	n = 7	n = 7	n = 8	n = 6	n = 8	n = 8	n = 5	n = 5	n = 6	n = 7
α = 0.931 ± 0.019	α = 0.991 ± 0.034	α = 0.965 ± 0.051	α = 0.940 ± 0.041	α = 0.995 ± 0.023	α = 0.913 ±	α = 0.899 ± 0.098	α = 0.997 ± 0.080	α = 0.919 ± 0.022	α = 0.967 ± 0.074	α = 0.965 ± 0.054	α = 0.999 ± 0.077
β = 0.945 ± 0.011	β = 0.978 ± 0.024	β = 0.923 ± 0.036	β = 0.905 ± 0.081	β = 0.963 ± 0.048	β = 0.998 ± 0.062	β = 0.962 ± 0.078	β = 0.879 ± 0.102	β = 0.974 ± 0.050	β = 0.934 ± 0.063	β = 0.971 ± 0.068	β = 0.998 ± 0.020
κ = 0.039 ± 0.016	κ = 0.269 ± 0.049	κ = 0.063 ± 0.022	κ = 0.295 ± 0.032	κ = 0.042 ± 0.021	κ = 0.048 ± 0.023	κ = 0.034 ± 0.014	κ = 0.034 ± 0.018	κ = 0.011 ± 0.009	κ = 0.683 ± 0.107	κ = 0.012 ± 0.008	κ = 0.168 ± 0.054
	p = 0.001		p = 0.002		p = 0.846		p = 0.998		p = 0.001		p = 0.027

p represents statistical comparison of κ between 0 Ca²⁺ and 1.8 Ca²⁺ conditions within groups. p was determined using the Mann–Whitney U test.

Next, we asked whether functional coupling required the diffusion of fluxed Ca²⁺. We pretreated cells with the fast-binding Ca²⁺ chelator BAPTA-AM and recorded on-cell unitary currents with 1.8 external Ca²⁺ (Fig. 2a). BAPTA and EGTA have similarly high affinity for Ca²⁺; however, they differ substantially (40-fold) in their Ca²⁺ association kinetics, such that BAPTA, but not EGTA, restricts Ca²⁺ diffusion to within several nanometers from the source. Compared with when EGTA-AM was used as the intracellular buffer, BAPTA-AM reduced the Ca²⁺-dependent shift in the correlation away from independence (Fig. 2b, top; 0 Ca²⁺: R² = 0.90, 1.8 Ca²⁺ R² = 0.91, F = 1.45, p = 0.191) and reduced coupling substantially to κ values similar to those observed in 0 Ca²⁺ (Fig. 2c). We conclude that NMDA receptor gating cooperativity required intracellular diffusion of fluxed Ca²⁺. These results are consistent with a mechanism where NMDA receptor Ca²⁺ flux sensitizes additional vicinal receptors to CDI.

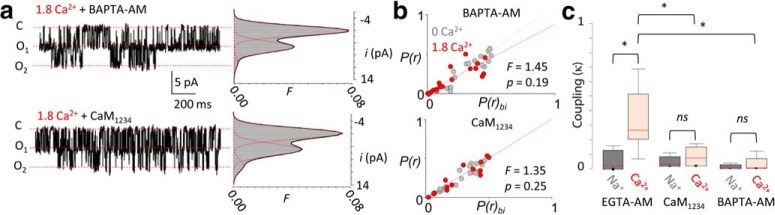
Figure 2.

Negative cooperativity of NMDA receptor currents is Ca²⁺ and CaM dependent. a, Representative unitary currents from cell-attached patches containing two GluN1-2a/GluN2A receptors in the presence of 1.8 mm Ca²⁺, in HEK293 cells pretreated with BAPTA-AM (20 μm, top) or coexpressing YFP-CaM₁₂₃₄ (bottom), and corresponding amplitude histograms superimposed by fitted Gaussian components (red dashed) and probability density function (black). b, Correlations between predicted conductance class occupancies from binomial distribution for each recorded file [P(r)_bi] and measured class occupancies [P(r)] show that intracellular buffering and CaM₁₂₃₄ reduce deviations from independence produced by Ca²⁺ (p determined by F test). c, Distributions of coupling coefficients, *p < 0.05, Mann–Whitney U test.

Given that CDI is dependent on Ca²⁺ binding to CaM, we asked whether channel cooperativity also required Ca²⁺ binding to CaM by overexpressing a Ca²⁺-insensitive CaM mutant (CaM₁₂₃₄; Fig. 2a; Peterson et al., 1999; Iacobucci and Popescu, 2017). We found that in these recordings, amplitude distributions conformed to the binomial distribution expected for independent gating (Fig. 2b, bottom; 0 Ca²⁺: R² = 0.93, 1.8 Ca²⁺ R² = 0.94, F = 1.35, p = 0.250), and the distribution of κ values collapsed near 0 (Fig. 2c, Table 1). Together, these results indicate that NMDA receptors display negative gating cooperativity that requires Ca²⁺ diffusion and Ca²⁺ binding to CaM, which is consistent with CDI being the mechanism mediating receptor coupling.

PSD-95 boosts NMDA receptor gating coupling and macroscopic CDI

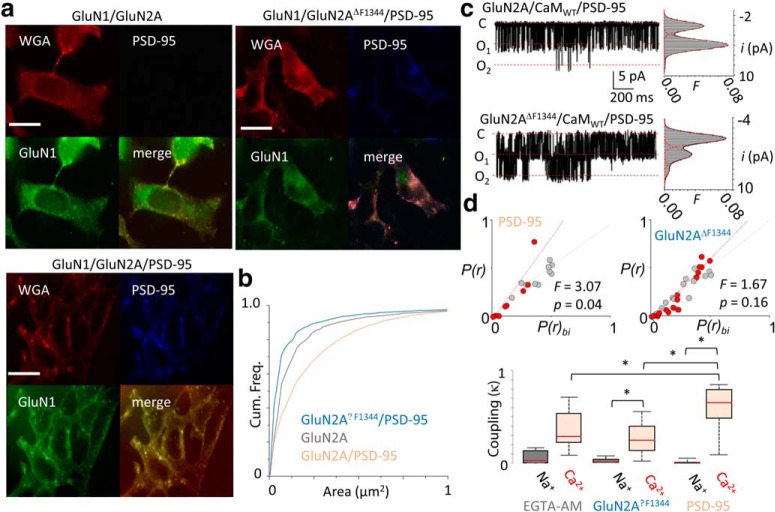
One hypothesis implicit in our model is that bringing channels into closer proximity would increase their negative cooperativity. PSD-95 is a synaptic scaffolding protein that clusters NMDA receptors into postsynaptic microdomains by direct interactions with C-terminal ESDV residues of GluN2A. We asked whether the expression of PSD-95 alters channel cooperativity. First, we tested whether PSD-95 overexpression affected the surface distribution of NMDA receptors in our system. Surface staining of HEK293 cells expressing GluN1–2a/GluN2A with anti-GluN1 antibody showed a pattern of diffusely dispersed small punctae (Fig. 3a,b; mean, 0.28 ± 0.02; N = 10 cells; n = 2046 punctae), which overlapped with a plasma membrane marker, WGA, consistent with surface location (data not shown; green/red channel correlation, R² = 0.82; Mander's overlap coefficient = 0.90). PSD-95 overexpression produced larger GluN1-positive punctae (Fig. 3a,b; mean, 0.37 ± 0.02; N = 10 cells; n = 4606 punctae; p = 0.0051); these also colocalized with WGA stain (data not shown; green/red channel, R² = 0.60; Mander's overlap coefficient = 0.78) and with PSD-95-positive punctae (data not shown; green/blue channel, R² = 0.60; Mander's overlap coefficient = 0.77). Finally, to test whether this redistribution of surface NMDA receptors was due to direct interactions of PSD-95 with the channel, we used a truncated GluN2A subunit (GluN2A^ΔF1344) that lacks the PSD-95 binding site (Kornau et al., 1995). Expression of GluN1-2a/GluN2A^ΔF1344 with PSD-95 reduced the size of GluN1-positive punctae below that observed for cells transfected with only wild-type (WT) channels (Fig. 3a,b; mean, 0.17 ± 0.01; N = 10 cells; n = 2577 punctae; p = 0.00004) and showed reduced colocalization with PSD-95 (data not shown; green/blue channel, R² = 0.37; Mander's overlap coefficient = 0.61). Together, these results are consistent with prior work demonstrating that PSD-95 overexpression increases surface clustering of NMDA receptor in HEK293 cells (Jeyifous et al., 2016).

Figure 3.

PSD-95 overexpression enhances negative cooperativity of NMDA receptor currents. a, Top, Representative immunofluorescence images of HEK293 cells expressing GluN1–2a, GluN2A, and PSD-95, as indicated, and stained for GluN1 (green), PSD-95 (blue), and WGA (red). Scale bar, 25 μm. b, Cumulative probability of GluN1-positive punctae area for the indicated constructs. c, Representative current traces recorded from a two-channel patch with 0 or 1.8 mm external Ca²⁺ in cells coexpressing CaM_WT and PSD-95, with corresponding amplitude histogram superimposed with fitted Gaussian components (red dashed) and probability density function (black). d, Top, Correlation of conductance class occupancies for GluN1-2a/GluN2A receptors (left) and GluN1-2a/GluN2A^ΔF1344 (right) coexpressed with PSD-95 showed substantial deviations from the predicted open conductance occupancies predicted from binomial distribution for independent gating (red dashed curves); *p < 0.05, Mann–Whitney U test compared with simulated datasets. Bottom, Distributions of κ values in the conditions indicated; *p < 0.05, Mann–Whitney U test.

Next, we tested whether channel clustering affected the NMDA receptor Ca²⁺-dependent gating cooperativity and CDI by recording unitary currents in multichannel patches in 0 and in 1.8 mm external Ca²⁺, as in Figure 1b (Fig. 3c). We found that PSD-95 overexpression resulted in significant deviations away from binomial predictions (Fig. 3d, top left; 0 Ca²⁺, R² = 0.58; 1.8 Ca²⁺, R² = 0.90; F = 3.07, p = 0.039). In contrast, the coexpression of PSD-95 with GluN2A^ΔF1344 did not show a Ca²⁺-dependent shift in the binomial correlation (Fig. 3d, top right; 0 Ca²⁺, R² = 0.80; 1.8 Ca²⁺, R² = 0.92; F = 1.67, p = 0.160). We next measured the degree of coupling and observed that the distribution of κ values was significantly higher upon PSD-95 overexpression, but not if the receptors lacked the PSD-95 binding domain (GluN2A^ΔF1344; Fig. 3d, bottom, Table 1). As expected in a mechanism where negative cooperativity is mediated by CDI, PSD-95 overexpression increased the CDI of macroscopic wild-type currents (Fig. 4a; CDI = 0.66 ± 0.09; p = 0.0402; n = 7) but not the CDI of GluN1-2a/GluN2A^ΔF1344 currents (Fig. 4a; CDI = 0.44 ± 0.08; p = 0.4774; n = 5).

Figure 4.

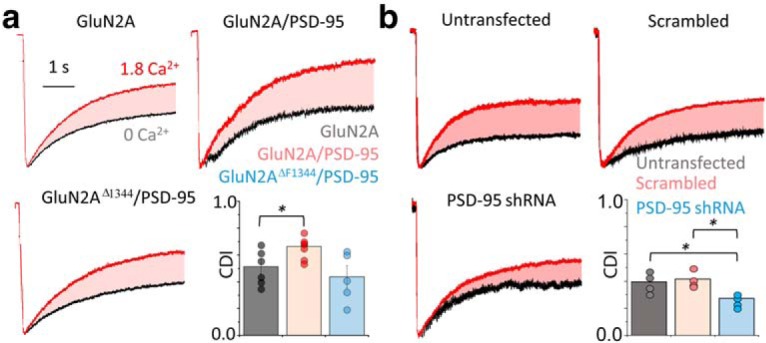
PSD-95 enhances CDI in recombinant and native receptors. a, Whole-cell current recordings from cells expressing GluN1–2a and the indicated GluN2A and PSD-95 constructs in 0 (black) and 1.8 mm Ca²⁺ (red), overlaid and normalized to peak; shaded area highlights CDI, and bar graph summary of data; *p < 0.05, Mann–Whitney U test. b, Whole-cell current recordings from dissociated hippocampal neurons (15–20 d in vitro) transfected with the indicated shRNA constructs. Glutamate elicited currents recorded in the continuous presence of CNQX and ifenprodil, and the bar graph summary of data; *p < 0.05, Mann–Whitney U test.

Because hippocampal neurons express PSD-95 endogenously, we sought to determine whether removal of endogenous PSD-95 affected the measured CDI of native receptors. We measured the CDI of NMDA receptor currents, in currents elicited by glutamate in the continued presence of the AMPA receptor inhibitor CNQX and the GluN2B-selective inhibitor ifenprodil, to isolate changes in GluN2A-mediated currents. We found that, compared with untransfected cells and cells transfected with a scrambled shRNA probe, PSD-95 knockdown reduced NMDA receptor CDI values (Fig. 4b).

PSD-95 reduces effective coupling distance between receptors

We have previously shown that the CDI of NMDA receptor currents develops quickly in response to locally fluxed Ca²⁺ and is mediated by Ca²⁺ binding to the apoCaM residing on the GluN1 C-terminal tail (Iacobucci and Popescu, 2017). Results presented here show that diffusible Ca²⁺ can increase the CDI of whole-cell NMDA receptor currents by a process that requires Ca²⁺ binding to CaM and that this process correlates with negative gating cooperativity as measured from single-channel currents.

This observation is surprising, first because the fast kinetics of Ca²⁺ binding to the resident apoCaM implies that a single channel opening would produce maximal CDI (Fig. 5a). Second, because although Ca²⁺ can bind CaM with lobe-specific kinetics, Ca²⁺ binding to either lobe is sufficient to displace actinin from C0 (Merrill et al., 2007) and produce maximal CDI values (Fig. 5b,c). To understand how it may be possible that each receptor becomes maximally inactivated during each opening but the ensemble response does not, we simulated CDI for a population of channels. We used a linear approximation of Ca²⁺ dynamics in the superpositioning of Ca²⁺ microdomains (Neher, 1998; Fig. 5d) and our previous measurements of the sensitivity of NMDA receptors currents to inhibition by intracellular Ca²⁺ (Iacobucci and Popescu, 2017). Further, controlling intracellular buffering with BAPTA restricts Ca²⁺ elevations to close distances from the pore, which also temporally synchronize with channel opening (Fig. 5e). To develop a model describing channel coupling, we consider surface channels distributed on a 2D membrane (Fig. 5f). The coupling model assumes that, in a population of channels, only a fraction will be preassociated with apoCaM (F_B < 1). This is a probable scenario, given the low affinity of apoCaM to the channel (Merrill et al., 2007) and that CaM is a mobile and limiting signaling molecule (Persechini and Stemmer, 2002; Petersen and Gerges, 2015). The model predicts that during channel opening, local Ca²⁺ influx will primarily bind the CaM molecules already residing on NMDA receptors and will preferentially inactivate this fraction of primed channels (F_B). In contrast, the Ca²⁺ signals from neighboring, CaM-free channels, will primarily bind to mobile CaM, which, having higher affinity for GluN2A, will associate with unprimed CDI-insensitive channels (1 − F_B) and cause them to inactivate. Finally, the model predicts that restricting Ca²⁺ diffusion with BAPTA will reduce the engagement of additional channels through mobile CaM, thus reducing coupling. To test this model, our predictions suggest that increasing BAPTA concentrations are effective at revealing the dynamic range of CDI (Fig. 5g).

To estimate F_B values in our system, we considered conditions where F_B ≈ 1 (CaM_WT overexpression) and measured CDI in the presence of the fast chelator 5 mm BAPTA to limit Ca²⁺ diffusion to nanometer distances from the fluxing pore (Fig. 6a). Under these conditions, we observed robust inactivation (CDI = 0.31 ± 0.02; Iacobucci and Popescu, 2017). This was significantly different from the CDI we observed when recording with BAPTA from cells containing only endogenous CaM (CaM_endo; CDI = 0.10 ± 0.01, p = 0.002). From these two measurements, we estimate the fraction of primed receptors as the ratio CDI_CaMendo/CDI_CaMWT (Ben Johny et al., 2013) and find F_B = 0.32 (Fig. 6b). This low fraction of receptors occupied by CaM is consistent with HEK293 cells containing a low basal expression level of CaM and CaM-associated proteins (Fig. 5b; Iacobucci and Popescu, 2017) and with the weak affinity of apoCaM to NMDA receptors (Akyol et al., 2004). To test the sensitivity of this metric, we dialyzed cells with 40 nm purified rat CaM_WT protein in 5 mm BAPTA and measured a slight boost in CDI (CDI = 0.13 ± 0.01). Consistent with low affinity of apoCaM with the receptor, this average increase in CDI predicts an F_B = 0.42 upon supplementation with defined CaM concentration above endogenous levels (Fig. 6b).

Using these conditions, BAPTA was dialyzed at increasing concentrations to reduce incrementally the spatial diffusion of Ca²⁺. We compared the CDI–[BAPTA] response curve of GluN1-2a/GluN2A receptors in cells with and without exogenously expressed PSD-95 (Fig. 6c), and we fit our model of CDI to these data. For cells not overexpressing PSD-95, our model predicted an average coupling distance of 26 ± 2 nm from bootstrap (Fig. 6d). In contrast, the overexpression of PSD-95 resulted in a predicted average coupling distance of 15.7 ± 0.6 nm from bootstrap (Fig. 6d). The robustness of this model was evaluated by systematically varying other model parameters and found that the predicted coupling distance was resistant to variability in these parameters (Fig. 6e). These values are consistent with findings of heterogeneous NMDA receptor cluster size estimated with optical methods (Yadav and Lu, 2018). Therefore, PSD-95 can boost channel CDI by shortening the coupling distance between channels. However, this is not necessarily the physical interchannel distance, because fluxed Ca²⁺ must first diffuse to a mobile CaM, which is not necessarily in the immediate vicinity of channel it subsequently inactivates. For any array of channels on the surface of the cell, their coupling distances will be widely distributed (Fig. 6f). Therefore, we modeled this parameter in our model as either a skewed Gaussian (model 2) or a weighted-exponential (model 3) distribution. Both models fit the data well and predicted similar shifts in the coupling distance (Fig. 6c).

Discussion

In this study, we build upon previous quantitative knowledge of NMDA receptor CDI and obtain novel insight into the mechanism of activity-dependent NMDA receptor modulation. We show that the CDI of NMDA receptor currents represent a means for the spatial coordination of channel activity. We provide electrophysiological evidence that individual channels can be inactivated by Ca²⁺ fluxed by their neighbors and that this mode of regulation has profound influence on ensemble NMDA receptor currents. Furthermore, we observed that the PSD-95 scaffold protein can strengthen this coordination by clustering channels in closer proximity. This additional level of regulation likely serves several physiological roles and may provide additional insights into neurological disease.

CDI as a spatiotemporal mechanism of control

In physiologic conditions and the continued presence of agonist, the ensemble activity of both native and recombinant NMDA receptors declines over time in a Ca²⁺ concentration-dependent manner (Legendre et al., 1993; Medina et al., 1995). We previously measured this time constant to be 0.5 s in physiological external Ca²⁺ (Iacobucci and Popescu, 2017). This time constant reflects the reciprocal of the rate of inactivation and, therefore, the average lifetime of a high-P_o active channel before shifting to a low-P_o inactivated state. Therefore, while the evolution of the CDI to maximal values occurs on the order of 0.5 s in physiological conditions, because this process follows exponential kinetics, a substantial fraction of channels will inactivate much faster, which is consistent with previous reports of fast NMDA receptor inactivation following Ca²⁺ influx through vicinal AMPA receptors (Rozov and Burnashev, 2016). Thus, while longer than the average synaptic event, the exponential nature of CDI onset over this interval provides dynamic temporal control of activity rather than complete inactivation with each synaptic event.

However, optical Ca²⁺ imaging reveals spatially heterogeneous distributions of glutamatergic channels along dendrites (Walker et al., 2017). Our data demonstrate diffusion-mediated, activity-dependent coupling of channel activity at the level of individual channels, which imparts channels with spatial activity control. Further, we show that PSD-95, a synaptic scaffold protein that clusters glutamatergic channels, reduces the coupling distance and strengthened NMDA receptor gating cooperativity (Fig. 6). Thus, the output of any given channel in the postsynaptic spine can be tuned not only by time-dependent autoinhibition, mediated by resident calmodulin molecules, but also by spatial coordination through the collective activity of neighboring channels, mediated by freely diffusing CaM.

Given that on a longer time scale Ca²⁺/CaM binding to PSD-95 (Zhang et al., 2014) can detach this scaffold protein from the postsynaptic density, the effects of CaM on the PSD-95-mediated clustering of NMDA receptors may have different roles during fast synaptic transmission and during slower events such as metaplasticity. As the physiological roles of these phenomena remain to be tested, one possibility is the formation of an activity-dependent feedback loop to adjust the activity of NMDA receptors by disengaging channels from PSD-95, thereby making channels less sensitive to the Ca²⁺ influx of their neighbors.

Microdomain versus nanodomain coupling

A continued obstacle in mechanistically understanding NMDA receptor CDI has been the variability in intracellular buffering conditions used between studies. For example, BAPTA concentrations as low as 1 mm have been reported to abolish CDI, whereas others have reported that much higher concentrations are needed. A portion of this variability is likely due to differences in the cell type-dependent properties such as endogenous buffering. We also observed variability in our κ measurements (Fig. 1), suggesting that the degree of coupling is not static. The typical on-cell pipette is ∼0.5–1 μm in diameter, providing ample room for lateral diffusion of channels during recording, which alters the physical distance between channels (Suchyna et al., 2009). At long distances between the Ca²⁺ source and sensor, loose coupling by Ca²⁺ microdomains (>100 nm) would predominate. These interactions would be both EGTA and BAPTA sensitive as EGTA is sufficient to quickly chelate low-amplitude Ca²⁺ elevations. In contrast, nanodomain coupling requires BAPTA for modulation (Eggermann et al., 2011). We observed that BAPTA-AM treatment abolished the coupling of individual channels while EGTA-AM did not. Although the actual intracellular concentration is not known, the analogy to fluorescent AM esters suggests a final concentration of >100 μm (Imredy and Yue, 1992). This is still substantially less than the BAPTA concentrations used in whole-cell experiments. Thus, variations in channel density may influence buffer saturation in these conditions at short interchannel distances and contribute to the observed functional variability. Because the GluN2A^ΔF1344 truncation resulted in smaller GluN1-positive punctae compared with wild-type channels, it is likely that HEK293 cells contain endogenous scaffolds (Fig. 3), such as SAP102, which mediate some degree of clustering (Sans et al., 2003).

NMDA receptor coupling is a physiological phenomenon

Signaling within Ca²⁺ microdomains is critical for chemical coordination in several physiological processes. However, one concern from our method is whether the Ω-shaped, cell-attached gigaseal creates a nonphysiological environment in which restricted diffusion within the patch artificially forces channels to cooperate. Such diffusion effects are worth considering as they have previously confounded interpretations of P2X receptor gating mechanisms (Li et al., 2015). To address this problem, we considered a channel modeled in an infinite planar lipid bilayer. The theoretical maximum conductance can be predicted by the total channel resistance as 1/R_channel (Hille, 2001), as follows:

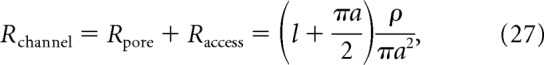where R_pore is the resistance through the pore, R_access is the access resistance on both sides of the pore, l is the length of the pore, a is the pore radius, and ρ is solution resistivity. Diffusion restriction due to seal formation would effectively increase the access resistance. This would have the following two consequences: (1) limited diffusion from the patch into the cell as well as (2) limited diffusion from the cell into the patch. The first consequence would be observed as a reduced channel conductance as ion buildup on the intracellular side of the patch. However, we observe no time-dependent change in unitary conductance in our recordings. Similarly, K⁺ flux through L-type Ca²⁺ channels can establish a unitary conductance of 250 pS (Kuo and Hess, 1992), which approaches the limiting conductance of 286 pS predicted through Equation 27, arguing against diffusion restriction effects with this approach. The second consequence predicts a prolonged time course needed for molecules to diffuse from the cell into the patch. However, previous reports showed that the activation of remote Ca²⁺-permeable channels led to a fast, reversible reduction of NMDA receptor activity in an on-cell patch (Legendre et al., 1993; Xin et al., 2005). Thus, diffusion of ions between the patch and the cell is likely unrestricted. Further, HEK293 cells express endogenous Ca²⁺ extrusion mechanisms, which have been shown to impact NMDA receptor CDI by preventing intracellular Ca²⁺ accumulation (Sibarov et al., 2015).

Insights into disease pathology

PSD-95 plays a crucial role in channel localization, synaptogenesis, and plasticity (Sheng and Hoogenraad, 2007). Perturbing PSD-95 interactions with its partners is associated with Huntington's disease, Alzheimer's disease, and schizophrenia (Purcell et al., 2014). We observe that PSD-95-mediated channel clustering is a factor in tuning channel activity. In Huntington's disease, brain lesions in patient brains resemble those resulting from kainic and quinolinic acid injection in animals studies (Coyle and Schwarcz, 1976; Beal et al., 1986). Similarly, Huntington's disease mouse models display hyperactive NMDA receptors (Levine et al., 1999). Polyglutamine expansion of the Huntingtin protein interferes with PSD-95 interaction with both NMDA and kainate receptors, resulting in hypersensitive channels and excitotoxic Ca²⁺ influx (Savinainen et al., 2001; Sun et al., 2001). Our results are consistent with a model whereby channel clustering strengthens activity-dependent regulation.

PSD-95 can also promote NMDA receptor activity (Lin et al., 2004). Consistent with this view, the sequestration of PSD-95 to prevent interaction with NMDA receptors was protective in an ischemic injury model (Aarts et al., 2002). Thus, PSD-95 likely has multimodal effects on channel activity. For example, it has been suggested that the route of Ca²⁺ entry rather than the bulk load is important for initiating excitotoxicity (Sattler et al., 1998). Similarly, synaptic and extrasynaptic NMDA receptors couple to distinct survival and apoptotic signaling pathways, respectively (Hardingham and Bading, 2010). How PSD-95 regulates these distinct channel populations and its physiological consequences remains unknown. PSD-95 is transcriptionally repressed during early development (Zheng et al., 2012). Thus, the effects of PSD-95 on NMDA receptors may be developmentally dependent and may explain why perturbing PSD-95–NMDA receptor interactions in young neurons had no effect on synaptic plasticity (Lim et al., 2003).

In vertebrates, CaM is encoded by three genes. Several disease-associated CaM mutations reduce Ca²⁺ binding (George, 2015). Despite the importance of CaM in modulating NMDA receptor activity, neurological deficits have been inconsistently reported in these diseases (Crotti et al., 2013). This surprising absence of neurological symptoms in this class of disease may reflect the importance of low apoCaM affinity to channels in resting physiological conditions. In this way, Ca²⁺ influx activates only functional copies of CaM, which can inactivate NMDA receptors. This is in contrast to voltage-gated Ca²⁺ channels whose strong apoCaM affinity can lead to mutant CaM occluding access to the channel from wild-type CaM, thereby perturbing Ca²⁺ regulation (Limpitikul et al., 2014).

Pharmacological inhibition of NMDA receptors for treating neurological disorders has shown little success, with the notable exception of memantine, which has proven beneficial in the treatment of Alzheimer's and other disorders. Memantine has been shown to stabilize the Ca²⁺-dependent inactivated state (Glasgow et al., 2017). Not only does this suggest the importance of NMDA receptor CDI in disease pathogenesis, but highlights the importance of drug design targeted to specific receptor states in the successful treatment of disease. Combining the use of such receptor state-targeted therapeutic agents (Popescu, 2005) with methods to restrict delivery to defined cell types (Shields et al., 2017) will represent a major advance toward next-generation pharmaceutical design.