A ROADMAP TO INTEGRATE ASTROCYTES INTO SYSTEMS NEUROSCIENCE

Abstract

Systems Neuroscience is still mainly a neuronal field, despite the plethora of evidence supporting the fact that astrocytes modulate local neural circuits, networks, and complex behaviors. In this article, we sought to identify which types of studies are necessary to establish whether astrocytes, beyond their well-documented homeostatic and metabolic functions, perform computations implementing mathematical algorithms that sub-serve coding and higher-brain functions. First, we reviewed Systems-like studies that include astrocytes in order to identify computational operations that these cells may perform, using Ca²⁺ transients as their encoding language. The analysis suggests that astrocytes may carry out canonical computations in a time scale of sub-seconds to seconds in sensory processing, neuromodulation, brain state, memory formation, fear, and complex homeostatic reflexes. Next, we propose a list of actions to gain insight into the outstanding question of which variables are encoded by such computations. The application of statistical analyses based on machine learning, such as dimensionality reduction and decoding in the context of complex behaviors, combined with connectomics of astrocyte-neuronal circuits, are, in our view, fundamental undertakings. We also discuss technical and analytical approaches to study neuronal and astrocytic populations simultaneously, and the inclusion of astrocytes in advanced modeling of neural circuits, as well as in theories currently under exploration such as predictive coding and energy-efficient coding. Clarifying the relationship between astrocytic Ca²⁺ and brain coding may represent a leap forward towards novel approaches in the study of astrocytes in health and disease.

Graphical Abstract

1. Systems Neuroscience is primarily a neuronal field

The study of the central nervous system (CNS) encompasses different levels of analysis: molecular, cellular, anatomical, behavioral, cognitive and systems. Systems Neuroscience aims at integrating these former fields, which have mostly grown independently. For example, Molecular Neuroscience has traditionally focused on the smallest functional level without a connection to cognition, whereas Behavioral Psychology and Psychophysics have typically studied cognition separately from its molecular and neuronal underpinnings. The overarching goal of Systems Neuroscience is to understand how neural circuits give rise to cognitive functions, emotions and behavior by simultaneously recording neuronal activity and behavior at the highest spatiotemporal resolution possible.

Systems Neuroscience is arguably a field of neurons. A proof of this can be found in recent editions (2015–2017) of the three international conferences dedicated to Systems and Computational Neuroscience—here we will not dwell on what is ‘Systems’ and what ‘Computational’ since the two fields are highly overlapping and complementary. The conferences are the ’Conference and Workshop on Neural Information Processing Systems’ (NIPS), the ‘Organization for Computational Neurosciences’ (OCNS) and ‘Computational and Systems Neuroscience (COSYNE). Of approximately 3000 communications, fewer than 1% included non-neuronal cells. The pervasive use of the phrase ‘neural circuit’ in the programs most of the time refers to computational integration of information embedded in neuronal biophysical substrates. The scarce attention to non-neuronal cells is puzzling, at least from the perspective of the astrocyte field, given the evidence that astrocytes contribute to circuit-based phenomena at the synaptic (Araque et al., 2014) and network (Poskanzer & Yuste, 2016) levels. Although efforts are being made in the US Brain Initiative and the European Human Brain Project to develop studies incorporating non-neuronal cells, it seems as though progress in astrocyte biology has advanced in parallel to systems neuroscience, and astrocytes have been excluded from unified theories of brain function, as previously noted (Poskanzer & Molofsky, 2018). Although extensive modeling of astrocytic Ca²⁺ fluxes exists (Manninen et al., 2018), and sporadic studies have explored the application of astrocyte-based computations to artificial intelligence (Alvarellos-Gonzalez et al., 2012; Porto-Pazos et al., 2011), astrocytes are characteristically missing from advanced in silico modeling of neural circuits (Capone et al., 2017; Deneve et al., 2017; Gjorgjieva et al., 2016; Markram et al., 2015).

Is this exclusion justified because the mechanisms underlying the well documented impact of astrocytes on neural circuits fall within the realm of intercellular signaling, homeostasis and metabolism, which, although essential for the maintenance of neural circuits, may not qualify as ‘computing’ processes? Or, are astrocytes fundamental to the computational foundations of the brain? Later we will elaborate on what is and what is not computation, but rather than struggling to define ‘computation’ we ask, instead, whether processes that take place in astrocytes participate in the implementation by neural circuits of processes sub-serving coding, complex behaviors, and higher-brain functions. In other words, if computation is an emerging property of a given neural network (Yuste, 2015), do astrocytes help to shape such property beyond providing metabolic and homeostatic support? If they do, specific questions are whether there are niche(s) in Systems Neurosciences that would particularly profit from astrocyte idiosyncrasies, and whether the impressive techniques and theoretical armamentarium deployed by Systems Neuroscience could be used—and are sufficient—to unravel possible astrocyte-based computations. In an early article in Computational Neuroscience, it was argued that anatomical features provide valuable insights about how the CNS operates because ‘the nervous system is a product of evolution, not design. The computational solutions evolved by nature may be unlike those that humans would invent, if only because evolutionary changes are always made within the context of a design and architecture that already is in place (Sejnowski et al., 1988). It follows that the unique anatomical arrangement between astrocytes and neurons might be part of computational solutions refined by evolution that have made the brain a highly efficient task-performing system. In this article we will explore the possible computations carried out by astrocytes. First, we will succinctly describe the fundamentals (section 2) and current challenges (sections 3 and 4) of Systems Neuroscience. We will continue by reviewing Systems-like studies involving astrocytes (sections 5 and 6). We will then propose a to-do list to further integrate astrocytes in Systems Neurosciences, thus helping to dissipate the historical and perhaps no longer tenable gap between astrocytes and neurons (section 7). We do not touch upon other glial cells because, as discussed earlier (Masgrau et al., 2017), the cells grouped under this name are molecularly and morphologically distinct; hence, their contribution to higher-brain functions deserves individual attention.

2. Computational foundations of the CNS

What is computation?

When we say that the brain computes we mean that it creates and stores representations of physical and conceptual entities, and performs operations on these representations in order to carry out discrete tasks underlying behavior. The goal of Computational/Systems Neuroscience is to describe these processes in mathematical and computational terms. In this framework, it is believed that the mathematical treatment of the representations is possible precisely because computation implies abstraction, thus permitting generation of internal models of the world using biophysical substrates (Marr, 1976). The action of generating representations is known as encoding because the brain converts physical and conceptual entities into a code, that is, a combination of symbols representing variables. Symbols can be discrete, continuous and distributed among numerous neurons and brain areas. A prime example of what is and is not computation can be found in action potentials. Their generation is caused by fine homeostatic adjustments of membrane voltage that per se may not qualify as a computation (Stuart et al., 1997), but complex combinations of action potentials constitute the ‘symbols’ of the ‘alphabet’ used by the brain to compute. Examples of variables encoded by the brain are the position, color and shape features of a given object (Seymour et al., 2010), sound categories (Tsunada & Cohen, 2014), the distance between the eyes in face recognition (Chang & Tsao, 2017), and the reward value of a choice during decision making (Saez et al., 2018). The information embedded in neural biophysical substrates can be decoded and transferred (‘rerouted’), possibly transformed into different formats and neural substrates. Examples are the on-line holding of memory during decision making (Hasson et al., 2015), and memory replay during memory consolidation (Foster, 2017). It is worth stressing that the current computational view of the brain is not an established truth, but a simplified framework highly influenced by information theory, computer science and linguistics to guide experimental testing.

Computation takes place at several hierarchically organized levels.

Levels include from brain areas, nuclei, maps, columns, circuits, single neurons, and sub-neuronal compartments, such as dendrites, spines, somas and axons (Mesulam, 1998). Levels, moreover, interact in specific temporal and topological patterns (Betzel & Bassett, 2017) (Vidaurre et al., 2017). A hierarchical organization is, in essence, a modular organization of computation (D. Meunier et al., 2009), such that a successful general theory of the brain will have to explain how tasks performed at one module(s) give rise to tasks performed by the larger module(s). Currently, a widely assumed premise is that most components of cognition emerge from the level of transiently active circuits—some authors prefer to speak about ensembles of neurons or cell assemblies (Buzsaki, 2010)—whose dynamics arise, in turn, from complex interactions involving the three classical building blocks: neuronal intrinsic excitability, synaptic efficiency, and connectivity (Gjorgjieva et al., 2016). Simply put, circuit dynamics within the range of millisecond to minutes control fast behaviors such as perception and decision making (Khani & Rainer, 2016), whereas synaptic changes lasting hours and days control learning and memory (Sweatt, 2016). Connectivity includes two main patterns: feed-forward, supporting a unidirectional flow of information, and recurrent, composed of positive and negative feedbacks that lead to self-sustained multiple activity patterns (Duarte et al., 2017). Connections are mostly selective but they can be random as well, giving rise to complex, slow dynamics that include chaotic interactions (Mastrogiuseppe & Ostojic, 2018). Another widely assumed premise is that local circuits, however dynamic, are too anatomically fixed to adapt their behavior to contexts that need to be globally broadcast, for instance, sleep-wake cycles, mood, reward, and attention during perception and decision making. To circumvent this problem, neuromodulation has been suggested as a solution. Neuromodulation refers to the relatively rapid (in the range of seconds) functional reconfiguration of circuits throughout the brain by acetylcholine, dopamine, noradrenaline and serotonin, which are released by subcortical and brainstem nuclei: the nucleus basalis of Meynert (NBM), the striatum, the locus coeruleus, and the Raphe nucleus (Avery & Krichmar, 2017). Neuromodulation participates in working memory, attention, brain state and plasticity (C. N. Meunier et al., 2017; Sara, 2009; Thiele & Bellgrove, 2018).

Neural substrates of brain computations.

The ultimate goal of Systems/Computational Neuroscience is to explain how electrical and chemical signals are used in the brain to represent and process information (Sejnowski et al., 1988). Currently, a widely accepted assumption is, as noted, that external variables are encoded into action potentials. Theories and empirical evidence point to firing rates (average number of action potentials per unit of time)(Gerstner et al., 1997), action-potential timing (length of time between action potentials) (Panzeri et al., 2001), population coding (joint activity of several neurons) (Panzeri et al., 2015), and neural dynamics (the way electrical activities evolve with time and space) (Shenoy et al., 2013), as potential features of action potentials that, in infinite amount of combinations, have enough breadth to constitute the basis of the brain code(s). A key implication of the multi-level organization of the brain is that code(s) are multi-level, too. This means that external variables are encoded by the collective activity of numerous simpler elements, which carry either synergistic or complementary information (Panzeri et al., 2015). This principle is the driving premise in population and dynamic coding, and has informed the development of methods for recording from large populations of neurons, including multi-electrode arrays, which can record up to 10³ neurons (Einevoll et al., 2012), Ca²⁺ imaging, which can simultaneously record over 10⁴ neurons (Sofroniew et al., 2016)(Pachitariu et al., 2016), and functional resonance magnetic imaging (fRMI), which makes use of BOLD (blood-oxygen-level contrast imaging) to unravel functional connectivity among regions encompassing over 10⁵ neurons (Fox & Raichle, 2007). It is worth stressing that the measurable signals in the latter two approaches are not action potentials, but single-cell Ca²⁺ rises and regional oxygen consumption, respectively. Although the premise for using large-scale Ca²⁺ imaging in neurons is that single-neuron Ca²⁺ signals represent slower non-linear encoding of the underlying action potentials (Vogelstein et al., 2010) (Lutcke et al., 2013), non-electrical signals, as well as global voltage oscillations measured with field potentials and electroencephalograms, plausibly carry additional information that is computationally relevant. For example, it has been proposed that synaptic facilitation mediated by neuronal Ca²⁺ signals sustains working memory (Mongillo et al., 2008). All in all, biophysical substrates of brain computations other than the ones directly or indirectly based on neuronal activity will plausibly arise in the future, including, we posit, astrocyte-based computations.

Contemporary brain theories.

According to the number of publications, one of the most influential brain frameworks is predictive coding, which aim to account for core principles underlying adaptive circuit remodeling. The key tenets of predictive coding are the following. First, representationalism, the brain operates by building models of the outer world, conceptual categories and expected outcomes of actions. Second, evaluation of new information against embedded models is at the core of many brain operations besides decision making, including perceptual discrimination, voluntary selective attention and learning. Third, the nature of such evaluations is probabilistic, since the underlying algorithms weigh in pros and cons and similarity of the novel information with respect to internal models. A central notion is that ‘organisms care less about representing what is actually out there in the world than about how this reality conflicts with their predictions about what should be there’ (Fitch, 2014). An apparent virtue of this strategy is minimization of data storage since it takes fewer bits to represent the mean and deviations from it than to attempt de novo representations (Fitch, 2014). Fourth, the brain tries to minimize its prediction errors such that internally-generated predictions are constantly optimized with external inputs in an iterative process. In predictive coding, neuromodulation is proposed as computing part of the statistics of errors made by predictions (Lau et al., 2017; Stephan et al., 2015). The bulk of empirical support for predictive coding lies in the domains of perception, reward learning, and decision making, as documented in humans, monkeys, and rodents (Summerfield et al., 2008; Wacongne et al., 2011) (Kok & de Lange, 2014; Markov et al., 2014) (Diederen et al., 2017; Nasser et al., 2017) (Leinweber et al., 2017), whereas the framework appears to be under exploration in memory consolidation (Cross et al., 2018) and emotion (Barrett, 2017). Other general CNS frameworks worth mentioning are global workspace theory, which describes the basic circuit from which consciousness emerges (Baars, 2005), and liquid computing, which states that neural circuits have the capacity to store information of previous perturbation(s), analogous to the ripples generated on the surface of a pond when stones are thrown into it (Maass et al., 2002). Finally, influential theoretical constructions about basic operative principles of the brain—compatible with global frameworks—include brain oscillations (Buzsaki & Draguhn, 2004), efficient coding (Chalk et al., 2018), energy-efficient coding (Laughlin, 2001), neural integrators (Mazurek et al., 2003), inhibitory/excitatory balance (Brunel, 2000; Litwin-Kumar & Doiron, 2012), noise (Arieli et al., 1996), and circuit degeneracy (Sporns, 2013).

3. Challenges, obstacles, and growth areas in Systems Neuroscience.

Despite the progress in the last decade, understanding brain computations remains a central challenge of modern Neuroscience. The readily observable behavioral variables that are used experimentally to study brain encoding, for instance, rewards, choices and stimulus features, represent the tip of the iceberg, because the vast majority of variables used by the brain in complex behaviors and higher-brain functions, are typically latent. However, this should not distract us from the impressive predictive power that analytical tools are achieving in Systems Neuroscience. Examples of success can be found in neuroprosthetics, where the electrical activity of the brain of a human user is decoded into motor commands (Cangelosi & Invitto, 2017); decision-making, in which decision outputs can be predicted from action potentials with 80% accuracy in monkeys before a response is observed (Kiani et al., 2014), and with 70% accuracy in rats, even before stimulus onset (Nogueira et al., 2017), and face recognition. Here, the face seen by a Rhesus monkey can be reproduced with 90% accuracy by tracking neuronal activity in the inferior temporal cortex (Chang & Tsao, 2017). Although the achievements are remarkable, there is still room to improve these numbers. In the workflow of Systems Neuroscience from signal capture to deciphering the brain code, areas of improvement include signal recording, signal processing, data analyses, and astrocyte-focused studies (Fig. 1). Key issues are briefly described next.

Figure 1. Workflow in Systems Neuroscience.

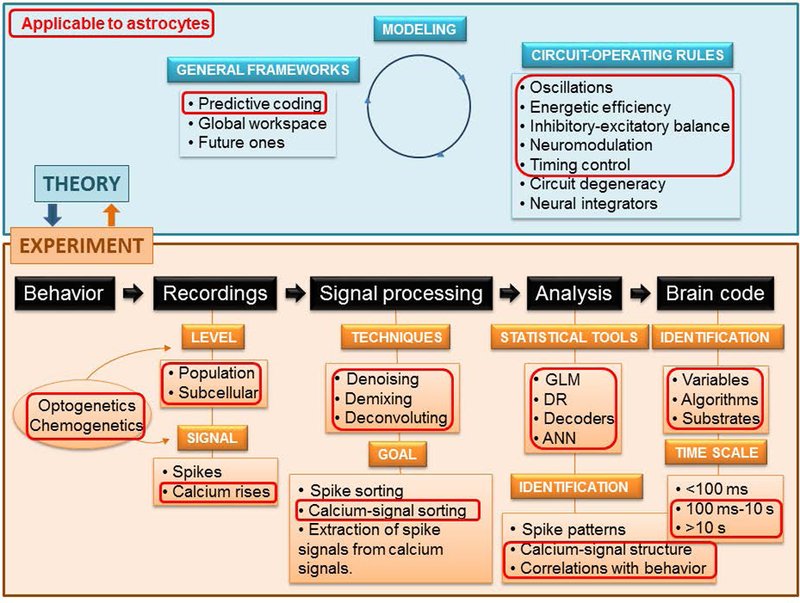
A central problem in Neuroscience is to explain how electrical and chemical signals are used in the brain to represent and process information. The workflow depicts the stages and tools currently used to decipher neuronal codes. In red squares we highlight the elements that are relevant to the study the role of astrocytic Ca²⁺ in neuronal coding.

Data load in large-scale recordings.

The trend of improving predictions by simultaneously recording more neurons has created a serious challenge: the ever-increasing size of the data seriously hampers storage, processing and analysis. In order to simplify and reduce data size of recordings, several methods exist to extract low-dimensional mathematical representations from multi-neuronal electrical recordings (Aljadeff et al., 2016; Cunningham & Yu, 2014). The obstacle is all the more complex in Ca²⁺ imaging, which has become a dominant method for recording from large populations of neurons, because special methods are necessary to extract the coarse-grained and noisy Ca²⁺ data prior to data analysis. Algorithms such as Suite2p (Pachitariu, 2016), and CNMF (Constrained and/or nonnegative matrix factorization, (Pnevmatikakis et al., 2016)), represent advances in the simplification of imaging data processing prior analysis. Caveats of current calcium imaging data processing are discussed in (Stringer & Pachitariu, 2018). Alternatively, shot-gun statistics unravels network connectivity information from recording at only 10% of the neurons at a given time, thus simplifying the experimental load of large-scale recordings (Soudry et al., 2015). Data-sharing and collaborative solutions have been proposed as well to manage the surge of data (Paninski & Cunningham, 2018).

Statistical tools for understanding data.

The standard problem is to determine how behavioral variables are encoded by neurons, and how this information is decoded, either by downstream neurons, or by an external observer. Different statistical tools address encoding and decoding. For encoding, generalized linear models (GLMs), a generalization of multiple linear regression, regress neuronal activity against behavioral variables to determine the set of variables that explain more neuronal activity (Aljadeff et al., 2016) (Nogueira et al., 2017). Decoding techniques, typically linear classifiers (Arandia-Romero et al., 2017; Quian Quiroga & Panzeri, 2009), as well as more recent artificial neural networks (ANNs) (Paninski & Cunningham, 2018) are used to predict, trial-by-trial, values of behavioral variables from neuronal activity, either using single neuronal activity, or the individual activity of large neuronal populations recorded from multi-electrode-arrays or Ca²⁺ imaging. These methods are supervised machine learning tools because both behavioral and neuronal variables are preselected and labelled. Also, unsupervised tools such as dimensionality reduction have been developed, and used in parallel, in order to reduce data complexity by identifying low-dimensional latent factors, where relevant behavioral variables could be represented (Cunningham & Ghahramani, 2015). Of note, detection of relevant subspaces of neuronal activity, and optimal selection of behavioral features to regress against neuronal data, will facilitate the discovery of computational principles. An elegant example is the aforementioned study by (Chang & Tsao, 2017), in which successful face identification in non-human primates was possible with 50-dimensional data, and recordings of 200 neurons. Likewise, feature selection can be adaptively improved with artificial intelligence (Yamins & DiCarlo, 2016). As with signal processing, data load is a challenge in signal analysis, for the number of observations per condition does not necessarily grow in parallel with the growth of complexity and number of dimensions of the data. For example, recording 20 neurons for 30 min produces the same number of observations per neuron than recording 1000 neurons during the same amount of time, but the number of dimensions increases 50-fold with the larger neuronal population. This means that encoding, decoding and dimensionality reduction techniques need to be constrained by specific structural and anatomical knowledge of the neural substrates to be operationally useful.

Optogenetics and chemogenetics.

These anatomically precise and reversible tools allow establishing cause-effect relationships between the electrical activity of single neurons, or neuronal populations, and behavioral parameters. Optogenetics is based on the expression of light-sensitive regulators of transmembrane conductance (ion channels and chloride pumps) coupled with fiber optic- and laser diode-based light delivery (Boyden et al., 2005; Li et al., 2005). Cell type specificity is accomplished by targeting the light sensitive channels with cell-type specific promoters. Light-activation of neurons expressing channels like channelrhodopsins (ChR1, ChR2) result in neuronal depolarizations due to import of cations such as Na⁺, K⁺, and Ca²⁺—the latter at trace levels. By contrast, optical stimulations of archaerhodopsin (Arch) and halorhodopsins (NpHR) pumps cause hyperpolarization of neurons by exporting H⁺, or by importing chloride ions, respectively. An alternative approach to classic opsins is the light-sensitive G-coupled receptor, also called OptoGq/Gs, which modulates receptor-initiated biochemical signaling pathways (Airan et al., 2009). Chemogenetics is based on the use of Designer Receptors Exclusively Activated by Designer drugs (DREADDs), a family of G protein-coupled receptors (GPCRs) that are solely activated by a pharmacologically inert drug, clozapine N-oxide (CNO) (Alexander et al., 2009). DREADDs can also be targeted to neurons with viral or transgenic delivery systems using neuron-specific promoters. Relevant insights into behavior, cognition and basic brain homeostasis have been gained with neuron-targeted optogenetic and chemogenetic approaches (Deisseroth, 2015) (Roth, 2016).

Subcellular computations.

Increasing the number of recorded neurons may not be the only solution for obtaining better data. Insofar each and every neuron must integrate and convert thousands of synaptic inputs into a single output (London & Hausser, 2005), concerns have been raised about the oversimplification of neurons as ‘integrate-and-fire’ nodes in large-scale recordings and in silico simulations, and a plea exists to pay renewed attention to the great computational potency of single neurons (Fitch, 2014). Spine computations and biophysical substrates are reviewed in (Yuste, 2013), and a recent example of the computational relevance of dendritic shafts is the finding that non-linear dynamics based on dendritic conductance can help sharpen time and rate codes in grid cells, thereby improving the accuracy of space representation (Schmidt-Hieber et al., 2017). In the context of imaging, voltage dyes represent a growth area allowing for recording at subcellular resolution at multiple points along dendrites and axons (Xu et al., 2017). The data, combined with whole-cell reconstructions with electron microscopy (Vishwanathan et al., 2017), will arguably improve the understanding of dendritic computations and network connectivity.

A need for theoretical frameworks and modeling.

The wealth of descriptive data will not advance knowledge unless analyses are guided by hypotheses and complemented with modeling. Computational/Systems Neuroscience is thus engaged in a virtuous cycle whereby data generate models, and models make predictions that can be tested ad infinitum against new proposed experiments. The trade-offs of increasing the realism of models by incorporating more biophysical variables versus developing simplifying models, as discussed in (Sejnowski et al., 1988), are still debated (Marder, 2015). Whatever the approach, in vivo models, and their in silico counterparts, need to be informed by large-scale hypotheses combined with simpler questions, in order to advance on the outstanding question of how the brain processes information with such energetic efficiency. We discussed the remarkable production of studies informed by predictive coding and other theoretical constructions. Other theories will plausibly arise in the future.

4. Astrocyte-based computations as a growth area in Systems Neuroscience.

We posit that variables used in brain coding may be partially embedded in astrocyte biophysical substrates, such that the incorporation of astrocytes as computational building blocks in neural circuits may help advance Systems Neurosciences. Significant gaps of knowledge, however, exist. First, there is no evidence that astrocytes gate, transform, store and reroute information in the brain by carrying out processes that can be described in abstract mathematical terms. Astrocytes do participate in brain state (Poskanzer & Yuste, 2016), neuromodulation (Magistretti & Morrison, 1988) (Paukert et al., 2014) (Srinivasan et al., 2015), and in a wide variety of naturally-occurring recurrent circuits, where they have been proposed as carrying out spatiotemporal integration of multicellular inputs (Araque et al., 2014). Examples indeed exist of discrimination and integration of synaptic information by astrocytes (Perea & Araque, 2005), but the underlying algorithms and their behavioral correlates remain undetermined. Second, if astrocytes compute, are Ca²⁺ transients a biophysical substrate of astrocyte-based computations? The intuition that they are already exists in the field, resting on a wealth of studies that, since the 1990s, have used Ca²⁺ imaging to assess astrocyte activation at increasing spatiotemporal resolution, thanks to the unremitting refinement of fluorescent indicators and optical imaging (reviewed in Kastanenka et al.(K. V. Kastanenka, Arbel-Ornath, M., Hudry, E., Galea, E., Xie, H., Backskai, B.J., 2016) and (Bazargani & Attwell, 2016)). However, although in silico modeling documents that astrocytes can encode extracellular cues into variables in Ca²⁺ transients (De Pitta et al., 2008), the statistical methods currently used to encode and decode neuronal action potentials (Section 3) have not been applied to astrocyte data obtained in vivo. Third, it is not known whether the subcellular Ca²⁺ microdomains in astrocytes would carry out different functions within distinct circuits associated with different complex behaviors, nor whether astrocytes would perform similar computations throughout the brain, or are as functionally heterogeneous as neurons. It is worth mentioning that in the last decade controversies have arisen concerning the regulation and consequences of Ca²⁺ signaling in astrocytes. Specifically, whether Ca²⁺ comes from endoplasmic reticulum and mitochondria, or from the extracellular milieu, the very notion of Ca²⁺-dependent gliotransmission, the role of astrocytes in long-term potentiation (LTP), and whether D-serine is a gliotransmitter have been debated—reviewed in (Bazargani & Attwell, 2016; Savtchouk & Volterra, 2018). Currently, the prevailing notion reconciling these discrepancies is that Ca²⁺ responses are highly complex and context-dependent, such that the signaling leading to Ca²⁺ rises, the sub-cellular source of such Ca²⁺, the speed of transients, as well as the downstream effects, are dependent on the subcellular astrocyte compartment(s), and the neural circuit (Savtchouk & Volterra, 2018). In this piece we do not focus on mechanistic issues, but rather on whether and how astrocytes may perform computations using Ca²⁺ transients.

5. Systems-like studies in astrocytes

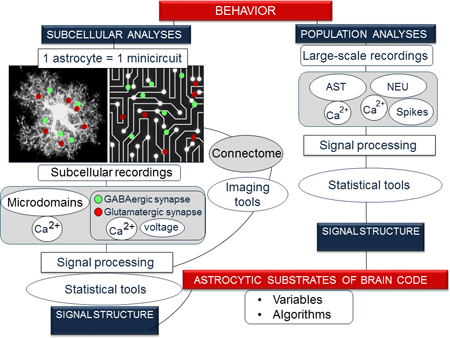
A prototypical study in Systems Neuroscience includes three components: (i) recording of electrical activity in multiple neurons, (ii) computerized analysis to decode information embedded in action-potential firings, and (iii) simultaneous measurement of a cognitive or behavioral function. The statistical analyses reveal correlations and, increasingly often, causal relationships between changes in patterns of neuronal-population firing and specific behavioral or cognitive responses (Sections 2 and 3). There are no studies, to our knowledge, recording the Ca²⁺ activity of multiple astrocytes, followed by analysis with GLM or decoders in the context of a behavioral paradigm defined by distinct features that can be correlated with patterns of astrocytic Ca²⁺ activity. Among studies linking astrocytes and behavior (for reviews (Oliveira et al., 2015; Santello et al., 2019)), in section 5.1 we discuss the ones closer to the neuron-focused experimental design in Systems Neuroscience, for they include recordings of Ca²⁺-based astrocyte excitability, as well as electrical or optical recordings of neuronal activity, in the context of complex behaviors or neuromodulation. Conversely, in Section 5.2 we focus on studies showing modulation of local brain circuits associated with complex behaviors, or brain state, by transient optogenetic or chemogenetic astrocyte activation. In section 6, we extract computational lessons from these studies, and identify gaps of knowledge, taking into account, when appropriate, previous and recent studies that, although lacking any of the aforementioned components, support our computational insights. Table 1 summarizes the analysis. In Fig. 1 we highlight in red approaches within the general workflow of Systems Neuroscience including signal capture, processing and analysis that could be used with astrocytic data.

Table 1.

System-like studies in astrocytes

Direction of experimental manipulation	Stimulation	Neural circuits	Readouts	References	Predicted canonical computations
BEHAVIOR ↓ ASTROCYTES	Sensory stimulation	Barrel cortex	Astrocytic Ca2+; LFP; local postsynaptic activity	(X. Wang et al., 2006)	• Filtering • Thresholding • State switching
			Astrocytic Ca2+; LFP; brain state	(Takata et al., 2011)*
		Visual cortex	Astrocytic Ca2+; neuronal Ca2+; hemodynamic responses	(Schummers et al., 2008) (Stobart et al., 2018)
			Astrocytic Ca2+; EPSP; IPSP; SIC; patch-clamp recordings; visual response selectivity	(Perea et al., 2016)*	• Gain control
		Hippocampus	Astrocytic Ca2+; LTP; CA1 post-synaptic depolarization	(Navarrete et al., 2012)	• Thresholding • Coincidence detection • Gain control
	Neuromodulation	Cholinergic
			Astrocytic Ca2+; LFP; brain state	(Takata et al., 2011)*	• Thresholding • Coincidence detection • Gain control • E/I balance
		Noradrenergic	Astrocytic Ca2+; EcoG	(Ding et al., 2013)
			Astrocytic Ca2+; locomotion; electromiography	(Paukert et al., 2014)
ASTROCYTES ↓ BEHAVIOR	Optogenetics	Cerebellum	Glutamate release; EPSP; LTD; motor behavior	(Sasaki et al., 2012)	• Gain control
		Somatosensory cortex	Astrocytic Ca2+; neuronal Ca2+; LFP; glutamate release; brain state	(Poskanzer & Yuste, 2016)	• Gain control • E/I balance • State switching
		Visual cortex	Astrocytic Ca2+; EPSP; IPSP; SIC; patch-clamp recordings; visual response selectivity	(Perea et al., 2016)*	• Gain control
		Brain stem	Astrocytic Ca2+; ATP release; neuronal membrane potentials; EPSC; breathing	(Gourine et al., 2010)	• Gain control • Gain control • E/I balance
		Hypothalamus	Sleep	(Pelluru et al., 2016)
			Adenosine release; open-field behavior; food intake	(Sweeney et al., 2016)
			Astrocytic Ca2+; patch clamp recordings; IPSC; food intake	(Chen et al., 2016; L. Yang et al., 2015)
		Hippocampus	Astrocytic Ca2+; LTP; EPSC; memory acquisition; contextual and spatial memory	(Adamsky et al., 2018)
	Chemogenetics
		Amygdala	Astrocytic Ca2+; IPSC; EPSC; fear-expression	(Martin-Fernandez et al., 2017)	• Gain control • E/I balance

LFP, Local field potentials, LTD, long-term depression, LTP, long-term potentiation, EPSP, excitatory postsynaptic potential, IPSP, inhibitory postsynaptic potential, ECoG, electrocorticogram recordings, SIC, slow inward currents

^*Belonging to more than one category

5.1. Activation of Ca²⁺ transients in astrocytes by sensory stimulation and neuromodulation

Studies in the mouse barrel cortex have shown activation of Ca²⁺ in astrocyte somata after whisker stimulation using fluorescent Ca²⁺ dyes (X. Wang et al., 2006) (Takata et al., 2011) and genetically-encoded Ca²⁺ indicators (Stobart et al., 2018). Astrocytic Ca²⁺ increases are delayed with respect to Ca²⁺ rises in neurons (Stobart et al., 2018). Also, astrocytic Ca²⁺ rises are dependent on whisker stimulation frequency, and they are blocked by inhibitors of metabotropic glutamate receptors, indicating that they are caused by glutamate released from neurons (X. Wang et al., 2006). Whisker stimulation-dependent Ca²⁺ rises in astrocytes are detected as early as at 2 s when dyes are used, and at 120 ms in the case of faster, genetically encoded indicators, although peak responses range between 3–12 s regardless of the Ca²⁺ indicator. Likewise, visual stimulation triggers neuron-dependent somatic Ca²⁺ transients in astrocytes in the visual cortex of ferret, with a delay of 1–3 s and a peak at 6 s (Schummers et al., 2008). Importantly, the latter study demonstrates that astrocyte activation is highly tuned to orientation maps at a single-cell resolution, and documents that astrocytes mediate hemodynamic signals in the visual cortex, which was confirmed in another study in the barrel cortex (Stobart et al., 2018). The study by (Takata et al., 2011) is also relevant because it demonstrates the following. First, cholinergic neuromodulation originating in the NBM potentiates the activation of local field potentials elicited by whisker stimulation. Second, neuromodulation is strictly dependent on Ca²⁺ rises in astrocytes, as shown by the disappearance of neuronal-activity potentiation in mice lacking IP3R2-dependent signaling. Crucially, abrogation of Ca²⁺ signaling in astrocytes in these mice shifts brain state to a desynchronized mode, as assessed with local field potentials in cortex. The impact of cholinergic neuromodulation on astrocyte Ca²⁺ responses is also documented in hippocampus. Specifically, the increase in Ca²⁺ rises triggered by somatosensory stimulation in rat hippocampal astrocytes is mediated by cholinergic neurotransmission, since it is blocked by the cholinergic inhibitor atropine (Navarrete et al., 2012). Astrocyte activation, in turn, induces the long-term potentiation (LTP) of field EPSPs in CA3-CA1 synapses (Navarrete et al., 2012). These data support the notion that, in addition to setting circuit dynamics for attention in sensory processing, cholinergic neuromodulation participates in the encoding of new information during memory formation (Hasselmo & McGaughy, 2004). The importance of neuromodulation via astrocytic Ca²⁺ in sensory cortical processing has also been reported for the locus coeruleus (Ding et al., 2013) (Paukert et al., 2014) (Srinivasan et al., 2015). This brain-stem nucleus amplifies as well the effect of locomotion on Ca²⁺ rises in Bergman glia in the cerebellum (Paukert et al., 2014). Timewise, neuromodulation-elicited Ca²⁺ rises in astrocytes occur in the range of a few seconds, with regards to both onset and peak after sensory stimulation (Ding et al., 2013) (Srinivasan et al., 2015).

5.2. Modulation of behavior and brain state by optogenetic and chemogenetic stimulation of astrocytes

As in neurons, important insights into causal relationships between astrocytic Ca²⁺ signals and behavioral outcomes are emerging from optogenetics and chemogenetic studies. These technologies allow temporally-precise and reversible modulation of astrocyte activity, in contrast to permanent loss- or gain-of-function genetic manipulations. In mice, optogenetic stimulation of astrocytes using ChR½, Arch and OptoGq has been reported to modulate breathing according to pH changes in the respiratory system (Gourine et al., 2010), induce long-term depression in Purkinje cells and motor behavior (Sasaki et al., 2012), modulate response selectivity of the visual cortex (Perea et al., 2016), inhibit food intake (Sweeney et al., 2016), induce sleep (Pelluru et al., 2016), promote a switch to the slow-oscillation state by triggering the UP state of slow waves (Poskanzer & Yuste, 2016), and enhance memory acquisition (Adamsky et al., 2018).

A key issue is that the downstream consequences of optogenetic activation of astrocytes are not well understood. In the case of neurons, since they are excitable cells that can operate via all-or-nothing changes in membrane voltage driven by fast-acting voltage-gated channels (although they also have subthreshold voltage fluctuations), the probability of neuronal firing is decreased by activation of NpHR and Arch, and increased upon activation of ChR2 (Yizhar et al., 2011). However, astrocytes are not as electrically excitable as neurons. In the first report of successful modulation of neuronal activation (with no behavioral consequences) upon optogenetic manipulation of nearby ChR2-expressing astrocytes, it was assumed, but not shown, that the response was mediated by Ca²⁺ fluxes through ChR2 (Gradinaru et al., 2009). Two subsequent studies confirmed Ca²⁺ rises using Ca²⁺ indicator dyes (Perea et al., 2014) (Pelluru et al., 2016), yet it is unclear how these rises can occur, considering that ChR2 has a relatively low Ca²⁺ permeability, is only open during a few milliseconds —decay constant is ~10 ms—, and presents depolarization-dependent slowing of deactivation (Nagel et al., 2003; Yizhar et al., 2011). One possibility is that it is the entry of Na⁺ through ChR2 that causes Ca²⁺ uptake by reverse activity of the Na⁺/Ca⁺ exchanger (J. Yang et al., 2015). Further, the possibility exists that the effects of ChR2 activation are due to undetected Ca²⁺ rises in astrocyte processes, of which somatic Ca²⁺ might be a consequence (Bernardinelli et al., 2011). In this regard, the use of Arch combined with genetically-encoded Ca²⁺ indicators represents a technical refinement because this opsin induces, after 5 s of photo-stimulation in the mouse cortex, fast Ca²⁺ transients in astrocyte arbors reminiscent of spontaneous activity (Poskanzer & Yuste, 2016). Still, how such a brief photo-stimulation of Arch, whose decay constant is ~9 ms (Yizhar et al., 2011), translates into ~20-s-long Ca²⁺ rises after a delay of ~10 s is unclear (Poskanzer & Yuste, 2016). Plausibly, Arch-elicited hyperpolarization engages voltage-sensitive elements in astrocyte processes. All in all, optogenetics clearly activates astrocytes, although clarification of underlying mechanisms will help optimize this approach for Systems-level basic and clinical studies.

A DREADD receptor that successfully triggers Ca²⁺ transients in astrocytes is hM3Dq (Bonder & McCarthy, 2014; Chen et al., 2016). Studies using hM3Dq in astrocytes have shown: (i) changes in neuronal activity, either reduced or increased firing, in the mouse arcuate nucleus with opposing effects on feeding behavior, perhaps stemming from CNO dose differences, which, in turn, might launch complex feedback loops leading to paradoxical data (Chen et al., 2016; L. Yang et al., 2015), (ii) regulation of excitatory and inhibitory neurotransmission in the amygdala, with a net effect of reduced fear expression in a fear-conditioning paradigm (Martin-Fernandez et al., 2017); and (iii) potentiation of the amplitude of evoked EPSC and, when chemogenetic activation is carried out at specific stages during learning paradigms, improvement of contextual and spatial memory acquisition (Adamsky et al., 2018). As with optogenetics, caution has to be exerted about the resemblance of the Ca²⁺ signaling elicited by chemogenetics to physiological signaling. Also, the CNO metabolite clozapine, and not CNO, might be the real activator of DREADD, as shown with radioligand receptor occupancy measurement, and in vivo positron emission tomography (Gomez et al., 2017). Since clozapine has multiple targets, this recent evidence raises doubts about the specificity of DREADD-based approaches (Gomez et al., 2017). That said, these studies offer several computational insights, to be discussed below.

6. Computational lessons learned from Systems-like studies in astrocytes

First, time scales of Ca²⁺ responses and filtering effect.

According to Ca²⁺-based dynamics, the time scale of astrocyte activation after a physiological input ranges from hundreds of milliseconds to tens of seconds, while the earliest reported effect on nearby neurons after optogenetic stimulation of astrocytes is at 500 ms (Gourine et al., 2010). The onset of hemodynamic response is within 1–3 s from the onset of Ca²⁺ responses (Otsu et al., 2015). Upon sensory stimulation, astrocytes are activated after neurons in cortex, suggesting that neurons reroute information to astrocytes. The observation that Ca²⁺ response curves in astrocytes are qualitatively similar but narrower than those in neurons, as shown by local field potentials (Schummers et al., 2008; X. Wang et al., 2006), suggests that astrocytes filter neuronal activity. Filtering can be either in terms of rectification (high pass filtering), cut-off (low pass filtering) or both (band pass filtering). The latter appears to be the case since astrocytes are not responsive to the highest and lowest frequencies of neuronal input. Interestingly, adaptive modulation of breathing by pH is the only context in which astrocytes directly compute external stimuli, for astrocytes sense changes in pH, even if local neurons are inactivated with tetrodotoxin (Gourine et al., 2010). In other paradigms, astrocyte activation is either secondary to neuronal activation (section 5.1), or the result of gain-of-function induced by optogenetics and chemogenetics in the context of already active circuits (section 5.2).

Second, existence of short- and long-term modalities in Ca²⁺ responses.

The computational and homeostatic functions of astrocytes manifest themselves in at least two broad modalities, depending on time range, nature of inputs, and the intracellular location of Ca²⁺ rises. One modality is the fast rising Ca²⁺ signals that originate within 0.2–5 s from stimulus onset, are short-lived (up from 0.3–10 s), are usually reported in peripheral processes and end-feet (e.g., (Stobart et al., 2018), and are sufficiently fast to locally mediate task-relevant regulation of blood flow (Otsu et al., 2015), metabolic coupling, and neurotransmitter supply (Agarwal et al., 2017; Otsu et al., 2015; Tani et al., 2014), as well as short-term modulation of synaptic efficacy (Perea et al., 2016). The second modality corresponds to robust somatic Ca²⁺ transients that can last tens of seconds, have a slow rise time, and have been reported in the context of cholinergic (Navarrete et al., 2012; Takata et al., 2011) and noradrenergic (Ding et al., 2013) (Paukert et al., 2014) (Srinivasan et al., 2015) neuromodulation, as well as upon ChR2-based optogenetics and by chemogenetics (Adamsky et al., 2018). In hippocampus, the functional consequences of this modality are long-lasting effects on synaptic connections (Adamsky et al., 2018; Navarrete et al., 2012), plausibly associated with memory formation. In cortex, we reason that astrocytic Ca²⁺ rises, as reported by (Takata et al., 2011), participate in a well-accepted role of neuromodulation: control of arousal and attention, which involves recruitment of large, spatially-distributed neuronal populations (Thiele & Bellgrove, 2018). Importantly, the two modalities reveal the existence of threshold heterogeneity in Ca²⁺ responses in astrocytes, which might be of computational importance. Consider, for example, the relative ease with which minimal synaptic stimuli trigger Ca²⁺ transients in astrocytic processes (Haustein et al., 2014; Panatier et al., 2011), which is consistent with a relatively low threshold for activation. This suggests that, in microdomains, the number of synaptic inputs may be of little importance, so that a microdomain could invariantly get activated, either by individual synapses or by an ensemble thereof, akin to the logical OR function. Conversely, the phenomenon of coincidence detection in which activation of cortical sensory neurons (Paukert et al., 2014; Takata et al., 2011) and postsynaptic hippocampal neurons (Navarrete et al., 2012), needs to coincide with neuromodulation to trigger somatic Ca²⁺ transients, and, similarly, the requirement for high inter-neuronal activity to promote astrocytic Ca²⁺-dependent facilitation of excitatory synaptic transmission in the hippocampus (Perea et al., 2016), may be regarded as examples in which the threshold for astrocytic activation is high, and astrocytes will become activated only if multiple inputs impinge together on them, akin to the logical AND function. Density of IP3R2 (De Pitta et al., 2018) and baseline Ca²⁺ levels (Zheng et al., 2015) may be among the factors setting thresholds of stimulation. Plausibly, the described modalities of astrocytic Ca²⁺ responses are the extremes of a context-dependent spectrum, encompassing mixed regimes in terms of number of astrocytic domains involved, and short versus long-term effects. Key questions emerge: how are different astrocytic microdomains recruited, which neural circuits are activated as a consequence of different response modalities, and, finally, do specific computations, other than thresholding, operate in different modalities? In section 7, we propose gaining insight into these questions by treating single astrocytes as mini-circuits, and by identifying relevant patterns of Ca²⁺ responses with dynamical-systems statistics approaches such as dimensionality reduction.

Third, regulation of neuronal gain.

This appears to be a computation carried out by astrocytes throughout a variegated collection of circuits and behavioral contexts. Signal coincidence detection of sensory stimulation and neuromodulation by cortical astrocytes is one example that may have implications in attention (Paukert et al., 2014; Takata et al., 2011). Computationally, attention consists of a gain change (in amplitude of response or contrast) that results in the prioritization of relevant inputs over irrelevant information (Thiele & Bellgrove, 2018). Input prioritization is called top-down (or inside-out) because the process is shaped by internal models and goals conveyed to the sensory areas by neuromodulators (Thiele & Bellgrove, 2018)—note the influence of predictive coding in this assumption. The modulation of gain is facilitated by a normalization mechanism whereby neurons’ responses are reduced in proportion to the activity of neighboring neurons by the joint activation of inhibitory and excitatory neurons (Reynolds & Heeger, 2009). Instructed by signal coincidence detection, astrocytes might help prioritize information by regulation of gain via modulation of excitatory synaptic drive by Ca²⁺-dependent glutamate uptake (Schummers et al., 2008), gliotransmission (Takata et al., 2011), intrinsic neuronal excitability (Sasaki et al., 2012), and co-modulation of excitatory and inhibitory neurotransmission (Perea et al., 2014).

In the case of brain state, a gain change might account for the transition from an asynchronous to a synchronous mode through a change in the network’s ratio of excitation versus inhibition, according to the general theory of neural networks (Brunel, 2000). Hence, a possible mechanism whereby astrocytes might synchronize brain state through gain control is regulation of excitatory-synaptic strength, either by reducing glutamate uptake (Poskanzer & Yuste, 2016), releasing ATP/adenosine and glutamate in a Ca²⁺ dependent manner (Halassa et al., 2009) (Fellin et al., 2009), or taking up GABA via GAT-3 transporters (Shigetomi et al., 2011).

Memory-related tasks in hippocampus can also be interpreted as a phenomenon of gain control. Thus, chemogenetic and optogenetic stimulations of hippocampal astrocytes result in increased frequency and potency of mEPSCs in local neurons, leading to long-term potentiation of excitatory synaptic connections (Adamsky et al., 2018). Significantly, astrocyte-mediated NMDA-dependent long-term potentiation appears to be: (i) task-specific insofar as fear-conditioned mice, but not home-caged ones, show synaptic potentiation, and (ii) stage-selective, for it very precisely affects distinct phases along the memory-formation continuum, such as memory allocation. Likewise, the interneuron-induced potentiation of excitatory neurotransmission mediated by astrocytes might be one example of neuronal gain (Perea et al., 2016). Intriguingly, a dual mechanism in which astrocyte-mediated depression of excitatory synapses combines with potentiation of inhibitory ones seems at play in afferents to neurons in the medial central region of the amygdala (Martin-Fernandez et al., 2017). The ensuing net increase of inhibitory drive to these neurons (i.e., a case of negative gain) was then shown to correlate with transient reduction of fear conditioning and anxiety

Finally, the role of astrocytes in reflex homeostatic behaviors modulating feeding and breathing can be explained in terms of use of gain modulation to adapt behavior to stimuli intensity. Thus, the presence of food modulates the synaptic efficacy of neurons in the hypothalamus (Chen et al., 2016; L. Yang et al., 2015), whereas pH acidification induces adaptive neuronal firing in the brain stem which, in turn, activates breathing (Gourine et al., 2010).

Fourth, decoding and rerouting of information.

Coincidence detection of sensory cortical and neuromodulatory subcortical neuronal inputs (Takata et al., 2011) (Paukert et al., 2014), transformation of inhibitory neurotransmission into synaptic facilitation in hippocampus (Perea et al., 2016), and the transformation of neuronal inputs into potentiation or inhibition, depending on the duration and frequency of the inputs (Covelo & Araque, 2018), might be three examples of decoding of neuronal signals by astrocytes, and rerouting of decoded information to other neurons. Plausibly, the information rerouted by astrocytes is gliotransmitter-dependent (Covelo & Araque, 2018). Since neuronal action potentials and astrocytic Ca²⁺ transients have utterly different temporal resolutions, it is improbable that variables represented in trains of action potentials are represented in astrocytic Ca²⁺ without significant loss of information. Rather, we posit that what astrocytes ‘hear’ from neurons are instructions to ‘tell’ other neurons to modify their activity via canonical computations. In computational science, canonical computations are fundamental operations carried out in circuits in a variety of contexts. We have hitherto identified a few: signal filtration, thresholding (implicating AND/OR functions and coincidence detection), gain, and control of the balance between excitation and inhibition. It is not clear whether synaptic scaling should be added, because this function might be performed by microglia rather than astrocytes (Stellwagen & Malenka, 2006). In the roadmap we propose to use decoding approaches from machine learning to identify possible variables encoded by astrocyte computations.

Fifth, astrocytes could act as switches in brain state transitions.

The causal implication of astrocytes in cortical slow oscillations (<1 Hz) (Takata et al., 2011) (Poskanzer & Yuste, 2016) supports the relevance of astrocytes in network activity beyond tripartite synapses. Slow waves have been hypothesized to represent the default mode of cortical network activity (Sanchez-Vives et al., 2017). During UP states, there is synchronization in beta and gamma frequencies, synaptic gain modulation, modulation of replay and memory formation, and some cortical features might inform about transitions between unconsciousness and consciousness (reviewed in (Sanchez-Vives et al., 2017)). An intriguing paradox exists in that astrocytes induce a synchronized state, but also mediate cholinergic and noradrenergic neuromodulations, which are characteristically associated with asynchronous, high-rate activity that facilitates sensory processing (Lee & Dan, 2012). We posit that astrocytes might act as switches whose default action is to sustain UP states, whereas neuromodulation-driven attention renders astrocytes independent of the cortical oscillator, and shifts their action towards short-term plasticity related to sensory processing. Indeed, network theory predicts that a key parameter in setting asynchronous versus synchronous network activity, as well as the frequency of eventual oscillations, is afferent synaptic activity (Brunel, 2000; Ledoux & Brunel, 2011). Coincidence detection can be thus regarded as a scenario of afferent stimulation—specifically mediated by neuromodulation—whereby astrocytes induce the network’s transition to the asynchronous state. Finally, although astrocytes are particularly attuned to slow oscillations because their internal dynamics, as judged by Ca²⁺ transients, fall within a time scale of seconds, they are also involved in the generation of faster waves such as theta (4–12 Hz) and slow gamma (30–50 Hz) (Perea et al., 2016; Sardinha et al., 2017). The effect of astrocytes on fast waves may be due to cross-frequency coupling, a mechanism whereby global slow oscillations modulate local fast oscillations, usually their amplitude (Canolty & Knight, 2010), which happens to be the predominant effect of astrocytes on fast waves (Perea et al., 2016; Sardinha et al., 2017). By regulating fast waves, astrocytes will have an impact on neuronal encoding, because fast rhythms provide temporal reference frames for local and large-scale computations (Hawellek et al., 2016). Dimensionality reduction (below) may reveal specific astrocytic Ca²⁺ regimes associated with coincidence detection, oscillations, and brain state transitions.

7. A roadmap to advance the integration of astrocytes into Systems Neuroscience

7.1. Theoretical and conceptual improvements

Is there a minimal astrocyte-neuronal circuit?

Anatomical, molecular and functional factors matter when considering astrocytes from a computational point of view. From an anatomical perspective, a single astrocyte can be regarded by itself as a ‘mini-circuit’, in light of the subcellular compartmentalization of calcium signals (Bazargani & Attwell, 2016), along with the consideration that one astrocytic anatomical domain may comprise numerous neurons, dendrites and synapses. Estimations in the mouse hippocampus are: 1–20 neurons (Halassa et al., 2007), 300–600 dendrites (Halassa et al., 2007), and 140,000 synapses in (Bushong et al., 2002) and 50,700–75,200 in (Chai et al., 2017). Recently, a FRET-based study reports dynamic interactions of astrocytic distal processes with different types of synaptic inputs (Octeau et al., 2018). Moreover, because astrocytes are characteristically territorial, they give rise to a tiled arrangement of the brain space, which can be then seen as a patchwork of mini-circuits. The function of tiling is an outstanding question. From a molecular perspective, according to single-cell gene profiling, and unbiased hierarchical clustering in mouse brains, astrocyte populations are not as functionally heterogeneous as neuronal populations (Zeisel et al., 2015). Thus, in the mouse somatosensory cortex and hippocampal CA1 region, there are 29 types of neurons including pyramidal cells, glutamatergic neurons, and interneurons, as opposed to just two types of astrocytes (Zeisel et al., 2015). This suggests that, although both neurons and astrocytes are molecularly specialized cells, additional and extensive sub-specialization exists among neurons but not astrocytes. On the other hand, the lack of molecular definition may provide astrocytes with greater adaptive capacity to operate in a variety of circuits (Poskanzer & Molofsky, 2018), which may explain phenotypical differences of astrocytes from region to region (Martin et al., 2015) (Chai et al., 2017). We thus argue that neurons imprint functional signatures on networks by encoding, for example, odors, position, images, words, abstract categories and executive functions, whereas the size, anatomical arrangement and molecular makeup of astrocytes suggest that they might be designed to operate canonical computations (Section 6, Table 1) in local mini-circuits within larger-scale networks—as well as homeostatic and metabolic support. Support for the hypothesis that astrocytes perform canonical computations comes from studies showing that astrocyte-based computations such as synaptic potentiation, a type of gain control, improve the performance of ANNs (Alvarellos-Gonzalez et al., 2012; Porto-Pazos et al., 2011). Additional support comes from recent theoretical studies in computer science, and formal language theory, which showed that canonical filtering of synaptic transmission by astrocytes (described as ‘astrocyte-like control’) facilitates the generation of the so-called logic gates (Song et al., 2017), which are basic building blocks in neural circuits performing logic Boolean operations such as AND, OR, NOT, XOR and NAND (Binder et al., 2007). According to these studies, simple ensembles of astrocytes and synapses reminiscent of our mini-circuits might account for all elementary logical functions and, properly combined, allow, in principle, computation of any real-world function in a scalable manner (Song et al., 2017). It should be kept in mind that multiple strategies are likely at play across species in shaping astrocytic mini-circuits, and their possible computational functions. For example, although single-cell genomics is not yet available in humans, the fact that human astrocytes are larger, more complex (including 270,000–2 million synapses), and present more morphological variants than mouse astrocytes (Oberheim et al., 2009), together with the striking observation that engraftment of human astrocytes into mouse brains enhances synaptic plasticity and learning (Han et al., 2013), suggests that more complex astrocytic mini-circuits are present in humans, possibly underpinning a larger variety of canonical computations. All in all, it appears that in order to reinforce the presence of astrocytes in Systems Neuroscience, we must zoom out at astrocyte populations as well as zoom into single-astrocyte mini-circuits. This is akin to neuron-focused studies that, as noted, should cover both systems-wide and sub-cellular computations. Indeed, the latter should be considered as part of the computations within astrocyte mini-circuits, for spines and dendrites are inextricably embedded in an astrocyte ‘matrix’.

Where might the ‘slow’ spatiotemporal dynamics of astrocytic Ca²⁺ enter Systems Neuroscience?

The question of which time scales are relevant for neuronal computations has long been debated. Action potentials of individual neurons are characteristically fast and short-lived voltage depolarizations in the range of 1–2 ms. The speed and all-or-nothing nature of these responses, as well as their lack of attenuation due to axonal myelination, makes them well suited to transmitting information throughout the brain in milliseconds. Currently, the minimal temporal resolution of the neuronal code appears to be on a millisecond time scale, as shown in sensory processing in the auditory system of mammals (Butts et al., 2007) (Kayser et al., 2010), and in basic human cognitive capabilities, including semantic abstract categorization of images (e.g., identifying an image as a ‘dog’)(Vanmarcke et al., 2016). This means that stimuli arriving within intervals of a few milliseconds are distinguished as individual entities by neurons that fire individual, millisecond-long spikes in response to each stimulus. Clearly, if astrocyte Ca²⁺ transients are the astrocytic substrate of neural computing—and they are the best candidate thus far—they are too slow to encode ultrafast representations. However, the brain characteristically operates in parallel on a gradient of time scales that are nested and hierarchically organized (Murray et al., 2014). Thus, attention and decision making can last seconds, emotions can arise within seconds, and mood changes in minutes. In prediction coding, the slow contextual changes in the prefrontal brain under which fast sensory representations are interpreted require seconds (Kiebel et al., 2008). Also, there are circadian time scales affecting sleep and global homeostasis, and very long time scales in the range of hours, weeks, or years affecting learning and memory (Hari & Parkkonen, 2015). This means that, complex operations ought to exist prolonging the effect of ultrafast (up to 10 ms) and fast (<100 ms) neuronal time scales up to minutes, which precludes structural changes caused by gene expression. Working memory during decision making is a prototypical example of the need for sustained activity in the short-term scale. The question is how several discrete, millisecond-long events related are engaged in a continuum of network activities that last up to hundreds of seconds (Hasson et al., 2015). Since there is no external input during delays (time between input and action), working memory must arise from the intrinsic dynamics of neural circuits. Computational neuroscience identified this problem over 20 years ago (Seung, 1996), and has since struggled to provide answers using realistic neuronal parameters (Chaudhury and Fiete, 2016). Answers include: (i) biophysical properties of neurons such as the slow ‘membrane-time constant’, which reflects the time during which information can be maintained by neuronal voltage without a substantial leak, estimated to last between 5–20 ms, (ii) intervention of NMDA receptors, which are ideally suited to enlarge ‘memory’ capabilities of neurons beyond their membrane time constants because they are active around 100 ms after the synaptic input (X. J. Wang, 1999), (iii) short-term synaptic plasticity (Abbott & Regehr, 2004), (iv) an effective computational solution called long short-term memory (Hochreiter & Schmidhuber, 1997), and (v) sustained firing rate of neurons, or ‘persistent activity’, achieved upon the exquisite tuning of recurrent circuits such that an input re-entering a synapse exactly matches the decay of the neuron, keeping its firing rate for a prolonged time (Goldman-Rakic, 1995) (Renart et al., 2007). These solutions present limitations. Slow time constants need to be reset, and, at present, slow time constants in neurons do not seem to have that capability. The time constant of the NMDA receptor is appropriate to maintain memories up to 1–5 s, but not longer. Long short-term memory works very well in current machine learning applications, but its application to natural circuits is unclear. Finally, it is also unclear how the exact timing of feedback loops in persistent activity is achieved. Clearly, additional solutions are in order, perhaps including astrocytes.

Inclusion of astrocytes in current theoretical frameworks and circuit-operating principles.

The temporal dynamics of Ca²⁺-based excitability make astrocytes suitable to operate in circuit computations running in the sub-second to a supra-second scale, including the ones already mentioned such as short-term plasticity, neuromodulation, and slow rhythms. Interestingly, computations such as signal-coincidence detection and oscillation control imply detection of the order and interval of arrival of time-varying signals, suggesting that astrocytes might encode time. Theoretical models of timing in the brain such as oscillators (Goel & Buonomano, 2014) and liquid state (or liquid computing) (Maass et al., 2002) may be useful to explore this idea. Astrocytes might also have a role in predictive coding. As shown in silico renditions (Deneve et al., 2017), the core idea of the framework is that neural circuits are error-driven, such that differences between predictions and new inputs are computed as prediction errors, which might be transformed (i.e., ‘rerouted’) into changes in synaptic strength by short-term plasticity. The greater the error, the more synaptic changes would be needed in order to ‘update’ circuit information. The quality of prediction errors is computed by the variable ‘precision’, which is akin to the standard error in the t-Student test, and is hypothesized to occur in a scale of seconds, and to be encoded by neuromodulators (Friston, 2009; Stephan et al., 2015). Since astrocytes participate in neuromodulation (Navarrete et al., 2012; Takata et al., 2011) (Ding et al., 2013) (Paukert et al., 2014), the possibility emerges that astrocytes might encode precision, perhaps by temporally decoding prediction errors from multiple synapses in the astrocyte mini-circuit, in order to ensure sufficient statistics. It is tempting to speculate that the aforementioned canonical computations carried out by astrocytes are manifestations of computation of error-related statistics and/or time in different contexts. These computations would be canonical, for they would occur throughout the brain. Decoding analyses (below) may provide information about the specific computations carried out by astrocytes in complex behaviors where issues like timing, temporal holding of information, and error between predictions and real outcomes, are particularly prominent.

Astrocytes and energy-efficient coding.

Circuit modeling and biophysical analyses support the idea that neuronal circuits are designed to produce energy-efficient codes because action potentials are energetically demanding; hence, energy supply becomes a relevant constraint in information processing (Laughlin, 2001). Three reasons justify a revision of the adjustment of coding to energy constraints from the perspective of astrocytes. First, astrocytes may lessen the metabolic constraint by facilitating lactate to neurons during task-elicited glutamatergic neurotransmission (Magistretti & Allaman, 2015). Of note, lactate qualifies as a gliotransmitter, and hence may be harvested for computational signaling tasks, because it instructs memory acquisition (Suzuki et al., 2011), and stimulates neurons by a mechanism independent of its uptake, perhaps receptor-mediated (Tang et al., 2014). Second, as noted in (Magistretti & Allaman, 2015), the anatomical arrangement of local neurons, projections from neuromodulatory nuclei and astrocytes within cortical columns, points to optimized circuit design to facilitate energetic coupling between neurons and astrocytes. Here we extend this notion to astrocyte mini-circuits, and argue that they might represent a coding strategy to optimize energy utilization, for example, by integrating sparse coding, which is coding distributed among many synapses to reduce individual computational load, and has been described as a solution to energy limitations (Laughlin, 2001). Third, whether energy is also a constraint in Ca²⁺based computations in astrocytes is an outstanding question. There is currently no estimation of the energy demand of Ca²⁺signaling in astrocytes. ATP-consuming steps are: (i) in the context of IP3R2-mediated Ca²⁺-release, re-uptake of cytosolic Ca²⁺ back into the endoplasmic reticulum via Ca^2+/ATPase pumps, which are crucial in dictating the period of Ca²⁺ fluctuations/oscillations, as well as their shape and duration; (ii) the plasmalemma Ca^2+/ATPase pump involved in capacitive Ca²⁺ entry/flux; (iii) Na⁺/K⁺-ATPase activity dependent on glutamate uptake (Pellerin & Magistretti, 1997), which appears to critically influence Ca²⁺ rises in sensory processing (Schummer et al., 2018); (iv) V-ATPase dependent uptake of Ca²⁺ into acidic stores; and (v) neuronal-activity dependent Ca²⁺ rises in astrocytic microdomains in distal processes, as shown in mice with membrane-anchored GCaMP3 (Agarwal et al., 2017). This study documents a critical link between energy metabolism and Ca²⁺-based excitability, because it shows that Ca²⁺ rises in microdomains are the result of Ca²⁺ efflux from mitochondria, which, in turn, is triggered by short events (‘mitoflashes’) of superoxide production during oxidative phosphorylation. Still, the need for ATP for several critical processes is an open question, a prime example of which is gliotransmission: the exact source of gliotransmitters such as ATP, glutamate, and D-serine, and the energy expenditure involved in their production, is unknown. All in all, it is worth stressing that fatty acids are a fuel for oxidative metabolism in astrocytes (Eraso-Pichot et al., 2018). Since fatty-acid oxidation yields over 50 times more ATP molecules than glycolysis, astrocyte metabolism might be optimized to undertake costly computations from the point of view of energy requirements.

Ca²⁺-independent computations.

Although productive, the adoption of Ca²⁺ signaling as a readout of astrocyte excitability should not blind us to the possibility that, similar to Ca²⁺ transients in neurons following action potentials, the astrocytic Ca²⁺ response might be a late manifestation of yet undiscovered signals. If we recover classic perspectives of biophysics (Barlow, 1996; Destexhe, 1999), many components of the astrocytic response could potentially encode stimulations and perform computations. This is the case of second messenger molecules such as IP₃ or cAMP that are conventionally associated with GPCR-mediated astrocytic Ca²⁺ signaling (DePittà, 2019) but also other ion-based signals. Among the latter, Na⁺ is an emerging candidate because it presents activity-dependent fluctuations, although advanced fluorescent probes are necessary to fully establish this ion as a novel readout of astrocyte excitability (Rose & Verkhratsky, 2016).

7.2. Technical and analytical improvements

7.2.1. Zooming into astrocyte mini-circuits

Dimensionality reduction of Ca²⁺ data.

We posit that single-astrocytes and astrocyte populations are dynamical systems governed by function-specific regimes resulting from coordinated changes in Ca²⁺ signaling. At the single-astrocyte level, the local and global activation modalities described earlier might be the extremes of a spectrum of possible regimes. Dimensionality reduction is a statistical method developed in machine learning to facilitate analysis of the characteristically multidimensional (i.e., multivariate) dynamical systems. What dimensionality reduction does is to identify key variables determining relationships within the data (the so-called latent variables), thereby reducing input data to low-dimensional representations defined by such latent variables. In Systems, dimensionality reduction has been applied to neuron-population recordings in decision making, movement, odor perception, working memory, visual attention, audition, rule learning, and speech (reviewed in (Cunningham & Yu, 2014). The complex spatiotemporal patterns of spontaneous and evoked Ca²⁺ transients in single astrocytes, which now can be measured with 3-dimensional Ca²⁺-imaging (Bindocci et al., 2017), represent a multidimensional data set that will benefit from dimensionality reduction techniques. Thus far, Ca²⁺ transients in astrocytes have been simplified for quantification purposes by using a single Ca²⁺ readout (Perea et al., 2014), the average of calcium signals detected in multiple ROIs pooled from a population of astrocytes (Poskanzer & Yuste, 2016), the categorization of these signals by spatial location and averaging within subcellular compartments (Chai et al., 2017), and machine-learning based identification of true signals (Agarwal et al., 2017). Although these approaches have already yielded useful insights into correlations between astrocytic and neuronal activities and behaviors—as described in Section 6—they have not revealed possible canonical spatiotemporal computations within and between astrocytes, in distinct experimental paradigms. Dimensionality reduction will thus facilitate detection of noise (stochastic Ca²⁺ transients), indicate whether some of the manually selected ROIs based on visual inspection are not independent, and hence can be considered as the same ROI, and reveal correlations and anti-correlations of distant regions belonging to the same ROI. The latter can occur when distant regions are synchronized due to oscillations or synchronous inputs that regularly occur in those regions. Thus, dimensionality reduction of single-astrocytes may help to reveal and select dimensions, that is, the minimum number of ROIs (e.g., 5–10 from up to 200 original ones), in which fluctuations are more pronounced and meaningful, thus paving the way for population analyses, which will require the simplification of Ca²⁺ signals per astrocyte with the minimal loss of relevant information. Linear methods for dimensionality reduction that can be used in astrocytes include simple principal component analysis (PCA), the prime linear method (Cunningham & Yu, 2014), as well as factor analysis, as used with neuronal Ca²⁺ (Paninski & Cunningham, 2018).

Machine learning.

Non-linear methods such as ANNs are increasingly being used to replace stages in signal processing and analysis in neuronal populations, as well as a method for dimensionality reduction (Paninski & Cunningham, 2018). Thus, ANNs could a priori uncover latent variables that best account for Ca²⁺ data from astrocyte mini-circuits, and are non-linearly related. Current ANNs appear well-suited to extract latent variables from Ca²⁺ imaging of large populations of neurons (Paninski & Cunningham, 2018), and their application to multidimensional astrocytic Ca²⁺ data should be explored. Conversely, ANNs can be also used as generative models, that is, models that infer classes of inputs from a low number of latent variables (Dosovitskiy, 2015). Another statistical tool of machine learning that holds promise is Bayesian hierarchical modeling (Bishop, 2006). The general idea is to build a graph that hierarchically and probabilistically relates relevant variables related to Ca²⁺ and to other data from connectomics. Indeed, if the graphs are well-informed about the connectome within mini-circuits, they can be used as an inverted model to infer the values of the latent variables accounting for Ca²⁺ signals. One advantage of these methods is that the number of free parameters is typically lower than in standard ANNs, which might require massive amounts of data for training.

Connectomics.

Providing an accurate picture of the synaptic contacts within astrocyte mini-circuits, in rodents and humans, and in different brain regions, is necessary to help interpret and model in silico Ca²⁺-based regimes defined by dimensionality reduction, and to identify constraints that could be incorporated into machine-learning algorithms. Specific questions are the density of excitatory and inhibitory synapses (and subtypes of the latter), their functional interplay in distinct astrocyte regimes defined by Ca²⁺. For example, astrocyte mini-circuits might adopt feed-forward, recurrent or mixed patterns, depending on the behavioral task, and present hierarchical organizations between astrocytic and neuronal elements, as well as topological/functional ‘motifs’ and wiring rules—as shown in the analysis of small neuronal networks (Schroter et al., 2017). Tools for connectomics include graph theory (Fornito, 2016), Bayesian hierarchical modeling (Bishop, 2006), and topological tools (Kanari et al., 2018; Reimann et al., 2017). In all these approaches, both morphological and functional readouts could serve as input data. Morphological readouts of the synaptic architecture of astrocyte mini-circuits at meso- and micro-scales can be obtained with array tomography, a form of light microscopy based on the serial sectioning of ultrathin (hundreds of microns) sections, which permits 3D reconstructions at a micrometer/nanometer resolution (Micheva et al., 2010). Array tomography can be complemented with automated 3D electron microscopy techniques, such as serial block-face ANNs electron microscopy (SBFSEM). Crucially, fixation methods must not distort contacts within mini-circuits (Korogod et al., 2015). Functional analyses are more challenging, for they will require development of improved optical tools and probes to simultaneously monitor the activities of excitatory and inhibitory neuronal populations, as well as those of astrocytes. The emerging combination of 2-photon calcium imaging with SBFSEM for examining neural circuits at cellular resolution may pave the way for subcellular analyses (Vishwanathan et al., 2017). Finally, recent multiplex Ca²⁺ imaging at a single synapse-astrocyte interface (J. P. Reynolds et al., 2018), application of nanotechnology to voltage recording in neurons (Jayant et al., 2017), and FRET-based analysis of contacts between synapses and astrocytes (Octeau et al., 2018), are advances towards integrating structure and function in astrocyte mini-circuits.

7.2.2. Zooming out to astrocyte populations

Decoding astrocytes in complex behavioral tasks.

The identification of a astrocytic Ca²⁺-based code is a prime objective that, importantly, can be started with current statistical tools developed to study neuron-based encoding and decoding. Moreover, we argue that the increased interest in neuronal Ca²⁺ as a tool to decipher the brain code (the reason being that the number of neurons recorded with optical tools is one order of magnitude higher than with multi-electrode arrays, see Section 2) benefits the analysis of Ca²⁺-based astrocyte computations. For simplicity, here we focus on decoding approaches, which specifically seek to predict external variables from signal patterns, although tools to study encoding can be also considered (Section 3). Decoding astrocyte signals entails measuring Ca²⁺ activity populations in behavioral paradigms in which several time scales, including those in the range of action defined for Ca²⁺-based signaling in astrocytes (hundreds of milliseconds to tens of seconds), are relevant for the task at hand. One such paradigm is reward-associated decision making over variable contexts in which an animal must associate stimuli with choices (responses) to obtain an immediate reward. The association can be abruptly reversed, as in the case of reversal learning, where in a given context 1, stimulus A leads to reward and stimulus B does not lead to reward, whereas in another context 2, stimulus B predicts reward (Schoenbaum et al., 2002). The performance in such varying contexts involves tracking variables at both fast and slow time scales. Variables such as ‘immediate reward’, ‘confidence’, ‘option values’ and ‘choice’ are fast, represented in the millisecond time scale, whereas the deliberation occurring before a decision is taken lasts hundreds of milliseconds to seconds, and even up to minutes if this deliberation involves inference about the current context. During this time, the brain computes correlations between fast variables, and represents differences between the prediction based on previous experience and the real outcome as ‘error’. We argue that the precise computation of prediction error is key in the identification of a true association between stimulus and reward, such that varying contexts plausibly require more complex computations. Frontal areas are expected to track the mixture of relevant variables in the form of ‘cognitive maps’. In rat, the orbitofrontal cortex encodes the millisecond-long fast variables (Rolls et al., 1996) (Nogueira et al., 2017). It is unclear, however, how transitions between contexts and associated deliberations are represented at the much slower time scale of seconds. We posit that the network may use astrocytes as a buffer to help represent the prior history of rewards and choices, which is necessary to infer the true nature of the current context. Specifically, astrocytes may temporally integrate error signals, or somehow influence behavior based on accumulated information through canonical computations such as gain modulation. Along these lines, dopaminergic neuromodulation, which signals reward prediction error (O’Doherty et al., 2017), might serve to gate information from neurons to astrocytes, and vice versa.

Technical and analytical challenges associated with large-scale recordings of Ca²⁺ rises in astrocytes and neurons.

The specific experimental design we propose involves the simultaneous recording of Ca²⁺ activity in astrocytes with 2-photon microscopy in awake animals (Srinivasan et al., 2015), and Ca²⁺ or electrophysiological responses in neurons (Poskanzer & Yuste, 2016). From previous work indicating that with tens of neurons it is possible to predict animal choices with high accuracy (Kiani et al., 2014; Nogueira et al., 2017), we reason that tens of astrocytes will suffice to observe statistically significant trends that can be used to guide subsequent recordings and analyses. At this time, optimal selection of paradigms and analytical methods may be more helpful to make significant leaps towards understanding astrocyte-based computations than massively increasing the number of astrocytes recorded. Data acquisition, signal processing and increased dimensionality of the data present additional challenges when there is a need to perform recordings of two cell types with different Ca²⁺ dynamics. As to data acquisition, although recent advances have pushed the boundaries of multi-photon imaging, with significant improvements that enable imaging in multiple brain areas, across laminae, and in non-head-fixed configurations (Yang & Yuste, 2017), since these imaging methodologies have been developed specifically to record the activity of neuronal populations, they may not always be translatable to astrocyte populations. For example, many of the technologies used to carry out 3D two-photon imaging rely on source separation algorithms that assume the Ca²⁺ signals are non-propagative and spatially static. While this is true for Ca²⁺ imaging of neuronal somata, astrocyte Ca²⁺ imaging data obviously do not obey these rules. Thus, new 2-photon imaging methodologies born from an astrocytic perspective, particularly those that allow imaging multiple laminae simultaneously, are necessary to advance our understanding of these cells within larger, meso-scale circuits. Another area of improvement for large-scale Ca²⁺ recording in astrocytes and spike-recording in neurons is the development of new electrophysiological approaches, including flexible polymer probes (Chung et al., 2018) and clear electrode arrays (Thunemann et al., 2018), to solve the current problem posed by the large equipment necessary to carry out single-neuron recordings, which precludes astrocyte imaging. Despite the advances in Ca²⁺ imaging, single-neuron electrophysiological measurements are preferable, for Ca²⁺ transients lack temporal resolution to reveal single-action potentials. With regards to signal processing, we described earlier the state-of the-art in signal processing in large-scale recordings in neurons, including methods to denoise, demix and simplify Ca²⁺ data. As to astrocytes, readouts to be assessed per astrocyte are Ca²⁺ signals in microdomains measured in dynamic ROIs (Wang et al., 2016) (Agarwal et al., 2017), and/or processed with dimensionality reduction techniques as explained above. A priori, dimensionality reduction and decoding techniques can be used with data from astrocyte and neuronal populations. Possible experimental scenarios are paired Ca²⁺ imaging from both cell types (e.g., low-dimensional data per astrocyte could be paired with one optical or electrophysiological signal per neuron). Dimensionality reduction may reveal pools of neurons interacting with specific astrocytes. Similarly, linear and non-linear decoders could be trained to predict relevant behavioral variables from neuron-astrocyte networks, and to study which sets of neurons and astrocytes are more relevant for that decoding. Linear decoding techniques could be used even if the amount of behavioral data is not massive, such that around ten trials per stimulus-choice condition might suffice to obtain a description of astrocyte-neuronal interactions at behaviorally relevant time scales.

7.3. Translation: Clinical Systems Neuroscience

When it comes to treatments for CNS diseases, molecular and cellular approaches should not be abandoned, because they have successfully led to current therapeutic venues. For example, in multiple sclerosis, relapses are mitigated by immunotherapy against specific populations of immune cells (Torkildsen et al., 2016), and in Alzheimer’s disease, promising anti-β−amyloid treatments are being tested in clinical trials (K. V. Kastanenka et al., 2016; Sevigny et al., 2016). However, there are no effective preventive or disease-modifying treatments for neurodegenerative and psychiatric disorders, suggesting that reductionist approaches aimed at fighting disease one molecule or one cell at a time might be insufficient. Moreover, degeneration of neuromodulatory nuclei (Kelly et al., 2017; Liu et al., 2015), as well as large-scale network disarrangement (Westerberg et al., 2012), are hallmarks of psychiatric and neurodegenerative diseases. Clearly, brain diseases are associated with dysfunction of neural systems. Although the outstanding question persists of whether such dysfunction is cause, consequence, or epiphenomenon, the notion that Systems-oriented research will prove more fruitful than traditional approaches to discovering, and thus manipulating, the biological underpinnings of diseases, has already been voiced for autism (Rosenberg et al., 2015), and motivates therapeutic approaches such as deep brain stimulation in Parkinson’s disease (Ashkan et al., 2017). We anticipate that optogenetic and chemogenetic stimulations will be the most productive avenues in the emerging field of Clinical Systems Neuroscience (K. V. Kastanenka, Herlitze, S., Boyden, E.S., Tsai, L-H and Bacskai, B.J., 2017). First, these approaches offer the advantage of selective actions at the network and cellular levels—critically allowing the assessment of neuronal versus astrocytic effects—since viral vectors may be targeted at specific regions through stereotaxic surgery. Second, they enable preclinical research in rodents and primates to demonstrate causality between network dysfunction and disease hallmarks (K. V. Kastanenka et al., 2017). Third, advances in viral vector technology for gene transfer significantly reduce vector-associated cytotoxicity and immune responses (Lundstrom, 2018), rendering chemogenetics and optogenetics amenable for clinical use in human patients.

8. Concluding remarks

We started this perspective article by posing several questions to guide the analysis of the role of astrocytes within Systems Neurosciences. We looked for initial answers in available studies that include measurements of astrocyte Ca²⁺ activity, targeted optogenetic and chemogenetic manipulations, and complex behaviors or neural networks. We asked whether astrocytes are as functionally heterogeneous as neurons. We contend that they are not. We put forth anatomical, molecular, and computational arguments in support that astrocytes may operate modules akin to mini-circuits in large scale networks, performing canonical computations throughout the brain. Mathematical analyses of in vivo data together with in silico modeling will be necessary to firmly establish the existence, and nature, of astrocytic computations, and whether they encode specific variables. We may get closer to the answer using decoding approaches in reward-associated decision making over variable contexts, a complex behavioral paradigm in which the brain needs to perform difficult computations within the slow time scale of astrocytic Ca²⁺ signals. Another question was whether astrocytes use Ca²⁺ to carry out spatiotemporal integration of multicellular signals. A first insight is that there is behavior-dependent integration in a time scale of sub-seconds to supra-seconds, perhaps driven by signal thresholding and timing control. We propose to use dimensionality reduction, a tool developed in the context of machine learning, to identify the minimum amount of ROIs that carry independent information in Ca²⁺ transients in different contexts. This is a mandatory step towards finding structure in these transients, with the assumption that astrocytic Ca²⁺ responses behave like a dynamical system that can adopt multiple regimes. Thus, the question of whether subcellular compartments in astrocytes perform different functions ought to be reformulated to whether there are function-specific Ca²⁺ regimes. Further, we identify technical and analytical shortages in joint astrocyte- and neuron-population imaging, and ensuing data processing algorithms. Finally, we point to theoretical frameworks used by Systems Neurosciences that might benefit from the inclusion of astrocytes. Many avenues of exploration remain. To cite two, we have the role of astrocyte-based computations in long-term processes underlying memory, perhaps by intervening in memory replay in the so-called resting brain, and the failure of neural circuits including astrocytes in neurodegenerative and psychiatric diseases. Decoding astrocytes may represent a leap forward towards novel approaches in the study of astrocytes in health and disease.

Main points.

• Astrocytes may use Ca2+ signals to perform canonical computations in complex behaviors on a time scale of sub-seconds to seconds.

• Statistical tools from Systems Neuroscience could be used to unravel variables and algorithms encoded by astrocytic Ca²⁺.