Turbulence induces clustering and segregation of non-motile, buoyancy-regulating phytoplankton

Abstract

Turbulence plays a major role in shaping marine community structure as it affects organism dispersal and guides fundamental ecological interactions. Below oceanographic mesoscale dynamics, turbulence also impinges on subtle physical–biological coupling at the single cell level, setting a sea of chemical gradients and determining microbial interactions with profound effects on scales much larger than the organisms themselves. It has been only recently that we have started to disentangle details of this coupling for swimming microorganisms. However, for non-motile species, which comprise some of the most abundant phytoplankton groups on Earth, a similar level of mechanistic understanding is still missing. Here, we explore by means of extensive numerical simulations the interplay between buoyancy regulation in non-motile phytoplankton and cellular responses to turbulent mechanical cues. Using a minimal mechano-response model, we show how such a mechanism would contribute to spatial heterogeneity and affect vertical fluxes and trigger community segregation.

1. Introduction

The spatial distribution of aquatic microorganisms has profound effects on the ecology of our oceans [1,2] affecting fundamental ecological interactions, population stability, species diversity [3] and, hence, affecting the functioning of whole marine food webs [4]. Highly sparse non-uniform spatial distributions, or patchiness, have distinct origins at different scales: while at the mesoscale, it is mostly driven by reproduction, grazing, nutrient availability [5] and advection by currents [6], at smaller scales (from the scale of the cell up to the order of a metre), the interplay between biological and physical factors plays a major role. These include microorganismal motility and its interaction with fluid flows and, among other processes, it shapes encounter rates [7,8], the formation of thin layers [9], cell clustering [10] and segregation [11]. Small-scale patches also serve as hotspots of microbial activity facilitating, for instance, interaction with bacteria in the ‘phycosphere’, influencing global carbon and nutrient cycling, and regulating ecosystem productivity [12,13].

Recent efforts have clearly established that motile marine microorganisms are patchily distributed in the presence of turbulent flows [14]. Cell motility and the response to chemical and mechanical landscapes conspire with fluid flows to accumulate and disperse cells in different spatial environments. However, and despite non-motile species comprising two of the most important ecological groups in the ocean (cyanobacteria, essential for nitrogen fixation [15,16], and diatoms, carrying out about one-fifth of the total photosynthesis on Earth [17]), a largely unanswered question concerns the response of non-motile cells to the same turbulent cues and how it affects their sinking dynamics, of paramount importance for global biogeochemical cycles.

Motivated by the physiological regulation of buoyancy prevalent in non-motile phytoplankton species [18–21], here we investigate, by means of direct numerical simulations, the dynamics of active but non-motile cells in a three-dimensional turbulent flow. In particular, we focus on cells’ response to mechanical stresses such as those locally induced by fluid forces. Although non-motile species possess the required mechanosensitive machinery to display rapid active responses to imposed mechanical stresses (triggering, for instance, the production of cytosolic Ca²⁺ [22]), the effect of hydrodynamic stresses in buoyancy regulation has been largely overlooked. Overcoming adverse environmental conditions, including light and nutrient limitations, has been considered as the most relevant driver for buoyancy regulation [23–25]. While certainly important, more recent work suggests this is only part of the story: even under nutrient replete conditions, transcriptional analysis reveals rapid changes in gene expression solely associated with the exposure to turbulent flows. These include an increase in the fatty acid biosynthesis pathways (which may also serve as buoyancy regulators) and other determinants of cellular metabolic state [26]. Moreover, fast and active physiological responses are also known to directly regulate cells’ instantaneous sinking speeds [25]. While none of these studies disentangles the mechano-transduction pathway linking physiological responses to changes in cell density, they unambiguously show that non-motile cells are able to perceive, and actively respond to, mechanical stimuli in short times. Since buoyancy regulation is the only known mechanism for non-motile species to control their position in the water column, the above results render mechano-induced buoyancy regulation as a plausible hypothesis that serves as the starting point for our minimal model.

Here we show that, in contrast to passive tracers, a simple law for buoyancy regulation leads to cell clustering and species segregation, and we demonstrate how these processes depend on physical parameters such as the cells’ settling speed. Finally, we discuss its implication for the ecology of marine phytoplankton.

2. Mathematical model

We consider the motion of small spherical particles of radius a and variable density ρ_p immersed in three-dimensional turbulent flows described by the incompressible Navier–Stokes equations

$$\begin{array}{rl}\mathrm{\nabla }\cdot \mathit{u}& =0\\ \text{and}{\mathrm{\partial }}_t\mathit{u}+\mathit{u}\cdot \mathbf{\nabla }\mathit{u}& =-\frac{1}{\rho }\mathbf{\nabla }p+\nu {\mathrm{\nabla }}^2\mathit{u}+\mathit{f}.\end{array}\}$$ 2.1

Here u(x, t) is the fluid velocity, p(x, t) the pressure, ρ the uniform fluid density and ν its kinematic viscosity. The forcing term, f, represents a zero-mean, temporally uncorrelated, Gaussian forcing which injects energy at large scales at a given rate, ɛ, necessary to sustain a statistically stationary state. Together with the kinematic viscosity, the energy injection rate defines the Kolmogorov scales for the length, η = (ν³/ɛ)^1/4, time, τ_η = (ν/ɛ)^1/2, and velocity, u_η = η_k/τ_k = (νɛ)^1/4 [27]. These scales will be used to make physical quantities dimensionless.

Small spherical particles follow the Maxey–Riley equation [28]. In our case, as the Reynolds number Re_p based on the particles’ radius a and the characteristic velocity U_a (i.e. the maximum between particle sedimentation velocity and the characteristic velocity fluctuation at the scale of the particle) is very small, Re_p = U_a a/ν ≪ 1, derivatives computed following the particles, d/dt, are well approximated by derivatives along fluid streamlines, D/Dt. Furthermore, we neglect Faxen corrections and the Basset history terms, following standard approaches justified for very small relaxation time [29–31]. Finally, the acceleration of the particle is written as

$$\frac{\text{d}{\mathit{u}}_{\hspace{0.17em}p}}{\text{d}t}=\beta \frac{\text{d}\mathit{u}}{\text{d}t}-\frac{{\mathit{u}}_{\hspace{0.17em}p}-\mathit{u}}{{\tau }_{\hspace{0.17em}p}}-(1-\beta )g\hat{\mathit{k}},$$ 2.2

where u_p = dx_p/dt is the particle velocity, β = 3ρ/(2ρ_p + ρ) is the ratio of the fluid density to the particle density ρ_p, τ_p = a²/(3νβ) is the Stokes relaxation time and g represents the acceleration of gravity.

We further simplify the equations taking into account the fact that particles are almost neutrally buoyant (β ≃ 1), that g ≫ |du/dt|—a typical condition in the ocean—and that the Stokes time (order 10⁻³ s for Stephanodiscus rotula, a ∼ 50 × 10⁶ m, ρ ∼ 1020 kg m⁻³ [32]) is usually much smaller than the smallest time scale in the flow (range from 0.1 s in coastal regions ɛ ∼ 10⁻⁴ W kg⁻¹ to 10 s in the open ocean ɛ ∼ 10⁻⁸ W kg⁻¹ [33]). Under these conditions, the equation of motion (2.2) reduces to an equation for particle position

$$\frac{\text{d}{\mathit{x}}_{\hspace{0.17em}p}}{\text{d}t}={\mathit{u}}_{\hspace{0.17em}p}=\mathit{u}-v_s\hat{\mathit{k}},$$ 2.3

where v_s = (1 − β)τ_pg is the particle sinking speed in still fluid and $\hat{\mathit{k}}$ represents the vertical direction.

For particles with constant density, ρ_p, the motion described by (2.3) is identical to that of ideal fluid tracers in the presence of an additional constant vertical drift due to buoyancy forces. Dynamics under these conditions cannot produce particle clustering as the relative motion between particles is identical to that of fluid elements. More formally, in this case, the effective velocity field u_p is divergence free and therefore the rate of contraction in physical space is zero [34]. This dynamics does not hold in the case of particles which are able to regulate their density (buoyancy) as is the case of diatoms and cyanobacteria. In the following, we will describe our model for buoyancy regulation in response to fluid mechanical stresses, following that discussed in [21]. To be specific, we assume that the particle density is dependent on the norm S of the local strain tensor ${\mathcal{S}}_{ij}=1/2({\mathrm{\partial }}_i{u}_{\hspace{0.17em}j}+{\mathrm{\partial }}_{\hspace{0.17em}j}{u}_i)$, and in particular, we employ the Frobenius norm $S={[tr(\mathcal{S}{\mathcal{S}}^t)]}^{1/2}$. Since a change in the density of particles corresponds to a change in sedimentation velocity, the latter will depend on the flow strain rate computed on the particle position v_s = v_s(S_p). As the detailed mechanism responsible for how intracellular responses translate into the regulation of buoyancy is still unclear, we will analyse two possible scenarios differing in the sign of the response: we refer to cells whose density decreases (increases) with the mechanical stresses as shear-thinning (shear-thickening), respectively [21].

To model how cell sedimentation velocity changes with the local strain rate, we take inspiration from Michaelis–Menten kinetics. We choose a response function of the form f(S) = S/(S + S_H), where S_H is the strain rate half-saturation constant. Examples of this response function are shown in figure 1 together with a typical steady distribution of strain rate in a turbulent flow obtained from the integration of (2.1). We further assume that the density of the particle varies linearly with the response function f(S) in the range ρ ≤ ρ_p ≤ 2ρ [21], where the minimum density corresponds to a neutrally buoyant particle. Thus, the density law for the shear-thinning case is ρ_p = ρ[2 − f(S)], whereas for the shear-thickening case it is ρ_p = ρ[1 + f(S)]. These density laws provide the variation of the still fluid sedimentation velocity with the norm of the strain rate for the shear-thinning case, v_s(S) = [1 − S/(S + S_H)]v_s,max and the shear-thickening case v_s(S) = [S/(S + S_H)]v_s,max, where v_s,max = 2a²g/(9ν) is the still fluid sedimentation velocity at the maximum density ρ_p = 2ρ. Note that at the half-saturation constant we have v_s(S_H) = v_s,max/2. The choice of 2ρ for the maximum density is not restrictive since v_s is given by a combination of ρ and a and the results for a different maximum density would be equivalent to those obtained for a cell of different size. We emphasize that in deriving the model of buoyancy, we have assumed that the particle regulates its buoyancy immediately. This is in agreement with the characteristic time scale measured in the back-and-forth transition in the sinking rate in [25] and the measured time response to other environmental signals [22]. It is important to clarify that the buoyancy model derived therein does not include any adaptive response to mechanical stresses and that, in [25], buoyancy regulation is seen as a mechanism able to enhance nutrient uptake by altering the nutrient-deplete boundary layer around the cell, regardless of the external flow. However, this does not mean that this process is not relevant or does not take place within a turbulent environment (where the boundary layer argument at the basis of [25] would be less stringent). Indeed, it was recently shown that motile phytoplankton are able to actively modify their migration strategy to evade turbulent layers [35], while non-motile phytoplankton (e.g. diatoms) modify their gene expression to trigger energy storage pathways when exposed to turbulent flows [26].

Figure 1.

Probability density function of the Eulerian strain rate. Coloured dots indicate six different values of S_H used in our direct numerical simulations: S_Hτ_η = 0.06, 0.18, 0.3, 0.47, 1.36, 3.0. Insets show the response function for shear-thickening (a) and for shear-thinning (b) particles, with different colours corresponding to the values of S_H indicated in the main panel: S_H1τ_η = 0.06 (violet), S_H4τ_η = 0.47 (orange) and S_H6τ_η = 3.0 (red). (Online version in colour.)

3. Numerical results

We have performed a numerical investigation of the statistical properties of several populations of both shear-thinning and shear-thickening cells. By means of direct numerical simulations of the Navier–Stokes equations (2.1) using a fully dealiased pseudo-spectral code [36], we obtain the incompressible velocity field. Statistical stationarity of the flow is guaranteed by a white-in-time forcing f acting at a large scale only. Simulations are done at three different resolutions N = 64, 128, 512 (N is the number of grid points per side on the periodic cube of size L_B) corresponding to three different Reynolds numbers or turbulence intensities. Resolutions are chosen such that the maximum wavenumber available k_max satisfies the relation k_maxη > 1.8 to guarantee sufficient accuracy at small scales at the different turbulence intensities. In stationary conditions, a population of N_c cells is initialized with uniform random positions x_p in the domain. Particle trajectories are obtained by the simultaneous integration of (2.1) and (2.3) where the velocity field and the strain rate at the cell positions are obtained by a third-order polynomial interpolation. After the particle distribution has reached a statistically steady state, we collect data for several large-scale eddy turnover times to ensure statistical convergence.

The numerical populations differ both in the relative sensitivity to the hydrodynamic cues and in the maximum sedimentation velocity they can reach. We have chosen 1 ≤ Π ≤ 30 (where $\mathit{\Pi }=v_{s,\max }/u_{\eta }$), which corresponds to 0.18 ≤ v_s,max ≤ 5.4 mm s⁻¹ when we rescale time and space such that ɛ = 10⁻⁹ W kg⁻¹, so that we can cover rather well the range of typical oceanic values of settling speed [37]. The range of reported values is quite wide, since there is a significant variation in terms of diatom species, methods for analysing sinking speeds and experimental conditions (nutrients, light, temperature, flows) [25,37–42]. In order to choose a set of values of S_H that represent different relevant situations, we computed the Eulerian strain rate of the turbulent flow. Numerical results are presented at fixed intermediate turbulence level ɛ, except for §3.2 where the effects of different turbulent intensities on the sedimentation time are discussed. Figure 1 shows the probability density function (PDF) of S; coloured dots on the PDF curve indicate the six different values of the strain constant S_H used in the simulations of the adaptive cells.

3.1. Clustering and preferential sampling

We first discuss the formation of cell clusters as a result of buoyancy regulation. We measure inhomogeneities in the spatial distribution of a population by its correlation dimension D₂, defined as the scaling exponent of the probability to find two particles at a distance less than $r\hspace{0.17em}:\hspace{0.17em}P(|{\mathit{X}}_1-{\mathit{X}}_2|<r)\propto r^{D_2}$, as r → 0. D₂ is directly related to encounter rates between cells, which is a crucial determinant for ecological interactions [7]. If a given type of interaction happens only once, cells are at a certain distance $\overline{r}$, the rate at which two cells get close enough for such interaction to occur is proportional to (i) the probability density for the cells to be at exactly that distance $P(r=\overline{r})$ and (ii) the typical relative velocity of cells at that distance [43,44]. The former is simply given by the probability density for the particles to be on a spherical surface of radius $\overline{r}$, which is $\propto {\overline{r}}^{D_2-1}$. In short, if D₂ < 3, the probability of having particles at small distances decays more slowly as r → 0 than in a homogeneously distributed population and, as a result, encounter rates increase.

For a homogeneous distribution in a space of dimension d (here d = 3), one has D₂ = d, while D₂ < d indicates fractal clustering. In the absence of buoyancy regulation, our simulations show no clustering, as is expected since in this case particle velocity is given by a constant downwards term added to an incompressible velocity field. When regulation is switched on, we observe parameter-dependent clustering for both shear-thinning and shear-thickening cells (see the example in figure 2). In figure 3, we plot the correlation dimension computed for both modes of regulation as a function of Π and for different values of S_H. In both cases, when the sedimentation velocity is small, we find D₂ ≃ 3, signalling that distributions remain homogeneous regardless of S_H. On the other hand, for large values of Π clustering strongly depends on the response to hydrodynamic stresses.

Figure 2.

Snapshot of 3 × 10⁵ thinning particles, with Π = 30, S_H = S_H1 and ɛ = 10⁻⁹ W kg⁻¹. Each particle is coloured according to the ratio of the local number density around it to the average density. (Online version in colour.)

Figure 3.

Correlation dimension as a function of Π = v_s,max/u_η for shear-thickening cells (a) and for shear-thinning cells (b). Inset shows the correlation dimension as a function of the strain rate half-saturation constant in the case of thickening cells with Π = 10 (grey) and Π = 20 (black). (Online version in colour.)

In the shear-thickening case, clustering is maximum (i.e. D₂ is minimum) for large values of Π and S_H, while D₂ ≃ 3 when S_H is very low. In this limit, cells tend to become very heavy (v_s ∼ v_s,max) and fast saturation means that correlation with the flow rapidly becomes very weak. As a consequence, cells behave very similarly to the unregulated case and mostly sink with a constant speed. In the opposite limit (large S_H), we have that v_s ∼ S(v_s,max)/S_H and observe clustering. In this case, regulation is very sensitive and variations in sedimentation speed are strongly correlated with the flow. However, in order to have a relevant degree of clustering, v_s,max has to be large to balance the large values of S_H, otherwise particles behave as slow sinkers with a consequent reduction in fractal clustering compared to the other S_H curves at same value of Π. The non-monotonic behaviour of D₂ with S_H is shown in the inset of figure 3 for thickening cells at Π = 10 and Π = 20.

In a similar way, shear-thinning cells display stronger clustering by increasing the sedimentation velocity, while the dependency from the strain constant is opposite compared to the first case. Indeed in the limit of large S_H cells tend to sink since v_s ∼ v_s,max and we find D₂ ≃ 3, while for small S_H fractal clustering can take place. The latter limit is not obvious because it would seem that particles behave like passive tracers (v_s ∼ 0), but from the shear-thinning density law we obtain that v_s ∼ v_s,max(S_H/S), so regulation is a first-order effect, although v_s,max has to be large to compensate for the small value of strain rate constant similarly to that discussed about shear-thickening cells for the curve at S_H6.

Small-scale clustering is often accompanied by a preferential sampling of regions characterized by certain properties of the flow. This behaviour has been observed both in inertial particles [45–47] and in swimming phytoplankton [14,48,49] and it is also present in this case. Figure 4 depicts the average vertical velocity of the fluid, 〈u_z〉, calculated on the particle positions as a function of the mean sedimentation speed 〈v_s〉. While shear-thinning cells appear to spend more time in regions of upwards flow velocity, shear-thickening particles preferentially sample downwards velocities. This effect does not affect deeply the cells’ dynamics, since the contribution of the average vertical fluid velocity is small compared to the average sedimentation speed, and it is related to the different buoyancy response. Indeed in both cases, the preferential sampling is larger for the same values of S_H for which the strongest clustering occurs, that means the largest shear half-saturation constant for shear thickening particles and lowest S_H for thinning cells.

Figure 4.

Average vertical fluid velocity as a function of mean sedimentation velocity (both divided by Kolmogorov velocity scale). Different colours represent different S_H, while solid (dashed) lines correspond to shear-thickening (thinning) cells. (Online version in colour.)

3.2. Sedimentation time

We explore the effects of buoyancy regulation on sinking particles by looking at the distribution of sedimentation times, defined as the time T_s needed to cover a certain vertical distance L which we will take as a multiple of L_B. We compare each population of thinning/thickening cells with passive particles sinking at the respective maximum speed v_s,max without regulation.

The average time needed by the passive particles to cover the distance L is known a priori and it is smaller than for active cells. Figure 5 shows the comparison between the PDFs of T_s for the active populations, normalized with the average sedimentation time for passive cells ${\overline{T}}_{\hspace{0.17em}p}=L/v_{s,\max }$, for both shear thickening and thinning cells for the case Π = 10 and for L = 4L_B. It is evident that there is a remarkable difference between the PDFs’ maxima: as expected, buoyancy control allows cells to sink more slowly compared to maximum density passive particles. The mean sedimentation time of shear-thickening particles increases for larger values of S_H, while the opposite is true for shear-thinning cells. The major effect of buoyancy regulation in this respect is to lower the time-averaged ‘instantaneous cell density’ (and, hence, the instantaneous sinking speed) well below the maximum passive value, effectively keeping cells suspended for much longer times before ultimately sinking to the deep ocean. Moreover, it is evident that not only does the mean sedimentation time increase (since the comparison is made with unregulated cells with v_s = v_s,max) but also the distribution becomes broader, with wider tails in the PDFs. In other words, buoyancy regulation does not simply shift rigidly the PDF of the sedimentation time but also modifies its shape: this implies that in the shear-thickening (thinning) case, for large (small) S_H a number of cells, contributing to the right tail of the PDF, will remain suspended for a time significantly larger than the average population.

Figure 5.

Probability distribution of the sedimentation time T_s (divided by ${\overline{T}}_{\hspace{0.17em}p}$, the mean sedimentation time of passive cells) for shear-thickening cells (a) and for shear-thinning cells (b) on a log–log scale. Π = 10 and L = 4 L_B in both cases. Black solid lines represent the inverse Gaussian prediction, while squares are numerical data. Black ones refer to maximum density passive cells, orange to S_H4, dark blue to S_H5, red to S_H6, while on the right green is S_H2 and light blue is S_H3. (Online version in colour.)

This behaviour can be rationalized by considering the vertical motion of sinking particles as a stochastic process with drift. Indeed, we can replace the deterministic vertical motion described by (2.3) with a stochastic version with a drift given by the average of the vertical component of particle velocity V_d = 〈u_p,z〉 and a diffusion coefficient D_z which takes into account the turbulent fluctuations (assumed Gaussian), including the fluctuations of S which induce the modulations of v_s. In this way, we can recast the problem as a standard first-passage problem [50] where the PDF of the sedimentation times takes the form of an inverse Gaussian function [51] (detailed derivation is given in the electronic supplementary material)

$$P(T_s)=\frac{L}{{(4\pi D_z{T}_s^3)}^{1/2}}{\text{e}}^{-{(V_d{T}_s-L)}^2/4D_z{T}_s}.$$ 3.1

In figure 5, we plot this analytical prediction with the only free parameter, D_z, fixed by the value of the variance of sedimentation times which, according to (3.1), is given by $⟨T_s^2⟩-{⟨T_s⟩}^2=2D_{z}L/V_d^3$. As mentioned above, buoyancy regulation affects the shape of the PDFs resulting in an increase of D_z (i.e. wider tails of PDFs) as a consequence of the turbulent fluctuations that, through S variations, control v_s. This provides an excellent agreement with the numerical data, which confirm the validity of our approach.

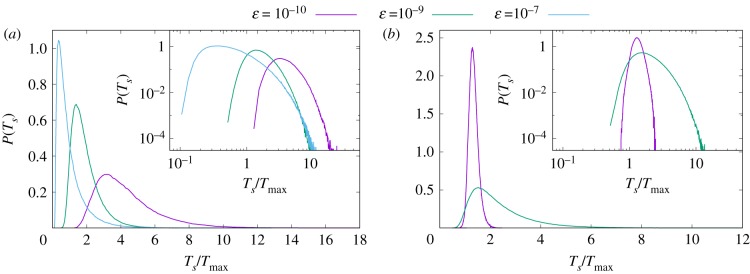
In a realistic physical situation, phytoplankton cells will face different flow environments, with possibly vastly different turbulent intensities on a seasonal or even daily basis. It is, therefore, interesting to study how the sedimentation time of a cell with a fixed set of parameters depends on the strength of the turbulent flow. To this aim, we performed simulations at three values of energy dissipation rate ɛ ≃ 10⁻¹⁰, 10⁻⁹ and 10⁻⁷ W kg⁻¹, numerically obtained by increasing the intensity of the forcing at constant viscosity. We remark that this scenario is not equivalent to simply taking into consideration different values of S_H, as done in figures 1–5, since the statistics of the strain changes with Re. Figure 6 shows the sedimentation time statistics for cells with Π = 10 and S_H = S_H4 in the flows of different intensities. When turbulence is more intense, particles experience, in general, larger values of the local shear. One can parametrize such effect, for example, by non-dimensionalizing S_H with the value S_peak corresponding to the maximum in the PDF of strain in each run. The three cases considered have S_H/S_peak = 3.76, 1.02 and 0.07, respectively. As a consequence, more intense turbulence produces faster sedimentation for shear-thickening particles. On the contrary, when shear-thinning particles experience intense turbulence, they become extremely light, almost neutral, leading to large sedimentation times. Since the longest sedimentation times are observed at the largest Re, which is, in turn, more computationally expensive, we present here only the statistics for the two lower values of ɛ in the shear-thinning case. For the same reason, sedimentation times are computed for L = L_B. It can be appreciated, from figure 6a, that shear-thickening cells develop wider tails as the flow Re increases. For the case of shear-thinning cells, increased shear slows down the sedimentation. However, increased turbulence also widens the distribution of sedimentation times, so that many cells sediment faster or slower than the average. This is probably the most remarkable consequence of this kind of buoyancy regulation for diatoms living in a changing turbulent environment: different levels of shear, indeed, would not only change the average sedimentation speed, but also affect the shape of the distribution of sedimentation times.

Figure 6.

Probability distribution of the sedimentation time T_s (divided by T_max, the sedimentation time of a particle sinking with Π = 10) for shear-thickening cells (a) and for shear-thinning cells (b). Different colours represent different values of ɛ. The insets show the same data but in log–log scale. (Online version in colour.)

3.3. Segregation

Having determined that both shear-thickening and shear-thinning cells show small-scale clustering, we then focus on the relative spatial distribution of different populations. Community segregation (or the degree of spatial overlap) is a hallmark of biological diversity as it facilitates the competition for resources by allowing distinct populations to explore different ecological niches. Here, we look at how community segregation depends on the clustering properties of the individual populations. We quantify segregation by the metric defined in [52]:

$$S_{1,2}(r)=\frac{1}{N_1+N_2}\sum _{i=1}^{M(r)}|n_i^1-n_i^2|,$$ 3.2

where M(r) is the number of cubes in which the volume L³ is partitioned (since this approach is based on a coarse graining over a scale r). We computed the segregation between one shear-thickening and one shear-thinning population characterized by different parameters (S_H, Π). We indicate by N₁ and N₂ the total number of particles of each type, while $n_i^1$ and $n_i^2$ are the number of particles of either population contained in each cube i. The observable in equation (3.2) varies in the range [0, 1]; S_1,2(r) = 0 implies that the total number of the two types is the same at scale r, while the limit S_1,2(r) = 1 means that there is no overlapping between the two distributions at the considered scale. Complete separation is expected at very small scale, giving that lim_r→0 S_1,2(r) = 1, while no structure can be observed on the scale of the numerical box, with lim_r→L S_1,2(r) = 0. Finally, we define the segregation length scale—the scale up to which the two distributions do not overlap—as R* = r(S_1,2 = 1/2). At scales below R*, one population is sensibly more abundant than the other and, hence, cross-population encounters will be depleted except on the boundaries of such areas.

We consider here both populations with maximum clustering and having quasi-homogeneous distributions. For the case of homogeneously distributed particles, we take those having correlation dimension closer to 3 and sedimentation velocity close to zero, representing Poissonian samples. As examples of inhomogeneous distributions, we have considered the case of the strongest clustering: shear-thickening cells characterized by the largest S_H and thinning particles with the smallest strain constant, in both cases setting Π = 30. Figure 7 shows the comparisons just described. Furthermore, we have compared the values S_H = S_H1 and Π = 30 for thinning cells with different Π for thickening particles (while the condition S_H = S_H6 has not changed), in order to study how the segregation length scale varies with the parameters. The top inset of figure 7 shows the segregation length, rescaled by the Kolmogorov length scale, for the different parameter combinations as a function of the non-dimensional maximum sedimentation velocity. The bottom inset of figure 7 shows the cells in a thin slab taken from the numerical box, for the case of maximum clustering and consequently maximum segregation.

Figure 7.

S_1,2(r) curves calculated between a population of shear-thinning cells with S_H = S_H1 and Π = 30 and shear-thickening cells with constant S_H = S_H6 and Π = 30 (dark violet), Π = 20 (green), Π = 10 (light blue), Π = 7 (orange), Π = 3 (red) and Π = 1 (dark blue). Solid black line corresponds to homogeneously distributed particles and dashed line to S_1,2(r) = 1/2. Bottom inset: horizontal section of a typical particle distribution for the clustered case (dark violet solid line in the main plot); red and green refer to thinning and thickening particles, respectively; in both cases, dark/light red (green) indicates high/low cell concentration. Top inset: segregation length R* defined by S_1,2(R*) = 1/2, as a function Π, the same colours as the main plot. Dashed line represents the value of R* associated with the case of homogeneously distributed particles. (Online version in colour.)

Although the correlation dimension of the attractors for the two individual populations characterized by the maximum clustering is, under the chosen set of parameters, almost identical, their dynamics follow very different rules. As a consequence, the two attractors are not necessarily overlapping, leading to well-segregated populations, as shown in figure 7. It is also possible to appreciate how the correlation length R* reduces accordingly to the decrease of clustering.

4. Conclusion

In this paper, we present the first analysis of the impact of turbulence on the spatial inhomogeneous distribution of non-motile, but actively responsive, phytoplankton in the ocean. By means of thorough numerical simulations of a minimal model of active buoyancy regulation of cells embedded in three-dimensional isotropic turbulence, we show that the nonlinear interplay between advection by turbulent flows and cellular activity leads to cell clustering in low dimensional patches (fractal manifolds), it affects average sinking rates and it promotes the segregation of distinct populations. Clustering prompts encounter rates which are key to ecological processes fundamental for population survival, such as sexual reproduction, grazing avoidance or chemical signalling. At the same time, clustering accelerates physical coagulation mechanisms and, ultimately, the formation of marine snow, coupling buoyancy control with global biogeochemical cycles through the regulation of vertical fluxes of organic carbon in the ocean (i.e. the biological carbon pump). Community segregation, on the contrary, facilitates the competition for resources by allowing distinct populations to explore different ecological niches. We also observed a preferential sampling of certain regions of the flow based on the sign of the vertical component of fluid velocity. This effect could, in principle, be relevant in the case of intense, coherent structures. One such example is Langmuir circulation [53,54]. In the latter case, the proposed mechanism could lead to accumulation along the upwelling and downwelling regions between the circulation rolls. The ecological relevance of inhomogeneous planktonic distributions (which can be produced by many different dynamics [55,56]) along Langmuir circulation has been noted by several authors (see [55] for a review).

In order to emphasize the significance of active cell mechano-responses in spatial inhomogeneities, we have intentionally left out of our minimal description any other biological processes affecting population dynamics. However, as soon as the characteristic time of sinking becomes of the order of the characteristic time of population growth, the interplay between purely biological (growth of the population) and physico-biological mechanisms (buoyancy control) becomes relevant. This interplay should be addressed in future studies. Furthermore, a detailed experimental characterization of cell responses to mechanical stresses, beyond qualitative first accounts [22], is still pressing. In particular, quantifying physiological responses to hydrodynamic stresses by directly measuring changes in the sinking rate when cells are exposed to different flow conditions is paramount. Finally, we would like to remark once again that a similar, hypothetical mechanism of buoyancy regulation would likely be much more complex than the minimal model considered here, as it would depend on many factors, including environmental conditions and the physiological state of the cell. If buoyancy regulation similar to the model proposed is found to be realized in phytoplankton, our analysis would provide a further example of the role played by turbulence in shaping oceanic community structure not solely through its large-scale direct effect on phytoplankton dispersal but also through less explored subtle physical–biological coupling at the single-cell level.

Data accessibility

Scripts and data used to produce figures can be found at: https://github.com/mborgnino/data-buoyancy-regulating-phytoplankton.git.

Authors' contributions

All authors contributed equally to this study.

Competing interests

We declare we have no competing interests.

Funding

This article is based upon work from COST Action MP1305, supported by COST (European Cooperation in Science and Technology). We acknowledge the support by the Departments of Excellence grant (MIUR). HPC Center CINECA is gratefully acknowledged for computing resources, within the INFN-Cineca agreement INF18-fldturb and IscrC-DnT project. We acknowledge the support from the Spanish Ministry of Economy and Competitiveness (AEI, FEDER EU) grant nos. FIS2016-77692-C2-1-P (I.T.) and CTM-2017-83774-D (J.A.), and the subprogram Juan de la Cierva no. IJCI-2015-26955 (J.A.).