The golden age of arthropods: ancient mechanisms of colour production in body scales

Abstract

Insect colour is extremely diverse and produced by a large number of pigmentary and nanostructural mechanisms. Considerable research has been dedicated to these optical mechanisms, with most of it focused on chromatic colours, such as blues and greens, and less on achromatic colours like white and gold. Moreover, studies on the evolution of these colours are less common and largely limited to inferences from extant organisms, in part because of the limited amount and types of available fossil material. Here, we directly compare nanostructure and colour of extant and amber-preserved (approx. 15 and 99 Myr old, respectively) gold-coloured representatives of micromoths (Lepidoptera: Micropterigidae) and springtails (Collembola: Tomoceridae). Using electron microscopy, microspectrophotometry and finite domain time difference optical modelling, we show that golden coloration in the extant micromoth is produced by nanometre-scale crossribs that function as zero-order diffraction gratings and in the springtail by a diffraction grating without crossribs. Surprisingly, nanostructure and thus predicted colour of the amber-preserved specimens were nearly identical to those of their extant counterparts. Removal of amber enabled direct colour measurement of the fossil micromoth and further revealed that its colour matched both that of the extant specimen and the predicted colour, providing further support for our optical models. Our data thus clearly show an early origin and striking conservation of scale nanostructures and golden coloration, suggesting strong selection pressure either on the colour itself or on the mechanisms that produce the colour. Furthermore, we show the thus-far untapped potential for the use of amber-preserved specimens in studies on the evolution of organismal coloration.

1. Introduction

Terrestrial arthropods are one of the most ubiquitous and ancient animal groups dating back to at least the Ordovician (approx. 450 Ma) [1]. Insects, in particular, are incomparably diverse, with an exquisite variety of colours that are produced by a magnificent array of underlying colour-producing mechanisms [2,3]. While the colours and colour-producing mechanisms of extant insects are fairly well studied, those insects known only from fossils are not. This is because fossilized optical nanostructures are relatively rare and subject to alteration during diagenesis that reduces the certainty of colour reconstructions [4]. Amber provides a unique preservation of colours and pigments/nanostructures that could enable more reliable colour reconstructions.

A defining characteristic of all arthropods is the presence of a hard exocuticle, a light but strong layer that provides protection and support [5] and frequently contains scales, or chitinous laminar structures that often produce the brightest colours of the animal [6]. Typical scales are characterized by a series of longitudinal ridges often traversed by crossribs sculpting a basal lamina [7]. In some cases, the scale is hollow and contains pigment granules or, in more specialized scales, elaborate reflecting elements [7–9].

Colours and their optical bases have been most heavily investigated in Lepidoptera, the butterflies and moths. Structural colours, such as those in butterfly wings, are produced when light is selectively reflected, diffracted or scattered by ordered nanostructures [9,10] (reviewed in [3]).

Cuticular scales are not exclusive to lepidopterans, and indeed are present in many other arthropods [11]. Scales on insect bodies vary in shape and size but seem to all have longitudinal ridges that are either straight or adorned with ridge-lamellae [12]. Despite numerous accounts of scales in numerous insect groups across the literature and their obvious evolutionary importance, the study of their optical properties is scant.

Structural colour has been identified in the fossil record in several insects (mostly beetles, e.g. [13–15]). Some of those studies have examined exceptionally well-preserved scales and cuticles such as those from the mid-Eocene Messel oil shale of Germany (47 Ma) [16,17] and from lepidopteran scales in Jurassic rock (approx. 200 Ma) [18]. Those studies indicate that structural colour and its mechanistic basis are an ancient feature in at least butterflies and moths. Investigating whether these colour production mechanisms are shared among other groups of scale-bearing insects and the origins of these structures are needed to elucidate the evolution of structural colours and scales in general.

Moreover, optical models to reconstruct fossil colour have been based on nanostructures preserved from rock samples only. Amber specimens may enable us to not only reconstruct colour from nanostructure but also test those predictions against preserved colour.

Here we used optical and electron microscopy, spectrophotometry and optical modelling to investigate how colour is produced on scales of two species of arthropods: a micromoth Micropterix calthella (Lepidoptera: Micropterigidae) and a springtail Tomocerus vulgaris (Collembola: Tomoceridae). Both species display a dense array of body scales with brilliant golden coloration and are ancient clades that originated early in the evolution of Hexapoda [19]. To identify potential evolutionary changes in these scales, we then compared the structural characteristics of scales of two fossil specimens from mid-Cretaceous Burmese amber (99 Ma) that are closely related to our extant species: one micromoth (Lepidoptera: Micropterigidae) and one springtail (Collembola: Tomoceridae).

2. Material and methods

2.1. Sample collection and imaging

We obtained three dry individuals of the micromoth M. calthella from a private entomological collector in Belgium. The primitive micromoth family Micropterigidae is currently regarded as the most ancestral taxon of the Lepidoptera [20]. Ten individuals of the springtail T. vulgaris (Collembola: Tomoceridae) were sourced from a laboratory-reared population at the University of Ghent. The Collembola are an ancient group of hexapod arthropods. The oldest known fossil species is about 380 Myr old, which makes them among the oldest terrestrial animals [21,22].

The amber moth was obtained from an amber mine located near Noije Bum Village, Tanaing Town. The U–Pb dating of zircons from the volcanoclastic matrix of the amber gave a maximum age of 98.8 ± 0.6 Myr [23,24]. The amber springtail is from the mid-Miocene (approx. 14.8 Ma) Zhangpu amber in southeastern China [25].

We pulled individual golden scales from the dorsal side of the wing of the extant micromoth and the dorsal surface of the abdominal segments of the springtail. We mounted individual scales on glass slides and imaged them on a dissecting microscope (Leica M60, Germany). We extracted an entire wing of the amber micromoth using chloroform. Under a fume hood, we placed the specimen in a sterile glass 35 mm Petri dish and we added enough volume of chloroform (trichloromethane) to cover the amber piece (approx. 3 ml). We continuously monitored the specimen to achieve a partial extraction (the most superficial region of the left upper wing). After 35 min, we removed the solvent and let the specimen air-dry. We took reflectance measures of the extracted wing and imaged it using electron microscopy. For scanning electron microscopy (SEM), we mounted one entire individual of each extant specimen on an aluminium stub, coated them with Au/Pd and viewed them with a FEG-SEM (FEI Quanta 200F, Netherlands) under an accelerating voltage of 10 kV and a working distance of 9.5 mm.

For transmission electron microscopy (TEM), we embedded scales following the protocol described in [26]. Briefly, scales were dehydrated using 100% ethanol (20 min) twice and infiltrated with 15, 50, 70 and 100% Epon (24 h each step). Infiltrated scales were placed in block moulds and polymerized at 60°C for 16 h. We cut thin (100 nm) cross sections using a Leica UC-6 ultramicrotome (Leica Microsystems, Germany). To image the fossil micropterigid, the piece of amber was directly trimmed and sectioned without further processing. The piece of amber containing the fossil springtail was embedded prior to sectioning, using LR White resin and sectioned after dipping the trimmed sample in an ice bath for 5 min. We stained the sections in Uranyless/lead citrate and examined them with a JEOL JEM 1010 (Jeol Ltd, Tokyo, Japan) transmission electron microscope.

2.2. Reflectance measures

We measured the reflectance of individual scales at normal incidence on their dorsal surface using a CRAIC AX10 UV–visible micro-spectrophotometer (CRAIC Technologies, Inc., USA). We obtained three measurements of each scale and sampled on average 15 scales per specimen. Polarization-dependent reflectance is characteristic of multilayered (one-dimensional) structures [27], two-dimensional photonic crystals [28] and diffraction gratings (e.g. scale ridges) [18]. Thus, to better understand the nature of the colour-producing nanostructure, we measured reflectance as a function of light polarization: we measured specular reflectance at two different polarizations, with incident light polarized parallel (TM) and perpendicular to scale ridges (TE).

2.3. Finite-difference time-domain modelling

To recognize the contribution of different structural components of scales to colour production, we used the finite-difference time-domain (FDTD) modelling method on idealized three-dimensional models. We built three-dimensional models using dimensions extracted from electron micrographs in a commercial Maxwell equation solver from Lumerical Solutions, Inc. For M. calthella, we created three models of scale crossribs.

Model 1 is a ‘simulation cell’ containing parallel ridges running longitudinally along scales, thereby creating concavities between them (electronic supplementary material, figure S1).

Model 2 is a crossrib grid, as seen on wing scales of Type I (figure 2d).

Figure 2.

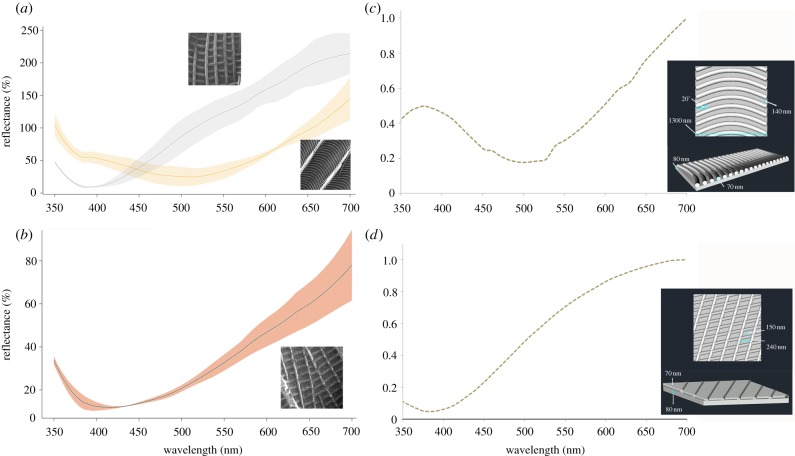
Reflectance spectra and optical simulation of micromoth scales. (a) Measured reflectance spectra of M. calthella Type I scales with crossribs arranged in square grids (grey line) and Type II long scales with herringbone crossribs (yellow line). (b) Reflectance spectra of wing scales from the fossil micropterigid, the scales display crossribs in a square grid pattern. Shaded areas illustrate 95% CI envelope around the average. (c) Optical modelling showing the reflectance spectra (for excitation at normal incidence) of simplified scale crossrib topography corresponding to a model of the herringbone array. (d) Optical model showing the simulated reflectance corresponding to the three-dimensional model of crossribs in square grid crossrib pattern. (Online version in colour.)

Model 3 is a crossrib herringbone pattern of wing scales Type II (figure 2c).

Additionally, we modelled a simple chitin thin film of 150 nm (the observed thickness of wing scales). For the springtail T. vulgaris, we created a three-dimensional model representing parallel pigmented ridges on the scales and a scale thickness of 450 nm (figure 4a).

Figure 4.

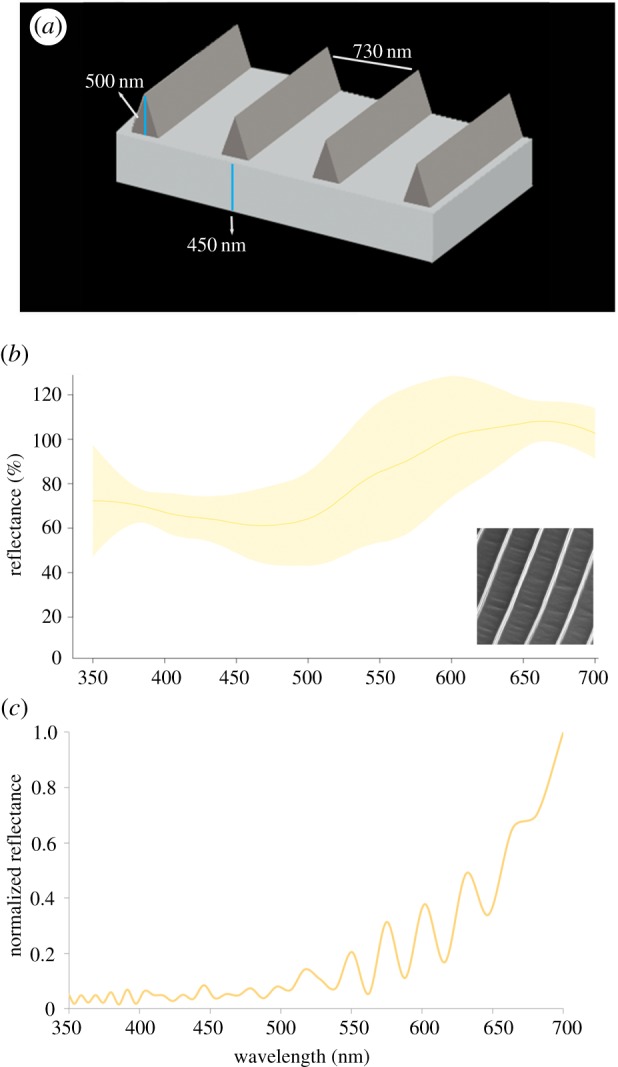
Reflectance of individual scales of T. vulgaris. (a) Three-dimensional model used for optical simulations showing the pigmented ridges (dark grey) overlaying the scale's surface (light grey). (b) Measured reflectance spectra of body golden scales under normally incident light, average reflectance (solid line) and 95% CI envelope (shaded area). (c) Reflectance spectra (for excitation at normal incidence) corresponding to simulation of the three-dimensional model. (Online version in colour.)

We used perfectly matched layers [29] to absorb electromagnetic waves from the top and bottom of the simulation cell and periodic boundary conditions on the sides to simulate infinite periodic structures. We used previously reported values of the refractive index of chitin [30] and melanin [31]. The light source covered a wavelength range of 350–700 nm and corresponded to an unpolarized plane wave at normal incidence unless otherwise indicated. To verify that diffraction is limited to zero order (as reported by [32]), we calculated the power scattered into the zero order of the grating structures using the grating order transmission script from the FDTD solver.

3. Results

3.1. Scale morphology and colour in the micromoth

Two types of scales cover both fore- and hind wings on M. calthella. Type I are short lamellar scales on the surface of the wing. Type II scales are elongated lamellar scales with pointed tips, situated on the margin of the wings (figure 1b). A third type, the piliform scales, cover legs, head, thorax and abdomen.

Figure 1.

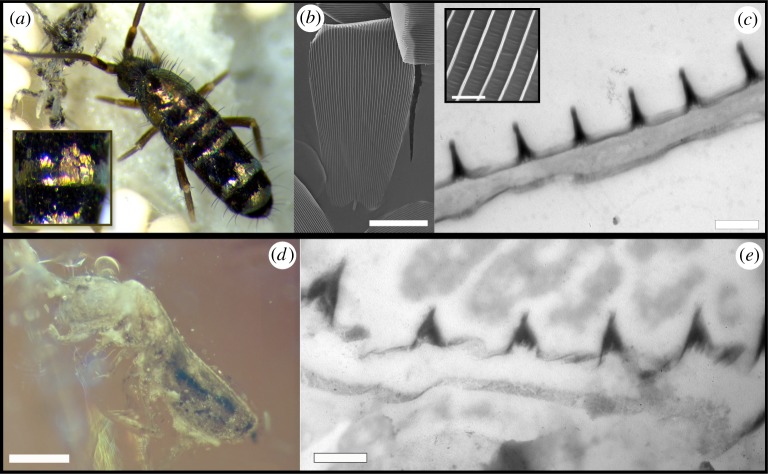
Morphology of extant and fossil micromoth wing scales. (a) M. calthella displaying golden coloration over its entire body. (b) Type I short scales covering the central portion of the wing surface (white dot) and Type II elongated lamellar scales located at the distal ends of the wing (black dot). (c) Topography of Type II scales showing herringbone pattern formed by crossribs extending across parallel ridges. (d) Type I scales have a topography consisting of a square grid of crossribs. (e) Fossil micropterigid from mid-Cretaceous Burmese amber. (f) Chloroform-extracted upper wing from the fossil micromoth showing golden coloration. (g) TEM of cross section of a wing scale from the fossil micromoth showing main ridges and crossribs on the scale. (h) SEM of extracted fossil scales showing crossribs forming a square grid pattern. Scale bars: (a,e) 500 µm, (b) 200 µm, (c,d,g,h) 1 µm, (f) 300 nm. (Online version in colour.)

Scales of the wings have two different surface topographies (figure 1c,d). Short lamellar scales have parallel ridges spaced 1400 nm (±30 nm) apart, which appear slanted on both sides along their long axis and extend 950 (±35) nm in height. The concave valleys between ridges are connected by small crossribs arranged in semi-rectangular grids (figure 1d). In long lamellar and piliform scales, the parallel ridges are also present, but the arrangement of crossribs resembles a herringbone pattern (figure 1c). All types of scales display an intense gold colour (figure 2a). Type II scales show a higher UV–violet chroma (350–430 nm) than the broadband silver–gold spectra of the Type I scales (figure 2a).

The wing scales’ optical properties were polarization-dependent. Two different colours are visible when scales were illuminated with a normal directional light source. Under TE-polarized light, the scales appeared golden, while under TM-polarized light, they appeared magenta indicating that some of the UV, purple and red light has undergone polarization (electronic supplementary material, figure S2a).

3.2. Scale morphology and colour in the Tomocerus springtail

The cuticle of T. vulgaris contains numerous lamellar scales aligned like roof tiles and arranged in alternating black and gold bands. Scales have round apical margins and decrease in size from the distal region. Golden scales have parallel ridges that protrude 500 (±12) nm in height and are spaced 730 (±28) nm apart. Unlike the scales of the moth, the springtail scales do not show prominent crossribs in between ridges, so the valleys between ridges appear smooth (figure 3b,c). The ridges contain melanin (figure 3c; and electronic supplementary material, figure S4). When seen under an optical microscope, some golden scales display patches with multicolour radial bands running parallel to the scale ridges (electronic supplementary material, figure S5a); when juxtaposed ridges cannot be seen individually, they combine into a broadband golden colour. This synthesis is demonstrated in the spectrum of individual scales, which show broadband reflectance along the visible lengths with a maximum peak at 660 nm; there is considerable variation in reflectance between scales (figure 4b).

Figure 3.

Morphology of scales of living and fossil springtails. (a) Image of T. vulgaris showing black and golden bands delineated by scales on the abdominal segments of the animal. (b) Scanning electron micrograph showing the lamellar scales with notable parallel ridges running longitudinally on the scale's surface. (c) Transmission electron micrograph of the cross section of a scale showing the electron-dense ridges, indicating the presence of pigment, overlaying a lower, unpigmented and solid lamina. Inset shows smooth valleys in between ridges. (d) Fossil Tomocerus springtail embedded in amber. (e) Transmission electron micrograph of the cross section of a fossil scale showing a similar morphology to the extant springtail scales. Scale bars: (b) 25 µm, (c) 500 nm, (d) 500 µm, (e) 400 nm. (Online version in colour.)

We observed the weak polarization-dependent reflection of springtail scales. When we observed the scales under TE-polarized normal incident light, the scales appear golden but under TM-polarized light, the yellow reflected light is extinguished and a substantial amount of violet light remains (electronic supplementary material, figure S5a).

3.3. Optical modelling of gold colour in moths and springtails

The simulated reflectance obtained from Model 1 (parallel ridges) did not match the measured reflectance of scales (electronic supplementary material, figure S1) of M. calthella, as the reflectance is highest in short wavelengths and decreases drastically towards longer wavelengths, opposite to the observed reflectance. This indicates that the parallel ridges are unlikely to explain the observed gold coloration of the scales. By contrast, an idealized rectangular grid of crossribs (Model 2; figure 2d) as seen in M. calthella Type I wing scales produces a reflectance spectrum with a maximum of 0.99 at 687 nm. The simulated spectrum is independent of light polarization and matches the measured reflectance of scales relatively well (figure 2). The simulation also shows that virtually all of the incident power goes into the zero-diffracted order (specular reflectance; electronic supplementary material, figure S3). The exclusive propagation of the zeroth order can be easily demonstrated for subwavelength gratings using the classic diffraction grating equation (electronic supplementary material, figure S3c).

A herringbone pattern of crossribs (Model 3; figure 2c) produced a reflectance spectrum with a small peak in the UV (380 nm) and a maximum peak at 700 nm. This spectrum matched the measured reflectance of scales with a herringbone pattern but showed some polarization dependence: under TE polarization, there were two distinctive peaks, one with a maximum at about 375 nm, the second broader and closer to 700 nm. The TM response was similar but the peak in short wavelengths was absent (electronic supplementary material, figure S2c). As with Type I scales, only the zeroth order is propagated (electronic supplementary material, figure S3). A simulated chitin (RI = 0.56) thin film of 150 nm (the average thickness we observe in wing scales of M. calthella) produces a reflectance spectrum that also corresponds to a golden coloration but with a much higher peak in the UV (electronic supplementary material, figure S2).

The model based on pigmented ridges on scales of T. vulgaris produced a highly oscillating reflectance spectrum that increases towards long wavelengths, consistent with a broadband gold colour (figure 4c). The simulated spectrum showed several intense peaks beyond 500 nm. The TE- and TM-polarized light models yielded only slightly different spectra, where the peaks are not observed in the TE-polarized response but only a smooth increase in reflectance towards longer wavelengths (electronic supplementary material, figure S5b). A modelled 450 nm thin film does not correspond to the observed scale reflectance (electronic supplementary material, figure S5b). The application of a standard diffraction grating analysis to these scale ridges demonstrates that the zeroth order is propagated but an evanescent first order is also diffracted (electronic supplementary material, figure S6).

3.4. Fossil scales

In the fossil micromoth, we observed wing scales with a similar structure to Type I scales of the extant micromoth. Scales of the central part of the wings are 150 (±8) nm thick and show ridges 550 (±30) nm high and separated by 2000 (±100) nm from one another (figure 1g). After the extraction from the amber matrix, we were able to observe the precise topography and colour of scales. The micromoth shows finer crossribs in a square grid pattern as observed in Type I scales of the extant micromoth (figure 1h). The crossribs have almost the same spacing (160 nm × 250 nm compared to 150 nm × 240 nm) as M. calthella. The scales on the extracted wing also showed a golden colour (figure 1f) and produced a reflectance spectrum similar to that of golden Type I scales (Figure 2b).

The fossil springtail has body scales varying in size similar to those of the living springtail. Many of the scales were loose and located just above the body (figure 3d). The scales were on average 400 (±2) nm thick and appeared to be solid laminae. Parallel ridges were 380 (±20) nm high and separated by 820 (±30) nm from each other. Just as in the extant Tomocerus, the scale ridges have higher electron density than the rest of the scale and thus likely contain melanin (figure 3e).

4. Discussion

We have shown that bright golden coloration of both species is produced largely by nanostructured scales that are virtually identical in extant and fossil specimens, despite the separation of nearly 100 Myr. As far as we know, we provide the first direct and objective measurement of preserved colours of fossils and showed that they match both the predicted colours and those of their extant counterparts. These data clearly demonstrate an early origin and strong stasis of structural colour in these arthropod clades.

Although their scales show corresponding longitudinal, parallel ridges, the scales of the micromoth differ in the presence of crossribs arranged in two different topographies. These two patterns of crossribs (observed in short and long wing scales) can explain the observed specular broadband reflection. However, our models show that the contribution of a thin film cannot be disregarded; the observed colour most likely arises through the interaction of diffractive scattering (from the periodicity in crossribs) and thin-film interference (from the scales' lower lamina acting as a UV–orange reflector).

The parallel ridges in moth scales do not contribute much to the broadband reflection, in contrast to the models previously reported for metallic scales of Micropterix aruncella by Zhang et al. [18]. Instead, our simulations support Brink et al. [32], who proposed that a zero-order diffraction process results from the regularly spaced crossribs (organized in a herringbone pattern), and this process is responsible for the metallic yellow and specular reflection by scales of the moth Trichoplusia orichalcea. The thickness of the crossribs in M. calthella is 70 nm and with an average grating period of 210 nm, a length scale in agreement with the conventions of multilayer interference and diffraction grating [33]. The parallel ridges, however, might produce most of the observed polarization-dependent reflectance.

We did not observe crossribs between the parallel ridges of springtail scales, but the ridges show dimensions and a grating period sufficient to act as a multilayer reflector producing broadband reflectance. The polarization effects observed on individual scales, however, were not successfully explained by longitudinal ridges. Even though submicrometre gratings (such as parallel cylinders [34]) sometimes display substantial polarization-dependent reflectance [35], this is not the case here and the cause of the polarized reflectance remains unclear.

4.1. Ancient origins of scale microstructures

We have shown that an amber micromoth and Tomoceridae show a dense layering of cuticular scales with parallel ridges. Furthermore, the micromoth scales have crossribs with an identical square grid pattern to that of scale spacing to extant Micropterigidae (this study) and to the herringbone crossribs producing the gold patches on the wings of the moth T. orichalcea [32]. Based on the perceived golden colour, measured reflectance and observed scale topography of the extracted scales, we can conclude that just as in living micromoths, fossil Micropterigidae produced broadband reflection and displayed golden wing coloration. Importantly, after being extracted from amber, scales still showed golden coloration despite erosion and absence of the parallel ridges (figures 1f and 2b). This provides further evidence that the diffraction grating formed by the crossribs, and not the parallel ridges, is the primary source of colour.

Cuticular scales in many hexapod arthropods (e.g. Archaeognatha, Zygentoma, Psocoptera, Culicidae, Lepidoptera, Collembola) also have parallel ridges [12] (this study) that frequently produce a satiny silver or golden appearance. These patterns reflect convergent evolution, suggesting similar selection pressures (perhaps sexual selection) across clades. Apart from producing colour, the scales’ microstructure might serve a variety of functions. For example, the parallel ridges could increase the fracture toughness of scales and thereby their resistance to crack propagation, similar to the reinforcement of insect wings by radiating veins [36]. Alternatively, by efficiently trapping and absorbing light and/or heat [37], the ridges may affect thermoregulation. Further studies are needed to elucidate the functional and evolutionary significance of structurally coloured insect scales. Our demonstration here that scale ultrastructure (SEM and TEM) and colour of amber specimens can be directly measured confirms that they are an important source of samples for these endeavours.

Data accessibility

Additional data can be found in the electronic supplementary material.

Competing interests

We declare we have no competing interests.

Funding

We received funding through grants FA9550-18-0477 and FWO G007117N.