Abstract
Personalized models of the gut microbiome are valuable for disease prevention and treatment. For this, one requires a mathematical model that predicts microbial community composition and the emergent behaviour of microbial communities. We seek a modelling strategy that can capture emergent behaviour when built from sets of universal individual interactions. Our investigation reveals that species–metabolite interaction (SMI) modelling is better able to capture emergent behaviour in community composition dynamics than direct species–species modelling. Using publicly available data, we examine the ability of species–species models and species–metabolite models to predict trio growth experiments from the outcomes of pair growth experiments. We compare quadratic species–species interaction models and quadratic SMI models and conclude that only species–metabolite models have the necessary complexity to explain a wide variety of interdependent growth outcomes. We also show that general species–species interaction models cannot match the patterns observed in community growth dynamics, whereas species–metabolite models can. We conclude that species–metabolite modelling will be important in the development of accurate, clinically useful models of microbial communities.
Keywords: microbiome, microbial ecology, pairwise modelling, metabolite-mediated modelling
1. Introduction
The microbial communities of the human body, collectively called the ‘human microbiome’, act on the host in a symbiotic relationship, which can have profound effects on health and disease [1–7]. This can be seen in the impact of bacterial colonization on the development of the adaptive immune system [7] as well as the many observed microbiome alterations in diseases ranging from multiple sclerosis [8] to colorectal cancer [4]. Importantly, these changes go beyond the presence or absence of a single species, but derive from more complex shifts in community composition. One prime example of this is the presence of pathogenic bacteria among the microbiota of disease-free asymptomatic individuals [7]. It is clearly not enough to identify and target a single species when attempting to explain the impact of the microbiome on host health. Instead, we must understand the interactions within a microbial community. These interactions determine whether a potentially pathogenic bacterium behaves as a beneficial, neutral or pathogenic member of the microbial community. Because these properties arise from the broader community, rather than the individual species, we call these emergent properties. Identifying and predicting microbial community composition and the resultant emergent properties are an important part of disease prevention, diagnosis and treatment in the burgeoning world of data-driven and individualized medicine.
In order to understand the composition of the microbiome, we must understand the dynamic process of growth, invasion and extinction which leads to a stable microbiome in healthy individuals, as well as the dynamic responses of the microbiome to changes in host health and diet. Such an understanding would give us the fundamental rules by which to alter the microbiome in an effective and stable way. We may then prevent disease and improve disease outcome by formulating these rules into a model of how microbiome composition changes in response to perturbation and use this model to design treatments to manipulate the microbiome.
The goal of this article is to identify a modelling framework for recapitulating community growth dynamics from sets of fundamental interactions. This modelling framework must be extensible, that is, it must allow us to directly combine models of smaller communities to create models of composite communities without discovering new parameters. As part of this goal, we would like this model to be ‘as simple as possible but no simpler’. These properties would allow us to generate a clinically useful dynamical model of the microbiome—one that can predict community composition dynamics from individualized information, such as initial composition and environmental perturbations due to treatment. It is worth noting that, in this setting, a single patient cannot, in general, provide enough data to accurately parameterize a purpose-built model. Instead, an individualized model needs to be built using the parameters generated from previous experiments or other datasets.
This contradiction can be overcome by using a modelling framework that infers whole community dynamics from simple, fundamental interactions that are assumed to be universal. Universal building block interactions could be used to construct purpose-built predictive dynamical models in an ‘n of 1’ manner, meaning built with data from a single patient [9,10]. It is as yet an open question as to the nature of these building blocks, and indeed if any can be found [11–15]. Here, we examine two popular modelling frameworks, species–species interaction (SSI) and species–metabolite interaction (SMI) models, and evaluate them using interdependent growth experiments of single species, pairs and trios from Friedman et al. [16]. These growth experiments were carried out on flat-bottomed plates with an experimental growth medium and serial dilution. We assume well-mixed, spatially homogeneous interactions and growth. We are, therefore, testing this on the simplest possible situation—pair and trio growth experiments, asking whether or not a modelling strategy can recapitulate the observed outcomes of these experiments.
Perhaps the most popular candidate for a set of fundamental modelling building blocks is the set of interactions between species of microbes [16–21]. We call such models SSI models. This strategy follows from microbial co-occurrence networks, which can be inferred from 16s rRNA gene or metagenomic sequencing data [22,23]. Focusing on SSIs is notably the strategy of the popular Lotka–Volterra (LV) model and its generalizations [16–19]. The LV model reproduces the dynamics of interacting species according the law of mass action [24,25]. Therefore, it is an appropriate model of direct interaction between species in a well-mixed and stable environment. The LV model and SSI models, in general, may, therefore, be useful when fitted to stable environments.
SSI models can capture some of the emergent behaviour of composition dynamics, but fail to capture higher order interactions which require more than two species [26,27]. We find, in general, that SSI models imply a strict condition on growth dynamics that is not observed in data. Furthermore, we find that the quadratic SSI model, usually called the generalized Lotka–Volterra (gLV) model, is not capable of recapitulating the entire set of pair and trio growth outcomes, using a single parameterization. Although the gLV model may be useful when fitted to whole communities [19–21], our work suggests that this model lacks the necessary complexity to be predictive when built from building blocks assumed to be universal.
Alternatively, the microbiome can be modelled by SMI models, which are constructed using the interactions of individual microbes with a shared metabolite pool [11,14,28–30]. SMI models follow from networks which include both microbiota and metabolites, which may be inferred from the literature [30] or from genome-scale metabolic networks [31]. In 2017, Momeni et al. [11] proved that SMI models are strictly more complex than SSI models. Like SSI models, SMI models may include arbitrary complexity in interaction terms; saturating kinetics (e.g. Michaelis–Menten or Hill kinetics) are a particularly common choice [28,29,32]. We show that a simpler quadratic species–metabolite interaction (QSMI) model can recapitulate the growth experiment outcomes of Friedman et al. [16] with a single parameterization.
It is worth noting explicitly that our work does not explore the accuracy of specific modelling tools [33–36], but instead examines whether the mathematical formulation of the model could ever be used to recapitulate the biological dynamics. A positive answer means that the mathematical form of the model is potentially useful, indicating promise for future endeavours; a negative answer indicates that the basic formulation of the model is inappropriate for predictive models of microbial communities. We investigate this question by inspecting to what extent models of simple communities can be used to build accurate models of larger communities. Precisely, we asked whether these models have the capacity for a parameterization that recapitulates the qualitative outcome of both pair and trio growth experiments.
2. Model definitions and background
2.1. Species–species interaction models
SSI models are dynamical models of the composition of a community of organisms i, j, k, etc., built by assuming a direct interaction between species. We model this by assuming that the population size of some species changes as the product of some per-organism growth rate and the current population size. This per-organism growth rate is then determined by interactions with other species.
SSI models are popular in ecology, including in the study of the microbiome, because they are computationally simple to create and analyse [16–18,20,37–39]. They are often fitted to large communities of microbiota, and interactions between species are assumed from this fitting [19,21]. This fitting implies a relationship between species, and these relationships are often classified as competitive, mutual or parasitic [40]. In the study of the human microbiome, discovering interactions between species is an active area of research [40], and automated tools [18,20,41] for the construction of SSI models are used [18,42–44]. It is, therefore, of interest to understand whether or not these interactions are preserved as the community changes, and so can be used as universal building blocks.
The general form of an SSI model is as follows:
| 2.1 |
where xi represents the biomass of organism i and the functions fi(xi) and hij(xi, xj), respectively, represent lone growth of organism i and the effect of organism j on the growth of organism i. Note that we allow complete generality, including the case of distinct functions hij for each pair i, j. It is convenient to write SSI models as a product of current population size xi and a per-organism growth rate . The number of interaction terms in an SSI model scales with the number of pairs of N microbes, and so scales as N2 − N.
In this article, we require that hij(xi, xj) satisfy hij(xi, 0) = 0 and that hij(xi, xj) do not switch sign (i.e. hij(xi, xj) ≥ 0 or hij(xi, xj) ≤ 0 for any non-negative population sizes xi, xj). This simply means that species j must be present to have an effect on the growth of i and that species j either increases the growth of species i or decreases this growth (or has no effect), regardless of the population sizes of species i and species j, while the strength of this effect may depend on population sizes.
2.1.1. The generalized Lotka–Volterra model
The simplest SSI model assumes direct, pairwise interactions proportional to species concentration, and is called the gLV model. In this model, the per-organism growth rate of a population changes proportionally to the size of each other population. Such changes may be positive or negative, indicating mutualism, parasitism, predation and competition.
The gLV model faithfully models direct pairwise interactions between agents (e.g. physically interacting organisms or reactants in an industrial reactor) under the assumption of mass action kinetics [24,25], but does not include any possible environmental variation in the interaction. It is, therefore, a fair representation of SSI in a controlled environment. Because of this, the gLV model is well studied and its parameters are often inferred from correlations seen in available 16S rRNA gene or metagenomic sequencing data [20,22]. Furthermore, the gLV model is commonly used to infer relationships between species and model the microbiome [18,37–39,42–44].
This model is typically written [16,27] as follows:
| 2.2 |
where ri > 0 is the intrinsic growth rate of the community of organism i, Ki > 0 is the carrying capacity of the environment for the organism and αij is the interaction between species. In this formulation, we may have αij > 0, meaning that the interaction between species i and j increases the growth of species i; αij < 0, meaning that the interaction between species i and j decreases the growth of species i; or αij = 0, meaning this interaction has no effect on the growth of species i. Although pairwise and linear in per-organism growth rate, this model can display a wide range of behaviours seen in nature, including invasion, competitive exclusion, coexistence and multi-stability (i.e. stable long-term outcomes that are dependent on initial community sizes even for fixed parameters) [27,45].
2.2. Species–metabolite interaction models
SMI models, also called metabolite (or resource)-mediated models, use the interaction of a microbe with an environmentally available metabolite as their fundamental interaction [14,28]. Similar to SSI models, we assume that the population size of some species changes as the product of some per-organism growth rate and the current population size. In SMI models, per-organism growth rate depends on available metabolites rather than a fixed carrying capacity. Additionally, metabolites are used and produced by individual species, in many cases as a by-product of some process involving another metabolite. Interactions between microbes are then possible through the manipulation of the shared metabolite pool.
SMI models have recently become of interest in the study of the human microbiome as data on the metabolite pool have become available [32,46,47]. Techniques for integrating species abundance and metabolomic data are now being developed to understand the mechanisms of microbiota organization [40,48].
We define an SMI model to be any model of the type
| 2.3 |
and
| 2.4 |
where n is the number of microbial species and m is the number of metabolites modelled, xi represents the biomass of organism i and yj is the concentration or biomass of metabolite j. As species and metabolites are added to the model, the number of terms could grow as large as NM + NM2, where N is the number of species and M is the number of metabolites included.
The simplest SMI model has competition for resources, leading to the well-known competitive exclusion principle, which states that an environment cannot support more species than it has food sources. However, metabolite-mediated models have more versatility, and do not need to hold to that principle [29].
Popular choices of interaction terms and include sigmoidal (i.e. saturating) kinetics, such as Michaelis–Menten or Hill kinetics [29,32], which have a diminishing change in effect as concentrations of metabolite increase and polynomial kinetics.
2.2.1. The quadratic species–metabolite interaction model.
The simplest SMI model is quadratic and includes the consumption and production of metabolites by microbes. This model assumes that the per-organism growth rate of the microbiota changes proportionally to the amount of each metabolite that it interacts with.
Similar to the gLV model, the QSMI model is a faithful model of interacting components of a well-mixed system [24,25], without allowing for any variation in environmental variables. In order to model stable growing communities, we include constant dilution of microbiota and metabolites. The QSMI model is the closest analogue among SMI models to the gLV model, as both are quadratic polynomials that faithfully model well-mixed interacting actors.
The general model for n species and m metabolites is as follows:
| 2.5 |
and
| 2.6 |
where a standard competition model would have κij = ψij ≥ 0. This model assumes that a microbial population’s growth rate depends on the availability of the resources being metabolized for growth, and these resources are depleted as this growth happens. The terms allow for the possibility that metabolites are produced as the by-products of some microbial metabolic pathway.
3. Results
Recall that our goal is a model of a composite community that can be built by directly combining models of smaller communities without discovering new parameters. We, therefore, analyse SSI, gLV, SMI and QSMI models with the goal of demonstrating which of these frameworks has the capacity for such a model. We find that gLV, and even general SSI models, cannot achieve this goal. However, the additional complexity of QSMI models is enough to allow a model which recapitulates the outcomes of pair and trio growth experiments from Friedman et al. [16] with a single parameter set. We conclude that SMI models show most promise in the building models of larger microbial communities.
3.1. Reversal of qualitative effects in general SSI models
One consequence of SSI models, regardless of the specific choices of interaction functions hij, is that they imply a classification of the interaction between two microbes. That is, the sign of hij(xi, xj) indicates if microbe j has a positive effect on microbe i (hij(xi, xj) > 0), or a negative effect on microbe i (hij(xi, xj) < 0); recall that hij(xi, xj) does not change sign for non-negative xi, xj. Generally, relationships are classified using both hij(xi, xj) and hji(xj, xi) [40]. SSI models allowed in some cases imply the sign of the combined effects of two microbes on a third. Precisely, if two microbes have the same qualitative effect on the growth of a third, SSI models imply that their combined effect should be qualitatively the same (although, of course, different in magnitude). For example, if hij(xi, xj) > 0 and hik(xi, xk) > 0, then clearly hij(xi, xj) + hik(xi, xk) > 0 for all non-negative xi, xj, xk, and we should observe increased growth in microbe i when in a trio with these two other species as compared with when grown alone.
We estimate the effects on the growth of microbes in pairs and trios by using the time-course data from Friedman et al. [16] to directly estimate the per-organism growth rate term of equation (2.1). We can, therefore, compare the effect on the per-organism growth rate of organism i of being grown with species j or species k with the effect of being grown with both j and k. We expect that if j and k both increase the per-organism growth rate of species i, then the combined effect of species j and k is to increase the per-organism growth rate of i, as in figure 1a. However, we do not always see this. In fact, we find that 11 of the 54 trios have at least one reversal of effect. Figure 1b shows an example in which two species have a positive effect on the growth of a third when grown in pairs, but when grown in a trio there is reduced growth in the third species. All of the implied pairwise relationships are shown in figure 2a. The list of all trios with pair and trio estimated effects can be found in qualitative.csv and the 11 reversals in reversals.csv at https://github.com/jdbrunner/model_comparisons.
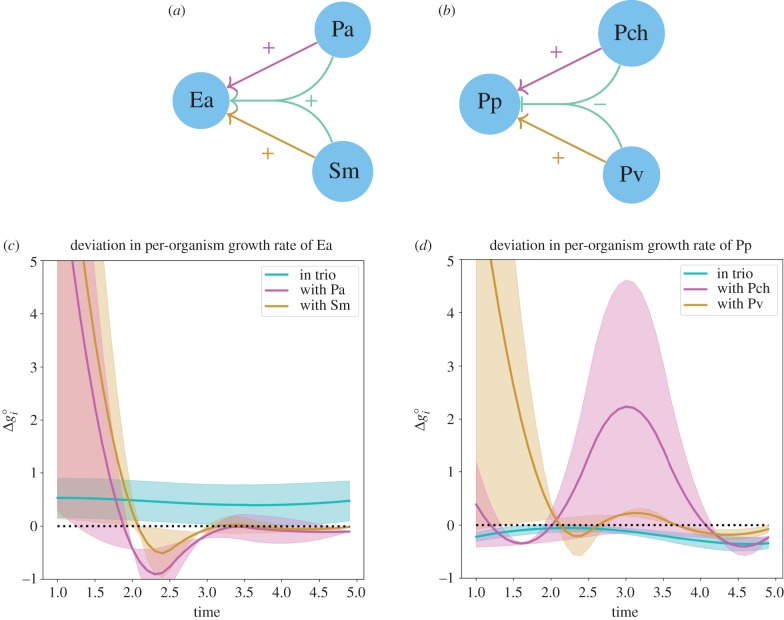
Figure 1.
(a,b) Arrows indicate influence on per-organism growth rate, as determined by deviation from growth rate when grown alone. Combined arrows represent the implied sum of influences. (c,d) Deviation in per-organism growth, estimated from time-course data reported in Friedman et al. [16] (dashed line showing no deviation). (a,c) Pa (Pseudomonas aurantiaca, ATCC 33663) and Sm (Serratia marcescens, ATCC 13880) both have positive effects on the growth of Ea (Enterobacter aerogenes, ATCC 13048) when grown in a pair. When these three are grown in a trio, the growth of Ea is promoted relative to its growth when grown alone. This trio makes sense in the context of SSI models. (b,d) Pch (Pseudomonas chlororaphis, ATCC 9446) and Pv (Pseudomonas veronii, ATCC 700474) both have positive effects on the growth of Pp (Pseudomonas putida, ATCC 12633) when grown in a pair. However, when these three are grown in a trio, the growth of Pp is reduced compared with its growth when grown alone. This trio does not make sense in the context of SSI models. (Online version in colour.)
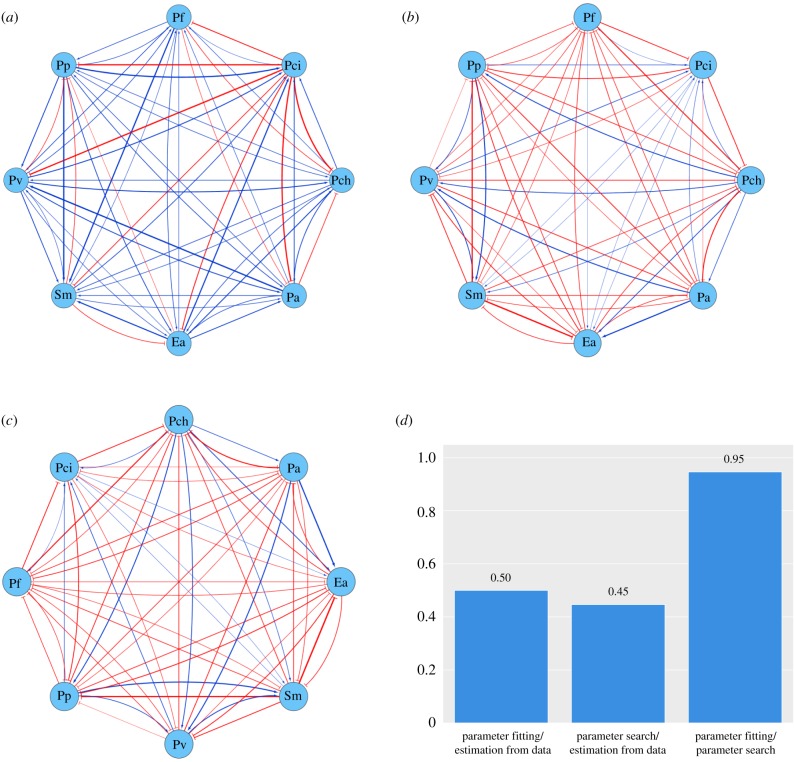
Figure 2.
(a) Relationships between microbial species as implied by estimating the average per-organism growth rate from growth data. (b) Relationships between microbial species as implied by parameters of the gLV model fitted to pair growth experiments. (c) Relationships between microbial species as implied by parameters of the gLV model from a computational search for parameters to explain all experimental outcomes. (a–c) Blue pointed arrows indicate a positive influence on growth; red T-shaped arrows indicate a negative influence; and nodes are labelled with the species used, as abbreviated in Friedman et al. [16] (Ea (Enterobacter aerogenes, ATCC 13048), Pa (Pseudomonas aurantiaca, ATCC 33663), Pch (Pseudomonas chlororaphis, ATCC 9446), Pci (Pseudomonas citronellolis, ATCC 13674), Pf (Pseudomonas fluorescens, ATCC 13525), Pp (Pseudomonas putida, ATCC 12633), Pv (Pseudomonas veronii, ATCC 700474) and Sm (Serratia marcescens, ATCC 13880)). (d) Proportion of edges in the network which match qualitatively (i.e. have the same sign) for each pair of networks from (a), (b) and (c). (Online version in colour.)
3.2. Parameter fitting in the gLV model
We showed above that SSI models, in general, will not match the dynamics of the growth experiments from Friedman et al. [16]. However, it may be that SSI models, including the popular gLV model, give the correct qualitative outcomes in terms of the survival and extinction over long time scales. In order to determine if this is the case, we fit a parameter set (the set of αij in equation (2.2)) to the time-course data of pair growth experiments, and ask if the model’s asymptotic stability correctly predicts the outcome of the trio growth experiments. That is, we take as a model’s ‘prediction’ the result of linear asymptotic stability analysis (see §4.2).
We find that parameters fitted to pair growth experiments explain trio experiments for half of all trios, meaning that the model correctly predicts survival/extinction outcomes for half of all trios. Note that Friedman et al. [16] report that parameters fitted to pairs lead to accurate predictions of 84% of trios. However, this was calculated using a different definition of model prediction (see §4.2 for details). Figure 2b shows the interactions implied by this parameter fitting. Interestingly, these interactions do not match the network of interactions determined using change in time-averaged growth, shown in figure 2a.
Additionally, we inspect long-time simulations of the gLV model for trios using parameters fitted to pair growth experiments in order to determine if oscillatory behaviour is predicted. We observe no oscillatory behaviour in the simulations.
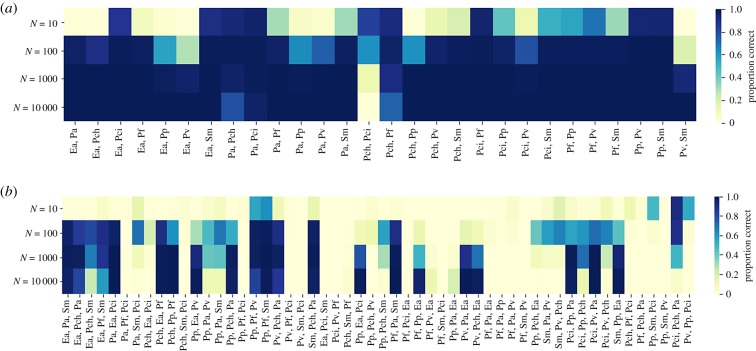
In order to determine if the model’s failure to recapitulate experiments is the result of random fluctuations in growth, we use a stochastic version of the gLV model with the same parameter set. We determine the likelihood of the observed experimental outcome according to the stochastic gLV model, and see in figure 3 that many outcomes have very low likelihood. Our experiment with the stochastic gLV model shows that random fluctuations in growth are unlikely to explain the failure of the LV model to match the growth experiment data.
Figure 3.
Monte Carlo experiments of the stochastic gLV model, with parameters fitted to a deterministic pair model. Darker colour indicates that a larger proportion of the 1000 trials used matched the observed growth experiment outcomes. Pairs and trios are abbreviated as in Friedman et al. [16]. (a). Pair experiments with population size 10, 100, 1000, 10 000. (b) Trio experiments with population size 10, 100, 1000, 10 000. (Online version in colour.)
3.3. The gLV model’s capacity to recapitulate experimental outcomes
We next determine if the gLV model has the capacity to recapitulate the outcome of the trio growth experiments while keeping a single parameter set that recapitulates pair experiment outcomes. We define the outcome of trio growth experiments in a binary fashion as reported by Friedman et al. [16], and similarly define the outcome of pair growth experiments based on the final time point of the experiment.
Finding a single set of αij such that the model correctly predicts every pair and trio growth experiment would imply that the gLV model has the necessary complexity to match the qualitative outcomes of the growth experiments, if not the dynamics. However, we are unable to find this parameter set using a computational search with a pseudo-genetic algorithm (see §4.4). Indeed, with the parameters resulting from this search, the model correctly predicts only 59% of the trio outcomes. This suggests that the set of parameters for the gLV model which cause it to recapitulate the growth experiments is small or empty.
To reduce the search space, we divide the growth experiments and attempt to find a parameter set for each group that predicts all of the qualitative outcomes of the growth experiments in that group. We use as groups all of the experiments involving one or both of some pair of microbial species (note that these groups are overlapping, but treated independently). For only nine of the 28 pairs, parameters could be found that explained each trio involving that pair. Figure 4 shows the proportion of trios involving a given pair which can be correctly predicted.
Figure 4.
Proportion of the explained trios as a result of each pair experiment, using the fitted interaction between that pair and varying the interactions involving the third member of a trio. For some pairs, parameters that explained the data are found for any third microbe, while for some pairs parameters cannot be found for most third microbes. Pairs and trios are abbreviated as in Friedman et al. [16]. (Online version in colour.)
3.4. A quadratic species–metabolite interaction model to recapitulate growth experiments
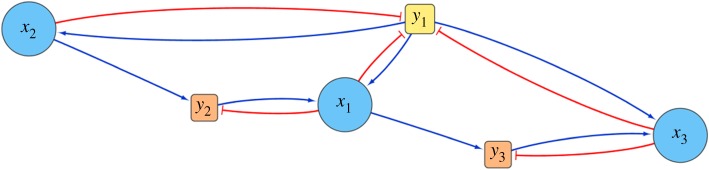
We ask if there exists a quadratic species–metabolite model which can match the qualitative outcomes of the growth experiments presented in Friedman et al. [16]. As with the gLV model, we seek a single parameter set that can explain the interdependent growth experiments. We can build such a model by assuming the existence of one initially present metabolite along with additional molecules produced by the microbiota. These additional molecules allow us to form cross-talk chains, as shown in figure 5. This model also demonstrates that the situation detailed by figure 1b can be modelled by a QSMI model, using the mechanism of figure 5 with y3 acting instead as a poison to reduce the growth of x3.
Figure 5.
Network representation of a cross-feeding chain in which metabolism of y1 by x2 produces a by-product which x1 can metabolize for growth, and this process, in turn, produces a by-product which x3 can metabolize for growth. Note that the production of y2 by x2 only occurs when y1 is present, and the production of y3 by x1 only occurs when y2 is present, so that this chain does not have an effect on other trios involving a subset of three species in the chain. For simplicity, this dependency is not shown, nor is it included in figure 6. (Online version in colour.)
To recapitulate the pair experiments of Friedman et al. [16], we need to add 19 cross-feeding molecules, bringing the total number of metabolites to 20. The pair models lead to trios for which we need to add cross-feeding chains to prevent a single extinction for four trios and prevent two extinctions for one trio. We also must implement cross-poisoning to cause a single extinction for 19 trios. For one trio, we need to adjust the model to cause one extinction and prevent another.
In total, we have a single model of eight microbes and 72 molecules which are part of 19 pair-specific and 25 trio-specific cross-talk pathways. This model, when restricted by initial state to only two or three microbial species, recapitulates the outcomes of the growth experiments.
Figure 6 shows the network of metabolite-mediated interactions of the QSMI model. In this model, every microbe grows on a single metabolite, labelled y1, and various pair or trio cross-talk chains alter that growth by providing extra resources (cross-feeding) or inhibiting a microbe’s growth (cross-poisoning).
Figure 6.
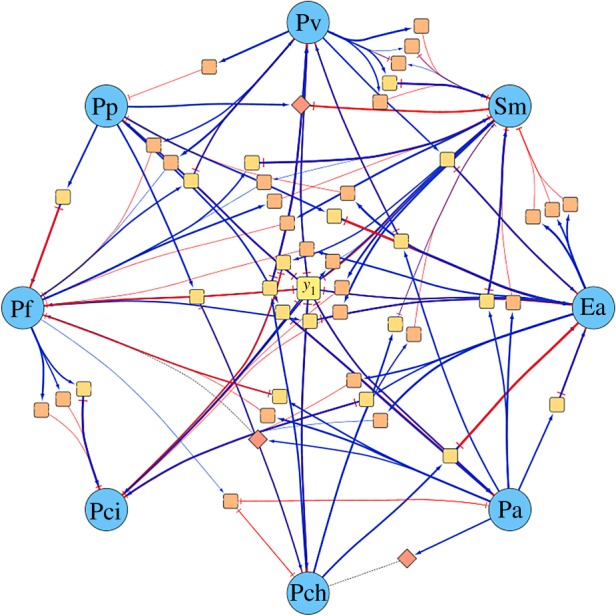
Schematic of the full QSMI model that recapitulates growth experimental outcomes. This model contains the eight microbes grown in Friedman et al. [16], as well as 69 metabolites (squares) and three signalling molecules (diamonds). Blue pointed arrows from metabolite to microbe indicate that the microbe uses that metabolite to grow, while red T-shaped arrows from metabolite to microbe indicate that the metabolite inhibits the growth of the microbe. Blue pointed arrows from microbe to metabolite indicate production, and red T-shaped arrows from microbe to metabolite indicate consumption or degradation. To match qualitative outcomes of growth experiments in Friedman et al. [16], the model is run with only y1 initially present, and initial microbial populations according to the growth experiment. (Online version in colour.)
3.5. Complexity of the quadratic species–metabolite interaction model that recapitulates trio experiments
We wish to estimate the complexity of a QSMI model that explains a given set of growth experiments. To do this, we reduce our set of allowable QSMI models to those that only include direct cross-talk as well as simple cross-talk chains such as that shown in figure 5 and detailed in equations (4.11) and (4.12). This restriction allows us to automate the construction of a model that explains all but two of the trio experiments from Friedman et al. [16] using only 17 metabolites (this network can be viewed in min_met_network.csv at https://github.com/jdbrunner/model_comparisons).
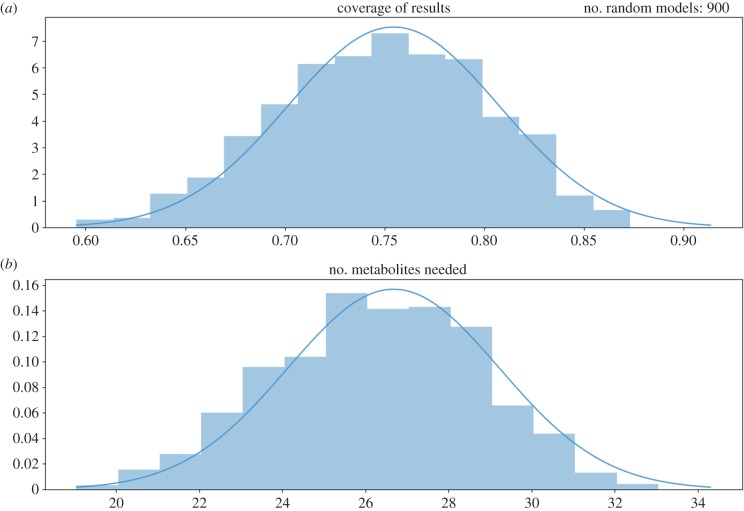
We next estimate the required complexity of a general QSMI model that recapitulates experiments. For a randomly generated set of growth outcomes, we determine how well an automatically generated QSMI model can recapitulate these outcomes, and how complex such a model must be. We hope that the best model generated for a given outcome set is of reasonable accuracy, explaining most or all of the dataset, and complexity, requiring not too many metabolites. Figure 7 shows a histogram of the coverage of (i.e. what proportion of a set of outcomes is recapitulated) and the number of metabolites needed in the best model we generate for each of 900 randomly generated ‘experimental’ outcomes. The coverage achieved follows roughly a normal distribution with mean 0.754 and standard deviation 0.053, while the number of metabolites also follows roughly a normal distribution with mean 26.67 and standard deviation 2.54. This experiment demonstrates that QSMI models have the power to explain the majority of outcomes in a dataset with a reasonable number of metabolites, and without pathways more complex than the one shown in figure 5.
Figure 7.
Histogram of (a) coverage of randomized experimental outcome and (b) number of necessary metabolites in an automatically generated QSMI model. Models are built to recapitulate randomly generated experimental growth outcomes and maximize prediction accuracy while minimizing the number of metabolites. (Online version in colour.)
4. Methods
4.1. Growth data used
We use data from growth experiments published in Friedman et al. [16]. These experiments were carried out in flat-bottomed plates and grown in 48 h growth–dilution cycles. Cell density was assessed using optical density (OD), and relative abundance was assessed by plating and colony counting. For this study, we use units of OD computed by multiplying total culture OD by a fraction of each species. Growth data are available in friedman_et_al_data at https://github.com/jdbrunner/model_comparisons. For single microbe and pair growth experiments, Friedman et al. [16] provided intermediate time-course data. However, for trio growth experiments, only beginning and endpoints were reported, and so used here.
4.2. Defining model prediction
We define model prediction by the behaviour of the model as the time approaches infinity for any positive initial conditions. We compare this model prediction with experimentally observed extinction and coexistence, as reported in Friedman et al. [16].
All models that we consider are ordinary differential equations (ODEs), with the exception of a stochastic analogue to an ODE model. For an ODE model, we define a model’s outcome from the asymptotic stability of equilibrium, using standard methods (see for example [27]). That is, we write any ODE in the form
| 4.1 |
where x and f may be vector valued, and consider a point in the phase-space x* the ‘outcome’ or ‘prediction’ of the model if
| 4.2 |
and some solutions to equation (4.1) approach x* as t → ∞. Note that it is possible for there to exist more than one such x* for a single model (and parameter set), a condition known as bi-stability [27]. In this case, we consider all such x* to be model outcomes.
For details on this process, see electronic supplementary material, appendix A.1.
In Friedman et al. [16], model outcome is defined using simulation up to the end time of the experiments. The discrepancy between reported accuracy of the gLV model in that article and the current one is a result of slow convergence to stable equilibrium.
4.3. Qualitative effect on growth
We use pair growth experiments to determine the qualitative effect of one species on another. That is, we find the difference between the time-averaged per-organism growth rate of species i alone and in various pairs or trios.
We label the difference between per-organism growth rate in species i when grown in some set of species and per-organism growth rate in species i when grown alone as
where, for example, ° is j for species i grown in a pair with species i, and · is j, k for species i grown in a trio with j and k. Then, we observe that the additivity of equation (2.1) and the assumption that the functions hij, hik do not switch sign imply that if the microbiota grows according to equation (2.1), then
| 4.3 |
and
| 4.4 |
In other words, if two species have the same qualitative effect on the growth of a third, their combination will have that same qualitative effect. We simply compare these quantities in the data to find examples for which this does not hold. We call such an instance a ‘reversal’. Note that the serial dilution of the growth experiment means that a reversal of effect is not the result of crowding.
4.4. Generalized Lotka–Volterra parameter fitting
We use nonlinear least-squares procedures to fit parameters of the gLV model to the time-course experimental data. Additionally, we use a pseudo-genetic algorithm to attempt to find a single set of parameters {αij} which cause the model to recapitulate the growth experiment outcomes.
We fit a set of parameters from equation (2.2) to the time-course data. For individual growth parameters (ri, Ki in equation (2.2)), we use individual growth data and nonlinear least squares (implemented in python package scipy.optimize [49]) to fit a logistic curve. We fit the parameters αij to pair growth experiment data. We again use nonlinear least squares (implemented in python package scipy.optimize [49]), computing solution curves for a given parameter set numerically in order to compute residuals. The parameters fitted, along with code to reproduce the fitting, can be found in the electronic supplementary material.
We also ask whether or not the model has the capacity to explain all of the growth experiment outcomes with a single parameter set by searching for such a parameter set. Note that the interdependence of the trios means that this is a stricter condition than the existence of a parameter set for each trio which correctly predicts the experimental outcome of just that trio, and also stricter than the existence of a single such parameter set for each trio and involved pairs.
We take advantage of qualitative analysis, detailed in electronic supplementary material, appendix A, to search for parameter values that explain all of the outcomes observed. To perform this search, we begin with parameter sets that explain 12 independent trios. We then use a pseudo-genetic algorithm, assessing the fitness of the parameter set by the magnitude of the eigenvalues of the various Jacobian matrices whose signs do not match the eigenvalues that would result in a model matching the observed data, to search for a parameter set which allows the model to recapitulate the experiments. In this algorithm, genes can be mutated with a continuous random variable, whereas in a standard genetic algorithm genes are generally taken over a discrete set [50]; see the electronic supplementary material for further explanation, the code and the parameters.
We next relax the search condition by attempting to find for each pair of species parameters that gave an accurate prediction of all the trios they are involved in without changing the interaction parameters between that pair. This is done in order to identify pairwise relationships that are consistent across different trios. To do this for a pair of species i, j, we first fix αij and αji as fitted to time-course data. Then, for each other species k, we seek αik, αjk, αki, αkj so that model asymptotic stability matches the observed outcome of the experiments. We again use a pseudo-genetic algorithm, taking advantage of some partial conditions for equilibrium stability given at https://github.com/jdbrunner/model_comparisons. We record for each pair the proportion of trios for which parameters can be found to explain the experimental outcomes. The result is shown in figure 4.
4.5. The stochastic generalized Lotka–Volterra model
We choose the stochastic process which has the property that as we increase the concentration of organisms modelled, we recover the deterministic gLV model [51]. This property means that, rather than simply ‘adding noise’ to the model, we have chosen the closest fully stochastic analogue to the model, which is also the standard choice of stochastic model for interactions between agents under the assumption of mass action kinetics [52–54]. See electronic supplementary material, appendix A.4, for details of the model.
We produce (exact) realizations of the stochastic process using Gillespie’s algorithm [55] (sometimes called the stochastic simulation algorithm), as shown in figure 8. Additionally, we perform Monte Carlo experiments to estimate the probability (±6%) of each observed outcome according to the stochastic model with parameters fitted to pairs. We use the τ-leaping algorithm from Anderson [56] for efficiency.
Figure 8.
(a,b) Exact realizations of the stochastic gLV model, with parameters fitted to a deterministic pair model for species Ea, Pa and Pch (as abbreviated in Friedman et al. [16]). Note that, in realization (b), we have an extinction event that is not implied by the deterministic model (shown dashed). (Online version in colour.)
4.6. Construction of QSMI Model
Starting with parameters given by models of individual growth, we can arrive at every possible pair outcome by assuming there are at most external metabolites used for growth, but only 1 is initially present. We build this model by adding cross-talk molecules to models of growth on a single nutrient. In our model, these cross-talk molecules are produced by one microbe and have some effect on another.
We do this systematically by adjusting pair or trio models separately. This means that we add a cross-talk pathway to a pair model so that it recapitulates the correct growth experiment outcome, and does so in such a way that the added cross-talk pathway will have no effect on any other pair, and likewise with trios. That is, any cross-talk pathway must require all members of the pair or trio to be present to have some effect. This restriction makes the construction systematic, but is not necessary.
We begin with a model of growth,
| 4.5 |
and
| 4.6 |
For each pair model, if the initial model formed simply by including both microbes does not match growth outcome, we add a metabolite to the model. Restricted to a pair, the model is then
| 4.7 |
| 4.8 |
| 4.9 |
| 4.10 |
where y2 serves as the cross-talk molecule; in this example produced by x2 and having some effect (determined by ψ12) on x1.
To adjust the model to account for trio growth experiments, we add trio-specific cross-talk pathways. Precisely, given a model of organisms x1, x2, x3 (assuming without loss of generality that x1 survives) which may already include pairwise cross-talk and cross-poisoning, we can introduce a trio-specific chain by introducing two new metabolites such that
| 4.11 |
and
| 4.12 |
where has some effect on x3. These equations model a situation in which is produced as a metabolic by-product of x1 metabolizing y1, and likewise is produced as a metabolic by-product of x2 metabolizing . Then, x1 and x2 must both be present for to be produced. This chain is specific to this trio as long as only has an effect on x3.
We must also for one trio change the model so that it predicts coexistence of the entire trio rather than two extinctions. This requires a signalling molecule and a positive feedback loop of cross-feeding. This model, therefore, needs three additional molecules.
Finally, there is one trio for which we need the model to predict one lone survivor instead of a different lone survivor. To do this, we use two signalling molecules that are never degraded or consumed, and cause one species to poison the other two species with a third molecule.
The complete model is detailed in the electronic supplementary material, and a schematic of the interactions in the model is shown in figure 6.
4.7. Estimation of quadratic species–metabolite interaction model complexity
To estimate QSMI model complexity, we reduce our set of allowed models to only those with one initial available metabolite and direct cross-talk between pairs as well as cross-talk chains as detailed in equations (4.11) and (4.12), allowing us to automatically generate a model which explains a large proportion (98% in the case of the data from Friedman et al. [16]—all trios beside the last two detailed above) of a set of pair and trio growth experimental outcomes. We attempt to maximize this coverage and minimize the number of molecules needed in order to estimate the complexity of QSMI models. In our construction, the number of additional pathways added is ultimately a function of the microbes' relative ability to metabolize the initial available metabolite. This observation allows us to optimize over the set of possible orders of these metabolic parameters.
We generate random trio and growth experiment outcomes by permuting the real experimental outcomes. In this way, we preserve the number of each possible qualitative outcome (i.e. coexistence, extinction and double extinction). We then generate the best possible model for each random outcome set.
5. Discussion
We would like to build a clinically useful model of the dynamics of the human microbiome. For this, we seek a modelling framework that infers community dynamics from fundamental interactions, so that data and discoveries from across studies can be incorporated into an individualized model using these interactions as building blocks. We, therefore, need a model that can be built without reparameterization and that can capture emergent properties of microbial community composition dynamics.
As a representative example of species–species modelling, we inspect the gLV model. Using this model, we see disagreement between trio growth experiments and model prediction based on pairwise fitted parameters, and we are unable to find a set of parameters which allow the model to recapitulate the qualitative outcomes of the interdependent growth experiments. This suggests that the gLV model has a high sensitivity to fitted parameters, even for qualitative results, and that the space of parameters which fit the entire set of qualitative growth experiments is small or does not exist.
In species–metabolite modelling, dynamics are modelled by the interactions of individual microbes with a shared metabolite pool. We find that this framework has the additional complexity necessary for capturing emergent behaviour through cross-feeding and cross-poisoning. We show that this framework does not adhere to the additive interaction assumption, and that a model can be found to fit interdependent growth data. We then use the mechanisms of cross-feeding and cross-poisoning to fit various competitive configurations to complex outcomes.
It is worth noting that SMI models are inherently more complex than SSI models, as proved by Momeni et al. [11]. Our result, which relates SSI and SMI modelling to experimental growth data, complements the conclusion of Momeni et al. [11] by showing that the dynamical complexity is indeed necessary for accurate modelling. The appeal of SMI models, however, goes beyond mere complexity. SMI models may provide better fundamental building blocks for inferring community dynamics because they better reflect the real biological building blocks of microbial community interactions. This allows us to build models for larger communities by simply combining models for smaller communities. In contrast, one might add higher order terms to an SSI model to account for interactions between more than two species. However, this approach requires that a model built for a large community has little relationship with models of sub-communities. Such an extension of SSI models, therefore, does not achieve our goal of individualized modelling.
Our work focuses on establishing the capacity of different modelling frameworks for recapitulating the emergent behaviour of relatively simple microbial communities. While this work provides an important starting point, it is nonetheless limited in applicability. For instance, it is fair to say that the procedure to build the QSMI model for the growth experiments in Friedman et al. [16] is not in the spirit of building a model in an individualized manner. In practice, cross-feeding and other interactions of the microbe with the metabolite pool might be discovered from, for example, metabolic modelling, and SMI models may be built from genome-scale metabolic models of individual microbial species [31,57,58]. In this way, high-throughput sequencing technology can be leveraged to better understand microbiome composition. Developing methods to build clinically useful species–metabolite models with available data remains an open and interesting area of research.
In addition, we investigate the complexity of the QSMI model by minimizing the number of metabolites needed to match most of a set of growth experiment outcomes. It would also be interesting to build the QSMI model with further ‘reality’ criteria in mind, such as using the minimum number of cross-talk pathways. In future work, we plan to establish a systematic method to build a QSMI model which matches some set of outcomes exactly and satisfies various reality conditions. It is also of interest to establish easily checkable conditions on a set of growth experiment outcomes which decide whether or not there exists a QSMI model which can recapitulate the experiments. While these questions are very interesting, they are fundamentally mathematical considerations and outside of the scope of this article, which attempts to determine model usefulness in the context of real data.
SMI models provide an intermediate level of complexity between fully detailed genome-scale models and fully simplified models such as SSI models. This level of complexity holds promise for individualized predictions in medicine.
Supplementary Material
Supplementary Material
Acknowledgements
We thank Dr Jonathan Friedman for his correspondence regarding the growth experimental data used in this article.
Data accessibility
Code for parameter estimation and searching, parameter values and a complete description of the QSMI model, as well as code for the stochastic experiments, is available at https://github.com/jdbrunner/model_comparisons.
Authors' contributions
J.D.B. carried out computational, statistical and mathematical analysis, and drafted the manuscript. N.C. directed the goals of the analysis, and critically revised the manuscript. Both authors gave final approval for publication and agree to be held accountable for the work performed herein.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by funding from the Andersen Family Foundation, National Cancer Institute grant no. R01 CA179243 and the Center for Individualized Medicine, Mayo Clinic.
References
- 1.Braundmeier AG. et al. 2015. Individualized medicine and the microbiome in reproductive tract. Front. Physiol. 6, 97 ( 10.3389/fphys.2015.00097) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Calcinotto A. et al. 2018. Microbiota-driven interleukin-17-producing cells and eosinophils synergize to accelerate multiple myeloma progression. Nat. Commun. 9, 4832 ( 10.1038/s41467-018-07305-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Walsh DM, Mert I, Chen J, Hou X, Weroha SJ, Chia N, Nelson H, Mariani A, Walther-Antonio MR. 2019. The role of microbiota in human reproductive tract cancers. Am. J. Phys. Anthropol. 168, 260–261. [Google Scholar]
- 4.Hale VL. et al. 2018. Distinct microbes, metabolites, and ecologies define the microbiome in deficient and proficient mismatch repair colorectal cancers. Genome Med. 10, 78 ( 10.1186/s13073-018-0586-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Flemer B, Lynch DB, Brown JM, Jeffery IB, Ryan FJ, Claesson MJ, O’Riordain M, Shanahan F, O’Toole PW. 2017. Tumour-associated and non-tumour-associated microbiota in colorectal cancer. Gut 66, 633–643. ( 10.1136/gutjnl-2015-309595) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ng KM. et al. 2013. Microbiota-liberated host sugars facilitate post-antibiotic expansion of enteric pathogens. Nature 502, 96–99. ( 10.1038/nature12503) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Round JL, Mazmanian SK. 2009. The gut microbiota shapes intestinal immune responses during health and disease. Nat. Rev. Immunol. 9, 313–323. ( 10.1038/nri2515) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen J. et al. 2016. Multiple sclerosis patients have a distinct gut microbiota compared to healthy controls. Sci. Rep. 6, 28484 ( 10.1038/srep28484) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guyatt GH, Keller JL, Jaeschke R, Rosenbloom D, Adachi JD, Newhouse MT. 1990. The n-of-1 randomized controlled trial: clinical usefulness: our three-year experience. Ann. Intern. Med. 112, 293–299. ( 10.7326/0003-4819-112-4-293) [DOI] [PubMed] [Google Scholar]
- 10.Lillie EO, Patay B, Diamant J, Issell B, Topol EJ, Schork NJ. 2011. The n-of-1 clinical trial: the ultimate strategy for individualizing medicine? Per. Med. 8, 161–173. ( 10.2217/pme.11.7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Momeni B, Xie L, Shou W. 2017. Lotka–Volterra pairwise modeling fails to capture diverse pairwise microbial interactions. eLife 6, e25051 ( 10.7554/eLife.25051) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang T, Goyal A, Dubinkina V, Maslov S. 2019. Evidence for a multi-level trophic organization of the human gut microbiome. (https://www.biorxiv.org/content/10.1101/603365v2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Erez A, Lopez JG, Weiner B, Meir Y, Wingreen NS. 2019 Nutrient levels and trade-offs control diversity in a model seasonal ecosystem. (https://arxiv.org/abs/1902.09039. )
- 14.Goyal A, Maslov S. 2018. Diversity, stability, and reproducibility in stochastically assembled microbial ecosystems. Phys. Rev. Lett. 120, 158102 ( 10.1103/PhysRevLett.120.158102) [DOI] [PubMed] [Google Scholar]
- 15.Goyal A, Dubinkina V, Maslov S. 2017. Microbial community structure predicted by the stable marriage problem. (http://arxiv.org/abs/quant-ph/1712.06042).
- 16.Friedman J, Higgins LM, Gore J. 2017. Community structure follows simple assembly rules in microbial microcosms. Nat. Ecol. Evol. 1, 0109 ( 10.1038/s41559-017-0109) [DOI] [PubMed] [Google Scholar]
- 17.Mounier J, Monnet C, Vallaeys T, Arditi R, Sarthou AS, Hélias A, Irlinger F. 2008. Microbial interactions within a cheese microbial community. Appl. Environ. Microbiol. 74, 172–181. ( 10.1128/AEM.01338-07) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fisher CK, Mehta P. 2014. Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. PLoS ONE 9, e102451 ( 10.1371/journal.pone.0102451) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stein RR, Bucci V, Toussaint NC, Buffie CG, Rätsch G, Pamer EG, Sander C, Xavier JB. 2013. Ecological modeling from time-series inference: insight into dynamics and stability of intestinal microbiota. PLoS Comput. Biol. 9, e1003388 ( 10.1371/journal.pcbi.1003388) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuntal BK, Gadgil C, Mande SS. 2019. Web-gLV: a web based platform for Lotka–Volterra based modeling and simulation of microbial populations. Front. Microbiol. 10, 288 ( 10.3389/fmicb.2019.00288) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Angulo MT, Moog CH, Liu YY. 2019. A theoretical framework for controlling complex microbial communities. Nat. Commun. 10, 1045 ( 10.1038/s41467-019-08890-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Faust K, Raes J. 2012. Microbial interactions: from networks to models. Nat. Rev. Microbiol. 10, 538–550. ( 10.1038/nrmicro2832) [DOI] [PubMed] [Google Scholar]
- 23.Müller H, Mancuso F. 2008. Identification and analysis of co-occurrence networks with NetCutter. PLoS ONE 3, 1–16. ( 10.1371/journal.pone.0003178) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Feinberg M. 1979. Lectures on Chemical Reaction Networks. See https://crnt.osu.edu/LecturesOnReactionNetworks.
- 25.Yu PY, Craciun G. 2018. Mathematical analysis of chemical reaction systems. Isr. J. Chem. 58, 733–741. ( 10.1002/ijch.v58.6-7) [DOI] [Google Scholar]
- 26.Billick I, Case TJ. 1994. Higher order interactions in ecological communities: what are they and how can they be detected? Ecology 75, 1529–1543. ( 10.2307/1939614) [DOI] [Google Scholar]
- 27.Edelstein-Keshet L. 2005. Mathematical models in biology. Classics in Applied Mathematics, vol. 46 Philadelphia, PA: SIAM. [Google Scholar]
- 28.Niehaus L. et al. 2019. Microbial coexistence through chemical-mediated interactions. Nat. Commun. 10, 2052 ( 10.1038/s41467-019-10062-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Posfai A, Taillefumier T, Wingreen NS. 2017. Metabolic trade-offs promote diversity in a model ecosystem. Phys. Rev. Lett. 118, 028103 ( 10.1103/PhysRevLett.118.028103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sung J, Kim S, Cabatbat JJT, Jang S, Jin YS, Jung GY, Chia N, Kim PJ. 2017. Global metabolic interaction network of the human gut microbiota for context-specific community-scale analysis. Nat. Commun. 8, 15393 ( 10.1038/ncomms15393) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chan SHJ, Simons MN, Maranas CD. 2017. SteadyCom: predicting microbial abundances while ensuring community stability. PLoS Comput. Biol. 13, 1–25. ( 10.1371/journal.pcbi.1005539) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hart SFM, Skelding D, Waite AJ, Burton JC, Shou W. 2019. High-throughput quantification of microbial birth and death dynamics using fluorescence microscopy. Quant. Biol. 7, 69–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Diener C, Gibbons SM, Resendis-Antonio O. 2019. MICOM: metagenome-scale modeling to infer metabolic interactions in the gut microbiota. (https://www.biorxiv.org/content/10.1101/361907v3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Henry CS, DeJongh M, Best AA, Frybarger PM, Linsay B, Stevens RL. 2010. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 28, 977–982. ( 10.1038/nbt.1672) [DOI] [PubMed] [Google Scholar]
- 35.Ebrahim A, Lerman JA, Palsson BO, Hyduke DR. 2013. COBRApy: constraints-based reconstruction and analysis for python. BMC Syst. Biol. 7, 74 ( 10.1186/1752-0509-7-74) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Röttjers L, Faust K. 2018. From hairballs to hypotheses—biological insights from microbial networks. FEMS Microbiol. Rev. 42, 761–780. ( 10.1093/femsre/fuy030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mougi A, Kondoh M. 2012. Diversity of interaction types and ecological community stability. Science 337, 349–351. ( 10.1126/science.1220529) [DOI] [PubMed] [Google Scholar]
- 38.Thébault E, Fontaine C. 2010. Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856. ( 10.1126/science.1188321) [DOI] [PubMed] [Google Scholar]
- 39.Allesina S, Tang S. 2012. Stability criteria for complex ecosystems. Nature 483, 205–208. ( 10.1038/nature10832) [DOI] [PubMed] [Google Scholar]
- 40.Dohlman AB, Shen X. 2019. Mapping the microbial interactome: statistical and experimental approaches for microbiome network inference. Exp. Biol. Med. 244, 445–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shaw GTW, Pao YY, Wang D. 2016. MetaMIS: a metagenomic microbial interaction simulator based on microbial community profiles. BMC Bioinf. 17, 488 ( 10.1186/s12859-016-1359-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chen WY, Ng TH, Wu JH, Chen JW, Wang HC. 2017. Microbiome dynamics in a shrimp grow-out pond with possible outbreak of acute hepatopancreatic necrosis disease. Sci. Rep. 7, 9395 ( 10.1038/s41598-017-09923-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shaw GTW, Liu AC, Weng CY, Chou CY, Wang D. 2017. Inferring microbial interactions in thermophilic and mesophilic anaerobic digestion of hog waste. PloS ONE 12, e0181395 ( 10.1371/journal.pone.0181395) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Džunková M. et al. 2018. Oxidative stress in the oral cavity is driven by individual-specific bacterial communities. NPJ Biofilms Microbiomes 4, 29 ( 10.1038/s41522-018-0072-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gause GF. 1934. The struggle for existence. Baltimore, MD: Williams & Wilkins. [Google Scholar]
- 46.Watrous J. et al. 2012. Mass spectral molecular networking of living microbial colonies. Proc. Natl Acad. Sci. USA 109, E1743–E1752. ( 10.1073/pnas.1203689109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pérez-Cobas AE. et al. 2013. Gut microbiota disturbance during antibiotic therapy: a multi-omic approach. Gut 62, 1591–1601. ( 10.1136/gutjnl-2012-303184) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Noecker C, Eng A, Srinivasan S, Theriot CM, Young VB, Jansson JK, Fredricks DN, Borenstein E. 2016. Metabolic model-based integration of microbiome taxonomic and metabolomic profiles elucidates mechanistic links between ecological and metabolic variation. MSystems 1, e00013–15. ( 10.1128/mSystems.00013-15) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jones E, Oliphant T, Peterson P. 2001. SciPy: Open Source Scientific Tools for Python. See http://www.scipy.org.
- 50.McCall J. 2005. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 184, 205–222. ( 10.1016/j.cam.2004.07.034) [DOI] [Google Scholar]
- 51.Kurtz TG. 1972. The relationship between stochastic and deterministic models for chemical reactions. J. Chem. Phys. 57, 2976–2978. ( 10.1063/1.1678692) [DOI] [Google Scholar]
- 52.Anderson DF, Kurtz TG. 2011. Continuous time Markov chain models for chemical reaction networks. In Design and analysis of biomolecular circuits (eds Koeppl H, Densmore D, Setti G, di Bernardo M), pp. 3–42. Berlin, Germany: Springer. [Google Scholar]
- 53.Anderson DF, Craciun G, Gopalkrishnan M, Wiuf C. 2015. Lyapunov functions, stationary distributions, and non-equilibrium potential for reaction networks. Bull. Math. Biol. 77, 1744–1767. ( 10.1007/s11538-015-0102-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Anderson DF, Kurtz T. 2015. Stochastic analysis of biochemical systems. Stochastics in Biological Systems, vol. 1.2. Berlin, Germany: Springer International Publishing. [Google Scholar]
- 55.Gillespie DT. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434. ( 10.1016/0021-9991(76)90041-3) [DOI] [Google Scholar]
- 56.Anderson DF. 2008. Incorporating postleap checks in tau-leaping. J. Chem. Phys. 128, 054103 ( 10.1063/1.2819665) [DOI] [PubMed] [Google Scholar]
- 57.Mendes-Soares H, Mundy M, Soares LM, Chia N. 2016. MMinte: an application for predicting metabolic interactions among the microbial species in a community. BMC Bioinf. 17, 343 ( 10.1186/s12859-016-1230-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zomorrodi AR, Islam MM, Maranas CD. 2014. d-OptCom: dynamic multi-level and multi-objective metabolic modeling of microbial communities. ACS Synth. Biol. 3, 247–257. ( 10.1021/sb4001307) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code for parameter estimation and searching, parameter values and a complete description of the QSMI model, as well as code for the stochastic experiments, is available at https://github.com/jdbrunner/model_comparisons.