Nonlinear phase coupling functions: a numerical study

Abstract

Phase reduction is a general tool widely used to describe forced and interacting self-sustained oscillators. Here, we explore the phase coupling functions beyond the usual first-order approximation in the strength of the force. Taking the periodically forced Stuart–Landau oscillator as the paradigmatic model, we determine and numerically analyse the coupling functions up to the fourth order in the force strength. We show that the found nonlinear phase coupling functions can be used for predicting synchronization regions of the forced oscillator.

This article is part of the theme issue ‘Coupling functions: dynamical interaction mechanisms in the physical, biological and social sciences’.

1. Introduction: phase description of forced and coupled oscillators

Models of coupled and forced self-sustained oscillators describe a variety of natural and social phenomena and effects in man-made devices, ranging from synchroni- zation of pendulum clocks, organ pipes and electronic circuits to the emergence of collective motion in popu- lations of spin-torque or nanomechanical oscillators, neurons, yeast cells, pedestrians on footbridges and synthetic genetic oscillators [1–12]. Probably the most important and frequently used theoretical tool for the analysis of forced and interacting self-sustained units is the phase reduction method [1,2,4,5,13–15]. This approach assumes that the force or the coupling is so weak that it does not essentially influence the amplitudes of the oscillators, but only their phases. The mathematical basis behind this assumption is the correspondence between the phase variable of an autonomous system and the neutrally stable direction (with zero Lyapunov exponent) along with the limit cycle, while the amplitudes correspond to stable transversal directions, quantified by negative Lyapunov exponents. Hence, the effects of weak forcing can be described solely by an equation for the phases, while the amplitudes are enslaved.

The phase dynamics approach became a useful and popular tool in the analysis of oscillators and oscillatory networks of different origin. It has been exploited to model and investigate, theoretically and experimentally, such distinct systems as crowds on pedestrian bridges [6], circadian clocks in animals and humans [16,17], physiological subsystems like cardiac and respiratory ones [18–20], neuronal populations [8,21] and even groups of socially interacting individuals, from insects to humans [22]. In particular, the phase dynamics framework provided an explanation and quantitative description for such an important effect as the emergence of collective mode in a highly interconnected network [2]. As interesting examples we mention use of the so-called phase response curves (PRCs) for accelerated recovery from jet lag [17] and modelling of deep brain stimulation in Parkinsonian patients [23].

The theory of phase reduction in the first order in the strength of the force is well established, see [14,15,24] for recent reviews. In such an approximate description, the corresponding term in the phase dynamics equations, called the coupling function, scales linearly with the forcing/interaction strength. On the other hand, if the variations of the amplitudes due to the forcing and/or interaction cannot be neglected, but still the dynamics in the state space is confined to the surface of a smooth torus, the dynamical description in terms of the phases is nevertheless possible. One cannot, however, expect the first-order perturbation theory to be valid for strong forcing, rather nonlinear effects should be visible. Although the derivation of the coupling functions with an account of relatively large deviations of the state space trajectory from the limit cycle of an unperturbed system remains a theoretical challenge (see, e.g. [14,24] and references therein), such nonlinear coupling functions can be estimated numerically, as have been demonstrated in our recent short communication [25]. Nonlinear coupling function depends non-trivially on the coupling strength, and, in contradistinction to the linear coupling function, also depends on the frequency of forcing. A numerical exploration of these dependencies is the main purpose of this paper.

2. Phase dynamics models

First, we briefly summarize the main results of the first-order phase approximation theory. Consider an autonomous self-sustained oscillator, described by an equation $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})$, where X is an N-dimensional, N≥2, state vector. Suppose that this system has a T-periodic limit cycle X_T(t + T) = X_T(t). Then, for all X in the basin of attraction of X_T, it is possible to introduce the phase φ(X) such that

$$\dot{\phi }(\mathbf{X})=\frac{2\pi }{T}=\omega .$$

Essential for the definition of the phase is the notion of isochrons [26] as the sets of constant phase. These are the (N − 1)-dimensional hypersurfaces I_φ such that φ(X) = const for X∈I_φ. Isochrons exist in a basin of attraction of a stable limit cycle, but only in some exceptional cases they can be expressed analytically.

Consider now a coupled or driven system, described by $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})+\epsilon \tilde{\mathbf{p}}(\mathbf{X},t)$, where ε quantifies the strength of coupling/driving. In this paper, we will consider the case of a periodic driving $\tilde{\mathbf{p}}(\mathbf{X},t)=\tilde{\mathbf{p}}(\mathbf{X},t+T_d)$. Then, one can introduce the phase of the driving according to $\dot{\psi }=\nu =2\pi /T_d$ and write the forcing term as a 2π-periodic function of this phase p(X, ψ). To perform the phase reduction in the first approximation, one writes the equation for the phase φ(X):

$$\begin{array}{rl}\dot{\phi }& =\frac{\mathrm{\partial }\phi }{\mathrm{\partial }\mathbf{X}}\dot{\mathbf{X}}=\frac{\mathrm{\partial }\phi }{\mathrm{\partial }\mathbf{X}}[\mathbf{F}(\mathbf{X})+\epsilon \mathbf{p}(\mathbf{X},\psi )]\\ & =\omega +\epsilon \frac{\mathrm{\partial }\phi }{\mathrm{\partial }\mathbf{X}}\mathbf{p}(\mathbf{X},\psi )\approx \omega +\epsilon {\frac{\mathrm{\partial }\phi }{\mathrm{\partial }\mathbf{X}}|}_{{\mathbf{X}}_{\mathbf{T}}}\mathbf{p}({\mathbf{X}}_{\mathbf{T}},\psi ).\end{array}$$ 2.1

Here in the last line one takes, in the first approximation in ε, the values of the derivative of the phase and of the force on the limit cycle, where X_T = X_T(φ). The resulting coupling term on the r.h.s. of equation (2.1) is thus a function of the phases φ, ψ:

$$Q_1(\phi ,\psi )={\frac{\mathrm{\partial }\phi }{\mathrm{\partial }\mathbf{X}}|}_{{\mathbf{X}}_{\mathbf{T}}}\mathbf{p}({\mathbf{X}}_{\mathbf{T}},\psi ).$$ 2.2

We now briefly discuss a special case when the direction of the force is constant and the force term does not depend on the state of the system, i.e. p(X, ψ) = sp(ψ), where s is a constant unity vector. Then, according to equation (2.2), the first-order coupling function can be written as a product, Q₁ = Z(φ)p(ψ), and the phase dynamics equation in the first approximation takes the so-called Winfree form [1]:

$$\dot{\phi }=\omega +\epsilon Z(\phi )p(\psi ).$$ 2.3

The function Z(φ) = ∂φ/∂X|_XT · s is called phase sensitivity function or PRC.

A further reduction of the phase dynamics, still in the first approximation, can be obtained if the norm of the function εQ₁ is small compared with ω. In this case, the phase evolution can be represented as a fast uniform rotation plus relatively slow additions. This allows for averaging over the basic period, keeping only resonant terms in the coupling function. The reason is that only such terms can cause large, though slow, deviations of the phase from a uniform rotation. Which terms are resonant depends on the relation between the autonomous frequency and the frequency of the forcing ν. Namely, if ω/ν ≈ m/n, then the averaging yields the Kuramoto–Daido model [2,27–31]:

$$\dot{\phi }=\omega +\epsilon h(n\phi -m\psi ).$$ 2.4

Now, we generalize the presented approach. It is natural to extend the model given by equations (2.1) and (2.2), representing the phase dynamics as a series expansion in powers of ε:

$$\dot{\phi }=\omega +Q(\phi ,\psi )=\omega +\epsilon Q_1(\phi ,\psi )+{\epsilon }^2{Q}_2(\phi ,\psi )+{\epsilon }^3{Q}_3(\phi ,\psi )+\dots .$$ 2.5

Noteworthy, the adopted representation relies on the definition of the phase for the autonomous system, i.e. for ε = 0; as mentioned above, an analytical relation between this phase and state variables X is generally unknown. As we have seen, the existing theory provides only the linear in ε term Q₁ in equation (2.5). Strictly speaking, the representation via a power series in ε remains a conjecture—we will support it by the numerical analysis below.

3. Phase reduction for the Stuart–Landau oscillator

Our basic model is the forced Stuart–Landau oscillator (SLO)

$$\dot{A}=(\mu +i\eta )A-(1+i\alpha )|A{|}^{2}A+\epsilon p(\psi ),$$ 3.1

where A = Re^iθ is the complex amplitude. This equation is widely used as a prototypic example of self-sustained oscillations, e.g. [14,24,32–37]. The main advantage of this model is that the phase and the first-order coupling function can be determined analytically, which simplifies the numerical analysis of higher-order terms. It is convenient to re-write the model as a system

$$\begin{array}{rl}& \dot{R}=\mu R-R^3+\epsilon p(\psi )\cdot \cos \theta \\ \mathrm{and}& \dot{\theta }=\eta -\alpha R^2-\epsilon p(\psi )\cdot \frac{\sin \theta }{R}.\end{array}\}$$ 3.2

Here, α is the non-isochronicity parameter. For the autonomous oscillator, parameter μ determines the radius $R_0=\sqrt{\mu }$ and stability of the limit cycle, while η, in combination with α, μ, determines the frequency of the oscillation.

As is well-known (see, e.g. [5]), the phase of the autonomous SLO is defined as

$$\phi =\theta -\alpha \ln \left(\frac{R}{R_0}\right).$$ 3.3

For the forced system, differentiating equation (3.3) with respect to time and substituting $\dot{R}$, $\dot{\theta }$ from equation (3.2), we obtain

$$\dot{\phi }=\omega -\frac{\alpha \cos \theta +\sin \theta }{R}\epsilon p(\psi ),$$ 3.4

where we introduced ω = η − αμ. If the forcing is so weak that the deviation from the limit cycle can be neglected, $R\approx R_0=\sqrt{\mu }$, then φ ≈ θ and equation (3.4) yields the known first-order phase dynamics reduction for the SLO in the Winfree form (see equation (2.3)), with the PRC

$$Z(\phi )=-\frac{\alpha \cos \phi +\sin \phi }{\sqrt{\mu }}.$$ 3.5

For a harmonic forcing p(ψ) = cosψ = cos(νt), we obtain

$$\begin{array}{rl}{Q}_1& =-(\alpha \cos \phi +\sin \phi )\frac{\cos \psi }{\sqrt{\mu }}\\ & =-\frac{\alpha }{2\sqrt{\mu }}[\cos (\phi -\psi )+\cos (\phi +\psi )]-\frac{1}{2\sqrt{\mu }}[\sin (\phi -\psi )+\sin (\phi +\psi )].\end{array}$$ 3.6

Next, we average Q₁ over the oscillation period, for ν ≈ ω. The terms dependent on the sums of phases have frequency ≈ 2ω and therefore disappear due to the averaging. On the contrary, the terms dependent on φ − ψ are slow and can be considered as unchanged within the oscillation period. Hence, averaging of Q₁ for ν ≈ ω yields

$$h(\phi -\psi )=-\frac{\sin (\phi -\psi )}{2\sqrt{\mu }}-\frac{\alpha \cos (\phi -\psi )}{2\sqrt{\mu }}.$$ 3.7

As is well-known, this coupling function determines the synchronization domain of 1:1 locking. Note that other locked states do not appear in the averaged first-order approximation.

4. Computing nonlinear coupling function

Here, we present our numerical approach for determination of the nonlinear coupling function for the SLO. We restrict ourselves, without loss of generality, to the case of harmonic driving p(ψ) = cos(νt), and proceed as follows. For some set of parameters μ, α, ε, ν, we solve numerically equation (3.2) and compute φ(t), $\dot{\phi }(t)$ with the help of equations (3.3) and (3.4). Next, we try to present $\dot{\phi }(t)$ in the form of equation (2.5). Since the term ω + εQ₁(φ, ψ) is known, we have to find only the nonlinear part of the coupling function

$${\epsilon }^2{Q}_2(\phi ,\psi )+{\epsilon }^3{Q}_3(\phi ,\psi )+\cdots =\dot{\phi }-\omega -\epsilon Q_1(\phi ,\psi ).$$

For this purpose, we compute the rest term ${\dot{\phi }}_r=\dot{\phi }-\omega -\epsilon Q_1(\phi ,\psi )$. As a result, we obtain a series of points $(\phi ,\psi ,{\dot{\phi }}_r)$. We use this set to fit the function ${\dot{\phi }}_r(\phi ,\psi )$ as a 2π-periodic function of variables φ, ψ. We denote the estimated function as Q_nlin. Practically, we perform a kernel-based estimation on a grid 100 × 100, see [19] for technical details. Another, almost equivalent option, could be representing the function ${\dot{\phi }}_r(\phi ,\psi )$ as a double Fourier series with unknown coefficients, and finding these coefficients from the minimization of the mean squared error. The error of the fit is quantified by

$$\sigma =\frac{\mathrm{std}[{\dot{\phi }}_r-Q_{nlin}(\phi ,\psi )]}{\mathrm{std}[\dot{\phi }]},$$ 4.1

where $\mathrm{std}[\xi ]={[\overline{{(\xi -\overline{\xi })}^2}]}^{1/2}$ and bar denotes the time averaging over the available time series. The error σ is due to a truncation of the series, to an error of the kernel estimator and to an error of the ODE solver. We emphasize that determination of Q_nlin can fail for large ε if, e.g. the SLO becomes entrained to the force. Indeed, in case of synchrony with the force, the trajectory does not cover the torus spanned by φ, ψ, and the function of these two variables cannot be recovered. Generally, a strong force can also result in destruction of the smooth torus or make the torus so ‘thick’ and shifted with respect to the original limit cycle that some loops cross one isochron twice, see a discussion in ref. [25]. In both latter cases, the approach also fails. This failure can be detected by monitoring the value of σ which is for good cases quite small.

The next task is to determine the basis functions Q_k in the power series representation by equation (2.5). For this goal, we perform the above described computation of Q_nlin for a fixed frequency ν = const, and a set of values of the force amplitude ε and then compute Q_k, k≥2, performing a polynomial fit in ε. (Recall that Q₁ is given by equation (3.6).) Practically, we truncate the series and obtain only three terms Q_2,3,4 by fitting each element of Q_nlin(φ, ψ;ε)/ε² by a second-order polynomial in ε, i.e. as Q_nlin/ε² ≈ Q₂ + εQ₃ + ε²Q₄. The quality of this step is quantified by

$$\gamma (\epsilon )=\frac{\mathrm{STD}[Q_{nlin}-{\epsilon }^2{Q}_2-{\epsilon }^3{Q}_3-{\epsilon }^4{Q}_4]}{\mathrm{std}\left[Q\right]}.$$ 4.2

Here, STD[ξ] = 〈(ξ − 〈ξ〉)²〉^1/2 and the averaging is performed as integration over the torus on which the coupling function is defined:

$$⟨w⟩={(4{\pi }^2)}^{-1}{\int }_0^{2\pi }\mathrm{d}\phi {\int }_0^{2\pi }\mathrm{d}\psi \hspace{0.17em}w(\phi ,\psi ).$$

5. Nonlinear coupling functions for the Stuart–Landau oscillator: results

(a). Full nonlinear coupling function

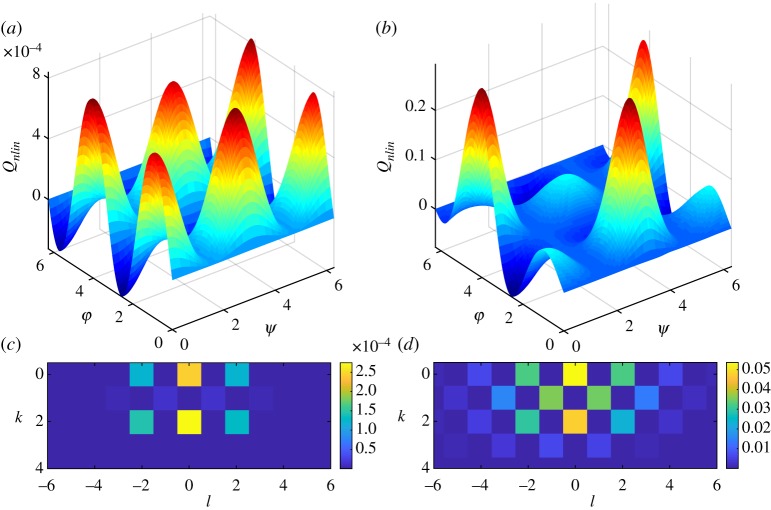
In the first tests, we compute the nonlinear coupling function Q_nlin and functions Q_2,3,4 for a fixed frequency of the force, ν = 0.3, and for different forcing amplitudes ε. Other parameters are η = 1, μ = 1, α = 0, and we used 10⁷ data points, i.e. ≈ 8000 oscillation periods, for construction of Q_nlin. We obtained a good reconstruction for ε≤0.55: the error of the fit σ, see equation (4.1), was smaller than 4 × 10⁻³. For stronger forcing, the system is close to being synchronized by the force; here, the reconstruction is poor and provides a non-smooth coupling function. The results are shown in figure 1. Here, together with the shapes of Q_nlin, we show the amplitudes of Fourier modes of these functions, defined according to

$$Q(\phi ,\psi )=\sum _{k,l}{F}_{(k,l)}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}k\phi +\mathrm{i}l\psi }.$$ 5.1

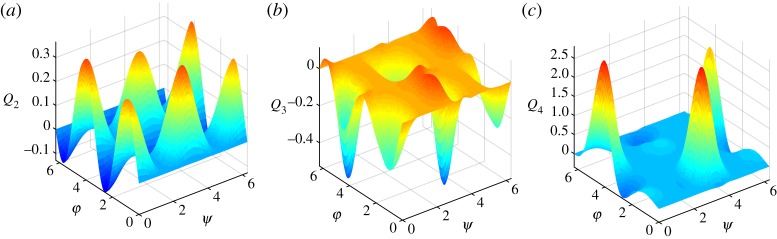
We remember that the first-order coupling function contains only harmonics k = ± 1, l = ± 1 (see equation 3.6). One can see that the shape of the nonlinear coupling function largely differs from the linear one and depends strongly on ε. The components Q_2,3,4 are illustrated in figure 2, all of them contain higher Fourier modes. (The error of the power series representation is γ(ε) < 6.5 × 10⁻³).

Figure 1.

Nonlinear part of the coupling function and the amplitudes of its Fourier modes (see equation (5.1)) for ν = 0.3 and ε = 0.05 (a,c) and ε = 0.55 (b,d). (Online version in colour.)

Figure 2.

The components (a) Q₂, (b) Q₃ and (c) Q₄ of the nonlinear coupling function for ν = 0.3, obtained via a polynomial fit in the range ε = 0.05, …, 0.55. Comparison with figure 1 shows that Q₂ dominates, as expected, for small ε, while Q₄ dominates for large ε. (Online version in colour.)

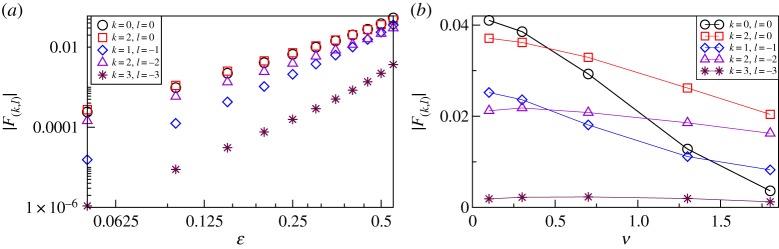
As discussed above, the novel essential feature of the nonlinear coupling function is its dependence on the frequency of the forcing ν. In figure 3, we show dependencies of several dominant Fourier modes of the coupling function on parameters ε and ν.

Figure 3.

Dependence of amplitudes of different Fourier modes on the amplitude ε (a) and on the frequency ν (b) of the forcing. (Online version in colour.)

Next, we analysed how the nonlinear coupling function varies with the parameter μ. As it follows from the first equation of (3.2), this parameter determines the radius of the limit cycle oscillation $R_0=\sqrt{\mu }$. Furthermore, linearization of this equation yields for a small radius deviation δ from the limit cycle $\dot{\delta }\approx -2\mu \delta +\epsilon p(t)\cos \theta$, so that the larger the value of μ, the more stable the cycle. We computed the nonlinear part of the coupling function for 0.5≤μ≤3 and fixed parameters of the forcing, ν = 0.1, ε = 0.4. (For μ < 0.5, the forcing becomes too strong to provide a reliable construction of Q_nlin.) The results are shown in figure 4. One can see that for large μ the norm of the nonlinear coupling function $N={(2\pi )}^{-1}{({\int }_0^{2\pi }{\int }_0^{2\pi }{Q}^2\hspace{0.17em}\mathrm{d}\phi \hspace{0.17em}\mathrm{d}\psi )}^{1/2}$ decays as ∼μ^−2.15, what means that the nonlinear effects become less visible in the μ → ∞ limit, because the linear part decays as ∼μ^−1/2.

Figure 4.

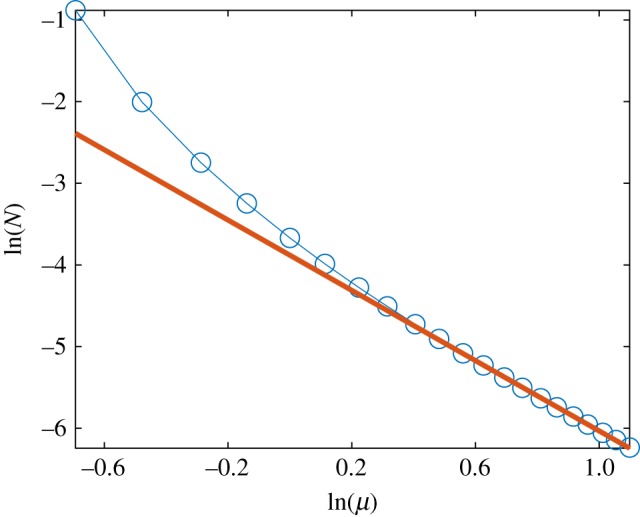
The norm of the nonlinear coupling function versus parameter μ for constant ε (circles). The bold line has slope −2.15. (Online version in colour.)

Finally, our simulations have shown no essentially interesting dependence on the parameter α≠0, only some quantitative changes.

(b). Validity of the Winfree and the Kuramoto–Daido forms

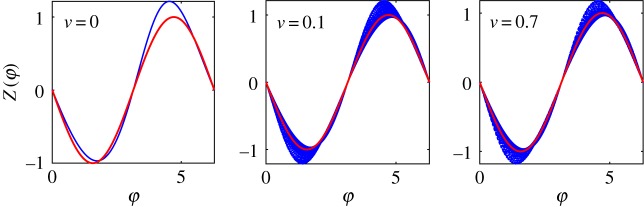
While the first-order coupling function for the forcing term adopted in this study can be represented in the Winfree form, this is no more valid for the full nonlinear coupling function. In order to check the validity of the Winfree representation for strong forcing, we estimate an ‘effective’ Z(φ) by plotting $(\dot{\phi }-\omega )/(\epsilon \cos (\nu t))$ versus φ for εcos(νt) > 10⁻⁵, cf. equation (2.3). The results for ε = 0.4 and three different values of ν are presented in figure 5. For a constant perturbation, ν = 0, this approach yields a curve that, as expected, deviates from the linear PRC given by equation (3.5). However, for harmonic driving, the points in the plot do not fall on a curve, what means that in the nonlinear regime the coupling function cannot be decomposed into a product Z(φ)p(ψ).

Figure 5.

Test for validity of the Winfree form of the phase coupling function for ε = 0.4 and different values of frequency ν. Red lines show the first-order PRC according to equation (3.5). Note that for ν≠0 the points do not fall on a single curve, which means that the Winfree form (see equation (2.3)) is not valid for strong forcing. (Online version in colour.)

One could find an approximate PRC by averaging the points in figure 5, or by neglecting all the Fourier components in the expansion (5.1) except for l = 1 (and taking only the real part of it). In this way one, however, neglects terms that are of the same order of magnitude as the preserved ones.

As was discussed in §2, there is no unique Kuramoto–Daido model, rather there is a set of models valid for different resonances ω/ν ≈ m/n. The coupling function for the resonance ω/ν ≈ m/n is obtained from the full coupling function (see equation (5.1)), as

$$h_{n,m}(n\phi -m\psi )=\sum _k{F}_{(kn,-km)}\exp [\mathrm{i}kn\phi -\mathrm{i}km\psi ].$$

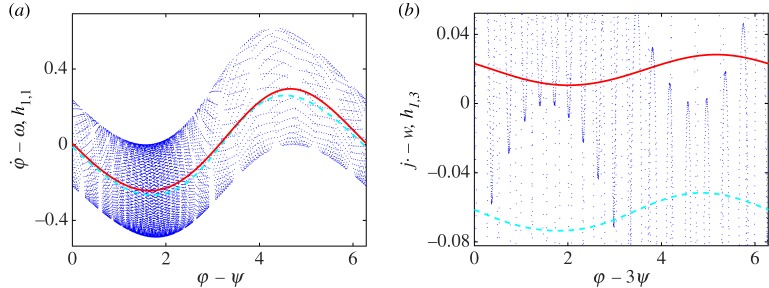
For example, the main resonance Kuramoto–Daido coupling function h_1,1 is described by the harmonics F_(0,0), F_{( ± 1,∓1)}, F_{( ± 2,∓2)}, F_{( ± 3,∓3)}, … In the first-order approximation, one has just the first harmonics terms (see equation (3.7)), while for the full nonlinear coupling function higher-order terms are also present for the main resonance. For other resonances, which are not present in the first order, nonlinear coupling provides effective averaged resonant forcing in higher orders in ε. Another way to construct the Kuramoto–Daido model is to perform a direct fit of $\dot{\phi }-\omega$ versus (nφ − mψ) mod 2π (e.g. representing the function as a Fourier series and finding the Fourier coefficients through minimization of the mean squared error); this approach has been adopted in ref. [38]. We illustrate the Kuramoto–Daido coupling functions h_1,1 and h_1,3 for ε = 0.5 in figure 6. While h_1,1 is rather close to the first-order Kuramoto–Daido model given by equation (3.7), the norm of the coupling for the resonance 1:3 is rather small.

Figure 6.

The Kuramoto–Daido models h(φ − ψ) constructed for ε = 0.5 and ν = 0.7 (a) and h(φ − 3ψ) for ε = 0.5, ν = 0.3 (b). Blue points show the exact values of the phase derivative. Solid and dashed curves are the results of two ways of averaging: the first one is obtained by taking the corresponding diagonal Fourier modes of the reconstructed full coupling function Q(φ, ψ), while the second one is obtained via a direct Fourier fit of blue dots. (Online version in colour.)

6. Predicting synchronization regions with nonlinear coupling functions

In this section, we demonstrate that the nonlinear phase model can be exploited to predict locking regions or Arnold tongues. We recall that we cannot construct the coupling function if the system is locked to an external force. However, it does not mean that the phase model is not valid in that parameter domain, but simply that our procedure for the coupling function construction fails. Nevertheless, we can use the coupling function obtained for coupling strength below the synchronization threshold to predict the domain of synchrony for stronger forcing (or for other frequencies of the forcing).

For small amplitudes of the forcing, only the main Arnold tongue with ν ≈ ω is relevant, and it is well captured by the Kuramoto–Daido representation of the phase dynamics in terms of phase differences, cf. equation (3.7). This form of coupling determines the only synchronization domain that has a triangular shape and touches the ν-axis. In the strongly forced regime, we can expect the appearance of further Arnold tongues. Indeed, the Devil's staircase computed for the full model (3.2) for ε = 0.7, exhibits not only 1:1 locking but also domains of 1:3 and 1:2 synchrony (see figure 7).

Figure 7.

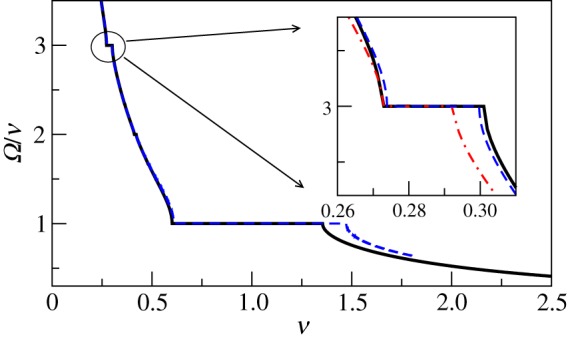
Synchronization domains of the forced SLO with ε = 0.7. The black solid line shows the true Devil's staircase and the blue dashed one shows the prediction by the full nonlinear phase model obtained for ν = 0.3 and ε≤0.55. The dashed-dotted line is obtained from the integration of the first-order phase approximation (see equation (3.6)); one can see that it provides a significantly worse prediction compared with the full model. (Online version in colour.)

Now, we check how this staircase can be reproduced by the phase model, constructed for ν = 0.3, ε≤0.55. (We remember that for ε > 0.55 the model construction failed because of synchrony.) Combining equation (2.5) with $\dot{\psi }=\nu ,$ we obtain

$$\frac{\mathrm{d}\phi }{\mathrm{d}\psi }=\frac{\omega +\epsilon Q_1+{\epsilon }^2{Q}_2+{\epsilon }^3{Q}_3+{\epsilon }^4{Q}_4}{\nu }.$$ 6.1

Next, we solve this equation numerically for ε = 0.7. Namely, using the Euler technique and precomputed Q_2,3,4, we find phase increase Δφ corresponding to a large phase increase Δψ and obtain the frequency ratio as Δφ/Δψ. The result is shown in figure 7. We see that the phase model obtained for ν = 0.3 describes very well the 1:3 locking domain and the left border of the 1:1 locking region, but exhibits an essential deviation at the right border of the latter. This can be explained by the frequency dependence of Q_nlin.

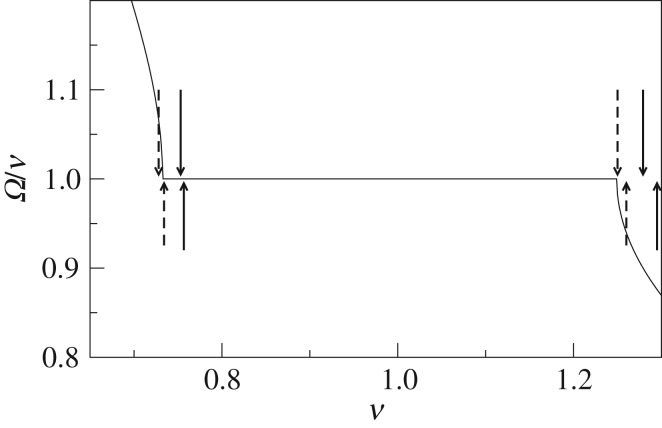
As has been discussed above, the Kuramoto–Daido model is expected to be good for small forcing only, because for large forcing the time-scale separation between the uniform phase rotation and deviations from it is not valid. Nevertheless, one can formally apply this model to check the quality of predictions of synchronization properties for large forcing amplitudes. We illustrate how well the model based on the coupling function h_1,1 predicts the boundaries of the main synchronization region 1:1 in figure 8. One can see that the prediction is quite reasonable, which indicates that for the synchronization properties many nonlinear features of the coupling function are not important. However, for the synchronization region 1:3 this is not the case. While the Kuramoto–Daido coupling function h_1,3, shown in figure 6b, correctly predicts the existence of the 1:3 locking domain, its position is so strongly shifted in ν with respect to the true one, that we do not depict it in figure 7.

Figure 8.

The 1:1 synchronization domain for the SLO forced with amplitude ε = 0.5 and its borders predicted by the Kuramoto–Daido model reconstructed for ν = 0.7 (arrows up) and for ν = 1.3 (arrows down). The solid curve shows the true locking region. The solid lines with arrows show the borders predicted by the model obtained from the Fourier coefficients of the coupling function; the dashed lines with arrows show the corresponding prediction of the model obtained via direct Fourier fit.

7. Conclusion

In summary, we have presented the concept of a nonlinear phase coupling function for a periodically forced self-sustained oscillator. It generalizes the approach of the phase reduction based on the first-order approximation in the forcing strength. For illustration, we have chosen the SLO, mainly for the reason of convenience of presentation, because for it the phase and the first-order phase reduction are known analytically. The method can be, however, straightforwardly applied to other systems, for which the dynamical equations are known. In such a case, the proper phase and its derivative should be determined numerically, see [25]. The case of a purely observational determination of the nonlinear coupling function (cf. [19,39]) requires additional efforts, as the reliable methods of the proper phase reconstruction from scalar signals are still missing.

We have demonstrated that the nonlinear coupling function has a shape quite different from that of the first-order approximation, with many more Fourier components present. A novel feature is a dependence of the nonlinear terms on the frequency of the forcing, in contradistinction to the first approximation which is frequency independent. We have also shown that many differences between the full nonlinear coupling function and its first-order approximation are not so important for determination of the synchronization regions, although the full nonlinear function provides better accuracy.

Finally, we compare our approach with the analytical technique for strongly perturbed limit cycle oscillators of ref. [40]. Except for the trivial fact that our reduction is merely numerical, we mention the essential difference: we rely on the unperturbed definition of the phase, i.e. we remain in the framework of the perturbation theory. On the contrary, the authors of [40] define a generalized phase, i.e. a family of phases for different values of a system's parameter. Next, they consider the case when the strong component of the forcing is very slow and then exploit the generalized phase to obtain a close equation in the adiabatic limit. Our approach is not restricted to slow forcing.

We foresee that the presented approach can be extended to the determination of the phase dynamics of coupled oscillators at strong coupling. An extra problem to be treated here is an additional dependence of the forcing waveform on the strength of the coupling. This study will be reported elsewhere.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors developed the numerical algorithms. M.R. performed computations and prepared the figures. Both authors have written and approved the manuscript.

Competing interests

We declare we have no competing interests.

Funding

M.R. thanks the Russian Science Foundation (grant no. 17-12-01534) for support of studies presented in $5. A.P. thanks the Russian Science Foundation (grant no. 19-12-00367) for support of studies in $6.